लंबक

लंबक : वस्तूच्या एका बिंदूला दोरी बांधून ती टांगली व नंतर तिच्या स्थिर स्थितीपासून बाजूला नेऊन तिला सोडून दिली, तर ती गुरुत्वाकर्षणी प्रेरणेमुळे आंदोलने करू लागते. या प्रकारच्या उपकरण योजनेला लंबक असे म्हणतात. एक आंदोलन पूर्ण करण्याकरिता लंबकाला जो एक ठराविक काळ लागतो त्यास त्याचा आवर्तन काल असे म्हणतात. (एका स्थितीतून लंबक विचलित झाल्यावर तो त्याच स्थितीत पुन्हा त्याच दिशेने आल्यावर एक आंदोलन पूर्ण होते). लंबकाच्या प्रत्येक आंदोलनास लागणारा वेळ सारखाच असतो. हा शोध १५८१ मध्ये ⇨गॅलिली गलिलीओ यांनी लावला. जर आंदोलन गतीचा परमप्रसर (स्थिर स्थितीपासून होणारे कमाल स्थानांतरण) जास्त मूल्याचा नसेल व संदमन परिणाम (हवेच्या घर्षणामुळे वा अन्य अडथळ्यामुळे आंदोलनाचा परमप्रसर हळूहळू कमी होण्याचा परिणाम) नगण्य प्रमाणाचा असेल, तर लंबकाचा आवर्तन काल आंदोलन गतीच्या परमप्रसरावर, लंबकाच्या द्रव्यमानावर व त्याच्या आकारमानावर अवलंबून नसतो. हा काल लंबकाची लांबी (याची व्याख्या खाली दिली आहे.) व त्या ठिकाणाचा गुरुत्वीय प्रवेग [g ⟶ गुरुत्वाकर्षण] या दोनच राशींमुळे निश्चित होत असतो. या कारणाकरिता लंबकाचा उपयोग घड्याळामध्ये कालमापनाकरिता करण्यात येऊ लागला. पृथ्वीवरील निरनिराळ्या ठिकाणच्या गुरुत्वीय प्रवेगाचे मूल्य प्रयोगाने मोजण्यासाठीही त्याचा उपयोग केला जातो. प्रयोगशाळेत लंबकाचे अनेक प्रकार वापरले जातात. त्यांपैकी काहींचे वर्णन खाली दिले आहे.

साधा लंबक : या लंबकामध्ये(आ. १) एकबिंदुवत द्रव्यमानाची जड वस्तू अत्यंत हलक्या, लवचिक व ताणल्या न जाणाऱ्या अशा दोरीच्या साहाय्याने टांगलेली असते.

ज्या बिंदूपासून लंबक टांगलेला असतो, त्या O या बिंदूला लंबन मध्य म्हणतात. वस्तूच्या P या गुरुत्वमध्यबिंदूपाशी वस्तूचे संपूर्ण द्रव्यमान केंद्रित झाले आहे असे मानले जाते. लंबन बिंदू व गुरुत्वमध्य यांतील OP या अंतरास लंबकाची लांबी (l) अशी संज्ञा दिली जाते. m – बिंदुवत वस्तूचे द्रव्यमान.

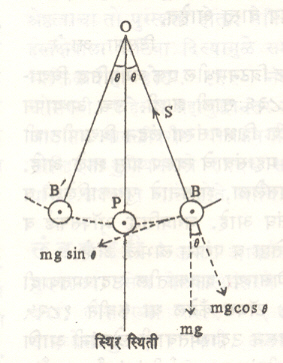B या ठिकाणी विचलित झालेल्या व दोरीने उभ्या दिशेशी θ कोन केलेल्या लंबकाचा विचार केला, तर त्यावर आकृतीत दाखविल्याप्रमाणे दोन प्रेरणा कार्य करीत असतात असे दिसते. यांपैकी mg cos θ हा प्रेरणा घटक दोरीमध्ये ताण (S) निर्माण करून त्यायोगे संतुलित होतो. mg sin θ या प्रेरणा घटकाची प्रवृत्ती लंबकाला परत आपल्या स्थिर स्थानाप्रत नेण्याकडे असते. या प्रेरणेला पुनःस्थापक प्रेरणा म्हणतात आणि तिची दिशा नेहमी स्थिर स्थानाकडे असते. लंबकाच्या कोनीय गतीकरिता खालील समीकरण यथार्थ असते.

(जर θ लहान असेल तर). येथे Ι – वस्तूचे लंबन बिंदूभोवतीचे निरुढी परिबल [⟶ यामिकी]. ही गती सरल हरात्मक स्वरूपाची [⟶ सरल हरात्मक गति] असून तिचा आवर्तन काल T

या सूत्राने मिळतो, असे दाखविता येते. 

दोन सेकंद आवर्तन काल असलेल्या साध्या लंबकाची लांबी g/n² इतकी असते आणि g = ९८१ सेंमी./सेकंद^२ घेतल्यास ही लांबी अगदी जवळजवळ एक मी. इतकी येते. असा लंबक उभ्या स्थितीतून बरोबर एक सेकंद कालावधीने (एकदा एका दिशेने व मग दुसऱ्या दिशेने) जातो म्हणून त्याला ‘सेकंद लंबक’ म्हणतात. g च्या मूल्यामध्ये स्थानपरत्वे बदल होत असल्याने या लंबकाच्या लांबीत किंचित फरक पडतो. एक सेकंद आवर्तन काल असलेल्या साध्या लंबकाची लांबी सेकंद लंबकाच्या एक-चतुर्थांश म्हणजे सु. २५ सेंमी. असते.

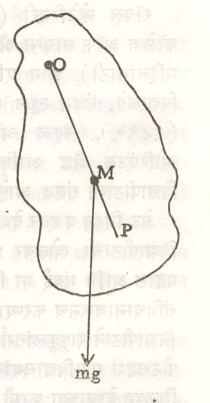स्थूल लंबक : कोणतीही एक दृढ वस्तू, तिला छेद करून जाणाऱ्या अक्षाभोवती आंदोलने करू शकेल अशा रीतीने टांगली असता तीमुळे स्थूल लंबक बनतो (आ. २). प्रत्यक्षातील सर्व लंबक बहुतांशी याच प्रकारचे असतात कारण बिंदुवत द्रव्यमान असणारी वस्तू ही एक केवळ आदर्शवादी कल्पना आहे. अशी वस्तू प्रत्यक्षात मिळत नाही.

आ. २ मध्ये एक स्वेच्छ आकाराची वस्तू O बिंदूमधून जाणाऱ्या अक्षाभोवती आंदोलने करू शकेल अशी दाखविली आहे. आकृतीमध्ये M द्रव्यमान मध्य व O लंबन मध्य असून OM = h  आहे. m – वस्तूंचे द्रव्यमान, I_m – M बिंदूमधून जाणाऱ्या अक्षाभोवतील वस्तूचे निरुढी परिबल (= mk²) असून k-M बिंदूमधून जाणाऱ्या अक्षाकरिता वस्तूची घूर्णीय त्रिज्या [⟶ यामिकी] आहे.

वस्तूच्या आंदोलनाकरिता T हा आवर्तन काल खालील सूत्राने मिळतो, असे दाखविता येते.

वरील सूत्रावरून हे स्पष्ट होते की, वरील स्थूल लंबकाच्या एवढाच आवर्तन काल असणाऱ्या साध्या लंबकाकरिता त्याची लांबी  l = k² + h²/ h एवढी असावयास पाहिजे.

द्रव्यमान मध्य M पासून  OM  रेषेवर k² + h²/h या अंतरावर जर एक बिंदू P घेतला, तर त्यास स्थूल लंबकाचा आंदोलन मध्य असे म्हणतात.

लंबन मध्य व आंदोलन मध्य या स्थानांना लंबकाच्या द्रव्यमान मध्याच्या सापेक्ष काही सममिती गुणधर्म असतात. O या लंबन मध्याकरिता P हा आंदोलन मध्य होत असेल आणि लंबक उलटा करून P या लंबन बिंदूवर टांगला, तर त्याकरिता O हा आंदोलन बिंदू होतो. स्थूल लंबकाकरिता  O किंवा P याचा लंबन बिंदू म्हणून उपयोग केला, तर लंबकाच्या आवर्तन कालामध्ये फरक पडत नाही. O व P बिंदूंची M पासूनची अंतरे अनुक्रमे h₁ व h₂ अशी असतील, तर  h₁ h₂ =k² व  h₁ + h₂ =  l. ( l-स्थूल लंबकाएवढाच आवर्तन काल असणाऱ्या साध्या लंबकाची लांबी).

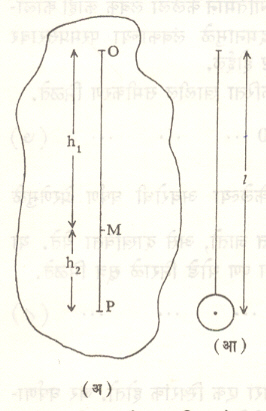कोणत्याही स्थूल लंबकाकरिता आंदोलन मध्याचे स्थान सोप्या प्रयोगाद्वारे निश्चित करता येते. या कार्याकरिता स्थूल लंबकाच्या शेजारी त्याच पातळीवरील लंबन बिंदूपासून एक साधा लंबक टांगतात. याची लांबी अशा रीतीने बदलतात की, साध्या व स्थूल या दोन्ही लंबकाचे आवर्तन काल एकाच मूल्याचे होतील. या परिस्थितीमध्ये साध्या लंबकाचा गोलक मध्य स्थूल लंबकाच्या आंदोलन मध्याच्या सरळ रेषेत येतो. वरील सर्व गोष्टींचा खुलासा आ. ३ मध्ये दाखविलेल्या स्थूल लंबकाच्या दुसऱ्या एका प्रकारावरून होईल.

स्थूल लंबकातील O व P या बिंदूंना आणखी एक सममितीय गुणधर्म असतो. जर O मधून जाणाऱ्या अक्षाशी वस्तू बंधित नसेल व ती आकृतीच्या प्रतलामध्ये मुक्तपणे संचार करु शकत असेल, तर अशा परिस्थितीमध्ये तिच्यावर O या बिंदूवर आवेगी प्रेरणा लावल्यास वस्तूची प्राथमिक गती P या बिंदूभोवतील परिभ्रमणाच्या स्वरूपात असते. त्यामुळे P या बिंदूला आघात केंद्र असेही म्हणतात. समजा ही वस्तू क्रिकेटची बॅट आहे. जर बॅट O येथे धरून चेंडूला P या बिंदूने टोला मारला, तर हाताला कमीत कमी झटका बसेल.

केटर व्युत्क्रमी लंबक : लंबन मध्य व आंदोलन मध्य यांपैकी कोणत्याही एका बिंदूमधून जाणाऱ्या अक्षाकरिता लंबकाचा आवर्तन काल एकाच मूल्याचा असतो या सिद्धांताचा उपयोग करून हेन्री केटर यांनी स्थूल लंबकाच्या साहाय्याने गुरुत्वीय प्रवेगाचे मापन केले. 

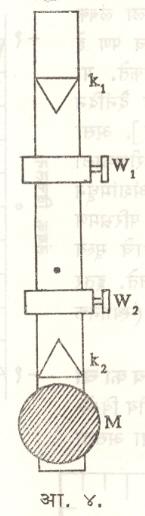या कार्याकरिता वापरलेला लंबक (आ. ४) एका धातूच्या दंडापासून बनविलेला असून त्याच्या एका टोकाशी एक वजनदार गोळा (M), दोन्ही बाजूंस खालीवर करता येण्याजोगी w₁ व w₂ ही वजने आणि k₁ व k₂ या दोन सुरीधारा असतात. कोण्त्याही एका सुरीधारेच्या साहाय्याने लंबकाला आंदोलन गती देता येते.

लंबक एकदा k₁ व नंतर k₂ या सुरीधारांच्या साहाय्याने आंदोलित करून w₁ व w₂ यांची स्थाने योग्य प्रकारे बदलून, लंबकाचे दोन्ही आवर्तन काल एकाच मूल्याचे केले जातात. अशा परिस्थितीमध्ये  l = h₁ +h₂ आणि T = २π √ l /g यांवरून g या राशीचे मूल्य काढले जाते.

परिपीडन लंबक : या उपकरणाला लंबक ही संज्ञा योग्य असत नाही कारण त्याच्या आंदोलनामध्ये गुरुत्वाकर्षणाचा काहीही संबंध नसतो. या उपकरणामध्ये एक उच्च मूल्याचे निरूढी परिबल असलेली तबकडी तारेच्या साहाय्याने टांगलेली असते. तबकडी क्षैतिज (क्षितिज समांतर) प्रतलात आंदोलने करते. तिला अक्षाभोवती फिरवून तारेला पीळ पडेल अशा तऱ्हेने सोडली की, ती हरात्मक आंदोलने करू लागते. अशा प्रकारची आंदोलने अनेक प्रकारच्या उपकरणांत आढळतात. उदा., ⇨गॅल्व्हानोमीटर, हातावरील घड्याळामधील तोलचक्र वगैरे.

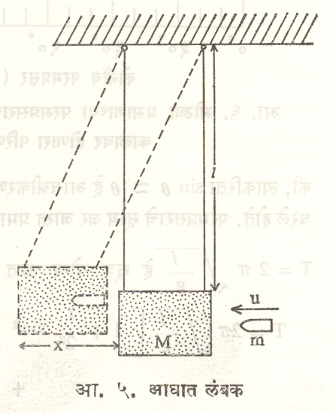आघात लंबक : या लंबकाच्या साहाय्याने आवेगी संवेग (दोन वस्तूंच्या जोरदार आघाताने निर्माण होणारा संवेग म्हणजे द्रव्यमान X वेग ही राशी) मोजता येतो (उदा., बंदुकीच्या गोळीचा संवेग व त्यावरून वेग). या उपकरणामध्ये M ही वाळूने भरलेली लाकडी पेटी असते. पेटी दोन दोऱ्यांच्या साहाय्याने टांगलेली असते (दोरीची लांबी =  l ). दोन दोऱ्या लावल्या असल्याने पेटीला बंदुकीच्या गोळीपासून मिळणाऱ्या संवेगामुळे ती आंदोलने करू लागते. u वेगाने जाणारी m द्रव्यमानाची बंदुकीची गोळी जोराने पेटीत शिरेल अशा दिशेत उडविली जाते. बंदुकीची गोळी पेटीमध्ये शिरल्यानंतर गतिशून्य होत असल्यामुळे गोळीचा संपूर्ण संवेग पेटीला दिला जातो. पेटी दोन दोऱ्यांच्या साहाय्याने टांगली असल्यामुळे तिला परिभ्रमण गती मिळत नाही, ती फक्त आंदोलनेच करते. आघातामुळे पेटी क्षैतिज दिशेत x अंतरामधून विस्थापित होत असेल,

 या सूत्राने गोळीचा प्रारंभिक वेग मिळविता येतो.

गोलीय अथवा फूको लंबक : जे. बी. एल्. फूको यांनी तयार केलेल्या या लंबकामध्ये एक जड गोलीय वस्तू लांब तारेच्या द्वारे अशा रीतीने टांगलेली असते की, त्यामुळे बनलेला लंबक उदग्र (उभ्या) प्रतलामध्ये आंदोलने तर करतोच पण हे आंदोलन प्रतल मुक्तपणे परिभ्रमण पण करू शकते. या लंबकाच्या साहाय्याने पृथ्वीच्या स्वतःभोवतीच्या दैनंदिन परिभ्रमण गतीचे दिग्दर्शन करता येते [⟶ पृथ्वी]. असा लंबक जर उत्तर ध्रुवावर ठेवला, तर पृथ्वीवरील निरीक्षकाला लंबकाचे आंदोलन प्रतल एका दिवसात ३६० अंशांमधून घटिवत (घड्याळातील काट्यांच्या गतीच्या दिशेने) परिभ्रमण करते, असे आढळते. दक्षिण ध्रुवाजवळ परिभ्रमणाचे मूल्य एवढेच असते पण परिभ्रमण गती प्रतिघटिवत असते. इतर कोणत्याही ठिकाणी परिभ्रमणाचा वेग १५^० × sin (स्थानिक अक्षांश), प्रती नाक्षत्र-तास एवढा असतो.

मोठ्या प्रमाणाच्या परमप्रसराकरिता लंबकाचा आवर्तन काल : लंबकाच्या आंदोलन गतीचे गणितीय विश्लेषण करताना त्याचा परमप्रसर इतका कमी मूल्याचा असतो की, त्याकरिता sin θ≈ θहे आसन्नीकरण यथार्थ असते, असे गृहीत धरले होते. परमप्रसराचे मूल्य जर जास्त प्रमाणाचे असेल, तर त्याकरिता

हे सूत्र वापरावे लागते.

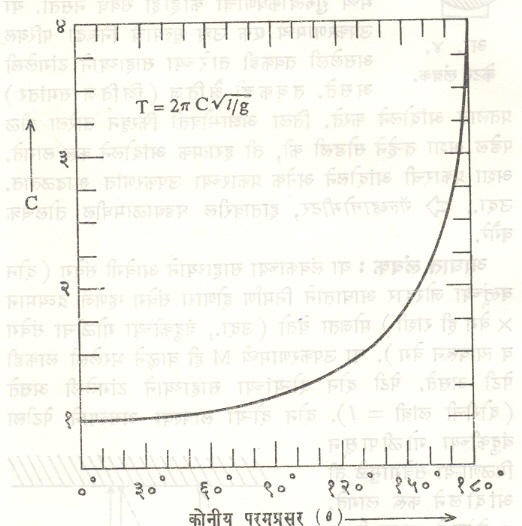
C या राशीचे मूल्य लंबकाच्या कोनीय परमप्रसराप्रमाणे कसे बदलते हे आ. ६ वरून स्पष्ट होईल.

संदमनाचा लंबकाच्या आवर्तन कालावर होणारा परिणाम : लंबकाच्या कोनीय हरात्मक आंदोलनाकरिता 

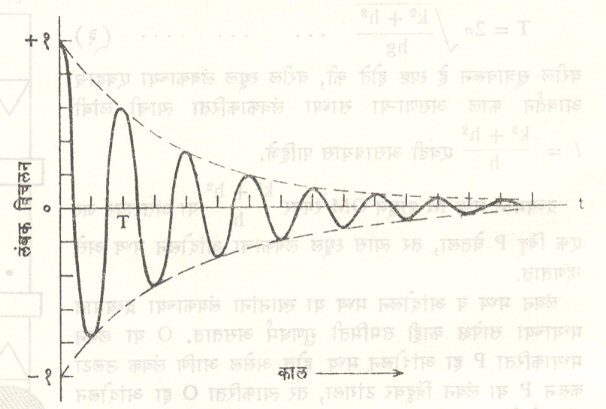
(I−लंबन बिंदूभोवतीचे गोलकाचे निरुढी परिबल) हे समीकरण यथार्थ ठरते. यामध्ये संदमन नगण्य प्रमाणाचे आहे, असे गृहीत धरलेले असते. लंबकाचा गोलक हवेतून संचार करतो तेव्हा त्यावर हवेचे घर्षण होत असल्यामुळे त्याच्या मूळ गतिज ऊर्जेचा सतत व्यय होत असतो. यामुळे त्याचा परमप्रसर कालानुसार सतत कमी होत जातो. या परिणामामुळेच एकदा गतिमान केलेला लंबक काही कालानंतर थांबून गतिशून्य होतो. संदमनामुळे लंबकाच्या परमप्रसरावर होणारा परिणाम आ. ७ स्पष्ट होईल.

संदमनासहित लंबकाच्या गतीकरिता खालील समीकरण मिळते.  

b dθ/dt या पदाने निर्देशित केलेल्या अवरोधी घर्षण प्रेरणेमुळे लंबकाचा परमप्रसर सतत कमी होत जातो, असे दाखविता येते. या परिस्थितीमुळे आवर्तन कालाकरिता पण थोडे निराळे सूत्र मिळते. 

 यामध्ये α लंबकाकरिता असणारा एक स्थिराक होतो. जर घर्षणामुळे निर्माण होणाऱ्या अवरोधी प्रेरणेचे मूल्य जास्त प्रमाणाचे असेल, तर (७) या समीकरनाकरिता आवर्तनी गती हा निष्कर्ष पण मिळत नाही. अशा परिस्थितीत वस्तूला तिच्या मूळ शून्यगती स्थानापासून विचलित केले, तर ती मूळ स्थानी हळूहळू सरळ परत येऊन स्थिर होते. हवेऐवजी लंबकाचा गोलक जर जास्त घनतेच्या श्यान (दाट) तेलात बुडवून ठेवून त्यास विचलित केले, तर त्याची गती आवर्तनी स्वरूपाची होत नाही. याबद्दल प्रत्यक्ष प्रयोगाने पडताळा मिळविता येतो. हवेमध्ये आंदोलन करणाऱ्या लंबकाकरिता जड गोलकाऐवजी जर कार्डबोर्डचा मोठा तुकडा वापरला, तर या पण परिस्थितीमध्ये आवर्तनी गती मिळत नाही, हे प्रयोगाने दाखविता येते.

संदर्भ : 1. Brown, R. C. A Textbook of Physics, London, 1962.

           2. Halliday. D. Resnick, R. Physics : For Students of Science and Engineering, New York, 1960.

चिपळोणकर, व. त्रिं. कुलकर्णी, दि. भि. 

“