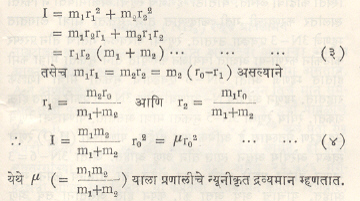रेणवीय संरचना

रेणवीय संरचना : पदार्थातून जाणाऱ्या प्रकाशाची किंवा अन्य ⇨विद्युत् चुंबकीय प्रारणाशी निगडित असलेली चुंबकीय व विद्युत् क्षेत्रे तरंगित होत असतात. या क्षेत्रांची व पदार्थात उपस्थित असणाऱ्या अणूंची किंवा रेणूंची परस्परक्रिया घडून येते. या परस्परक्रियांचा अभ्यास म्हणजेच ⇨वर्णपटविज्ञान होय. रेणूंच्या वर्णपटांचा अभ्यास म्हणजे रेणवीय वर्णपटविज्ञान. रेणूंच्या संरचनेचा व त्यांच्या वर्णपटांचा फार निकटचा संबंध आहे. एकोणिसाव्या शतकात प्रकाशमान वायूंच्या उत्सर्जन वर्णपटांचे निरीक्षण करताना वर्णपटात असलेल्या रेषांचा किंवा रेषांसमूहांचा संबंध वायूत उपस्थित असणाऱ्या अणूंशी किंवा रेणूंशी असतो, असे आढळून आले आणि या रेषा अणूंचे किंवा रेणूंचे विशिष्ट गुण (अभिलक्षणे) दर्शविणाऱ्या असतात असे आढळून आले. प्रारणातील विशिष्ट कंप्रतेचे (दर सेकंदास होणाऱ्या कंपन संख्येचे) किंवा तरंगलांबीचे ⇨फोटॉन (विद्युत् चंबकीय प्रारणांचे पुंजकण) ग्रहण केल्यामुळे अणूतील इलेक्ट्रॉनांची किंवा रेणूंची ऊर्जा पातळी वाढते आणि वर्णपटात विशिष्ट रेषा किंवा रेषासमूह दिसतात.

रेणवीय वर्णपट व रेणवीय संरचना : रेणवीय वर्णपटाचा व रेणूच्या संरचनेचा फार निकटचा संबंध असल्याने रेणवीय वर्णपटाचा अभ्यास करून रेणूची संरचना काढता येते. (रेणवीय संरचना काढण्याकरिता रेणवीय वर्णपटाखेरीज विद्युत् अपार्यता स्थिरांक, विद्युत् द्विध्रुवी परिबल, क्ष-किरण विवर्तन वगैरे पद्धतींचाही उपयोग करण्यात येतो. या पद्धतींचे विवरण ‘रेणवीय भौतिकी’ या नोंदीत दिलेले आहे). दृश्य प्रकाशात असलेल्या निरनिराळ्या तरंगलांब्याच्या किंवा कंप्रतांच्या फोटॉनांचे ज्याप्रमाणे शोषण केले जाते त्याचप्रमाणे इतर विद्युत् चुंबकीय प्रारणांपैकी रेडिओ तरंग, क्ष-किरण, लघुतरंग, गॅमा किरण इ. क्षेत्रांतील विशिष्ट तरंगलांबीच्या किंवा कंप्रतेच्या फोटॉनांचेही शोषण विशिष्ट प्रकारचे रेणू करीत असतात व त्यामुळे त्यांच्या वर्णपटातील रेषा त्या त्या विशिष्ट क्षेत्रातच आढळून येतात.

विद्युत् चुंबकीय तरंग एका विशिष्ट उद्‌गम बिंदूपासून निघून सरळ रेषेत पुढे जातात. त्यांचे स्वरूप हरात्मक तरंगांसारखे [⟶ तरंग गति] असल्याने ते खालील समीकरणांनी दाखविले जाते.

 X = A . sin v किंवा X = A . sin ωt किंवा

 X = A . sin 2πωt   …    …    …    …    (१)

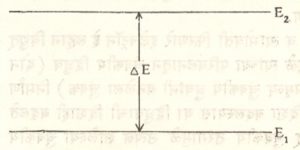
रेणूला एकाहून अधिक मुक्तता मात्रा (अवस्था निश्चित करण्यासाठी निर्देशित करावे लागणारे चल) असतात. रेणूची ऊर्जा स्वतःच्या गुरुत्वमध्यातून जाणाऱ्या अक्षाभोवती होणाऱ्या परिवलनामुळे, त्या रेणूत असलेल्या अणूंच्या स्थानपरिवर्तनाने उत्पन्न झालेल्या कंपनामुळे किंवा त्यात असलेल्या अणूंतील इलेक्ट्रॉनांच्या गतीमुळे उत्पन्न होते. या तीन प्रकारच्या ऊर्जांना अनुक्रमे परिवलनीय, कंपनीय व इलेक्ट्रॉनीय ऊर्जा म्हणतात. अणूमधील इलेक्ट्रॉनांच्या गतीमुळे उत्पन्न होते. या तीन प्रकारच्या ऊर्जांना अनुक्रमे परिवलनीय, कंपनीय व इलेक्ट्रॉनीय ऊर्जा म्हणतात. अणूमधील इलेक्ट्रॉनांच्या ऊर्जेचे ज्याप्रमाणे पुंजीकरण झालेले असते (म्हणजे तिला पृथक् मूल्येच असू शकतात) त्याचप्रमाणे रेणूची परिवलनीय, कंपनीय किंवा इलेक्ट्रॉनीय ऊर्जा ही पुंजीकृत असते. प्रत्येक रेणू एका ऊर्जा पातळीवरून दुसऱ्या (वरच्या किंवा खालच्या) ऊर्जा पातळीवर जाऊ शकतो पण अशी पातळी बदलताना हे कार्य एकाच उडीत करावे लागते. आ. १ मध्ये E₁ व E₂ अशा दोन ऊर्जा पातळ्या दाखविल्या आहेत. E₁ या ऊर्जा पातळीवर असलेला रेणू ऊर्जा ग्रहण करून E₂ या पातळीवर जातो. या दोन पातळ्यांतील ऊर्जातर ∆E असेल, तर ∆E एवढ्या ऊर्जेच्या विशिष्ट तरंगलांबीच्या किंवा कंप्रतेच्या फोटॉनापासून शोषण करावे लागते. माक्स प्लांक यांनी E₁, E₂, ∆E आणि ν (कंप्रता) यांचा संबंध समी. (२) ने दाखविला आहे.

येथे h हा प्लांक स्थिरांक आहे. E₁ या ऊर्जा पातळीवर असलेल्या रेणूंवर ν कंप्रतेच्या म्हणजेच एकवर्णी प्रकाश टाकल्यास तो रेणू ऊर्जा ग्रहण करून E₂ या ऊर्जा पातळीवर जाईल. पदार्थातून बाहेर पडणाऱ्या प्रकाशात या विशिष्ट तरंगलांबीच्या किंवा कंप्रतेच्या प्रकाशाची तीव्रता कमी होईल म्हणजेच शोषणामुळे वर्णपटात ही विशिष्ट रेषा दिसेल.

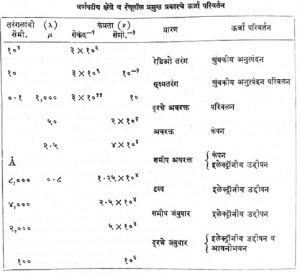विद्युत् चुंबकीय तरंगांचे त्यांच्या तरंगलांबीप्रमाणे किंवा कंप्रतेप्रमाणे निरनिराळे वर्ग पाडले आहेत. या वर्गांच्या सीमारेषा स्पष्ट नाहीत आणि या क्षेत्रांची परस्पर व्याप्तीही होत असते. कोष्टकामध्ये वर्णपटात येणारी विविध तरंगलांब्यांची क्षेत्रे, तरंगलांबी, कंप्रता, प्रारण आणि त्यामुळे रेणूंच्या ऊर्जेत होणारे परिवर्तन दाखविले आहे.

१ मायक्रॉन (μ) = १०^−४ सेंमी. १ अँगस्ट्रॉन (Å) = १०^−८ सेंमी. ‘चुंबकीय अनुस्पंदन’ याच्या स्पष्टीकरणासाठी ‘अनुस्पंदन’ ही नोंद पहावी. आयनीभवन म्हणजे विद्युत् भारित अणू, रेणू वा अणुगट यांत रूपांतरण.

अणूतील अणुकेंद्र व त्याभोवती फिरणारे इलेक्ट्रॉन हे लहान विद्युत् भारित कण असल्यामुळे त्यांच्या परिवलनातून चुंबकीय द्विध्रुव (दोन परस्परविरुद्ध परंतु सममूल्य चुंबकीय ध्रुवांनी बनलेला चुंबक) निर्माण होतो. परिवलनाची दिशा बदलल्यास या द्विध्रुवाची दिशाही बदलते आणि विशिष्ट विद्युत् चुंबकीय तरंगामुळे उत्पन्न झालेल्या चुंबकीय क्षेत्राशी त्याची क्रिया घडून येते व वर्णपट उत्पन्न होतो. प्रत्येक परिवलन दिशाबदलामुळे शोषण किंवा उत्सर्जन वर्णपट तयार होऊ शकतो. या रेषा रेडिओ तरंग क्षेत्रात दिसतात. संयुजी इलेक्ट्रॉनांची (अणूच्या बाह्यतम कवचातील इलेक्ट्रॉनांची) ऊर्जा वाढल्यामुळे  रेणूतील इलेक्ट्रॉनांत गती उत्पन्न होते आणि इलेक्ट्रॉन द्विध्रुवांची निर्मिती होऊन त्यांची परिवर्तित होणाऱ्या विद्युत क्षेत्राशी क्रिया घडते. यामुळे उत्पन्न होणाऱ्या रेषा दृश्य प्रकाशीय क्षेत्रात दिसतात. HCl सारख्या रेणूत हायड्रोजन व क्लोरीन हे अणू स्थायी रूपाने घन व ऋण विद्युत् भारित असतात आणि म्हणून HCl चा रेणू एक स्थायी द्विध्रुव बनतो. याउलट हायड्रोजनाच्या किंवा क्लोरीनाच्या रेणूंत विद्युत् द्विध्रुवी परिबल (विद्युत् भार व त्याचा स्थान सदिश यांच्या गुणाकारांची सर्व विद्युत् भारांकरिता केलेली सदिश बेरीज) शून्य असते. HCl सारख्या द्वि आणवीय रेणूच्या परिवलनामुळे त्याच्या द्विध्रुवाची दिशा बदलते आणि द्विध्रुवी परिबलाच्या दिशेतही बदल घडून येतो आणि प्रारणाच्या परिवर्तनीय चुंबकीय क्षेत्राशी त्याची क्रिया होते. यामुळे उत्पन्न होणाऱ्या वर्णपटातील रेषा लघुतरंग क्षेत्रात दिसतात. कंपनामुळे द्विध्रुवी परिबलात बदल होतात आणि रेणूचे बंध आकुंचन किंवा प्रसरण पावतात. अशा प्रकारे होणाऱ्या ऊर्जापरिवर्तनातून उत्पन्न झालेल्या वर्णपटातील रेषा अवरक्त क्षेत्रात दिसतात.

रेणूचे परिवलन : कोणत्याही दृढ रेणूचे अवकाशात होणारे परिवलन काहीसे जटिल असते. रेणूच्या गुरुत्वमध्यातून जाणारे व एकमेकांस काटकोन करणारे तीन सरळ रेषीय अक्ष कल्पून रेणूच्या परिवलन गतीचे या तीन दिशांत वियोजन केले, तर प्रत्येक दिशेत एक याप्रमाणे तीन प्रमुख निरूढी परिबले (द्रव्यमान व निर्देशित अक्षांपासूनच्या अंतरांचा वर्ग मिळणाऱ्या राशी) प्राप्त होतील. ही तीन निरूढी परिबले I_A, I_B व I_C अशी निदर्शित करण्याची प्रथा आहे. या तीन दिशांतील निरूढी परिबलांच्या तुलनात्मक मानांवरून म्हणजेच पदार्थाच्या आकारावरून किंवा आकृतीवरून रेणूंचे खालील वर्ग पडतात.

(अ) सरळ रेषीय रेणू : HCl किंवा O–C–S यांसारखे रेणू. अशा रेणूंचे तीन दिशांना होणारे परिवलन म्हणजे (१) रासायनिक बंधाला अक्ष कल्पून त्याभोवती आणि (२) व (३) एका टोकापासून दुसऱ्या टोकाकडे होणारे परंतु परस्पर काटकोन करणाऱ्या प्रतलांत होणारे परिवलन. (२) व (३) या परिवलनांचे प्रतिबल समान आहे, म्हणून I_B = I_C असे म्हणता येईल. यांच्या तुलनेत (१) या परिवलनाचे प्रतिबल जवळजवळ शून्याएवढे अल्प असल्याने I_A = 0. रेषीय रेणूचे वैशिष्ट्य म्हणजे I_A = 0 आणि I_B = I_C हे होय.

(आ) सममित घूर्णक रेणू : मिथिल फ्लुओराइडामध्ये कार्बन व हायड्रोजन यांचे बंध चतुःपृष्ठकाच्या टोकांकडे जाणारे बंध असतात. त्यामुळे एका टोकापासून दुसऱ्या टोकापर्यंत होणारे परिवलन रेषीय रेणूच्या परिवलनासारखेच असते, म्हणून I_B = I_C परंतु C – F बंधाला जोडणारी रेषा परिवलनाचा प्रमुख अक्ष असल्याने या अक्षाभोवती होणाऱ्या परिवलनाचे परिबल शून्य नसते. म्हणून अशा रेणूसाठी I_B = I_C ≠ I_A असे असून I_A ≠ 0 अशी स्थिती असते. या प्रकारच्या रेणूंचे दोन उपवर्ग पडतात. मिथिल फ्ल्युओराइडाच्या रेणूसारखे म्हणजेच बृहदशीय सममित घूर्ण रेणू I_B = I_C &gt I_A असते व दुसरा उपवर्ग लघु-अक्षीय सममित घूर्णक रेणू ज्यात I_B = I_C &lt I_A असते. बोरॉन ट्रायक्लोराइड (BCl3) हे दुसऱ्या अ वर्गातील रेणूचे उदाहरण असून यात I_A = 2 I_B = 2I_C असते.

(इ) गोलीय घूर्णक रेणू : अशा रेणूंची तिन्ही दिशांतील निरूढी परिबले सारखीच असतात. मिथेनाचा रेणू या वर्गाचे एक चांगले उदाहरण आहे. येथे I_A = I_B = I_C.

(ई) असममित घूरणक रेणू : बहुतेक रेणू या प्रकारात मोडतात. H₂O आणि H₂C = CHCl ही या प्रकारच्या रेणूंची उदाहरणे आहेत. या रेणूत I_A ≠ I I_B ≠ I_C असे असते.

परिवलनीय वर्णपट : द्वि-आणवीय (दोन अणूंपासून बनलेला) रेषीय रेणू विचारात घेऊ.

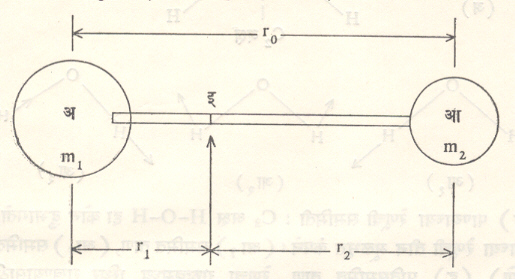
अ व आ या अणूंची द्वव्यमाने अनुक्रमे m₁ व m₂ असून ते एका दृढ बंधाने जोडलेले असू अआ हा रेणू बनतो. अ व आ या अणूंतील अंतर r_० असून इ या गुरुत्वमध्यापासून अ व आ यांची अंतरे

अनुक्रमे r₁= व r₂ आहेत, म्हणून r₀ = r₁ + r₂ आणि m₁r₁ = m₂r₂ इ बिंदूतून जाणाऱ्या अक्षाभोवती या रेणूचे निरूढी परिबल खालील समीकरणांनी दाखविता येईल.

श्रोडिंजर तरंग समीकरणाचा [⟶ पुंजयामिकी] उपयोग करून अशा प्रकारच्या दृढ रेणूच्या परिवलन ऊर्जेच्या अनुमत पातळ्या कोणत्या असतात हे काढता येते. खालील समीकरणात हे दर्शविले आहे.

येथे h = प्लांक स्थिरांक आणि I = निरूढी परिबल. I = I_B = I_C कारण I_B व I_C यांचे मान एकच असते. J = परिवलन पुंजांक (परिवलनांक). परिवलनामुळे उत्पन्न झालेल्या वर्णपटातील रेषांचा उल्लेख त्यांच्या तरंगसंस्थेने (तरंगलांबीच्या व्यस्तांकाने) केला जातो म्हणून वरील समीकरणाचे स्वरूप तरंगसंस्थेत खालीलप्रमाणे होईल.

c = प्रकाशाचा वेग व e हे चिन्ह ऊर्जा/रेणू सेंमी ⁻¹ मध्ये याकरिता वापरले आहे. याच समीकरणात 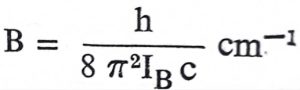घातल्यास त्याचे लघुरूप e_J = B (J + 1) cm⁻¹ (J = 0, 1, 2, … ……) असे होईल. I_B च्या ठिकाणी I_C पण घालता येईल.

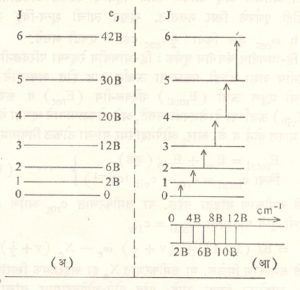
आ. ३ (अ) मध्ये या ऊर्जा पातळ्या दाखविल्या आहेत आणि (आ) मध्ये दृढ द्वि आणवीय रेणूची कोणत्या ऊर्जा पातळ्यांत संक्रमणे होऊ शकतात आणि त्यांपासून उत्पन्न होणारा वर्णपट यांचे चित्रण केले आहे.

वर्णपटात असलेल्या रेषांचा विचार करताना या ऊर्जा पातळ्यांतील ऊर्जांतर किती असते, याची माहिती करून घेणे आवश्यक आहे. J = 0 म्हणजेच ऊर्जेची सर्वांत खालची पातळी. या पातळीवर असताना परिवलन होत नसते म्हणजेच ही पातळी स्थायी ऊर्जा पातळी आहे. रेणूवर पडलेल्या प्रारणातील फोटॉन ग्रहण केल्यामुळे त्याची ऊर्जा पातळी J = 0 वरून J = 1 झाली अशी कल्पना केल्यास यासाठी लागणाऱ्या ऊर्जेचे मान e_J = 1−e_J = ० = 2B cm⁻¹ होईल.

श्रोडिंजर तरंग समीकरणाचा उपयोग करून सिद्ध करता येते की, J च्या मूल्यात एकाचा फरक असणारी परिवर्तनेच शक्य असतात. इतर परिवर्तने वर्णपटविज्ञानाच्या दृष्टीने असंभवनीय ठरतात. म्हणून दृढ द्वि-आणवीय घूर्णकासाठी निवड नियम ∆J = ± 1 या सूत्राने दर्शविला जातो. श्रोडिंजर तरंग समीकरणाचा उपयोग अदृढ रेणूंच्या  ऊर्जा पातळ्या काढण्यासाठीही केला जातो. रेणूचा परिवलनीय वर्णपट उत्पन्न होण्यासाठी त्याच्या द्विध्रुवी परिबलात परिवर्तन होणे आवश्यक आहे. असममित किंवा विषम अणुकेंद्रीय रेणूंचाच परिवलनीय वर्णपट दिसतो. HCl किंवा CO हे रेणू परिवलनीय वर्णपट उत्पन्न करतात परंतु N₂ किंवा O₂ च्या बाबतीत हे शक्य नसते.

बहु-आणवीय रेणू : OCS किंवा HC ≡ CCI सारख्या रेणूंच्या वर्णपटातील रेषा लघुतरंग क्षेत्रात दिसतात. या रेणूंच्या बाबतीत I_B = I_C आणि I_A = 0 असल्याने त्यांचा वर्णपट द्वि आणवीय रेणूसारखाच असतो.

रेणूंचे कंपन : जेव्हा दोन अणू एकमेकांशी संयोग पावून सहसंयुजी रेणू निर्माण करतात, तेव्हा त्यांच्यात उपस्थित असलेल्या इलेक्ट्रॉनांची पुनर्रचना होते. रेणूमध्ये असलेले अणू जास्तीत जास्त जवळ आल्यावर आंतर अणुकेंद्रीय प्रेरणांचा समतोल होऊन रेणूची ऊर्जा सर्वांत कमी होते. अशा स्थिर अवस्थेत असलेल्या अणूचे एकमेकांपासून असलेले अंतर r_eq ने दर्शविले जाते. या अणूंना जोडणारा बंध कधी ताणला जातो, तर कधी आकुंचन पावतो. एखाद्या स्प्रिंगेला एक गोळा जोडल्यावर होणाऱ्या आकुंचन प्रसरण क्रियेशी याची तुलना केल्यास हुक यांचा नियम [⟶ स्थितिस्थापकता]या क्रियेसही लावता येतो आणि

f = − k (r – r_eq)     …     …     …     …  (७)

असे समीकरण मांडता येते. येथे f = पूर्वस्थितीवर आणणारी किंवा पुनःस्थापक प्रेरणा, k = प्रेरणा स्थिरांक, r = दोन अणुकेंद्रांमधील अंतर या प्रकारचा कंप पावणारा द्वि आणवीय रेणू सरल हरात्मक आंदोलकासारखा [⟶ पुंजयामिकी] असतो परंतु सामान्यपणे रेणू या समीकरणाचे तंतोतंत पालन करीत नाहीत या रेणूच्या आंदोलनाची कंप्रता ω_osc असल्यास तिचे मूल्य

या समीकरणाने काढता येते. K = प्रेरणा स्थिरांक व μ = न्यूनीकृत द्रव्यमान आहे. कंप्रतेऐवजी तरंगसंस्थेचा उपयोग केल्यास प्रकाशाच्या वेगाने (c ने) भागून समीकरणाचे स्वरूप खालीलप्रमाणे होईल.

कंपनीय ऊर्जाही पुंजीकृत असल्याने तिचे मूल्य किती असू शकते हे श्रोडिंजर तरंग समीकरणावरून काढता येते. V हा कंपन पुंजांक असल्यास

(v = 0, 1,  2,   …   …   …) वर्णपटविज्ञानीय एककात हे समीकरण खालीलप्रमाणे मांडता येईल.

द्वि आणवीय रेणूंच्या कंपनीय ऊर्जेचे मूल्य शून्य कधीच होत नाही. श्रोडिंजर तरंग समीकरणाचा उपयोग करून काढलेला निवड नियम ∆v = ± 1, ± 2, ±3, … …. या सूत्राने दर्शविला जातो. रेणूत असलेले अणू आपले स्थान नेहमीच बदलत असतात. ते कधी ही पूर्णपणे स्थिर नसतात. म्हणून त्यांची शून्य बिंदू ऊर्जा  जूल किंवा  एवढी असते.

 द्वि-आणवीय कंपनीय : घर्णक द्वि आणवीय रेणूच्या परिवलनीय व कंपनीय अशा दोन्ही प्रकारच्या ऊर्जांत वाढ होत असल्याने त्या रेणूची एकूण ऊर्जा (E_total) परिवलनीय (E_rot) व कंपनीय (E_vib) ऊर्जांच्या बेरजेएवढी असते, असे ठोकळमानाने म्हणता येईल.

माक्स बोर्न व जे. आर्. ओपेनहायमर यांच्या ठोकळ नियमाप्रमाणे

असे समीकरण मांडता येईल. या समीकरणात  e_rot आणि e_vib यांची मूल्ये घातल्यास e_total = e_J,v 

असे समीकरण मिळेल. या समीकरणात X_eहा अहरात्मक स्थिरांक व ϖ_e आंदोलन कंप्रता आहे; परंतु बोर्न-ओपेनहायमर यांचा हा ठोकळ नियम सामान्यपणे पदार्थांत आढळून येणाऱ्या रेणूंना लावता येत नाही. कारण या रेणूंची परिवलन गती सरल हरात्मक गती नसल्याने परिवलन होत असताना रासायनिक बंधांची लांबी सतत बदलत असते.

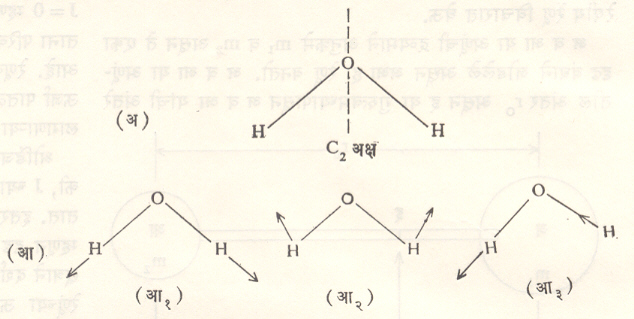
बहु-आणवीय रेणूंचे कंपन : N अणूंपासून बनलेल्या रेणूचा विचार करताना प्रत्येक अणूचे त्रिमितीय स्थान निश्चित करावे लागेल. यासाठी परस्पर काटकोन करणाऱ्या तीन कार्तीय अक्षांची [⟶ भूमिति] आवश्यकता असते म्हणजेच त्या रेणूच्या मुक्तता मात्रांची संख्या 3N होईल. अशा प्रकारचा रेणू त्रिमितीय अवकाशात आपला आकार न बदलता भ्रमण करू लागेल. या रेणूच्या गुरुत्वमध्याचे स्थान निश्चित केल्यास कोणत्याही क्षणी होणारे त्याचे भ्रमण जाणून घेणे शक्य होते परंतु गुरुत्वमध्याचे स्थान निश्चित करताना तीनही अक्षांवरील त्याची स्थिती काढावी लागते. यासाठी म्हणजेच रेणूची अक्षाभोवती न फिरता स्थलांतर करण्याची गती काढण्यास तीन मुक्तता मात्रा लागतात म्हणजे 3N−3 एवढ्या उरतात. रेणूच्या परिवलन गतीचे तीन परस्पर काटकोन करणाऱ्या अक्षांत नियोजन करण्यात तीन मुक्तता मात्रा कमी होतात म्हणजे आता 3N−6 एवढ्याच मुक्तता मात्रा शिल्लक राहतात. म्हणून अरेषीय  N−आणवीय रेणू 3N−6 प्रकारे कंपित होऊ शकतो. रेषीय रेणूला 3N−5 मुक्तता मात्रा असतात. पाण्याच्या रेणूचे उदाहरण घेतल्यास हे अधिक स्पष्ट होईल. पाण्याच्या (H₂O) रेणूचे स्वरूप अरेषीय असून त्यात तीन अणू आहेत. आता 3N−6 = 3 म्हणून तीनच प्रकारे त्याचे कंपन होईल. या सामान्य कंपन गती आहेत. याचाच अर्थ असा की, कंपन होत असताना सर्व एणू एकाच कलेत (एखाद्या स्वेच्छ संदर्भाच्या सापेक्ष एकाच स्थितीत) असून त्यांची कंप्रताही सारखीच असते.

रेणूच्या संरचनेच्या अभ्यासासाठी दृश्य, अवरक्त, सूक्ष्मतरंग, क्ष-किरण, गॅमा किरण, जंबुपार वर्णपटांशिवाय रामन वर्णपटही फार महत्त्वाचा ठरतो. [⟶ रामन परिणाम वर्णपटविज्ञान].

अमोनियाच्या रेणूने लघुतरंगाचे शोषण केल्यावर त्याच्या कंपन गतीत परिवर्तन होते आणि अधिक ऊर्जा ग्रहण केल्यास या रेणूत प्रतिलेमन (तेच घटक पण निराळी संरचना असलेल्या प्रकारात रूपांतर) कसे घडून येते याचा विचार करू.

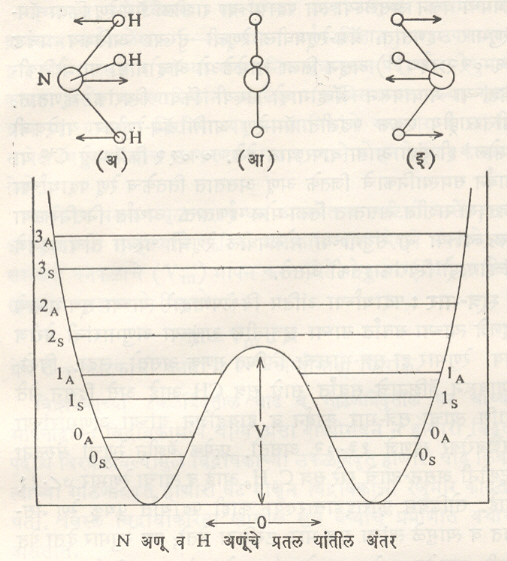
अमोनियाचा रेणू प्रसूच्याकृती (पिरॅमिडाच्या आकाराचा) असून H−N−H हा कोन १०६^° ४२’ असतो. या रेणूतील तिन्ही हायड्रोजन अणू एकाच प्रतलात असतात, मात्र नायट्रोजन रेणूची एकाच सरळ रेषेत हायड्रोजनाचे अणू असणाऱ्या प्रतलाकडे आणि तेथून परत होणारी गती होय. आ. ५ मध्ये वरच्या बाजूस दाखविल्याप्रमाणे (अ) प्रमाणे गती असते पण अधिक ऊर्जा ग्रहण केल्यास नायट्रोजन अणू हायड्रोजन अणूंच्या प्रतलातच जाऊन बसतो. ही ऊर्जा सर्वोच्च ऊर्जा होय. त्यानंतर नायट्रोजन अणू उलट दिशेने गतिमान होतो [(आ) व (इ) मध्ये दाखविल्याप्रमाणे]. यालाच अमोनिया रेणूचे प्रतिलोमन म्हणतात. ग्रहण केलेली ऊर्जा आणि नायट्रोजन व हायड्रोजन अणू यांच्यात असलेल्या अंतराचा आलेख आकृतीत दिला आहे. प्रत्येक ऊर्जा पातळीचे दोन भाग असतात. A ने दाखविलेली पातळी असममित रेणूसाठी असून तिचे मान सममित ऊर्जा पातळी S पेक्षा थोडे जास्त असते. शून्य ऊर्जा पातळीचे 0_S ⟶ 0_A असे रूपांतर होण्यास १·५७६ × १०^−२३ जूल प्रती रेणू एवढी किंवा ९·५० जूल प्रती मोल एवढी ऊर्जा लागते. ही ऊर्जा लघुतरंगांच्या शोषणातून प्राप्त केली जाते आणि २३,७८६ मेगॅहर्जझची शोषण रेषा दिसते. या कंप्रतेला प्रतिलोमन कंप्रता म्हणतात. अमोनिया रेणूच्या अवरक्त वर्णपटातील रेषांवरून गणिताने काढलेली अनुमाने प्रत्यक्ष प्रयोगावरून काढलेल्या मूल्यांशी जुळतात.

रामन व अवरक्त वर्णपटांच्या संयुक्त अभ्यासाने रेणूंची संरचना ठरविता येते. प्रथम AB₂ सारख्या त्रि-आणवीय रेणूचा विचार करू. या रेणूची संरचना ठरविताना हा रेणू रेषीय अथवा अरेषीय आहे, तो B–A–B असा सममित आहे की B–B–A असा असमित आहे, याचा विचार करावा लागतो. हे जाणून घेताना रेणूचा वर्णपट अवरक्त व रामन वर्णपट क्षेत्रात दिसतो किंवा नाही हे महत्त्वाचे ठरते. यासाठी परस्पर अपवर्जन नियमाचा उपयोग करावा लागतो. या नियमाप्रमाणे कोणत्याही सममिती केंद्र असणाऱ्या रेणूच्या कंपनामुळे रामन रेषा दिसत असतील, तर अवरक्त क्षेत्रात रेषा दिसत नाहीत. याच्या उलट जर अवरक्त क्षेत्रात रेषा असतील, तर रामन वर्णपटात रेषा दिसणार नाहीत. जर रेणूला सममिती केंद्र नसेल, तर मात्र रामन आणि अवरक्त या दोन्ही क्षेत्रांत रेषा कंपनामुळे दिसतात. CO₂ रेणूत सममिती केंद्र असल्याचे तसेच N2O (N–N–O) रेणूत नसल्याचे त्यांच्या वर्णपटावरून दिसून येते कारण रामन व अवरक्त क्षेत्रांत N₂O च्या रेषा असतात.

आधुनिक वैज्ञानिक विकासाबरोबर वर्णपटांचा अभ्यास करण्यासाठी नवनवीन उपकरणे उपलब्ध होऊ लागली आहेत. यामुळे या क्षेत्रात जोमाने संशोधन कार्य होत आहे. ⇨लेसर किरणांचा उपयोग करून रामन वर्णपटविज्ञानाचा नवनवीन प्रकाराने उपयोग करून घेणे हा याच विकासाचा एक टप्पा आहे. [⟶ वर्णपट विज्ञान].

संदर्भ :

• Banwell, C. N., Fundamentals of Molecular Spectroscopy, London, 1972.
• Bunker, P. R., Molecular Symmetry and Spectroscopy, New York, 1979.
• Crookes, J. E., The Spectrum in Chemistry, London, 1978.
• Dixon, R. N., Spectroscopy and Structure, London, 1965.
• Flygare, W. H., Molecular Structure and Dynamics, Englewood Cliffs N. J., 1978

लेखक : वैद्य, वि. गो.