रासायनिक गतिविज्ञान

रासायनिक गतिविज्ञान : रासायनिक विक्रियांचा वेग आणि विक्रियाकारकांचे अंतिम उत्पादितांत कसकसे क्रमवार रूपांतर होते, याचा अभ्यास रासायनिक गतिविज्ञानात केला जातो. आपल्या सभोवती असलेल्या वातावरणात, पाण्यात तसेच भूपृष्ठभागावर असंख्य रासायनिक पदार्थ विखुरलेले आहेत. त्यांपैकी काही पदार्थांचा परस्पर संयोग होतो व नवीन पदार्थ निर्माण होतात. काही पदार्थांचे अपघटन (रेणूचे तुकडे होण्याची क्रिया) होऊनही नवीन पदार्थ निर्माण होतात. काही पदार्थ मात्र एकमेकांच्या सान्निध्यात राहूनही त्यांच्यात रासायनिक विक्रिया घडत नाही. पृथ्वीच्या वातावरणात प्रामुख्याने असलेल्या नायट्रोजन व ऑक्सिजन या वायूंत प्रदीर्घ काळापासून एकत्र राहूनही सामान्य परिस्थितीत रासायनिक विक्रिया घडून येत नसल्याचे आपणास माहीत आहे परंतु आकाशात विजा चमकू लागल्या की, या वायूंचा परस्पर संयोग होतो व येणाऱ्या पावसाच्या पाण्याबरोबर त्यांच्या संयोगातून उत्पन्न झालेले नायट्रिक अम्ला भूपृष्ठावर पोहोचते. पदार्थाच्या संयोगातून अथवा अपघटनातून नवीन पदार्थ निर्माण करणाऱ्या रासायनिक विक्रिया कधी अत्यंत जलद तर कधी अतिशय संथ वेगाने होत असतात. या रासायनिक विक्रिया का घडतात व कोणत्या विक्रिया कशा परिस्थितीत घडतात, याचा अठराव्या शतकाच्या अखेरीपासून अभ्यास केला जात आहे.

प्रत्येक रासायनिक विक्रिया विशिष्ट परिस्थितीत ठराविक वेगाने होताना दिसते. हा वेग प्रामुख्याने विक्रियाकारकांची संहती (एकक घनफळातील प्रमाण), तापमान, उत्प्रेरकाची (विक्रियेचा वेग बदलणाऱ्या पदार्थाची) किंवा विक्रियारोधकाची उपस्थिती, वापरलेला विद्रावक (विरघळविणारा द्रव पदार्थ) इत्यादींवर अवलंबून असल्याने आढळते. रासायनिक विक्रियेच्या वेगावरून तसेच त्या विशिष्ट विक्रियेची यंत्रणा जाणून घेतल्याने तीत निर्माण होणारे विशिष्ट पदार्थ प्रयोगशाळेत किंवा औदयोगिक प्रमाणावर मिळविताना तापमान, दाब, उत्प्रेरक इत्यादींची योग्य निवड करता येते.

साधारणपणे पदार्थांच्या रेणूंत वा अणूंत परस्परक्रिया करून नवीन रेणू निर्माण करण्याची प्रवृत्ती दिसून येते पण अशा प्रकारची विक्रिया घडेल किंवा नाही हे ठरविताना ⇨ऊष्मागतिकीच्या सिद्धांताचा उपयोग करावा लागतो. विक्रियाकारकांच्या तुलनेत उत्पादितांची मुक्त ऊर्जा [प्रणालीची अंतर्गत ऊर्जा उणे तिचे तापमान व तिची एंट्रॉपी यांचा गुणाकार ⟶ ऊष्मागतिकी] कमी असेल तर विक्रिया घडते.

नॉर्वेजियन शास्त्रज्ञ सी. एम्. गुलबॅर व पी. व्हॉग यांनी १८६४ मध्ये असे दाखवून दिले की, रासायनिक विक्रियेचा वेग संबंधित विक्रियाकारकांच्या क्रियाशील संहतीच्या सम प्रमाणात असतो. अर्थात जसजशी संहती कमी होत जाईल तसतसा विक्रियेचा वेगही कमी होत जाईल. विक्रियाकारकांच्या एखाद्या गुणधर्मावरून त्याची संहती विक्रियेच्या आरंभ काळापासून मोठ्या कालांतराने मोजतात. विक्रियाकारकांची संहती आणि प्रारंभापासूनचा कालावधी यांचा आलेख काढतात. या आलेखावरून आलेख रेषेला दिलेल्या कोणत्याही कालक्षणाच्या बिंदूवर स्पर्शरेषा काढतात. त्यावरून त्या क्षणीचा विक्रिया वेग कळतो. त्यावरून विक्रिया वेग व कालावधी यांचा आलेख काढतात. कालावधीऐवजी विक्रियाकारकाची संहती आलेख काढताना वापरता येते. गतिकीय दृष्टीने रासायनिक विक्रियांचे वर्गीकरण (१) रेणवीयता (विक्रियेत एकत्र येणाऱ्या रेणूंची संख्या) पद्धतीने किंवा (२) विक्रिया कोटीच्या स्वरूपात केले जाते. सरल एकाच पायरीत घडणाऱ्या विक्रियेत विक्रियाकारकाचे एक, दोन वा (क्वचित) तीन रेणू एकत्र येऊन जर विक्रिया घडत असेल, तर त्या विक्रियेला एक-, द्वि- किंवा त्रि-रेणवीय विक्रिया म्हणतात. विक्रियेच्या रासायनिक समीकरणावरून याचे अनुमान करणे नेहमीच शक्य होईल असे नाही.

विक्रिया वेग व कोटी : प्रायोगिक मापनावरून विक्रियेचा वेग तीत सहभागी असणाऱ्या विक्रियाकारकांच्या कोणत्या घातांकाच्या प्रमाणानुसार आहे, हे ठरवितात. याप्रमाणे सहभागी विक्रियाकारकांच्या संहतीच्या मिळणाऱ्या वेगनिर्धारक घातांकांची बेरीज म्हणजे त्या विक्रियेची कोटी होय.

समजा A ⟶ B या विक्रियेत A चा एक रेणू B च्या एका रेणूत रूपांतर पावतो म्हणजे एकाच पायरीने होणाऱ्या या विक्रियेची रेणवीयता एक आहे, कारण एकच रेणू या रूपांतर विक्रियेला प्रवृत्त करतो. तसेच या विक्रियेचा वेग हा A च्या मोल संहतीच्या (ग्रॅम –रेणुभाराच्या पदातील संहतीच्या) सम प्रमाणात आढळतो. म्हणून ही विक्रिया प्रथम कोटीचीही आहे H₂+I₂ ⟶ 2 HI या विक्रियेत H₂व I₂ हे रेणू (योग्य परिस्थितीत पुरेशा ऊर्जेने व योग्य सापेक्ष दिशेने) परस्पर आघात करून एकाच पायरीत विक्रिया देतात, म्हणून ही विक्रिया द्वि-रेणवीय विक्रिया होय. या विक्रियेच्या दरम्यान H₂व I₂ यांच्या परस्पर आघातातून H–H व I–I बंध तयार होतात.

आ. १ मध्ये या विक्रियेची यंत्रणा दाखविली आहे. प्रयोगावरून असे आढळून येते की, H₂+I₂ ⟶ 2 HI यातील बाणाच्या दिशेने

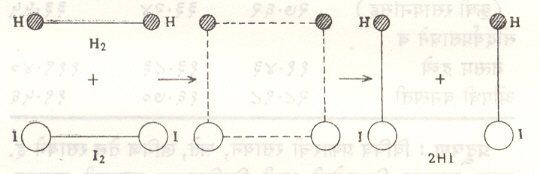
होणाऱ्या अग्रगामी विक्रियेचा वेग [H₂] व [I₂] या विक्रियाकारकांच्या एकघातात्मक मोल संहतींच्या गुणाकाराबरोबर असतो. म्हणून ही विक्रिया द्वितीय कोटीची आहे.

वरील उदाहरणात विक्रियेची रेणवीयता व कोटी सारखेच असल्याचे दिसून आले, तरी प्रत्येक विक्रियेत ते सारखेच असतात असे समजणे चूक होय. सरळ गुंतागुंतीच्या नसलेल्या विक्रियांच्या बाबतीतच त्यांची रेणवीयता व विक्रिया कोटी यांत एकवाक्यता दिसून येते. विक्रियेची कोटी प्रयोगाद्वारेच निश्चित करावयाची असते. ती अपूर्णांकही असू शकते किंवा शून्यही असू शकते. विक्रिया अनेक पायऱ्यांच्या साखळीतून झाल्यास रेणवीयता व विक्रिया कोटी यांची फारकत होते, कारण रेणवीयता एकाच पायरीच्या संदर्भात असते. विक्रियेची ती एकच पायरी असेल किंवा अनेक जलद पायऱ्यांसह होणाऱ्या संथ विक्रियेची ती एकच पायरी असेल, तर समग्र विक्रियेचीही ती रेणवीयता ठरते.

एखाद्या विक्रियेचे समीकरण सहज लिहिता येत असेल, तरी त्यातील विक्रियाकारकांच्या सहगुणकांचा व त्या विक्रियाकारकांच्या क्रियाशील घातांकांचा सरळ संबंध नसल्यास प्रयोगावरून विक्रियेचे वेग समीकरण काढावे लागते. या वेग समीकरणातील विक्रियाकारकांच्या संहतीचे जे घातांक प्रयोगात परिणामी आढळतात ते निवडूनच ते समीकरण बनविलेले असते. एखाद्या विक्रियेचा वेग A, B व C या विक्रियाकारकांच्या [A][ B] व [C]^1/2 या प्रमाणात असेल, तर हीच पदे वेग समीकरणात असतील. आता प्रयोगाने याप्रमाणे मिळविलेल्या वेग समीकरणाशी जुळेल अशी विक्रिया यंत्रणा सुचवावी लागते. या यंत्रणेवरून सैद्धांतिक पायावर वेग समीकरण रचले म्हणजे ते प्रायोगिक वेग समीकरणाशी तुल्य आढळल्यास सुचविलेल्या विक्रिया यंत्रणेची संभाव्यता विश्वसनीयतेच्या पातळीशी येते. याचा अर्थ असा नव्हे की, सुचविलेली विक्रिया यंत्रणा प्रत्यक्षात घडणाऱ्या विक्रियेच्या यंत्रणेप्रमाणेच आहे. सैद्धांतिक वेग समीकरण व प्रायोगिक वेग समीकरण यांची तुल्यता ही सुचविलेल्या विक्रिया यंत्रणेच्या बरोबर असू शकते एवढेच दर्शविते. ती बरोबरच असली पाहिजे असा निष्कर्ष काढणे योग्य ठरत नाही.

प्रथम कोटीच्या विक्रियेसाठी हे सामान्य वेग समीकरण आहे. यात c ही संहती, k हा वेग स्थिरांक व t हा काल आहे. या विक्रियेत t = ० असताना c = a असेल व t = t असताना x भाग विक्रियाकारक वापरला गेला असेल, तर त्या विक्रियेचा वेग त्या कालावधीनंतर (a – x) च्या प्रमाणात असेल. म्हणजे हेच समीकरण असे लिहिता येईल. त्याच्या समकलनाने [⟶ अवकलन व समाकलन] 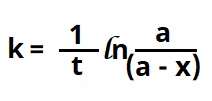किंवा 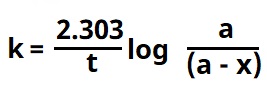हे समीकरण मिळेल. [येथे In हा e आधारांकास असलेला व Iog हा १० आधारांक असलेला लॉगरिथम आहे ⟶ लॉगरिथम]. हे प्रथम कोटीच्या विक्रियेचे गतिकीय समीकरण आहे. ते (a–x) = ae^-kt किंवा c_t = c_o e^-kt या स्वरूपातही लिहीता येईल. येथे विक्रियाकारकाची प्रारंभिक संहती c_o असून t कालावधीनंतर ती c_t आहे. अर्धी विक्रिया पार पाडण्यास t_1/2 = ln 2 एवढा वेळ लागेल. यावरून प्रथम कोटीच्या विक्रियांच्या बाबतीत हा वेळ प्रारंभिक संहतीवर अवलंबून नसल्याचे लक्षात येते.

याचप्रमाणे द्वितीय किंवा तृतीय कोटीच्या विक्रियांसाठी समीकरणे मांडता येतात.

कोटी काढण्याच्या पद्धती : रासायनिक विक्रियांची कोटी काढण्यासाठी खालीलपैकी एखादी पद्धती वापरता येते :

(१) भिन्न कालावधीनंतर विक्रिया प्रणालीतील विक्रियाकारकांच्या संहती विश्लेषणाने काढून त्यांची मूल्ये प्रथम, द्वितीय व तृतीय कोटीच्या वेग समीकरणात घालतात. जे वेग समीकरण (प्रथम, द्वितीय किंवा तृतीय कोटीच्या विकियेचे) स्थिरांक देईल त्याच कोटीची ती विक्रिया समजतात.

(२) अर्धी विक्रिया संपण्यास लागणारा कालावधी प्रयोगाद्वारे मोजतात. त्यासाठी सर्व विक्रियाकारक प्रारंभी एकाच संहतीचे घेणे सोईचे असते. प्रथम कोटी विक्रिया अर्धी होण्यास लागणारा वेळ विक्रियाकारकाच्या संहतीवर अवलंबून नसतो. द्वितीय, तृतीय आदि कोटींच्या विक्रियांसाठी t_1/2 α I    असे असते. येथे t_1/2 हा अर्धी विक्रिया घडून येण्यासाठी लागणारा वेळ असून a ही विक्रियाकारकाची प्रारंभिक                                                                                                                  a^n-1

संहती व n ही विक्रिया कोटी आहे. द्वितीय कोटीच्या विक्रियेसाठी t_1/2 = 1 असे समीकरण मिळते.

ka

(३) जे. एच्. व्हांट−हॉफ यांच्या पद्धतीनुसार n कोटीच्या रासायनिक विक्रियेचा वेग (सर्व विक्रियाकारक समान संहतीचे घेतल्यास) संहतीच्या n घातांकाच्या प्रमाणात असतो. म्हणून

– dc  = kcⁿ

dt

c₁ व c₂ या दोन संहतींसाठी – dc₁ = kc₁ⁿ व

dt

– dc₂= kc₂ⁿ आणि म्हणून लॉगरिथम वापर

dt

n =   log(–dc₁)– log(–dc₂)

dt                    dt

log c₁ – log c₂

(४) विक्रियेत जेवढे विक्रियाकारक असतात त्यांच्या संहतीच्या कोणत्या घातांकाच्या प्रमाणावर विक्रियेचा वेग अवलंबून आहे, हे प्रयोगाने मोजल्यास त्या विक्रियेची कोटी तिच्यातील सहभागी विक्रियाकारकांच्या अशा क्रियाशील संहतीच्या घातांकाच्या बेरजेएवढी असते. एफ्. डब्ल्यू. ओस्टव्हाल्ट यांनी यासाठी एक सोपा मार्ग अवलंबिला. या पद्धतीला ओस्टव्हाल्ट विलगीकरण पद्धती म्हणतात. विक्रियाकारकांचे मिश्रण अशा प्रकारे केले जाते की, फक्त एकाच विक्रियाकारकाची प्रारंभिक संहती इतर विक्रियाकारकांच्या तुलनेत फार अल्प असते. जलजशी विक्रिया घडते तसतशी या विक्रियाकारकाची संहती बर्यारच मोठ्या प्रमाणात बदलते. प्रारंभिक अवस्थेत तरी इतर विक्रियाकारकांची संहती बदलत नाही, असे म्हणता येईल. जे विक्रियाकारक फार विपुल प्रमाणात घेतले जातात त्यांची संहती न बदलल्यामुळे विक्रियेच्या वेगावर त्यांचा प्रभाव पडत नाही. त्यामुळे अल्प व मोजक्या प्रमाणात घेतलेल्या विक्रियाकारकाच्या संदर्भात विक्रियेची कोटी कळते. क्रमाक्रमाने प्रत्येक विक्रियाकारक मोजक्या प्रमाणात घेऊन आणि अन्य सर्व विपुलतेने घेऊन प्रयोग करतात. नंतर त्या सर्वांची बेरीज म्हणजेच समग्र विक्रियेची कोटी होय. सामान्यपणे या विक्रियेसाठी वेग समीकरण खालीलप्रमाणे असते.

dx = k (a – x)ⁿ¹ . bⁿ² . cⁿ³ = k¹ (a – x)ⁿ¹

dt

आभासी कोटी : विद्रावातील विक्रियांत विलगीकरण पद्धती वापरण्यासारखी परिस्थिती अनेक वेळा आढळून येते. विशेषतः अशा विक्रियांत जेथे एक विक्रियाकारक विद्रावकच असतो तेथे ही पद्धत उपयुक्त ठरते. या संदर्भात एथिल असिटेटाची पाण्याबरोबर होणारी जलीय विच्छेदनाची (पाण्यामुळे रेणूचे तुकडे होण्याची) विक्रिया एक चांगले उदाहरण म्हणून देता येईल. या विक्रियेत एस्टराची

CH₃COOC₂H₅ + H₂O ⟶   CH₃COOH   +   C₂H₅OH

एथिल असिटेट पाणी ॲसिटिक अम्ल एथिल अल्कोहॉल प्रारंभिक संहती पाण्याच्या तुलनेत फारच अल्प असते. ही विक्रिया प्रथम कोटीची असल्याने दिसून येते. पाण्याच्या संहतीत जवळजवळ काहीच बदल होत नसल्याने विक्रियेच्या वेगावर पाण्याचा काहीच परिणाम दिसत नाही. अशा विक्रियेला आभासी प्रथम कोटीची विक्रिया म्हणतात.

वेगावर प्रभाव पाडणारे घटक : रासायनिक विक्रियांच्या वेगावर कोणत्या घटकांचा प्रभाव पडतो हे पाहणे महत्त्वाचे आहे.

(१) १८८७ च्या सुमारास एन्. ए. मेन्शुटकीन यांची ट्रायएथिल अमाइन व एथिल आयोडाइड यांमधील विक्रियेचे भिन्न विद्रावकातील वेग मोजले. त्यावरून त्यांनी असा निष्कर्ष काढला की, विद्रावकाचा विद्युत्‍.अपार्यता स्थिरांक [⟶ विद्युत् अपारक पदार्थ ] व त्या विद्रावकातील विक्रियेचा वेग यांचा सरळ संबंध असतो. विद्युत् अपार्यता स्थिरांक वाढला की, विक्रियेचा वेगही वाढतो. काही विक्रियांबाबत याउलटही घडते, म्हणजेच विद्युत् अपार्यता स्थिरांक मोठा असलेल्या विद्रावकात विक्रियेचा वेग कमी होतो.

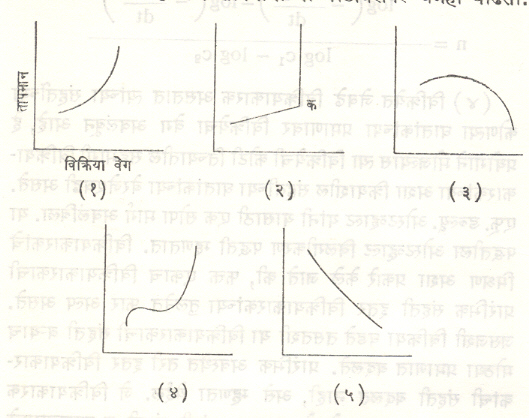(२) विक्रियेच्या वेगावर तापमानाचा परिणाम होतो. सामान्यतः १०^० से. तापमान वाढविले, तर विक्रियेचा वेग दुप्पट ते तिप्पट होतो. तापमान व विक्रिया वेग यांचे आलेख आ. २ मध्ये दिलेले आहेत. सामान्यतः बहुतेक विक्रियांचे आलेख आकृतीमधील (१) प्रमाणे असतात म्हणजेच तापमान वाढीबरोबर वेगही वाढतो.(२) मध्ये प्रथमतः वेग वाढतो पण क बिंदूजवळ एकदम वेग वाढतो व स्फोट होतो. (३) असा आलेख एंझाइमांच्या (जीवरासायनिक विक्रिया घडवून आणण्यास मदत करणाऱ्या प्रथिनांच्या) विक्रियांत आढळतो. (४) कार्बन व ऑक्सिजन यांची विक्रिया दाखवितो. (५) हा NO व O₂ यांच्या विक्रियेचा आलेख आहे.

एस्. ए. अऱ्हेनियस यांनी वेग स्थिरांक व तापमान यांचा संबंध खालील समीकरणाने दर्शविला.

---

d (ln k) = Ea

dT             RT²

येथे Ea − सक्रियण किंवा उद्दीपन ऊर्जा, R− वायू स्थिरांक [⟶ स्थिति समीकरण], T−निरपेक्ष तापमान व k−हा वेग स्थिरांक आहे. या समीकरणाचे समाकलन केल्यास

log k =− Ea    + स्थिरांक

2.303 RT

याचा अर्थ असा की, log k व 1/T यांचा आलेख एक सरळ रेषा राहील व रेषेचा उतार  Ea असेल. यावरून Ea ऊर्जेचे मूल्य मिळू शकते.

2.303 RT

वरील समीकरणास ‘अऱ्हेनियस समीकरण’ म्हणतात. हे कोणत्याही उपपत्तीवर आधारलेले नसून अनुभवसिद्ध आहे.

(३) विक्रियेच्या वेगावर बंदिस्त पात्रात आसलेल्या गतिमान रेणूच्या एकमेकांवर होणाऱ्या आघातांचाही प्रभाव पडतो. हा प्रभाव कसा पडतो ते समजण्यासाठी एका वायुरूप द्विरेणवीय विक्रियेचे उदाहरण घेऊ. विक्रिया होणारा वायू मात्र एकच आहे असे मानू. वायूचे दोन रेणू एकत्र आल्याविना विक्रिया होणार नाही. वायूंच्या गत्यात्मक सिद्धांतानुसार [⟶ द्रव्याचा गत्यात्मक सिद्धांत] वायूचे रेणू गतिमान असल्याने त्यांचे एकमेकांवर आघात होत असतात. दर सेकंदास असे अनेक आघात होतात. वायू एका बंदीस्त पात्रात आहे असे कल्पिल्यास अशा आघातांची संख्या Ö2 pσū n² असते.  येथे σ हा गोल वायू रेणूचा व्यास, ū रेणूंचा सरासरी वेग व n ही रेणूंची संख्या आहे. वायूच्या निरपेक्ष तापमानावर रेणूंचा वेग अवलंबून असतो. सर्व रेणूंचा वेग एकसारखा नसून काहींचा अल्प तर काहींचा फार जास्त असतो. या वेग भिन्नत्वामुळे रेणूंच्या गतिज ऊर्जाही भिन्न असतात. दोन रेणूंचे एकमेकंवर आघात झाल्याबरोबर त्यांची विक्रिया अल्पावधीत पूर्ण व्हायला हवी, पण प्रत्यक्षात बहुतेक विक्रियांप्रमाणे या विक्रियेसही काही काळ लागतो. यावरून प्रत्येक आघात फलदायी होत नाही, असे मानावे लागते. दोन रेणूंचा आघात होताना त्या रेणूंची किमान समग्र ऊर्जा पुरेशी असल्यासच विक्रिया होते. या आघाताच्या वेळी या ऊर्जेमुळे रेणू सक्रियित होतात म्हणूनच या ऊर्जेस सक्रियण ऊर्जा म्हणतात. या ऊर्जेचे मूल्य अऱ्हेनियस (समीकरणीतील) ऊर्जेबरोबर (E_a) असते असे मानल्यास आणि मॅक्सवेल व बोल्टस्मान सिद्धांताचा [⟶ द्रव्याचा गत्यात्मक सिद्धांत] उपयोग केल्यास दर सेकंदास फलदायी आघातांची संख्या

Ö2 pσū n² e–^Ea/RT इतकी होईल. तसेच ती वेग स्थिरांकाच्या मूल्याएवढी होईल. म्हणजे k = Ö2 pσū n² e^–Ea/RT = Z e^–Ea/RT (येथे Z = Ö2 pσū n²). या समीकरणाचा उपयोग करून वेग स्थिरांकाचे मान काढता येते. ५५६^० से. तापमानावर हायड्रोजन आयोडाइड या वायूच्या अपघटनाच्या विक्रियेचा वेग स्थिरांक k हा ३·५ × १०^–७ ग्रॅम-रेणू दर लिटर दर सेकंद इतका असतो, असे प्रयोगाने दिसून येते. वरील समीकरणाचा उपयोग करून हेच मूल्य k = ५·२ × १०^–७ ग्रॅम-रेणू द.लि.द.से. येते. प्रायोगिक व समीकरणावरून काढलेल्या मूल्यांत आढळणारी समानता फारच समाधानकारक आहे परंतु सर्वच विक्रियांच्या बाबतीत अशी एकवाक्यता आढळत नाही.

विक्रिया वेगावर उत्प्रेरक व दाबात केलेले परिवर्तन यांचाही प्रभाव पडतो. [⟶ उत्प्रेरण].

व्युत्क्रमी विक्रिया : सैद्धांतिक दृष्ट्या सर्वच विक्रिया व्युत्क्रमी (उलटसुलट दोन्ही दिशांनी होणाऱ्या) असतात म्हणजेच विक्रियाकारकांच्या होणाऱ्या विक्रियेतून उत्पन्न झालेले उत्पादित पदार्थ परस्पर क्रिया करून मूळ विक्रियाकारक निर्माण करतात. समजा, पदार्थ A पासून पदार्थ B निर्माण होतो. समीकरण मांडून ही विक्रिया पुढीलप्रमाणे दर्शविता येते : A ⟶ B. विक्रियेच्या प्रारंभी A ची संहती अधिक असल्याने अग्रगामी विक्रियेचा वेग जास्त असतो पण जसजशी B ची संहती वाढते. त्याच प्रमाणात पश्चगामी विक्रियांचा वेग वाढतो. अग्रगामी व  पश्चगामी विक्रियांचे वेग सारखे झाले की, समतोल स्थापन होतो. समतोल स्थापन होण्यापूर्वीची अवस्था

K₁

A ⇌ B या समाकरणाने दर्शविता

K₂

येते. गतिकीय दृष्ट्या या दोन्ही विक्रियांचा विचार करावा लागतो. समजा या दोन्ही विक्रिया प्रथम कोटीच्या आहेत. अग्रगामी विक्रियेचा वेग स्थिरांक k₁ व पश्चगामी विक्रियेचा k₂ आहे असे मानल्यास या विक्रियेचे वेग समीकरण dx = K₁ (a – x) – k₂ (b + x) असे होईल. येथे A

dt

व B यांच्या प्रारंभिक संहती अनुक्रमे a व b आहेत आणि t कालावधीनंतर A चा x भाग विक्रियेत खर्च होऊन B ची संहती x ने वाढली आहे, असे वरील समीकरणावरून दिसून येते. विक्रयेच्या समतोलाच्या क्षणी K₁ (a–x) = K₂ (b+x) असेल. वरील पदावरून व t_o व t या काली A च्या संहती x_o व x समजून समाकलित वेग समीकरण (k₁ + k₂) t = ln x_e–x_o असे मिळते. xe ही समतोल स्थितीतील संहती आहे.  [⟶ समतोल, रासायनिक].                                                                                                                                                                  x_e–x                                                                                                                                                                                                                                                                                                           ॲसिटिक अम्ली व एथिल अल्कोहॉल यांपासून एथिल ॲसिटेट व पाणी हे पदार्थ मिळतात. अग्रगामी विक्रिया प्रारंभ होताच मिळालेले उत्पादीत पदार्थ पश्चगामी विक्रिया करतात व मूळ विक्रियाकारक प्राप्त होतात. याचे समीकरण

K₁

CH₃COOH     + C₂H₅OH   ⇌   CH₃COOC₂H₅ +   H₂O

ॲसिटिक अम्ल एथिल अल्कोहॉल  K₂    एथिल ॲसिटेट     पाणी

असे मांडता येईल सुरुवातीला एस्टर व पाणी नसल्याने पश्चगामी विक्रियेचा वेग फार कमी असतो. म्हणून या विक्रियेचा प्रारंभिक वेग dx

dt

= k₁ C CH₃COOH × C C₂H₅OH असतो. उलट विक्रिया सुरू होताच हेच समीकरण dx = k₁ C CH₃COOH × C C₂H₅OH – k₂

dt

C CH₃COO C₂H₅ × CH₂O असे असे.

एकाच वेळी उलटसुलट विक्रिया होऊ शकतात. तशाच दिलेल्या विक्रियाकारकाच्या दोन वा अधिक भिन्न विक्रियाही होऊ शकतात. तसेच एकापाठोपाठ विक्रिया घडून समग्र विक्रिया गुंतागुंतीची ठरू शकते.

---

स्वयं-उत्प्रेरित विक्रिया : या विक्रियांत आरंभिक विक्रियाकारकापासून मिळालेली उत्पादिते त्या विक्रियेचे उत्प्रेरण करू लागतात व विक्रियेचा वेग थोड्याच वेळात लक्षणीय प्रमाणात वाढताना दिसतो. क्लोरो-असिटिक अम्ल व सिल्व्हर नायट्रेट यांपासून मिळणारे सिल्व्हर क्लोराइड त्यांच्यामधील विक्रियेचे उत्प्रेरण करून वेग वाढविते. ऑक्झॅलिक अम्ल. व पोटॅशिअम परमॅंगॅनेट यांतील विक्रिया अगदी संथ असते. विक्रिया होत आहे किंवा नाही हेही प्रथम कळत नाही पण काही वेळाने तिचा वेग वाढतो. याचे कारण विक्रियेचा प्रारंभ झाल्यावर उत्पन्न होणारे मॅंगॅनस आयन विक्रियेचे उत्प्रेरण करतात. विक्रियाकारक मिसळल्यापासून त्यांची विक्रिया एकदम त्वरेने सुरू होण्यापर्यंतच्या कालावधीला प्रवर्तन काल म्हणतात. बहुधा मुक्त अणू व मुक्त मूलके [⟶ मूलके] मध्यस्थ म्हणून उत्पन्न होताच ते उत्प्रेरक बनतात आणि त्यामुळे विक्रियेचा वेग एकदम वाढतो.

जटिल विक्रिया : एकच एक आणि एकाच पायरीची विक्रिया असे रासायनिक विक्रियेचे स्वरूप क्वचितच आढळते. अनेक विक्रिया गुंतागंतीच्या असतात. त्यांत अस्थायी मध्यस्थ तयार होऊन वापरले जातात किंवा अनेक शाखांनी विक्रिया होताना दिसते. रासायनिक गतिविज्ञान अशी सर्व गुंतागुंत शोधून तिचा उलगडा करते. शाखांनी होणाऱ्या विक्रिया परस्परांच्या प्रतिस्पर्धी असतात. फिनॉलावरील नायट्रिक अम्लातची विक्रिया अशाच स्वरूपाची आहे. 2NO+O₂ 2NO₂ ही विक्रिया अशीच जटील विक्रिया असून ती तिसऱ्या कोटीची असल्याचे प्रयोगाने आढळते. येथे वेग समीकरण – dC_NO = ke kC²_NO . C_O2 असे आहे. (येथे k_e हा विक्रिया समतोलावस्थेत असतानाचा

dt

वेग स्थिरांक आहे) पण या विक्रियेत 2NO ⇌ N₂O₂ अशी द्विवारीकीकरणाची पहिली पायरी असून नंतर N₂O₂ + O₂ ⟶ 2NO₂ अशी विक्रिया होताना दिसते. वरील दोन पायऱ्यांवरून समग्र विक्रियेसाठी – dCNO = dCNO₂ = k_obs C²_NO . C_O2 असे वेग

dt             dt

समीकरण लिहिता येईल (येथे K_obs हा प्रयोगातील निरीक्षणाने मिळालेला वेग स्थिरांक आहे) पण ke = C_N2O2 असल्यामुळे प्रयोगाने

C²NO

पडताळा घेता येईल असे समीकरण K_obs =K₂ K_e असे असेल.

जटील विक्रियेत प्रयोगाने वेग समीकरण मिळविले जाते. त्यात संबंधित विक्रियाकारकांच्या संहतीच्या कोणत्या घातांकाच्या प्रमाणात त्या विक्रियेचा वेग आहे, हे प्रयोगाद्वारे मोजले जाते. विक्रियेची प्रगती दाखविणारा भौतिक गुणधर्म कालांतराने मोजला जातो. नवनवीन इलेक्ट्रॉनीय उपकरणांच्या साहाय्याने आता निरनिराळे भौतिक गुणधर्म मोजणे सोपे झाले आहे. या पद्धतीत जास्त अचूकपणे मोजमाप करता येते. विक्रिया प्रणालीचा अल्पांश मोजून निराळा काढून घेतात. तो थंड करून पुढील विक्रिया थोपवून उत्पादिताचे प्रमाण रासायनिक विश्लेषणाने ठरवितात. याच कामासाठी आता नवनवीन उपकरणे उपलब्ध असल्याने असा अल्पांश वेगळा न काढताही विक्रियेची प्रगती मोजणे शक्य झाले आहे नंतर जटील विक्रियेसाठी कल्पकतेने व अनुभवाच्या सूक्ष्म दृष्टीने अनेक पायऱ्यांची यंत्रणा सुचविली जाते. या यंत्रणेच्या पायऱ्यावरून समग्र विक्रियेसाठी गत्यात्मक सिद्धांताच्या पार्श्वभूमीवर गणिताने एक वेग समीकरण तयार करता येते. हे सैद्धांतिक वेग समीकरण जर प्रायोगिक समीकरणाशी जुळले, तर सुचविलेली यंत्रणा मान्य केली जाते पण भविष्यात अधिक तपशिलाच्या आधारे अधिक सयुक्तिक यंत्रणा सुचविली जाण्याची शक्यता मात्र नाकारता येत नाही.

अम्लाच्या उत्प्रेरणाने शर्करेचे (सुक्रोजाचे) जलीय विच्छेदन होऊन ग्लुकोज व फ्रुक्टोज तयार होतात. या विक्रियेत हायड्रोजन आयनांची केवळ उत्प्रेरक म्हणूनच गरज असते. त्यांचा विक्रियेच्या वेगावर परिणाम होतो, पण विक्रिया घडत असताना H⁺ आयनाच्या संहतीत बदल होत नाही. तथापि H⁺ च्या भिन्न संहती विक्रियेचा वेग स्थिरांक भिन्न मूल्यांचा देतात. वेग स्थिरांक मोजण्यासाठी ध्रुवणमापकाचा [⟶ ध्रुवणमिति ] वापर केला जातो. वेग स्थिरांक शर्करेच्या संहतीच्या प्रमाणात आढळतो. चौकोनी कंस प्रती लिटर मोल संहती दाखवितो. या

K₁

विक्रियेत प्रथम पायरी प्रोटॉनीकरणाची आहे. C₁₂H₂₂O₁₁ + H⁺ ⇌ (C₁₂H₂₂O₁₁) H⁺. ही पायरी एवढी जलद होते की, प्रायः लगेच ती

K₂

समतोल गाठते पण दर क्षणी (C₁₂H₂₂O₁₁) H⁺ भंग पावत असल्याने हा खरा समतोल नव्हे.

K₃

(C₁₂H₂₂O₁₁) H⁺ + H₂O ⟶ C₆H₁₂O₆ + C₆H₁₂O₆ + H⁺

ग्लुकोज     फ्रुक्टोज

ही जलीय विच्छेदन विक्रिया समग्र विक्रियेचा वेग निश्चित करते. ही विक्रिया प्रोटॉनीकरणाच्या तुलनेत फारच सावकाश घडते. समग्र विक्रियेचा वेग स्थिरांक त्यावरूनच मिळतो.

 

विक्रिया   वेग = k₃ [(C₁₂H₂₂O₁₁ ) H⁺] [H₂O]

येथे पाणी विपुल प्रमाणात उपलब्द असल्याने विक्रिया घडताना त्याच्या संहतीत फारसा फरक पडत नाही. म्हणून विक्रियेच्या वेगावर त्याचा प्रभाव प्रभाव पडत नाही. वेग शर्करेच्या संहतीच्याच प्रमाणात असल्याचे आढळून येते. पायऱ्यापायऱ्यांतील समतोल कल्पून हीच गोष्ट अशी मांडता येईल.

C₁₂H₂₂O₁₁ + H⁺ ⇌ (C₁₂H₂₂O₁₁) H⁺

यावरून k_eq = k₁ = [(C₁₂H₂₂O₁₁)H⁺] कारण अग्रगामी विक्रियेचा वेग = k₁ [C₁₂H₂₂O₁₁] [H⁺] असून पश्चभागी विक्रियेचा वेग = k₂  C₁₂H₂₂O₁₁) H⁺] असेल. समतोल स्थापन होताच हे वेग समान होतील. मध्यस्थ विक्रियाकारकांची संहती अशी मिळेल.

[(C₁₂H₂₂O₁₁) H⁺] = k₁ [(C₁₂H₂₂O₁₁) ] [H⁺]

k₂

या समीकरणातील उजवीकडची सर्व पदे मोजता येतात. प्रोटॉनीकृत शर्करा रेणूची जलीय विच्छेदन विक्रिया k₃ [(C₁₂H₂₂O₁₁) H⁺] [H₂O]या पदाच्या प्रमाणात घडेल. वरील दोन समीकरणांवरून अग्रगामी विक्रियेचा वेग k₃ k₁ [C₁₂H₂₂O₁₁] [H⁺] [H₂O] असेल.

k₂

आता प्रयोगाने आढळणारा वेग = k'[C₁₂H₂₂O₁₁]. प्रायोगिक वेग मोजणीवरून ही विक्रिया पहिल्या कोटीची ठरते, तर गणिताने ती तृतीय कोटीची आहे, असा निष्कर्ष निघतो. या फरकाचे कारण एवढेच की, प्रत्येक प्रयोगात [H⁺] ची संहती स्थिर असते व पाण्याच्या संहतीत [H₂O] होणारा बदल नगण्यप्राय असतो. अर्थात अम्लत संपर्कात शर्करेची जलीय विच्छेदन विक्रिया गुंतागुंतीची असली, तरी प्रयोगाने ती प्रथम कोटीचीच ठरते.

---

दुसऱ्या एका गतिकीय दृष्टीकोनातून असे मानण्यात येते की, विक्रियाकारकातून प्रथम एक अस्थायी समतोल तयार होतो व तो लगेच

k₁

अपघटन पावून विक्रियेची अंतिम उत्पादिते देतो. या भूमिकेनुसार C₁₂H₂₂O₁₁+ H⁺ ⇌ (C₁₂H₂₂O₁₁) H⁺ हा खरा समतोल स्थापन होत

k₂

नाही पण पहिली पायरी (C₁₂H₂₂O₁₁) H⁺ देते. व त्याची निर्मिती एवढ्या त्वरेने होते की, त्याचा वापर जलीय विच्छेदनाच्या पायरीत तेवढा जलद होत नाही. विक्रिया सुरू होताच काही सेकंदातच या मध्यस्थाची संहती निश्चित पातळीला येते व स्थिर होते. म्हणजेच d

dt

[(C₁₂H₂₂O₁₁) H⁺] = ०

ज्या विक्रियेत (C₁₂H₂₂O₁₁ )H⁺ बनते व ज्यात ते वापरले जाते. त्यांचे वेग सारखेच असले पाहीजेत म्हणूनच

d [(C₁₂H₂₂O₁₁) H+ ] = ०

dt

= k₁[C₁₂H₂₂O₁₁ ] [H⁺] – k₂ [(C₁₂H₂₂O₁₁) H⁺] – k₃ [C₁₂H₂₂O₁₁ ] [H₂O].

सुलभीकरणाने

[(C₁₂H₂₂O₁₁) H⁺] = k₁[C₁₂H₂₂O₁₁] [H⁺] येथे k2 फार लहान असेल k₂&lt &lt k₃ [H₂O] म्हणून वरील समीकरणावरून जलीय

k₂ + k₃ [H₂O]

विच्छेदन वेग = k₁ k₃ [C₁₂H₂₂O₁₁] [H⁺] [ H₂O] = k₁ [C₁₂H₂₂O₁₁] [ H⁺] होईल. पाणी विपुल असता व [H⁺] ची संहती अम्लागच्या

k₃ [ H₂O]

उत्प्रेरक कार्यामुळे स्थिर असल्याने ही गुंतागुंतीची विक्रिया प्रथम कोटीची ठरते. प्रत्यक्षात वेग स्थिरांकाचे मूल्य [H⁺] च्या मूल्यावर असेल.

शृंखला विक्रिया : H₂ व I₂ यांत होणारी विक्रिया एकाच पायरीने होणारी द्विरेणवीय व द्वितीय कोटीची विक्रिया आहे परंतु H₂ व CI₂ यांची प्रकाशप्रेरीत विक्रिया आणि H₂ व Br₂ यांची उष्णतेने उत्तेजित केलेली विक्रिया या दोन्ही शृंखला विक्रिया आहेत. अशा विक्रियेत (१) प्रथम अणू किंवा मुक्त मूलक तयार होतात, (२) ते विक्रियाकारकाशी विक्रिया देण्याचे व मुक्त मूलक निर्मिण्याचे कार्य बऱ्याच काळ शृंखलेसारखे करतात. (३) अखेर अणू वा मुक्त मूलक यांची परस्परक्रिया होऊन शृंवखलेने विक्रिया करणारे घटक वापरले जाऊन शृंखला तुटते.

उष्णता

(१) शृंखलेचा प्रारंभ : Br₂ ⟶ 2Br. (अणू वा मुक्त मूलक)

(२) शृंखलेचे सातत्य : Br. + H₂ ⟶ HBr + H.

H. + Br₂ ⟶ HBr+ Br.

H. +HBr ⟶ H₂+Br.

(3) शृंखलेची समाप्ती : Br.+ Br. ⟶ Br₂

अल्प प्रमाणात Br. चे अणू बनताच किंवा बाहेरून विक्रिया प्रणालीत मिसळल्यास शृंखला विक्रियेस प्रारंभ होऊन विक्रियेचा वेग व क्षमता एकदम वाढतात.

निरपेक्ष विक्रियावेग : रासायनिक विक्रिया होण्यापूर्वी प्रथम सक्रियित (संमिश्र) रेणू तयार होतात. हे सक्रियित रेणू व इतर आरंभिक पदार्थ यांचा समतोल असून सक्रियित रेणूंचे अपघटन होऊन उत्पादिते मिळतात. सक्रयित रेणूंच्या आधारे विक्रियांचा वेग किंवा निरपेक्ष वेग काढता येणे शक्य आहे, ही कल्पना प्रथम १९३२ साली एच्. पेल्झर व ई. विग्नर या शास्त्रज्ञांनी मांडली. १९३५ मध्ये एच्. आयरिंग व त्यांचे सहकारी यांनी या कल्पनेचा विस्तार करून निरपेक्ष वेग काढण्याची समीकरणे मांडली. ही उत्पत्ती उपयुक्त ठरली आहे. या उपपत्तीस ‘संक्रमणावस्था उपपत्ती’ असेही म्हणतात. ही उपपत्ती सांख्यिकी (संख्याशास्त्र) व ⇨पुंजयामिकी यांवर आधारलेली आहे. या उपपत्तीनुसार A व B अशा दोन वायूंची विक्रिया विचारात घेतल्यास प्रथमतः [AB]* असे संमिश्र सक्रियित रेणू तयार होतील व मग त्यांचे अपघटन होऊन उत्पादिते प्राप्त होतील.

K

A +B ⇌ [AB]* ⟶ उत्पादिते

वरील उत्पत्तीच्या आधारे आयरिंग यांनी (विक्रियेची रेणवीयता कोणतीही असली तरी ) विक्रियेचा वेग स्थिरांक खालील समीकरणाने दाखविता येतो, असे सिद्ध केले :

k = RT   k*

Nh

येथे R – वायुस्थिरांक, T – निरपेक्ष तापमान, N –ॲव्होगाड्रो संख्या (पदार्थाच्या ग्रॅम रेणुभारातील रेणूंची संख्या), h – प्लांक स्थिरांक व k* – हा संमिश्र सक्रियित रेणू आणि आरंभिक पदार्थ यांचा समतोल स्थिरांक होत.

विद्रावातील विक्रिया : विद्रावात होणाऱ्या विक्रियांचे वेग स्थिरांक फार उपयुक्त ठरले आहेत. विरल विद्रावातील विद्रुतांचे (विरघळलेल्या पदार्थांचे) गुणधर्म व वायुस्थितीतील गुणधर्म यांमध्ये फार साम्य दिसून येते. यावरून वायुस्थितीतील विक्रियावेग आणि विद्रावातील विक्रियावेग जवळजवळ सारखेच असणे संभवते. क्लोरीन मोनॉक्साइड व ओझोन (क्लोरीन साहाय्यक) वापरून एथिलीन आयोडाइडाचे औष्णिक अपघटन वायुरूप स्थितीत किंवा कार्बन टेट्राक्लोराइडच्या विद्रावात एकाच वेगाने होते. त्याचप्रमाणे काही सावकाश होणाऱ्या विक्रिया उदा., ट्रायएथिल अमाइन व एथिल आयोडाइड, एथिल अल्कोहॉल व ॲसिटिक ॲनहायड्राइड यांच्या विक्रिया वायुस्थितीत अथवा विद्रावावस्थेत एकाच वेगाने होतात.

पदार्थांच्या विरल विद्रावातच असे आढळून येते, पण पदार्थांच्या संहती क्षीण नसून जास्त असल्यास संहतीच्या ऐवजी पदार्थांच्या क्रियाशीलता विचारात घेतल्या पाहिजेत.

अतिजलद विक्रिया : काही विक्रियांचा वेग इतका प्रचंड असतो की, त्या घडल्याची जाणीवही होत नाही. रॉबर्ट नॉरिश व जॉर्ज पोर्टर या शास्त्रज्ञांनी १९४९ मध्ये अतिजलद घडणाऱ्या प्रकाश रासायनिक विक्रियांचा अभ्यास केला. त्यांना यासाठी चमक प्रकाश विश्लेषण पद्धतीचा उपयोग केला. यात विक्रिया होत असताना विक्रिया प्रणालीतील पदार्थांवर चमक टाकून उत्पन्ना होणाऱ्या पदार्थाची संहती विश्लेषण करून काढली जाते. चमकेचा काळ हा फारच अल्प म्हणजे सेकंदाच्या एक दशसहस्त्रांश भागाएवढाच असतो. विश्लेषणासाठी पदार्थाच्या वर्णपटाचा उपयोग केला जातो.

काही रासायनिक विक्रिया एवढ्या जलद घडतात की, विक्रियाकारकात होणारे बदल जाणून घेण्यासाठी सेकंदाचा एक कोट्यांश भागही मोठाच वाटतो. या प्रकारच्या अत्यधिक जलद विक्रियांचा अभ्यास आता ⇨लेसर किरणांच्या साहाय्याने केला जात आहे. यासाठी विशिष्ट प्रकारचे लेसर वापरले जातात. त्यांमधून उत्पन्न होणाऱ्या चमकेचा काळ सेंकदाच्या एक दशकोट्यांश भागाएवढा अल्प असतो. ही पद्धती वापरून ⇨प्रकाशसंश्लेषणामध्ये हरित द्रव्य (क्लोरोफिल ) कशा प्रकारे कार्य करते यासंबंधी संशोधन करण्यात येत आहे.

पहा : उत्प्रेरण रासायनिक विक्रिया.

संदर्भ : 1. Berrow, G. M. Physical Cheistry, Tokyo, 1979.

2. Bernasconi, C. F. Relaxation Kinetics, New York, 1976.

3. Glasstone, . S. Textbook of Physical Chemistry, London, 1964.

4. Hamill, W. H. Williams, R. R. Principles of Physical Chemistry, Edinburgh, 1959.

5. Hammes, G. G., Ed., Investigations of Rates and Mechanisms of Reactions, New York, 1974.

6. Laidler, K. J. Reaction Kinetics , 2 Vols., New York, 1963.

7. Moore, W. J. Physical Chemistry. Burnt Mill, Essex, 1972.

भिडे, ब. वा. करबेलकर, ना. वि. वैद्य, वि. गो.

“