भूगणित

भूगणित : (जिओडेसी). पृथ्वीचा (किंवा तिच्या मोठ्या भागाचा) आकार, आकारमान, वक्रता तसेच भूपृष्ठावर गुरुत्वाकर्षणामध्ये होणारे बदल यांचा अभ्यास करणारे व ⇨ भूभौतिकीशी निगडीत असलेले शास्त्र. पुढील उद्दीष्ट्ये डोळ्यासमोर ठेवून भूगणिताचा अभ्यास केला जातो : (१) पृथ्वीसंबंधीची विविध परिमाणे (उदा., त्रिज्या, परिघ इ.) मोजणे तसेच गणिताद्वारे अचूकपणे स्थाननिश्चिती केलेल्या बिंदूंच्या साहाय्याने नकाशे, आलेख, बांधकामे, मार्गनिर्देशन (विमाने, जहाजे इ. वाहनांना इष्ट स्थळी पोहोचण्याचे मार्ग निर्देशित करणे) इ. कामांसाठी लागणारे समोच्च रेषांचे ( एकाच उंचीचे बिंदू–स्थाने–जोडणाऱ्या रेषांचे) नियंत्रक जाळे प्रस्थापित करणे. (२) भूकंपमापनाद्वारे [⟶भूकंप] मिळालेल्या भूवैज्ञानिक स्वरुपाच्या व इतर माहितीच्या संदर्भात भूकवच व प्रावरण (कवच व गाभा यांच्या दरम्यानचा पृथ्वीची सु. ३,४८० किमी. खोलीपर्यंतचा भाग) यांच्या संरचनेचा अभ्यास करण्यासाठी गुरुत्वाकर्षणामध्ये होणाऱ्या बदलाचा अभ्यास करणे. (३) गुरुत्वाकर्षण मापनाच्या साहाय्याने भूभौतिकीय पूर्वेक्षण [⟶खनिज पूर्वेक्षण] करण्याकरिता गुरुत्वीय प्रवेगांचे संदर्भ-जाळे तयार करणे. (४) कृत्रिम उपग्रहाची कक्षा बिनचूकपणे काढण्यासाठी गुरुत्वीय क्षेत्राची अचूक माहिती मिळविणे.

  

भूगणितातील प्रश्न सोडविण्यासाठी अनुसरलेल्या मार्गानुसार त्याचे भूमितीय, भूभौतिकीय, ज्योतिषशास्त्रीय व कृत्रिम उपग्रहीय असे विभाग पाडले जातात. पहिल्या तीन विभागांना मिळून सामान्यतः ‘अभिजात भूगणित’ म्हटले जाते. चौथ्या विभागाचे अध्ययन १९५७ सालापासून सुरू झाले आहे.

  

भूगणितातील सर्वेक्षणे अतिशय अचुकपणे केली जातात. त्याकरिता पृथ्वीची वक्रता लक्षात घेऊन भूपृष्ठावरील रेषेची लांबी व दिशा काढतात. भूपृष्ठावरील स्थिर बिंदूचे स्थान पृथ्वीसापेक्ष सहनिर्देशकांमध्ये देतात आणि बिंदूंचे स्थान निश्चित करण्यासाठी वापरण्यात येणारे अक्षांश, रेखांश, समुद्रपातळीपासूनची उंची इ. सहनिर्देशक काढण्यासाठी अचूक ज्योतिषशास्त्रीय वेध घ्यावे लागतात. हे वेध घेताना पृथ्वीच्या ध्रुवाच्या भ्रमणामुळे [⟶ध्रुव-२] रेखांशात होणारे सूक्ष्म बदल, तसेच जवळच्या डोंगरपर्वताच्या गुरुत्वाकर्षणामुळे उद्‌भवणाऱ्या त्रुटीही लक्षात घेतात. अक्षांश, रेखांश इत्यादींची मूल्ये पृथ्वीच्या आकारानुसार बदलत असल्याने ती काढणे हेही भूगणिताचे कार्य आहे. शिवाय एखाद्या स्थानाची उंची ठरविण्यासाठी त्या ठिकाणच्या गुरुत्वाकर्षणाची दिशा व तीव्रता माहीत असाव्या लागतात. त्यामुळे पृथ्वीच्या गुरुत्वीय क्षेत्राचे मापन करणे हेही भूगणिताचे एक कार्य ठरते. अशा प्रकारे यामध्ये एकूण भूपृष्ठाचा अभ्यास अभिप्रेत असल्याने या विज्ञान शाखेला आंतरराष्ट्रीय स्वरूप प्राप्त झाले आहे. आता तर पृथ्वीलगतच्या खस्थ पदार्थांचे (उदा., चंद्र, मंगळ इ.) आकार, आकारमान, गुरुत्वीय क्षेत्र इ. निश्चित करण्यासाठीही भूगणितीय पद्धतींचा वापर केला जातो.

  

सर्वेक्षण करताना उद्‌भवलेल्या अडचणींचे निराकरण करण्याच्या प्रयत्नांमधून भूगणिताचा विकास झाला व त्याला भूविज्ञान, ज्योतिषशास्त्र, मानचित्रण (पृथ्वीच्या विविध क्षेत्रांचे नकाशे तयार करणे), भौतिकी वगैरे इतरही विज्ञान शाखांचे साहाय्य झाले उदा., अक्षांश, रेखांश इ. ठरविताना ज्योतिषशास्त्रीय वेधांचा व इतर माहितीचा वापर करावा लागतो तसेच ⇨ अक्षांदोलनामुळे पृथ्वीच्या दैनिक गतीत होणारा ०.०३ सेकंद एवढा फरकही भूगणितीय मापने घेताना विचारात घ्यावा लागतो. उलट १९६० नंतर भूकवचामध्ये होणाऱ्या उभ्या वा आडव्या दिशांतील हालचालींचे मापन भूगणितीय पद्धतींमुळे अचूकपणे करता येऊ लागले आहे. अशा प्रकारे भूगणिताचा ज्योतिषशास्त्र व भूविज्ञानाशी संबंध येतो. रॉकेट व लांब पल्ल्याची क्षेपणास्त्रे यांचा गतिमार्ग काढणे, खनिज पूर्वेक्षणातील मापने घेणे वगैरेमध्येही अतिशय अचूक मापनासाठी भूगणितीय पद्धतींचा वापर करतात.

  

इतिहास : मानवाला खूप प्राचीन काळापासून पृथ्वीच्या आकाराविषयी कुतूहल वाटत आले आहे. प्रथम पृथ्वी म्हणजे नद्या, समुद्र व पर्वत यांनी युक्त असा घनाकार वा गोलाकार ठोकळा मानीत. बॅबिलोनियन लोक कुशल ज्योतिर्विद होते व त्यांच्यापैकी काहीनी ग्रहणाच्या वेळी चंद्रावर पडणारी पृथ्वीची वक्राकार छाया पाहिली असावी तसेच दक्षिणेकडे जाताना आकाशातील ताऱ्यांची मांडणी बदलते, उत्तरेकडील नेहमी दिसणारे तारे दिसेनासे होतात व दक्षिणेचे नवीन तारे दिसू लागतात, असे त्यांना आढळले होते. यावरुन त्यांच्यापैकी काहींना तरी पृथ्वी गोलाकार असावी, निदान तिचे पृष्ठ वक्र असावे असे वाटले असावे. मात्र पृथ्वी सपाट आहे, अशीच त्यांची श्रध्दा होती. दूर जाणारे जहाज खालीही जाताना दिसते हे पाहून काही नावाड्यांना तरी भूपृष्ठाच्या वक्रतेची कल्पना आली असावी. पार्मेनिडीझ (इ. स. पू. पाचवे शतक) या ग्रीक तत्त्वज्ञांनी पृथ्वी गोल असल्याचे प्रथम सांगितले होते. तथापी पृथ्वी गोलाकार असल्याची कल्पना मांडण्याचे श्रेय सामान्यपणे पायथॅगोरस (इ. स. पू. सू. ५७५–४९५) आणि त्यांचे सहकारी यांना देण्यात येते. प्लेटो (इ. स. पू. सू. ४२८–३४८) पृथ्वी गोलाकार असल्याचे मानीत, तर ॲरिस्टॉटल (इ. स. पू. सू. ३८४–३२२) यांनी ग्रहणात चंद्रावर पडणारी पृथ्वीची वक्र छाया हा तिच्या गोलाकाराचा एक पुरावा दिला होता व इतर स्वस्थ पदार्थांच्या मानाने पृथ्वी विशेष मोठी नसल्याचेही त्यांनी सांगितले होते. टॉलेमी (इ. स. सु. ९०–१६९) यांच्या काळी अक्षांश-रेखांशयुक्त नकाशे व मार्गनिर्देशक नाविक चार्ट वापरात होते परंतु कोलंबस (सु. १४५१-१५०६) यांच्या काळातच पृथ्वीचा आकार लक्षात घेऊन काढलेल्या नकाशांची निकड भासू लागली.

आयझॅक न्यूटन (१६४२-१७२७) व क्रिस्तीआन हायगेन्झ (१६२९-९५) यांच्यापासून भूगणिताचे नवे युग सुरु झाले. अक्षीय परिभ्रमणामुळे पृथ्वीच्या विषुववृत्तीय भागातील गुरुत्वाकर्षण किंचित कमी होऊन त्यामुळे पृथ्वीचा विषुववृत्तीय अक्ष तिच्या ध्रुवीय अक्षापेक्षा किंचित मोठा असलाच पाहिजे, असे न्यूटन यांनी प्रिन्सिपिया या ग्रंथात नमूद केले होते. १६७२ साली झां रीशे यांनी दक्षिण अमेरिकेतील कायएन (फ्रेंच गियाना) मोहिमेत लंबकाचा आंदोलनकाल (एका आंदोलनास लागणारा काळ) अक्षांशानुसार बदलतो, हे शोधून काढले. यावरुन पृथ्वी पूर्ण गोलाकार नसावी हे दिसून आले. झां डॉमीनीक कासीनी (१६२५-१७१२) यांच्यासारख्या काहींचे मत पृथ्वी विषुववृत्ताशी चापट असली पाहिजे असे होते. ही परस्परविरुद्ध मते तपासून पाहण्यासाठी पेरू व लॅपलँड येथे भूगणितीय मोहिमा पाठविण्यात आल्या. त्यांच्या निरीक्षणांवरून पृथ्वी ध्रुवांशी चापट असल्याचे कळून आले. पृथ्वी आपल्या अक्षाभोवती फिरत असल्याने तिच्यावर केंद्रोत्सारी (केंद्रापासून दूर लोटणारी) प्रेरणा कार्य करीत असते हा कोपर्निकस यांचा सिद्धांत सतराव्या शतकात मान्यता पावल्यावर पृथ्वी पूर्णपणे गोलाकार आहे ही संकल्पना मागे पडली. तसेच पृथ्वी ध्रुवांपाशी चापट व विषुववृत्ताशी फुगीर असल्याचे सिद्ध झाले. अशा प्रकारे पृथ्वी लघु-अक्षीय विवृत्तज म्हणजे लघु-अक्षीय गोलाभ (विवृत्त-दीर्घवर्तुळ त्याच्या लघु-अक्षाभोवती फिरविल्यास निर्माण होणारे पृष्ठ) असल्याचे मानले जाऊ लागल्यावर तिचा परिघ काढण्याच्या पद्धतीमध्ये सुधारणा होऊ शकल्या.

डब्ल्यू. स्नेल (१५८०-१६२६) यांनी त्रिकोणीकरणाची पद्धती [⟶सर्वेक्षण] शोधून मापने घेण्याच्या पद्धतीत क्रांती घडवून आणली तर १६६९ साली झां पीकार यांनी अक्षांश निश्चित करण्यासाठी व त्रिकोणाचे कोन मोजण्यासाठी दूरदर्शकाचा (दुर्बिणीचा) वापर करण्यास सुरुवात केली. त्यांनी पृथ्वीची त्रिज्या सु. ६,४०३ किमी. एवढी काढली होती. १७९१ साली मीटर या एककाची लांबी ठरविण्याचे प्रयत्न करण्यात आले व त्यासाठी पृथ्वीचे आकारमान अचूकपणे ठरविणे आवश्यक झाले. अशा प्रकारे यानंतर उपकरणे व पद्धती यांची परिशुद्धता वाढत गेली आणि पृथ्वीचा आकार व आकारमान अधिक अचूकपणे ठरविता येऊ लागले.

  

इ. स. १९१९ मध्ये इंटरनॅशनल जिओडेटिक अँड जिओफिजीकल युनियनची स्थापना झाली व नंतर भूगणितीय अध्ययनाशी संबंधित इतरही संस्था स्थापन झाल्या. १९५७ साली पृथ्वीभोवती पहिला कृत्रिम उपग्रह सोडल्यावर पृथ्वीच्या आकाराविषयी अधिक अचूकपणे अभ्यास करणे शक्य झाले. कृत्रिम उपग्रहांच्या कक्षांच्या निरीक्षणांवरुन पृथ्वी काहीशी उलट्या पेरूच्या (किंवा नासपतीच्या) आकाराची म्हणजे उत्तर ध्रुवाशी काहीशी फुगीर व दक्षिण ध्रुवाशी किंचित खोलगट असल्याचे दिसून आले तसेच भूपृष्ठावरील पुष्कळ उंचवट्यांची व खोल भागांची नव्याने माहिती झाली. अवकाशयुग व आंतरखंडीय क्षेपणास्त्रे यांच्या उदयामुळे अधिक अचूकतेची गरज वाटू लागली आणि १९६०-७० या काळातील प्रगतीमुळे अशी अचूकता शोधणे बऱ्याच प्रमाणात शक्य झाले. यासाठी नवीन उपकरणे बनविण्यात आली, तसेच मिळालेल्या माहितीवर संगणकांद्वारे (गणकयंत्राद्वारे) संस्करण करण्यात येऊ लागल्याने कामाची गती वाढली. परिणामी या काळात पृथ्वीचा आकार, आकारमान व गुरुत्वीय क्षेत्र यांच्या माहितीत चांगलीच भर पडली. नंतरच्या काळातील माहितीच्या आधारे याबाबतीत अधिक सूक्ष्म माहिती मिळू लागली आहे.

  

पृथ्वीविषयक परिमाणे काढण्याचे आधीचे प्रयत्न : परिघ, व्यास, त्रिज्या, इ. पृथ्वीची परिमाणे काढण्याचे प्रयत्न पुष्कळांनी केले आहेत. पैकी एराटॉस्थीनीझ (इ. स. पू. २७६-१९४) यांच्या पृथ्वीची परिघ काढण्याचा प्रयोग महत्वाचा आहे. ॲरिस्टॉटल यांनी पृथ्वीचा व्यास ४ लाख स्टेडिया (या लांबीच्या एककाचे एकवचन स्टेडियम असे असून त्याचे मूल्य निरनिराळ्या प्रदेशांत भिन्नभिन्न असावे मात्र सर्वसाधारणपणे १ स्टेडीयम = १८५ मी. मानतात), तर आर्किमिडीज यांनी सु. १५,०३१ किमी. इतका काढला होता. पॉसिडोनिअस (इ. स. पू. सु. १३५-५०) यांनी काढलेला पृथ्वीचा व्यास प्रत्यक्षापेक्षा ११% जास्त आला होता व टॉलेमींनी पृथ्वीचा परिघ १.८ लाख स्टेडिया काढला होता. सिंजार पठारावर प्रयोग करून अब्दुल्ला अल मामून (७८६-८३३) व त्यांच्या सहकाऱ्यांनी काढलेला पृथ्वीचा व्यास प्रत्यक्षातल्यापेक्षा ३.६% जास्त होता तर झां फेर्नेल (१४९७-१५५८) यांनी काढलेला पृथ्वीचा व्यास प्रत्यक्ष व्यासापेक्षा फक्त १२८ किमी. जास्त होता.

  

पृथ्वीवरील दोन गावांची भूगोलावरील स्थाने निश्चित करता आली व त्यांच्यातील अंतर (चाप) किंवा त्यांनी पृथ्वीच्या मध्याशी केलेला कोन काढता आला, तर गणिताने पृथ्वीची विविध परिमाणे काढता येतील, अशी एराटॉस्थीनीझ यांची कल्पना होती. साईनी (आताचे आस्वान, ईजिप्त) येथे २१ जूनच्या सुमारास विष्टंभाच्या वेळी (सूर्य विषुववृत्ताच्या जास्तीत जास्त उत्तरेस असताना) जेव्हा सूर्य सरळ माथ्यावर आला, तेव्हा ॲलेक्झांड्रिया गावी पडलेले सूर्यकिरण उदग्र (उभ्या) दिशेशी ७०.२ इतका कोन करतात, असे त्यांना आढळले. सूर्यकिरण समांतर मानल्याने या दोन गावांनी पृथ्वीच्या मध्याशी केलेला कोन ७०.२ आला. पृथ्वी गोलाकार मानल्याने हा कोन म्हणजे वर्तुळाकार भूपृष्ठाचा ५० वा भाग आला. म्हणजे या दोन गावांमधील भूपृष्ठावर मोजलेल्या अंतराच्या (५,००० स्टेडिया) ५० पट (२.५ लाख स्टेडिया किंवा ३९,५२० किमी.) पृथ्वीचा परिघ आला व तो प्रत्यक्ष परिघाशी (३९,७७६ किमी.) पुष्कळ जुळणारा आहे.

[⟶एराटॉस्थीनीझ]. 

पृथ्वीचा चापटपणा : पृथ्वी ध्रुवांपाशी चापट आहे ही कल्पना स्वीकारली जाणे ही भूगणिताच्या इतिहासातील ठळक घटना आहे. पृथ्वीच्या विषुववृत्तीय (a) व ध्रुवीय (b) त्रिज्यांमधील फरक भागिले विषुववृत्तीय त्रिज्या अशी पृथ्वीच्या चापटपणाची व्याख्या करतात म्हणजे चापटपणा

= f =     a-b

                 a

पृथ्वीच्या चापटपणाचा अभ्यास विषुववृत्तीय फुगवट्याने उद्‌भवणाऱ्या परिणामांच्या आधारे केला जातो. त्यामुळे भूपृष्ठावरील मापने, चंद्राचे वेध, कृत्रिम उपग्रहांच्या गती व स्कायलॅब या अवकाशात सोडलेल्या वेधशाळेवरून केलेली निरीक्षणे यांच्या साहाय्याने हा चापटपणा ठरविण्यात आला आहे.

न्यूटन यांनी पृथ्वीच्या चापटपणाचे सैद्धांतिक मूल्य १/२३० एवढे काढले होते. या मूल्याची शहानिशा करण्यासाठी पृथ्वीच्या चापाची लांबी प्रत्यक्ष मोजण्याचे प्रयत्न सुरू झाले. याकरिता फ्रेंच ॲकॅडेमी ऑफ सायन्सेसने १७३० च्या सुमारास लॅपलँड व पेरू येथे मोहिमा पाठविल्या. लॅपलँडला गेलेल्या तुकडीने चापटपणाचे मूल्य १/१७६, तर पेरुला गेलेल्या तुकडीने ते १/१७९ ते १/२६६ यांच्या दरम्यान काढले. नंतर अधिकाधिक अचूक मूल्य मिळविण्याचे प्रयत्न झाले व मीटरची लांबी ठरविताना चापटपणा काढण्याच्या दृष्टीने अनेक मापने घेण्यात आली होती. १८६६ साली ब्रिटीश भूगणिती अलेक्झांडर क्लार्क यांना हे मूल्य १/२९४.१७२३०८३ एवढे, तर १९०९ साली अमेरिकेतील जे. एफ्. हेफर्ड यांना ते १/२९७.१ हे मूल्य अवकाशयगाच्या आधीचे सर्वोत्तम मूल्य होते. चंद्र, कृत्रिम उपग्रह वगैरेंच्या निरीक्षणांद्वारे चापटपणाचे मूल्य अधिक अचूकपणे ठरविता येऊ लागले असून हल्ली १/२९८.२५ हे चापटपणाचे मूल्य स्वीकारण्यात येते.

  

पृथ्वीचा आकार : पृथ्वीचा आकार व आकारमान काढणे हे भूगणिताचे एक कार्य असून असे करताना उदग्र दिशेतील परिणामांचाही विचार करतात. पृथ्वीवरील खंड व पर्वत लक्षात घेतल्यास पृथ्वीच्या आकाराची बाह्य रेखा वेडीवाकडी येते. म्हणून पृथ्वीची भूमितीय व इतर वैशिष्ट्ये दर्शविण्यासाठी पृथ्वीच्या आकाराला जवळचा असा नियमित आकार संदर्भ-आकृती म्हणून निवडावा लागतो आणि त्याच्या संदर्भात पृथ्वीची परिणामे (उदा., अंतरे, दिशा इ.) देतात. पृथ्वीच्या मोठ्या क्षेत्राचे सर्वेक्षण करून पुष्कळ ठिकाणचे अक्षांश-रेखांश ठरविण्यासाठी ताऱ्यांचे वेध घेतात. रूढ आकाराला अनुसरून मोजमापे गृहीत धरून काढलेल्या मूल्यांशी या वेधांची तुलना करतात आणि पडणाऱ्या फरकांचा क्रमवार विचार करुन अधिक चांगला (गोलाभ) निवडतात व स्थानिक बदल लक्षात घेऊन पृथ्वीचा आकार ठरवितात. अशा प्रकारे १९६० सालापर्यंत आकार ठरविताना खंडाएवढ्या क्षेत्राचा विचार केला जाई तद्नंतर एकूण पृथ्वीचा विचार करण्यात येऊ लागला. पृथ्वीचा आकार पेरुसारखा आहे, हे जॉन ओकीफ यांनी शोधून काढले व विषुववृत्त वर्तुळाकार नसल्याचे इम्रे इझाक यांनी सांगितले (१९६०). पृथ्वीच्या संदर्भात खालील तीन आकार विचारात घेतले जातात.

गोल : गोल ही सर्वांत साधी संदर्भ-आकृती आहे. द्रायुरूप (द्रव व वायुरूप) ग्रहाला केवळ गुरुत्वाकर्षणाचेच नियम लागू पडत असतील, तर त्याला गोलाकार प्राप्त होईल. पृथ्वी दर्शविणाऱ्या अशा गोलाची त्रिज्या ६३,७१,०२७ मी. येईल. असा गोल व प्रत्यक्ष भूपृष्ठ यांच्यात ३०० भागांत १ भाग एवढा फरक असेल व हा फरक बहुत करुन ध्रुवांजवळील चापटपणामुळे पडेल.

  

लघु-अक्षीय विवृत्तज : पृथ्वीचे द्रव्य पूर्णपणे दृढ नाही, भूकवचात वस्तुमानाची वाटणी विषमपणे झाली आहे. पृथ्वी स्वतःभोवती फिरत असते व पृथ्वीवर वेलीय (भरती-ओहोटीसदृश) प्रेरणा असतात. या गोष्टीमुळे पृथ्वीचा आकार गोल न होता तिला काहीसा लघु-अक्षीय विवृत्तज (नोंदीच्या यापुढील भागात याचा निर्देश ‘विवृत्तज’ असा संक्षेपाने केलेला आहे) म्हणजे लघु-अक्षीय गोलाभ आकार आला आहे. हा आकार प्रत्यक्ष पृथ्वीशी गोलापेक्षा अधिक जुळणारा आहे. विवृत्तजाचे पृष्ठ व भूपृष्ठाची सरासरी पातळी यांच्यामध्ये ७० हजार भागांत १ भाग एवढा फरक पडू शकतो. ही संदर्भ-आकृती गणितीय कृत्ये करण्यास सोयीची असून ती व प्रत्यक्ष आकार यांच्यातील फरक अल्प असल्याने दुरुस्ती सहजपणे करता येते. अर्थात गणितीय दृष्ट्या ही आकृतीही परिपूर्ण व आदर्श नाही. १९६७ साली इंटरनॅशनल ॲसोसिएशन ऑफ जिओडेसी या संघटनेने पृथ्वीच्या अशा संदर्भ-आकृतीची पुढील परिणामे मान्य केली होती : विषुववृत्तीय त्रिज्या (a)= ६,३७१.१६ किमी., ध्रुवीय त्रिज्या (b)= ६,३५६.७७४ किमी. व चापटपणा (f)= १/२९८.२४७१६७४.

भूरूप : पृथ्वीच्या वैशिष्ट्यांचे स्पष्टीकरण करणारा अधिक परिपूर्ण आकार म्हणजे भूरूप वा भू-आकार (जिऑइड) होय. भूगणितात भूरूप या संकल्पनेला मूलभूत महत्त्व आहे. ज्या पृष्ठाच्या संदर्भात गुरुत्वीय प्रेरणा व पृथ्वीचे अक्षीय परिभ्रमण ही पूर्णतया संतुलित झालेली असतात अथवा ज्या पृष्ठावर पृथ्वीचे गुरुत्वाकर्षण व अक्षीय परिभ्रमण यांच्यामुळे येणाऱ्या प्रवेगांमुळे उद्‌भवणारे एकत्रित वर्चस् (स्थितिज ऊर्जा) स्थिर असते त्या पृष्ठाला समवर्चसी पृष्ठ म्हणतात आणि असे जे पृष्ठ माध्य (सरासरी) समुद्रपातळीशी सर्वात चांगल्या प्रकारे जुळते त्या पृष्ठाला ‘भूरूप’ म्हणतात. महासागरांची सरासरी पातळी १ मी. पेक्षा जास्त बदलत नाही. त्यामुळे महासागर खंडांखालीही गेले आहेत (अथवा महासागर ते सर्व खंड असा सलग कालवा खोदला आहे), अशी कल्पना केल्यास व महासागर शांत आहेत असे मानल्यास त्यांच्या पातळीने येणारी पृथ्वीची आकृती म्हणजे भूरूप होय. भूरूपावरील कोणत्याही बिंदूशी असणारी गुरुत्वीय ओढ ही त्याला लंब दिशेत असते, हे भूरूपाचे वैशिष्ट्य आहे. पृथ्वीतील वस्तूमानाच्या विषम वाटणीनुसार भूरूपाचे पृष्ठ बदलते. प्रत्यक्षात पृथ्वीच्या वास्तव पृष्ठाशी सर्वांत चांगले जुळणारे विवृत्तज व भूरूप यांच्या पृष्ठांत १०० मी. पेक्षा जास्त फरक पडत नाही. त्यामुळे अशा विवृत्तजापासूनच्या भूरूपाच्या अंतरावरून भूरूपाची व्याख्या करतात. इंटरनॅशनल ॲस्ट्रॉनॉमिकल युनियन व इंटरनॅशनल युनियन फॉर जिओडेसी अँड जिओफिजिक्स या संघटनांनी स्वीकारलेली व कृत्रिम उपग्रहांद्वारे मिळालेल्या माहितीवरून काढलेली संदर्भ विवृत्तजाची परिमाणे अशी आहेत : विषुववृत्तीय त्रिज्या (a)= ६,३७८.१६५ किमी. व चापटपणा (f)= १/२९८.२५. या संदर्भ विवृत्तजापासूनच्या अरीय (त्रिज्यीय) अंतराने (N) भूरूपाचा आकार देण्याची प्रथा आहे. भूपृष्ठावर या अंतरामध्ये १०० मी. पेक्षा कमी फरक पडतो. हा फरक भूरूप व भूपृष्ठ यांच्यातील १० किमी. पर्यंतच्या फरकाच्या (H) मानाने अल्प आहे (आ.१).

  

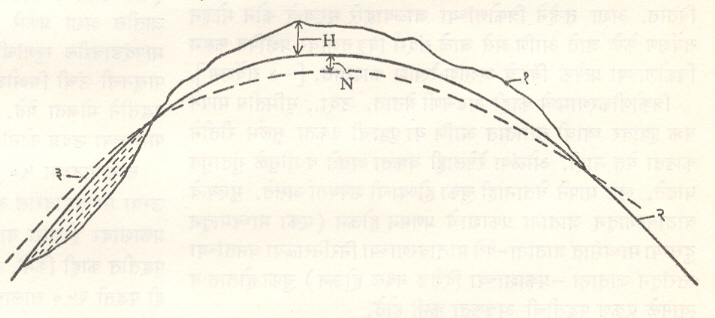आ. १. संदर्भ विवृत्तज, भुरूप व भूपृष्ठ यांच्यातील संबंध : (१) भूपृष्ठ, (२) भूरूप, (३) संदर्भ विवृत्तज N- भूरूप व संदर्भ विवृत्तज यांमधील फरक, H- भूरूप व भूपृष्ठ यांमधील फरक.पर्वत व महासागरांच्या द्रोणी यांच्या वेगवेगळ्या गुरुत्वाकर्षणामुळे भूरूप काहीसे वेगळे येते. ते आधार मानून जमीन व सागरतळ यांच्यावरील उंचवटे व खोलगट भाग यांचे सर्वेक्षण करतात आणि अशा तऱ्हेने भूरूपानुसार समोच्च रेषा नकाशे काढतात. मानचित्रणासाठी पृथ्वीच्या वा तिच्या कोणत्याही भागाच्या सर्वांत जवळचा असा गोलाभ हे भूरूप मानतात. 

  

कृत्रिम उपग्रहांच्या कक्षांच्या माहितीवरून असे दिसून आले आहे की, उत्तर ध्रुवाजवळील वक्रतेची त्रिज्या दक्षिण ध्रुवावरील वक्रतेच्या त्रिज्येपेक्षा सु. ३० मी. जास्त आहे. तसेच विषुववृत्त वर्तुळाकार नसून किंचित विवृत्ताकार आहे आणि त्याच्या वक्रता त्रिज्यांमधील फरक १५० मी. (पर्यंत) आहे.

भूरूप प्रत्यक्ष भूपृष्ठाशी थोड्याच ठिकाणी जुळते व भूरूपाशी जुळणारी मापने काढणे अवघड असते. म्हणून भूरूपाची कल्पना टाळावी असे काहींचे मत असून म्यिखाईल एस्. मोलोडेन्स्की हे त्यापैकी प्रमुख आहेत. त्यांनी एक सिद्धांत मांडला असून त्याच्या आधारे गुरुत्वाकर्षण मापनाच्या साहाय्याने नैसर्गिक भूपृष्ठाचा आकार सरळ मिळू शकतो.  

  

भूगणितीय निरीक्षण पद्धती : भूरूपाचा आकार, आकारमान तसेच पृथ्वीशी संबंधित इतर परिमाणे ठरविण्याच्या विविध पद्धती असून येथे त्यांचे वर्णन थोडक्यात दिले आहे.

क्षैतिज मापन : या पद्धतीतील सर्वेक्षणामध्ये अक्षांश, रेखांश इ. सहनिर्देशक निश्चित केले जातात. मोठ्या क्षेत्रांचे सर्वेक्षण करताना त्यांचे अनेक त्रिकोणांत विभाजन करणारी त्रिकोणीकरणाची पद्धती वापरतात. तिच्या आधारे दोन स्थानांतील अंतरे व दिशा काढतात. त्रिकोणाची किमान एक बाजू व दोन कोन माहीत असल्यास त्रिकोणमीतीय गणिताने उरलेल्या दोन बाजू व तिसरा कोनही काढता येतात [⟶→ त्रिकोणमिति], हे त्रिकोणीकरणाचे तत्त्व आहे. अशा प्रकारे त्रिकोणीकरणाने मोठ्या क्षेत्रांची लांबी ठरविता येते व त्यांचे सर्वेक्षण करता येते. डब्ल्यू. स्नेल यांनी १६१५ मध्ये प्रथम असे सर्वेक्षण अचूकपणे केले. झां पीकार यांनी पॅरिसचे माध्यान्हवृत्त काढण्यासाठी ही पद्धती वापरली होती. झाक कासीनी (१६७७–१७५६) यांनी हिच्यात सुधारणा केल्या.

  

त्रिकोणीकरणामध्ये सामान्यतः  एकमेकांपासून दिसणारी ३-४ किमी. अंतर असलेली दोन केंद्रे (स्थाने) निवडतात. त्यांचे अक्षांश व रेखांश ज्योतिषशास्त्रीय पद्धतीने काढतात (उदा., ⇨ खस्वस्तिक दूरदर्शकाने अक्षांश तर ⇨ याम्योत्तर संक्रमणमापकाने रेखांश काढतात). या दोन केंद्रातील अंतर म्हणजे आधार रेषा असून ते अतिशय अचूकपणे मोजतात. आधार रेषेशी तिसऱ्या केंद्राने केलेले कोन मोजून त्याचे स्थान ठरवितात आणि गणिताने या त्रिकोणाच्या उरलेल्या दोन बाजू (म्हणजे पहिल्या दोन केंद्रांची तिसऱ्यापासूनची अंतरे) काढतात. नंतर याच बाजू आधार रेषा मानून आणखी त्रिकोण सोडवितात. अशा तऱ्हेने त्रिकोणांच्या जाळ्यांद्वारे मुख्यत्वे कोन मोजून सर्वेक्षण केले जाते आणि असे जाळे संदर्भ विवृतजावर प्रक्षेपित करुन त्रिकोणाच्या प्रत्येक बिंदूचे अक्षांश-रेखांश काढतात. [⟶सर्वेक्षण].

त्रिकोणीकरणामध्ये काही अडचणी येतात. उदा., भूमितीय मापने वक्र पृष्ठावर घ्यावी लागतात आणि या पृष्ठाची वक्रता सुलभ रीतीने काढता येत नाही. ओळंबा रेषेलाही वक्रता असते व तीमुळे गुंतागुंत वाढते. खुद्द मापने घेतानाही चुका होण्याची शक्यता असते. मुख्यत्वे वातावरणातून जाताना प्रकाशाचे प्रणमन होऊन (एका माध्यमातून दुसऱ्या माध्यमात जाताना–येथे वातावरणाच्या निरनिराळ्या घनतांच्या स्तरांतून जाताना–प्रकाशाच्या दिशेत बदल होऊन) चुका होतात व त्यामुळे एकूण पद्धतीची अचूकता कमी होते.

  

त्रिकोणीकरणात पहिल्या आधार रेषेची लांबी मोजणे हेच तेवढे रेखीय मापन असते व ही लांबी अतिशय अचूकपणे मोजावी लागते. त्याकरिता अशी आधार रेषा बहुधा वाजवी सपाट अशा पृष्ठावर घेतात. अंतरे मोजण्यासाठी सतराव्या शतकात लाकडी दांडे, अठराव्या शतकात लोखंडी गज, एकोणिसाव्या शतकात विशिष्ट दंड (आइस्ड बार) व विसाव्या शतकाच्या प्रारंभी पोलादी वा इनव्हारची (लोखंड आणि निकेल यांच्या एका मिश्रधातूची) मोजफीत (टेप) वापरीत. मात्र यामुळे खर्च वाढतो व वेळही जास्त लागतो. आता अंतरे मोजण्यासाठी विद्युत् चुंबकीय तरंग (उदा., प्रकाश) वापरतात. ते लांब अंतरासाठी व उंचसखल प्रदेशासाठी उपयुक्त ठरले आहेत. इलेक्ट्रॉनीय अंतरमापक उपकरणांच्या साहाय्याने लांब अंतरे प्रकाशसेकंदात (एका सेकंदात प्रकाश जितके अंतर जातो–म्हणजे सु. ३ लक्ष किमी.–त्या अंतराच्या एककात) काढतात. मात्र प्रकाशावर वातावरणाचा परिणाम होत असल्याने त्यात काही दुरुस्त्या करून घ्याव्या लागतात. या उपकरणांनी काढलेल्या १५ किमी. अंतरात केवळ २ सेंमी. पर्यंत चूक असू शकते. ⇨ लेसरच्या साहाय्याने ४० किमी. पर्यंतचे अंतर धुक्यातही मोजता येते, तर सूक्ष्मतरंगाद्वारे पावसात व छोटे अडथळे असणाऱ्या भागातीलही ७० किमी. पर्यंतचे अंतर मोजता येते आणि या मापनाची अचूकता ५० किमी. अंतरात १५ सेंमी. पर्यंत असते. विमानातील उपकरणांद्वारे तर कित्येकशे किमी. पर्यंतचे अंतर मोजता येते.

आडवा व उभा कोन मोजण्यासाठी अचूक व सूक्ष्मग्राही थिओडोलाईट हे उपकरण वापरतात. टाळता न येणाऱ्या चुका कमी करण्यासाठी एकाच कोनाची अनेक मापने घेऊन त्यांचे माध्य मूल्य घेतात. 

  

अंतरे अतिशय अचूकपणे मोजण्याच्या इलेक्ट्रॉनीय व लेसर पद्धतींचा विकास झाल्याने त्रिकोणीकरणाच्या जागी हळूहळू त्रिपार्श्वन व वेढा पद्धती प्रचारात येत आहेत [⟶सर्वेक्षण]. त्रिपार्श्वन पद्धतीत ज्यांच्या सर्व बाजू इलेक्ट्रॉनीय अंतरमापकांनी मोजलेल्या आहेत अशा त्रिकोणांचे अध्यारोपण करतात. वेढा पद्धतीत लागोपाठच्या दोन बिंदूतील अंतर व या प्रत्येक बिंदूशी आधीच्या व नंतरच्या बिंदूनी होणारे कोन मोजून त्यांची सापेक्ष स्थाने ठरवितात. १९४६ साली यर्जो व्हायसाला यांनी त्रिमितीय त्रिकोणीकरणाचे तंत्र सुचविले होते. त्यासंबंधात अमेरिकेने १९६० नंतर एको-१, एको-२, पॅजिऑस हे उपग्रह सोडले होते. प्रगत गणितीय पद्धती व संगणकाचा वापर यांमुळे कामाची गती, कार्यक्षमता व अचूकता वाढली आहे.

मर्यादित क्षेत्रातील समुद्रतळाचे अंतर काढण्यासाठीही ही पद्धती वापरतात. जहाजाच्या स्थानाची निश्चिती दुसऱ्या पद्धतीने करतात व जहाजापासूनचे तळाचे अंतर ध्वनिमापक उपकरणांनी काढतात. 

  

उदग्र मापन : उभ्या दिशेतील अंतर मोजण्यासाठी प्रमाणभूत पद्धती म्हणजे संतलन होय. या पद्धतीत काळजीपूर्वक संतलित केलेल्या (सर्व उदग्र व क्षैतिज कोन खऱ्या उदग्र व क्षैतिज प्रतलांत मोजले जातील अशा प्रकारे जुळवणी केलेल्या) दूरदर्शकाच्या साहाय्याने मापदंडावरील खुणांची मापने घेतली जातात. माध्य समुद्रपातळीपासूनची उंची थिओडोलाइटापेक्षा संतलन उपकरणाने अधिक अचूक पद्धतीने मोजता येते. याकरिता उन्नतांशांमधील (बिंदूच्या क्षितिजापासूनच्या उदग्र कोनांमधील) फरक काढतात. 

  

लागोपाठच्या ५० ते १०० मी. अंतरावर उंचीत पडणारा फरक उभ्या मापदंडावरील आडव्या रेषा पाहून पुनःपुन्हा मोजतात. त्यामुळे प्रकाशावर होणारा वातावरणाचा परिणाम किमान करता येतो. या पद्धतीत काही किमी. अंतरामागे थोडे मिमी. इतकी चूक होऊ शकते. ही पद्धती २५० सालाच्या सुमारास ॲलेक्झांड्रियाचे हीरो यांनी शोधून काढली असून तिच्यात नंतर थोड्याच सुधारणा करण्यात आल्या व ती अजूनही वापरात आहे. उंचसखल प्रदेशाच्या सर्वेक्षणासाठी त्रिकोणमितीय संतलन पद्धती वापरावीच लागते.  

  

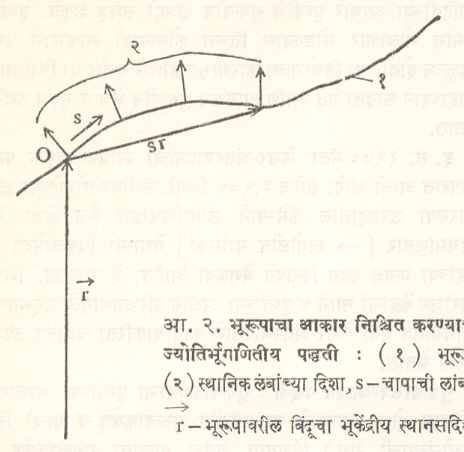
ज्योतिर्भूगणितीय पद्धती : भूरुप निश्चित करण्यासाठी दीर्घकाळ ही एकमेव पद्धती वापरात होती. हिच्यात समवर्चसी पृष्ठावरील लंब (स्थानिक उदग्र दिशा) व भूपृष्ठाच्या भागाची (चापाची) लांबी मोजतात. तसेच भूपृष्ठावरील बिंदूचा गुरुत्वाकर्षण सदिश (गुरुत्वाकर्षणाची महत्ता व दिशा दर्शविणारी रेषा) व उत्तर ध्रुव यांच्या दिशाही काढतात. ज्याचा स्थानसदिश (संदर्भबिंदूपासूनचे–येथे भूकेंद्रापासूनचे–अंतर व दिशा दर्शविणारी रेषा) माहीत आहे अशा बिंदूपासून (उदा., आ.२ मधील O बिंदूपासून) सुरू झालेल्या व परस्परांशी निगडीत अशा बिंदूच्या मालिकेविषयी वरील प्रकारची माहिती मिळाल्यास आ. २ मध्ये दाखविल्याप्रमाणे भूरूप काढता येऊ शकते. या पद्धतीत लंबांच्या दिशा ज्योतिषशास्त्रीय वेधांच्या साहाय्याने ठरवितात. त्यामुळे त्या दिशा पृथ्वीच्या ध्रुवाच्या माध्य दिशेच्या आणि ग्रिनिच रेखांशाच्या संदर्भात देण्यात येतात. वातावरणातील प्रकाशाच्या अनियमित प्रणमनामुळे उद्‌भवणाऱ्या चुका कमीत कमी करण्यासाठी अनेक ताऱ्यांचे अचूक वेध घेण्यात येतात.

आ.२. भूरूपाचा आकार निश्चित करण्याची ज्योतिर्भूगणीतीय पद्धती : (१) भूरूप, (२) स्थानिक लंबाच्या दिशा, s-चपाची लांबी, ⟶ r –भूरुपावरील बंदूचा भूकेंद्रीय स्थानसदिशअलाकडेपर्यंत चापांची लांबी त्रिकोणीकरणाने ठरवीत असत. १९५० नंतर जिओडीमीटर, टेल्यूरोमीटर ही उपकरणे वापरात आल्यामुळे लांब अंतरे थोडक्या काळात मोजता येऊ लागली. परिणामी त्रिकोणाच्या कोनांऐवजी बाजू मोजून अधिक अचूक माहिती मिळू लागली आहे. दोन बिंदूमधील अंतर कापण्यास प्रकाशाला लागणारा वेळ जिओडीमीटरद्वारे मोजतात तर टेल्यूरोमीटरमध्ये सूक्ष्मतरंग (१० सेंमी. तरंगलांबीचे रडार तरंग) वापरतात. ५० किमी. पर्यंतच्या अंतराच्या बाबतीत या उपकरणांची अचूकता १ लाख भागात १ भाग एवढी असते. शिवाय दोन व्यक्ती टेल्यूरोमीटरने सु. ६५ किमी. अंतर केवळ अर्ध्या तासात मोजू शकतात व या उपकरणांनी दिवसा, रात्री वा धुक्यातही मापने घेता येतात. जमिनीवरील मापनांसाठीच ज्योतिर्भूगणितीय पद्धती वापरतात. उत्तर अमेरिका, यूरोप, ऑस्ट्रेलिया व भारत यांच्यासारख्या चांगले भूगणितीय सर्वेक्षण झालेल्या अनेक प्रदेशांत ही पद्धती वापरण्यात आलेली आहे. तथापी या पद्धतीची अचूकता मर्यादित आहे, असे आढळून आले आहे.

आ. ३. कृत्रिम उपग्रहाच्या एकाच वेळी घेतलेल्या वेधांद्वारे सर्वेक्षण जाळ्यांची जोडणी करण्याची पद्धती : (१) तारा, (२) कृत्रिम उपग्रह.

भूकेंद्रीय सहनिर्देशकांची पद्धती : या पद्धतीत कृत्रिम उपग्रह, अवकाशीय अन्वेषक यान (दूर अवकाशात प्रक्षेपित केलेले व संशोधनास उपयुक्त असे वेध घेणाऱ्या उपकरणांनी युक्त असलेले यान) किंवा चंद्र यांच्या वेधांचा वापर करून भूपृष्ठावरील अनेक स्थानांचे भूकेंद्रीय (पृथ्वीच्या केंद्राच्या संदर्भात निश्चित केलेले) सहनिर्देशक प्रत्यक्ष मोजतात. हे काम दोन प्रकारे करता येते. पहिल्या प्रकारात वेध्य वस्तू (उदा., कृत्रिम उपग्रह) अवकाशातील स्वेच्छ बिंदू मानून एकाच वेळी तिचे विविध केंद्रावरून वेध घेण्यात येतात. दुसऱ्या प्रकारात या वस्तूंच्या कक्षासंबंधीच्या माहितीचा उपयोग करतात. पहिल्या प्रकारात पृथ्वीवरील बिंदूची सापेक्ष स्थाने मिळतात, तर दुसऱ्या प्रकाराने त्यांची निरपेक्ष स्थाने ठरविता येतात.

  

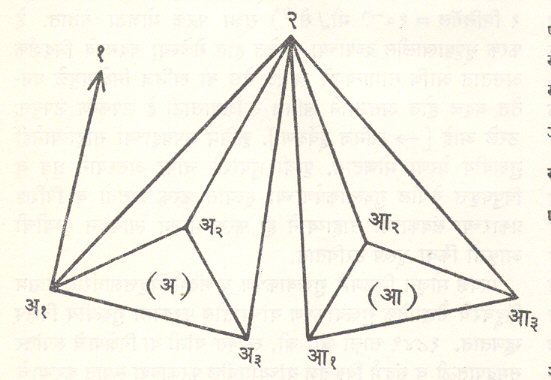
पहिल्या प्रकाराचे तत्त्व आ. ३ मध्ये दाखविले आहे. अ आणि आ ही त्रिकोणीकरणाची जाळी असून त्यांमध्ये अ१, अ२, अ३ आणि आ१, आ२, आ३ हे त्याच क्रमाने येणारे बिंदू मानले आहेत. अ जाळ्यापासून कृत्रिम उपग्रहाच्या निरपेक्ष दिशा, तसेच अ चे भूकेंद्रीय सहनिर्देशक माहीत असल्यास भूकेंद्रीय सहनिर्देशकांनी या उपग्रहाचे स्थान ठरविणे शक्य होते. नंतर आ जाळ्यापासून उपग्रहाच्या साहाय्याने वेध घेतल्यास अ च्या सहनिर्देशक प्रणालीमध्ये आ चे स्थान मिळते. एकाच वेळी घेतलेल्या वेधांचा एक संच अ च्या संदर्भातील आ ची स्थिती ठरविण्यास तत्त्वत: पुरेसा असतो. जर उपग्रहाची दोनापेक्षा जास्त स्थाने माहीत झाली, तर वरीलसारख्या केंद्राच्या जोड्यांची सापेक्ष स्थाने शोधून काढणे शक्य होते.

आ.४. कृत्रिम उपग्रहाच्या कक्षेतील लागोपाठच्या स्थिती : ⟶ r -निरीक्षण केंद्रचा भूकेंद्रीय स्थानसदिश ⟶ ⟶ s1, s2 –वेगवेगळ्या दोन वेळी असलेले उपग्रहाचे भूकेंद्रीय स्थानसदिश ⟶ ⟶ k1, k2 निरीक्षण केंद्रापासूनचे उपग्रहाचे एकक सदिश.

कृत्रिम उपग्रहांच्या वेधांच्या बाबतीत सलगता राहील अशा तऱ्हेने भूपृष्ठावरील केंद्रांची वाटणी केल्यास भूकेंद्रीय सहनिर्देशकांच्या संदर्भातील सापेक्ष स्थाननिश्चिती पूर्णतः करता येऊ शकेल आणि त्यामुळे गणिताने भूरूपाचा तंतोतंत आकार काढता येईल. स्मिथसोनियन ॲस्ट्रोफिजिकल ऑब्झर्व्हेटरीने या पद्धतीचा सर्वांधिक विस्तृत विकास केला असून त्यासाठी जगभर ५० केंद्रे उभारली आहेत. 

  

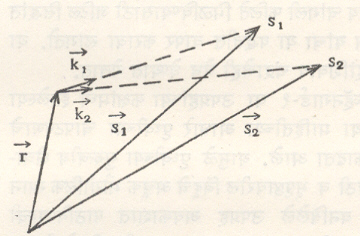
कृत्रिम उपग्रहाच्या कक्षेसंबंधीच्या माहितीचा उपयोग करणाऱ्या पद्धतीचे तत्त्व आ. ४ मध्ये विशद केले आहे. तीमध्ये हा ज्याचे स्थान निश्चित करावयाचे आहे त्या बिंदूचा (निरीक्षण केंद्राचा) स्थानसदिश आहे. s1 व  s2ही वेगवेगळ्या दोन वेळी असलेली उपग्रहाची स्थाने आणि 

व हे त्याचे त्या वेळचे भूकेंद्रीय स्थानसदिश आहेत.

व  हे निरीक्षण केंद्रापासून उपग्रहाच्या दिशेतील एकक सदिश आहेत. r हा सदिश पुढील सूत्राने मिळतो.

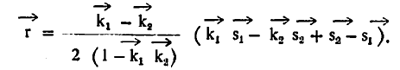
भूरूपाचा आकार ठरविण्याचा सर्वांत सरळ मार्ग म्हणजे ही पद्धती असून या पद्धतीत उपगहांचे (अथवा अन्वेषक यानांचे) ५ मी. पर्यंत अचूकतेचे वेध घ्यावे लागतात. ते घेण्यात बराच वेळ जातो व थोड्याच महत्त्वाच्या केंद्रांमधून ते सध्या घेता येतात. तथापि माणकाच्या स्फटिकाचा उपयोग करणाऱ्या आणि अतिशय अरुंद व तीव्र तांबड्या प्रकाशाची शलाका निर्माण करणाऱ्या लेसरांचा विकास झाल्याने त्यांच्या साहाय्याने कृत्रिम उपग्रहांचे पृथ्वीपासूनचे अंतर १ मी. इतक्या अचूकतेने मोजता येते. 

  

कृत्रिम उपग्रहांचे मार्ग-निरीक्षण : भूगणिताला हे एक खात्रीशीर तंत्र लाभलेले आहे. त्यामुळे पृथ्वीच्या आकाराविषयीची मोजमापे चांगल्या प्रकारे घेता येऊ लागली आहेत. गुरूत्वाकर्षण व अक्षीय परिभ्रमण यांच्या एकत्रित वर्चसाचे मिळणारे समवर्चसी पृष्ठ म्हणजे भूरूप या वस्तूस्थितीचा उपयोग भूरूपाचा आकार ठरविण्यासाठी होऊ शकतो. पृथ्वीलगतच्या सर्व अवकाशातील एकत्रित वर्चसाची मूल्ये माहीत असल्यास दिलेल्या वर्चसाच्या मूल्याचा बिंदूपथ काढणे शक्य असते. कृत्रिम उपग्रहांच्या कक्षांच्या वेधांवरून पृथ्वीलगतच्या गुरूत्वाकर्षणाचे वर्चस् मिळते व त्यावरून भूरूपाचा आकार निश्चित करणे शक्य असते. या पद्धतीने भूरूपाच्या सर्वसाधारण वैशिष्ट्यांचेच निरीक्षण करता येते म्हणजे त्याचा सूक्ष्म तपशील मिळू शकत नाही. कारण ज्या उंचीवर उपग्रह फिरत असतात त्या उंचीवर पृथ्वीच्या द्रव्याच्या जलदपणे बदलणाऱ्या घनतेमुळे होणारे परिणाम सौम्य होऊन त्यांच्यातील तफावत विशेष राहत नाही. परिणामी भूरूपाच्या आकाराची केवळ स्थूल रूपरेषा मिळते. शिवाय चांगली फलिते मिळविण्यासाठी जटिल सिद्धांत व पुष्कळ प्रकारचे वेध यांचा या पद्धतीत वापर करावा लागतो. या पद्धतीत कृत्रिम उपग्रहांशिवाय चंद्राचेही वेध घेण्यात येतात. 

  

एक्स्फ्लोअरर-१ व व्हॅनगार्ड-१ या उपग्रहांच्या कक्षांमध्ये झालेल्या बदलांवरून मिळालेल्या माहितीच्या आधारे पृथ्वीच्या चापटपणाचे अधिक अचूक मूल्य काढता आले. यामुळे पृथ्वीच्या गुरूत्वीय क्षेत्रातील बदल मोजण्यासाठी व भूपृष्ठावरील बिंदूचे अचूक भौगोलिक स्थान ठरविण्यासाठी खास बनविलेले उपग्रह अवकाशात पाठविण्याची योजना मार्गी लागली. कृत्रिम उपग्रह हा अवकाशातील त्रिकोणीकरण बिंदू (केंद्र) असून पृथ्वीवरील स्थिर केंद्रावरून त्याची दिशा, कक्षा व गती ठरवितात. पृथ्वीच्या वस्तुमान केंद्राच्या संदर्भातील निरीक्षण केंद्राच्या स्थानाची चूक, तसेच पृथ्वीच्या गुरूत्वाकर्षणामुळे उपग्रहाच्या कक्षेत होणारे विक्षोभ यांचा या वेधांवर परिणाम होतो. कारण गुरूत्वीय विक्षेपांचा (आढळलेले गुरुत्वाकर्षण व सैद्धांतिक वा अपेक्षिलेले गुरुत्वाकर्षण यांच्यातील फरकाचा) उपग्रहांच्या गतीवर पुष्कळ परिणाम होतो. उदा., पृथ्वीच्या चापटपणामुळे उपग्रहांच्या कक्षेचे प्रतल (पातळी) ध्रुवीय अक्षाबोवती दररोज काही अंशानी फिरते. प्रणमनाचा परिणाम किमान करण्यासाठी स्थिर ताऱयांच्या पार्श्वभूमीवर उपग्रहांची छायाचित्रे घेतात. उपग्रहाची फिरण्याची गती सेकंदाला ८ किमी. असल्याने भूपृष्ठावरील अनेक केंद्रावरून त्याची एकाच वेळेला छायाचित्रे घेतात. परिणामी भूपृष्ठावरील बिंदूंच्या स्थानांची तुलना अचूकपणे करता येते. एको व पॅजिऑस यांच्यासारखे काही भूगणितीय उपग्रह परावर्तित सूर्यप्रकाशाने चकाकतात, तर काहींवर ठराविक कालावधीने उघड-मीट होणारे अतिप्रखर दिवे असतात.

विषुववृत्त किंचित विवृत्ताकार असावे असे या पद्धतीने दिसून आले आहे. या पद्धतीने पृथ्वीच्या विवृत्तजाची त्रिज्या व चापटपणा १० लाख भागांत १ भाग इतक्या अचूकतेने तर जमिनीवरील केंद्राचे पृथ्वीच्या गुरुत्वमध्याच्या संदर्भातील स्थान १० मी. इतक्या अचूकतेने ठरविता येते. शिवाय भूरूपाचा नकाशा पुरेसा तपशीलवारपणे बनविणे शक्य होते. या पद्धतीचे इतर काही फायदे असे आहेत : अगदी दूरच्या केंद्रावरून उपग्रहाचे वेध घेता येतात व इतक्या उंचीवरील विरळ वातावरणात प्रकाशाचे प्रणमन अत्यल्प होते. या पद्धतीत कोणतेही संदर्भ विवृत्तज वापरावे लागत नाही वा उदग्र दिशेपासून होणाऱ्या विचलनाची भीती नसते. उपग्रह त्रिकोणीकरणाने केवळ सापेक्ष स्थाने कळतात मात्र उपग्रहांच्या कक्षांच्या माहितीवरून भूपृष्ठावरील केंद्राचे निरपेक्ष भूमितीय सहनिर्देशक काढता येऊ शकतात. उपग्रहासंबंधीच्या माहितीच्या आधारे पृथ्वीचे गुरुत्वीय क्षेत्रही समजू शकते. पृथ्वीचा समांग गोलाकार सोडल्यास तिच्या कोणत्याही आकाराने उपग्रह विक्षुब्ध होतो. या विक्षोभाला कारणीभूत होणारे वर्चस् या विक्षोभाच्या साहाय्याने काढता येते आणि त्यावरून गुरुत्वीय क्षेत्र व भूरूप ठरविता येतात.

इ. स. १९७० नंतर लेसर-अंतरमापनाची अधिक अचूक पद्धती वापरात आली आहे. तसेच ३,५०० किमी. उंचीवर सोडलेल्या फुग्यासारख्या उपग्रहातील कॅमेऱ्याने छायाचित्रांद्वारे वेध घेऊन केप्लर नियमांनुसार [⟶खगोलीय यामिकी] येणाऱ्या विवृत्तापेक्षा उपग्रहांच्या प्रत्यक्ष कक्षा कितपत वेगळ्या आहेत, हे पाहतात. शिवाय निरीक्षण केंद्राची स्थाने व पृथ्वीच्या अक्षीय परिभ्रमणामुळे उद्‌भवणारी अनियमित गती लेसर-अंतरमापनाने काढण्याकरिता चंद्राचा उपयोग करून घेतात.

गुरूत्वाकर्षणमापन पद्धती : गुरूत्वाकर्षणाचा पृथ्वीच्या आकारावर परिणाम होत असल्याने या पद्धतीत गुरुत्वाकर्षण व त्याची दिशा (ओळंब्याची रेषा) मोजतात. तसेच भूपृष्ठावर गुरुत्वाकर्षण कसे बदलत जाते, याचेही सर्वेक्षण करतात. जमिनीवरील व समुद्रावरील अशा गुरुत्वाकर्षणमापनांचा उपयोग पृथ्वीचा आकार आणि संदर्भ विवृत्तजाचा चापटपणा काढण्यासाठी होतो. गुरुत्वाकर्षणाचे निरपेक्ष मापन करणे अतिशय अवघड असून थोड्याच ठिकाणी ते केले आहे. लंबकाची आंदोलने किंवा निर्वातामध्ये वस्तू पडण्यास लागणारा वेळ मोजून अशी मापने घेतात. गुरुत्वाकर्षणाचे सापेक्ष मापन सहजपणे करता येते व विसाव्या शतकात कित्येक देशांतील केंद्रात गुरुत्वाकर्षण मापने घेण्यात आलेली आहेत. दुसऱ्या महायुध्दानंतर गुरूत्वाकर्षणमापक हे उपकरण उपलब्ध झाल्यावर गुरूत्वाकर्षण मापनाचे क्षेत्र विस्तृत झाले. अशी उपकरणे प्रथम खनिज तेलाच्या पूर्वेक्षणासाठी बनविण्यात आली होती. ती हलकी, वापरावयास सोपी व अतिशयअचूक आहेत. समुद्रावर वापरावयाचे लंबक व गुरुत्वाकर्षणमापके, तसेच जहाजात व विमानात वापरता येतील अशी उपकरणेही बनविण्यात आली आहेत. वाहनातील उपकरणाने मोजलेल्या गुरुत्वाकर्षणात फरक येतात म्हणून अशा वेळी प्रगत ⇨ प्रवेगमापकांचा उपयोग करतात.

स्प्रिंगेला लावलेल्या वजनावरील गुरुत्वीय प्रेरणेच्या प्रमाणात तिची लांबी वाढते या तत्त्वानुसार गुरुत्वाकर्षणमापकाचे कार्य चालते. या उपकरणाने ०.०१ मिलिगॅलपर्यंतचे (मिलिगॅल हे प्रवेगाचे एकक असून १ मिलिगॅल = १०-५ मी./से.२) सूक्ष्म फरक मोजता येतात. हे फरक भूपृष्ठाखालील द्रव्याच्या घनतेत होत गेलेल्या बदलाचे निदर्शक असतात आणि सामान्यपणे खनिज तेल वा खनिज निक्षेपामुळे घनतेत बदल होत असल्याने खनिज सर्वेक्षणासाठी हे उपकरण उपयुक्त ठरले आहे [⟶खनिज पूर्वेक्षण]. कृत्रिम उपगहाच्या साहाय्यानेही गुरूत्वीय प्रेरणा मोजतात. पृथ्वी ध्रुवांशी चापट असल्याने ध्रुव व विषुववृत्त येथील गुरुत्वाकर्षणाच्या मूल्यांत फरक असतो व विशिष्ट प्रकारच्या लंबकाच्या साहाय्याने हा फरक मोजून त्यावरून पृथ्वीची आकृती किंवा भूरूप ठरवितात.

प्रत्यक्ष मोजून मिळणारे गुरुत्वाकर्षण व संदर्भ विवृत्तजावरील तत्सम बिंदूवरचे सैद्धांतिक गुरुत्वाकर्षण यांच्यातील फरकाला गुरुत्वीय विक्षेप म्हणतात. १८४९ साली जी. जी. स्टोक्स यांनी या विक्षेपाचे रूपांतर समुद्रपातळी व संदर्भ विवृत्तज यांच्यामधील फरकाच्या रूपात करण्याचे ‘स्टोक्स सूत्र’ तयार केले. त्याच्या साहाय्याने समुद्रपातळीने येणाऱ्या पृष्ठाचा आकार काढता येतो. ज्याच्या प्रत्येक बिंदूवरील स्थितिज ऊर्जा एकच असते त्या पृष्ठाला समवर्चसी पृष्ठ म्हणतात. अशा पृष्ठाला अनुसरून कोणताही गुरुत्वाकर्षण घटक कार्य करीत नसतो. म्हणजे तेथे ओळंबा रेषा पृष्ठाला काटकोनात असते. या समवर्चसी पृष्ठावरील गुरुत्वाकर्षणाचे मूल्य व त्या पृष्ठाचा आकार ही एकमेकांशी निगडीत असतात. त्यामुळे अनेक केंद्रावरील गुरुत्वाकर्षणाचे मूल्य काढल्यास त्यांच्या साहाय्याने समवर्चसी पृष्ठाचा आकार ठरविता येऊ शकेल. तसेच बऱ्याच क्षेत्राचे गुरुत्वाकर्षण मापन झालेले असेल, तर संदर्भ विवृत्तजापासूनचे भूरूपाचे अंतर काढता येते किंवा या दोन आकारांची तुलना करता येते. जमिनीच्या विस्तृत भागाचे गुरुत्वीय सर्वेक्षण झालेले असून गुरुत्वाकर्षणाची ०.५ मिलिगॅल इतक्या अचुकतेपर्यंतची मूल्ये मिळाली आहेत. तथापी समुद्रावरील गुरुत्वाकर्षण मापनात ५ ते १० मिलिगॅलपर्यंतच अचूकता येऊ शकते (शिवाय ही निरीक्षण केंद्रे पृथ्वीच्या भागावर अनियमितपणे वाटली गेलेली असल्यानेही अडचणी येतात). या मर्यादांमुळे गुरुत्वाकर्षण मापनाच्या आधारे गणिताने भूरूप काढण्याचे काम पृथ्वीच्या काही भागांपुरतेच झाले आहे. म्हणजे एकूण भूरूपाचा आकार निश्चित करण्याच्या दृष्टीने ही पद्धती उपयुक्त नाही निश्चित करण्याच्या दृष्टीने ही पद्धती उपयुक्त नाही परंतु कृत्रिम उपग्रहांद्वारे मिळालेल्या माहितीच्या संदर्भात एखाद्या स्थानिक क्षेत्राची अधिक तपशीलवारपणे माहिती देण्याकरिता ही पद्धती पूरक ठरू शकते.

भूपृष्ठावरील चंद्र-सूर्याच्या वेलीय परिणामाची (भरती-ओहोटी सदृश होणाऱ्या परिणामाची) तसेच भूरूपाकरिता समुद्राची माध्यपातळी आधारभूत धरीत असल्याने महासागरांच्या भरती-ओहोटीची माहीती भूरूप निश्चित करण्यासाठी आवश्यक असते. यामुळे पृथ्वीचे गुरुत्वीय क्षेत्र, त्याचा भूरूपाच्या आकारावरील परिणाम आणि चंद्र-सूर्याचा पृथ्वीवरील वेलीय परिणाम यांचा अभ्यास भूगणितात केला जातो. गुरुत्वाकर्षणात चांद्र वेलांमुळे ०.१६८ मिलिगॅल तर सौरवेलांमुळे ०.०७५ मिलिगॅलपर्यंत बदल होतात. चांद्र परिणामामुळे भूरूपात कमाल उंचवटा ३६ सेंमी. व कमाल खोलवटा १८ सेंमी. पर्यंत येऊ शकतो तर एकूण सौर परिणामामुळे भूरूपात २५ सेंमी. पर्यंत फरक पडतो. चंद्र-सूर्यामुळे पडणारा एकत्रित फरक अमावस्येला व पोर्णिमेला ७९ सेंमी. असू शकतो.

भूपृष्ठावरील उंच भागांखाली द्रव्याची घनता अपेक्षेपेक्षा कमी तर खोलगट भागाच्या खालील द्रव्याची घनता अपेक्षेपेक्षा जास्त असल्याचे आढळते. म्हणजे भूपृष्ठावर दिसणाऱ्या अनियमितपणाची (उंचसखलपणाची) भरपाई खालील द्रव्याने झालेली आढळते. अशा स्थितीला ⇨ समस्थायित्व म्हणतात. गुरुत्वीय विक्षेपावरून पृथ्वीचे वस्तुमान कोणत्या भागात कमी वा जास्त आहे ते समजते व त्यावरुन समस्थायित्वीय समतोल किती प्रमाणात प्रस्थापित झालेला आहे, त कळते. अशा तऱ्हेने समस्थायित्व या कल्पनेचा पूर्वी भूगणितीय अध्ययनात उपयोग होई. आता कृत्रिम उपग्रहांच्या साहाय्याने सरळ भूरूप ठरविता येऊ लागल्याने समस्थायित्वाचे भूगणितातील महत्त्व कमी झाले आहे. [⟶समस्थायित्व]. 

भूरूपाविषयी निष्कर्ष व पृथ्वीचे प्रचल : (दिलेल्या अटींच्या संचानुसार स्थिर मूल्य धारण करणाऱ्या व अटी बदलल्यास हे मूल्य बदलणे शक्य असलेल्या भौतिक राशीला प्रचल म्हणतात). वरील सर्व पद्धतींद्वारे मिळालेल्या माहितीचे एकत्रीकरण करुन तिच्या साहाय्याने भूरूपाचा सर्वोत्कृष्ट आकार ठरविता येईल. या दृष्टीने ई. एम्. गापशिकीन व के. लॅमबेक यांनी १९७० साली प्रयत्न केले होते. त्यांनी कृत्रिम उपग्रह व अवकाशीय अन्वेषक याने यांद्वारे मिळालेले भूकेंद्रीय सहनिर्देशक व गतिकीय गुरुत्वाकर्षणाची माहिती यांचा एकत्रितपणे वापर करुन भूरूपाचा नकाशा तयार केला. त्यावरुन हे भूरूप व त्याच्याशी सर्वाधिक जुळणारे विवृत्तज यांच्यात सु. +८१ मी. ते -११३ मी. इतका फरक पडल्याचे आढळले. पृथ्वीच्या त्रिज्येशी तुलना केल्यास हा फरक १० लाख भागांत ३० भाग एवढा आहे. विषुववृत्ताच्या संदर्भात हे भूरूप असममित असून ते उत्तर ध्रुवापाशी २० मी. वर तर दक्षिण ध्रुवालगत तितकेच खाली गेलेले आढळते. भूरूपात रेखांशानुसार पद्धतशीर बदल होत गेल्याचेही आढळले. या भूरूपाचा सर्वांत उंच भाग + १४० पूर्व व – १० पूर्व रेखांशांदरम्यान तर सर्वांत खोलगट भाग + ८० पूर्व व – १२० पूर्व रेखांशांच्या क्षेत्रात येतो. या भूरूपाचे उंच भाग ऑस्ट्रेलियाच्या उत्तरेस (+ ८१ मी.), यूरोपच्या वायव्य भागात (+ ६० मी.) व मॅलॅगॅसीच्या (मादागास्करच्या) दक्षिणेस (+ ५५ मी.) येतात आणि याचे खोल भाग भारताच्या दक्षिण टोकास (-११० मी.) , पॅसिफिक महासागराच्या अगदी दक्षिणेकडील भागात (- ६० मी.) व वेस्ट इंडीजलगतच्या भागात (- ५० मी.) येतात.

  

भूगणितीय माहितीच्या आधारे काढलेली पृथ्वीसंबंधीच्या परिणामांची व प्रचलांची मूल्ये भूरूप अनियमित असल्याने आसन्नीकरण (अचूक मूल्याच्या पुरेसे जवळचे मूल्य काढण्याची क्रिया) करुन देण्यात येतात. अक्षांश, पृथ्वीचा स्वतःभोवती फिरण्याचा वेग, भूकवचाची विशेषतः  आडव्या दिशेत होणारी हालचाल व भूवेला या राशीमध्ये कालपरत्वे बदल होऊन पृथ्वीच्या परिणामांची मूल्ये बदलतात (यामुळे भूगणितात या राशींचे मापन केले जाते). म्हणून या मूल्यांचे मानकीकरण (प्रमाणभूत मूल्ये मिळविण्याची क्रिया) होणे व अद्ययावत माहितीच्या संदर्भात अचूक असणे आवश्यक असते. यासाठी इंटरनॅशनल युनियन ऑफ जिओडेसी अँड जिओफिजिक्स आणि इंटरनॅशनल ॲस्ट्रॉनॉमिकल युनियन या संघटनानी अद्ययावत माहितीच्या आधारे प्रमाणभूत केलेली मूल्येच विचारात घेतली जातात. अशा प्रकारे १९७५ साली मान्य झालेली पृथ्वीची विषुववृत्तीय (किंवा कमाल) त्रिज्या ६३,७८,१४४ ± ४ मी. व चापटपणा १/२९८.२५७ इतका होता. 

उपयोग : भूगणितीय अध्ययनाद्वारे अचूकपणे स्थाननिश्चिती केलेल्या बिंदूचे जाळे मिळते. त्याचा उपयोग नकाशे, मार्गनिर्देशन, अभियांत्रिकीय तसेच भूभौतिकीय सर्वेक्षण यांमध्ये होतो. उदा., नवीन धरण बांधल्याने नेमकी किती जमीन त्याच्या पाण्याखाली जाईल हे समजण्यासाठी, भौतिक स्थिरांक मोजण्यासाठी, खनिजांचे पूर्वेक्षण करण्यासाठी व मोठे रस्ते बांधताना अचूक भूगणितीय माहिती उपयुक्त ठरते. काही स्थानांमध्ये कालपरत्वे झालेला बदल भूगणितीय निरीक्षणांमूळे समजतो आणि अशा माहितीचा उपयोग भूकवचाचे वेलीय विरुपण (रूप बदलणे), ⇨ खंडविप्लव व पृथ्वीच्या भ्रमणाक्षाचे सरकणे यांसारखे प्रश्न सोडविण्यासाठी होऊ शकतो. अपोलो-११ अवकाशयानाबरोबर गेलेल्या अंतराळवीरांनी चंद्रावर एक लेसर परावर्तक ठेवला आहे. त्यामुळे पृथ्वी व चंद्र यांच्यातील अंतर ५० सेंमी. पर्यंत अचूकपणे मोजता येऊ लागले. परिणामी ध्रुवाची गती, खंडविप्लव वगैरेसारख्या पृथ्वीवरील सूक्ष्मपणे होणाऱ्या आविष्कारांचे या परावर्तकाच्या साहाय्याने दीर्घकाळ अध्ययन केल्यास त्यांच्याविषयी अधिक माहिती मिळू शकेल तसेच चंद्राची अनियमित गती आणि चंद्र-पृथ्वीतील दिशाविषयक बाबी यांच्याबद्दलही अधिक माहिती मिळू शकते.

मार्गदर्शित क्षेपणास्त्रांच्या प्रणालीत रडाराची अचूक अभिस्थापना करण्यासाठी भूगणितीय सर्वेक्षणाने मिळालेल्या अचूक माहितीचा उपयोग होऊ शकतो. कारण असे क्षेपणास्त्र सोडताना केवळ लक्ष्याचे अंतर व दिशा हीच माहिती उपलब्ध असून चालत नाही, तर क्षेपणास्त्रांवर होणारा गुरुत्वाकर्षणाचा परिणामही माहीत असावा लागतो आणि तो भूगणितीय माहितीच्या आधारे मिळू शकतो. कृत्रिम उपग्रहांचा मागोवा घेण्यासाठी पृथ्वीच्या गुरुत्वीय क्षेत्राची रचना व मार्ग-निरीक्षण केंद्रांचे स्थान लक्षात घ्यावे लागते आणि त्याबद्दलची माहिती भूगणितीय अध्ययनाने अचूकपणे मिळते. तसेच यामुळे पृथ्वीच्या स्थितिस्थापकतेविषयी (लवचिकतेविषयी) अधिक माहिती मिळते. उदा., उत्तर ध्रुव स्थिर बिंदूपासून जास्तीत जास्त १० मी. दूर जातो. जर पृथ्वी दृढ असती, तर या दूर जाण्याला १० महिने लागले असते. मात्र प्रत्यक्षात हा कालावधी १४ महिने आढळला. याचा अर्थ पृथ्वी पूर्णतया दृढ नाही असा होता. भूगणितीय माहितीच्या आधारे भावी काळात भूकवचाची अल्पशी हालचाल व गुरुत्वाकर्षणामधील सूक्ष्म बदल मोजणे शक्य होईल, असा अंदाज आहे. शिवाय गुरुत्वाकर्षणातील बदलांच्या साहाय्याने पृथ्वीच्या अंतरंगाच्या रचनेविषयी अंदाज बांधणे शक्य होईल.

  

चंद्रावर योग्य ठिकाणी व सुरक्षितपणे उतरण्यासाठी चंद्राचे गुरुत्वीय क्षेत्र माहीत असणे आणि चंद्राचा नकाशा तयार केलेला असणे आवश्यक असते. पृथ्वीवरील भूगणितीय अध्ययनाने मिळालेले निष्कर्ष चंद्राला लावून हे साधता येते.  

  

चंद्र व इतर ग्रह : अवकाशयुगापूर्वी चंद्र तसेच पृथ्वीशिवाय इतर ग्रह यांचे आकार, आकारमान व गुरुत्वीय क्षेत्र हे ज्योतिषशास्त्रीय वेधांच्या साहाय्याने काढण्यात येत असत. आता प्रत्यक्ष चंद्रावर व ग्रहावर उपकरणे पाठवून आणि वरील प्रकारची तंत्रे वापरून त्यांच्याबद्दलची अशी माहिती मिळविता येऊ लागली आहे. अचूक नकाशे व गुरुत्वाकर्षणाची अचूक माहिती उपलब्ध झाल्यावरच चंद्रावर माणूस पाठविणे शक्य झाले. चंद्रावर ठेवण्यात आलेल्या उपकरणांनी पाठविलेल्या माहितीच्या आधारे चंद्राचे आकारमान काढण्यात आले आहे. पृथ्वीवरून घेतलेल्या ज्योतिषशास्त्रीय वेधांद्वारे चंद्राची त्रिज्या १,७३८ किमी. आली होती. तिच्या आधारे काढलेल्या अपेक्षित काळापेक्षा रेंजर या कृत्रिम उपग्रहांना चंद्रावर पोहचण्यास जास्त काळ लागल्याचे आढळले. यावरून चंद्राची पृथ्वीच्या दिशेतील प्रत्यक्ष त्रिज्या गणिताने काढलेल्या त्रिज्येपेक्षा ३ किमी. एवढी कमी असल्याचे दिसून आले. ल्यूनर ऑरबाइटर मालिकेतील अवकाशयानांच्या चंद्राभोवतीच्या गतीत झालेल्या बदलांवरून चंद्राच्या गुरुत्वीय क्षेत्राची अचूक माहिती प्रथमच उपलब्ध झाली.

  

भूगणिताच्या दृष्टीने चंद्र पुढील दोन बाबतींत पृथ्वीपेक्षा वेगळा आहे : (१) चंद्रावर महासागर नसल्याने पृथ्वीच्या भूरूपाशी तुल्य व भौतिकीय दृष्ट्या ओळखू येईल असे समवर्चसी पृष्ठ तेथे नाही. (२) चंद्राच्या विषुववृत्तालगत (किंवा इतरत्रही) पृथ्वीच्या विषुववृत्तावरील फुगवट्याएवढा मोठा फुगवटा नाही. त्यामुळे तेथील उंची दर्शविण्यासाठी गोल ही संदर्भ-आकृती पुरेशी आहे. अशा सर्वोत्कृष्ट जुळणाऱ्या हल्लीच्या गोलाची त्रिज्या १,७३६ किमी. येते. तथापि भूरूप जेवढे संदर्भ विवृत्तजाशी जुळते तेवढा हा गोल चंद्राशी जुळत नाही.

  

चंद्राभोवती फिरणाऱ्या उपग्रहाचा मागोवा त्याच्या अर्ध्या कक्षेइतकाच अखंडपणे घेता येण्याइतका चंद्र पृथ्वीपासून दूर आहे म्हणून अशा उपग्रहाचा प्रवेग चंद्राच्या बदलत्या गुरुत्वीय क्षेत्राच्या सम प्रमाणात बदलतो, असे म्हणता येते. प्रवेगात होणाऱ्या अशा बदलांवरून घनतेत होणाऱ्या बदलांचा नकाशा मिळतो. त्याच्या साहाय्याने चंद्राच्या पृष्ठाखालील वस्तुमानाच्या एकत्रिकरणातील असंगतीची कल्पना येते. चंद्राभोवतीच्या कृत्रिम उपग्रहांची गती स्पष्टपणे  समजण्यासाठी अशी माहिती असावी लागते. मात्र वस्तुमानांतील असंगतीची रचना, वाटणी, खोली व महत्त्व यांच्याविषयी अजून मतभेद आहेत.

  

मंगळाभोवती फिरणाऱ्या अवकाशयानांचे निरीक्षण केले असता मंगळावरील गुरुत्वीय विक्षेप हे चंद्रावरील अशा विक्षेपांसारखे असल्याचे दिसून आले आहे. इतर काही ग्रहांकडे पाठविण्यात आलेल्या अवकाशयानांच्या साहाय्याने त्यांचा आकार, आकारमान व गुरुत्वीय क्षेत्र यांबद्दलची माहीती मिळविण्याचे प्रयत्न चालू आहेत.

  

पहा : पृथ्वी भूभौतिकी.

  

संदर्भ : 1. Bomford. G. Geodesy, New York, 1980. 

            2. Heiskanen, W. A. Morits, H. Physical Geodesy. London, 1967. 

            3. King-Hele, D. Observing Earth Satellites, London, 1966. 

            4. Mueller, I. I. Introduction to Satellites Geodesy, New York, 1964. 

            5. Todhunter, I. A History of the Mathematical Theories of Attraction and the Figure of the Earth, New York,1962

पवार, कृ. भ. ठाकूर, 

“