प्रावस्था नियम

प्रावस्था नियम : बहुजिनसी घटकांच्या प्रणालीमधील समतोलाची उकल करण्यासाठी ⇨ ऊष्मागतिकीच्या सिद्धांतावरून ⇨जोसिआ विलर्ड गिब्ज (१८३९-१९०३) यांनी हा अत्यंत महत्त्वाचा नियम शोधून काढला. द्रव्याच्या स्वरूपाविषयी त्यात कोणतीच गृहीतके अध्याहृत नसल्याने तो विविध प्रणालींना लागू पडतो व अनेक क्षेत्रांमध्ये त्याचे अनुप्रयोग होऊ शकतात.

गिब्ज यांनी प्रथम आपला नियम एका अप्रसिद्ध नियतकालिकात प्रकाशित केल्यामुळे (१८७४-७८) पुढे २० वर्षेपर्यंत अज्ञातच राहिला. पुढे जे. एच्‌. व्हांट-हॉफ, डब्ल्यू. ओस्टव्हाल्ट आणि मुख्यतः एच्‌. डब्ल्यू. बी. रोझेबोम यांनी या नियमाचे विविध अनुप्रयोग स्पष्ट केले या नियमाला प्रसिद्धी प्राप्त करून दिली.

काही संज्ञा : या नियमाची चर्चा करण्यापूर्वी त्यात येणाऱ्या काही संज्ञांचा खुलासा करणे योग्य होईल.

 प्रावस्था : द्रव्याच्या वायुरूप, द्रवरूप व घनरूप या तीन अवस्था सर्वांना माहीतच आहेत. ‘अवस्थे’पेक्षा प्रावस्थेची कल्पना बरीच वेगळी आहे. विशिष्ट प्रणालीमधील रासायनिक व भौतिक दृष्ट्या स्वतंत्र (अलग करता येईल अशा) व संपूर्णपणे एकविध (एकसारख्या) अशा प्रत्येक विभागाला ‘प्रावस्था’ असे म्हणतात.

विशिष्ट प्रावस्थेत किती द्रव्य अंतर्भूत असेल याबद्दल काहीही निर्बंध नाही. त्याचप्रमाणे विशिष्ट प्रावस्था संपूर्णपणे एकसंध असेल किंवा छोट्या छोट्या तुकड्यांच्या स्वरूपातही असू शकेल (उदा., बर्फ ही प्रावस्था एका मोठ्या शिळेच्या किंवा चुऱ्याच्या स्वरूपातही असेल) प्रावस्था रासायनिक दृष्ट्या शुद्ध असण्याची जरूरी नाही. (उदा., एखादी प्रावस्था म्हणजे एक विद्राव किंवा अनेक वायूंचे मिश्रण असेल). परंतु एखादा रासायनिक पदार्थ घनावस्थेत असून त्याच्या वेगवेगळ्या स्फटिकीय संरचना अस्तित्वात असतील (उदा., गंधक), तर प्रत्येक स्फटिकावस्था ही वेगळी प्रावस्था मानावी लागेल. अशा एक किंवा अधिक प्रावस्थांची मिळून एक प्रणाली बनते.

घटक संख्या : प्रावस्था नियमाच्या संदर्भात घटक ही संज्ञा एका खास मर्यादित अर्थाने वापरली जाते. विशिष्ट प्रणालीतील प्रत्येक प्रावस्थेचे रासायनिक संघटन ज्या किमान संख्येच्या रासायनिक जातींनी (अणू किंवा रेणू यांनी) निश्चित करता येते, त्या संख्येला ‘घटक संख्या’ असे म्हणतात. उदा., बर्फ-पाणी-बाष्प या प्रणालीत तीन प्रावस्था असून त्यांपैकी प्रत्येकीचे रासायनिक संघटन एकच (H₂O हे) आहे. म्हणून येथे घटक संख्या एक आहे.

प्रावस्था नियमाच्या उपयोगात केव्हा केव्हा वेगवेगळ्या जाती घटक मानता येतात, तरी अंती घटक संख्या मात्र तीच येते. उदा., उष्णतेने कॅल्शियम कार्बोनेटाचे (CaCO₃) अपघटन होऊन कॅल्शियम ऑक्साइड (CaO) व कार्बन डाय-ऑक्साइड (CO₂) तयार होतात आणि परस्परांशी समतोलात येतात. सकृत्‌-दर्शनी येथे तीन वेगळे घटक दिसले, तरी त्यांना जोडणारे एक समीकरण (CaCO₃ ⇌ CaO + CO₂) असल्याने घटक संख्या दोनच येते. त्यासाठी वरील तिहींपैकी कोणतेही दोन रेणू मूळ घटक मानले तरी चालतील, हे पुढील समीकरणांवरून स्पष्ट होईल.

CaO व CO₂ हे घटक मानल्यास त्यांच्या संदर्भात तीनही प्रावस्थांचे संघटन पुढील समीकरणांनी देता येते, म्हणून घटक संख्या दोनच होते.

CaCO₃ = CaO + CO₂ CaO  = CO₂ + 0 CaCO₃

                      CO₂ = CaO + 0 CaCO₃.

येथे 0 याने त्या त्या घटकाचे प्रमाण शून्य टक्के असल्याचे दर्शविले आहे. 

त्याचप्रमाणे CaCO₃ व CaO हे मूळ घटक मानल्यास तीनही प्रावस्थांचे संघटन पुढील समीकरणांवरून देता येईल.

CaCO₃ = 0 CaO + CaCO₃ CO₂ = CaCO₃ – CaO

               CaO = 0 CaCO₃ + CaO.

त्याचप्रमाणे CaO व CaCO₃ हे दोन घटक मुख्य मानून त्यांच्या संदर्भात तीनही प्रावस्थांचे संघटन व्यक्त करता येईल. यावरून हे स्पष्ट होईल की, घटक संख्या निश्चित करताना कोणते घटक मुख्य मानावेत याला काहीच महत्त्व नाही.

घटक संख्या निश्चित करण्यासाठी पुढील सोपा नियम वापरता येईल. ‘प्रणालीतील सर्व रासायनिक जातींची संख्या काढून तिच्यामधून या जातींना संलग्न करणाऱ्या अशा स्वतंत्र रासायनिक समीकरणांची संख्या वजा करावी. ही वजाबाकी म्हणजेच घटक संख्या होय’. वरील उदाहरणात (CaCO₃, CaO व CO₂ या) तीन रासायनिक जाती असून त्यांना जोडणारे एकच (CaCO₃  ⇌ CaO + CO₂) हे स्वतंत्र समीकरण आहे. म्हणून घटक संख्या = ३ – १ = २ झाली.

मुक्तता मात्रा किंवा विचरण : विशिष्ट प्रणालीमधील समतोल बिघडू न देता ज्या ऊष्मागतिकीय चल राशींची मूल्ये स्वतंत्रपणे बदलता येतात, त्या राशींच्या संख्येला मुक्तता मात्रा किंवा विचरण असे म्हणतात. या राशी बदलल्या, तरी प्रणालीतील प्रावस्थांची संख्या बदलत नाही.

तापमान, प्रणमनांक (प्रकाशाचा निर्वातातील वेग आणि त्याचा दिलेल्या पदार्थातील – माध्यमातील – वेग यांचे गुणोत्तर), संहती (दिलेल्या घनफळातील वा वजनातील प्रमाण), दाब यांसारख्या कित्येक राशी एकूण पदार्थ किती घेतला आहे त्यावर अवलंबून असत नाहीत (उदा., विशिष्ट द्रव्यमानाचे पाणी घेऊन त्याच्यात मध्यभागी एक पडदा घालून त्याचे दोन सारखे भाग केले आहेत असे समजा. यांपैकी प्रत्येक भागाचे तापमान, प्रणमनांक इ. गुणधर्म पूर्वीइतकेच राहतील). अशा राशींना तीव्रतादर्शक गुणधर्म असे म्हणतात. मुक्तता मात्रा या तीव्रतादर्शक गुणधर्मच असतात.

 सर्वसामान्य प्रणालींच्या बाबतीत असे दिसते की, दाब, तापमान व प्रणालीतील घटकांच्या संहती याच मुक्तता मात्रा प्रभावी असतात. काही अपवादात्मक प्रणालींच्या बाबतीत विद्युत्‌ किंवा चुंबकीय क्षेत्र, पृष्ठ ऊर्जा, प्रकाश तीव्रता या राशीही परिणामकारी होतात व त्यांचाही अंतर्भाव करावा लागतो. येथे अशा प्रणाली विचारात घेतलेल्या नाहीत.

मुक्तता मात्रा निश्चित करताना स्वंतत्रपणे बदलता येण्याजोग्या किती राशी आहेत त्यांचीच संख्या लक्षात घेतली पाहिजे. एकूण प्रावस्था संख्या P असून त्या प्रत्येकात C घटक संख्या असल्यास प्रत्येक प्रावस्थेतील एकेका घटकाची संहती ही एक एक मुक्तता मात्रा होईल परंतु प्रत्येक प्रावस्थेतील C-1 घटकांच्या संहती दिल्यास त्यावरून उरलेली एक संहती आपोआपच निश्चित होते. प्रत्येक प्रावस्थेत C-1 व म्हणून एकूण प्रणालीत P (C–1) संहती स्वतंत्रपणे बदलण्याजोग्या राहतात. या संख्येत दाब व तापमान या दोन मुक्तता मात्रा मिळविल्यास एकूण मुक्तता मात्रांची संख्या P (C – 1) + 2 होते.

ऊष्मागतिकीय समतोल : जेव्हा एखादी प्रणाली ऊष्मागतिकीय समतोलात असते, तेव्हा (१) प्रणालीतील सर्व अंतर्गत प्रेरणा आणि तीवर कार्य करणाऱ्या बाह्य प्रेरणा या संतुलित झालेल्या असल्या पाहिजेत (यामिकीय समतोल) (२) प्रणालीतील अंतर्गत तापमान सर्वत्र एकसारखेच असून ते प्रणालीच्या परिसराच्या तापमानाइतके असले पाहिजे (औष्णिक समतोल) (३) प्रणालीतील कोणत्याही विभागाची संरचना व रासायनिक संघटन यांमध्ये बदल होता कामा नये (रासायनिक समतोल). म्हणजेच प्रणालीत विसरण (पदार्थातील कणांची म्हणजे अणू व रेणूंची स्वयंस्फूर्त हालचाल व विखुरणे), रासायनिक विक्रिया यांसारख्या घटना होता कामा नयेत.

रासायनिक समतोल होण्यासाठी प्रणालीतील कोणत्याही घटकाची प्रत्येक प्रावस्थेमधील रासायनिक वर्चसे सममूल्य असली पाहिजेत. एखाद्या प्रावस्थेतील विशिष्ट घटकाचे रासायनिक वर्चस्‌ हे त्या घटकाच्या ती प्रावस्था सोडून दुसऱ्या प्रावस्थेत जाण्याच्या प्रवृत्तीचे माप असते. समजा की, १ व २ या दोन प्रावस्थांत a या घटकाची रासायनिक वर्चस्‌ मूल्ये अनुक्रमे μ₁^a व μ₂^a आहेत. μ₁^a &gt μ₂^a असल्यास त्या घटकाचे १ या प्रावस्थेकडून २ या प्रावस्थेकडे अभिवहन होईल. उलट μ₂^a &gt μ₁^a असल्यास २ कडून १ कडे अभिवहन होईल  परंतु रासायनिक समतोलात असे अभिवहन अजिबात होता कामा नये. त्यासाठी μ₁^a = μ₂^a असणे आवश्यक आहे. प्रावस्थांची एकूण संख्या P असल्यास, μ₁^a = μ₂^a  = … = μ_p^a असे समीकरण मिळेल. प्रत्येक घटकाच्या बाबतीत असेच समीकरण मिळेल. (प्रत्येक रासायनिक वर्चस्‌ हे तापमान, दाब व घटकांच्या संहती यांचे फलन असते म्हणजे संबंधदर्शक गणितीय नियमाने जोडलेले असते). या अटीमुळे आपणाला तापमान, दाब व संहती यांना जोडणारी C (P–1) स्वंतत्र समीकरणे मिळतात. या समीकरणांमुळे वेगवेगळ्या घटकांच्या संहतीमध्ये काही निश्चित संबंध प्रस्थापित होतात व त्यामुळे स्वतंत्रपणे बदल होऊ शकणाऱ्या चल राशींची म्हणजेच मुक्तता मात्रांची संख्या C (P–1) ने कमी होते.

प्रावस्था नियम : ऊष्मागतिकीय समतोलात असलेल्या प्रणालीच्या बाबतीत F = C – P + 2 येथे F =  मुक्तता मात्रा, P = प्रावस्थांची संख्या व C = प्रणालीतील घटकांची संख्या. हे समीकरण म्हणजेच गिब्ज यांचा प्रावस्था नियम होय. या समीकरणाची सिद्धता पुढील सोप्या पद्धतीने करता येते. वर दर्शविल्याप्रमाणे P प्रावस्थांनी युक्त अशा C घटकांच्या प्रणालीच्या एकूण मुक्तता मात्रांची संख्या P (C – 1) + 2 असते. रासायनिक समतोलासाठी जरूर त्या अटी पुऱ्या होत असतील, तर तदनुषंगाने मिळणाऱ्या समीकरणांमुळे मुक्तता मात्रांची संख्या C (P – 1) ने कमी होते. म्हणून परिणामी शिल्लक राहणाऱ्या मुक्तता मात्रांची संख्या खालीलप्रमाणे येते.

F = P (C – 1) + 2 – C (P – 1) = C – P + 2

ऊष्मागतिकीय समतोलात असलेल्या बहुजिनसी प्रणालींचे वर्तन कसे होईल, त्याचे निदान या नियमावरून करता येते. निसर्गात नेहमी समतोलावस्थेत जाण्याकडे प्रवृत्ती असते, हे लक्षात घेता असमतोलात असलेल्या बहुजिनसी प्रणालींमध्ये कोणत्या दिशेने फेरफार होतील त्याचेही दिग्दर्शन या नियमाने केले जाते. या नियमाचे उपयोजन काही उदाहरणांनी स्पष्ट करण्यापूर्वी प्रावस्था आकृतीची कल्पना समजणे आवश्यक आहे.

प्रावस्था आकृती : प्रत्यक्ष प्रयोगावरून (वेगवेगळ्या द्रवांचे वेगवेगळ्या तापमानांना) बाष्पदाब, उकळबिंदू, वितळबिंदू, क्रांतिक तापमान किंवा क्रांतिक दाब (ज्या तापमानाला वा दाबाला समतोलात असलेल्या पदार्थाच्या द्रव व बाष्प प्रावस्था एकरूप होतात), विद्राव्यता (विरघळविण्याची क्षमता) इ. राशींचे मापन करता येते. अशा मापनावरून घटकांच्या त्या त्या गुणधर्मांचे आलेख काढता येतात. या आलेखांना ‘प्रावस्था आकृती’ असे म्हणतात. घटकांच्या संख्येनुसार हे आलेख द्विमितीय, त्रिमितीय, बहुमितीय असे असू शकतात. जितक्या मिती जास्त तितकी ही आकृती काढण्याला व समजण्याला जास्त अवघड होते परंतु या आकृतींच्या साहाय्यानेच प्रावस्था नियमाचे उपयोजन करून घटक अलग करणे, (द्रव्याचे) शुद्धीकरण करणे, द्रव्ये तयार करणे अशांसारख्या क्रियांसाठी कोणती स्थिती अनुकूलतम होईल ते समजू शकते. या सर्व गोष्टी पुढील उदाहरणांवरूनच समजू शकतील.

 प्रणालीतील घटकांच्या संख्येनुसार त्यांचे एकघटकी, द्विघटकी, त्रिघटकी इ. प्रकार पाडता येतात. घटक संख्या जितकी कमी तितकी प्रावस्था आकृती जास्त सोपी होते.

एकघटकी प्रणाली : सर्वांत सोपी प्रणाली म्हणजे एकघटकी, एक प्रावस्थायुक्त प्रणाली (उदा., शुद्ध पाणी). येथे P = 1 व C = 1 म्हणून प्रावस्था नियमानुसार F = 1 – 1 + 2 = 2 म्हणजेच येथे दोन मुक्तता मात्रा आहेत. उदा., पाण्याचे तापमान व दाब या दोन्ही राशी स्वतंत्रपणे बदलता येतील.

परंतु एकघटकी दोन प्रावस्थायुक्त प्रणाली घेतल्यास (उदा., बर्फ-पाणी, किंवा पाणी-बाष्प किंवा बर्फ-बाष्प) P = 2 म्हणून F = 1 – 2 + 2 = 1. येथे मुक्तता मात्रा फक्त एक आहे. म्हणजेच तापमान किंवा बाष्पदाब यांपैकी एकच कोणतातरी प्रचल (विशिष्ट परिस्थितीत अचल राहणाऱ्या राशी) स्वतंत्रपणे बदलता येईल (येथे प्रत्येक प्रावस्था १०० टक्के ‘पाणीमय’ असल्याने संहती हा प्रचल आपोआपच गळून गेलेला आहे) व त्यानुसार उरलेल्या प्रचलाचे मूल्य आपोआपच निश्चित होईल. उदा., शुद्ध पाण्याच्या बाबतीत तापमान बदलत गेल्यास प्रत्येक तापमानाला (दोन्ही समतोलात असतील तर) त्याच्या बाष्पदाबाचे निश्चित मूल्य असते. त्याचप्रमाणे बर्फ व बाष्प यांच्या समतोलात प्रत्येक तापमानानुसार बर्फाचा निश्चित असा बाष्पदाब असतो.

परंतु बर्फ, पाणी व बाष्प या तीनही प्रावस्थांमध्ये समतोल असेल, तर P = 3 म्हणून F = 1 – 3 + 2 = 0. म्हणजे या संहतीची मुक्तता मात्रा शून्य होईल. एका निश्चित बाष्पदाबाखाली (= ४·५८ टॉर) व निश्चित तापमानालाच (=२७३°·१६ के.) हा समतोल राहू शकेल. यालाच पाण्याचा ‘त्रिक बिंदू’ असे म्हणतात. यासाठीच १ अंश केल्व्हिनची व्याख्या देण्यासाठी शुद्ध पाण्याच्या त्रिक बिंदूचे तापमान हे मानक म्हणून घेण्यात आले आहे [→ तापमापन].

(पाण्याचे) तापमान व बाष्पदाब यांचे आलेख काढून त्यांवरून वरील सर्व गोष्टी जास्त स्पष्ट होतील (आ. १). 

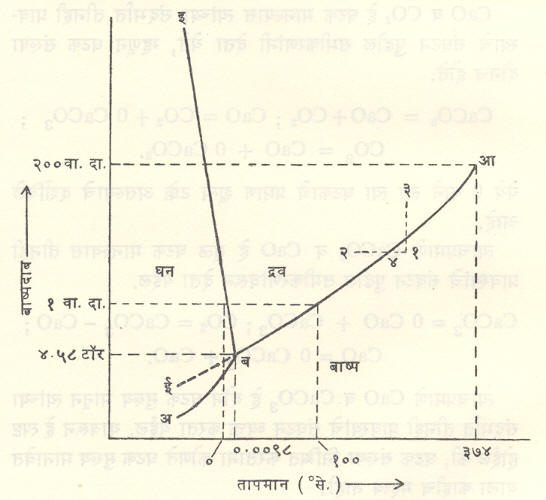
अब हा वक्र बर्फ व त्यावरील बाष्प समतोलात असतानाचा तापमान-दाब वक्र आहे (घन-वायू समतोल वक्र किंवा संप्लवन वक्र). या परिस्थितीत उष्णता दिल्यास बर्फाचे एकदम बाष्पातच रूपांतर होते. बआ हा पाणी व बाष्प यांचा समतोल दर्शविणारा वक्र आहे (द्रव-वायू समतोल वक्र किंवा बाष्पीभवन वक्र), तर बई हा बर्फ व पाणी समतोलात असताना तापमान व दाब दर्शविणारा वक्र आहे (घन-द्रव्य समतोल किंवा द्रवीभवन वक्र). अशा तऱ्हेने यांपैकी प्रत्येक वक्रावर १ च मुक्तता मात्रा आहे. बई व बआ यांच्यामधील भाग फक्त द्रव प्रावस्था (पाणी) दर्शवितो. त्यासाठी मुक्तता मात्रांची संख्या २ आहे परंतु ब येथे तीनही वक्र एकत्र मिळतात. तेथे तीनही प्रावस्था परस्पर समतोलात असल्याने मुक्तता मात्रांची संख्या शून्य आहे. हाच त्रिक बिंदू होय. या बिंदूच्या परिस्थितीत प्रणालीला उष्णता देणे किंवा तीमधून उष्णता काढून टाकणे अथवा तिच्यामधील कोणत्याही एका प्रावस्थेचे घनफळ कमीअधिक करणे अशा क्रियांनी वेगवेगळ्या प्रावस्थांची द्रव्यमाने बदलतील किंवा त्यांच्यात अंतर्भूत झालेल्या उष्णतेचे मान बदलेल परंतु जोपर्यंत तीनही प्रावस्था परस्परांच्या संपर्कात उपस्थित आहेत तोपर्यंत प्रणालीचा दाब व तापमान यांत यत्‌किंचितही बदल होत नाही.

 आकृतीमधील १ हा (बाष्प प्रावस्थेमधील) बिंदू घ्या. तापमान स्थिर ठेवून बाष्पावरील दाब वाढवीत गेल्यास होणारा बदल १-३ या रेषेने दर्शविला जातो. ही रेषा बआ ला जेथे छेदते तेथे बाष्पाचे द्रवात रूपांतर होण्यास प्रारंभ होईल. ३ या बिंदूशी सुसंगत दाब होईल तेव्हा त्याचे संपूर्णपणे द्रवात रूपांतर झालेले असेल. त्याचप्रमाणे दाब स्थिर ठेवून तापमान कमी करीत गेल्यास होणारे बदल १-२ या रेषेने व्यक्त होतील. ही रेषा बआ ला ४ या बिंदूत छेदते. येथे बाष्पाचे द्रवात रुपांतर सुरू होईल. संपूर्ण बाष्पाचे द्रवात रूपांतर होईतो तापमान स्थिर राहील. म्हणजेच तद्‌दर्शक बिंदू ४ येथेच राहील. त्यानंतरच या द्रवाचे तापमान कमी होऊ लागेल व रेषेचा ४-२ हा भाग आरेखिला जाईल. अवस्था बदल होतान शुद्ध पदार्थाचे तापमान स्थिर राहते, हे सर्वज्ञातच आहे.

बआ हा वक्र आ येथे एकदम तुटतो. आ ला क्रांतिक बिंदू म्हणतात. या बिंदूशी ३७४°·२ से. हे तापमान व २१८·३ वातावरण दाब संलग्न आहेत. या स्थितीत पाणी व त्याचे बाष्प यांच्यामधील भेद नष्टच होतो. पाण्याचे मुक्त पृष्ठ नाहीसे होते आणि द्रव व बाष्प यांची घनता एकच होते.

तापमान व दाब यांच्या मूल्यांत योग्य तो बदल करून अशीच प्रावस्था आकृती घन-द्रव-बाष्प अवस्थांत उपलब्ध होणाऱ्या इतर शुद्ध पदार्थांनाही लागू पडेल.

आ. १ ही पाण्याला मर्यादित दाब दिला जात असल्यासच लागू पडते. अती उच्च दाब दिल्यास (नवीन घन प्रावस्था) वेगळ्या स्फटिक संरचनेचे बर्फाचे अनेक प्रकार तयार होऊ शकतात (याचे वर्णन पुढे आले आहे),

अती स्वच्छ पाणी गुळगुळीत भांड्यात ठेवून त्याला धक्का न लागू देता थंड करीत गेल्यास त्याचे बर्फ न होताही ते ०° से. या खाली नेता येते. हा बदल आ. १ मधील बई या वक्राने दाखविला असून या घटनेला ‘अतिशीतन’ असे म्हणतात. या वक्रावरील पाण्याच्या स्थितीला ‘अंशस्थिर स्थिती’ असे म्हणतात. या स्थितीत पाण्याला अगदी सूक्ष्म धक्का दिला किंवा त्याच्यात एखादा घन कण सोडला तरी एकदम स्फोटकपणे पाण्याचे बर्फात रूपांतर होते.

कार्बन डाय-ऑक्साइडाच्या प्रावस्था आकृतीचे सर्वसामान्य स्वरूप पाण्यासारखेच आहे परंतु त्याच्या त्रिक बिंदूच्या ठिकाणचा दाब इतका जास्त आहे की, नेहमीच्या परिस्थितीत घन कार्बन डाय-ऑक्साइडाचे (म्हणजेच ‘शुष्क बर्फा’ चे) एकदम वायुरूपातच परिवर्तन होते.

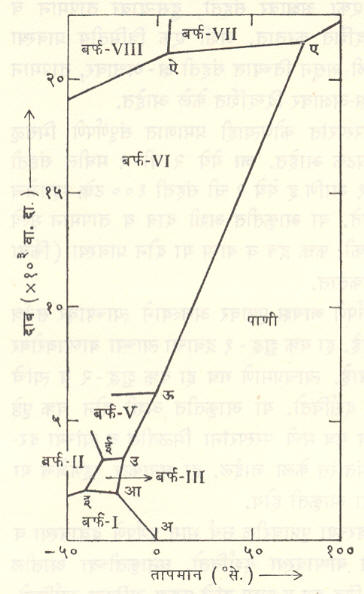बहुरूपी पदार्थ : गंधक, फॉस्फरस, कार्बन, लोखंड इ. पदार्थांच्या घनावस्थेत परिस्थितीनुसार वेगवेगळ्या स्फटिकीय संरचना असू शकतात. याला ⇨ बहुरूपता असे म्हणतात. उच्च दाबाखाली पाण्याचे  बर्फही  हा गुणधर्म दर्शविते. अशा पदार्थांच्या प्रावस्था आकृतीचे स्वरूप समजण्यासाठी वानगीदाखल पाण्याचीच प्रावस्था आकृती आ. २ मध्ये दिली आहे. नेहमीचे बर्फ हे बर्फ-I म्हणून ओळखले जाते. सुयोग्य उच्च दाबाखाली त्याचे बर्फ- II, बर्फ- III, …, बर्फ- VIII असे ७ प्रावस्था प्रकार मिळू शकतात. मधला बर्फ -IV हा प्रकार फक्त ‘जड पाण्या’च्या (हायड्रोजनाच्या ड्यूटेरियम या जड समस्थानिकाचे म्हणजे भिन्न अणुभार असलेल्या प्रकारचे प्रमाण जास्त असलेल्या पाण्याच्या) बाबतीतच मिळतो व तो अंश स्थिर आहे म्हणून तो या आकृतीत दाखविलेला नाही. बर्फाचे हे वेगवेगळे प्रकार ज्या वेगवेगळ्या तापमान-दाब पल्ल्यांमध्ये स्थिर राहू शकतात, हे आकृतीत वेगवेगळ्या विभागांनी दाखविले आहेत (आश्चर्य वाटण्यासारखी गोष्ट म्हणजे बर्फ – VII याचा वितळबिंदू १००° से. च्याही वर आहे).

या आकृतीतील अआ हा वक्र म्हणजे आ. १ मधील बई वक्र होय आणि अ हा बिंदू त्या आकृतीमधील त्रिक बिंदू होय. याशिवाय या आकृतीत आ, इ, ई, उ इत्यादी अनेक त्रिक बिंदू दिसतील. उदा., आ येथे पाणी, बर्फ-I व बर्फ-III हे समतोलात आहेत, तर इ येथे बर्फ-I बर्फ-II व बर्फ-III या तिघांचा समतोल झाला आहे. इआ हा वक्र बर्फ-I व बफ-III यांच्यामधील समतोल दर्शवितो. योग्य तापमानाला बर्फ-I वरील दाब वाढवून त्याचे बर्फ-III मध्ये दाब कमी करून बर्फ-III चे बर्फ-I मध्ये रूपांतर होऊ शकेल.

ग्रॅफाइट व हिरा ही कार्बनाची दोन रुपे आहेत. प्रावस्था नियमाच्या संदर्भात त्यांचे परस्परसंबंध बर्फ-I व बर्फ-III यांच्याप्रमाणे आहेत. म्हणूनच उच्च तापमानाला प्रचंड दाब देऊन ग्रॅफाइटाचे हिऱ्यात रूपांतर होऊ शकते. सर्वसामान्य दाब व तापमानावर हिरा ही प्रावस्था सुस्थिर नसून तिचे हळूहळू ग्रॅफाइटात रूपांतर व्हावयास हवे परंतु या रूपांतराची त्वरा इतकी अत्यल्प आहे की, हिरा सुस्थिरच आहे असे वाटते. अशा स्थितीला अंशस्थिर स्थिती असे म्हणतात.

द्विघटकी प्रणाली : दोन घटकांच्या प्रणालींमध्ये तापमान व दाब यांच्याशिवाय (एका घटकाची दुसऱ्याच्या संदर्भात) संहती हा तिसरा बदलक्षम प्रचल कार्यवाहीत येतो. अशा परिस्थितीत प्रावस्था आकृती काढण्यासाठी त्रिमितीय आकृतीचा वापर करावा लागतो. हिच्यामध्ये एका अक्षावर संहती, दुसऱ्यावर तापमान व तिसऱ्यावर दाब दिग्दर्शित करतात. अशी एक त्रिमितीय प्रावस्था आ. ३ मध्ये दाखविली असून तिच्यात संहती क्ष-अक्षावर, तापमान ब-अक्षावर व दाब झ-अक्षावर दिग्दर्शित केले आहेत.

येथे १ व २ हे परस्परांत कोणत्याही प्रमाणात संपूर्णपणे मिसळू शकणारे दोन द्रव हे घटक आहेत. आ येथे २ ची १ मधील संहती शून्य म्हणजेच शुद्ध-१ आणि इ येथे २ ची संहती १०० टक्के म्हणजेच शुद्ध-२ दिग्दर्शित होते. या आकृतीत अशी दाब व तापमान मूल्ये गृहीत धरली आहेत की, फक्त द्रव व बाष्प या दोन प्रावस्था (किंवा त्यांपैकी एक) येऊ शकतात.

कख हा वक्र संपूर्णपणे आयझ पृष्ठावर असल्याने त्याच्यावर सर्वत्र २ ची संहती शून्य आहे. हा वक्र शुद्ध-१ द्रवाचा त्याच्या बाष्पाबरोबर समतोलदर्शक वर्क आहे. त्याचप्रमाणे गघ हा वक्र शुद्ध-२ व त्यांचे बाष्प यांचा समतोल दर्शवितो. या आकृतीत अशी दोन वक्र पृष्ठे आहेत की, ती कख व गघ मध्ये परस्परांना मिळतील व त्यांच्या दरम्यान एक घनाकार अंतरित केला जाईल. हा घनाकार म्हणजेच या परिस्थितीतील प्रावस्था आकृती होय.

या घनाकृतीच्या वरच्या पृष्ठावरील सर्व भाग पूर्णपणे द्रवावस्था व खालचा भाग पूर्णपणे बाष्पावस्था दर्शवितो. घनाकृतीच्या आतील भागातील कोणताही बिंदू द्रव व बाष्प यांचे एकत्र अस्तित्व दर्शवितो.

या स्वरूपात या आकृतीवरून काही उपयुक्त निष्कर्ष काढणे मुष्किल आहे. त्याकरिता या आकृतीचे विशिष्ट दिशेने छेद घेणे जास्त सोयीचे होते. हे छेद सामान्यतः विशिष्ट स्थिर दाबाकरिता (आ. ३ मधील च हा छेद दा या दाबासाठी आहे) किंवा स्थिर तापमानाकरिता (आ. ३ मधील छ हा छेद त तापमानाकरिता आहे) किंवा क्वचित स्थिर संहतीकरिता घेतले जातात. च आणि छ हे भिंगाकार छेद आ. ४ (स्थिर दाब) व आ. ५ (स्थिर तापमान) मध्ये वेगळे काढून दाखविले आहेत.

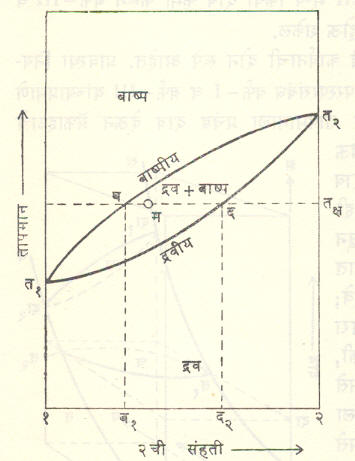
 आ. ४ मध्ये दा या स्थिर दाबाला त_१, हा शुद्ध-१ चा व त_२ हा शुद्ध-२ चा उकळबिंदू आहे. (त_१ &lt त_२ म्हणून १ हा जास्त बाष्पनशील आहे). त_१ व त_२ या वक्राला ‘बाष्पीय’ असे म्हणतात. त्याच्यावरून वेगवेगळ्या तापमानांना बाष्पातील १ व २ यांचे प्रमाण मिळते. त्याच्यावरील सर्व भाग संपूर्णपणे बाष्पस्थिती दर्शवितो. त्याचप्रमाणे त_१, द त_२ या वक्रावरून दा या दाबाखालील वेगवेगळ्या संहतीच्या  द्रवाचा उकळबिंदू मिळतो. या वक्राला ‘द्रवीय’ असे म्हणतात. द्रवीयाच्या खालचा सर्व भाग द्रवस्थिती दर्शवितो. द्रवीय आणि बाष्पीय यांच्यामधील भागात द्रव व बाष्प या दोन्ही स्थिती परस्परांच्या साहचर्यात असू शकतात.

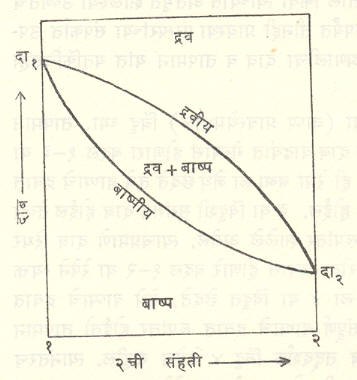
आ. ५ मध्ये त या स्थिर तापमानाला दा_१, आणि दा_२ हे अनुक्रमे शुद्ध-१ व शुद्ध-२ यांचे बाष्पदाब आहेत. संहतीच्या बदला बरोबर बाष्पदाब कसा बदलतो, हे आकृतीवरून समजते. द्रवीय, बाष्पीय इत्यादींचे अर्थ आ. ४ मधल्याप्रमाणेच आहेत. या दोन आकृत्यांची तुलना करता आ. ५ ही आ. ४ च्या उलट आहे, हे लक्षात येईल.

आ. ४ मध्ये म हा (द्रवीय व बाष्पीय यांच्यामधील भागातील) कोणताही बिंदू घ्या. म मधून संहतिदर्शक अक्षाला समांतर काढलेली रेषा बाष्पीय व द्रवीय यांना अनुक्रमे ब आणि द मध्ये छेदते. या बिंदूंशी संलग्न त_क्ष हे आहे. याचा अर्थ असा की द_२ या संहतीचे द्रवमिश्रण घेतल्यास दा दाबाखाली ते त_क्ष या तापमानाला उकळू लागेल व त्यापासून निघणाऱ्या बाष्पाची संहती ब_१ इतकी असेल, म्हणजे उकळणाऱ्या द्रवापेक्षा त्यामधून निघणाऱ्या बाष्पात १ ची, म्हणजे जास्त बाष्पनशील घटकाची संहती जास्त असेल, हे बाष्प एकसारखे काढून घेत गेल्यास (उदा., ऊर्ध्वपातनामध्ये म्हणजे द्रवांचे मिश्रण उकळून मिळणारे बाष्प थंड करून मिश्रणातील घटक अलग करण्याच्या क्रियेमध्ये) शिल्लक राहिलेल्या द्रवात २ चे प्रमाण वाढत जाईल व त्याचा उकळबिंदू वाढत जाईल. शेवटी जेव्हा उळकबिंदू त_२ इतका होईल तेव्हा शिल्लक द्रव हा शुद्ध-२ असेल. त्याचप्रमाणे १ चे प्रमाण जास्त असलेले बाष्प थंड करून पुन्हा उकळावे. ही क्रिया पुनःपुन्हा केल्यास थंड करून मिळणाऱ्या द्रवात १ चे प्रमाण उत्तरोत्तर वाढत जाऊन शेवटी शुद्ध-१ मिळू शकेल. यालाच ‘भागशः ऊर्ध्वपातन’ असे म्हणतात. उदा., मिथिल अल्कोहॉल-पाणी किंवा ॲसिटोन-पाणी या प्रणालीची वैशिष्ट्ये वर वर्णन केल्याप्रमाने असतात व ते घटक एकमेकांपासून या पद्धतीने अलग करता येतात.

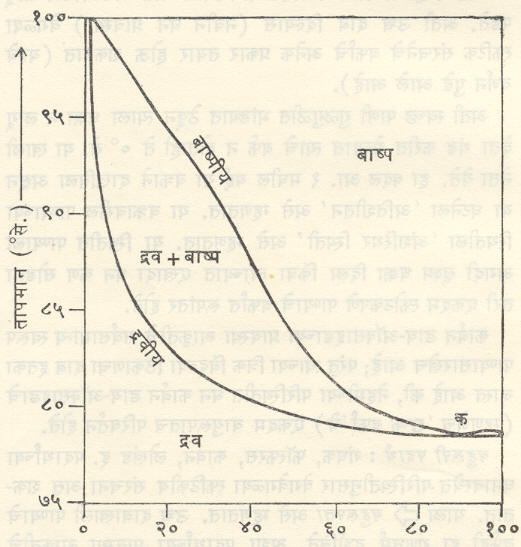
सहबाष्पी मिश्रण : (विशिष्ट परिस्थितीत द्रव मिश्रण व त्याचे बाष्प यांच्या संहती समानच असतात असे द्रवमिश्रण). आ. ४ व ५ मध्ये दाखविलेल्या आकाराच्या आकृती ज्या द्रवांच्यासाठी मिळतात त्यांना ‘आदर्श द्रव’ म्हणतात. अशा आकृती न देऊ शकणाऱ्या द्रवांना ‘अनादर्श (आदर्श नसलेले) द्रव’ असे म्हणतात. त्यांच्यासाठी स्थिर दाबाखाली मिळणारे संहति-उकळबिंदू आलेख दोन प्रकारचे असतात. एका प्रकारात संहती बदलत जाते तसा उकळबिंदू कमी होत जाऊन तो एका किमान मूल्याप्रत पोहोचतो व नंतर पुन्हा वाढू लागतो (आ. ६). दुसऱ्या प्रकारात तो कमाल मूल्याप्रत जाऊन मग कमी होऊ लागतो (आ.७).

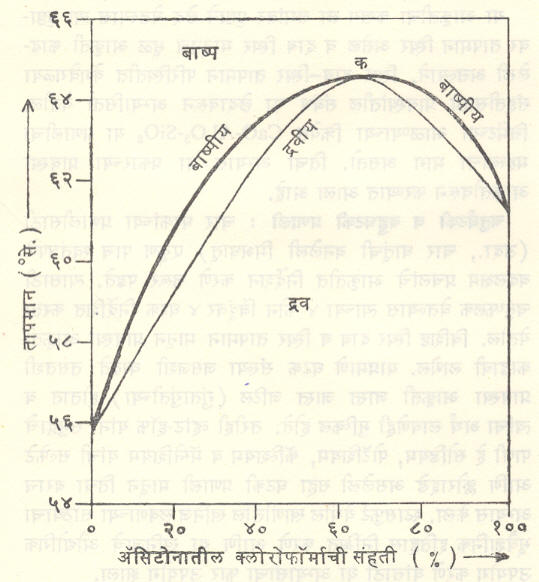
आ. ६ व ७ या दोन्ही आकृतींत बाष्पीय व द्रवीय वक्र क या बिंदूशी परस्परांना मिळतात (या बिंदूला ‘सहबाष्प बिंदू’ म्हणतात) या परिस्थितीत द्रवमिश्रण व त्याचे बाष्प यांच्या संहती समानच असतात आणि कितीही वेळ द्रवमिश्रण उकळले तरी त्याचा उकळबिंदू स्थिर राहतो. या परिस्थितीतील द्रवमिश्रणाला ‘स्थिर-उकळबिंदू मिश्रण’ असे म्हणतात. ऊर्ध्वपातनाने अशा द्रवमिश्रणातील घटक परस्परांपासून संपूर्णपणे अलग करता येत नाहीत.

शुद्ध अल्कोहॉलाची प्राप्ती : शर्करायुक्त विद्रावाचे किण्वन (आंबविण्याची क्रिया) करून जास्तीत जास्त १० टक्के अल्कोहॉलयुक्त पाणी मिळते. त्यातील अल्कोहॉलाची संहती भागशः ऊर्ध्वपातन करून जास्तीत जास्त म्हणजे सहबाष्प बिंदूशी असते तेवढीच (द्रवमानाने ९५ टक्क्यांपर्यतच) मिळविता येते. शुद्ध अल्कोहॉल मिळविण्यासाठी पाणी-अल्कोहॉल-बेंझीन यासारखी त्रिघटकी प्रणाली वापरतात.

शुद्ध द्रवाची कसोटी :वरील विवेचनावरून असे लक्षात येईल की, शुद्ध द्रवापेक्षा द्रवमिश्रणाचा उकळबिंदू वेगळा असतो. म्हणून द्रवाची शुद्धता समजण्याचा सोपा मार्ग म्हणून त्याचा उकळबिंदू मोजतात. 

दोन घन पदार्थांची प्रणाली :कोणत्याही प्रमाणात परस्परांशी संपूर्णपणे मिसळू शकणारे दोन घन पदार्थ (उदा., तांबे व निकेल) घेतल्यास मर्यादित तापमानापर्यंत त्यांचे वायुरूप होत नाही. फक्त घन व द्रव अवस्थाच संभवतात. अशा पदार्थांच्या प्रावस्था आकृती वरीलप्रमाणेच येतात. फक्त वरील आकृतीत बाष्पाऐवजी द्रव व द्रवाऐवजी घन असा बदल केला म्हणजे झाले. अशा मिश्रधातूंना एक निश्चित असा वितळबिंदू येत नाही. त्याचप्रमाणे शुद्ध धातूपेक्षा अशा मिश्रधातू कमी तापमानाला द्रवावस्थेत जातात. डाख लावण्यासाठी अशा मिश्रधातू वापरतात. [→ द्रवणक्रांतिक समतोलावस्था आकृत्या].

शीतकारी मिश्रणे : बर्फामध्ये मीठ (NaCI) किंवा कॅल्शियम क्लोराइड (CaCI₂) यासारखी लवणे मिसळून बर्फाच्या वितळबिंदूपेक्षाही नीच तापमाने मिळविता येतात. अशा मिश्रणांना ‘शीतकारी मिश्रणे’ म्हणतात. प्रावस्था आकृतीच्या साहाय्याने अशा मिश्रणाचे कार्य चांगले समजू शकते.

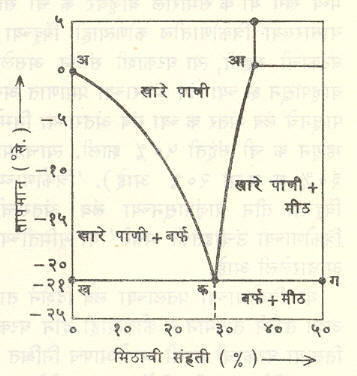आ. ८ मध्ये मीठ-पाणी या द्विघटकी प्रणालीसाठी वातावरणीय दाबाखाली संहति-तापमान आलेख दाखविला आहे. या आकृतीवरून पुढील गोष्टी स्पष्ट होतील : (१) तापमान कमी होत जाते त्याबरोबर खाऱ्या पाण्यातील मिठाची विद्राव्यता कमी होत जाते (वक्र आक). (२) तापमान कमी होत जाते त्याबरोबर खाऱ्या पाण्यातील शुद्ध बर्फाची विद्राव्यता कमी होत जाते (वक्र अक). (३) ०% ते १००% यांच्या दरम्यानच्या संहतीसाठी विद्रावाचा गोठणबिंदू शुद्ध मिठाच्या वा शुद्ध बर्फाच्याही वितळबिंदूच्या खाली असतो. उदा., समुद्राचे पाणी (मिठाची संहती १·५%) ०° से. तापमानाला किंवा त्याच्या थोडे खालीही गोठत नाही. सु.-१° से. तापमानाला त्या विद्रावातून शुद्ध बर्फ बाहेर पडू लागते व त्यामुळे उरलेल्या विद्रावाची संहती वाढत जाते. ही परिस्थिती -२१° से. तापमानापर्यंत चालू राहते. तापमान त्याच्याहीपेक्षा खाली नेल्यास बर्फ व मीठ दोन्ही विद्रावातून बाहेर पडू लागतात. क हा द्रवणक्रांतिक बिंदू (ज्या तापमानाला मिश्रणाचा नीचतम गोठणबिंदू येतो ते तापमान) आहे. मिठाऐवेजी कॅल्शियम, क्लोराइड वापरल्यास -५१° से. पर्यंत नीच तापमान मिळू शकते. 

थंड प्रदेशात रस्त्यावर पडलेले बर्फ वितळविण्यासाठी त्याच्यावर मीठ शिंपडतात. हे मीठ बर्फालगतच्या पाण्यात विरघळते व मग क हा बिंदू येईतो बर्फ वितळत जाते व तयार होणाऱ्या पाण्यात जास्त जास्त मीठ विरघळत जाते. कारण आता मीठ, बर्फ, बाष्प व खारे पाणी या चार प्रावस्था एकत्र येतात व त्यांचा समतोल फक्त क येथेच होऊ शकतो.

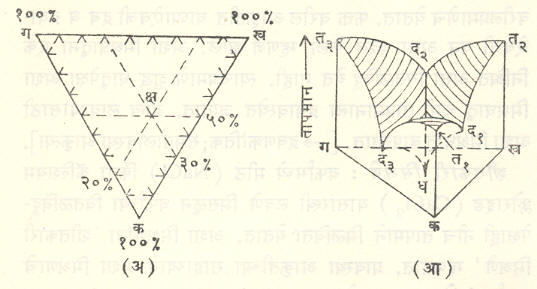त्रिघटकी प्रणाली : तीन घटकांची प्रणाली असल्यास वरील त्रिमितीय आकृतीचा उपयोग करता येत नाही. अशा प्रसंगी त्रिकोणी लोलकाकार घेऊन त्यात प्रावस्था आकृती सिद्ध करतात. आ. ९ वरून या आकृतीची सर्वसामान्य कल्पना येईल. अशा बहुतेक प्रणालींचे समतोल दाबावर फारसे अवलंबून असत नाहीत. म्हणून ती राशी विचारात न घेता फक्त तापमान व घटकांच्या संहती एवढ्यांचे दिग्दर्शन प्रावस्था आकृतीत करतात.

संबधित लोलकाचा पाया समभुज त्रिकोण घेतात. तीन घटकांचेच क, ख, ग असे नामकरण केल्यास लोलकाच्या पायाचे क, ख, ग हे शिरोबिंदू. त्या त्या घटकाची शुद्ध अवस्था किंवा १०० टक्के संहती व्यक्त करतात आणि त्या शिरोबिंदूसमोरील बाजूवर त्या घटकाचा अभाव किंवा शून्य टक्का संहती दर्शविली जाते [उदा., आ. ९ (अ) मध्ये खग या क समोरील बाजूवर क ची संहती शून्य आहे]. क्ष यासारख्या त्रिकोणातील कोणत्याही बिंदूच्या ठिकाणची कोणत्याही घटकाची संहती, त्या घटकाशी संलग्न असलेल्या शिरोबिंदूसमोरील बाजूपासून क्ष च्या लंब अंतराच्या प्रमाणात असते (उदा., क्ष चे खग पासूनचे लंब अंतर क च्या लंब अंतराच्या निम्मे म्हणजे ५०% आहे. म्हणून क ची संहती ५०% झाली. त्याचप्रमाणे तेथे ख ची संहती ३०% व ग ची २०% आहे). ‘त्रिकोणाच्या आतील कोणत्याही बिंदूच्या तीन बाजूंपासूनच्या लंब अंतरांची बेरीज नेहमी त्या त्रिकोणाच्या उंचीइतकी असते’ या भूमितीच्या सिद्धांतावर ही पद्धत आधारलेली आहे.

या त्रिकोणाच्या प्रतलाच्या लंब दिशेने तापमान दर्शविले जाते. अशा तऱ्हेने तापमान व कोणत्याही दोन घटकांच्या संहती (त्यामुळे तिसऱ्या घंटकाची संहती आपोआपच निश्चित होते) या तीन स्वतंत्र चल राशीचे आकृतीत निर्देशन करता येते.

आ. ९ (आ) मध्ये अशा प्रकारची एक प्रावस्था आकृती दाखविली आहे. आकृती सोपी व्हावी यासाठी क, ख, ग या तीन धातू (उदा., शिसे, जस्त व बिस्मथ) अशा घेतल्या आहेत की, द्रवरूपात त्या परस्परांत संपूर्णपणे मिसळू शकतात पण घनरूपात परस्परांपासून अलग राहतात. त_१, त_२ आणि त_३ हे (अनुक्रमे) या तीन शुद्ध धातूंचे वितळबिंदू आहेत. कखग या त्रिकोणाच्या प्रतलाला लंब दिशेने तापमान निर्देशित केले आहे. अशा रीतीने आकृतीत दर्शविल्याप्रमाणे एक त्रिकोणी लोलक तयार होतो.

या लोलकाच्या प्रत्येक उभ्या फलकावर दोनच धातूंचे मिश्रण निर्देशित होते. उदा., कख या रेषेवर ग ची संहती शून्य आहे. म्हणून कखत_२त_१ या फलकावरही सर्वत्र ग ची संहती शून्यच असणार. कखत_२त_१ या फलकांवर फक्त क आणि ख या दोन धातूंच्या संहतीच निर्देशित होतील. त्या फलकावरील त_१ द_१ त_२ हा क आणि ख या धातूंचा संहति-वितळबिंदू वक्र आहे आणि द_१ हा त्या मिश्रणाचा द्रवणक्रांतिक बिंदू आहे. उरलेल्या दोन फलकांवरील त_२द_२त_३ आणि त_३द_३त_१ या वक्रांचे याचप्रमाणे अर्थ आहेत.

या वक्रामधून जाणारी तीन वक्र पृष्ठे त्यांवर आडव्या रेषा मारून दिग्दर्शित केली आहेत. ही पृष्ठे लोलकाच्या अंतर्भागात खालच्या दिशेने वळत असून ती धद_१, धद_२ व धद_३ या रेषांत परस्परांना छेदतात (ही पृष्ठे हीच प्रावस्था आकृती होय). ध हा या तीन धातूंच्या मिश्रणाचा द्रवनक्रांतिक बिंदू असून आकृतीवरून हे स्पष्ट होईल की, ध ने दर्शविलेले तापमान द१, द२ किंवा द३ या तीनहीपेक्षा कमी आहे. म्हणजेच दोन धातूंच्या मिश्रणापेक्षा तीन धातूंच्या मिश्रणाचा द्रवणक्रांतिक बिंदू आणखी खाली येतो.

या आकृतीचा कखग ला समांतर पृष्ठाने छेद घेतल्यास त्या पृष्ठावर तापमान स्थिर असेल व दाब स्थिर मानूनच मूळ आकृती काढलेली असल्याने, स्थिर दाब-स्थिर तापमान परिस्थितीत वेगवेगळ्या संहतीसाठी प्रावस्थांतील संबंध या छेदावरून अभ्यासिता येतील. सिमेंटच्या आळण्याच्या क्रियेत C_aO-Al₂O₃-SiO₂ या प्रणालीचा महत्त्वाचा भाग असतो. तिचा अभ्यास या प्रकारच्या प्रावस्था आकृतीवरून करण्यात आला आहे.

चतुर्घटकी व बहुघटकी प्रणाली : चार घटकांच्या प्रणालीसाठी (उदा., चार धातूंची बनलेली मिश्रधातू) एकूण पाच स्वतंत्रपणे बदलक्षम प्रचलांचे आकृतीत निर्देशन करणे जरूर पडते. त्यासाठी चतुष्फलक घेतल्यास त्याच्या ४ कोन बिंदूवर ४ घटक निर्देशित करता येतील. विशिष्ट स्थिर दाब व स्थिर तापमान मानून प्रावस्था आकृती काढावी लागेल. याप्रमाणे घटक संख्या जसजशी वाढते तसतशी प्रावस्था आकृती जास्त जास्त जटिल (गुंतागुंतीच्या) होतात व त्यांचा अर्थ लावणेही मुष्किल होते. तरीही व्हांट-हॉफ यांनी समुद्राचे पाणी हे सोडियम, पोटॅशियम, कॅल्शियम व मॅग्नेशियम यांची सल्फेटे आणि क्लोराइडे असलेली सहा घटकी प्रणाली मानून तिचा बराच अभ्यास केला. श्टासफुर्ट येथील खाणीतील खनिज लवणाच्या साठ्याचा भूवैज्ञानिक इतिहास निश्चित करणे आणि या खनिजाचे औद्योगिक उपयोग करणे यांसाठी या अभ्यासाचा फार उपयोग झाला.

वैशिष्ट्ये व उपयोग : प्रावस्था नियमाचा वापर करण्यासाठी प्रणालीतील पदार्थांची रेणवीय संरचना माहीत असण्याची जरूरी नसते. त्याचप्रमाणे द्रव्याच्या संघटनाबद्दल कोणती गृहीतकेही या नियमात धरावी लागत नाहीत. या नियमाच्या साहाय्याने विविध प्रकारच्या प्रणालींचे त्यांच्या मुक्तता मात्रांनुसार वर्गीकरण करता येते.

वर पाहिल्याप्रमाणे अनेक प्रावस्था आकृती या क्ष-अक्षावर संहती व य-अक्षावर तापमान घेऊन काढलेले आलेख असतात. या प्रचलांच्या विविध मूल्यांसाठी प्रणालीचे स्वरूप दर्शविणारा प्रावस्था आकृती हा जणू काही एक नकाशाच असतो.

विशिष्ट प्रणालीच्या व्यवहारातील परिस्थितीत तापमान व संहती माहीत असतील, तर त्यांवरून प्रावस्था आकृतीत आपणाला ती स्थिती दर्शविणारा एक ठराविक बिंदू मिळतो. या बिंदूच्या स्थानावरून त्या परिस्थितीत कोणत्या प्रावस्था असतील ते समजू शकते. उपस्थित असणाऱ्या प्रावस्थांचे तौलनिक प्रमाण निश्चित करता येते. धातुविज्ञानामधील पोलादाला पाणी देणे अथवा त्याचे पाणी उतरविणे यांसारख्या क्रिया प्रावस्था आकृतीच्या अभ्यासाने जास्त चांगल्या तऱ्हेने करता येतात [⟶ पोलाद]. इष्ट गुणधर्माची मिश्रधातू तयार करण्यातही प्रावस्था आकृती मार्गदर्शक करू शकतात [⟶ मिश्रधातु कासे पितळ]. ओतकाम करताना होणाऱ्या स्थितिबदलाची चांगली कल्पना संबंधित प्रावस्था आकृतीवरून येते. द्रवांचे शुद्धीकरण, शुद्धता तपासणे, ऊर्ध्वपातनाने द्रवांचे निष्कर्षण, अंश शुद्धीकरणाने शुद्धीकरण इ. अनेक प्रक्रियांत या आकृतींचा उपयोग होतो. नीच तापमान मिळविण्यासाठी वेगवेगळी शीतकारी मिश्रणे या आकृतीवरून सिद्ध करता येतात.

संदर्भ : 1. Barrow, G. M. Physical Chemistry, New York, 1961.

            2. Maron, S. H. Principles of Physical Chemistry, New York, 1961.

            3. Van Vleck, L. H. Eements of Material Science, Reading. 1964.

            4. Zemansky, M. W. Heat and Thermodynamics, New York, 1957.

भिडे, ब. वा शेजवलकर, बा. ग. पुरोहित, वा. ल.

“