दाबविद्युत्

दाबविद्युत् : काही पदार्थांवर यांत्रिक प्रतिबल (एकक क्षेत्रफळावरील प्रेरणा) लावले असता विद्युत्‌निर्मिती होऊ शकेल, यासी. ए. कूलंब (१७३६–१८०६) यांच्या सूचनेवरून होवे व ए. एच्. बेक्रेल यांनी काही प्रयोग केले. प्रयोगान्ती त्यांना असे दिसून आले की, काही स्फटिकांवर प्रतिबल लावले असता विशिष्ट विद्युत्‌परिणाम दिसतात. त्यांच्या असल्या काही प्रयोगांना थोड्याफार प्रमाणात यश मिळाले असले, तरी दाबविद्युत् या शाखेच्या शोधाचे श्रेय निर्विवादपणे झाक क्यूरी व प्येअर क्यूरी (१८५९–१९०६ मारी क्यूरी यांचे पती) या बंधूंनाच दिले पाहिजे.

क्यूरी बंधूंनी १८८० मध्ये असा शोध लावला की, काही स्फटिकांवर विशिष्ट दिशांनी प्रतिबल लावले असता स्फटिकाच्या एका पृष्ठभागावर धन व दुसऱ्या पृष्ठभागावर ऋण विद्युत् भार उत्पन्न होतो (यालाच स्फटिकाचे विद्युत्‌ध्रुवण झाले असे म्हणतात). उत्पन्न होणारा विद्युत्‌भार हा लावलेल्या प्रतिबलाच्या प्रमाणात असतो व प्रतिबल काढून घेतले असता विद्युत्‌भारही अंतर्धान पावतो.

हा शोध म्हणजे क्यूरीबंधूंच्या उत्तापविद्युत् (काही पदार्थांच्या स्फटिकांच्या तापमानात बदल केला असता त्यातील निरनिराळ्या भागांवर विद्युत्‌भार निर्माण होतात) या विषयावरील अभ्यासाचे फल म्हणता येईल. या अभ्यासातून त्यांना दाबविद्युत् आविष्काराचा केवळ शोध लागला एवढेच नव्हे, तर कोणत्या दिशांनी प्रतिबल लावले असता स्फटिकाच्या कोणत्या भागावर विद्युत्‌भारांची अपेक्षा करावी, या संबंधीचे आडाखेही त्यांना आधीच मांडता येऊ लागले. क्यूरी बंधूंनी आपला शोध ज्या लेखात प्रसिद्ध केला त्या पहिल्याच लेखात स्फटिक विशिष्ट दिशांनी कापून त्याच्याच पट्या चकत्या कशा कराव्यात, त्यावर कथिलाचा वर्ख कसा लावावा व दोन विद्युत्‌वाहक विद्युत्‌ मापकाला कसे जोडावेत याचे वर्णन केले आहे. त्यानंतर झिंक ब्लेंड, सोडियम क्‍लोरेट, बोरॅसाइट, तोरमल्ली (टूर्मलीन), क्वार्ट्‌झ, टार्टारिक अम्ल, साखर व रोचेल लवण यांच्या स्फटिकांवर विशिष्ट दिशेत प्रतिबल लावले असता विद्युत्‌भार निर्मिती झाली असल्याचेही नमुद केले आहे. नंतरच्या लेखात त्या परिणामाची क्वार्ट्झ व तोरमल्लीयांच्या स्फटिकांवरील मोजमापे, या परिणामाचे उपयोग व त्याचा विरूद्ध परिणाम (म्हणजे स्फटिक विद्युत्‌क्षेत्रात ठेवल्यास क्षेत्राच्या दिशेनुसार त्याचे आकुंचन वा प्रसरणहोणे) यांसंबंधी क्यूरी बंधूंनी विवेचन केले आहे. या शाखेचे दाबविद्युत् (पिझो इलेक्ट्रिसिटी) असे नामकरण मात्र डब्ल्यू. जी. हँकेल या शास्त्रज्ञांनी केले व हे नाव क्यूरी बंधूसह सर्वांनी मान्य केले. उत्तापविद्युत्‌ हा परिणाम फार पूर्वीपासून श्रीलंकेतील लोकांना व भारतीयांना माहीत होता. दाबविद्युत्‌ ही शाखा त्यामधूनच निघालेली असली, तरी त्यातील फरक असा : काही स्फटिक तापविले असता त्यांच्या पृष्ठभागांवर विद्युत् भार उत्पन्न होतात म्हणजेच तापमानातील फरकामुळे स्फटिक पृष्ठावर होणाऱ्या विद्युत् निर्मितीस उत्ताप विद्युत् म्हणतात, तर स्फटिक पृष्ठावर लावलेल्या यांत्रिक प्रतिबलामुळे उत्पन्न होणाऱ्या विद्युत भारास दाबविद्युत् असे म्हणतात.

दाबविद्युती स्फटिक : या स्फटिकांची व्याख्या खालीलप्रमाणे करता येईल : ज्या विद्युत् अपारक स्फटिकावर यांत्रिक प्रतिबल लावले असता त्याच्या पृष्ठभागांवर विद्युत् भागांची उत्पत्ती होते किंवा विद्युत् ध्रुवण होते, तसेच जो विद्युत् क्षेत्रात ठेवला असता क्षेत्राच्या दिशेनुसार त्याचे आकुंचन अथवा प्रसरण होते, त्यास दाबविद्युती स्फटिक म्हणता येईल. अर्थात प्रतिबल लावले असता विद्युत् निर्मिती होणे हा सरळ दाबविद्युत् परिणाम असून त्याच्या उलट विद्युत् क्षेत्रामुळे स्फटिकाचे आकारमानातील होणारा फेरफार हा विरूद्ध दाबविद्युत् परिणाम होय.

वरील व्याख्येचे अधिक स्पष्टीकरण असे : धन प्रतिबलाऐवजी (म्हणजेच दाब) ऋण प्रतिबल (म्हणजेच ताण) लावले असता स्फटिक पृष्ठभागांवरील विद्युत् भारांची चिन्हे बदलतात (+ चे –आणि – चे +). साहजिकच असा प्रश्न उपस्थित होतो की, स्फटिकाच्या विशिष्ट पृष्ठावर कोणता विद्युत् भार केव्हा यावा हे कसे ठरते ? त्याकरिता स्फटिकात एक प्रकारचे ‘एकमार्गीत्व’ किंवा विशिष्ट प्रकारची स्फटिकाची बांधणी असली पाहिजे. त्यानुसार स्फटिकावर प्रतिबल लावल्यास त्याच्या विशिष्ट पृष्ठभागावर धन विद्युत् भार येणार की ऋण विद्युत् भार येणार ते ठरते. विरूद्ध दाबविद्युत् परिणामात सुद्धा या एकमार्गित्वानेच आकारमानात होणारा बदल हा प्रसरण की आकुंचन ते ठरत असते. येथे विरूद्ध दाबविद्युत् परिणाम व सकृत्दर्शनी त्यासारखाच वाटणारा ⇨ विद्युत् आकारांतर हा आविष्कार यांच्यामधील फरक लक्षात घेणे जरूर आहे. कोणताही विद्युत् अपारक पदार्थ विद्युत् क्षेत्रात ठेवला असता त्याच्या आकारमानात बदल होतो, या प्रकाराला विद्युत् आकारांतर असे म्हणतात. यामुळे होणारा बदल (१) त्यामानाने अल्प असतो (२) तो व्युत्क्रमी नसतो म्हणजे लावलेल्या विद्युत् क्षेत्राची दिशा उलट केली, तर मूळ आकुंचनाच्याऐवजी प्रसरण किंवा प्रसरणाच्याऐवजी आकुंचन असे होत नाही (३) होणारा बदल विद्युत् क्षेत्र तीव्रतेच्या वर्गाच्या सम प्रमाणात असतो आणि (४) अशा प्रकारच्या पदार्थाचे यांत्रिक प्रतिबल लावून आकारांतर केले, तर त्यावर विद्युत् भार निर्माण होत नाहीत.

 विरूद्ध दाबविद्युत् परिणामामुळे होणारा आकारमानातील बदल (१) तुलनेने जास्त असतो, (२) तो व्युत्क्रमी असतो व (३) तो क्षेत्र तीव्रतेच्या सम प्रमाणात असतो आणि (४) यांत्रिक प्रतिबलाने आकारांतर केल्यास पृष्ठभागावर विद्युत् भार निर्माण होतात.

सोप्या शब्दांत सांगावयाचे म्हणजे काही पदार्थ विद्युत् क्षेत्रात आकारमान बदलतात, पण त्यांच्यावर दाब देऊन त्यांच्या आकारमानात होणाऱ्या फरकाने विद्युत् निर्मिती होऊ शकत नाही, या परिणामास विद्युत् आकारांतर म्हणतात. दाबविद्युत् परिणाम दाखविणारे स्फटिक अर्धफलकीय (स्फटिक समूहाच्या महत्तम सममितीच्या, म्हणजे आकार आणि रचना यांत असणाऱ्या नियमितपणाच्या, दृष्टीने आवश्यक असणाऱ्या फलकसंख्येपेक्षा निम्मे फलक असणारे हेमिहेड्रल) जातीचे असतात. त्याचे पृष्ठभाग तिरपे असून ते सममिती दाखवितात. प्रतल ध्रुवित प्रकाशाचे (विशिष्ट प्रतलात कंप पावणाऱ्या प्रकाशाचे) घ्रुवण प्रतल फिरविण्याचा गुणधर्म त्यांच्या अंगी असतो. तोरमल्ली, क्वॉर्ट्‌झ, बोरॅसाइट, राेचे लवण हे दाबविद्युत् परिणाम दाखविणारे काही स्फटिक होत. पैकी राेचे लवणामध्ये हा परिणाम सर्वांत अधिक प्रमाणात दिसून येतो. तथापि क्वॉर्ट्‌झचा उपयोग या शाखेत सर्वांत अधिक प्रमाणात केला जातो. दाबविद्युत् परिणाम हा ‘मध्याची सममिती’ ज्या स्फटिकात नसते अशा स्फटिकातच दिसतो. स्फटिकांच्या एकूण ३२ वर्गांपैकी २१ वर्गांतील स्फटिकांत मध्याची सममिती नसते व त्यांपैकी २० वर्गांतील स्फटिक हा परिणाम दर्शवितात [→स्फटिकविज्ञान].

ज्या अक्षाभोवती एखाद्या स्फटिक १८० अंशांतून फिरवला असता त्याची नवी स्थिती तंतोतंत मूळच्या स्थितीप्रमाणे येत नाही, त्या अक्षाला स्फटिकाचा ध्रुवाक्ष असे म्हणतात (प्रत्येक स्फटिकाला असा ध्रुवाक्ष असेलच असे नाही). दाबविद्युती स्फटिकाचे एक महत्त्वाचे वैशिष्ट्य म्हणजे त्याला एक किंवा अधिक ध्रुवाक्ष असतात. स्फटिकाचे विरूपण केल्यास ध्रुवाक्षाच्या दिशेने त्याचे जास्तीत जास्त विद्युते घ्रुवण होते विद्युत् ध्रुवणाची दिशा कोणत्या प्रकारचे प्रतिबल स्फटिकावर लागू केले आहे, त्यावर अवलंबून राहते. उत्तापविद्युत् परिणाम दाखविणाऱ्या स्फटिकांचे दहा वर्ग दाबविद्युत् परिणाम दाखवितात. योग्य तापमानात लोहविद्युत् (ज्याप्रमाणे लोखंडाचा चुंबक बनू शकतो त्याप्रमाणे योग्य परिस्थितीत ज्याच्या दोन बाजूंना विरुद्ध प्रकारचे विद्युत् भार आपोआप येऊ शकतात अशा पदार्थाचे) स्फटिकदाबविद्युत् परिणाम दाखवितात.

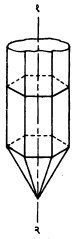
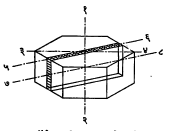
दाबविद्युत् परिणामाच्या अनुप्रयोगांमध्ये क्वॉर्ट्‌झच्या स्फटिकाच्या कापांचा मोठ्या प्रमाणावर उपयोग केला जातो. इच्छित परिणाम मिळविण्यासाठी काप योग्य त्या दिशेने काढणे आवश्यक असते. आ. १ मध्ये क्वॉर्ट्‌झचा नैसर्गिक स्फटिक दाखविला असून १–२ हा त्याचा प्रकाशीय अक्ष आहे, यालाच स्फटिकाचा झ–अक्ष असेही म्हणतात. या स्फटिकाचे १–२ ला लंबदिशेने दोन छेद घेतल्यास आ. २ मध्ये दाखविल्यासारखा षट्‍कोणी ठोकळा मिळेल. या षट्‌कोणाचे समोरासमोरचे कोणतेही दोन कोनबिंदू जोडणाऱ्या रेषेच्या दिशेला (उदा., ३–४) स्फटिकांचा विद्युत् अक्ष किंवा क्ष–अक्ष म्हणतात व षट्‌कोणाच्या प्रतलातील क्ष–अक्षाच्या लंबदिशेला स्फटिकाचा य–अक्ष म्हणतात.

या षट्‌कोणी ठोकळ्यातून आ. २ मध्ये दाखविल्यासारखी चौकोनी पट्टी कापल्यास तिची जाडी क्ष–अक्षाला समांतर येईल, तिला ‘क्ष–काप’ असे म्हणतात. त्याचप्रमाणे ‘य–काप’ व ‘झ–काप’ यांचा अर्थ समजावा. उपयोजनेमध्ये कापाची आंदोलने जाडीच्या दिशेने व्हावयाची असल्यास क्ष–काप वापरतात, तर लांबीच्या दिशेने आंदोलनासाठी य–काप वापरतात.

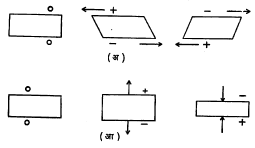
एखाद्या दाबविद्युती स्फटिकाच्या कापाच्या पृष्ठांवर प्रतिबले लावल्यामुळे प्रकट होणाऱ्या विद्युत् भारांचे स्वरूप हे (१) स्फटिकाचे द्रव्य, (२) स्फटिकाच्या अक्षांच्या संदर्भात कापाची दिशा व (३) प्रतिबलाचे स्वरूप या गोष्टींवर अवलंबून असते. आ. ३ वरून हे स्पष्ट होईल.

 स्फटिक कापण्याचे तंत्र : सुरुवातीच्या काळात स्फटिक विशिष्ट प्रकारच्या करवतीने कापीत असत पण लवकरच तिची जागा तांब्याच्या किंवा मऊ पोलादाच्या चाकीने (चकतीने) घेतली. फिरत्या चाकीवर एखाद्या द्रव्यात मिसळलेली कार्बोरंडमची पूड टाकून तिने स्फटिक कापण्यात येतात. नंतरच्या काळात हिऱ्याची पूड लावलेल्या चाक्या अधिक चांगले काम देतात, असे आढळून आले. कापण्याच्या कडेवर केरोसिनाची बारीक धार धरली असता कापणे अधिक सुलभ होते. कापलेला तुकडा मिळताच तो जुळ्या क्वार्ट्‌झचा तुकडा आहे काय ते पहावे लागते. यानंतर या कापाची लांबी–रुंदी हवी तेवढी मिळेपर्यंत स्फटिक घासावा लागतो. हे तंत्र बरेचसे दूरदर्शकाचा (दुर्बिणीचा) मुख्य अंतर्गोल आरसा घासण्याच्या तंत्राप्रमाणे असते. लांबी–रुंदी अचूक मिळण्यासाठी शेवटी नाजूकपणे घासण्याकरिता एक बाजू किंवा दोन्ही बाजू घासणारी यंत्रे असतात. घासण्याकरिता अधिकाधिक बारीक अशी कार्बोरंडमची पूड, साबण व पाणी पाणी किंवा पातळ तेलाबरोबर वापरतात. अगदी शेवटचा हात फिरविताना अल्युमिनियमाचे ऑक्साइड किंवा रूज (चकाकी आणणारी फेरिक ऑक्साइडाची तांबूस पूड) वापरतात. हे शेवटचे घासणे बहुधा हातांनी करणे आवश्यक असते. लांबी–रुंदी बरोबरच स्फटिकाच्या अक्षाशी पृष्ठभागाचा कोन योग्य आहे की नाही ते क्ष–किरण पद्धतीने तपासावे लागते. कमी कंप्रतेच्या (दर सेकंदास होणाऱ्या कंपनांच्या संस्थेच्या) कापांच्या बाबतीत लांबी–रुंदी महत्त्वाची असते, तर जास्त कंप्रतेच्या काप्रांच्या बाबतीत जाडी काटेकोरपणे घासून घ्यावी लागते. साधारणपणे ०·०००५ मिमी. इतकी अचूकता जाडीच्या बाबतीत आवश्यक असते. एक दशलक्ष हर्ट्‌झ कंप्रता असलेल्या क्ष–अक्षीय सिलिकॉन स्फटिकावरून सिलिकॉनाच्या अणूचा एक थर काढला असता, स्फटिकाची कंप्रता एक दशांशाने वाढेल. विशेष अचूक आंदोलकात (स्फटिकाच्या बाजूंवर प्रत्यावर्ती, म्हणजे उलटसुलट दिशेने कार्य करणारा, विद्युत् दाब लावला असता स्फटिक कंप पावू लागतो, या गुणधर्माचा उपयोग करून विद्युत् प्रवाहांची आंदोलने निर्माण करण्याकरिता वापरण्यात येणाऱ्या साधनात) हा फरकसुद्धा त्याची नोंद घेण्याइतका महत्त्वाचा असतो हे लक्षात घ्यावे. स्फटिक आंदोलकाची कंप्रता काटेकोरपणे राखावयाची असल्यास त्याचे तापमान बदलू न देणे आवश्यक असते. कारण तापमान बदलल्यास कंप्रता बदलते. म्हणून स्फटिक बऱ्याच वेळा निर्वात डबीत बंद करून, त्याचे तापमान विद्युत् तापकाने थोडेसे वाढवून, तापनियंत्रकाच्या साहाय्याने तो योग्य त्या तापमानास ठेवलेला असतो. स्फटिकाच्या अक्षाशी विशिष्ट कोन करून (मात्र हा कोन फारच काटेकोरपणे साधावा लागतो) स्फटिक कापला असता त्याची कंप्रता तापमान बदलले तरीसुद्धा जवळजवळ तीच राहते.

क्ष–कापांच्या आकाराने सर्वांत मोठ्या असलेल्या पृष्ठभागावर कथिलाचा वर्ख चिटकवला व या वर्खाला विद्युत् मापक जोडला, तर स्फटिकाच्या आ. २ मध्ये दाखविलेल्या ३–४ या दिशेने दाब प्रतिबल लावले असता, पृष्ठभागावर विद्युत् भार आलेला दिसून येईल. गेल्या काही वर्षांत मुलामा चढविलेले स्फटिक अधिक वापरात आलेले आहेत. या प्रकारात स्फटिकावर धातूची विद्युत् अग्रे बाष्पिभवनाने पक्की बसविलेली असतात. अल्युमिनियम, चांदी किंवा सोन्याचा ०·०००५ मिमी. जाडीचा बाष्पीभूत थर स्फटिकावर दिलेला असतो. विशिष्ट पद्धतीने फॉस्फर ब्राँझची तार विद्युत् अग्रांच्या मध्यावर पक्की बसविलेली असते. या तारेवरही स्फटिक लोंबत असतो. अशा प्रकारे कंप्रता अधिक स्थिर करून संदमन (रोधामुळे कंपनात होणारी घट) कमी केलेले असते. स्फटिक व त्यावर जोडलेल्या तारा एका काचेच्या किंवा धातूच्या नळीत किंवा डबीत बसवितात. काही वेळा डबी निर्वात असून तिच्यात विद्युत् तापक असून तापमानाचे नियमन केलेले असते.

विद्युत् भार व स्फटिकाची कंप्रता : प्रयोगावरून असे सिद्ध झाले आहे की, उत्पन्न होणारा विद्युत् भार हा लावलेल्या प्रतिबलाच्या सम प्रमाणात असतो.

 येथे भा = विद्युत् भार, प्र = प्रतिबल, क हा त्या त्या स्फटिकाचा दाबविद्युत् मापांक असतो.

प्रकाशीय अक्षाला समांतर दिशेत प्रतिबल लावले असता कोणत्याही प्रकारची विद्युत् निर्मिती होत नाही तसेच विरूद्ध दाबविद्युत् परिणामात, प्रकाशीय अक्षाच्या दिशेने लावलेल्या विद्युत् दाबामुळे आकारमानावर काही परिणाम होत नाही. अन्य दिशांनी विद्युत् दाब दिला असता यांत्रिक प्रतिबल निर्माण होऊन स्फटिकाच्या आकारमानात बदल होतो. एका दिशेने विद्युत् दाब लावला असता लांबी वाढून रुंदी कमी होते, तर दुसऱ्या दिशेने विद्युत् दाब दिला असता लांबी कमी होऊन रुंदी वाढते. लांबी–रुंदीत होणारा बदल हा लावलेल्या विद्युत् दाबाच्या सम प्रमाणात असतो.

दाबविद्युत् सिद्धांताच्या गणितात सदिश (दिशा व मूल्य असणारी राशी) व प्रदिश [एका सहनिर्देशक व्यूहातून दुसऱ्या व्यूहात विशेष नियमाधारे रूपांतरित होणाऱ्या फलनांचा संच → प्रदिश] यांचा समावेश असल्यामुळे ते गणित फार क्‍लिष्ट आहे. म्हणून दाबविद्युत् मापांक कसा काढावा व स्फटिकाची नैसर्गिक कंप्रता कशी काढावी, याची मूलग्राही व सोपी पद्धत आणि त्या अनुषंगाने येणारे सोपे गणित पुढे दिले आहे. आ. ४ मध्ये स्फटिकावर २–३ या दिशांनी प्रतिबल लावले असता त्याच्या पृष्ठभागावर विद्युत् निर्मिती होते. पृष्ठभागावर विद्युत् अग्रे जोडली असल्याने त्यांवरील विद्युत् भार विद्युत् मापकाने दाखविला जाईल. विद्युत् भार किती आहे हे ४ हे प्रमाण धारित्र (विद्युत् भार साठवून ठेवणारे साधन) मंडलात जोडून मोजता येईल. धारित्र मंडलात जोडलेले नसताना मंडलातील विद्युत् धारणा धा_१ आहे असे समजू. धारित्र आकृतीत दाखविल्याप्रमाणे जोडल्यावर विद्युत् धारणा वाढून धा_२ होईल असे मानू. लावलेल्या प्र प्रतिबलामुळे विद्युत् मापकाने (मंडलात ४ जोडले नसताना) वि_१ आणि (मंडलात ४ जोडल्यावर) वि_२ अशी विचलने (कोनीय स्थानांतरणे) दाखविली, तर उत्पन्न झालेला विद्युत् भार भा हा पुढील समीकरणाने दाखविता येईल.

मंडलातील धारित्राची विद्युत् धारणा धा_० इतकी असल्यास

समीकरणे (२) व (३) वरून

(२), (३) व (४) समीकरणावरून

या समीकरणाच्या उजव्या बाजूची सर्व पदे प्रयोगावरून काढता येत असल्यामुळे क हा स्फटिकाचा दाबविद्युत् मापांक काढता येईल, मात्र प्रयोगात काही ठिकाणी विशेष काळजी घ्यावी लागते.

स्फटिकाच्या चपट्या पट्टीची नैसर्गिक कंप्रता ही (१) तिच्या कंपने होणाऱ्या दिशेतील स्थितीस्थापकीय (विकृती निर्माण करणाऱ्या प्रेरणा काढून घेतल्यावर पदार्थ मूळ अवस्थेत येण्याच्या गुणधर्मासंबधीच्या) मापांकावर, (२) स्फटिकाच्या घनतेवर व (३) स्फटिकाच्या जाडीवर अलवंबून असते.

समीकरणाच्या भाषेत :

येथे स = स्फटिकाचा स्थितीस्थापकीय मापांक, घ = स्फटिकाची घनता आणि वे = स्फटिकातील अन्वायाम (ज्यातील कंपन दिशा प्रसाराच्या दिशेला समांतर आहे अशा) तरंगांचा वेग. स्फटिकपट्टी जर तिच्या मूलभूत रीतीने कंप पावत असेल म्हणजेच जर तिची जाडी (जा) तरंगलांबीच्या (त) अर्धी असेल (जा = त/2 ) आणि कंप्रता न असेल, तर

समीकरणे (७) व (८) वरून

या समीकरणाची उजव्या बाजूची पदे स्फटिकावरून माहीत होत असल्याने त्याची मूलभूत कंप्रता काढता येते. 

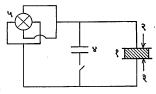
 उपयोग : कोणत्याही पदार्थास त्याची स्वत:ची अशी आंदोलन कंप्रता असते ती त्या पदार्थाच्या लांबी–रुंदीवर व त्याच्या स्थितीस्थापकतेवर अवलंबून असते. या सर्वसामान्य नियमास अनुसरून प्रत्येक स्फटिकालाही त्याची विशिष्ट दोलन कंप्रता असते. हिला नैसर्गिक कंप्रता असेही म्हणतात. आंदोलन कंप्रता स्फटिकाच्या भिन्न दिशांत भिन्न असते, कारण भिन्न दिशांत स्फटिकाचे स्थितिस्थापकीय मापांक भिन्न असतात. स्फटिकाला ज्या दिशेत विद्युत् क्षेत्र लावायचे त्या दिशेतील स्फटिकाची नैसर्गिक कंप्रता व विद्युत् क्षेत्र बदलण्याची कंप्रता या दोन्हीही समान झाल्यास स्फटिकात अनुस्पंदन (दोन कंप्रता समान झाल्यामुळे एकमेकींस पूरक होणारा परिणाम) चालू होऊन स्फटिक जोरदारपणे कंप पावू लागतो. अर्थात ही गोष्ट विरुद्ध दाब विद्युत् परिणामामुळे घडून येते. जोरदार कंपनांमुळे प्रतिक्रिया म्हणून सरळ दाबविद्युत् परिणामामुळे विद्युत् आंदोलने जास्त जोरदार होतात हे दाखविणारे विद्युत् मंडळ आ. ५ मध्ये दिले आहे, या मंडलास दाबविद्युत् आंदोलक किंवा स्फटिक आंदोलक असे म्हणतात [ → आंदोलक, इलेक्ट्रॉनीय]. यातील स्फटिक हाच दाबविद्युती अनुस्पंदकाचे काम करतो. मूलत: अशा प्रकारच्या मंडलाचा उपयोग जेथे जेथे कंप्रतेवर काटेकोरपणे नियंत्रण ठेवण्याची आवश्यकता असते, अशा ठिकाणी करतात. उदा., रेडिओ प्रेषक, स्फटिकी घड्याळे वेगैरे.

स्फटिकी घड्याळाकरिता वापरण्याच्या स्फटिकात संदमन कमी असणे हा प्रमुख गुण असावा लागतो. शिवाय त्यात तापमानाच्या बदलामुळे होणारा कंप्रतेतील बदल कमीत कमी असावा. एकूण स्फटिकी घड्याळ बरेच गुंतागुंतीचे असले, तरी त्यातील मुख्य भाग म्हणजे काटेकोर कंप्रता असणारा स्फटिक हाच असतो [→ घड्याळ].

श्राव्यातीत (२० किलोहर्ट्‌झपेक्षा जास्त कंप्रतेच्या) कंपनांचे प्रेषण किंवा ग्रहण करण्याकरिता दाबविद्युती क्वॉर्ट्‌झच्या स्फटिकाचा उपयोग करता येतो. त्याचा मुख्य फायदा हा की, स्फटिकाच्या पृष्ठभागावरून काटकोनात जे तरंग निघतात, ते त्याच दिशेत प्रकाशाच्या समांतर किरणशलाकेप्रमाणे त्यामधील कोन फारसा न वाढता प्रवास करतात. याकरिता अट अशी की, प्रेषण करणाऱ्या स्फटिकाची लांबी–रुंदी प्रेषित होणाऱ्या तरंगांच्या तरंगलांबीपेक्षा कमी असली पाहिजे. या तत्त्वावर पॉल लांजिवीन या फ्रेंच शास्त्रज्ञांनी १९१८ मध्ये पाण्याखालून श्राव्यातीत तरंग पाठविण्यात यश मिळवले. या तंत्रात पुढे अनेक सुधारणा झाल्या व स्फटिक तरंगाचा उपयोग खोल पाण्यातील तळाचा ठाव घेणे, पाणबुडीची जागा शोधणे, हिमखंडांचा तलास लावणे वगैरे कामांकरिता केला जाऊ लागला. यातील तत्त्व म्हणजे तरंगांचा एक स्पंद सोडून तो पाण्याखालील पृष्ठभागावर आपटून परत येण्यास लागणारा वेळ मोजणे आणि या तरंगांचा पाण्यातील वेग माहीत असल्याने वेग = अंतर/वेळ या समीकरणावरून अंतर काढणे हे होय.

ग्रामोफोनमधील उद्‌ग्राहकामध्ये (पिक–अपमध्ये) वापरण्यात येणाऱ्या स्फटिकावर सुई तबकडीतून फिरताना उत्पन्न होणाऱ्या कमीजास्त प्रतिबलामुळे त्या प्रमाणात विद्युत् निर्मिती होते. ती विवर्धित करून तीपासून ध्वनिनिर्मिती होते. स्फटिक कंपनाने द्रवात स्थिर तरंग उत्पन्न करून त्याचा जालकाप्रमाणे (अनेक समसमांतर पृष्ठांच्या मालिकेप्रमाणे) उपयोग करतात. शिवाय पायसीकरण (एकमेकांत न मिसळणाऱ्या दोन द्रवांपैकी एक दुसऱ्यात सूक्ष्म कणरूपात पसरविणे), पदार्थ निर्जंतुक करणे, कपड्यांवरील धूळ झाडणे, ओतीव कामामधील दोष काढणे, ध्वनिग्राहक (मायक्रोफोन), दूरध्वनी इत्यादींत दाबविद्युत् स्फटिकांचा उपयोग होतो. स्फटिकांच्या कापाच्या साहाय्याने अत्यंत अचूक अशा विद्युत् गाळण्या बनविता येतात, त्यांचा दूरध्वनी तंत्रात मोठ्या प्रमाणावर उपयोग होतो. त्याचप्रमाणे संकेतवहनाच्या मार्गात ‘विलंबकारक’ म्हणून या स्फटिकांचा उपयोग होतो. बेरियम टिटॅनेटाचे मानवनिर्मित मृदीय स्फटिक दाबविद्युत् परिणाम मोठ्या प्रमाणावर दाखवितात. त्यांच्यावर दाब देऊन मोठा (२५,००० व्होल्ट) विद्युत् वर्चोभेद (विद्युत् पातळ्यांमधील फरक) निर्माण होऊ शकतो. त्याचा उपयोग एंजिनातील ठिणगी गुडद्या (स्पार्क प्‍लग) कार्यन्वित करणे, हातबाँबचा आपटल्याबरोबर स्फोट होण्याची योजना करणे, गुरामेंढरांचे कळप (विद्युत् झटका देऊन) नियंत्रित करणे अशा अनेक ठिकाणी करण्यात येतो.

संदर्भ : 1. Cady, W. G. Piezoelectricity, 2 Vols., New York, 1964.

            2. Wooster, W. A. Experimental Crystal Physics, Oxford, 1957.

कुलकर्णी, प्र. वा.

“