अंकगणित : अंकगणितात प्रामुख्याने धन पूर्णाकांच्या (म्हणजे १, २, ३, ४… या नेहमीच्या स्वाभाविक संख्यांच्या) गुणधर्मांचा अभ्यास केला जातो. धन पूर्णांकांची बेरीज, वजाबाकी, गुणाकार, भागाकार इ. गणितकृत्ये तसेच क्षेत्रफळ, घनफळ, व्याज, सरासरी, शेकडेवारी इ. व्यवहारोपयोगी प्रश्नांमध्ये उपयुक्त असणारी सूत्रे व त्यांचा वापर करण्याच्या विविध पद्धती यांचा अंक गणितात विशेष उपयोग होतो. अंकगणितात वापरली जाणारी सूत्रे तर्क कठोरपद्धतीने सिध्द करण्यावर फारसा भर दिला जात नाही तर ती गृहीत धरून त्यांचा नित्य व्यवहारातील प्रश्न सोडविण्यासाठी कसा उपयोग करता येईल याकडे विशेष लक्ष दिले जाते. संख्यांच्या व्याख्या आणि त्यांचे गुणधर्म यांचा ⇨संख्या सिद्धांत या गणितीय शाखेत विचार करण्यात येतो व या दृष्टीने अंकगणित हे संख्या सिद्धांताचे प्राथमिक स्वरूप आहे असे म्हणण्यास हरकत नाही.
संच या संकल्पनेच्या आधारे धनपूर्णांक व यांची बेरीज म्हणजे काय हे सुलभतेने मांडता येते. १, २, ३, ४,… ही अंक चिन्हे सुपरिचित आहेत. त्यांच्या संचास ध म्हणतात. आता कोणत्याही दिलेल्या संचास किती घटक आहेत हे कसे मोजतात ते पाहू. समजा का या संचात 
या चिन्हांनी निर्देशित असे घटक आहेत. म्हणजेच का = { } या संचातील कोणताही एक घटक घेऊन त्याच्याशी १ या अंकचिन्हाची जोडी लावली. नंतर दुसरा घटक घेऊन त्याच्याशी २ या अंकचिन्हाचा संबंध जोडला आणि राहिलेल्या घटकाशी ३ ची जोडी जमवली. अशा प्रकारे दिलेल्या का या संचाशी {१, २, ३} या ध च्या उपसंचाशी एकास-एक संबंध प्रस्थापित झाला. उपरोक्त उपसंचातील शेवटचे अंकचिन्ह ३ म्हणजेच का मधील घटकांची संख्या होय. हेच, का चा संचांक ३ आहे असेही मांडतात. याचप्रमाणे दुसऱ्या एखाद्या खा संचांक {१, २, ३…, १०, ११} या ध च्या उपसंचाचा एकास-एक संबंध जोडता येत असेल तर खा मध्ये ११ घटक आहेत किंवा खा चा संचांस ११ आहे असे म्हणता येईल. याच पद्धतीने कोणत्याही दिलेल्या संचासाठी संचांक (म्हणजे त्यात असलेल्या घटकांची संख्या) काढता येईल. यामध्ये संचातील वस्तू कोणत्या प्रकारच्या आहेत याला महत्त्व नाही हे सहजच लक्षात यावे [→ संच सिद्धांत].
आता दोन धन पूर्णांकांची बेरीज म्हणजे काय ते पाहू. समजा का आणि खा हे दोन वियुक्त संच आहेत (म्हणजेच या दोन संचांमध्ये कोणताही घटक समाईक नाही). या का आणि खा या दोन संचांचे सर्व घटक एकत्रित करून गा हा संच बनवला तर गा ला का आणि खा यांचा युतिसंच असे म्हणतात, व तो का U खा असा दर्शवतात. या युतिसंचातील घटकांच्या संख्येस (का U खा च्या संचांकांस) ग म्हटले, आणि का, खा चे संचांक अनुक्रमे क आणि ख आहेत असे मानले तर ग ही संख्या क आणि ख ची बेरीज आहे असे म्हणतात, आणि हेच ग = क + ख असे लिहितात.
धन पूर्णांकांच्या बेरीज या गणितकृत्यासाठी पुढील नियम मिळतात.
(१) धन पूर्णांकांची बेरीज करताना ती कोणत्याही क्रमाने केली तरी अंतिम उत्तरात त्यामुळे फरक पडत नाही. या नियमाला ‘क्रमनिरपेक्ष नियम’ म्हणतात. म्हणजेच क + ख = ख + क. उदा., ५ + ७ = ७ + ५.
(२) तीन धन पूर्णांकांची बेरीज करताना प्रथम पहिल्या दोन धन पूर्णांकांची बेरीज करून ती तिसऱ्यात मिळविली किंवा पहिल्या धन पूर्णांकांत राहिलेल्या दोन धन पूर्णांकांची बेरीज करून मिळविली तरी अंतिम बेरजेत फरक पडत नाही. या नियमाला ‘सहयोग नियम’ म्हणतात. म्हणजेच
क + (ख + ग) = (क + ख) + ग
उदा., ३ + (४ + ७) = (३ + ४) + ७
या नियमाचे अधिक धन पूर्णांकांकरिताही व्यापकीकरण करता येते.
क आणि ख या धन पूर्णांकांसाठी ग हा असा धन पूर्णांक अस्तित्वात असेल की, क = ख + ग आहे, तर ‘क गुरूत्तर ख,’ क > ख असे म्हणतात. हेच ‘ख लघुतर क,’ ख < क असेही म्हणतात. कोणत्याही क, ख या दोन धन पूर्णांकांसाठी क > ख, क = ख, क < ख या तीनपैकी एक (आणि एकच) सत्य असते. याला ‘त्रिभाजन गुणधर्म’ म्हणतात.
क + क + … + क (ख वेळा) या पुनरावृत्त बेरजेस ‘ख आणि क चा गुणाकार’, ख X क (ख गुणिले क) म्हणतात. ख X क हा गुणाकार ख. क किंवा खक असाही लिहितात. बेरजेप्रमाणे गुणाकार या गणितकृत्यासाठीही क्रमनिरपेक्ष नियम आणि सहयोग नियम मिळतात :
(१) कख = खक, क्रमनिरपेक्ष नियम.
उदा., ३ X ८ = ८ X ३
(२) क (खग) = (कख) ग, सहयोग नियम.
उदा., ४ X (७ X ९) = (४ X ७) X ९
गुणाकाराकरिता आणखी तिसरा नियम म्हणजे दोन धन पूर्णांकांच्या बेरजेला तिसऱ्या धन पूर्णांकांने गुणावयाचे असल्यास बेरजेतील प्रत्येक धन पूर्णांकाला गुणून नंतर या गुणाकारांची बेरीज केल्यास चालते. यालाच ‘वितरण नियम’ म्हणतात.
(क + ख) ग = कग + खग
उदा., (५ + ७) X ३ = (५ X ३) + (७ X ३).
क X क X… X क (ख वेळा) असा पुनरावृत्त गुणाकार घेतल्यास तो कख असा लिहतात. क ला ‘पाया’ आणि ख ला ‘घातांक’ म्हणतात. ‘कख हे क घात ख’ किंवा ‘क उन्नीत ख’ असे वाचतात.
घातांकांसाठी पुढील नियम सिद्ध करता येतात : क,ख,प,फ हे धन पूर्णांक असल्यास
(१) क प X क फ = क प+फ,
(२) (क प)फ = क प फ,
(३) (क X ख)प = क प Xख प,
बेरीज, गुणाकार व घात या गणितकृत्यांच्या उलट अनुक्रमे वजाबाकी, भागाकार आणि घातमूल ही गणितकृत्ये आहेत. दिलेल्या क आणि ख, (क > ख) या धन पूर्णांकांकरिता जर क = ख + क्ष असेल तर क्ष ला ‘क, ख ची वजाबाकी’ म्हणतात व ती क – ख (क वजा ख) अशी लिहतात.
फी हा रिक्त संच असेल तर त्याचा संचांक शून्य (०) आहे असे मानतात. कोणत्याही का या संचासाठी का U फी = का असे असल्याने क + ० = क असते. म्हणजेच क – क = ० असे मिळते.
समजा, क मधून ख, भ वेळा वजा केला तर वजाबाकी ग मिळते. हेच क = भख + ग असे लिहितात. जर ग < ख असेल तर यालाच क ला ख ने भागिले असता ‘भ हा भागाकार असून ग ही बाकी (शेष) आहे’ असे म्हणतात. ज्याप्रमाणे बेरजेच्या पुनरावृत्तीने गुणाकार मिळतो त्याचप्रमाणे वजाबाकीच्या पुनरावृत्तीने भागाकार मिळतो, हे वरील विवरणावरून लक्षात येईल.
जर क = ख. ग असेल तर क ला ख ने भागिले असता बाकी शून्य राहून भागाकार ग येईल हे वरील विवेचनावरून स्पष्ट आहे. हेच
| क | = ग असे लिहितात. अर्थात | क | = ख | असेही लिहिता येईल हे उघड आहे. |
| ख | ग |
क = ख. ग असेल तर ‘ख आणि ग हे क चे अवयव आहेत’ असे म्हणतात. हेच (ख। क), (ग । क) असे लिहितात. १ या अंकाला ‘अविकारक घटक’ म्हणतात. कोणत्याही क साठी क = १. क असल्याने १ हा क चा अवयव आहे किंवा (१ । क) आहे. जर ख > १, ग > १ आणि क = ख. ग असेल तर क ला ‘संयुक्त संख्या’ म्हणतात. १ आणि संयुक्त संख्या यांव्यतिरिक्त सर्व धन पूर्णांकांस ⇨अविभाज्य संख्या म्हणतात.
खाली दिलेले काही सामान्य नियम अवयव शोधताना वा भागाकार करताना उपयोगी पडतात:
(१) ज्या संख्येच्या शेवटी ०, २, ४, ६ किंवा ८ असा सम अंक असेल त्या संख्येस २ ने भाग जातो.
(२) ज्या संख्येच्या शेवटच्या दोन अंकांनी बनलेल्या संख्येस ४ ने भाग जातो त्या संख्येचा ४ हा अवयव असतो. त्याचप्रमाणे शेवटच्या तीन अंकांनी बनलेल्या संख्येस ८ ने भाग गेल्यास दिलेल्या संख्येस ८ ने भाग जातो.
(३) ज्या संख्यांमधील अंकांच्या बेरजेस ३ किंवा ९ ने भाग जातो त्या संख्यांना अनुक्रमे ३ किंवा ९ ने भाग जातो.
(४) दिलेल्या संख्येतील पहिल्या, तिसऱ्या, पाचव्या इ. अंकांची बेरीज जर दुसऱ्या, चौथ्या, सहाव्या इ. अंकांच्या बेरजेबरोबर असेल तर किंवा त्यांच्या वजाबाकीस ११ ने भाग जात असेल तर त्या संख्येस ११ ने भाग जातो.
अशा प्रकारचे आणखीही अनेक नियम अभ्यासाने बसविता येतात.
म.सा.वि. आणि ल.सा.वि : दिलेल्या सर्व संख्यांना ज्या संख्येने नि:शेष भाग जातो अशा बऱ्याच संख्या असू शकतात. त्यांपैकी सर्वांत मोठ्या संख्येस दिलेल्या संख्यांचा ‘महत्तम साधारण विभाजक’ (म. सा. वि.) म्हणतात. जर दिलेल्या संख्यांचा (म. सा. वि.) १ असेल तर त्या संख्या सापेक्षतः अविभाज्य असतात. याचप्रमाणे दिलेल्या संख्यांनी भाग जाऊ शकेल अशाही बऱ्याच संख्या असतात व त्यांपैकी सर्वांत लहान संख्येस दिलेल्या संख्यांचा ‘लघुतम साधारण विभाज्य’ (ल. सा. वि) म्हणतात.
दिलेल्या संख्यांचे अवयव पाडून सर्व संख्यांना समाईक असलेल्या अवयवांचा गुणाकार केल्यास म. सा. वि. मिळतो. तसेच प्रत्येक अवयव जितक्या जास्तीत जास्त वेळा आलेला असेल तितक्या वेळा घेऊन त्यांचा गुणाकार केल्यास ल. सा. वि. मिळतो.
उदा., १२६ = २ X ३ X ३ X ७, ३०८ = २ X २ X ७ X ११
यावरून १२६ आणि ३०८ या संख्यांचा
म. सा. वि. = २ X ७ = १४
आणि ल. सा. वि. = २ X २ X ३ X ३ X ७ X ११ = २७७२.
यूक्लिडीय गणनविधी : या पद्धतीने दिलेल्या संख्यांचे अवयव न पाडता त्यांचा म. सा. वि काढता येतो. क, ख हे धन पूर्णांक (क > ख) असतील तर क = ख. भ + ग; o< ग < ख, असे लिहिता येईल [भ—भागाकार,ग—बाकी]. येथे (क, ख) चा आणि (ख, ग) चा म. सा. वि. एकच असतो. पुन्हा ख = ग. भ१ + ग१ असे लिहता येईल. (ख, ग) चा आणि (ग, ग१,) चा म. सा. वि. एकच असेल. याचप्रमाणे शून्य बाकी उरेपर्यंत केले असता त्यापूर्वी जी बाकी असेल तो (क, ख) चा अपेक्षित म. सा. वि. होय.
वर दिलेले उदाहरण यूक्लिडीय गणनविधिपद्धतीने पुढीलप्रमाणे सोडविता येईल:
३०८ = १२६ X २ + ५६
| १२६ = ५६ X २ + | १४ |
५६ = १४ X ४ + ०
यावरून ३०८ व १२६ यांचा म. सा. वि. १४ आहे.
| अपूर्णांक :ख ने क ला नि:शेष भाग जात नसेल तर | क | या संख्येस‘व्यवहारी अपूर्णांक’ म्हणतात. क आणि ख ला अनुक्रमे ‘अंश’ | ||
| ख | ||||
| आणि ‘छेद’ म्हणतात. जर क < ख असेल तर | क | याला ‘युक्त अपूर्णांक’ म्हणतात. | ||
| ख | ||||
| व्यवहारी अपूर्णांकांचे गुणधर्म : (१) | क | = | प क | हे समीकरण कोणत्याही प साठी खरे असते. यावरून एकच व्यवहारी | |||||
| ख | प ख | ||||||||
| अपूर्णांक विविध रितींनी दर्शविता येतो असे दिसून येई . उदा., | २ | = | ७ X २ | = | १४ | ||||
| ३ | ७ X ३ | २१ | |||||||
| (२) | क | आणि | प | यांची बेरीज पुढीलप्रमाणे करतात : ख आणि फ यांचा ल.सा.वि. ल काढतात. |
| ख | फ |
समजा, ल = रख = गफ आहे, तर
| क | = | र क | आणि | प | = | ग प | असे लिहून | क | + | प | र क | + | ग प | |
| ख | र ख | फ | ग फ | ख | फ | र ख |
| = | र क | + | ग प | = | र क + ग प | ||||
| ल | ल | ल |
अशी बेरीज मिळते. व्यवहारी अपूर्णांकांच्या बेरजेकरिता क्रमनिरपेक्ष आणि सहयोग नियम पूर्णांकांप्रमाणेच सिद्ध करता येतात.
| (३) | क | , | प | यांचा गुणाकार | क प | असा लिहितात. तसेच |
| ख | फ | ख फ | ||||
| क | ÷ | प | = | क प | हे भागाकाराचे सूत्र मिळते. | |
| ख | फ | ख फ |
| (४) | क | ( | प | + | र | ) | = | क प | + | क र |
| ख | फ | ल | ख फ | ख ल |
(५) पूर्णांकांप्रमाणेच अपूर्णांकांचे घात व घातांकांसंबंधीचे नियम आहेत.
दशांश अपूर्णांक : सर्व प्रकारच्या अपूर्णांकांत गणितीय कृत्यांच्या दृष्टीने दशांश अपूर्णांक सोयीचे असतात. अशा अपूर्णांकांचे छेद १०, १००, १०००, … इ. म्हणजे १० चे घात असतात. यामध्ये छेद दर्शविण्यासाठी त्यात १ वर जितकी शून्य असतील तितके अंशातील अंक उजवीकडून सोडून एक टिंब देतात. या टिंबास ‘दशांशचिन्ह’ म्हणतात.
| उदा., | ४५ | = | .४५. |
| १०० |
दिलेल्या दशांश अपूर्णांकात दशांशचिन्हानंतर जेवढी स्थळे असतील तितका १० चा घात म्हणजे १ वर शून्ये छेदात लिहून मग दशांशचिन्ह काढून टाकले, की दशांश अपूर्णांकाचे व्यवहारी अपूर्णांकात रूपांतर होते.
| उदा., ·७ = | ७ | , | ·०४७ = | ४७ |
| १० | १००० |
दशांश अपूर्णांकांची बेरीज करताना दिलेल्या प्रत्येक अपूर्णांकाची दशांशस्थळे प्रथम सारखी करावीत व दशांशचिन्हे एकाखाली एक येतील अशा प्रकारे संख्या मांडून मग त्यांची बेरीज करावी.
| उदा., | ·७, ·६३ आणि ०·४७ यांची बेरीज करण्यासाठी | ||||||
| ·७ | = | ७०० | = | ·७०० | व ·६३ | = ·६३० मांडून | |
| १००० | |||||||
| ·७०० | |||||||
| + ·६३० | |||||||
| + ०·४७ | |||||||
| १.३७७ | अशी बेरीज येईल. | ||||||
दशांश अपूर्णांकांचा गुणाकार करताना दिलेल्या सर्व संख्यांतील दशांश चिन्हे वगळून त्या संख्यांचा नेहमीप्रमाणे गुणाकार करावा व मग सर्व संख्यांत मिळून जितकी दशांशस्थळे असतील तितकी गुणाकारात द्यावीत. उदा., ·३ X २·९ X ·०७ यात ३ X २९ X ७ = ६०९ व एकूण दशांशस्थळे चार, म्हणून गुणाकार ०·०६०९ असा होईल.
दोन दशांश अपूर्णांकांचा भागाकार करताना प्रथम त्यांना पूर्णांकी रूप देऊन साधा भागाकार करावा. भागाकारात दशांशचिन्ह कोठे द्यावे हे ठरविण्याची पद्धती खालील उदाहरणांवरून स्पष्ट होईल :
| (१) | ९·३६१ | = | ९३६१ | × | १० | = | ९३६१ | × | १ |
| २·३ | १००० | २३ | २३ | १०० | |||||
| = | ४०७ | × | १ | = | ४·०७ | ||||
| १०० | |||||||||
| (२) | ९३६·१ | = | ९३६१ | × | १०० | = | ९३६१ | × | १० |
| ·२३ | १० | २३ | २३ | ||||||
| = | ४०७ | × | १० | = | ४०७० | ||||
काही वेळा जरूर तितक्या अचूकतेसाठी दशांश अपूर्णांकाचे मूल्य काही विशिष्ट दशांशस्थळांपर्यंतच मांडणे आवश्यक असते. उदा., एखाद्या राशीचे मूल्य .१८५७१४३५ असे असेल व चार दशांशस्थळांपर्यंत अचूकता पुरेशी असेल तर या अपूर्णांकाचे मूल्य ·१८५७ होईल. हे मूल्य अर्थात मूळ मूल्यापेक्षा कमी अचूक असते. याकरिता ‘ज्या दशांशस्थळापर्यंत मूल्य पाहिजे असेल त्यापुढील अंक ५ किंवा ५ पेक्षा मोठा असेल तर त्याअगोदरचा अंक एकाने वाढवावा आणि तो ५ पेक्षा कमी असेल तर अगोदरचा अंक तसाच ठेवाव’ असा नियम आहे. वरील दशांश अपूर्णांकाचे पाच दशांशस्थळांपर्यंतचे मूल्य ·१८५७१ आणि दोन दशांशस्थळांपर्यंत ·१९ होईल.
आवर्तदशांश : व्यवहारी अपूर्णांक दशांशरूपात मांडल्यास त्यात काही अंकमालिका पुन्हा पुन्हा येत राहतात.
| उदा., | १ | = ०·३३३ … | ||||
| ३ | ||||||
| ३ | = | ०·२७२७२७ …, | १ | = ०·१४२८५७१४२८५७ … या पुन्हा | ||
| ११ | ७ | |||||
पुन्हा येणाऱ्या अंकांना ‘आवर्तअंक’ म्हणतात. असे आवर्त अपूर्णांक मांडताना त्यातील एकच अंक पुन्हा पुन्हा येत असेल तर त्याच्या डोक्यावर टिंब देऊन आणि काही अंकांचा गट पुन्हा पुन्हा येत असल्यास त्यातील पहिल्या व शेवटच्या अंकांवर टिंबे देऊन दर्शवितात.
| उदा., | १ | = | ०·३ | १ | ०·१४२८५७. |
| ३ | ७ |
दिलेल्या आवर्तदशांशाच्या बरोबरचा व्यवहारी अपूर्णांक कढण्याची पद्धती खालील उदाहरणावरून स्पष्ट होईल.
समजा, ३·१८१८१८… या आवर्तदशांशाच्या बरोबरचा व्यवहारी अपूर्णांक क्ष आहे.
| समजा, ३·१८१८१८ … या आवर्तदशांशाच्या बरोबरचा व्यवहारी अपूर्णांक क्ष आहे. | |||||||||
| क्ष | = | ३·१८१८ … | |||||||
| १०० क्ष | = | ३१८·१८१८ … | |||||||
| ९९क्ष | = | ३१५ | |||||||
| ∴ | क्ष | = | ३१५ | = | ३५ | ||||
| ९९ | ११ | ||||||||
हा प्रश्न सोडविण्यासाठी क + क ग + क ग२+ … ही अनंत गुणोत्तरश्रेढीही वापरता येते. येथे ग हा १ पेक्षा लहान असल्यास या श्रेढीची सीमांत 
बेरीज आहे असे मानतात. या स्वरूपात ३·१८१८… हा आवर्तदशांश पुढीलप्रमाणे मांडता येईल:
|
३·१८१८ … =३
|
+ |
१८ |
+ |
१८ |
+ |
१८ |
+ |
… |
|
|
|
१०० |
१००२ |
१००३ |
|
|||||||
|
= |
३ |
+ |
१८ |
} |
१ |
+ |
१ |
+ |
१ |
+… } |
|
१०० |
१०० |
१००२ |
||||||||
| = | ३ + | १८ | × | १ | = ३ + = | ३५ | ||
| १०० | १ − | १ | ११ | |||||
| १०० | ||||||||
घातमूले, करणी संख्या : घातमूलकृत्य म्हणजे एखाद्या संख्येचे वर्गमूळ, घनमूळ, पंचमूळ इ. काढणे. घातमूल व घात ही कृत्ये एकमेकांच्या उलट आहेत.उदा., ५ X ५ X ५ = ५३ = १२५ म्हणून ५ हे १२५ चे घनमूळ होय. २ ८ = २५६ म्हणून २ हे २५६ चे अष्टमूळ होय. हे कृत्य 
असे लिहितात. म्हणजे जे मूळ काढावयाचे आहे तो आकडा √ या करणी चिन्हाच्या डाव्या बाजूच्या खाचेत दर्शवितात. नुसते वर्गमूळ दर्शविताना २ हा आकडा लिहीत नाहीत. उदा., 
काही संख्यांचे मूळ क/ख (क आणि ख पूर्णांक) अशा स्वरूपात मांडता येत नाही. अशा संख्यांना ‘करणी संख्या’ म्हणतात. उदा., √२,√३, 
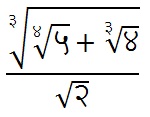करणी संख्यांचा शोध वेदकालातील आहे. शूल्वसूत्रात 
या करणी संख्या दिलेल्या आढळतात. 
असे दिलेले असून ते पाच दशांशस्थळांपर्यंत बरोबर आहे. करणी संख्येचे मूल्य काढण्याकरिता दशांश अपूर्णांक वापरणे सोयीचे असते, तथापि ते शेवटच्या दशांशस्थळापर्यंत काढणे शक्य नसते. त्यामुळे अशा संख्यांचे मूल्य जरूर तितक्या दशांशस्थळांपर्यंत काढून ते मूल्य आसन्न आहे हे दर्शविण्यासाठी त्यामागे ≒ असे चिन्ह लिहिले जाते उदा., √२≒ १·४१४२, √५ ≒२·२३६.
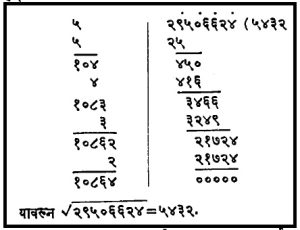
वर्गमूळ : दिलेल्या संख्येचे वर्गमूळ काढण्याची रीत पुढीलप्रमाणे आहे :
दिलेल्या संख्येतील एकम् स्थाळाच्या अंकावर टिंब द्यावे. त्या अंकापासून डावीकडे प्रत्येक दुसऱ्या अंकावर टिंब द्यावे. अशा प्रकारे दिलेल्या संख्येचे प्रत्येकी दोन अंकांचा एक असे भाग होतील. डावीकडील पहिला भाग फक्त एकाच अंकाचाही असू शकेल. संख्या दशांश अपूर्णांकी असल्यास दशांशचिन्हापासून उजवीकडे पुढे प्रत्येक दुसऱ्या अंकावर टिंब द्यावे व शेवटी राहिलेल्या अंकावर दोन अंक पूर्ण करण्यासाठी आवश्यक असल्यास शून्य देऊन शेवटच्या अंकावर टिंब द्यावे.
डावीकडे प्रथम भागातील संख्येपेक्षा लहान पण त्या संख्येच्या जवळचा सर्वांत मोठा वर्ग शोधून त्याचे वर्गमूळ उजवीकडे भागाकाराच्या ठिकाणी लिहावे. नंतर शोधून काढलेला सर्वांत मोठा वर्ग त्या प्रथम भागातून वजा करावा आणि जी बाकी राहील तिच्यापुढे दिलेल्या संख्येचा दुसरा भाग लिहावा. ही नवी संख्या म्हणजे नवे भाज्य होय.
भाजकाकरिता वर लिहिलेले मूळ दुप्पट करून लिहावे आणि भाज्याचा उजवीकडील एक अंक सोडून राहिलेल्या भाज्यातून हा भाजक किती वेळा जातो ते शोधावे आणि ती संख्या भाजक आणि भागाकार यांच्या उजवीकडे दोन्ही ठिकाणी लिहावी. अशा प्रकारे नवा भाजक मिळतो.
वाढविल्या गेलेल्या भाजकास त्या शेवटच्या संख्येने गुणून भाज्याच्या खाली लिहून वजाबाकी करावी. नंतर जी बाकी राहील तिच्या पुढे अगोदर घेतलेल्या भागाच्या पुढचा भाग लिहावा. हा नवा भाज्य होय. भाजकात नवीन संख्या मिळवावी. नव्या भाज्यातील एक आकडा वगळून येणाऱ्या संख्येस भाजकाने किती वेळा भाग जातो ती संख्या भागाकारात व भाजकात उजवीकडे लिहावी. ह्याचप्रमाणे दिलेल्या संख्येतील सर्व भाग संपेपर्यंत क्रिया करीत रहावे. म्हणजे भागाकाराच्या जागी येणारी संख्या हे इष्ट वर्गमूळ होय. खालील उदाहरणावरून ही पद्धती स्पष्ट होईल :
| . . . . | |||||||||
| ५ | २९५०६६२४ (५४३२ | ||||||||
| ५ | २५ | ||||||||
| १०४ | ४५० | ||||||||
| ४ | ४१६ | ||||||||
| १०८३ | ३४६६ | ||||||||
| ३ | ३२४९ | ||||||||
| १०८६२ | २१७२४ | ||||||||
| २ | २१७२४ | ||||||||
| १०८६४ | ००००० | ||||||||
यावरून 
डाव्या बाजूकडील स्तंभातील शेवटचा आकडा हा वर्गमूळाच्या दुप्पट आहे हे सहज पडताळून पहाता येईल. वर दिलेली वर्गमूळ काढण्याची रीत (क + ख)२= क २ + (२ क + ख) ख या बैजिक सूत्रावर आधारलेली आहे.
घनमूळ : दिलेल्या संख्येचे घनमूळ काढण्याची रीत खालीलप्रमाणे :
(१) दिलेल्या संख्येचे डावीकडे दोन स्तंभ पाडावे व उजवीकडे भागाकारदर्शक कंस करावा.
(२) वर्गमूळ काढण्याच्या पद्धतीप्रमाणेच दिलेल्या संख्येचे भाग पाडावेत, मात्र येथे प्रत्येक भागात दोनऐवजी तीन अंक घ्यावेत. येथे डावीकडील पहिल्या भागात १ किंवा २ अंकही असू शकतील. तसेच दिलेल्या संख्या दशांश अपूर्णांकी असल्यास शेवटी राहिलेल्या अंकावर तीन अंक पूर्ण करण्याकरिता एक किंवा दोन शून्ये लिहावी लागतील.
(३) पहिल्या भागातून ज्याचा घन वजा जाईल असा सर्वांत मोठा अंक शोधून तो भागाकाराच्या ठिकाणी लिहावा. हाच अंक घनमूळातील पहिला अंक होय. त्याचा घन पहिल्या भागातून वजा करावा व बाकी राहिलेल्या संख्येवर दुसरा भाग लिहावा. ही संख्या नवे भाज्य होईल.
(४) घनमूळातील पहिल्या अंकाची तिप्पट पहिल्या स्तंभात मांडावी व त्या अंकाच्या वर्गाची तिप्पट दुसऱ्या स्तंभात लिहून त्यावर दोन शून्य मांडावीत. ही संख्या वरील नव्या भाज्याचा शोधक भाजक होय.
(५) या भाजकाचा वरील नव्या भाज्यास किती वेळा भाग जातो तो अंक ठरवावा. हा अंक घनमूळातील दुसरा अंक असून तो भागाकारात द्वितीय स्थळी लिहावा. तोच अंक पहिल्या स्तंभातील अंकावर लिहावा व अशा प्रकारे मिळालेल्या संख्येस त्या अंकाने गुणून तो गुणाकार दुसऱ्या स्तंभातील संख्येखाली मांडून त्यांची बेरीज करावी. ही बेरीज म्हणजेच नव्या भाज्याचा भाजक होय. तिला वरील अंकाने गुणून गुणाकार (३) मधील नव्या भाज्यातून वजा करावा. बाकी राहील त्या संख्येवर दिलेल्या संख्येतील तिसरा भाग लिहावा. अशा प्रकारे मिळालेली संख्या हे दुसरे नवे भाज्य होय.
(६) वरील अंकांची दुप्पट पहिल्या स्तंभातील संख्येखाली मांडून त्यांची बेरीज करावी ही बेरीज भागाकारातील संख्येची तिप्पट असेल. वरील अंकाचा वर्ग दुसऱ्या स्तंभातील संख्येखाली लिहून हिच्यासह स्तभांतील वरील तीन संख्यांची बेरीज करावी. ती भागाकारातील संख्येच्या वर्गाची तिप्पट असेल. या संख्येवर दोन शून्ये द्यावीत. अशी संख्या नवा शोधक भाजक होईल.
(७) या शोधक भाजकाने (५) मधील नव्या भाज्यास भाग शोधावा. हा नवा अंक भागाकारात तृतीय स्थळी मांडावा. तोच पहिल्या स्तंभातील संख्येवर लिहावा. अशा संख्येस नवीन अंकाने गुणून गुणाकार दुसऱ्या स्तंभातील शेवटच्या संख्येखाली लिहून त्यांची बेरीज घ्यावी. ही बेरीज (५) मधील नव्या भाज्याचा पुरा भाजक होय. या नव्या भाजकाला नवीन अंकाने गुणून गुणाकार या भाज्यातून वजा करावा. बाकी राहिलेल्या संख्येवर पुढील चौथा भाग घ्यावा.
(८) यापुढील क्रिया (६) व (७) प्रमाणेच दिलेली संख्या संपेपर्यंत कराव्यात.
(९) भागाकाराच्या ठिकाणची संख्या इष्ट घनमूळ होय. त्यात योग्य ठिकाणी दशांशचिन्ह द्यावे.
वरील पद्धतीनुसार ९२६८५९.३७५ या संख्येचे घनमूळ काढून दाखविले आहे :
| स्तंभ १ | स्तंभ २ | संख्या | घनमूळ | |||||||
| २७७ | २४३०० | ९२६८५९·३७५ | (९७·५ | |||||||
| १४ | १९३९ | ७२९ | ||||||||
| २९१५ | २६२३९ | १९७८५९ | ||||||||
| ४९ | १८३६७३ | |||||||||
| २८२२७०० | १४१८६३७५ | |||||||||
| १४५७५ | १४१८६३७५ | |||||||||
| २८३७२७५ | ००००००० | |||||||||
म्हणून 
वरील रीत (क + ख)३ – क ३ = (३ क २+ कख+ ख २) ख
या बैजिक सूत्रावर आधारलेली आहे.
गुणोत्तर व प्रमाण: अंकगणितात गुणोत्तर व प्रमाण यांच्या कल्पना व मांडणी हा महत्त्वाचा टप्पा आहे.
दोन राशींची तुलना करण्यासाठी गुणोत्तराचा उपयोग होतो. या राशी एकाच प्रकारच्या व परिमाणाच्या असणे आवश्यक आहे. उदा., दोन रेषांच्या लांबीचे गुणोत्तर मांडण्यासाठी त्या एकाच परिमाणात म्हणजे दोन्ही रेषा फूट किंवा मीटर किंवा मैल अशा एकाच मापात दर्शविणे आवश्यक आहे. गुणोत्तर व्यवहारी अपूर्णांकाच्या स्वरूपात (त्याच्या किमान पदात) किंवा भागाकार करून दशांश अपूर्णांकात मांडले जाते.
| ४५ मी. व ३० मी. यांचे गुणोत्तर | ४५ | = | ३ | = १·५ असे येईल. |
| ३० | २ |
गुणोत्तर ही केवळ एक संख्या असून दोन राशींचे गुणोत्तर मांडल्यावर त्या राशींची मूळ मुल्ये व त्यांचे परिणाम यांना महत्त्व उरत नाही.
दोन निरनिराळ्या जातींच्या राशींची गुणोत्तरे समान असल्यास त्यांतील राशी एकाच प्रमाणात आहेत असे म्हणतात. प्रमाणात मांडलेल्या चार राशींपैकी कोणत्याही तीन दिलेल्या असल्यास उरलेली राशी काढता येते. या प्रश्नास ‘त्रैराशीक’ म्हणतात. यातील पहिल्या जातीची राशी कमी वा अधिक झाल्यास दुसऱ्या जातीची राशी कमी व आधिक झाली तर या राशी सम प्रमाणात आहेत असे म्हणतात.
उदा., ३ रूपयांना १५ आंबे मिळतात तर ५ रूपयांना किती मिळतील?
यात राशींचा क्रम पुढीलप्रमाणे लिहितात :
| रूपये | : | रूपये | : : | आंबे | : | आंबे |
| ३ | ५ | १५ | ? |
येथे अधिक रूपयांना अधिक आंबे मिळणार हे उघड असल्याने या राशी सम प्रमाणात आहेत.
रूपयांचे गुणोत्तर = आंब्यांचे गुणोत्तर
| ३ | = | १५ |
| ५ | ? |
| यावरून इष्ट आंबे = | ५X१५ | =२५ आंबे |
| ३ |
अशा त्रैराशिकाला ‘सम त्रैराशिक’ म्हणतात व ते + + असे दर्शवितात. याच उदाहरणात ‘२ रूपयांस किती आंबे?’ असे विचारल्यास ते त्रैराशिक — असे दर्शवितात. पहिल्या जातीची राशी अधिक वा कमी झाल्यास दुसऱ्या जातीची राशी त्याच्या उलट म्हणजे अनुक्रमे कमी वा आधिक होत असेल तर या राशी व्यस्त प्रमाणात आहेत असे म्हणतात. उदा., ४ माणसांना एक काम करण्यास १५ दिवस लागतात तर १२ माणसांना तेच काम करण्यास किती दिवस लागतील?
| माणसे | : | माणसे | : : | दिवस | : | दिवस |
| ४ | १२ | १५ | ? |
येथे माणसे आधिक असल्यास काम पूर्ण करण्यास कमी दिवस लागतील यामुळे ह्या राशी व्यस्त प्रमाणात आहेत. म्हणून दिलेल्या राशींचे म्हणजे माणसांचे गुणोत्तर उलटे करून प्रमाण
| १२ | = | १५ | असे लिहिले पाहिजे. यावरूण इष्ट दिवस | |
| ४ | ? | |||
| = | १५ X ४ | = | ५ दिवस. | |
| १२ | ||||
अशा त्रैराशिकास‘व्यस्त त्रैराशिक’ म्हणतात व ते + – किंवा – + असे दर्शविले जाते.
दिलेले त्रैराशिक सम आहे की व्यस्त, हे ठरविण्यासाठी त्यातील राशींसंबंधी प्रत्यक्ष ज्ञान असणे आवश्यक असते.
त्रैराशिकाप्रमाणेच पंचराशिक (पाच राशी दिलेल्या असल्यास सहावी राशी काढणे), सप्तराशिक (सात राशी दिलेल्या असल्यास आठवी राशी काढणे) इ.बहुराशिके वरीलप्रमाणेच मांडून व त्यातील प्रमाणे सम वा व्यस्त आहेत हे ठरवून सोडविता येतात.
सरासरी : दिलेल्या निरनिराळ्या राशींच्या मूल्यांची बेरीज करून तिला राशींच्या संख्येने भागले असता मिळणाऱ्या संख्येस त्या राशींच्या मूल्यांची सरासरी म्हणतात. सरासरी काढताना दिलेल्या राशी एकाच जातीच्या व त्या एकाच परिमाणात मोजणे आवश्यक असते. उदा., एखाद्या वर्गातील विद्यार्थ्यांच्या वजनांची सरासरी काढावयाची असल्यास त्यांच्या वजनांची परिमाणे सारखीच असणे जरूर आहे.
पर्जन्यमान, देशाचे वार्षिक उत्पन्न, विविध वस्तूंचे वार्षिक उत्पादन यांसारख्या राशींची आकडेवारी सरासरीने दर्शविली जाते. निरनिराळ्या वयोमानांनुसार वजन व उंची यांचे प्रमाण काय असावे, हे दर्शविणाऱ्या कोष्टकातील आकडे सरासरीवरच आधारलेले असतात. सरासरी दर्शविण्यासाठी जितक्या जास्तीत जास्त राशी लक्षात घेतल्या असतील तितकी ती सरासरी जास्त विश्वसनीय होईल. विम्याचे गणित पुष्कळ अंशी सरासरीवर अवलंबून असते.
शेकडेवारी : मूळ संख्या कितीही मोठ्या वा लहान असल्या तरी १०० हे मान घेऊन प्रमाण मांडणे उपयुक्त ठरते. या प्रमाणास ‘शेकडाप्रमाण’ किंवा ‘शेकडेवारी’ म्हणतात. शेकडेवारी दर्शविण्यासाठी % अशी खूण करण्यात येते. व्यवहारात शेकडेवारीचा अनेक ठिकाणी उपयोग करण्यात येतो. उदा., परीक्षेतील उत्तीर्ण विद्यार्थ्यांची शेकडेवारी, व्यापारातील नफा वा तोटा यांची शेकडेवारी, वस्तूंच्या उत्पादनातील विशिष्ट कसोटीला उतरणाऱ्या वस्तूंची शेकडेवारी इत्यादी.
समजा, एका वर्गातील ४०विद्यार्थ्यांपैकी ३२ उत्तीर्ण झाले व दुसर्‍या वर्गातील ५६ विद्यार्थ्यांपैकी ४२ उत्तीर्ण झाले. पहिल्या वर्गातील उत्तीर्ण
| विद्यार्थ्यांची शेकडेवारी= | १०० X ३२ | = ८० % व दुसर्‍या वर्गातील |
| ४० |
| उत्तीर्ण विद्यार्थ्यांची शेकडेवारी | १०० X ४२ | = ७५ % इतकी येते. |
| ५६ |
यावरून पहिल्या वर्गातील उत्तीर्ण विद्यार्थ्यांचे प्रमाण अधिक आहे असे दिसून येते. अशा प्रकारे शेकडेवारीच्या साहाय्याने निरनिराळ्या प्रमाणांची तुलना करणे सुलभ होते.
सोयीनुसार १०० ऐवजी इतर संख्याही प्रमाण दर्शविण्यासाठी वापरल्या जातात. लोकसंख्येतील जन्ममृत्यूचे प्रमाण दर हजारी सांगितले जाते. विशिष्ट रोगाने आजारी असणाऱ्या व्यक्तींचे प्रमाण दर दहा हजारी वा दर लक्षात मांडले जाते.
सरळ व्याज व चक्रवाढ व्याज : एखाद्या व्यवहारात गुंतविलेल्या मूळ रकमेस ‘मुद्दल’ म्हणतात. यावरील व्याजाचा दर सर्वसाधारणपणे ‘दर साल दर शेकडा’ असा निर्देशित करतात. मुद्दल व एका वर्षानंतर त्यावर मिळणारे व्याज यांच्या बेरजेस एका वर्षानंतरची ‘रास’ म्हणतात.
एका वर्षानंतर झालेले व्याज देऊन पुढील वर्षाकरिता मूळ मुद्दलच व्याजाच्या हिशेबासाठी लक्षात घेतल्यास त्या व्याजास ‘सरळ व्याज’ म्हणतात.
एका वर्षानंतर झालेले व्याज न देता मूळ मुद्दलात ते जमा करून पुढील वर्षाकरिता ही रास व्याजाच्या हिशेबाकरिता मुद्दल म्हणून विचारात घेतल्यास त्या व्याजास ‘चक्रवाढ व्याज’ म्हणतात.
समजा, आज १०० रू. द. सा. द. शे. ५ रू ने व्याजी दिले. एक वर्षानंतर मुद्दल व व्याज मिळून १०५ रू येणे झाले. या १०५ रू. वर (म्हणजे पहिल्या वर्षाच्या राशीवर) दुसऱ्या वर्षाचे व्याज आकारावयाचे म्हणून दुसऱ्या वर्षाच्या शेवटी होणारी रास काढण्यासाठी पुढीलप्रमाणे त्रैराशिक मांडता येईल:
| मुद्दल रु. | : | मुद्दल रु. | : : | रास रु. | : | रास रु. |
| १०० | १०५ | १०५ | ? |
| इष्ट रास = | १०५X१०५ | = | (१०५२) | रु. |
| १०० | १०० |
| याचप्रमाणे तिसऱ्या वर्षाच्या शेवटी | (१०५)३ | रु. व चौथ्या वर्षाच्या |
| (१००)२ |
| शेवटी | (१०५)४ | रु. रास होईल. अर्थात ही रास मूळच्या १०० रु. |
| (१००)३ |
| मुद्दलाची होय. म्हणून १ रु.मुद्दलाची रास २ वर्षांनी | ( | १०५ |
)२ ·०५)२ |
| १०० |
रु., ३ वर्षांनी (१·०५)३ रु. व ४ वर्षांनी (१·०५)४ रु. होईल यावरून सामान्यनियम असा बसविता येईल,
| की चक्रवाढ व्याजाचा दर द असेल तर ववर्षांनी १ रु. ची रास | ( | १ | + | द | )व |
| १०० |
रु. होईल. साध्या गुणाकाराने हे उत्तर काढणे जिकीरीचे असते. त्याकरिता लॉगरिथमपद्धतीचा वापर करणे सोयीचे असते.
आ. १
क्षेत्रफळ, घनफळ,पृष्ठफळ: सुतारकाम, गवंडीकाम, स्थापत्य इ. अनेक प्रकारच्या दैनंदिन व्यवहारांत विविध आकारांच्या व आकारमानांच्या भूमितीय आकृत्यांचे क्षेत्रफळ, घनफळ, वा पृष्ठफळ काढणे आवश्यक असते. याकरिता अंकगणितातील विविध कृत्यांचा उपयोग कसा होतो हे खालील उदाहरणांवरून स्पष्ट होईल.
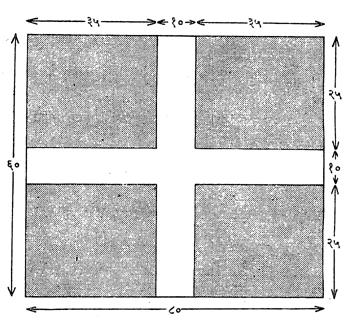
उदा. १: एका बागेचे क्षेत्र आयताकृती असून तिची लांबी ८० मी. व रुंदी ६० मी. आहे. या क्षेत्रात लांबी-रुंदीला समांतर असे १० मी. रुंदीचे रस्ते मधोमध ठेवलेले आहेत, तर प्रत्यक्ष बागेचे क्षेत्रफळ किती? (आ.१).
येथे प्रत्यक्ष बागेसाठी ३५ X २५ चे चार आयत शिल्लक रहातात व ते सर्व जोडून (३५ X २५) X ४ = ३,५०० चौरस मी. क्षेत्रफळाची बाग होते. म्हणजे या गणिताचे उत्तर (८० – १०) X (६० – १०) हे होय. अर्थात क्षेत्राच्या परिमाणांतून रस्त्यांची रुंदी वजा करुन मग गुणाकार करणे हे याचे सूत्र झाले.
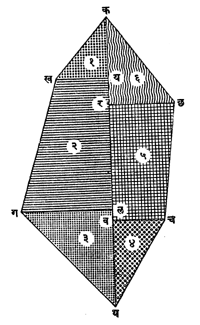
उदा. २ क ख ग घ च छ या जागेचे क्षेत्रफळ काढण्यासाठी क घ जोडून तिच्यावर खय, छर, गल आणि चव हे लंब टाकावे. नंतर बाजूंची व लंबांची तसेच कय, यर, रल आणि लव ही मापे घ्यावीत येथे (१) , (३), (४), व (६) हे काटकोन त्रिकोण आणि (२) व (५) हे समलंब चौकोन आहेत (आ.२) या दोन आकृत्यांच्या सूत्रांवरून सबंध आकृतीचे क्षेत्रफळ काढता येईल.
आ. २
ताळा : प्रत्येक उदाहरणात काही गोष्टी पक्ष म्हणून दिलेल्या असतात व काही साध्य करावयाच्या असतात. आपणास प्राप्त झालेले उत्तर हेच पक्ष धरुन ज्या कृत्यांची उदाहरण सोडविलेले असेल त्याच्या उलट कृत्ये करुन मूळच्या पक्षातील एखादी बाब शोधून काढणे व ती दिलेल्या बाबीशी पडताळून पाहणे हे ताळा करण्याचे तत्त्व होय. ताळा केल्याने उदाहरणाच्या उत्तराची खात्री पटते. गुणाकाराचा ताळा भागाकाराने व भागाकाराचा गुणाकाराने, घातमूलाचा घाताने व घाताचा घातमूलाने- थोडक्यात म्हणजे दोन व्युत्क्रम कृत्यांनी परस्परांचा ताळा होऊ शकतो.
उदा.: एका सुताराने १६० रु. स एक कपाट बनविले व ते २०० रु. स विकले, तर त्याला शेकडा किती नफा झाला?
| मूळ किंमत रु. | मूळ किंमत रु. | नफा रु. | नफा रु. | |
| १६० : | १०० : | : | : ४० | : ? |
| १००X४० | = २५ % नफा | |
| १६० |
ताळा – आता १६० रु. मूळ किंमत व २५ % नफा धरून विक्रीची किंमत काढू.
| मूळ किंमत रु. | मूळ किंमत रु. | विक्रीची किंमत रु. | विक्रीची किंमत रु. |
| १०० : | १६० : | : १२५ | : ? |
| १६०X१२५ | = २०० रू. विक्रीची किंमत. | |
| १०० |
तसेच २०० रू. विक्रिची किंमत व २५% नफा धरून मूळ किंमत काढू.
| विक्रीची किंमत रु. | विक्रीची किंमत रु. | मूळ किंमत रु. | मूळ किंमत रु. |
| १२५ : | २०० : | : १०० : | ? |
| २००X१०० | = १६० रू. मूळ किंमत. | |
| १२५ |
ताळ्यावरुन काढलेली ही दोन्ही उत्तरे पक्षाशी जुळतात म्हणून दिलेल्या गणिताचे काढलेले उत्तर (२५% नफा) हे बरोबर होय.
पहा : अंक गणित संख्यासिद्धांत संचसिद्धांत महत्वमापन.
संदर्भ : 1. Bakst, A. Arithmetic for the Modern Age, New York, 1960.
2. Gurjar, L. V. Ancient Indian Mathematics and Vedha, Poona, 1947.
३. गोखले, गो. कृ. अंकगणित, पुणे, १९०७.
४. छत्रे, के. ल. अंकगणित, मुंबई, १८७९.
५. जार्विस, जी. आर. अंकगणित, मुंबई, १८५८.
गुर्जर, ल. वा. देशपांडे, कृ. के.