आव्यूह सिद्धांत : आव्यूह म्हणजे काही [सत् किंवा सदसत्, →संख्या] संख्यांची एका विशिष्ट तऱ्हेने केलेली आयताकार मांडणी. ज्या संख्यांनी आव्यूह तयार होतो त्यांना त्या आव्यूहाचे घटक म्हणतात. खाली दाखविलेल्या अ ह्या आव्यूहात ग x म संख्या ग पंक्तीत आणि म स्तंभांत मांडल्या आहेत. अशा आव्यूहास ग x म क्रमी आव्यूह म्हणतात. सुलभतेसाठी प व्या पंक्तीतील आणि स व्या स्तंभातील घटक अपस असा लिहिला आहे.
| अ= | अ११ | अ१२ | अ१३ | … | अ१स | … | अ१म |
| अ२१ | अ२२ | अ२३ | … | अ२स | … | अ२म | |
| अ३१ | अ१२ | अ३३ | … | अ३स | … | अ३म | |
| . | . | . | … | . | … | . | |
| अप१ | अप२ | अप३ | … | अपस | … | अपम | |
| . | . | . | … | . | … | . | |
| अय१ | अय२ | अय३ | … | अयस | … | अयम |
वरील आव्यूहातील अपस हा लक्षण घटक समजून अ=[ अपस] यxम असे थोडक्यात लिहितात. जेव्हा पंक्तीची आणि स्तंभांची संख्या (ग,म) संदर्भावरून स्पष्ट असेल, तेव्हा नुसते आ = [ अपस] असे लिहितात. एकच पंक्ती असलेल्या आव्यूहास पंक्ति-सदिश आणि एकच स्तंभ असलेल्या आव्यूहास स्तंभ-सदिश म्हणतात. जर पंक्तीची आणि स्तंभांची संख्या समान असेल (ग=म), तर अशा आव्यूहास म-क्रमी चौरस आव्यूह म्हणतात. ज्या चौरस आव्यूहात, कोणत्याही प,स साठी अपस= असप असेल, तर त्यास सममित आव्यूह म्हणतात आणि जर अपस= – असप असेल, तर त्यास वितल सममितआव्यूह म्हणतात. अ११, अ२२,… … …., अमम या घटकांनी म-क्रमी चौरस आव्यूहाचा कर्ण तयार होतो. वितल सममित आव्यूहाच्या कर्णाचे सर्व घटक शून्य असणार हे उघड आहे.
कर्ण आव्यूह : जर चौरस आव्यूहात कर्णातील घटकांखेरीज इतर सर्व घटक शून्य असतील, म्हणजेच अपस हा घटक प्रत्येक प ≠स करिता शून्य असेल, तर त्या आव्यूहास कर्ण आव्यूह म्हणतात. असा आव्यूह, कर्ण (अ११, अ२२,……, अमम) असा दर्शवितात.
त्रिकोणी आव्यूह : जर प्रमुख कर्णाच्या एका बाजूचे सर्व घटक शून्य असतील (म्हणजेच जर प > स, तर अपस = ० किंवा दुसरी शक्यता जर प < स, तर अपस= ०), तर त्यास त्रिकोणी आव्यूह म्हणतात.
पक्षांतरित आव्यूह : अ या ग x म क्रमी आव्यूहाच्या पंक्ती आणि स्तंभ यांची अदलाबदल केली म्हणजेच कोणत्याही प,स साठी अपस हा स व्या पंक्तीत आणि प व्या स्तंभात ठेवला तर जो म x ग क्रमी आव्यूह मिळतो त्यास अ चा पक्षांतरित आव्यूह (अ’) म्हणतात. अर्थात अपस = अ’सप हे उघड आहे.
संयुग्मी आव्यूह : अ च्या प्रत्येक घटकाच्या जागी त्याच्या संयुग्माची [ज्या दोन सदसत् संख्यांचा गुणाकार सत् संख्या असतो त्या संख्यांना संयुग्मी संख्या म्हणतात, → संख्या] स्थापना केली असता जो आव्यूह तयार होईल त्याला अ चा संयुग्मी आव्यूह म्हणतात व तो अ असा दर्शवितात.
समानता :अ आणि क या दोन आव्यूहांतील पंक्तिसंख्या आणि स्तंभसंख्या समान असतील आणि कोणत्याही प, स साठी अपस = कपस असेल, तर अ आणि क हे आव्यूह समान असतात (अ = क).
जर अ हा सममित आव्यूह असेल, तर अ=अ’ असे दाखविता येईल. जर अ =अ’ असेल, तर अ ला हरमाईटीय आव्यूह (हरमाईट या गणितज्ञाच्या नावावरून) म्हणतात. अ चे सर्व घटक सत् असतील, तर तो हरमाईटीय असणारच हे सहज लक्षात येईल.
शून्य आव्यूह : ज्याचे सर्व घटक शून्य आहेत, अशा आव्यूहास शून्य आव्यूह (०) म्हणतात.
बेरीज : अ आणि क या दोन ग x म क्रमी आव्यूहांची बेरीज म्हणजे ख हा असा आव्यूह असतो की, कोणत्याही प,स साठी खपस = अपस + कपस. हेच अ + क = ख असे लिहितात.
ऋण आव्यूह : जर अ + क = ० असेल, तर क ला ऋण अ (किंवा – अ) म्हणतात. असे होण्यास कपस = – अपस असले पाहिजे. म्हणजेच अ च्या प्रत्येक घटकाचे चिन्ह बदलल्यास जो आव्यूह मिळेल त्यास –अ म्हणतात.
वजाबाकी : क + (-अ) म्हणजेच क–अ ही क आणि अ या दोन आव्यूहांची वजाबाकी होय. अर्थातच जर ख = क – अ असेल, तर खपस = कपस – अपस असेल.
अदिश गुणाकार : अ च्या सर्व घटकांना द या अदिशाने (केवळ महत्ता असलेल्या राशीने) गुणले असता द अ हा अदिश गुणाकार सिद्ध होतो. जर ख = द अ असेल, तर खपस = द अपस असले पाहिजे.
आव्यूहांचे घटक सत् किंवा सदसत् संख्या असल्यामुळे आणि आव्यूहांची बेरीज ही त्यांच्या घटकांच्या बेरजेने व्याख्यात (व्याख्या केलेली) केली असल्यामुळे ती क्रमनिरपेक्षी (खालील नियम – १ पहावा) आणि सहयोगी (नियम – २) असते. तसेच अदिश गुणाकारास वितरण नियम (नियम – ३) लागू पडतो. म्हणजेच कोणत्याही अ, क, ख या आव्यूहांसाठी व द या अदिशासाठी खालील नियम लागू होतात.
(१) अ +क = क + अ,
(२) (अ + क) + ख =अ + (क + ख),
(३) द (अ + क) = द अ + द क.
आव्यूह गुणाकार :अ आणि क यांचा अ क हा गुणाकार सिद्ध होण्यासाठी अ च्या स्तंभांची संख्या क च्या पंक्तींच्या संख्येइतकी असणे आवश्यक आहे. या अटीचे पालन झाल्यास अ क या गुणाकाराची व्याख्या पुढीलप्रमाणे करतात.
अ क या गुणाकार आव्यूहातील प व्या पंक्तीतील आणि स व्या स्तंभातील घटक (अ क) पस म्हणजे अ मधील पव्या पंक्तीतील घटक आणि क मधील स व्या स्तंभातील घटक यांचा अनुक्रमाने गुणाकार करून त्या गुणाकारांची बेरीज होय. उदा., (अक)२३ पाहिजे असल्यास अ ची दुसरी पंक्ती आणि क चा तिसरा स्तंभ घेऊन त्यांच्या घटकांच्या गुणाकारांची बेरीज घ्यावयाची. समजा, अ हा ग x म क्रमी आणि क हा म x न क्रमी आहे, तर वरील व्याखेनुसार (अ क)२३ = अ२१ क१३ + अ२२ क२३ + अ२३ क३३+…….+अ२म कम३ होईल. हेच सूत्ररूपाने
| म | ||
| (अ क)पस = | ∑ | अपइकइस असे लिहितात. यावरून अ-च्या पंक्तीतील घटकांची संख्या आणि कच्या स्तंभातील घटकांची संख्या समान असली तरच वर दिलेल्या गुणाकाराच्या |
| इ=१ |
व्याख्येस अर्थ आहे असे दिसून येईल. अ हा ग x म क्रमी आणि क हा म x न क्रमी असल्यास अ क हा ग x न क्रमी असतो असे दाखविता येईल.
वरील विवेचनावरून असे दिसून येते की, दोन आव्यूहांच्या गुणाकारांचे गुणधर्म सत् किंवा सदसत् संख्यांच्या गुणधर्मांहून वेगळेच आहेत. एक तर वाटेल त्या दोन आव्यूहांचा गुणाकार करता येईलच असे नाही. दुसरे म्हणजे अ क हा गुणाकार करता आला तरी क अ हा गुणाकार शक्य होईलच असे नाही व तिसरे म्हणजे अ क आणि क अ हे दोन्ही गुणाकार शक्य असले, तरी ते समान असतीलच असे नाही.
आतापर्यंत दिलेले आव्यूहांचे गुणधर्म खालील उदाहरणांवरून स्पष्ट होतील.
असेल तर अ श =०, अ त =त अ= अ. यावरून शून्य आव्यूहाने गुणले असता गुणाकार शून्य येतो.
तत्समक आव्यूह : समजा अ = [अपस] ग x म हा कोणताही आव्यूह असून, त = कर्ण[१, १, …, १] असा म-क्रमी चौरस आव्यूह आहे. यावरून
| म | |||
| (अ त)पस = | ∑ | अपइतइस | असे लिहिता येते. पण जर इ ≠ स, तर तइस = ० आणि जर इ = स, तर तइस = १ |
| इ=१ |
असल्याने (अत)पस = अपस असे उत्तर येईल. हेच कोणत्याही प,स करता असल्याने अ त = अ हे सिद्ध होते. यावरून त हा असा आव्यूह आहे की, अ ला त ने गुणले असता गुणाकार अ च मिळतो. म्हणून त ला दक्षिण तत्समक आव्यूह म्हणतात. जर ग ≠ म असेल, तर त अ शक्य होणार नाही. याचप्रमाणे जर त हा वरीलप्रमाणे कर्ण [१,१,…,१] असून ग-क्रमी असेल, तर त अ = अ असून अ त शक्य होणार नाही. यावेळी त ला वाम तत्समक आव्यूह म्हणतात.
जर अ हा म-क्रमी चौरस आव्यूह असून त हा म-क्रमी चौरस कर्ण [१,१, …,१] आव्यूह असेल, तर अ त = त अ = अ हे वरीलप्रमाणे दाखविता येईल. येथे त हा म-क्रमी तत्समक आव्यूह होय. सामान्य सत् किंवा सदसत् संख्या संचात शून्य आणि एक यांचे जे स्थान आहे (शून्य आणि एक हे संख्यांच्या बेरजेसाठी आणि गुणाकारासाठी तत्समक आहेत) तेच नेमके स्थान म–क्रमी चौरस आव्यूहांच्या समष्टीत (समूहात) म–क्रमी शून्य आव्यूह आणि म-क्रमी तत्समक आव्यूह (किंवा एकाव्यूह) यांचे आहे.
द हा अदिश असल्यास द त या आव्यूहास अदिश आव्यूह म्हणतात. याचा कोणत्याही चौरस आव्यूहाशी केलेला गुणाकार क्रमनिरपेक्षी असतो.
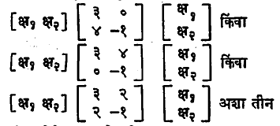
शून्य भाजक: दोहोंपैकी एक आव्यूह जरी शून्य असेल तरी त्यांचा गुणाकार शून्यच असणार हे सहज पडताळून पाहता येईल. परंतु जर दोन आव्यूहांचा गुणाकार शून्य असेल तर त्या दोहोंपैकी एक तरी शून्य असेलच असे नाही. म्हणजेच दोन अशून्य आव्यूहांचा गुणाकार शून्य असणे शक्य आहे. उदा.,
| [ | ब ० | ] X [ | ० ० | ] = [ | ० ० | ] |
| भ ० | र ह | ० ० |
अशा आव्यूहांना शून्याचे भाजक किंवा शून्य भाजक म्हणतात. अशा शून्य भाजकांचे अस्तित्व हे आव्यूहांचे वैशिष्ट्य आहे. सामान्य संख्या संचात शून्य भाजक अस्तित्वात नसतात.
आव्यूहांचे खंडकरण : समजा, अ = [अपस] ग X म आणि क = [कपस] म X न यांचा गुणाकार करावयाचा आहे. जर ग, म आणि न या संख्या बऱ्याच मोठ्या असतील, तर अ आणि क चे खंड करणे सोयीचे ठरते. अ च्या स्तंभांचे म१, म२,…, मर स्तंभ असलेले र भाग करा. यामुळे अ चे (आ१ आ२…आर) अशा उपआव्यूहात र खंड पडतील. तसेच क च्या पंक्तींचे म१, म२, …, मर पंक्ती असलेले (का१ का२…कार) असे उपआव्यूहात खंड पाडा. आता
असे लिहिले, तर अ क हा गुणाकार अ क = आ१ का१ + आ२का२ + … + आर कार असा लिहिता येईल. या उपआव्यूहांतील काही शून्य वा तत्समक असल्यास गुणाकार करणे आणखी सुलभ होईल.
व्यस्त आव्यूह : जर अक = क अ = त असेल तर अ आणि क एकमेकांचे व्यस्त आव्यूह आहेत असे म्हणतात. अ चा व्यस्त आव्यूह अ-१ असाही लिहितात. म्हणजेच क= अ-१ किंवा अ = क-१ असे लिहिता येईल. अर्थातच अ आणि क हे दोन्ही समानक्रमी चौरस आव्यूह असले पाहिजेत. दिलेल्या कोणत्याही चौरस आव्यूहास त्याचा व्यस्त आव्यूह अस्तित्वात असेलच असे नाही. ज्या आव्यूहास असा व्यस्त आव्यूह नाही त्यास एकमात्र आव्यूह म्हणतात. तसेच ज्यास व्यस्त आव्यूह आहे त्यास नैकमात्र आव्यूह म्हणतात.
चौरस आव्यूह आणि निर्धारक : कोणत्याही चौरस आव्यूहाशी [अपस] त्याचा निर्धारक |अपस| निगडीत असतो [→निर्धारक]. मात्र आव्यूह आणि निर्धारक यांतील मूलभूत फरक लक्षात ठेवणे जरूर आहे. [अपस] या आव्यूहात त्याच्या घटकांची मांडणी महत्त्वाची असून त्यातील एका घटकाची जरी जागा वा मूल्य बदलले तरी आव्यूह तोच राहणार नाही. निर्धारक सोडवून त्याचे मूल्य काढता येते. म्हणजेच निर्धारक म्हणजे एक संख्या होय. त्यातील घटक विशिष्ट तऱ्हेने बदलले तरी त्याच्या मूल्यात (म्हणजेच निर्धारकात) काही फरक पडत नाही.
|अपस| या निर्धारकातील अपस चा सहअवयव अ*पस असा लिहिला असता आणि [अपस] या आव्यूहातील प्रत्येक घटकाच्या जागी त्याचा निर्धारकातील सहअवयव लिहिला असता जो आव्यूह मिळेल त्याचा पक्षांतरित आव्यूह [अ*पस ]असा लिहिल्यास त्याला [अपस] चा संलग्नी आव्यूह म्हणतात.
अ आणि क या दोन म-क्रमी चौरस आव्यूहांच्या अ क या गुणाकाराचा निर्धारक |अ क| हा |अ | आणि |क| या निर्धारकांच्या गुणाकाराबरोबर असतो. |अ क| = |अ | |क|. अर्थातच अ X अ–१ = त आणि |त|= १ असल्याने |अ | X |अ -१|=१ असले पाहिजे. निर्धारकांच्या गुणधर्मावरून |अ*|= |अ |म-१ असे सिद्ध करता येते. तसेच अ आणि त्याचा संलग्नी आव्यूह अ* यांच्या गुणाकारातील लक्षण घटकांसंबंधी, जर प ≠ स, तर (अ.अ*)पस = ० आणि जर प = स, तर (अ.अ*) पस = |अ | असे सिद्ध
| करता येईल. यावरून असे सिद्ध करता येते की, अ. | अ* | = | अ* | अ = त म्हणजेच अ-१ = | १ | अ*. |
| |अ| | |अ| | |अ| |
यावरून अ-१ अस्तित्वात असण्यासाठी म्हणजेच अ नैकमात्र असण्यासाठी |अ| ≠ ० ही अट आवश्यक आहे असे दिसून येईल.
जात्य आव्यूह : जर क हा आव्यूह असा असेल की, क.क’ = क’.क = त, तर क ला जात्य आव्यूह म्हणतात. म्हणजेच क’ = क–१ असेल, तर क जात्य होतो. क जात्य असून
आव्यूहाची कोटी : अ या ग X म क्रमी आव्यूहाची प्रत्येक पंक्ती म्हणजे प-युत सदिश समजले, तर अशा ग सदिशांचा संग्रह मिळेल. हे सर्व सदिश एकघाती निरवलंबी (म्हणजे या सदिशांची कोणतीही एकघाती पदावली शून्याबरोबर नसणे) असतीलच असे नाही. या संग्रहातील एकघाती निरवलंबी सदिशांचा महत्तम संख्येस अ ची पंक्ति कोटी, कोप (अ), म्हणतात. हेच दुसऱ्या शब्दात सांगावयाचे म्हणजे या ग पंक्ती सदिशांपैकी कोणतीही पंक्ती कोटीइतक्या निरवलंबी पंक्तींच्या एकघाती पदावलीच्या बरोबर लिहिता येईल. याचप्रमाणे स्तंभ कोटी कोस्त (अ) ची व्याख्या करता येईल. कोणत्याही आव्यूहाची पंक्ती कोटी व स्तंभ कोटी सारख्याच असतात हे सिद्ध करता येते. यामुळे अ ची कोटी को(अ) अशी नि:संदिग्धपणे लिहिता येते [ → सदिश अवकाश].
अ हा म-क्रमी चौरस आव्यूह नैकमात्र असण्यासाठी को (अ) = म असावयास पाहिजे असे सिद्ध करता येते. तसेच याचा व्यत्यास म्हणजे कोटी म असल्यास तो आव्यूह नैकमात्र आहे हेही सिद्ध करता येते. कारण को (अ) = म असेल, तर |अ| ≠ ० असलेच पाहिजे. यावरून सिद्ध करता येते. कारण की,को (अ) ही अ च्या अशून्य निर्धारक असणाऱ्या उप-चौरस आव्यूहाच्या महत्तम क्रमाइतकी असते. उदा., या
आव्यूहाची कोटी २ आहे.
अनेकवर्णी एकघाती समीकरणे व आव्यूह : आव्यूह कोटीचा आणि व्यस्त आव्यूहाचा उपयोग एकघाती म-वर्णी (म बदलत्या राशी म्हणजे चल असलेली) समीकरणे सोडविण्यासाठी, तसेच ती समीकरणे सुसंगत आहेत किंवा नाहीत हे तपासण्यासाठी होतो. अशा तर्‍हेची समीकरणे सदिश अवकाशांच्या एकघातील रूपांतरणांत आढळतात.
समजा, क्ष१, क्ष२,…,क्षम या म चलपदांची ग समीकरणे खालील प्रमाणे दिलेली आहेत :
अ११ क्ष१ + अ१२ क्ष२ + … + अ१म क्षम = क१
अ२१ क्ष१ + अ२२ क्ष२ + … + अ२म क्षम = क२
. . . . … . . .
अग१ क्ष१ + अग२ क्ष२ + … + अगम क्षम = कग
येथे अ११, अ१२, …, अगम हे स्थिरांक आहेत. जर अ = [अपस] हा ग X म क्रमी आव्यूह आणि
असे आव्यूह घेतले, तर दिलेली ग समीकरणे अ क्ष = क या एकाच आव्यूह समीकरणाने दाखविता येतात. ही समीकरणे सोडवताना क=0 आणि क ≠० या दोन पर्यायांचा वेगवेगळा विचार करावा लागतो.
(१) क = ० म्हणजेच क१ = क२ = कग = ० असल्यास वरील ग समीकरणांना समघाती समीकरणे म्हणतात, यांचा एक निर्वाह (समीकरण सोडवून काढलेले उत्तर) क्ष१= क्ष२ = …= क्षम = ० हे उघडच आहे. याखेरीज दुसरा निर्वाह अस्तित्वात असण्यासाठी म–को (अ) > ० असणे हे आवश्यक व पर्याप्त (पुरेसे) आहे असे सिद्ध करता येते. अर्थातच ग = म = को (अ) असल्यास या समीकरणांचा क्ष = 0 याशिवाय दुसरा निर्वाह मिळणार नाही.
(२) क ≠ ० असल्यास क१, क२, … , कग यांपैकी एकतरी अशून्य असेल. अशा समीकरणांस असमघाती समीकरणे म्हणतात. या समीकरणांचा एकही निर्वाह अस्तित्वात नसणे शक्य आहे. समीकरणास एकतरी निर्वाह आहे किंवा कसे हे अ आणि क यांच्या घटकांवरून ठरते. अ या ग X म आव्यूहामध्ये म + १ वा स्तंभ हा क च्या स्तंभ सदिशरूपाने मांडला तर होणाऱ्या (अ|क) या ग X (म + १) क्रमी आव्यूहास वरील समीकरणांचा आवर्धित आव्यूह म्हणतात.
को (अ | क)=को (अ) असल्यास वरील समीकरणांना निर्वाह असतो आणि ती समीकरणे सुसंगत असतात असे सिद्ध करता येते.
तथापि वरील समघाती किंवा असमघाती समीकरणांचे निश्चित एकमेव निर्वाह असण्यासाठी ग = म = को (अ) हे आवश्यक व पर्याप्त आहे. अशा वेळी साहजिकच निर्वाह क्ष = अ–१ क असा आव्यूहाच्या स्वरूपात मांडता येतो.
त्रिमिती अवकाशातील उदाहरणे :
(१) अ११ क्ष१ + अ१२ क्ष२ + अ१३ क्ष३ = ०,
अ२१ क्ष१ + अ२२ क्ष२ + अ२३ क्ष३= ०,
अ३१ क्ष१ + अ३२ क्ष२ + अ३३ क्ष३ = ०
ही तीन प्रतले (पातळ्या) आहेत, जर को (अ) = ३ असेल, तर क्ष१ = क्ष२ = क्ष३ = ० हा एकमेव निर्वाह संभवतो. म्हणजेच तिन्ही प्रतलांना फक्त आदिबिंदू (संदर्भ अक्षांचा छेदबिंदू) समाईक आहे. जर को (अ) = २ असेल, तर आदिबिंदूतून जाणाऱ्या एका विशिष्ट रेषेवरील सर्व बिंदू समाईक असतात. म्हणजेच तिन्ही प्रतले एकाच रेषेतून जातात किंवा दोन प्रतले एकच असतात. जर को (अ) = १ असेल, तर एका विशिष्ट प्रतलावरील सर्व बिंदू समाईक असतात. म्हणजे तीन प्रतले भिन्न नसतील.
(२) २क्ष१ + क्ष२ + ५क्ष३= ४,
३क्ष१ – २क्ष२ + २क्ष३= २ आणि
५क्ष१– ८क्ष२– ४क्ष३= १
या प्रतलांच्या समीकरणांत अ आणि (अ|क) यांच्या कोटी समान नसल्याने निर्वाह मिळणार नाही. म्हणजेच ही प्रतले एकाच बिंदूत मिळत नाहीत.
(३) २क्ष१ – क्ष२ + ३क्ष३ = ३,
क्ष२= – २, २क्ष१ + क्ष२ + क्ष३ = १ यांमध्ये
को (अ) = को (अ|क) = ३ असल्याने
क्ष१ = २, क्ष२= – २ क्ष३= – १ असा एकमेव निर्वाह मिळतो. म्हणजेच तिन्ही प्रतले (२, –२, –१) या बिंदूतून जातात.
आव्यूह बहुपदी : अ हा म क्रमी चौरस आव्यूह असल्यास अ अ, अ अअ, … हे सर्व गुणाकार करता येतात. याबद्दल अनुक्रमे अ२, अ३,… असे मांडल्यास आणि अ०= त असे मानल्यास त्या संकेतनाचा अर्थ स्पष्ट होईल. सदिशांप्रमाणेच आव्यूहांमध्ये एकघातील निरवलंबी संग्रहाची कल्पना केल्यास अ० , अ, … , अम२ हे म२+१ आव्यूह एकघाती निरवलंबी नसतात असे दाखविता येईल. म्हणजेच ठ च्या पुरेशा मोठ्या मूल्याकरिता अठ + क१ अठ-१ + क२अठ-२+ .. + कठ-१ अ + कठत = ० असे समीकरण मिळेल. अशा प्रकारच्या ठ च्या शक्य त्या मूल्यांत जर ठ चे कमीत कमी मूल्य घेतले तर हेच सहगुणक (म्हणजे क१, क२, …, कठ) घेऊन मांडलेल्या क्षठ+ क१ क्षठ-१ + … + कठ-१ क्ष + कठ या अधिश बहुपदीस (अनेक पदे असलेल्या राशीस) अ ची अल्पिष्ठ बहुपदी म्हणतात व ही प्रत्येक आव्यूहाकरिता एकमेव असते.
लाक्षणिक बहुपदी : आव्यूहाशी संबद्ध असलेली आणखी एक बहुपदी आहे. अ हा म–क्रमी आव्यूह, क्ष हा म X १ सदिश आव्यूह आणि द हा अदिश असेल, तर अक्ष = दक्ष हे समीकरण सोडविता येईल. हेच समीकरण अक्ष = द तक्ष म्हणजेच (अ – दत) क्ष = ० असे लिहिता येईल. जर |अ – दत| ≠० असेल. तर या समीकरणाचे क्ष = ० एवढा एकच निर्वाह संभवेल. पण जर |अ – दत| =० असेल, तर याचे क्ष१, क्ष२ … इ. निर्वाह मिळतील. |अ – दत| = ० हे द या प्रचलातील म -घाती समीकरण आहे. |अ – दत| या बहुपदीस अ ची समीकरणास लाक्षणिक बहपदी आणि |अ – दत| = ० या समीकरणास लाक्षणिक समीकरण व त्याच्या बीजांस अ ची लाक्षणिक बीजे म्हणतात. ही बीजे द१, द२,…, दम अशी असल्यास अक्षइ = दइ क्षइ या समीकरणातील क्ष१, क्ष२, …, क्षम या सदिशांना अ चे लाक्षणिक सदिश म्हणतात. द१, द२, …, दम यांना लाक्षणिक मूल्ये म्हणतात.
केली व हॅमिल्टन यांचे प्रमेय : प्रत्येक चौरस आव्यूह त्याच्या लाक्षणिक समीकरणाची पूर्तता करतो. आव्यूहाची अल्पिष्ठ बहुपदी ही त्याच्या लाक्षणिक बहुपदीचा एक गुणक असतो हेही सिद्ध करता येते. या प्रमेयाचा उपयोग करून व्यस्त आव्यूहही काढता येतो.
सरूप आव्यूह : अ हा म-क्रमी आव्यूह आणि घ हा नैकमात्र म-क्रमी आव्यूह असेल आणि क = घ अ घ-१असेल, तर अ आणि क हे सरूप आव्यूह आहेत असे म्हणतात. सरूप आव्यूहांची कोटी निर्धारक समान असतात असे सिद्ध करता येते.
प्राथमिक रूपांतरणे : कोणत्याही आव्यूहासाठी खालील क्रियांना प्राथमिक रूपांतरणे म्हणतात. (१) कोणत्याही दोन पंक्तीची अदलाबदल, (२) कोणत्याही पंक्तीतील सर्व घटकांना एकाच अशून्य संख्येने गुणणे, (३) एका पंक्तीतील सर्व घटकांना एकाच संख्येने गुणून दुसऱ्या पंक्तीतील घटकांशी अनुक्रमाने बेरीज करणे. याचप्रमाणे तिन्ही क्रिया स्तंभांसाठीही करता येतील.
प्राथमिक आव्यूह : वर दिलेल्यापैकी एक किंवा अधिक प्राथमिक रूपांतरणे जर त या तत्समक आव्यूहावर केल्या तर जो आव्यूह तयार होईल त्यास प्राथमिक आव्यूह म्हणतात.
अ या एखाद्या आव्यूहातील र आणि ल या पंक्तींची अदलाबदल करून अरल हा आव्यूह मिळाला असे समजू. हेच प्राथमिक रूपांतरण त या तत्समक आव्यूहावर केले असता तरल हा आव्यूह तयार होईल. अरल = तरल अ हे सहज दाखविता येईल. तसेच जर इ आणि ज या स्तंभांची अदलाबदल केली असती, तर अइज = अ. तइज असे समीकरण मिळाले असते. यावरून प्राथमिक रूपांतरणे आणि त्या त्या प्रकारच्या प्राथमिक आव्यूहाने गुणणे या एकच क्रिया आहेत, असे दिसून येईल.
एखाद्या आव्यूहाचे जर प्राथमिक रूपांतरण केले तर त्याची कोटी बदलणार नाही हो कोटीच्या व्याख्येवरून आणि निर्धारकांच्या गुणधर्मांवरून दाखविता येईल. कोणताही नैकमात्र आव्यूह हा प्राथमिक आव्यूहांच्या गुणाकाराबरोबर दाखविता येतो.
आव्यूहाचे प्रसामान्य आव्यूहात संक्षेपण : वर दिलेल्या प्राथमिक रूपांतरणांचा (योग्य अशा) उपयोग करून कोणत्याही अ ह्या आव्यूहाचे रूपांतर 
अशा विभागित आव्यूहात करता येते. या ठिकाणी तर हा र-क्रमी तत्समक आव्यूह असून र = को(अ) होय आणि ० हे योग्य क्रमी शून्य उपआव्यूह दर्शवितात. या रूपांतरण क्रियेस प्रसामान्यीकरण म्हणतात. काही आव्यूहांचे प्रसामान्यीकरण कर्ण-आव्यूहात होऊ शकते. यास कर्ण-आव्यूह रूपांतरण म्हणतात.
आव्यूहाचा कर्णयोग: म-क्रमी अ या चौरस आव्यूहातील 
या कर्ण घटकांच्या बेरजेस आव्यूहाचा कर्णयोग म्हणतात. जर अ आणि क हे आव्यूह सरूप असतील तर कर्णयोग अ = कर्णयोग क म्हणजेच Σअइइ = Σकइइ असे दाखविता येते. कर्णयोगाच्या साहाय्याने आव्यूहाचे इतर काही गुणधर्मही समजतात.
द्विघाती रूपे : जर अपस हे अदिश असतील आणि क्ष१, क्ष२, क्ष३, ही चलपदे असतील तर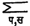 
अपसक्षप क्षस यास द्विघाती रूप म्हणतात. जर क्ष’ हा आव्यूह [क्ष१ क्ष२ …… क्षम] असा घेतला व क्ष हा त्याचा पक्षांतरित आव्यूह असेल आणि अ = [ अपस] हा म-क्रमी आव्यूह घेतला, तर वरील द्विघाती रूप क्ष’ अ क्ष असे लिहिता येते. निरनिराळ्या तर्‍हेने अ सदृश आव्यूह घेऊन असे लिहिता येईल पण सामान्यत: अ हा सममित आव्यूह घेतात.
उदा., ३क्ष१२+ ४क्ष१क्ष२ – क्ष२२ हे द्विघाती रूप
तऱ्हांनी दाखविता येईल. पण शेवटचे रूप सामान्यत: वापरतात.
जर क्षप च्या निरनिराळ्या अशून्य मूल्यांसाठी 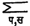अपस क्षप क्षस > ० असेल तर त्या द्विघाती रूपास धनात्मक निश्चित द्विघाती रूप म्हणतात. तसेच जर क्षप च्या सर्व अशून्य मूल्यांसाठी 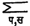अपसक्षप क्षस > ० असेल, तर त्याला ऋणात्मक निश्चित द्विघातील रूप म्हणतात. अर्थातच क्ष१= क्ष२ …= क्षम =0 असल्यास द्विघाती रूपाचे मूल्य शून्यच येईल. इतर प्रकारांत द्विघाती रूप अनिश्चित आहे असे म्हणतात.
द्विघाती रूपे साधारणपणे खालील संदर्भात आढळतात :
(१) अवकाशातील दोन बिंदूंमधील अंतर दर्शविण्यासाठी
| d र२ = Σ कपस d क्षप d क्षस |
| प,स |
(२) शांकवजांच्या [शांकव कुलातील वक्रांच्या भ्रमणापासून मिळणारी पृष्ठे, → शंकुच्छेद; पृष्ठ] द्विघाती समीकरणात.
(३)वस्तुमानांची गतिज (गतीमुळे प्राप्त होणारी) किंवा स्थितीज (स्थितीमुळे प्राप्त होणारी) ऊर्जा दर्शविण्यासाठी. उदा., ∑१/२वप क्षंप२ इत्यादी.
द्विघाती रूपांचे प्रसामान्य रूपांत संक्षेपण :
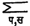अपस क्षप क्षस या द्विघाती रुपाऐवजी 
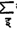कइक्षइ२ हे द्विघाती रूप वापरण्यास सोपे असते. म्हणजेच येथे अ चे कर्ण आव्यूहात रूपांतर केलेले आहे. कोणत्याही सत् संख्येच्या सममित आव्यूहाचे कर्ण आव्यूहात सरूप रूपांतर करता येते हे सिद्ध करता येते. यास ‘मुख्याक्ष सिद्धांत’ म्हणतात. जर द१, द२, …, दम ही अ ची लाक्षणिक बीजे असतील आणि जर यांपैकी द१, द२,…, दप ही धन असतील दप+१, दप+२,…, दर [को (अ) = र ] ही ऋण असतील व दर+१, दर+२,…, दम ही शून्य असतील, तर अ चे रूपांतर, कर्ण आव्यूह [द१, द२, …, दम] असेल हे दाखविता येते. म्हणजेच दिलेले द्विघाती रूप द१ क्ष१२ + … + दपक्षप२ + दप+१क्ष२ प+१ +…+दरक्क्षर२ असे रूपांतरित होईल. येथे मापप्रमाण बदलून हेच रूप क्ष१२ + क्ष२२ +…+क्षप२+१ – क्षप२+२ …– क्षर२ असेही लिहिता येईल. या शेवटी लिहिलेल्या रूपाला दिलेल्या मूळ द्विघाती रूपाचे प्रसामान्य रूपातील संक्षेपण म्हणतात. यामध्ये र [= को (अ)] यास रूपाची कोटी म्हणतात. र ≤ म हे उघड आहे. प्रसामान्य रूपात प पदे धन आणि र-प पदे ऋण असतील, तर
प – (र – प) = २ प – र या संख्येस द्विघाती रूपाचे चिन्हक म्हणतात.
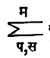अप क्षप क्षस हे दिलेले द्विघाती रूप धनात्मक निश्चित असण्यासाठी त्याची कोटी आणि चिन्हक म असणे आवश्यक व पर्याप्त आहे असे सिद्ध करता येते. तसेच अ हा आव्यूह अ = घ घ’ असा एका नैकमात्र आव्यूहाचा व त्याच्या पक्षांतरित आव्यूहाचा गुणाकार म्हणून मांडता येतो असेही सिद्ध करता येते.
काही वेळा क्षअक्ष’ आणि क्षकक्ष’ अशा दोन निरनिराळ्या द्विघाती रूपांचा एकाच वेळी विचार करावा लागतो. जर अ चे कर्ण आव्यूहात रूपांतर केले, तर त्याच नियमांनी क चेही कर्ण आव्यूहात रुपांतर होईल असे नाही. दोन्ही आव्यूहांचे कर्ण आव्यूहात एकाच वेळी रूपांतर होण्यासाठी अक = कअ असणे आवश्यक व पर्याप्त आहे हे सिद्ध करता येते. अशा प्रकारचे एक उदाहरण पुढीलप्रमाणे आहे : एखादा वस्तुमान समूह जेव्हा स्थिर समतोल अवस्थेत असतो आणि जेव्हा त्याची या अवस्थेभोवती लहान दोलने होतात तेव्हा त्यांचा आवर्तकाल (एका दोलनास लागणारा काल) इ. गुणधर्म जाणण्यासाठी त्यांच्या गतिज आणि स्थितिज ऊर्जांसंबंधी माहिती लागते. ही दोन द्विघाती रूपांनी दिली जात असल्याने या दोन द्विघातील रूपांचे एकाच वेळी प्रसामान्यीकरण करावे लागते.
अनुप्रयोग : आव्यूह सिद्धांताचा विविध शाखांत उपयोग केला जातो. साध्या यामिकीमध्ये(प्रेरणांची वस्तूंवर होणारी क्रिया व त्यामुळे निर्माण होणारी गती यांचा अभ्यास करणाऱ्या शास्त्रामध्ये) तसेच ⇨ पुंजयामिकीमध्ये आव्यूहांचा उपयोग करतात. विशेषत: आव्यूह गुणाकार क्रमनिरपेक्षी नसल्याने परिभ्रमण इत्यादींच्या संदर्भात त्यांचा उपयोग होतो. पुंजयामिकीमध्ये काही निरीक्षणयोग्ये विसंगत असतात हा गुणधर्म अक्रमनिरपेक्षतेशी संबद्ध करता येतो. भौतिकी, रसायनशास्त्र, वर्णपटविज्ञान, स्फटिक रचना, स्थापत्य, स्थितिस्थापकता,विद्युत् संवाहकांची जाळी इत्यादींच्या अभ्यासात आव्यूह वापरले जातात. सांख्यिकी, जीवविज्ञान, मानसशास्त्र, समाजशास्त्र, अर्थशास्त्र यांत तसेच ⇨ खेळ सिद्धांत, रैखिक कार्यक्रमण [→ संगणक] यांसारख्या आधुनिक गणितीय शाखांत आव्यूहांचा उपयोग होतो.
संदर्भ : 1. McDuffe, C. C. Theory of Matrices, New York, 1946.
2. McDuffe, C. C. Vectors and Matrices, New York, 1943.
3. Shanti Narayan, A Text Book of Matrices, New Delhi, 1962.
4. Thrall, R.M.; Tornheim, L. Vector Spaces and Matrices, 1957
देशपांडे, श्री. वि.