चतुर्दली

चतुर्दली : (क्वाटर्नियन). चतुर्दली म्हणजे सत्‌ संख्यांच्या [⟶ संख्या] क्षेत्रावर आधारित असा चतुर्मिती एकघाती बीजावकाश होय [⟶ बीजगणित, अमूर्त]. सर विल्यम रोवान हॅमिल्टन यांनी १८४३ साली याचा शोध लावला. विसाव्या शतकाच्या सुरुवातीपर्यंत चतुर्दलीचा विशेष असा अभ्यास झाला. पुढे मात्र बीजावकाश या अधिक व्यापक संकल्पनेच्या प्रसारामुळे, एक विशिष्ट प्रकारचा बीजावकाश एवढेच त्याचे स्वरूप राहिले. भूमिती आणि गणितीय भौतिकी यांमध्ये होणाऱ्या उपयोगामुळे चतुर्दलीस महत्त्व प्राप्त झाले. चतुर्दलीचे  ⇨ पुंजयामिकी, संख्या सिद्धांत, ⇨ गट सिद्धांत  इ. शाखांमध्येही पुष्कळ उपयोग आहेत.

सदसत्‌ संख्या क्ष ＋i य, (i = √^—-१) अशा लिहितात. त्याचप्रमाणे (क्ष, य) अशा सत्‌ संख्यांच्या क्रमित युग्माच्या रूपातही लिहिता येतात. सदसत्‌ संख्यांची बेरीज व गुणाकार यांची नेहमीची व्याख्या घेतल्यास, सदसत्‌ संख्यांचा संच बेरीज आणि गुणाकार या कृत्यांसाठी क्षेत्र असण्यास आवश्यक असणाऱ्या अटींची पूर्तता करतो. हे क्षेत्र द्विमिती असून ते द्विमिती ⇨सदिश अवकाशाशी समरूप असते. याचप्रमाणे त्रिमिती क्षेत्र तयार होऊ शकेल काय या प्रश्नाचा विचार गणितज्ञ करीत होते. त्रिमिती सदिशांच्या बेरजेची व्याख्या करणे शक्य आहे. ती अशी

(क्ष,य,झ) + (क्ष’, य’, झ’) = (क्ष+क्ष’, य+य’, झ+झ’).

यामुळे क्षेत्रास आवश्यक असणारे एक द्विमान कृत्य (जे कृत्य दोन घटकांवर केले असता तिसरा घटक मिळतो असे कृत्य) उपलब्ध होते; परंतु त्यांचे क्षेत्र होऊ शकेल अशा प्रकारे त्यांच्यात गुणाकाराची व्याख्या करणे शक्य नाही.

[(क्ष, य, झ) ⋅ (क्ष’, य’, झ’)] = (क्ष·क्ष’, य·य’, झ·झ’) अशी गुणाकाराची व्याख्या दृष्टीपुढे येते पण असा गुणाकार क्रमनिरपेक्षता, साहचर्य, वितरण हे नियम पाळत असला तरी ‘प्रत्येक शून्येतर घटकाला व्यस्त असणे’ या क्षेत्र होण्यास आवश्यक गुणाचा अभाव दिसून येतो]. म्हणून दोनहून अधिक मितींचे क्षेत्र बनवण्यासाठी चतुर्मिती सदिशांचाच विचार केला पाहिजे. यातूनच हॅमिल्टन यांना चतुर्दलीचा शोध लागला. चतुर्दलीला ‘उच्च कोटीच्या सदसत्‌ संख्या’ असेही म्हणतात. मात्र यापेक्षा उच्चतर कोटीच्या–क्षेत्र बनवण्यालायक अशा–सदसत्‌ संख्या अस्तित्वात असणे शक्य नाही असे प्रस्थापित झालेले आहे.

चतुर्दलीला आधारभूत असे चार एकघाती निरवलंबी एकक घटक १, ट, ठ, ड असे दर्शवितात. त्यांचे गुणधर्म खाली दिलेल्याप्रमाणे आहेत.

       १^२= १, ट^२ = ठ^२ =ड^२ = ट ठ ड = –१

                                             ट (ठ ड) = (ट ठ) ड = ट ठ ड;

                                             १·ट = ट·१, १·ठ = ठ·१, १·ड = ड·१;

                                             ट ठ ≠ ठ ट, ठ ड ≠ ड ठ, ड ट ≠ ट ड.

जर स ही सत्‌ संख्या असेल तर, स ट=ट स, स ठ=ठ स, स ड=ड स.

ट ठ = – ठ ट = ड, ठ ड = – ड ठ = ट, ड ट = – ट ड = ठ.

वर दिलेले आधार घटक घेऊन पुढे दिल्याप्रमाणे च ही चतुर्दली मिळते.

च = स+ट क+ठ ख+ड ग

यामध्ये स, क, ख, ग या सत्‌ संख्या आहेत. जर स = ० असेल तर च हा सदिश होतो. तसेच क = ख = ग = ० असल्यास च अदिश होतो. च’=स–(ट क+ठ ख+ड ग), यास च ची संयुग्मी चतुर्दली म्हणतात. च · च’ = च’ · च = स^२ + क^२ + ख^२ + ग^२ =  ण हे सहज दाखवता येईल. ण ला च चा मानांक म्हणतात. √^—ण = त या सत्‌ संख्येला च चा प्रदिश म्हणतात आणि क, ख, ग यांना च चे सहनिर्देशक म्हणतात.

                 च_१ = स_१ + ट क_१ + ठ ख_१ + ड ग_१ 

आणि           च_२ = स_२ + ट क_२ + ठ ख_२ + ड ग_२ 

या दोन चतुर्दली असतील तर पुढील गोष्टी, वर दिलेल्या नियमांवरून मिळतात.

(१) च_१ = च_२ असेल, तर स_१ = स_२, क_१ =क_२, ख_१ = ख_२, ग_१=ग_२.

(२) च_१ · च_२ = ० असेल, तर च_१ = ० किंवा च_२ = ० किंवा च_१ = च_२= ०.

(३) च_१ · च_२ = स_१ स_२ – (क_१क_२+ख_१ख_२+ग_१ग_२)

                                +ट (स_१क_२+क_१स_२+ख_१ग_२–ग_१ख_२)

                               +ठ (स_१ख_२+ख_१स_२+ग_१क_२–क_१ग_२)

                               +ड (स_१ग_२+ग_१स_२+क_१ख_२–ख_१क_२)

तसेच च_२·च_१ = स_१स_२ –(क_१क_२+ख_१ख_२+ग_१ग_२)

                               +ट (स_१क_२+क_१स_२ – ख_१ग_२+ग_१ख_२)

                              +ठ (स_१ख_२+ख_१स_२ – ग_१क_२+क_१ग_२)

                              +ड (स_१ग_२+ग_१स_२ – क_१ख_२+ख_१क_२)

∴ ( च_१·च_२) – ( च_२·च_१) = २ [ट (ख_१ग_२ – ग_१ख_२) + ठ(ग_१क_{२ –} क_१ग_२)+ड (क_१ख_२ – ख_१क_२)]

यावरून असे दिसून येते की,

जर ख_१ग_२–ग_१ख_२ = ग_१क_२ – क_१ग_२ = क_१ख_२– ख_१क_२ = ० ह्या विशेष परिस्थितीतच, च_१·च_२ = च_२·च_१ असेल. म्हणजेच सामान्यपणेच च_१·च_२ ≠ च_२·च_१ म्हणजेच चतुर्दलींचा गुणाकार क्रमनिरपेक्ष नसतो.

(४) च = स + ट क + ठ ख + ड ग या चतुर्दलीत, क, ख, ग यांपैकी कोणतेही दोन शून्य मूल्याचे असतील तर च ही सदसत्‌ संख्याच होईल. जर क = ख = ग = ० असेल, तर च ही सत्‌ संख्या होईल. यावरून असे म्हणता येईल की, सदसत्‌ आणि सत्‌ संख्या यांची क्षेत्रे चतुर्दलीची उपक्षेत्रे समजता येतील. पण चतुर्दलींचे क्षेत्र क्रमनिरपेक्ष नाही.

आता चतुर्दलींच्या भागाकाराचा विचार करू. खाली दिलेले नियम सहज लक्षात यावे.

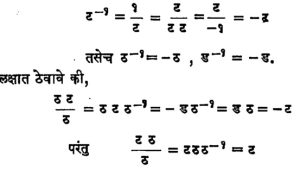
याचा अर्थ छेदस्थानातील घटक उणे घात देऊन योग्य जागी लिहिल्यास भागाकार सहज करणे शक्य होईल.

समजा, च = स + ट क + ठ ख + ड ग ≠ ०

आणि    संयुग्मी च’ = स – टक –ठ ख – ड ग आहेत

तर        च·च’ = स^२+क^२+ख^२+ग^२ = ण

आता छ ही दुसरी एक चतुर्दली असेल, तर

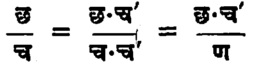
यावरून दोन चतुर्दलींचा भागाकार करावयाची एक रीत मिळते.

अर्थात छ·च’ ≠ च’·छ हे सामान्यपणे असणार हे उघड आहे.

हॅमिल्टन यांनी निश्चित दिशा दिलेला सरळरेषाखंड अशी सदिशाची व्याख्या केली. परस्पर लंब अक्ष त्रिकूटावर ट, ठ, ड असे एकक सदिश कल्पून र_१ = ट क्ष_१+ ठ य_१ +ड झ_१ आणि र_२ = ट क्ष_२ +ठ य_२ + ड झ_२ असे दोन सदिश घेतले तर,

र_१ र_२ = – (क्ष_१ क्ष_२ + य_१ य_२ + झ_१ झ_२) + [ट (य_१ झ_२–य_२ झ_१) + ठ (झ_१ क्ष_२ – झ_२ क्ष_१) +    ड (क्ष_१ य_२ – क्ष_२ य_१)]

र_२ र_१ = – (क्ष_१ क्ष_२ + य_१ य_२ + झ_१ झ_२) – [ट (य_१ झ_२ – य_२ झ_१) + ठ (झ_१ क्ष_२ – झ_२ क्ष_१) + ड (क्ष_१ य_२-क्ष_२य_१)]

अशी समीकरणे मिळतात. त्यावरून र_१ र_२ आणि र_२ र_१ चतुर्दली आहेत असे दिसून येते. असमांतर सदिशांचा गुणाकार क्रमनिरपेक्ष नाही.

तसेच र_१ र_२ + र_२ र_१ = – २ (क्ष_१ क्ष_२ + य_१ य_२ + झ_१ झ_२)

यात   क्ष_१= क्ष_२, य_१ = य_२, झ_१ = झ_२ असल्यास

       र_१^२ = – (क्ष_१^२+य_१^२+झ_१^२).

आता भागाकार कसा मिळतो ते खाली दिले आहे.

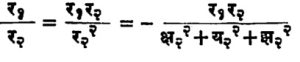
म्हणजे ^र_१/_र२ याची निःसंदिग्ध एकमेव किंमत येते, (फक्त क्ष_२ = य_२ = झ_२ = ० असता कामा नये) म्हणजे दोन सदिशांचा भागाकार देखील गुणाकारासारखाच चतुर्दली आहे. यावरून, दोन सदिशांचा गुणाकार वा भागाकार म्हणजे चतुर्दली अशी व्याख्या करता येईल.

आणखी लक्षात ठेवण्यासारखी गोष्ट म्हणजे,

                             च = स + (ट प + ठ फ + ड ब)

आणि त्याचे संयुग्मी च’ = स – (ट प + ठ फ + ड ब) असता,

               च·च’ = स^२+प^२+फ^२+ब^२=त^२, (अदिश)

                           च+च’ = २ स, (अदिश)

हेच असे म्हणता येईल की,

                          च, च’ ही क्ष^२ – २ स क्ष + त^२ = ०

या द्विघाती समीकरणाची बीजे आहेत.

क्ष = स ± √^—–(प^२ +फ^२+ ब^२). ही मूल्ये सदसत्‌ संख्या क्षेत्राचे घटक आहेत.

चतुर्दलीच्या साहाय्याने क^२ + ख^२ +ग^२ + घ^२ = (प^२+ फ^२+ ब^२ + भ^२) (क्ष^२+ य^२+ झ^२ + र^२)

हे ऑयरल यांचे सुप्रसिद्ध सूत्र सहज सिद्ध करता येते. येथे दोन चतुर्दलींच्या गुणाकाराचा मानांक = त्यांच्या मानांकांचा गुणाकार; या गुणधर्माचा उपयोग करावा लागतो व ह्या सूत्रावरून ‘प्रत्येक पूर्णांक चार वर्गांच्या (पूर्णाकांच्या) बेरजेच्या रूपात व्यक्त करता येतो’, याची सिद्धता देता येते.

चतुर्दलींचा सदिश (एकघाती) अवकाश होतो.

जर च = स + ट क + ठ ख + ड ग अशी चतुर्दली घेतली,

तर च = (स, क, ख, ग) असा चतुर्मिती सदिश म्हणूनही मांडता येईल. बेरजेची व्याख्या पूर्वीप्रमाणेच करता येईल. म ही सत्‌ संख्या असेल तर म च = (म स, म क, म ख, म ग) अशी आदिशाने गुणण्याची व्याख्या करता येईल. वरील दोन क्रियांच्या संदर्भात सर्व चतुर्दलींचा सत्‌ सदिश अवकाश बनतो.

चतुर्दलींचा गुणाकार व्याख्यात (व्याख्या केलेला) असल्याने व त्याकरिता चतुर्दलींचा संच संवृत असल्याने (म्हणजे गुणाकार करून येणारा घटक संचातच असण्याचा गुणधर्म असल्याने) चतुर्दलींचा बीजावकाश बनतो. मात्र तो क्रमनिरपेक्ष नसतो.

चतुर्दलीचे आधार घटक आणि त्यांचे ऋण चिन्हांकित घटक यांचा न-आबेलीय गट होतो. या गटात आठ घटक असून त्याला चतुर्दली गट म्हणतात. यामध्ये एक घटकी असा एक आणि प्रत्येकी चार घटक असलेले एकूण तीन चक्रीय उपगट असतात [⟶ गट सिद्धांत].

चतुर्दलींच्या अवकाशाचे आधार घटक द्विकोटिक किंवा चतुष्कोटिक आव्यूहांच्या रूपात मांडता येतात [⟶ आव्यूह सिद्धांत]. त्यांच्या साहाय्याने चतुर्दलींचे निदर्शन करता येते. उदा.,

(१) सिल्व्हेस्टर यांची पद्धत :

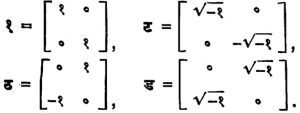
ह्या आव्यूहांना पुंजयामिकीचे परिवलन आव्यूह असे म्हणतात.

(२) एडिंग्टन यांची पद्धत :

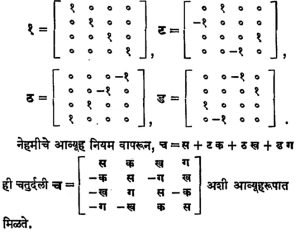
तसेच |च| = (स^२ +क^२ + ख^२ + ग^२)^२ हे सहज पडताळून पाहता येईल.

संदर्भ :

1. Hamilton, W. R. Elements of Quaternions, 1966.

2. Hardy, G. H. Wright, E. M. An Introduction to Theory of Numbers, Oxford, 1945.

3. MacDuffe, C.C. An Introduction to Abstract Algebra, New York, 1940.

गुर्जर, ल. वा.