कारक सिद्धांत

कारक सिद्धांत : कारक म्हणजे सत्‌ किंवा सदसत्‌ मूल्य[→संख्या]असलेल्या एका फलनाचे (गणितीय संबंधाचे) दुसऱ्या फलनात रुपांतर करणारा नियम असे स्थूलमानाने म्हणता येईल. उदा., (१) एखाद्या अवकलनीय फलनाचे[→अवकलन व समाकलन]त्याच्या अवकलांकात रूपांतर करणारा कारक. हा सामान्यपणे D असा लिहितात. जसे D(क्ष^३) = ३क्ष^२. (२)फ हे क्ष,य आणि झ या चलांचे दोनदा आंशिक अवकलन करण्याजोगे फलन असेल आणि जर

असेल तर हेच भ=  फ असे लिहितात. येथे हा फ चे भ मध्ये रुपांतर करणारा कारक होय. (३) जर,

असेल (सीमेचे अस्तित्व गृहीत धरल्यास) आणि हेच जर भ (य) = क cअसे लिहिले, तर क हा फ (क्ष) चे भ (य) मध्ये रुपांतर करणारा कारक होय. याला फूर्ये कारक म्हणतात. याचा आंशिक ðअवकल समीकरणे सोडविण्यासाठी विशेष उपयोग होतो. (४) जर,

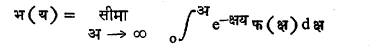
असेल (सीमेचे अस्तित्व गृहीत धरल्यास) आणि हेच जर भ (य) = क [(फ) क्ष]  असे लिहिले, तर क हा फ (क्ष) चे भ (य) मध्ये रूपांतर करणारा कारक होय. यास लाप्लास कारक म्हणतात. एकघाती अवकल समीकरणे, अविभाज्य संख्या सिध्दांत, अनंतवर्ती श्रेणी [→श्रेढी], घात श्रेढी संयुती (बेरीज) इ. विविध गणित शाखांमध्ये त्याचा उपयोग केला जातो.

कोणतेही अवकल किंवा समाकल समीकरण क (फ) = क्ष असे लिहिता येते. यामध्ये कारक क आणि फलन क्ष माहीत असेल, तर फलन फ शोधून काढणे म्हणजेच समीकरण सोडविणे होय.

कारकांसंबंधीचे नियम व व्याख्या : समजा, कारक ग हा फ या फलनाचे ह मध्ये रुपांतर करतो, म्हणजेच हग (फ) आणि दुसरा एक कारक क, ह फलनाचे रुपांतर भ मध्ये करतो, म्हणजेच भक (ह). ही रुपांतरे भक  ग (फ)  अशी एकत्र लिहिता येतील. म्हणजेच या कारकांमुळे फ चे भ मध्ये रुपांतर होते. हेच रुपांतर घ या एकाच कारकाने होते असे मानल्यास भ घ (फ) होईल. येथे कारक घ म्हणजे क आणि ग या दोन कारकांचा गुणाकार क ग आहे असे म्हणतात. यात कारकांचा अनुक्रम महत्त्वाचा आहे, कारण कग ग क असेलच असे नाही. याच तऱ्हेने क², क³,…… इत्यादींचा, तसाच क्ष₀ अ₁ क अ₂ क²…… अपकप या साध्या घातश्रेढींचा अर्थ विशद करता येईल.

जर क, ग आणि घ हे तीन कारक असतील, तर त्यांच्या गुणाकाराचा गुणधर्म (क ग) घ क (गघ) हा सहज सिद्ध करता येतो. अशाच प्रकारे जो कारक फ चे रुपांतर क (फ) ग (फ) या फलनात करतो त्यास क आणि ग ची बेरीज म्हणतात आणि ती क ग अशी लिहितात. कारकांच्या बेरजेचे पुढील नियम सहज सिद्ध करता येतातः क ग ग क(क ग) घ क (ग घ). म्हणजेच बेरजेकरिता कंसाचा उपयोग केला नाही तरी चालतो.

अशा तऱ्हेने बीजगणितातील बरेचसे नियम कारकांना लागू पडतात व त्यामुळे कारकांचे स्वतंत्र बीजगणितही तयार करता येते. कारकांच्या अभ्यासास महत्त्व येण्याचे हे एक मोठे कारण आहे. कारकांच्या उपयोगाने पुष्कळशा गणितीय समस्यांची चर्चा करणे अतिशय सोपे व सुटसुटीत होते.

क फ या फलनाला फ ची क – कारककृत प्रतिमा म्हणतात. फ, ह,… इत्यादी फलनांच्या क – कारककृत प्रतिमा जर क (फ), क (ह),… इत्यादी असतील, तर {फ, ह, ……} या संचास क चा प्रांत आणि {क (क), क (ह),……} या प्रतिमा संचास क ची व्याप्ती म्हणतात. प्रांत आणि व्याप्ती एकच संचही असू शकेल किंवा व्याप्ती प्रांताचा उपसंचही असू शकेल.

त, द हे कोणतेही स्थिरांक असता, प्रांतामधील फ, ह या कोणत्याही फलन घटकांसाठी जर क (त फ द ह) त क (फ) द क (ह) असेल, तर क ला एकघाती कारक म्हणतात किंवा दुसऱ्या शब्दात म्हणजे ज्या कारकांमुळे फलनांच्या एकघाती पदावलीची प्रतिमा ही त्या फलनांच्या तशाच एकघाती पदावलीसारखी असते त्यांना एकघाती कारक म्हणतात. अनेक फलनांच्या एकघाती पदावलीविषयीही असेच म्हणता येईल.

गणितशास्त्राच्या वेगवेगळया शाखांतील समस्यांच्या संदर्भात कारकांचा उपयोग होत असल्यामुळे अमूर्त अवकाशाच्या अनुषंगाने कारकांच्या अभ्यासासही चालना मिळाली. बैजिक आणि वैश्लेषिक दृष्टया कारकांचा अमूर्त अवकाशी घटक अशा स्वरुपात अभ्यास केल्यास लाभदायक ठरतो. अशा व्यापक अर्थाने, एका ⇨ सदिश अवकाशाचे दुसऱ्या सदिश अवकाशात चित्रण करणारे फलक म्हणजे कारक अशी व्याख्या करतात. एकघाती कारकाची व्याख्या वरील व्याख्येच्या अनुरोधाने करता येते. सामान्यतः एकघाती कारकच प्रचारात आहेत.

जर प्रांत अवकाश सांत-मितीय असेल तर व्याप्ती अवकाशही सांत मितीय असले पाहिजे. जर व्याप्ती अवकाश एक-मितीय असेल तर त्या कारकांना फलनके म्हणतात  [→फलनक विश्र्लेषण].

कारक सिध्दांत आणि भौतिक शास्त्रे यांच्यातील समस्यांमधील कारकांच्या अनुप्रयोगातील एक महत्वाचा भाग म्हणजे लाक्षणिक मूल्ये होय. जर क (अ) ते अ असेल, तर अ ला (त ह्या लाक्षणिक) मूल्यास अनुलक्षून) क चा लाक्षणिक सदिश म्हणतात. निरनिराळया लाक्षणिक मूल्यांचे लाक्षणिक सदिश एकघाती निरवलंबी असतात. म्हणजेच लाक्षणिक मूल्यांची संख्या त्या सदिश अवकाशाच्या मितीपेक्षा जास्त असू शकणार नाही. लाक्षणिक मूल्यांच्या माहितीमुळे कारकांविषयीचे बरेचसे ज्ञान प्राप्त होते. सदिश अवकाशातील कोणताही सदिश जर या लाक्षणिक मूल्याच्या एकघाती पदावलीच्या रूपात मांडता आला, तर ते फार सोईचे ठरते.

हेच सदिश अवकाश मानीय (म्हणजे ज्यांच्या बाबतीत, अंतराशी साम्य असणारे गुणधर्म असणाऱ्या एका अ-ऋण सत्‌ मूल्यी फलनाची व्याख्या मांडता येईल असे, मेट्रिक) असतील, तर अशी मांडणी फार महत्त्वाची ठरते व त्यांचा अभ्यास प्रगत गणितीय शाखांतून होतो. तसेच संस्थितिक एकघाती अवकाशातील फलन आणि अनंतमितीय अवकाशातील कारक हेही प्रगत अभ्यासाचे विषय आहेत.

इतिहास : एकोणिसाव्या शतकाच्या अखेरीस व विसाव्या शतकाच्या सुरुवातीस सिल्व्हेस्टर व केली यांनी ⇨निर्धारक आणि [→ आव्यूह सिध्दांत] यांच्या साहाय्याने सांत अवकाशाच्या उपपत्तीसंबंधी बरेच संशोधन केले. विसाव्या शतकाच्या सुरुवातीला हिल्बर्ट, श्मिट आणि रीझ यांनी समाकल समीकरणांसंबंधी (विशेषतः फ्रेडहोम व व्होल्तेर्रा समीकरणांसंबंधी) केलेल्या अभ्यासामुळे कारक उपपत्तीने प्रगतीचा मोठा पल्ला गाठला. याच अनुषंगाने हिल्बर्ट यांनी हिल्बर्ट अवकाशातील कारक आणि भूमिती यांचा सुसूत्र अभ्यास केला. पूर्णतः संतत स्वसंलग्नी कारकांसंबंधीचे सुप्रसिद्ध वर्णपटी प्रमेय हे हिल्बर्ट यांच्या अभ्यासाचे महत्त्वपूर्ण फल होय. याच सुमारास रीझ यांनी संतत एकघाती फलनके आणि कारक यांच्यासंबंधी बरेच संशोधन केले. १९३० च्या सुमारास मानीय अवकाश व तद्‌विषयक कारक यासंबंधीही बरेच संशोधन झाले. बनाख यांनी यासंबंधी प्रसिद्ध केलेला प्रबंध आजही प्रमाणभूत मानला जातो. फोन नॉयमान यांचे संशोधन व स्टोन यांच्या हिल्बर्ट अवकाशातील रुपांतरे आणि त्यांचे वैश्लेषिक अनुप्रयोग या विषयावरील ग्रंथाने आधुनिक कारक उपपत्तीतील नवे पर्व सुरू झाले. नॉयमान यांनी कारक-वलयांच्या अभ्यासास चालना दिली, तसेच हिल्बर्ट अवकाशातील अमर्याद कारकांसंबंधी बरेच संशोधन करून त्यासंबंधीचे वर्णपटी प्रमेयही मांडले. विंटनर यांनी अनंतमितीय आव्यूहांच्या दृष्टीने कारकांचा अभ्यास केला. कारक-वलये हा आजतागायत संशोधनाचा विषय होऊन बसला आहे.

संदर्भ :- १.Dickinson, D.R.Operators, London, १९६७.

२.Indritz, J.Methods in Analysis, London, १९६३.

३.Pipes, L.A.Applied Mathematics for Engineering and Physics, New York १९५८.

आगाशे, क.म.

“