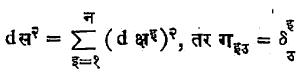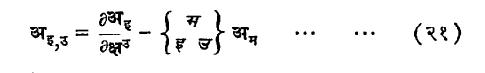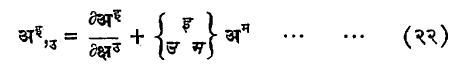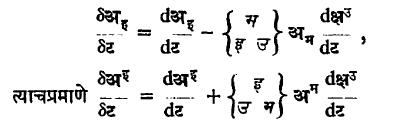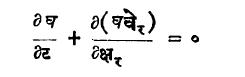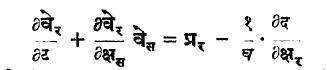प्रदिश : (टेन्सॉर). सदिश विश्लेषणातून [⟶ सदिश] व्यापकीकरणाने विकसित झालेली प्रदिश विश्लेषण ही एक गणित पद्धती आहे. प्रदिश संकल्पनेचा उदय सी. एफ्. गौस, जी. एफ्. बी. रीमान व ई. बी.क्रिस्टोफेल यांनी एकोणिसाव्या शतकाच्या उत्तरार्धात केलेल्या अवकल भूमिती विषयक [⟶ भूमिती] अभ्यासातून झाला आणि १९०१ मध्ये इटलीतील सी. जी. रीत्ची व त्यांचे शिष्य टी. लेअव्हि-चिव्हिता यांनी व्यवस्थित व शास्त्रशुद्ध पायावर ‘प्रदिश विश्लेषणा’ची (किंवा ‘शुद्ध अवकल गणिता’ची) उभारणी केली. निरनिराळ्या सहनिर्देशक पद्धतींमध्ये [⟶ भूमिती] काही गणितीय विधाने निश्चल राहतात. अशा विधानांचा रूपांतरण पद्धतीने अभ्यास करणे हे प्रदिश विश्लेषणाचे प्रमुख कार्य आहे. भौतिकीतील सत्य विधाने स्वभावतः शास्त्रज्ञांनी वापरलेल्या कोणत्याही संदर्भ व्यूहावर अवलंबून नसणारच परंतु त्यांचे वर्णन करण्यास सहनिर्देशकांची आवश्यकता असते. म्हणून अशा नियमांना गणितीय सूत्रांचे रूप देण्यास प्रदिश विश्लेषण अत्यावश्यक आहे. ॲल्बर्ट आइन्स्टाइन यांनी प्रदिशांच्या साहाय्याने आपल्या व्यापक सापेक्षता सिद्धांताची [⟶ सापेक्षता सिद्धांत] मांडणी अतिशय प्रभावीपणे केल्यापासून ही गणित पद्धती सर्वमान्य झाली. रीमानीय अवकल भूमितीच्या अभ्यासात तर प्रदिशांचा आधार घेतल्याशिवाय चालतच नाही आणि गतिकी (प्रेरणा कशा प्रकारे गती निर्माण करते याचा अभ्यास करणारी अनुप्रयुक्त गणिताची शाखा), स्थितिस्थापकताशास्त्र (वस्तू ताणल्यानंतर, दाबल्यानंतर वा विकृत केल्यानंतर पुन्हा मूळ आकार वा आकारमान धारण करण्याच्या तिच्या प्रवृत्तीसंबंधीचे शास्त्र), द्रायुगतिकी (द्रव व वायू यांसंबंधीची गतिकी), विद्युत् चुंबकत्व (चुंबकत्व व विद्युत् प्रवाह यांतील संबंध आणि त्यांचे गुणधर्म यांसंबंधीचे शास्त्र) इ. अनेक शास्त्रशाखांच्या उच्च सैद्धांतिक अभ्यासात प्रदिश विश्लेषणाला विशेष महत्त्व आहे.
न-मितीय अवकाश व रूपांतरण सूत्रे : त्रिमितीय अवकाशातील बिंदूंची निश्चिती (क्ष१, क्ष२, क्ष३) या अनुक्रमित तीन सत् संख्यांनी [⟶ संख्या] होते (या ठिकाणी १, २, ३ हे शिरांक असून घातांक नाहीत). या कल्पनेचे व्यापकीकरण करून प (क्ष१, क्ष२, …….., क्षन) हा एक न-मितीय अवकाशातील बिंदू कल्पिल्यास क्षइ (इ = १, २, ……. , न) हे त्याचे सहनिर्देशक होतील. क्षइ याला सर्व सत् मूल्ये दिल्यास जो बिंदुसंच मिळतो त्याला न-मितीय अवकाश म्हणतात व त्याचा निर्देश वन या चिन्हाने करतात.
(क्षइ) व (क्ष¯इ) हे वन मधील बिंदूचे, दोन निरनिराळ्या पद्धतींत सहनिर्देशक असल्यास त्यांच्यातील अन्योन्य संबंधदर्शक न-समीकरणे थोडक्यात दिल्यास
क्ष¯इ = क्ष¯इ (क्ष१, क्ष२, …….., क्षन )
} इ = १, २, …, न.
क्षइ = क्षइ (क्ष¯१, क्ष¯२, ……..,क्ष¯न )
… …. (१)
ही सहनिर्देशक रूपांतरण सूत्रे मिळतात.
गणितीय कृत्यांच्या सोयीकरिता या गणित पद्धतीत खालील संकेत रूढ आहेत.
(१) संयुती संकेत:
|
अ१ क्ष१ + अ२ क्ष२ + … + अन क्षन |
न |
|
Σ अस क्षस … (२) |
|
|
स = १ |
ही बेरीज संयुती चिन्ह Σ वगळून अस क्षस अशी लिहिण्याची पद्धती आहे. याच पद्धतीने एकाच पदात स हा प्रत्यय (शिरांक व पादांक म्हणून) दोन वेळा आल्यास ती बेरीज समजावी. याला आइन्स्टाइन यांचा संयुती संकेत म्हणतात. येथे स ऐवजी कोणताही प्रत्यय वापरला तरी संयुतीचे मूल्य बदलत नाही.
|
(२) क्रोनेकर डेल्टा : δइ |
= 0, इ ≠ उ |
} … … (३) |
|
उ |
= १, इ = उ |
या चिन्हाला एल्. क्रोनेकर या जर्मन गणितज्ञांच्या नावावरून क्रोनेकरडेल्टा म्हणतात.
|
संयुती संकेताप्रमाणे |
δस |
= न हे स्पष्ट होईल. |
|
स |
(३) वरील परिच्छेदांत वापरलेला संकेत म्हणजे
क्ष¯र = Φर (क्ष१, क्ष२, …….., क्षन ) यात र = १, २, ……. , न असे गृहीत धरतात.
सहचल व प्रतिचल सदिश आणि प्रदिश : वन अवकाशात प(क्षइ) आणि प(क्षइ + d क्षइ) हे सन्निध बिंदू घेतले, तर d क्षइ यास न-मितीय सदिश म्हणतात.
क्षइ⟶`क्ष¯इरूपांतरण केले, तर
|
dक्ष¯इ = |
∂`क्ष¯इ |
d क्षस … … … (४) |
|
∂क्ष-स |
हे समीकरण मिळते.
यावरून अ(अ¯इ) हा अनुक्रमित अइ (इ = १, २, …., न) फलनांचा सदिश घेऊन अ¯ (अ¯इ) हा त्याचा रूपांतरित सदिश खालील सूत्राने देता आल्यास,
|
अ¯इ = |
∂क्षइ |
अस … … (५) |
|
∂`क्षस |
अला ‘प्रतिचल सदिश’ म्हणतात. या ठिकाणी स शिरांक व पादांक म्हणून आल्याने संयुती संकेताप्रमाणे बेरीज अभिप्रेत आहे. तसेच Φ (क्ष१, क्ष२, …….., क्षन ) हे अदिश फलन घेतले, तर
|
∂Φ |
= |
∂Φ |
. |
∂क्षस |
, (इ = १, २, …, न) … (६) |
|
∂क्षइ |
∂क्षस |
∂क्षइ |
असे सूत्र मिळते. ब (बइ) असा अनुक्रमित फलन सदिश घेऊन, त्याचा रूपांतरित सदिश ब (बइ)
|
ब¯इ = |
∂क्षस |
बस … … … (७) |
|
∂क्ष¯इ |
या सूत्राने देता आल्यास ब ला ‘सहचल सदिश’ म्हणतात.
म(क्षइ) हे फलन रूपांतरणाने बदलत नसेल, तर त्यास निश्चल किंवा अदिश म्हणतात. उदा.,
|
म ≡ अस बस, म¯ ≡अ¯ बस |
||||||||
|
म¯ ≡अ¯स ब¯स = अट |
∂क्ष¯स |
. |
∂क्षठ |
बठ |
||||
|
∂क्षट |
∂क्षस |
|||||||
|
= अट |
∂क्षठ |
बठ = अट δठ ट |
बठ |
|||||
|
∂क्षट |
||||||||
|
= अट बट = म … … … (८)
|
||||||||
प्रतिचल व सहचल सदिशांप्रमाणे द्विप्रत्ययांकित
|
अइउ, अइउ, अउइ इ, उ = १, २, ……, न |
अशी द्विकोटिक फलने घेऊन त्यांची रूपांतरण सूत्रे अनुक्रमे
अशी असल्यास त्यांना अनुक्रमे द्विकोटिक प्रतिचल, सहचल व मिश्र प्रदिश म्हणतात.शिरांकाला प्रतिचल प्रत्ययांक व पादांकाला सहचल
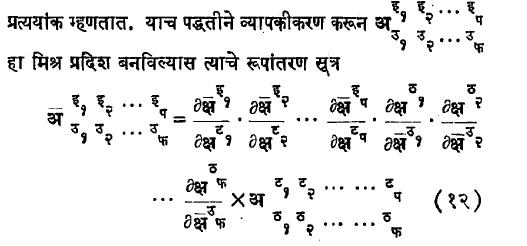
असे मिळते. येथे अ हा प्रदिश प प्रतिचल कोटिक व फ सहचल कोटिक आहे. यावरून अदिश शून्य कोटिक व सदिश एक कोटिक प्रदिश होत.
सममित व विषममित प्रदिश : दोन प्रतिचल किंवा सहचल प्रत्ययांकांच्या अदलाबदलीने प्रदिश बदलत नसेल, तर त्या दोन प्रत्ययांकापुरता तो सममित आहे असे म्हणतात. अशा कोणत्याही दोन प्रत्ययांकांच्या अदलाबदलीने प्रदिश बदलत नसेल, तर त्याला सममित प्रदिश म्हणतात. वरील प्रकारच्या अदलाबदलीने त्या प्रदिशाच्या अवयवांची फक्त बैजिक चिन्ह बदलत असेल, तर त्यास विषममित प्रदिश म्हणतात. शिवाय सहनिर्देशक रूपांतरण सूत्रे समघाती असल्याने प्रदिशाचे अवयव एका सहनिर्देशक पद्धतीत शून्य असल्यास कोणत्याही सहनिर्देशक पद्धतीत शून्य असले पाहिजेत. उदा.,
मूलभूत कृत्ये : दोन प्रदिशांचे शिरांक व पादांक समान असतील, तर त्यांची बेरीज व वजाबाकी म्हणजे घटकांची बेरीज आणि वजाबाकी करून मिळणारा त्याच कोटीचा प्रदिश होय. उदा.,
ह्याला दोन प्रदिशांचा बाह्य गुणाकार म्हणतात व त्यांची कोटी मूळ प्रदिशांच्या कोटींच्या बेरजेइतकी असते. बाह्य गुणाकारात एक शिरांक व एक पादांक (एक अ चा व एक ब चा) एकच घेतले, तर संयुती संकेतानुसार प्रदिशाची कोटी दोनने कमी होते. या क्रियेला संकोचन म्हणतात व मिळणाऱ्या प्रदिशास अंतर्गत गुणाकार म्हणतात.
प्रदिशत्वाची कसोटी : अइउट या फलन संचाचा कोणत्याही प्रदिशाशी अंतर्गत गुणाकार केल्यास तो जर प्रदिश असेल तर अइउट हाही प्रदिश असला पाहिजे. ह्या प्रदिशत्वाच्या कसोटीला भागाकार नियम म्हणतात.
रीमान मानीय (मेट्रिक) व प्रदिश अवकलन : त्रिमितीय अवकाशातील बिंदूचे कार्तीय सहनिर्देशक (क्ष, य, झ) घेतले, तर अल्पकंस dस करिता सूत्र dस२ = dक्ष२ + dय२ + dझ२ मिळते. क्ष, य, झ यांचे वक्र सहनिर्देशकात रूपांतरण केले, तर तेच सूत्र
d स२ = Σ गइउ d लइ d लउ
असे होईल. वक्र सहनिर्देशक अक्ष जात्य (एकमेकांना लंब) असल्यास
d स२ = ह१ d ल१२ + ह२ dल२२ + ह३ d ल३२
असे होईल. याचे व्यापकीकरण करून न-मितीय अवकाशातील (क्ष१, क्ष२, ….., क्षन) या सहनिर्देशक पद्धतीत dस करिता खालील सूत्र मिळते.
d स२ = ΣΣ गइठ d क्षइ d क्षउ = गइउ d क्षइ d क्षउ
(संयुती संकेतानुसार ) …. (१४)
या सूत्रास रीमान मानीय म्हणतात. येथे गइउ हा सममित द्विकोटिक प्रदिश असून तो सहचल असला पाहिजे. कारण dस२ ही अदिश राशी आहे.
जर एका विशिष्ट सहनिर्देशक पद्धतीमध्ये
आणि अशा अवकाशाला न-मितीय यूक्लिडीय अवकाश म्हणतात.
जर निर्धारक । गइउ । = ग असेल [⟶निर्धारक] आणि
|
गइउ= |
गइउ चा ग मधील सहअवयव |
… … … (१५) |
|
ग |
घेतला, तर गइउ हा सममित द्विकोटिक प्रतिचल प्रदिश मिळतो. त्याच्या व्याख्येवरून त्याला गइउ चा व्यस्त प्रदिश म्हणतात. कारण
|
गइउ गटउ = |
δटइ |
(निर्धारक नियमावरून). |
गइउ आणि गइउ या दोन प्रदिशांच्या साहाय्याने दिलेल्या सहचल किंवा प्रतिचल सदिशांचे सहानुगामी प्रतिचल किंवा सहचल सदिश मिळतात. उदा.,
|
अइ= गइम अम आणि अइ = गइम अम … … … (१६) |
एकाच सदिशाचे अइ आणि अइ हे अनुक्रमे सहचल किंवा प्रतिचलअवयव समजून सदिशाची लांबी व दोन सदिशांतील कोन यांची सुटसुटीत सूत्रे मिळतात.
(अधिक विवेचनासाठी ‘भूमिती’ या नोंदीतील ‘रीमानीय भूमिती’ विषयीची माहिती पहावी).
प्रदिशांचे अवकलज : फ(ट) हे निश्चल फलन व ट हा प्रचल (निरनिराळ्या परिस्थितीनुसार ठराविक मूल्य धारण करणारा स्थिरांक)
|
असेल, तर |
dफ |
हाही निश्चल असला पाहिजे. |
|
dट |
फ (क्षइ) हे क्षइ (इ = १, २, …, न) सहनिर्देशकांचे अदिश फलन असेल, तर समीकरण (६) वरून
|
∂फ |
हा सहचल सदिश असतो, हे स्पष्ट होईल परंतु |
|
|
∂क्षइ |
||
|
∂फ |
चा क्षट संबंधी अवकलज घेतल्यास त्यात |
|
|
∂क्षइ |
||
द्विकोटिक अवकलज येतो व तो प्रदिश होऊ शकत नाही. तेव्हा प्रदिश लक्षणाशी सुसंगत अशी प्रदिश अवकलनाची व्याख्या देण्याकरिता गइउ या रीमान प्रदिशाच्या साहाय्याने मिळणारी क्रिस्टोफेल चिन्हे वापरणे आवश्यक आहे. त्यांच्या व्याख्या अशा
यांना अनुक्रमे क्रिस्टोफेल यांचे प्रथम चिन्ह व क्रिस्टोफेल यांचे द्वितीय चिन्ह म्हणतात. ही चिन्हे प्रदिश नाहीत, हे त्यांची रूपांतरण सूत्रे लिहून सहज ध्यानात येईल परंतु त्यांच्या साहाय्याने अइ या सहचल सदिशाचा सहचल अवकलज म्हणून
हा द्विकोटिक सहचल प्रदिश मिळतो. (इ व उ यांमधील स्वल्पविराम सहचल अवकलनाचा निदर्शक आहे).
त्याचप्रमाणे अइ या प्रतिचल सदिशाचा सहचल अवकलज खाली दिल्याप्रमाणे मिळतो.
हा द्विकोटिक मिश्र प्रदिश आहे.
|
अइ सदिशाचा |
δअइ |
हा, क्षउ = क्षउ (ट) या वक्रानुगामी अवकलज, |
|
δट |
|
dक्षउ |
वअइ चा सहचल अवकलज यांच्या अंतर्गत गुणाकाराने मिळतो. |
|
dट |
यांना अनुक्रमे अइ व अइ यांचे अंगभूत किंवा विशुद्ध अवकलज म्हणतात. याचप्रमाणे उच्चकोटिक सहचल किंवा प्रतिचल अवकलजांच्या व्याख्या देता येतात.
सहनिर्देशक पद्धती जात्य (यूक्लिडीय) असल्यास गइउ या निश्चल संख्या असल्यामुळे क्रिस्टोफेल चिन्हांची मूल्ये शून्य असणार. या पद्धतीमध्ये प्रतिचल व सहचल असा सदिशांमधील भेद करण्याची जरूरी नसते. शिवाय वरील अंगभूत अवकलज हा या पद्धतीत सामान्य पूर्ण अवकलज होतो व सहचल अवकलज सामान्य आंशिक अवकलज होतो. गइ व गइउ यांचे सहचल अवकलजही या पद्धतीत शून्य असतात. उदा., गतिमान बिंदूचे सहनिर्देशक्षइ घेतल्यास त्याचा
|
वेग सदिश वेइ |
dक्षइ |
|
dट |
हा सहचल सदिश होय. यावरून न्यूटन यांचा गती नियम
असा लिहिता येतो.
अल्पांतरी रेषा : न-मितीय अवकाशातील पृष्ठांवर अ आणि आ हे कोणतेही दोन बिंदू घेतले, तर त्यांस जोडणारे त्या पृष्ठावर अनेक वक्र संभवतात. त्यांतील लघुतम लांबी असलेल्या वक्रास अल्पांतरी रेषा म्हणतात. समजा च हा पृष्ठावरील वक्र असून त्याच्या लांबीसाठी स हे चल परिमाण वापरले आणि अ व आ या ठिकाणी स चे मूल्य अनुक्रमे स१ व स२ असेल, तर च या वक्राची अ पासून आ पर्यंतची लांबी खालील समाकलाने मिळते.
हे अल्पांतरी रेषेचे अवकल समीकरण होय.
स्थितिस्थापकताशास्त्रात प्रदिशांचा उपयोग : जात्य सहनिर्देशक पद्धतीनुसार स्थितिस्थापकतेची समीकरणे [⟶ स्थितिस्थापकता] पुढीलप्रमाणे आहेत:
या समीकरणांचे दुसऱ्या एखाद्या वक्र सहनिर्देशक पद्धतीत प्रदिश विश्लेषणाचे नियम वापरून रूपांतरण केले, तर आपल्याला जी समीकरणे मिळतील ती प्रदिश समीकरणे कोणत्याही सहनिर्देशक पद्धतीत सत्य ठरतील. म्हणजेच ही समीकरणे स्थितिस्थापकतेसंबंधी जी माहिती देतात जी सहनिर्देशक पद्धतीवर अवलंबून असणार नाही.
वरीलप्रमाणेच द्रायुगतिकीची मूलभूत समीकरणे पुढीलप्रमाणे आहेत.
(येथे घ-घनता, वे-वेग, प्र-बाह्य प्रेरणा, द-दाब, ट-काल आहेत).
यांचे कोणत्याही सहनिर्देशक पद्धतीत रूपांतरण केले असता जी प्रदिश समीकरणे मिळतील ती सहनिर्देशक पद्धतीवर अवलंबून असणार नाहीत.
पहा : अवकलन व समाकलन भूमिती स्थितिस्थापकता.
संदर्भ : 1. Pipes, L. A. Applied Mathematics for Engineers and Physicists, Tokyo, 1958.
2. Spain, B. Tensor Calculus, London, 1960.
3. Spain, B. Vector Calculus, London, 1965.
4. Weatherburn, C. E. An Introduction to Riemannian Geometry and the Tensor Calculus, Cambridge, 1963.
देशपांडे, कृ. के. आगाशे, क. म.
“