आरेखन, अभियांत्रिकीय

आरेखन, अभियांत्रिकीय : यंत्र व त्याचे भाग, जमिनीवरील व जमिनीखालील कोणतीही रचना, तिच्या निरनिराळ्या भागांचे आकार, मांडणी, जोडणी वगैरेंची त्यांच्या निर्मितीच्या दृष्टींनी सर्वांगीण कल्पना येईल अशी अंतर्बाह्य विविध दृश्ये अचूक व लहानमोठ्या मापात काढतात, त्यास अभियांत्रिकीय आरेख म्हणतात. ज्याचे आरेख काढावयाचे त्या आरेखन विषयात यंत्र, त्याचा प्रत्येक भाग, कोणत्याही प्रदेशाचे अंतर्बाह्य चित्रण, वास्तू, लोहमार्ग, रस्ते, पूल, पाण्याचे नळ व मलवाहिन्या यांचे मार्ग, धरणे, तलाव, बोगदे, कालवे इ. मानवाने निर्माण करावयाच्या वस्तूंचा व रचनांचा समावेश होतो. आरेखांवर अवश्य ती सर्व मापे मांडतात.

आरेखन साहित्य व उपकरण

आरेखन फलक : (आ. १). हा फलक उत्तमपैकी रापविलेल्या पाइन किंवा तत्सम लाकडाच्या फळ्यांचा बनवितात. कागद धरून ठेवणाऱ्या फलक-

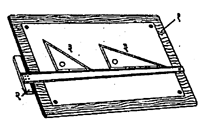
टोची फलकावर टोचून बसविता येतील इतपत फलकाचा पृष्ठभाग मऊसर असतो. कोणत्याही प्रकारच्या हवामानामुळे त्याच्या फळ्या वेड्यावाकड्या होऊन अगर फळ्यांचे जोड सुटून अलग होऊ नयेत, अशी त्याची बांधणी असते. त्याची डावी कड, टी-गुण्याचे खोड टेकवून सरकविण्याकरिता काटेकोरपणाने सरळ केलेली असते. तिला कामाची कड म्हणतात. कागदाला सर्वत्र सारखा आधार मिळावा म्हणून फलकाचा पृष्ठभाग तितक्याच काटेकोरपणाने सपाट ठेवतात. कामाच्या सोईकरिता हे फलक निरनिराळ्या मापाचे बनवितात. त्यांची लांबी ही रुंदीच्या सुमारे दीडपट असते.

टी-गुण्या : (आ. १). ह्याचा आकार इंग्रजीतल्या टी (T)अक्षराच्या आकारासारखा दिसतो म्हणून यास टी-गुण्या म्हणतात. हा नासपती किंवा मॅहॉगनी अगर तत्सम प्रकारच्या घट्ट मजबूत लाकडापासून बनवितात. ह्याचे दोन भाग म्हणजे खोड व त्याच्या काटकोनात घट्ट बसविलेले पाते. आरेखन फलकाच्या कामाच्या कडेवर खोड खेटून धरून टी-गुण्या आरेखन फलकावर खाली-वर सरकविता येतो. टी-गुण्याचा उपयोग फलकाच्या लांबीला समांतर आडव्या रेघा काढण्यासाठी व तिकोनी गुण्यांना आधार देण्यासाठी होतो.

तिकोनी गुण्ये : (आ. १). यांची नेहेमी एक जोडी असते. एकाचे कोन ४५^०, ९०^० व ४५^० व दुसऱ्याचे ६०^०, ९०^० व ३०^० असे असतात. हे 

सर्वसाधारणपणे पारदर्शक प्‍लॅस्टिकचे व लहानमोठ्या आकारांचे बनवितात व काहींच्या कोरी उतरत्या असतात. ह्या गुण्यांनी लंब किंवा तिरक्या समांतर रेषा सुलभतेने काढता येतात.

वक्रणी : (आ. २). हिचे अनेक लहानमोठे आकार व प्रकार आहेत. लाकूड, व्हल्कनाइट, प्‍लॅस्टिक वगैरेंच्या पट्ट्यांवर विविध वक्र कोरलेले असतात. वर्तुळाकार अगर त्याचा भाग नसतील अशा पाहिजे त्या प्रकारच्या वक्ररेषा काढण्याकरिता हिचा उपयोग होतो.

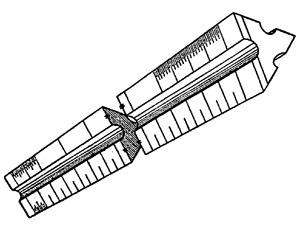
प्रमाणपट्ट्या : या उत्तम प्रतीचे लाकूड, पुठ्ठा किंवा प्‍लॅस्टिक यांच्या बनवितात. प्रमाणपट्टीवर एखादे विशिष्ट प्रमाणमाप रेखलेले असते. निरनिराळ्या प्रमाणमापांचा ६ ते ८ प्रमाणपट्ट्यांचा एक संच असतो किंवा त्रिधारी लाकडी पट्टीच्या कडांवर दोन्ही टोकांकडून निरनिराळ्या प्रमाणातील मापे असतात. एका पट्टीवर एकूण १२ प्रमाणमापे असतात (पहा आ. ३). आवश्यकतेप्रमाणे ठराविक प्रमाणपट्टी वापरून आरेखातील मापे वास्तव प्रमाणात मिळतात. मेट्रिक पद्धती प्रचारात आल्यापासून अशा प्रमाणपट्ट्यांची फारशी गरज राहिलेली नाही.

कोनमापक : हे अर्धवर्तुळाकार व वर्तुळाकार लहानमोठ्या आकाराचे प्‍लॅस्टिक, लाकूड किंवा पोलाद यांचे बनवितात. कोणत्याही ठराविक अंशाची कलती रेषा काढण्याकरिता किंवा दोन रेषांमधील कोन मोजण्याकरिता हा उपयोगी असतो.

आरेखन फलकसंच : सरळ उभे राहून काम करता येण्यासारखा, घोडीवर  

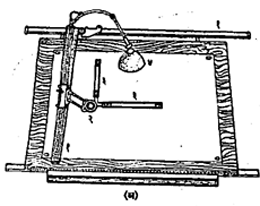
 उभारावयाचा फलक आ. ४ (अ) मध्ये दाखविला आहे. या फलकावर आडव्या व उभ्या समांतर रेघा काढण्याच्या मार्गदर्शक पट्ट्या, अचूक कोन काढण्याचे मापक व प्रमाणपट्ट्या हे साहित्य जोडलेले असते. याच्या साहाय्याने टी-गुण्या, तिकोनी गुण्ये व कोनमापक या सर्वांचे काम करता येते व आरेखन सोपे व सत्वर होते. फलकावर योग्य प्रकारे प्रकाश पडावा म्हणून स्वतंत्र विजेच्या दिव्याचीही सोय केलेली असते. या 

फलकावरील साहित्याचा मुख्य नियंत्रक भाग आ. ४ (आ) मध्ये दाखविला आहे, त्यावरून या साहित्याच्या उपयुक्ततेची कल्पना येईल. असा फलकसंच जेथे आरेखनाचे पुष्कळ कार्य असते तेथेच वापरला जातो.

पेन्सिल : शिशाच्या प्रतीप्रमाणे पेन्सिलीचे निरनिराळे प्रकार असतात. बी, २ बी, ३ बी, ४ बी वगैरे इंग्रजी अक्षरांनी ओळखल्या जाणाऱ्या पेन्सिलींचे शिसे क्रमशः वाढत्या प्रमाणात काळे व नरम असते. त्याचप्रमाणे एच, एचबी या अक्षरांनी दर्शविलेल्या पेन्सिलींचे शिसे मध्यम असते व २ एच, ३ एच, ४ एच म्हणून ओळखल्या जाणाऱ्या पेन्सिलींचे शिसे क्रमशः जास्त कडक असते.

अचूक रेषाकाम साधण्यासाठी पेन्सिलीला आवश्यक आकाराचे टोक करून घ्यावे लागते. अणकुचीदार व धारदार चपटे अशा दोन प्रकारची टोके असतात. घासकागदावर वेळोवेळी घासून किंवा दोन शून्य (००) वर्गाची कानस वापरून टोकाची धार कायम ठेवतात.

पेन्सिल तासण्यासाठी चाकू, आरेखनातील अनावश्यक रेघा खोडण्यासाठी मऊ प्रतीचे खोडरबर, खोडकामाचा कचरा झटकण्याकरिता वा साहित्य स्वच्छ ठेवण्याकरिता स्वच्छ कापड हे किरकोळ साहित्यही आवश्यक असते. आरेखन कागद फलकावर स्थिर बसविण्यासाठी फलकटोची किंवा चिमटे वापरतात. याच कामासाठी चिकटपट्टीचाही उपयोग करतात. त्यामुळे टी-गुण्या फलकावर वरपासून खालपर्यंत सरकवताना त्याला अडथळा होत नाही.

आरेखन कागद : रबराने खोडले असता तंतू निघणार नाहीत किंवा घडी पडली असता कागद सहजासहजी फाटणार नाही, असा चिवट व टिकाऊ कागद आरेखनासाठी वापरतात. त्यावर शाई पसरत नाही व त्यावरील आरेख दीर्घकाळ स्पष्ट राहतो, म्हणूनच कायम स्वरूपाचे आरेख यावर काढतात. ५५ ते ८० सेंमी. पर्यंत रुंदी व ८० ते १३५ सेंमी. पर्यंत लांबी अशा ७-८ आकारांचे कागद निरनिराळ्या संज्ञांनी व्यवहारात ओळखले जातात. मूळ आरेख अनुलेखन कागदावर किंवा अनुलेखन कापडावर अनुलेखित करून त्यावरून अवश्य तितकी छायामुद्रिते काढतात.

शाई : आरेखातील रेषा जास्तीत जास्त गडद उठतील व धुवूनही जाणार नाहीत अशी काळी शाई वापरतात. या शाईच्या रेषा फिक्या पडत नाहीत. शाईची रेषा समजाडीची काढण्याकरिता विशेष तऱ्हेचे निब किंवा शाई सामावणारे टोक असलेली आरेखलेखणी वापरतात. अशा आरेखलेखणीत रेषांची जाडी कमी जास्त करण्याची सोय असते. जाड किंवा तुटक्या रेषा नीट उमटतील अशी निरनिराळी निबे व टोके असतात (आ. ५ अ.). अक्षराच्या कोरीव फर्म्यावर एक टोक गिरवून दुसऱ्या टोकांनी लहान किंवा मोठी, उभी किंवा तिरकी अक्षरे काढता येणारी विशेष आरेखलेखणीही (आ. ५ आ) असते.

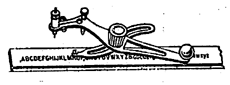
उपकरण पेटी : आरेखनास उपयुक्त अशी उपकरणे असलेली पेटी असते. या पेटीत सामान्यतः पुढील गोष्टी असतात. (१) पेन्सिलीचा मोठा कर्कट, (२) मोठा विभाजक, (३) पेन्सिलीचा स्प्रिंग

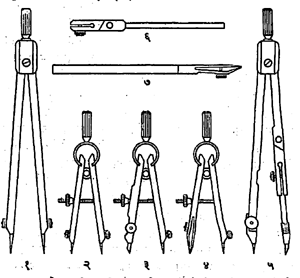
असलेला लहान कर्कट, (४) स्प्रिंग असलेला लहान विभाजक, (५) शाईचा स्प्रिंग असलेला लहान कर्कट, (६) कर्कटासाठी आरेखलेखणीचा उपायोज (वेगळा लावण्याचा भाग), (७) कर्कटासाठी विभाजकाचे उपायोज, (८) लांब त्रिज्या काढण्यासाठी दीर्घी (लांबी वाढविण्याचा भाग), (९) शाईकामासाठी लहान मोठ्या आरेखलेखण्या, (१०) घूर्णी कर्कट, (११) शिसे ठेवण्याची डबी, (१२) स्क्रू सैल-घट्ट करण्यासाठी पानापट्टी. आ. ६ मध्ये काही उपकरणे दाखविली आहेत कर्कटाचा उपयोग वर्तुळे, वर्तुळखंड, भूमिती पद्धतीने लंब व कोन काढण्यासाठी, रेषेचे किंवा कंसाचे समान भाग करण्यासाठी करतात. वर्तुळाची त्रिज्या मोठी असेल, तर कर्कटाच्या पायास जोडण्याकरिता दीर्घीचा उपयोग करतात.

आरेख प्रकार

आरेखन विषय त्रिमित असतात. त्यांची निरनिराळी द्विमित रूपे रेखाटून आरेखन विषयाचे बारकावे व त्यामधील अंतर यांची सुस्पष्ट कल्पना देता येते. द्विमित रूपात अधोदर्शन (वरून दिसणारा), पुरोदर्शन (पुढून दिसणारा), पार्श्वदर्शन (बाजूने दिसणारा), पश्चदर्शन (मागून दिसणारा) व उभे आडवे छेद हे आरेख मुख्यतः असतात व ते प्रक्षेप (एखाद्या वस्तूवर प्रकाशकिरण पाडून उत्पन्न केलेल्या छायेच्या जागी प्रकाश उगमाच्या बाजूने दिसणारा त्या वस्तूचा देखावा काढण्याच्या) पद्धतींनी काही निवडक पातळ्यांमध्ये काढले जातात.

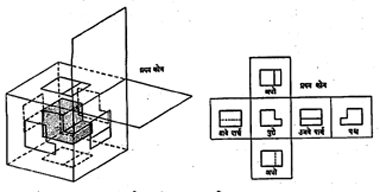
लंबजन्य प्रक्षेप : या पद्धतीत आडवी एक व उभ्या दोन अशा एकमेकींना काटकोनात असलेल्या पातळ्या प्रमुख असतात व त्यावर त्यांच्याशी काटकोन करणारे प्रक्षेप घेऊन आरेखन विषयाची निरनिराळी रूपे काढतात. उभी व आडवी पातळी एकमेकींना छेदते तेव्हा अवकाशाचे चार भाग होतात. त्यांना अनुक्रमे प्रथम, द्वितीय, तृतीय व चतुर्थ काटकोन म्हणतात. या चार भागांपैकी प्रत्येक भागात समोरासमोर समांतर पातळ्या काढल्या, तर पातळ्यांच्या चार पेट्या तयार होतात. त्यांपैकी तृतीय पातळीतील पेटीत (आ. ७) आरेखन विषय अधांतरी आहे असे कल्पून त्याच्या निरनिराळ्या बिंदूंपासून सभोवतालच्या पातळ्यांवर, पातळीशी काटकोन करणाऱ्या रेषा काढून पातळ्यांवर भिडविल्या, तर पातळ्यांवर आरेखन विषयाचे त्या त्या बाजूचे दृश्य तयार होते. कोणतीही पातळी दृष्टिपथाच्या काटकोनात धरली, तर माथ्याच्या किंवा तळच्या पातळीवर दिसणारे दृश्य म्हणजे आरेखन विषयाचे अधोदर्शन, आरेखन विषयाच्या लांबीशी समांतर असलेल्या पुढील पातळीवरील दृश्य ते पुरोदर्शन, मागील पातळीवरील दृश्य ते पश्चदर्शन व बाजूच्या पातळ्यांवरील ती पार्श्वदर्शने होत. तृतीय काटकोनातील अशी प्रक्षेप दृश्ये भारतीय मानक पद्धतीत प्रमाणभूत दृश्ये मानतात.

गास्पार माँझ (१७४६ – १८१८) या फ्रेंच गणितज्ञाला प्रक्षेप पद्धतीच्या शोधाचा मान दिला जातो. त्यांनी लिहिलेल्या Geometrie descriptive हा ग्रंथ जनतेसाठी १७९९ मध्ये प्रसिद्ध होईपर्यंत सु. तीस वर्षे ही पद्धती एक राष्ट्रीय गुपित म्हणून ठरविण्यात आलेली होती. यांत्रिक अभियांत्रिकीत या पद्धतीस विशेष महत्त्वाचे स्थान प्राप्त झालेले आहे [→ भूमिति].

साहाय्यक प्रक्षेप देखावे: सर्वसाधारण पद्धतीच्या लंबजन्य प्रक्षेप देखाव्यावरून जर मूळ वस्तूची नीट कल्पना येत नसेल, तर साहाय्यक प्रक्षेप घेतात. हे प्रक्षेप नेहमीच्या तीन पातळ्यांपेक्षा निराळ्या पातळ्यांवर घेतात.

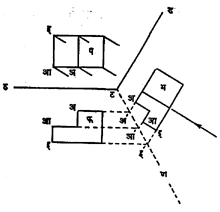
पहिला अथवा मूळ साहाय्यक देखावा घेण्याची पद्धत आ. ८ मध्ये दाखविली आहे. या आकृतीत फ हे मूळ वस्तूचे पुरोदर्शन आहे व प अधोदर्शन आहे. प या देखाव्याकडे बाणाच्या दिशेने पाहून तिच्या काटकोनात असलेल्या टड या रेषेवरील उभ्या पातळीवर जो नवा देखावा भ तयार होतो तो पहिला साहाय्यक देखावा होय. 

याकरिता फ देखाव्याची टठ रेषेने दर्शविलेली पातळी व पहिल्या साहाय्यक देखाव्याची टड रेषेनी दर्शविलेली पातळी यांमधील कोनाचा द्विभाजक टण याचे साहाय्य घेतात. फ वरील अ, आ, इ या बिंदूंचे प्रक्षेप टण या द्विभाजकावर घेऊन अ’, आ’, इ‘ बिंदू मिळतात. या बिंदूंपासून निघालेले प्रक्षेप प वरील अ, आ, इ या बिंदूंमधून टड या पातळीवर काढलेल्या प्रक्षेपांना ज्या ठिकाणी अनुक्रमाने छेदतात, त्यांवरून भ देखाव्यातील अ, आ, इ हे बिंदू निश्चित होतात. याचप्रमाणे इतर सर्व बिंदू निश्चित केले जातात.

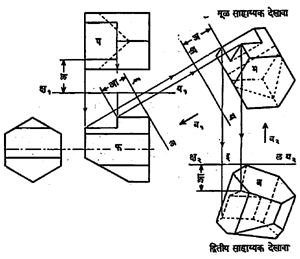
ज्या वेळी पहिल्या साहाय्यक देखाव्याची एखादी बाजू अधिक स्पष्ट करावयाची असेल, तेथे त्या बाजूकडे तिच्या लंब दिशेने पाहून आणखी एक साहाय्यक देखावा काढतात, त्यास दुसरा साहाय्यक प्रक्षेप देखावा म्हणतात. आ. ९ मध्ये भ हा पहिला साहाय्यक देखावा वरील पद्धतीनेच काढलेला आहे. या देखाव्यातील खालच्या बाजूकडे ब_२ या दिशेने पाहून क्ष_२ य_२ या रेषेने दाखविलेल्या उभ्या पातळीवर ब हा आणखी एक देखावा काढलेला आहे. त्यास द्वितीय साहाय्यक देखावा म्हणतात.

छेद देखावे: लंबजन्य प्रक्षेपांनी काढलेल्या दृश्यावरून आरेखन विषयाच्या अंतर्गत 

भागाचे स्वरूप व मापे कळू शकत नाहीत म्हणून छेद देखावे काढतात. प्रमुख पातळ्यांशी समांतर अशी एक पातळी आरेखन विषयामधून जाते, अशी कल्पना करून त्या छेद पातळीने आरेखन विषयाचे जे दोन भाग होतील, त्यांपैकी पुढील 

भाग बाजूला काढला, तर मागील भाग जसा दिसेल तो आरेखन विषयाचा छेद देखावा होय. अनुदैर्घ्य म्हणजे लांबीवरचे छेद देखावे व काट छेद देखावे हे प्रमुख छेद देखावे आहेत (पहा आ. १०). एकाच

पातळीत छेद देखावा घेताना आरेखन विषयातील इतर ठिकाणचे वैशिष्ट्य त्यात समाविष्ट होत नसेल, तर छेद पातळीचा काही भाग समांतर सरकवून, त्या विशिष्ट भागातून नेऊन, एकाच छेद देखाव्यात दाखवितात. आरेखन विषयाचा छेद कोठे घेतला हे

अधोदर्शन, पुरोदर्शन किंवा पार्श्वदर्शन यांपैकी कोणत्या तरी दृश्यावर बहुधा लघुरेषा व टिंब एका-पुढे एक काढलेल्या विभाजक रेषांनी दाखवतात. विभाजनामुळे कापला गेलेला जो भाग भरीव असतो, त्या भागावर समांतर व सम अंतरावर तिरक्या रेषा काढतात. अंतर्गत पोकळ भाग जसाच्या तसाच दाखवितात.

छेद देखाव्याचे अन्य प्रकार : यंत्राच्या घटक भागांचे आकार ठिकठिकाणी निरनिराळे असतात. यंत्राच्या मुख्य देखाव्यावर कोणत्याही जागेचा छेद त्याच दृश्यावर त्याच जागी

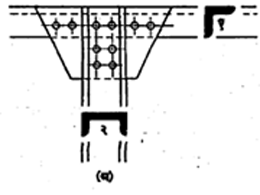
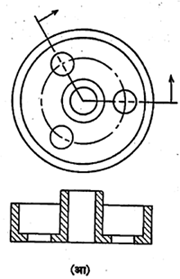
 काटकोनात फिरवून त्याच पातळीत दाखवितात (आ. ११ अ). आरेखन विषय मध्ये रेषेभोवती सममित (दोन्ही बाजूस सारखा) असेल, तर अर्ध्या भागाचा छेद व उरलेल्या अर्ध्या भागाचा मुख्य देखावा असे अर्धछेद देखावे काढतात. आरेखन विषय मध्य-बिंदूभोवती सममित असेल तर छेद पातळीची दिशा मध्यबिंदूपाशी सोईप्रमाणे बदलून घेतलेला छेद, एका पातळीत घेतलेल्या छेदाप्रमाणे एका ओळीत काढतात. ते एकपंक्ती छेद देखावे होत (आ. ११ आ).

लंबजन्य प्रक्षेप पद्धतीनी काढलेल्या दृश्यावरून व छेद देखाव्यावरून आरेखन विषयाच्या निरनिराळ्या भागांची पृथक्‌पणे सर्व माहिती मिळते पण सर्वसाधारण स्वरूपाची कल्पना येण्याकरिता तीनही दृश्ये एकवट दिसतील असा तुल्य देखावा अथवा तिर्यक् देखावा काढावा लागतो. वास्तुशिल्पशास्त्रात यथादर्शन (वस्तू प्रत्यक्षात जशा दिसतात तशाच कागदावर काढून दाखविलेले) देखावे काढून सर्वसाधारण स्वरूप दाखवितात.

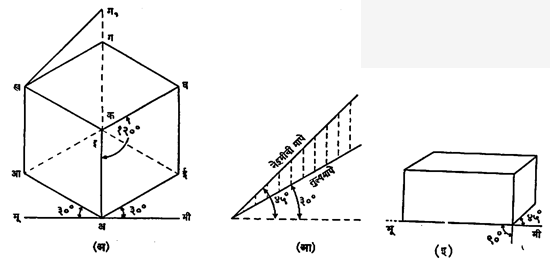
तुल्य देखावा : आ १२ (अ) मध्ये एका चौरस ठोकळ्याचा तुल्य (ज्यात मापे बदलत नाहीत असा) देखावा काढला आहे. ठोकळ्याची अ, आ, इ, ई ही बैठक भूमी या रेषेतून जाणाऱ्या आडव्या पातळीवर टेकून ठेवली. त्याच्या अआखक व अईघक या दोन बाजू भूमी या रेषेतून जाणाऱ्या उभ्या म्हणजे निरीक्षण पातळीतून दिसतील असा तो फिरविला. नंतर पुढच्या बाजूस तो इतका कलता करावयाचा की, त्याचा फक्त अ हा बिंदू आडव्या पातळीवर टेकेल, त्याची अक ही कड निरीक्षण पातळीवर टेकेल व तिचा वरचा क बिंदू व अगदी मागील गइ या कडेचा तळबिंदू इ हे एका रेषेत दिसतील, कर्ण इक निरीक्षण पातळीशी काटकोनात येईल. ठोकळ्याच्या या परिस्थितीत त्याच्या निरनिराळ्या बिंदूंपासून निरीक्षण पातळीवर तिच्याशी काटकोनात प्रक्षेप घेऊन जे दृश्य उमटेल तो तुल्य देखावा होय. यात ठोकळ्याचे क आणि इ हे बिंदू एकस्थित होतील तो प्रक्षेप बिंदू. निरीक्षण पातळीरेषा भूमी हिच्याशी ठोकळ्याच्या आडव्या कडरेषा ३०^० कोनात व उभ्या रेषा काटकोनात असतात. त्यांना तुल्य देखाव्याचे अक्ष म्हणतात. तिन्ही अक्ष परस्परांशी १२०^० कोन करतात.

तुल्य प्रमाणपट्टी : निरीक्षण पातळीशी समांतर नसलेल्या रेषांची खरी मापे मोजण्याकरिता विशिष्ट प्रमाणपट्टी तयार करतात (आ. १२ आ). एक आडवी रेषा काढून तिच्याशी ३०^० व ४५^० कोन करतील अशा दोन रेषा एकाच बिंदूतून काढतात. ४५^० च्या  रेषेवर नेहेमीची खरी मापे आखून त्यामधून उभे म्हणजे पहिल्या आडव्या रेषेच्या काटकोनात प्रक्षेप घेऊन ३०^० रेषेवर ते छेदतील त्या छेदावर क्रमशः वरील ४५^० च्या रेषेवरील मापे मांडून तुल्य प्रमाणपट्टी तयार होते.

आ. १२ (अ) मध्ये तुल्य लांबी खग = ०·८१६५ × खरी लांबी खग_१.

रूढ तुल्य देखाव्यात निरीक्षण पातळीशी समांतर नसलेल्या रेषासुद्धा आरेखन विषयाच्या त्या त्या बाजूच्या खऱ्या मापांच्या प्रमाणात काढतात. त्यामुळे आकार थोडासा विकृत दिसतो, पण आरेखातील सर्व मापे एकाच प्रमाणपट्टीने मोजून मिळू शकतात.

तिर्यक् देखावा:आरेखन विषयाच्या एका बाजूवर जेव्हा बहुसंख्य बारकावे समाविष्ट झालेले असतील व इतर बाजूंचा विस्तार कमी असेल तेव्हा ती एक बाजू निरीक्षण पातळीशी समांतर ठेवून तिर्यक् देखावा काढतात. या देखाव्यात निरीक्षण पातळीवर येणाऱ्या दोन अक्षांमधील कोन काटकोन असतो व तिसरा अक्ष सोईप्रमाणे तिरकस ठेवतात (आ. १२ इ). निरीक्षण पातळीवर घ्यावयाचे प्रक्षेप तिरकस अक्षाला समांतर घेतात. या पद्धतीत निरीक्षण पातळीवरील दृश्यातील सर्व मापे खऱ्या मापाच्या एकाच प्रमाणात असतात, ही सोय आहे.

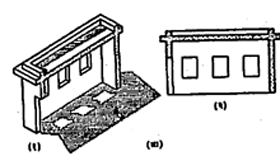
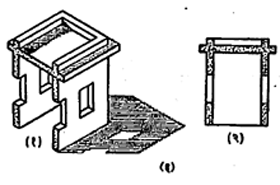
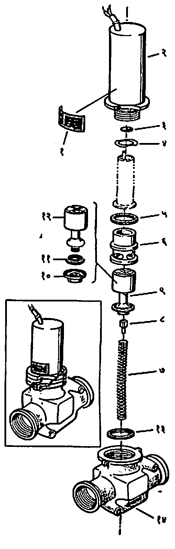
यंत्राचे निरनिराळे भाग क्रमशः कसे जोडतात हे दाखविण्यासाठी स्फुट जातीचे म्हणजे एकमेकांपासून क्रमशः दूर सरकवून ठेवलेल्या स्वतंत्र भागांचे आरेख काढतात (आ. १३).

स्थलदर्शक नकाशा:स्थापत्य अभियांत्रिकीत आरेखन विषयाचा विस्तार कधीकधी फार मोठा असतो. हा विस्तार त्याचा परिसर व परिसराचे प्राकृतिक स्वरूप यांची एकत्रित कल्पना देण्याकरिता स्थलदर्शक नकाशाच्या रूपात तयार केलेला असतो. या नकाशावर त्या प्रदेशाच्या समोच्चरेखा (समान उंची दर्शविणाऱ्या रेखा) दाखविलेल्या असतात. त्यावरून जमिनीचे चढउतार, पाण्याच्या प्रवाहाचे मार्ग, उंचवटे वगैरेंची कल्पना येते. या नकाशावर लोकवस्तीची ठिकाणे, रहदारीच्या व इतर सोयी दाखविलेल्या असतात. नकाशावर निरनिराळ्या रंगांनी धरणाच्या जागा, कालवे, पाण्याच्या नळांचे किंवा मलवाहिन्यांचे मार्ग, रस्ते, पूल, मोऱ्या, शुद्धीकरण किंवा निर्मिती-स्थाने वगैरे प्रस्तुत प्रकल्पांच्या अंगोपांगांच्या नियुक्त जागा दाखविलेल्या असतात. इमारतीच्या स्थलदर्शक नकाशात इमारतीच्या मर्यादा, सभोवारची मोकळी जागा, चतुःसीमा, रस्ते, पाण्याचे नळ, मलवाहिनी वगैरे प्रकारच्या सोयी समाविष्ट होतील इतका परिसर फक्त दाखवितात. प्रकल्पाच्या किंवा इमारतीच्या आरेखांचा एक संच असतो. प्रत्येक आरेखावर प्रकल्पाचे शीर्षक, आरेखाचे शीर्षक, आरेखाची संज्ञा किंवा क्रमांक, दिशानिर्देशक व आरेख प्रमाण मुख्यतः दिलेले असतात.

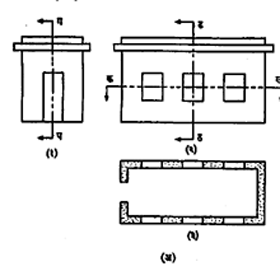
इमारतीचे आरेखसंच: इमारतीच्या जमिनीच्या वर सुमारे एक मीटर उंचीवर आडवा छेद घेतला व खाली राहणाऱ्या भागाकडे वरून पाहिले असता जे दृश्य दिसेल [आ. १० (अ-३) व १४] ते इमारतीचे अधोदर्शन होय. यात दालनांची मांडणी व मापे, भिंती, दरवाजे व खिडक्या हे ठराविक प्रमाणात दाखविलेले असतात. प्रत्येक मजल्याचे छप्पर उतरते असेल तर त्याचे, स्वतंत्र अधोदर्शन काढतात. दरवाजे, खिडक्या, कपाटे, संडास

वगैरे उपांगे संकेत चिन्हांनी अधोदर्शनावर दाखवितात. त्यांचे प्रकार व मापे दर्शविणारे सारणीबद्ध विवरण अधोदर्शनावर देतात. लांबीरुंदीची, परस्पर अंतरांची सर्व मापे अधोदर्शनावर व उंचीची मापे बाजूने, पुढून व मागून दिसणारे मुख्य देखावे व छेद यांवर दाखवितात. दालनांच्या मापांची उपयुक्तता पटविण्याकरिता अधोदर्शनावर घरातील सामानाची मांडणी अवश्य तर दाखवितात.

इमारतीचे इतर आरेख : जमिनीची पातळीरेषा काढून तीवर अधोदर्शनातील पुढील भागाच्या भिंतीवरील निरनिराळ्या बिंदूंपासून लंबजन्य प्रक्षेप घेतात. जोते, भिंती, खिडक्या, दरवाजे, छप्पर इत्यादींमधून निघालेल्या प्रक्षेप रेषांवर त्या त्या भागाची अपेक्षित उंची समप्रमाण दाखवून, त्यावर प्रत्येकाची बनावट संकेतरेषांनी दाखवून पुरोदर्शन देखावा तयार होतो. याचप्रमाणे बाजूच्या व मागील भिंतींवरून प्रक्षेप घेऊन अनुक्रमे पार्श्वदर्शन व पश्चदर्शन देखावे काढतात. इमारतीच्या आतील भिंती, दरवाजे वगैरे गोष्टी मुख्य देखाव्यावर दिसत नाहीत. त्यांची माहिती व्हावी म्हणून छेद देखावे त्याच पद्धतींनी काढतात व त्यात जमिनीखाली असलेला भागही दाखवितात (आ. १० व १४). भिंतींचे उभे छेद, दरवाजे, खिडक्या, कपाटे, छप्पर, जिना, काँक्रीटमधील प्रबलन (अधिक मजबुती आणण्यासाठी घातलेल्या पोलादी सळ्या), सजावट वगैरेंची व त्याच्या प्रत्येक भागाच्या रचनेची स्पष्ट कल्पना येईल, असे निरनिराळे मोठ्या आकाराचे आरेख काढतात. ते सविस्तर आरेख होत. इमारतीची उभारणी करताना पायाखोदाईपासून लागणारी विविध मापे दाखविणारे अधोदर्शन म्हणजे पायंडा अधोदर्शन होय. यावर इमारतीच्या भिंतींच्या मध्यरेषेवर आधारित लांबीरुंदीची मापे दिलेली असतात. वीज व पाणीपुरवठा, मैला व सांडपाणी विल्हेवाट वगैरे कामे अथपासून इतिपर्यंत दाखविणारे आरेख बहुधा संकेत चिन्हांनी स्वतंत्र काढलेले असतात.

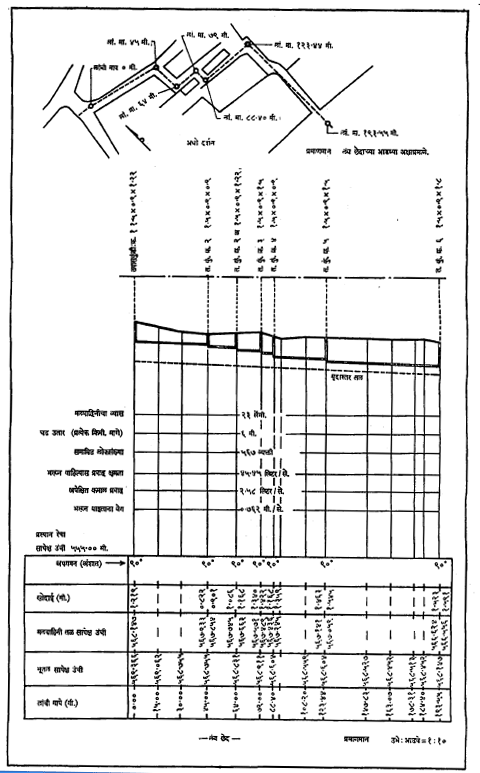
प्रकल्प आरेखसंच : स्थलदर्शक नकाशावर दाखविलेल्या निर तयार करतात. धरणे वगैरेंवर येणारे दाब पेलण्यायोग्य त्यांचा आकार, निराळ्या घटकांचे व त्यांच्या उपांगांचे आरेख, अवश्य तेथे सविस्तर रचना वगैरे निश्चित करण्याकरिता जे गणित केलेले असते ते दाखविणाऱ्या आरेखांपैकी स्थिरता आरेख हा एक असतो. रस्ते, पाण्याचे नळ, मलवाहिन्या वगैरेंचे चढउतार दाखविण्याकरिता अधोदर्शनाशिवाय मार्गांचे अनुदैर्घ्य छेद महत्त्वाचे असतात. त्यावर जमिनीची व संकल्पित घटकाच्या तळपातळीची सापेक्ष उंची, गणनातलरेषेवरील उंची, काम पार पाडण्याकरिता अवश्य असलेली खोदाई वा भराव, पूल, मोऱ्या वगैरे माहिती दाखविलेली असते (आ. १४). जमिनीच्या अनुदैर्घ्य छेदात किंवा काटछेदात उभ्या अंतराचे प्रमाण आडव्या अंतराच्या प्रमाणाच्या पंधरा ते वीसपट घेतात. अनुदैर्घ्य छेदाच्या काही विशिष्ट ठिकाणचे काटछेद अवश्य असतात व ते अनुदैर्घ्य छेदाच्या आरेखाच्या जवळच बहुधा काढतात.

आरेख छायामुद्रिते:निळ्या पार्श्वभूमीवर पांढऱ्या रेषांनी आरेखन उमटते अशा नील प्रती किंवा पांढऱ्या पार्श्वभूमीवर करड्या, जांभळ्या किंवा काळ्या रेषा उमटणाऱ्या अमोनिया प्रती असे आरेख छायामुद्रितांचे प्रकार असतात व ते अनुक्रमे फेरस किंवा अमोनिया रसायनांनी प्रभावित केलेल्या कागदांवर असतात. काळ्या शाईने अगर पेन्सिलीच्या गडद काळ्या रेषांनी केलेले अनुलेखन एका चौकटीत बसविलेल्या काचेवर, आरेख काढलेली बाजू काचेवर टेकेल असे पसरतात व त्यामागे त्याला चिकटून प्रभावित कागद पसरतात. दोन्ही एकमेकांना चिकटून बसावेत म्हणून त्यामागे नमदा (फेल्ट) व फळी घालून दाबून ठेवतात आणि काचेवर प्रकाश पाडतात. अनुलेखनातील काळ्या रेषांखेरीज इतर भागातून येणाऱ्या प्रकाशकिरणांचा परिणाम प्रभावित कागदावर होतो व परिणाम झालेल्या प्रभावित कागदाचे विकाशन करून (रासायनिक द्रव्यांच्या साहाय्याने मूळ आरेख दृश्यमान करून) छायामुद्रित तयार होते. परिणाम झालेला प्रभावित कागद धुऊन म्हणजे ओल्या पद्धतीने किंवा वाफारा देऊन कोरड्या पद्धतीने विकाशन करतात. विकाशनातील क्रिया एकामागून एक करणारी यंत्रेही उपलब्ध आहेत.

संदर्भ :  1. Greenhalgh, R. Modern Building Construction, Vol.1, London.

             2. Hornung, W. J. Blueprint Reading, Englewood Cliff, N. J. 1961.

             3. Pare, E. G. Engineering Drawing, New York, 1959.

             4. Schmidt, O. Technical Drawing, Bombay, 1964.

             5. Stevenson, G. A. Essentials of Drafting, Princeton. N. J., 1943.

               ६. दीक्षित, ल. वि. यांत्रिक चित्रकला, मुंबई, १९६१.

दीक्षित, ल. वि. ओक, भ. प्र.

“