गाठी : एका दोराचे (किंवा दोरीचे, नाडीचे वा इतर तत्सम वस्तूचे) टोक त्याच्या दुसऱ्या टोकाला किंवा दुसऱ्या दोराच्या टोकाला, किंवा कडीला, खुंटाला अथवा खांबाला किंवा अन्य वस्तूला घट्ट बांधून ठेवण्याची पद्धती. दोराच्या गाठी बांधण्याच्या अनेक पद्धती आहेत. विजारीच्या नाडीची टोके विशिष्ट पद्धतीने आवळून बांधली, तर नाडी आपोआप सुटत नाही परंतु नाडीचे विशिष्ट टोक ओढले, तर नाडीची गाठ चटकन सुटते. विहिरीतून पाणी काढण्यासाठी दोर-बादलीचा उपयोग करताना रहाटाच्या दोरीचे टोक बादलीच्या कडीमध्ये एका ठराविक पद्धतीने गुंतविले, तर पाण्याच्या वजनाने दोरीची गाठ सुटत नाही. परंतु गाठीतील दोरी एका विशिष्ट रीतीने मागे सरकवली, तर गाठ लवकर सुटते. गोठ्यातील गुरे खुंटांना बांधून ठेवण्यासाठी दोराच्या गाठी बांधाव्या लागतात. त्या गाठी योग्य पद्धतीने मारल्या तर गुरांनी दोर ओढला, तरी त्यांच्या मानेभोवती दोराचा फास बसत नाही.
बहुतेक सर्व प्रकारचे तंबू लवकर उभे करण्यासाठी तंबूच्या दोऱ्या जमिनीत पुरलेल्या खुंट्यांना जलद बांधाव्या लागतात व पाहिजे तेव्हा त्या जलद सोडवाव्याही लागतात. याकरिता सोईस्कर होईल अशी एक विशिष्ट पद्धत ठरविलेली आहे. धक्क्यावरील माल जहाजावर चढविण्यासाठी वापरीत असलेल्या दोरांना मालाच्या प्रकाराप्रमाणे निरनिराळ्या पद्धतींच्या गाठी बांधाव्या लागतात. गिर्यारोहक, बांधकाम करणारे कारागीर, कापड विणणारे कोष्टी, मासे धरणारे कोळी, पक्षी आणि लहान श्वापदे धरणारे पारधी अशी विविध धंद्यांतील लोकांना त्यांच्या विशिष्ट परिस्थितीप्रमाणे अनेक निरनिराळ्या प्रकारच्या गाठी बांधाव्या लागतात. शस्त्रक्रिया करणाऱ्या डॉक्टरांनाही फाडलेली त्वचा पुन्हा जुळवून सांधण्यासाठी विशिष्ट प्रकारच्या गाठी बांधाव्या लागतात. नेकटायची गाठ बांधण्याच्याही विविध पद्धती आहेत. शिडाच्या जहाजावर वापरीत असलेल्या दोरांना अनेक प्रकारच्या गाठी माराव्या लागतात. जहाजावर काम करणाऱ्या खलाशांना दोराच्या गाठी मारण्याची कला प्रत्यक्ष काम करून शिकावी लागते. निरनिराळ्या पद्धतींच्या गाठी मारणे ही एक उपयुक्त कला असल्यामुळे बालवीरांना ती मुद्दाम शिकविण्यात येते.
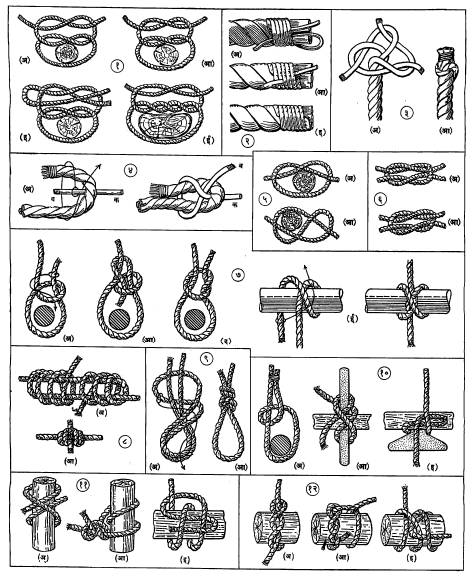
गाठींचे विविध प्रकार : आ. १ मध्ये रीफ जातीची एक पक्की गाठ दाखविली आहे. ती मुख्यतः जहाजावर उभारलेल्या शिडाचा काही भाग तात्पुरता गुंडाळून ठेवण्यासाठी वापरली जाते. घरगुती कामामध्ये तिचा उपयोग पिशव्यांची तोंडे, गुंडाळलेल्या गाद्या किंवा लाकडाच्या मोळ्या बांधून ठेवण्यासाठी करता येतो. ही गाठ योग्य पद्धतीने बांधली तरच तिचा चांगला उपयोग होतो. ही गाठ बांधण्याची उत्तम पद्धत आ.१ (अ) मध्ये दाखविली आहे. आ. १ (आ) मध्ये दाखविलेली पद्धत मध्यम प्रतीची आहे आणि आ. १ (इ) मध्ये सैल व सहज सोडवता येणारी गाठ पद्धत दाखविली आहे. आ. १ (ई) मध्ये दाखविलेली गाठ विशेषेकरून शस्त्रक्रियेतील जखमा बांधण्यासाठी वापरीत असलेल्या दोऱ्यामध्ये वापरतात.
अनेक बारीक दोऱ्या वळून बनविलेल्या जाड दोराची टोके नीट बांधून ठेवली नाहीत, तर त्यातील लहान दोऱ्या सैल होऊन विस्कटतात व दोराचे टोक निरुपयोगी होत जाते म्हणून ते दुसऱ्या बारीक पण मजबूत दोराने विशिष्ट पद्धतीने बांधून ठेवावे लागते. दोराचे टोक बांधून ठेवण्याच्या उत्तम पद्धती आ. २ मध्ये (अ), (आ) आणि (इ) या तीन आकृत्यांनी दाखविल्या आहेत.
दोराचे टोक मुद्दाम जाड करण्यासाठी दोरातील बारीक दोऱ्या जवळच्या दुसऱ्या दोऱ्यातून ओवून गुंडीसारखी गुंतवण करतात. त्या फुगवलेल्या भागाला गुंडीची गाठ म्हणतात. ही पद्धत आ. ३ मध्ये (अ) आणि (आ) या क्रमाने दाखविली आहे.
दोन दोरांची टोके एकमेकांबरोबर बांधावयाची असताना ते दोर जर फार निराळ्या व्यासाचे असतील, तर आ. ४ (अ) आणि (आ) मध्ये दाखविलेली कोष्टी गाठ वापरतात. ही गाठ बांधताना मोठ्या दोराचे टोक शक्य तितके वळवून त्याचा आकडा करतात आणि लहान दोराचे टोक आ. ४ (अ) मध्ये दाखविलेल्या बारीक तारेच्या मार्गाने आकड्याभोवती वळवून पुन्हा आकृतीत दाखविल्याप्रमाणे दोन दोरांच्या मधून ओढून बाहेर काढतात व दोन्ही मुख्य दोर ओढून गाठ पक्की करतात.
दोराचे टोक एकाद्या दांड्याला किंवा स्थिर खांबाला बांधून ठेवायचे असल्यास आ. ५ (अ) किंवा (आ) मध्ये दाखविलेली गाठ वापरतात. आ. ५ (आ) मध्ये दाखविलेली गाठ (अ) मधील गाठीपेक्षा घट्ट बसते व सहज सैल पडत नाही.
दोन सारख्या व्यासाचे दोर एकमेकांत गुंतवून एक सलग लांब दोर तयार करावयाचा असेल तर आ. ६ (अ) आणि (आ) मध्ये दाखविलेल्या पद्धती वापरतात. यांपैकी (अ) मध्ये दाखविलेली पद्धत (आ) पेक्षा अधिक चांगली आहे.
बांधकाम करताना लाकडे व दांडे उंचावर उचलावे लागतात किंवा ओढत न्यावे लागतात. अशा दांड्यांना दोराचे टोक बांधण्याच्या अनेक पद्धती प्रचारात आहेत. त्यांतील मुख्य पद्धती आ. ७ (अ), (आ), (इ) आणि (ई) मध्ये दाखविलेल्या आहेत. या गाठींना ‘राजगाठ’ म्हणतात.
मासे पकडण्याचा आकडा बांधण्यासाठी वापरीत असलेल्या दोन दोऱ्यांची टोके बांधून एकच लांब दोरी करण्यासाठी नळीची गाठ वापरतात. तिची रचना आ. ८ (अ) आणि (आ) मध्ये दाखविली आहे.
मासे धरण्यासाठी वापरीत असलेल्या दोरीच्या शेवटी फास करण्यासाठी वापरण्याची गाठ आ. ९ (अ) व (आ) मध्ये दाखविली आहे.
वजन टांगलेल्या दोरीचे टोक तात्पुरते अडकवून ठेवण्याच्या काही पद्धतींना फास म्हणतात. नाटकगृहातील पडद्यांच्या दोऱ्या बांधून ठेवण्यासाठी असे फास योजतात. या दोऱ्यांची टोके बांधून ठेवण्याच्या काही पद्धती आ. १० (अ), (आ) आणि (इ) मध्ये दाखविल्या आहेत. (अ) मध्ये दाखविलेली पद्धत विशेष प्रचारात आहे. या पद्धतीने बांधलेले फास पक्के होतात परंतु दांड्यावर कधीही आवळत नाहीत, त्यामुळे दोरीचे टोक पाहिजे तेव्हा दांड्यामधून सहज सोडवून घेता येते. आ. १० (आ) आणि (इ) मध्ये दाखविलेले फास सहज सोडता येणाऱ्या जातीचे आहेत.
शिडाचे दोर जहाजावरील खांबांना किंवा दांड्यांना बांधण्यासाठी आणि तंबूच्या दोऱ्या जमिनीमध्ये पुरलेल्या खुंट्यांना बांधण्यासाठी आ. ११ मध्ये दाखविलेले तीन प्रकारचे फास वापरतात.
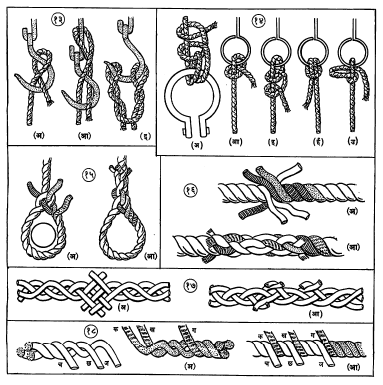
मोठ्या वजनाची लाकडे किंवा इतर जड वस्तू यारीने उचलण्यासाठी दोराचे अनेक प्रकारचे फास वापरात आहेत. त्यांपैकी लाकडे धरण्याचे मुख्य फास प्रकार आ. २ (अ), (आ) आणि (इ) मध्ये दाखविले आहेत आणि यारीच्या आकड्यात वापरण्याचे फास आ. १३ मध्ये दाखविले आहेत. तसेच धातूच्या कडीमध्ये दोराचे टोक ओवून बांधण्याचे फास आ. १४ मध्ये दाखविले आहेत.
जाड दोराच्या टोकावर कडीसारखे तोंड गुंफावयाचे असेल, तर दोराच्या शेवटच्या निरनिराळ्या दोऱ्या सोडवून त्या पाळीपाळीने मागच्या दोरातील घट्ट पेडांमधून ओवून गाठीसारखी गुंतवण करतात. घट्ट दोरातील पेड सैल करून वर उचलण्यासाठी दाभण किंवा टोच्यासारखे उपकरण वापरतात व दोर गुंडाळून धरण्यासाठी एखादा खुंटा वापरतात. ही पद्धत आ. १५ मध्ये दाखविली आहे.
तुटलेला दोर सांधण्यासाठी किंवा दोन दोरांची टोके जोडण्यासाठी दोराचा व्यास फारसा वाढू न देता दोन्हीकडील दोरांमधील शेवटचे पेड सोडवून ते दुसऱ्या बाजू्च्या घट्ट दोऱ्यामध्ये क्रमाक्रमाने ओवून गुंतवितात. ही पद्धत आ. १६ मध्ये दाखविली आहे. (अ) मध्ये पेड सोडवलेली टोके जवळ आणली आहेत व (आ) मध्ये पेड गुंतवलेले दाखविले आहेत.
तारेच्या दोराची टोके गुंतविण्याच्या दोन पद्धती आ. १७ आणि आ. १८ मध्ये दाखविल्या आहेत.
ओक, वा. रा.
गणितीय सिद्धांत : गौस (१७७७–१८५५) या जर्मन गणितज्ञांनी गाठींसंबंधी गणितीय दृष्टिकोनातून विचार केलेला होता. तथापि त्यांनी आपले संशोधनप्रसिद्ध केले नाही. जे. बी. लिस्टिंग (१८०२–१८८२) यांनी प्रथम ⇨संस्थितिविज्ञानाच्या (वाकविणे, ताणणे यांसारखी रूपांतरे केली तरीही भूमितीय आकारांत जे गुणधर्म कायम राहतात त्यांचा अभ्यास करणाऱ्या गणितीय शाखेच्या) दृष्टीने गाठींचा अभ्यास केला. पी. जी. टेट (१८३१–१९०१) यांनी आणवीय सिद्धांत आणि निरनिराळ्या रासायनिक मूलद्रव्यांतील फरक यांच्या संदर्भात गाठींच्या वर्गीकरणासंबंधी संशोधन केले.
संस्थितिविज्ञानाच्या दृष्टीने गाठ म्हणजे एक साधा त्रिमितीय बंद वक्र आहे. हा वक्र अवकाशातील एकाच बिंदूतून एकापेक्षा जास्त वेळा जात नाही. जर अवकाशाचे संतत विरूपण करून एका गाठीचे दुसऱ्या गाठीत रूपांतर करता येत असेल, तर त्या दोन गाठी एकाच वर्गातील आहेत असे म्हणतात. जर एखादी गाठ वर्तुळाच्या वर्गातील असेल, तर ती गाठ पूर्णपणे सुटलेली आहे असे म्हणतात. गाठीसंबंधी गणितीय विचार करताना थोडाफार नियमितपणा असलेल्या वक्रांचाच विचार करण्यात येतो. हे वक्र म्हणजे प्रत्यक्षात दोरे असून ते स्वेच्छ पिळलेले व गुंतवलेले असून त्यांची दोन टोके एकत्र जोडलेली आहेत असे मानता येते. या भौतिक दृष्टिकोनातून पाहिले असता दिलेल्या दोन दोऱ्यांपैकी एक दोरा कोणत्या परिस्थितीत वाकवून, ताणून व आकुंचित करून दुसऱ्या दोऱ्याच्या आकाराचा करता येईल, यावरून गाठींचे वर्गीकरण करता येणे शक्य आहे. तथापि दिलेल्या कोणत्याही दोन गाठी एकाच वर्गातील आहेत की नाहीत, हे ठरविण्यासाठी उपयोगी पडेल अशी व्यापक पद्धती अद्याप उपलब्ध नाही.
प्रत्येक गाठीत निरीक्षकाच्या स्थितीनुसार दोऱ्याचा एक भाग दुसऱ्या भागावरून गेलेला आहे, अशा भासमान छेदबिंदूंची ठराविक संख्या असते. ही भासमान छेदबिंदूंची संख्या गाठीचे विरूपण करून किंवा निरीक्षण कोन बदलूनही बदलता येते. पण कोणत्याही एखाद्या विशिष्ट गाठीच्या बाबतीत ती गाठ विरूपित करून छेदबिंदूंची एक किमान संख्या मिळते आणि त्यापेक्षा कमी छेदबिंदू मिळूच शकत नाहीत. या किमान संख्येला त्या गाठीची असंक्षेप्य छेदबिंदूंची संख्या म्हणतात. सर्वांत साधी गाठ म्हणजे शून्य छेदबिंदूची म्हणजेच पूर्ण सुटलेली गाठ होय. दिलेल्या कोणत्याही गाठीच्या असंक्षेप्य छेदबिंदूंची संख्या काढण्याचा व्यापक प्रश्न अद्याप सुटलेला नाही. असंक्षेप्य छेदबिंदूंच्या संख्येनुसार काही प्राथमिक स्वरूपाच्या गाठींचे वर्गीकरण टेट, कर्कमन, लिटल इत्यादींनी केलेले असून त्याची कोष्टकेही तयार करण्यात आलेली आहेत. तथापि ही कोष्टके केवळ अनुभवजन्य असल्यामुळे तितकीशी समाधानकारक नाहीत.
एम्. डेन यांनी १९१० मध्ये गाठीच्या गटाची व्याख्या मांडली. एफ्. रिडमाइस्टर यांनी १९२६ मध्ये व जे. डब्ल्यू. अलेक्झांडर यांनी १९२७ मध्ये गाठींच्या निरनिराळ्या प्रकारांतील फरक ठरविण्यासाठी काही निश्चल राशींच्या व्याख्या मांडल्या. तथापि या निश्चल राशीहीगाठींचे संपूर्ण वर्गीकरण करण्यास पुरेशा समाधानकारक नाहीत, असे आढळून आले आहे.
कोणतीही गाठ तीन प्रतल वक्रांनी निर्देशित करता येते व यांपैकी कोणत्याही वक्रांना दुहेरी बिंदू नसून ते वक्र एकमेकांना छेदत नाहीत, असे सिद्ध करण्यात आलेले आहे. सी. एफ्. क्लाइन यांनी असे सिद्ध केले आहे की, चौ-मितीमध्ये (तसेच २ प-मितींमध्ये प > २) गाठी अस्तित्वात असणे शक्य नाही. गाठींसंबंधी सी. डब्ल्यू. ॲश्ली यांचे द ॲश्ली बुक ऑफ नॉट्स (१९४७) हे पुस्तक सुप्रसिद्ध आहे.
भदे, व. ग.
“