विद्युत् चुंबकीय तरंग: प्रवेगित अगर आंदोलित असणाऱ्या विद्युत् भारामुळे विद्युत् चुंबकीय क्षेत्रामध्ये क्षोभ निर्माण होतो. माध्यमातून प्रसारित होणाऱ्या या क्षोभाला विद्युत् चुंबकीय तरंग असे नाव आहे. या तरंगांना निश्चित आवर्तकाल असतो आणि त्याचे मूळ क्षोभाशी दिशिक संबंध असतात. अशा तऱ्हेने प्रवेगित अगर आंदोलित विद्युत् भार असलेल्या भागापासून विद्युत् आणि चुंबकीय क्षेत्रांची प्रणाली बाह्य दिशेला प्रसार पावते. माध्यमातील द्रव्याचे निव्वळ स्थानांतरण (पुढे जाण्याची क्रिया) न होता अवकाशील एका बिंदूपासून वा स्त्रोतापासून जास्त दूरच्या, दुसऱ्या बिंदूपार्यंत क्षोभ प्रसारित होण्याच्या क्रियेला तरंग गती म्हणतात.
विद्युत् चुंबकीय तरंग ज्या माध्यमातून प्रवास करतात त्याला लवचिकता किंवा जडत्व नसते परंतु विद्युत् आणि चुंबकीय क्षेत्रांची ऊर्जा साठविण्याची क्षमता असते.
विद्युत् चुंबकीय वर्णपटाकडे पाहिल्यावर या तरंगांची व्याप्ती खूप विस्तृत आहे, हे लक्षात येते. भिन्न तरंगलांबी विभागांत या तरंगांचे स्वरूप भिन्न असते. प्रकाश, उष्णता, रेडिओ तरंग, क्ष-किरण ही या तरंगांची नेहमी आढळणारी उदाहरणे आहेत. यांशिवाय अवरक्त व जंबुपार (दृश्य वर्णपटातील तांबड्या आणि जांभळ्या रंगांपलीकडील अदृश्य) किरण, सूक्ष्मतरंग, गॅमा किरण हे अन्य तरंगलांबी विभाग होत. रडार आणि रेडिओ तरंग विभागात या तरंगांना विद्युत् किंवा हर्ट्झियन तरंग असे नाव आहे.
या तरंगांच्या रूपात विद्युत् चुंबकीय ऊर्जा प्रसारित होते. या ऊर्जेला, तिच्या ऊत्सर्जनाला व प्रसारणाला ⇨विद्युत् चुंबकीय प्रारण असे म्हणतात. अवरक्त प्रारण, उष्णता प्रारण, जंबुपार प्रारण, प्रकाश सूक्ष्मतरंग, क्ष-किरण या विद्युत् चुंबकीय तरंगांच्या प्रकारांवर मराठी विश्वकोशात स्वतंत्र नोंदी आहेत. रेडिओ तरंगांविषयीची माहिती ‘रेडिओ तरंग प्रसारण’, ‘रेडिओ प्रेषण’ व ‘रेडिओ संदेशवहन प्रणाली’ या नोंदीत आली हे. ‘प्रकाश’ व ‘विद्युत् चुंबकीय प्रारण’ या नोदींत आली हे. ‘प्रकाश’ व ‘विद्युत् चुंबकीय प्रारण’ या नोंदीमध्येही विद्युत् चुंबकीय तरंगांविषयीची काही माहिती दिलेली हे. शिवाय ‘तरंग गति’ अशीही स्वतंत्र नोंद आहे.
|
|
⟶ |
|
विद्युत् चुंबकीय तरंगात विद्युत् क्षेत्राची तीव्रता |
(E) आणि चुंबकीय क्षेत्राची तीव्रता |
| ⟶ | |
|
(H) |
या सदिश गुणकांचे मूल्य अवकाशातील प्रत्येक बिंदूपाशी व्यक्त करावे लागते. |
माध्यम एकजिनसी, समदिक् आहे [म्हणजे विद्युत् पार्यता (ϵ) आणि चुंबकीय पार्यता (μ) स्थिर अदिश आहेत], त्यात विद्युत् क्षेत्र लावलेले नसून माध्यमाची संवाहकता शून्य आहे (विद्युत् संवाहकता शून्याहून जास्त पण अनंताहून कमी असलेल्या माध्यमात विद्युत् चुंबकीय तरंग प्रसारण होऊ शकते), असे गृहीत धरून अशा माध्यमासाठी खालील क्षेत्र समीकरणे लिहिता येतात.
|
|
|
→ |
|
|
|
|
k |
. |
∂E |
= curl H … … …(१) |
||
|
c |
∂t |
||||
|
|
|
|
→ |
= curl E … … (२) |
|
|
– |
µ |
. |
∂H |
||
|
c |
∂t |
||||
|
Div H = O … … (३) |
|||||
|
Div E = O … … (४) |
|||||
(c ही निर्वात पोकळीतील तरंग प्रसारण गती आहे असे पुढे आढळेल. निर्वात पोकळीसाठी µ= k = 1).
वरील समीकरणांच्या संयोगातून यामिकीय तरंग समीकरण मिळविता येते, ही गोष्ट १८६३ च्या सुमारास जे. सी.मॅक्सवेल यांच्या लक्षात आली. त्यावरून त्यांनी विद्युत् चुंबकीय तरंगांच्या अस्तित्वाबद्दल प्राक्कथन केले. त्यापूर्वी या तरंगांबद्दल कोणालाच कल्पना नव्हती. त्यानंतरच्या काळातत विद्युत् चुंबकीय तरंग आणि प्रकाश तरंग अभिन्न आहेत, हे सिद्ध झाले.
(१) ते (४) समीकरणांच्या संयोगातून तरंग समीकरण (५) मिळते. निर्वात पोकळीत तरंग समीकरण (६) आणि (७) लागू पडते. या समीकरणात ∇2 हा अदिश प्रचालक असून त्याला लाप्लाशियन म्हणतात.
|
|
→ |
|
→ |
|
||
|
k µ |
∂2E |
= |
∇2E |
…… …(५) |
||
|
C2 |
∂t2 |
|||||
|
→ |
|
|
→ |
|
||
|
∂2E |
=c2 |
∇2 |
E |
… … (६) |
||
|
∂t 2 |
||||||
|
→ |
|
|
→ |
|
||
|
∂2H |
=c2 |
∇2 |
H |
… … (७) |
||
|
∂t2 |
||||||
|
∇2= |
∂2 |
+ |
∂2 |
+ |
∂2 |
… … (८) |
|
∂x2 |
∂y2 |
∂z2 |
||||
जात्य सहनिर्देशक पद्धतीमध्ये ∇2 चे पूर्ण रूप समी. (८) मध्ये दिले आहे. वृत्तचिती आणि गोलीय सहनिर्देशकांत ∇2 चे संपूर्ण रूप वेगवेगळे असते. १८८७ च्या सुमारास एच्. आर्. हर्ट्झ यांनी प्रयोदांद्वारे विद्युत् चुंबकीय तरंगांची निर्मिती करून त्यांचे प्रेषण केले व त्यांचे अभिज्ञानही केले. यामुळे या तरंगांना हर्ट्झियन तरंग असेही नाव आहे. हर्ट्झ यांच्या प्रयोगांमुळे या तरंगांच्या प्रायोगिक अभ्यासाला मोठी चालना मिळाली आणि त्याची झपाट्याने प्रगती झाली. त्याचप्रमाणे यामुळे संदेशवहन क्षेत्र विकसीत झाले.
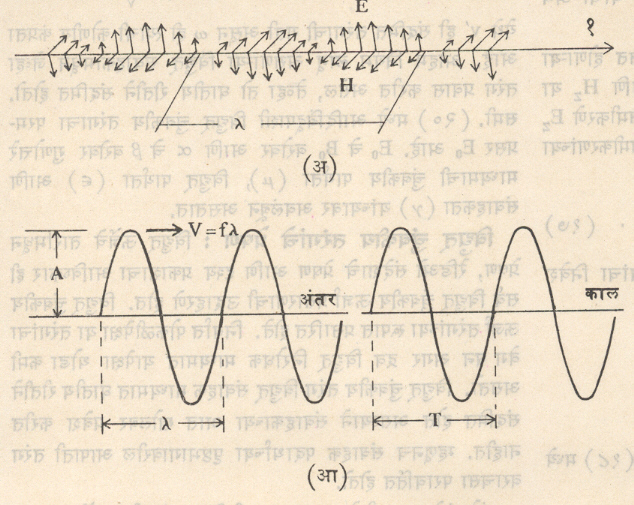
विद्युत् चुंबकीय तरंगांची वैशिष्ट्ये: विद्युत् चुंबकीय तरंगांची महत्त्वाची अंगे आकृतीमध्ये दाखविली आहेत. आकृती (अ) मध्ये विद्युत् आणि चुंबकीय क्षेत्रांची तीव्रता
|
→ |
→ |
|
|
E आणि |
H |
दर्शविणारे सदिश (तरंगाच्या प्रसारण दिशेत निरनिराळ्या बिंदूंजवळ) दाखविले |
आहेत. विद्युत् क्षेत्र प्रसारण दिशेशी लंबरूप, उदग्र (उभ्या) पातळीत असल्याने उदग्र दिशेमध्ये तरंग ध्रुवित झाला आहे. चुंबकीय क्षेत्राची तीव्रता (H) देखील प्रसारण दिशेशी लंबरूप परंतु क्षैतिज (आडव्या) प्रतलामध्ये विद्युत् असून तिची महत्ता/मान विद्युत् क्षेत्राच्या तीव्रतेच्या प्रमाणात समी. (९) मध्ये दिल्याप्रमाणे असते.
|
E |
= |
√ |
µ |
… … … (९) |
|
H |
∈ |
(येथे µ आणि ∈ अनुक्रमे माध्यमाची चुंबकीय आणि विद्युत् पार्यता आहेत).
दिलेल्या कालक्षणी E चे मान तरंग प्रसारण दिशेतील अंतराच्या ‘ज्या’ वक्रीय [त्रिकोणमितीतील ‘ज्या’ गुणोत्तराच्या वक्राच्या ⟶ त्रिकोणमिति] फलनाप्रमाणे बदलते. [⟶ तरंग गति].
विद्युत् क्षेत्राच्या तीव्रतेचे एकक व्होल्ट/मी. आणि चुंबकीय क्षेत्राच्या तीव्रतेचे एकक अँपिअर/मी. आहे. निर्वात पोकळीसाठी ∈ व µ यांचे मूल्य अनुक्रमे ∈ =८.८५४ ´ १०−१२ फॅराड/मी. आणि µ = ४ πx १०−७ हेन्ऱी/मी. इतके आहे. तेव्हा निर्वात पोकळीसाठी
|
E |
चे मुल्य ३७७ ओहमच्या जवळपास येते. |
|
H |
या गुणोत्तराला माध्यमाचा (निर्वात पोकळीचा) तरंग संरोध म्हणतात [⟶ मॅक्सवेल विद्युत् चुंबकीय समीकरणे].
 आकृतीमध्ये दाखविल्याप्रमाणे विद्युत् चुबंकीय तरंगांचा प्रवास सरळ रेषेत होतो. या रेषेतील दोन (डाव्या किंवा उजव्या) दिशांपैकी
आकृतीमध्ये दाखविल्याप्रमाणे विद्युत् चुबंकीय तरंगांचा प्रवास सरळ रेषेत होतो. या रेषेतील दोन (डाव्या किंवा उजव्या) दिशांपैकी
प्रसारणाची प्रत्यक्ष दिशा ठरविण्यासाठी दक्षिणहस्ती मळसूत्र त्या रेषेवर ठेवून तो
|
⟶ |
कडून |
⟶ |
|
E |
|
H |
कडे गोल फिरविल्यास त्याचे टोक ज्या दिशेकडे सरकेल त्या दिशेने ऊर्जेचे प्रसारण होते. तरंगांची गती समी. (१०) प्रमाणे मिळते.
|
V = |
1 |
… … (१०) |
|
√ µ ∈ |
निर्वात पोकळीत ही गती सु. ३ × १०८ मी./ सेकंद असते. हवेमध्ये ती यापेक्षा थोडी कमी असते.
तरंगाच्या लागोपाठ येणाऱ्या दोन समान बिंदूंतील प्रसारण दिशेत मोजलेले अंतर म्हणजे तरंगलांबी होय. ही दाखविण्यासाठी λ हे चिन्ह वापरतात.
एखाद्या स्थिर बिंदूवरून तरंग जसा पुढे सरकतो. तसे E आणि H यांचे त्या स्थिर बिंदूपाशी असलेले मूल्य ‘ज्या’ वक्रीय तऱ्हेने कालानुरूप बदलत राहते. या बदलण्याच्या एका आवर्तनात कालाला तरंगाचा आवर्तन काल (उदा., T सेकंद) असे म्हणतात. एका सेकंदात होणाऱ्या आवर्तन संख्येला कंप्रता (हर्ट्झमध्ये) म्हणतात. म्हणजेच कंप्रता
|
f = |
1 |
… … (११) |
|
T |
एका आवर्तन कालात v गतीने प्रवास करणारा तरंग एका तरंगलांबीइतके अंतर काटतो. म्हणून
λ= vT… … (१२)
किंवा समीकरण (११) वापरून
|
λ = |
v |
… … (१३) |
|
f |
तरंग गती ३ × १०८ मी/. सेकंद आहे असे मानल्यास ६० हर्ट्झ कंप्रतेच्या विद्युत् चुंबकीय तरंगाची तरंगलांबी ५ × १०६ मी . किंवा ४,९६० किमी होते. ३ मेगॅहर्ट्झ कंप्रतेला (म्हणजे ३ × १०६ हर्ट्झ) तरंगलांबी १०० मी. येते आणि ३,००० मेगॅहर्ट्झ कंप्रतेला १० सेंमी. येते. दृश्य प्रकाशाची कंप्रता ५ × १०१४ हर्ट्झच्या जवळपास असते आणि तंरगलांबी ६ × १०-५ सेंमी. इतकी कमी असते.
तरंगलांबी अगर कंप्रतेच्या संज्ञांमध्ये तंरगांचा उल्लेख करतात. आकृतीमध्ये λ, f, T, v आणि परमप्रसर (A) यांचे महत्त्व विशद केले आहे. यातील परमप्रसर म्हणजे तरंगातील बदलणाऱ्या राशीचे (उदा., विद्युत् क्षेत्राचे) महत्तम मूल्य होय. तरंग गतीचा मूलभूत गुणधर्म म्हणजे तरंगाची कंप्रता कोणत्याही परिस्थितीत स्थिर राहते. याला अपवाद म्हणजे जेव्हा निरीक्षक आणि तरंग स्त्रोत यांच्यात सापेक्ष गती असेल तेव्हा मात्र डॉप्लर परिणामामुळे कंप्रता जास्त अगर कमी होऊ शकते [⟶ डॉप्लर परिणाम]. याउलट प्रसारण गती माध्यमाच्या गुणधर्मावर आणि क्वचित प्रसंगी कंप्रतेवर सुद्धा अवलंबून असून गती कमीजास्त झाल्यास समी (१३) प्रमाणे तरंगलांबी बदलते.
|
विद्युत् क्षेत्राची ऊर्जाघनता |
∈E2 |
जूल/मी.३व चुंबकीय |
|
2 |
||
|
क्षेत्राची ऊर्जा घनता |
µ H 2 |
जूल मी.३ इतकी असते. समी (९) चा वापर करून खालील निष्कर्ष मिळतो. |
|
2 |
|
µ H2 |
= |
µ |
(E√ ∈/µ )2 = |
∈E2 |
… … (१४) |
|
2 |
2 |
2 |
विद्युत् चुंबकीय तरंगातील विद्युत् आणि चुंबकीय क्षेत्रांत समान ऊर्जा असते, असे समी. (१४) वरून स्पष्ट होते. तरंगातील ऊर्जा घनता
|
v = |
1 |
|
√ µ ∈ |
या त्वरेने स्थानांतरित केली जाते. म्हणजेच प्रसारण दिशेला लंबरुप प्रतलाच्या दर चौ. मी. पृष्ठभागातून ∈E2v वॉट/चौ. मी. या त्वरेने ऊर्जेचे वहन होते.
प्रतल तरंग :निर्वात पोकळीत सरल हरात्मक (म्हणजेच रेखीय ‘ज्या’ वक्रिय) गतीने [⟶ सरळ हरात्मक गति] फिरणारा विद्युत् भार साधे तरंग निर्माण करतो. स्त्रोतापासून दूर म्हणजे परमप्रसराच्या किती तरी पट अंतरावर ज्यामध्ये खूप आवर्तने झाली आहेत इतक्या दूर अंतरावर तरंग गोलाकार होतो परंतु जेव्हा तरंगाच्या निरीक्षणाखालील भाग गोलाच्या त्रिज्येच्या मानाने लहान असतो, तेव्हा त्याला प्रतल तरंग असे मानता येते.
प्रतल तरंगाच्या क्षेत्रात दिलेल्या प्रतलावरील सर्व बिंदूंपाशी विद्युत् आणि चुंबकीय क्षेत्रांशी तीव्रता आणि दिशा एकच असते. या प्रतलांना तरंगमुखे म्हणतात आणि त्यांना लंबरूप असणाऱ्या दिशेला तरंग लंब म्हणतात.
तरंग लंब दिशा क्ष-अक्ष घेतल्यास तरंगमुखे य-झ अक्षांच्या प्रतलाला समांतर असतात. E आणि H कोणत्याही तरंगमुखावर स्थिर असल्याने त्यांचे य आणि झ बरोबरील आंशिक अवकलज शून्य असले पाहिजेत (असतात). त्यामुळे क्षेत्र समी. (१५) आणि तंरग प्रसारण समी. (१६) खालीलप्रमाणे लिहिता येतात :
|
∂E× |
= |
∂E× |
= |
∂H× |
= |
∂H× |
= 0 … … (१५) |
|
∂t |
∂X |
∂t |
∂X |
Ex =Hx = 0 … … (१६)
समी. (१६) वरून हे स्पष्ट होचे की, विद्युत् आणि चुंबकीय क्षेत्रे तरंग लंब दिशेला म्हणजेच प्रसारण दिशेला लंबरूप असतात. याचा अर्थ विद्युत् चुंबकीय तरंग अनुतरंग नसून अवतरंग आहेत.
क्षेत्र समीकरणांपासून (समीकरणे १ ते ४) विकसित होणाऱ्या उरलेल्या चार समीकरणांपैकी दोन समीकरणे Ey आणि Hz घटकांमधील संबंध स्पष्ट करतात आणि उरलेली दोन समीकरणे Ez आणि Hy या घटकांच्या संबंधाबाबत आहेत. या चारी समीकरणांच्या संयोगातून एकमितीय तरंग समी (१७) मिळते.
|
∂2 |
( ) |
= C2 |
∂2 |
( ) |
… … … (१७) |
|
∂t2 |
∂x2 |
यातील कंसांमध्ये अनुक्रमे Ey,Ez आणि Hy, Hz यांचा निवेश करता येतो. जसे
|
∂2Ey |
= c2 |
∂2Ey |
|
∂2Ez |
=c2 |
∂2Ez |
|
∂t2 |
∂x2 |
∂t2 |
∂x2 |
|
∂2Hy |
=c2 |
∂2Hy |
|
∂2Hz |
=c2 |
∂2Hz |
|
∂t2 |
∂x2 |
∂t2 |
∂x2 |
समी. (१७) चा व्यापक निर्वाह वेगळ्या रुपात समी (१८) मध्ये लिहिला आहे.
Ey =F1 (x – ct) + F2 (x + ct) … … (१८)
यातील उजव्या बाजूचे पहिले + x दिशेने (प्रवास करणारा तरंग) आणि दुसरे पद – x दिशेने (प्रवास… … …) दर्शवितो.
स्थिर तरंग आणि अप्रगामी तरंग :एकच कंप्रता आणि परमप्रसर असणारे परंतु परस्परविरुद्ध दिशांनी प्रवास करणारे दोन तरंग एकत्र आल्यावर स्थिर तरंग निर्माण होतो. स्थिर तरंगात स्त्रोतापासून ऊर्जेचे दूर स्थानांतरण होत नाही. अप्रगामी तरंगाची निर्मिती देखील याच पद्धतीने होते. परंतु या ठिकाणी उलट दिशेने प्रवास करणारा म्हणजे स्त्रोताकडे येणारा तरंग (उदा., परावर्तन झाल्यानंतरचा तरंग) कमी परमप्रसर असणारा असतो. त्यामुळेच या दोन्ही तरंगांच्या मिलाफानंतर थोड्या ऊर्जेचे स्त्रोतापासून दूर स्थानांतरण होते. [⟶ तरंग गति].
गोलीय तरंग :परिमित व्याप्तीच्या अगर बिंदुमात्र स्त्रोताने समदिक्, एकजिनसी माध्यमात उत्सर्जित केलेले प्रारण स्त्रोतापासून दूर अंतरावर गोलीय तंरग होते. या तरंगाची मुखे गोलाकार असतात म्हणजे E आणि B/H क्षेत्रीय मूलघटकांचे मान, दिशा व कला गोलाच्या पृष्ठभागावर एकच (स्थिर) असते. गोलीय तरंगाचे समी. (१९) खाली दिलेले आहे.
|
F = r-1 Φ1 (θ, ψ ) f (r – vt) |
|
+ r-1 Φ2 (θ , ψ) f (r + vt)… … (१९) |
येथे F च्या जागी क्षेत्रीय मूल घटक
|
→ |
|
→ |
|
→ |
|
E |
आणि |
B |
किंवा |
H |
क्रमाक्रमाने लिहून प्रत्येक घटकाचे समीकरण मिळते. समी. (१९) मध्ये उजव्या बाजूकडील पहिले पद अपसारी दुसरे पद अभिसारी तरंग निर्देशित करतात.
संदमित तरंग :तरंगाचे प्रसारण होत असताना तरंग ऊर्जेचा व्यय होत असल्यास तरंगाचा परमप्रसर क्षीण होतो. अशा तरंगाला संदमित तरंग म्हणतात. ऊर्जाक्षय तरंग परमप्रसाराच्या वर्गाच्या समप्रमाणात असेल, तर तरंग घातीय रीतीने संदमित होतो. असा तरंग समी (२०) प्रमाणे निर्देशित करतात.
Ex = Eoe–azcos (ωt – βz) … … … (२०)
समी. (२०) मधील α ला क्षीणनांक स्थिरांक आणि β ला तरंगांक किंवा कला स्थिरांक म्हणतात.
|
कला स्थिराकांचे मूल्य |
ω |
इतके असते. |
|
v’ |
इतके असते. येथे v’ ही संदमित तरंगाची गती असून ω त्याची कोणीय कंप्रता आहे. ओहम नियम लागू असणाऱ्या विद्युत् संवाहाकामधून जेव्हा तरंग प्रवास करीत असेल, तेव्हा तो घातीय रीतीने संदमित होतो. समी. (२०) मध्ये आदिबिंदूपाशी विद्युत् चुंबकीय तरंगाचा परमप्रसर Eo आहे. Eo चे Bo बरोबर आणि α चे β बरोबर गुणोत्तरे माध्यमाची चुंबकीय पार्यता ( µ), विद्युत् पार्यता (∈) आणि संवाहकता (γ) यांच्यावर अवलंबून असतात.
विद्युत् चुंबकीय तरंगांचे प्रेषण :विद्युत् ऊर्जेचे तारांमधून प्रेषण, रेडिओ संदेशाचे प्रेषण आणि दृश्य प्रकाशाचा आविष्कार ही सर्व विद्युत् चूंबकिय ऊर्जा प्रसारणाची उदाहरणे होत. विद्युत् चुंबकीय ऊर्जा तरंगांच्या रूपात प्रसारित होते. निर्वात पोकळीपेक्षा या तरंगाचा वेग घन अगर द्रव विद्युत् निरोधक माध्यमात यापेक्षा थोडा कमी असतो. विद्युत् चुंबकीय तरंग विद्युत् संवाहक माध्यमात घातीय रीतीने संदमित होत असल्याने संवाहकाच्या आत खोलवर प्रवेश करीत नाहीत. म्हणूनच संवाहक पदार्थाच्या पृष्ठभागावरील आपाती तरंग बराचसा परावर्तित होतो.
संदेशांचे दूरस्थळी प्रेषण करण्यासाठी विद्युत् चुंबकीय ऊर्जेच्या वाहक म्हणून उपयोग केला जातो. याचे नेहमीच्या परिचयातील उदाहरण म्हणजे दूरध्वनी होय. स्थानिक दूरध्वनी तारा २०० ते ४,००० हर्ट्झ कंप्रतेचे तरंग वाहून नेतात. प्रथम या कंप्रतेच्या ध्वनितरंगांचे विद्युत् चुंबकीय तरंगात रुपांतर करतात आणि दोन तारांमार्फत ते पोहोचस्थानाकडे मार्गनिर्देशित केले जातात. दुसरे उदाहरण रेडिओ ग्राहीचे होय. मध्यम तरंग रेडिओमध्ये १० हर्ट्झ कंप्रतेच्या विद्युत् चुंबकीय तरंगाचा उपयोग केला जातो. यामध्ये विद्युत् चुंबकीय वाहक तरंगाचे ओळख पटविण्यायोग्य वैशिष्ट्य (गुणधर्म) बदलले जाते. उदा., वाहक तरंगाचा परमप्रसर अगर कंप्रता संदेश तरंगाच्या कमी अधिक तीव्रतेप्रमाणे अगर कंप्रतेप्रमाणे कमी जास्त केला जातो. हे बदललेले तरंग आकाशकामधून (अँटेनामधून) उत्सर्जित होतात व दूरस्थळी विस्तृत भागावर रेडिओ ग्राहीमध्ये ग्रहण केले जातात [⟶ रेडिओ प्रेषण विरुपण].
⇨रडारमध्ये १०१० हर्ट्झ कंप्रतेच्या तरंगाचा वापर केला जातो. त्याचप्रमाणे लेसर [प्रारणाच्या उद्दीपित उत्सर्जनाव्दारे विद्युत् चुंबकीय तरंगांचे विवर्धन करून मिळालेल्या अतिशय अरुंद, तीव्र शलाकेचा उपयोग करणाऱ्या ⟶ लेसर] संदेशवहनात रुबी लेसरमधून ४.३२ × १०१४ हर्ट्झ कंप्रतेचा प्रकाश उत्सर्जित केला जातो. विद्युत् चुंबकीय ऊर्जा प्रेषण करण्याचे तंत्र व ती दूरस्थळी ग्रहण केल्यावर तिचा वापर करण्याचे तंत्र तरंगलांबीवर अवलंबून असते. [⟶ लेसर रेडिओ संदेशवहल प्रणाली].
उपयोग :विविध तरंगलांबीचे विद्युत् चुंबकीय तरंग निरनिराळ्या कामांसाठी वापरले जातात. असे तरंग किती सहजपणे निर्माण करता येतात व ओळखता येतात, यांवर त्यांचे उपयोग अवलंबून असतात. या तरंगाची तरंगलांबी ऊर्जा-उद्गमातील इलेक्ट्रॉनांच्या आंदोलनांच्या त्वरेशी (कंप्रतेशी) निगडीत असते. कंप्रता किंवा आंदोलनांची त्वरा जेवढी कमी तेवढी तरंगलांबी दीर्घ (जास्त) असते. दीर्घ तरंग सहजपणे निर्माण करता येतात.
रेडिओ तरंग (सामान्यतः १०० किलोहर्ट्झ ते ६० मेगॅहर्ट्झ या कंप्रतेचे) संदेशवहनासाठी १९०० नंतर वापरण्यात येऊ लागले. १०० मेगॅहर्ट्झ कंप्रतेचे तरंग कंप्रता विरूपण नभोवाणी व दूरचित्रवाणी प्रेषणासाठी वापरले जातात. यांचा बिनतारी संदेशवहनासाठी वापर करता येईल, असे १८९२ साली दिसून आले आणि १८९६ साली सु. १.६ कि.मी अंतरापर्यंत असे संदेशवहन करण्यात यश आले. नाविक संदेशवहन व दिशानिश्चितीसाठी दीर्घ तरंग वापरतात. ३० मेगॅहर्ट्झपेक्षा उच्च कंप्रतेचे तंरग परावर्तनक्षम नसल्याने ते कमी अंतरावरील संदेशवहन ⇨ रडार (३० ते ३०,००० मेगॅहर्ट्झ), दूरचिरवाणी (३० ते ३०० मेगॅहर्ट्झ) इत्यादींकरिता वापरतात. [⟶ रेडिओ तंरग प्रसारण रेडिओ प्रेषण रेडिओ संदेशवहन प्रणाली] ३०,००० मेगॅहर्ट्झपेक्षा उच्च कंप्रतेचे तरंग हवेत जास्त प्रमाणात शोषले जातात व त्यामुळे त्यांचा विशेष उपयोग होत नाही. क्लायस्ट्रॉन, मॅग्नेट्रॉन यांसारख्या सूक्ष्मतंरग (सु.०.५ अब्ज हर्ट्झ वा त्याहून अधिक कंप्रतेचे) आंदोलकांचा [⟶ आंदोलक, इलेक्ट्रॉनीय] शोध लागल्यावर कमी तरंगलांबीच्या तरंगांचा प्रभावीपणे वापर होऊ लागला. तसेच अन्न शिजविण्यासाठीही सूक्ष्मतरंग वापरण्यात येऊ लागले.
१०−२ सेंमी. पेक्षा तरंगलांबीच्या किंवा ३ × १०१२ हर्ट्झपेक्षा अधिक कंप्रतेच्या तरंगांचे पुढीलप्रमाणे उपयोग होतात : ३ × १०-११ सेंमी.पेक्षा कमी तरंगलांबीचे गॅमा किरण कर्करोगावरील उपचारासाठी व अणूविषयक अध्ययनासाठी वापरतात. तर ३× १०−१० सेंमी. ते ३ × १०−९ सेंमी तरंगलांबीच्या क्ष-किरणांचा वापर कर्करोगावरील उपचार व क्ष-किरण छायाचित्रण (उदा., अस्थिभंगाचे स्वरुप समजण्यासाठी ) यांत होतो. जंबुपार किरणांचा उपयोग (तरंगलांबी ४ × १०−७ ते ४ × १०−५सेंमी) स्वयंप्रकाशी प्रयुक्ती, दिवे इत्यादींत तसेच जंतुनाशक म्हणून होतो. दृश्य प्रकाशाची तरंगलांबी ४ ×१०-७ ते ८ × १०-५ सेंमी. असून त्यामुळे आपल्याला दिसू शकते. अवरक्त किरण (तरंगलांबी ८ ×१०-५ ते १०-२ सेंमी) छायाचित्रण, उष्णता निर्माण करणे (उदा., एनॅमल भाजण्यासाठी), रोगोपचार (उदा., गुप्तरोग) वगैरेंमध्ये वापरतात.
इ. स १९६०-७० या दशकात लेसरविषयक अध्ययनात प्रगती झाल्याने लघुतरंगांचे नवनवीन उपयोग होऊ लागले. अशा प्रकारे जंबुपार वा अवरक्त किरण अथवा दृश्य प्रकाश यांपासून लेसर शलाका निर्माण करता येऊ लागल्या. तसेच लेसर शलाका दीर्घ अंतरापर्यंत न फैलावता रेखीव रहाते. यामुळे लेसरचा विविध क्षेत्रांत उपयोग होतो. उदा., शस्त्रक्रिया, कर्करोगावरील उपचार, छायाचित्रण, संदेशवहन (ध्वनिसंकेतांचे व दूरचित्रवाणी संकेतांचे प्रेषण), छपाई, औद्योगिक प्रक्रिया, शस्त्रनिर्मिता, प्रकाशकीय संस्करण, माहिती संस्करण (माहिती साठविणे व हवी तेव्हा परत मिळविणे), अवकाशविज्ञान वगैरे. [⟶ लेसर].
दृश्य प्रकाश आणि अवरक्त प्रकाश या तरंगांचा उपयोग करणाऱ्या व कृत्रिम उपग्रहावर बसविलेल्या प्रारणमापकाच्या साहाय्याने पृथ्वीभोवतालच्या ढगांचे सतत चित्रण वा छायाचित्रण केले जाते. दिवसातील ठराविक वेळी ढगांची घेतलेली अशी छायाचित्रे जगातील निरनिराळ्या वातावरणीय कार्यालयांकडे पाठवितात. या कामी दृश्य प्रकाशाचा उपयोग दिवसा, तर अवरक्त किरणांचा रात्रंदिवस करता येतो. ढगांच्या अशा छायाचित्रांवरुन वातावरणाच्या स्थितीविषयी महत्त्वाची माहिती मिळते.
पहा : अवरक्त प्रारण उष्णता जंबुपार प्रारण तरंग गति प्रकाश रेडिओ प्रेषण विद्युत् चुंबकीय प्रारण विश्वकिरण सूक्ष्मतरंग क्ष-किरण.
संदर्भ : 1. Kraus, J. D. Electromagnetic, 1982.
2. Lorrain, P. and others, Electromagnetic Fields and Waves, New York, 1989.
3. Paul, C. R. Nasar, S. A. Introduction to Electromagnetic Fields 1982.
4. Ramo, Winners, J, R: Van Dazzler, T. Fields as Waves in Communication Electronics, New York, 1965.
5. Raja sky, V. Electromagnetic Fields and Waves, New York, 1980.
6. Sadiku, M, Elements of Electromagnetic, New York, 1989.
कारेकर, र. न. आगाशे, वसंत वा.
“