स्थिति समीकरण : भौतिकी हे निसर्गातील विविध प्रणालींचा अभ्यास करणारे शास्त्र आहे. या प्रणाल्या विविध प्रकारच्या असू शकतात. उदा., एखाद्या डब्यात बंद करून ठेवलेला वायू ही एक प्रणाली आहे. भौतिकशास्त्रात तिचा अभ्यास केला जातो. साबणाच्या पाण्याचे एक अगदी पातळ पटल तयार होते किंवा अशा पातळ पटलाचे आवरण असणारे व हवेत विहार करणारे साबणाच्या पाण्याचे फुगे तयार होतात. भौतिकीच्या शास्त्रज्ञांना हीदेखील एक महत्त्वपूर्ण प्रणाली वाटते. त्याचप्रमाणे चुंबकीय गुणधर्म असलेले पदार्थ निसर्गातील एक प्रणाली दर्शवितात. अशा प्रणाल्यांचा अभ्यास केल्यावर खालील समान सूत्र शास्त्रज्ञांच्या लक्षात आले.
वर वर्णन केलेल्या प्रत्येक प्रणालीशी तीन चल पदे निगडित असतात. या तीन चलांच्या कोणत्याही क्षणी जी मूल्ये असतात ती, त्या प्रणालीची त्या क्षणाची स्थिती ( अवस्था ) दर्शवितात आणि या तीन चलांना एकमेकांशी जोडणारी समीकरणे असतात, ज्यायोगे दोन चलांच्या मूल्यांवरून उरलेल्या चलाचे मूल्य काढता येते. अशा समीकरणांना स्थिती समीकरण असे म्हणतात.
वर ज्या तीन प्रणाल्या वर्णन केल्या आहेत, त्यातील बंदिस्त वायूचे उदाहरण घेऊन ‘ चले ’, ‘ स्थिती ’ आणि ‘ स्थिती समीकरण ’ या संकल्पना अधिक स्पष्ट करता येतील. हे उदाहरण घेण्याचे महत्त्वाचे कारण हे की, या प्रणालीचा सरळ संबंध ‘औष्णिक एंजिना’शी आहे. या प्रणालीचा तपशिलाने अभ्यास करून शास्त्रज्ञांनी औष्णिक एंजिनांची कार्यपद्धती आणि कार्यक्षमता यांविषयी फार महत्त्वाचे निष्कर्ष काढले आहेत.
बंदिस्त वायूशी निगडित असलेली तीन चले म्हणजे त्या वायूचे आयतन ( घनफळ ) V, त्या वायूचा दाब P आणि त्याचे तापमान T. कोणत्याही क्षणी बंदिस्त असलेल्या वायूच्या P, V आणि T यांची मूल्ये माहीत असली तर त्या प्रणालीची स्थिती माहीत होते, असे म्हटले जाते. समजा, यातील कोणत्याही एका चलात ( उदा., दट्ट्या वर किंवा खाली हलवून V मध्ये ) फरक केला तर उरलेल्या दोन चलांची ( म्हणजे P आणि T यांची ) मूल्येही बदलतील. म्हणजेच प्रणालीची स्थिती बदलेल.
प्रत्यक्षात बंदिस्त वायूचे एक चल बदलले की उरलेली दोन्ही चले बदलतात. परंतु त्यांच्यातील संबंध नीट जाणून घेण्यासाठी शास्त्रज्ञांनी जे प्रयोग केले त्यात तीन चलांपैकी एक चल स्थिर ठेवण्यात आले व उरलेल्या दोघांचा एकमेकांमधील संबंध तपासण्यात आला. म्हणजे वरील उदाहरणात समजा, T स्थिर ठेवले आणि V बदलल्यावर P मध्ये कसा बदल होतो ते बघितले किंवा अशाच प्रकारे V स्थिर ठेवून P आणि T यांच्यातील आणि P स्थिर ठेवून T आणि V यांच्यातील संबंध प्रयोग करून तपासण्यात आला. या प्रयोगांच्या निष्कर्षांच्या आधारावर पुढील नियम बनविण्यात आले.
तापमान (T) स्थिर असेल तर बंदिस्त वायूचा ( ज्याचे द्रव्यमानही स्थिर असते ) दाब (P) आणि त्याचे आयतन (V) यांचा गुणाकार नेहमी स्थिर असतो. म्हणजेच, P.V = स्थिरांक, ( T व वायूचे द्रव्यमान स्थिर ).
त्याचप्रमाणे दाब (P) स्थिर असेल, तर बंदिस्त वायूचे ( ज्याचे द्रव्यमानही स्थिर असते ) आयतन (V) आणि तापमान (V) यांचे गुणोत्तर नेहमी स्थिर असते. म्हणजेच, ( V / T ) = स्थिरांक, ( P आणि वायूचे द्रव्यमान स्थिर ).
या दोन नियमांची सांगड घातली तर P, V आणि T या तिन्ही चलांना एकत्र जोडणारे समीकरण मिळते, जे पुढीलप्रमाणे आहे :
P.V = nRT.
या समीकरणाला या प्रणालीचे ‘ स्थिती समीकरण ’ असे म्हणतात.
यामध्ये P, V आणि T ही आधी सांगितल्याप्रमाणे प्रणालीशी निगडित असलेली तीन चले आहेत. नेहमी तापमान ° से. किंवा ° फॅ. यांमध्ये मोजतात. परंतु या समीकरणात ‘T’ हे चल निरपेक्ष तापक्रमात मोजलेले असावे लागते. वरील समीकरणात ‘n’ वायूचे द्रव्यमान दर्शविते. मात्र ते नेहमीप्रमाणे ग्रॅम किंवा किलोग्रॅम यामध्ये मोजलेले नसून त्यासाठी एक वेगळे एकक वापरले आहे, ज्याला ग्रॅम-रेणुभार किंवा किलोग्रॅम-रेणुभार म्हणतात. वायूच्या गॅ्र.मध्ये ( किंवा किगॅ्र.मध्ये ) असलेल्या द्रव्यमानाला त्या वायूच्या रेणुभाराच्या संख्येने भागले की त्या वायूचे ग्रॅम-रेणुभार ( किंवा किग्रॅ.-रेणुभार ) मिळतात. उदा., हायड्रोजन वायूचा रेणुभार २ आहे. त्यामुळे २ ग्रॅ. हायड्रोजन वायू म्हणजे १ ग्रॅ.- रेणुभार किंवा २ किग्रॅ. हायड्रोजन वायू म्हणजे १ किग्रॅ.- रेणुभार वायू होय. तसेच ऑक्सिजनाचा रेणुभार ३२ आहे. म्हणून ३२ ग्रॅ. ऑक्सिजन हा १ ग्रॅ.-रेणुभार इतका किंवा ३२ किग्रॅ. ऑक्सिजन हा १ किग्रॅ.-रेणुभार इतका ऑक्सिजन आहे. वरील समीकरणातील ‘R’ हा ‘ वैश्विक वायू स्थिरांक ’ आहे. त्याचे मूल्य ८.३४ जूल/के. इतके आहे.
वरील स्थिती समीकरणाच्या बाबतीत एक गोष्ट फार महत्त्वाची आहे. हे समीकरण ‘ आदर्श वायू ’ ला नेमकेपणाने लागू पडते. ज्या वायूच्या रेणूंचे आयतन शून्य असते व ज्याच्या दोन रेणूंमधील परस्पर आकर्षणाचे बल शून्य असते अशा वायूला आदर्श वायू म्हणतात. तापमान कितीही कमी केले व दाब कितीही वाढविला तरी आदर्श वायू हा वायू रूपातच राहतो.
प्रत्यक्ष वायूंच्या रेणूंचे आयतन अत्यंत लहान असते परंतु शून्य असणार नाही हे उघड आहे. तसेच त्याचे दोन रेणू जेव्हा एकमेकांच्या खूप जवळ येतात, तेव्हा त्यांच्यात तीव्र आकर्षणाचे बल निर्माण होते. तसेच प्रत्येक वायू एका विशिष्ट तापमानाच्या खाली नेल्यास द्रवरूपात रूपांतरित होतो. म्हणजेच प्रत्यक्ष अस्तित्वात असलेला कोणताही वायू हा आदर्श वायू नाही. असे असेल तर, वर जे स्थिती समीकरण दिले आहे त्याचा उपयोग काय ? असा प्रश्न पडतो.
या समीकरणाचा उपयोग होतो याचे कारण असे की, एखादा वायू जेव्हा त्याला द्रवीभूत होण्यासाठी लागते त्यापेक्षा खूपच वरच्या तापमानाला असतो, तेव्हा तो जवळजवळ आदर्श वायूप्रमाणेच वर्तणूक करतो आणि सर्वच वायूंचे द्रवीभूत होण्यासाठीचे तापमान इतके कमी आहे, की सर्वसामान्य तापमानाला ते जवळजवळ आदर्श वायूसारखे वागतात. त्यामुळे सर्वसामान्य तापमानाला किंवा त्यापेक्षा उच्च तापमानाला वरील स्थिती समीकरण सर्व वायूंसाठी वापरता येते. मात्र कमी तापमानाला ही परिस्थिती बदलते, हे लक्षात ठेवणे आवश्यक असते.
या बंदिस्त वायूच्या प्रणालीच्या P, V आणि T या तीन चलांमध्ये फरक करीत असताना जर V च्या मूल्यात वाढ झाली, तर त्याचा अर्थ वायू प्रसरण पावला असा होतो. अशा वेळेस त्या वायूकडून बाह्य कार्य घडते आणि त्यासाठी तो आपल्या जवळची उष्णता खर्च करतो. म्हणजेच ही प्रणाली औष्णिक एंजिन बनते. एंजिन जर सतत कार्यरत राहायचे असेल तर त्याला उष्णतेचा सतत पुरवठा करावा लागेल म्हणजे त्यासाठी एक उष्णतेचे उगमस्थान लागेल.
परंतु ⇨ निकोलास लेओनार्ट सादी कार्नो या फ्रेंच शास्त्रज्ञाने हेदेखील लक्षात आणून दिले की, एंजिन सतत कार्यरत राहण्यासाठी त्याची कार्यपद्धती चक्रीय असणे आवश्यक आहे. म्हणजेच व्यवस्था पुनःपुन्हा तिच्या मूळ स्थितीला येणे आवश्यक आहे. हे करण्यासाठी प्रत्येक चक्राच्या शेवटी प्रणालीला उष्णता बाहेर टाकावी लागेल आणि त्यासाठी उष्णतेचे विसर्जन करण्यासाठी एक विसर्जन स्थान किंवा कुंड असणे देखील तितकेच आवश्यक आहे. थोडक्यात औष्णिक एंजिन जर सतत कार्यरत ठेवायचे असेल तर त्यासाठी उष्णतेचे उगम स्थान आणि विसर्जन स्थान अशा दोघांची आवश्यकता असते. इतकेच नव्हे तर विसर्जन स्थानात टाकलेली उष्णता ही वाया गेलेली उष्णता आहे आणि तिचा उपयोग करता येणार नाही. औष्णिक एंजिनाच्या कार्यपद्धतीत अशा प्रकारे उष्णता वाया जाणे अपरिहार्य असल्यामुळे १००% कार्यक्षमतेचे औष्णिक एंजिन बनविणे तार्किक दृष्ट्या असंभाव्य आहे.
हा निष्कर्ष म्हणजे भौतिकीतील एक मूलभूत महत्त्वाचा नियम आहे व त्याला ‘ ऊष्मागतिकीचा दुसरा नियम ’ म्हणून ओळखले जाते. बंदिस्त वायूच्या प्रणालीचा अभ्यास करून हा नियम समजून घेता येतो, म्हणून या प्रणालीला महत्त्व आहे.
P.V = nRT हे समीकरण आदर्श वायूसाठीचे आहे. प्रत्यक्षातील वायूंसाठी स्थिती समीकरण कसे असेल याचा शोध ⇨ योहानेस डीडेरिक व्हॅन डर व्हाल्स या शास्त्रज्ञाने घेतला. आदर्श वायूंच्या रेणूंचे आयतन शून्य असते असे मानले जाते. तसेच आदर्श वायूच्या कोणत्याही दोन रेणूंमध्ये आकर्षण किंवा अपकर्षण यांचे बल नसते असे मानले जाते. या गृहीतकांच्या आधाराने आदर्श वायूच्या स्थिती समीकरणाची उपपत्ती मांडली जाते.
व्हॅन डर व्हाल्स यांनी प्रत्येक रेणूचे आयतन विचारात घेतले. एक ग्रॅम-रेणुभारामध्ये असलेल्या सर्व रेणूंचे एकूण आयतन b आहे असे मानले तर n ग्रॅम-रेणुभार वायूने व्यापलेले आकारमान nb एवढे असेल. म्हणजेच वायूच्या आयतनातून (V मधून ) या रेणूंचे आकारमान वजा करावे लागेल. तसेच त्यांनी वायूंच्या दोन रेणूंमधील आकर्षणाचे बलदेखील विचारात घेतले. या बलाचा परिणाम म्हणजे वायूचा दाब आधीच्या ( आदर्श वायूच्या ) समीकरणात होता त्यापेक्षा जास्त असतो. त्यामुळे प्रत्यक्ष वायूंचे समीकरण लिहिताना मूळच्या समीकरणातील ‘P’ आणि ‘V’ या चलांमध्ये सुधारणा कराव्या लागतात. नवीन समीकरण पुढीलप्रमाणे आहे.
| [ | P | + | an2 | ] | (V – nb) = | nRT |
| V2 |
या समीकरणास व्हॅन डर व्हाल्स यांचे समीकरण असे म्हणतात. यात a आणि b हे दोन स्थिरांक असून त्यांची मूल्ये प्रत्येक वायूसाठी वेगवेगळी असतात, ती प्रयोगांद्वारे ठरविली गेली आहेत. उदा., कार्बन डाय-ऑक्साइड ( CO2 ) वायूसाठीची ही मूल्ये खालीलप्रमाणे आहेत,
a = ०.३६४ जू. मी.३/( ग्रॅ.-रेणुभार )२,
b = ४.२७ × १०–५ मी.३/ ( ग्रॅ.-रेणुभार )
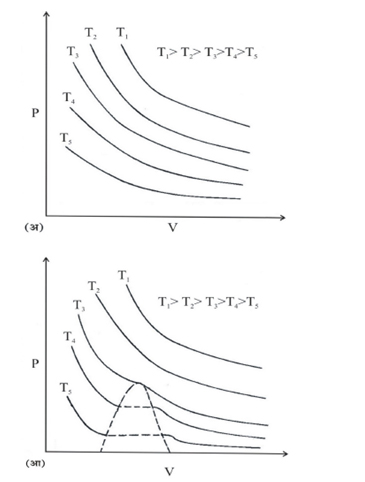
प्रत्यक्ष वायू आणि आदर्श वायू यांच्या वर्तणुकीतील फरक नेमका कधी आणि कसा होतो हे या दोन्ही वायूंचे P-V आलेख बघितले तर मागे समजून येते. हे आलेख वर दाखविले आहेत. त्यातून असे लक्षात येते की, कमी तापमानाला प्रत्यक्ष वायूच्या आलेखाचे तीन भाग पडतात. डाव्या बाजूला एक उभी चढण असलेली जवळजवळ सरळ रेषा आहे. येथे P मध्ये मोठा फरक केला, तर V मध्ये अगदी छोटा फरक होतो. अगदी उजव्या बाजूला एक वक्र रेषा आहे, जी खूप आडवी आहे. येथे P मध्ये थोडा फरक केला तरी V मध्ये मोठा फरक होतो. या दोन भागांना जोडणारी एक तुटक सरळ रेषा दाखविली आहे. या आलेखाचा अर्थ असा की, उजवीकडील भाग ही वायुरूपातील अवस्था आहे, जेथे दाब थोडा वाढविला तरी आयतन खूप कमी होते. डावीकडील भाग द्रवरूप अवस्था आहे, जेथे दाब खूप वाढविला तरी आयतनात नगण्य फरक होतो. मधला भाग या दोन भागांना जोडतो, जेथे द्रव आणि वायुरूप अशा दोन्ही अवस्था एकमेकींशी संतुलन साधून अस्तित्वात असतात. ( या भागात वायूची वर्तणूक इतकी चंचल असते, की त्याची विश्वासार्ह प्रायोगिक निरीक्षणे घेणे कठीण असते. म्हणून हा भाग तुटक सरळ रेषेने दाखवितात ).
म्हणजेच प्रत्यक्ष वायूच्या बाबतीत काय घडते? तापमान कमी असताना त्यावरील दाब वाढवावा तसे त्याचे आयतन कमी होत जाते आणि अशी एक पायरी येते की, वायूचे द्रव अवस्थेत रूपांतर होते. त्यानंतर वायूचे स्थिती समीकरण या द्रवाला लावता येत नाही. थोडक्यात तापमान कमी असेल तर दाब पुरेसा वाढविला की प्रत्यक्ष वायू द्रवरूप होतात. आदर्श वायू कधीच द्रवरूप होत नाही.
वरील आलेखावरून आणखी एक गोष्ट लक्षात येते. द्रव आणि वायू अवस्था एकत्रित असण्याचा जो भाग आलेखात दाखविला आहे ( तुटक रेषांचा भाग ), तो तापमान वाढते तसा कमीकमी होत जातो, आणि एका विशिष्ट तापमानाला ( आलेखातील T3 हे तापमान) तो शून्य होतो. या तापमानाला त्या वायूचे ‘ क्रांतिक तापमान ’ असे म्हणतात. प्रत्येक वायूचे ‘ क्रांतिक तापमान ’ वेगवेगळे असते. क्रांतिक तापमानाच्या वर कितीही दाब वाढविला तरी वायू द्रवीभूत होत नाही. म्हणजेच या तापमानाच्या वर तो प्रत्यक्ष वायू आदर्श वायूप्रमाणे वर्तणूक करतो.
वायूसंबंधीचा हा अभ्यास ‘ वायूंचा गत्यात्मक सिद्धांत ’ या भौतिकीच्या शाखेत केला जातो. त्यातून वायूंची वर्तणूक आणि औष्णिक एंजिने यांबाबत महत्त्वाचे निष्कर्ष काढता येतात.
पहा : उष्णता; ऊष्मागतिकी; द्रव्याचा गत्यात्मक सिद्धांत.
पानसे, सुधीर