मॅक्सवेल विद्युत् चुंबकीय समीकरणे : विद्युत् व चुंबकीय क्षेत्रे यांची स्थूल माध्यमातील स्वरूपे व त्यांचे परस्परसंबंध स्पष्ट करणारी सदिश संकेतनात [⟶ सदिश] मांडलेली समीकरणे. प्रयोगाद्वारे मिळालेल्या समीकरणांना जेम्स क्लार्क मॅक्सवेल यांनी १८६४ मध्ये त्यांचे सध्याचे व्यापक व मूलभूत स्वरूप दिले.
जर एखाद्या माध्यमाकरिता विद्युत् पार्यता ϵ व चुंबकीय पार्यता μ [⟶ एकके व परिमाणे] असेल आणि त्या माध्यमावर विद्युत् स्थितिक (स्थिर) क्षेत्र असेल, तर खालील सदिश समीकरणांपैकी (३) व (४) ही समीकरणे यथार्थ ठरतात आणि जर त्यावर कालपरिवर्ती (कालानुसार बदलणारे) विद्युत् क्षेत्र असेल, तर खालील सर्व म्हणजे (१) ते (४) समीकरणे यथार्थ ठरतात. ही समीकरणे सयुक्तिक एम. के. एस. पद्धतीनुसार [⟶ एकके व परिमाणे] दिलेली आहेत. माध्यमात वाहणाऱ्या विद्युत् प्रवाहाची घनता [विद्युत् प्रवाह मूल्य/माध्यमाच्या अनुप्रस्थ (आडव्या) छेदाचे क्षेत्रफळ] J या सदिशाने दर्शविली आहे.
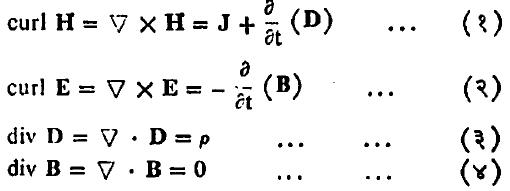
या समीकरणांमुळे विद्युत् क्षेत्र तीव्रता (E), विद्युत् भार घनता (ρ), विद्युत् प्रवाह घनता (J), चुंबकीय स्रोत घनता किंवा चुंबकीय प्रवर्तन (B), चुंबकीय क्षेत्र तीव्रता (H) व विद्युत् विस्थापन (D) या राशींतील संख्यात्मक परस्पर संबंध स्पष्ट केला गेला आहे ( curl व ∇ या संज्ञांच्या स्पष्टीकरणासाठी ‘सदिश’ ही नोंद पहावी).
देकार्तीय सहनिर्देशक पद्धतीकरिता [⟶ भूमिति] हीच समीकरणे अवकल निदर्शनात [⟶ अवकल समीकरणे] खालील स्वरूपे धारण करतात. यांत x, y, z या पादाक्षरांनी H, E, D व B यांचे अनुक्रमे X, Y, Z या अक्षांच्या दिशांतील घटक दर्शविले आहेत.
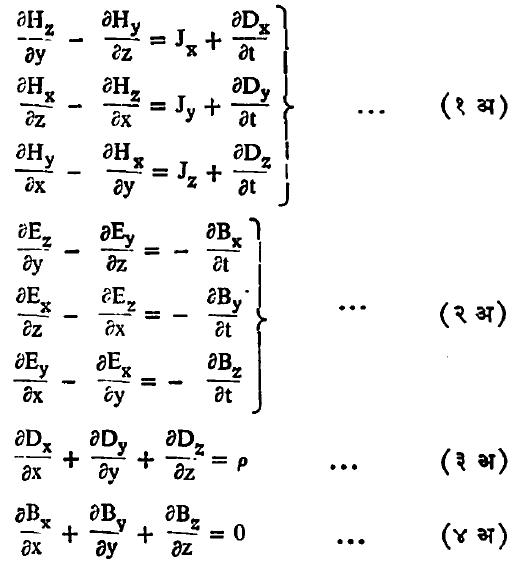
सदिश विश्लेषण नियमांचा वापर करून हीच समीकरणे खालील समाकल स्वरूपात [⟶ समाकल समीकरणे व रूपांतरे] मांडता येतात. या स्वरूपात यांचा अर्थ समजणे सुलभ होते.

प्रकाशाचा वेग) या सूत्राने परस्परांशी संबंधित असतात (मॅक्सवेल यांच्या वेळी E व H या राशी निरनिराळ्या एकक पद्धतीत निर्देशित केल्या जात असत).
वरील समीकरणांत येणाऱ्या चलांविषयीचे विशदीकरण खाली दिले आहे.
(२) व (२ अ) या समीकरणांत येणारे ऋण चिन्ह चुंबकीय स्रोत घनता B व प्रवर्तित झालेल्या विद्युत् प्रवाहामुळे मिळणारा चुंबकीय स्रोत यांच्या दिशा एकमेकींविरुद्ध असतात हे दाखविते. विद्युत् भार वाहकाच्या स्थान वितरणामुळे मिळालेली सरासरी विद्युत् भार घनता ρ या राशीने दर्शविली आहे. रूढ भौतिकीमध्ये सर्व विद्युत् भार बिंदु स्वरूपात असतात, असे गृहीत धरलेले असते. त्यामुळे पुष्कळ विद्युत् भार बिंदूंचा ज्यामध्ये समावेश आहे अशा एका अत्यंत लहान पण सांत (मर्यादित) घनफळाकरिता ρ याला अर्थ देता येईल, हे उघड आहे. घनफळ शून्योपगामी धरून त्याच्या अनुषंगाने एका बिंदुपाशी ρ चे मूल्य निर्धारित करावयाचा प्रयत्न केला, तर त्यापासून अनेक अडचणी निर्माण होतात असे आढळते. या कारणाकरिता मॅक्सवेल समीकरणाच्या विवेचनाकरिता माध्यमाचा एक प्राथमिक अत्यल्प पण सांत घनफल विभाग विचारात घेणे जास्त बरोबर ठरते.
निरोधक माध्यमामध्ये विद्युत् प्रवाह वाहक उपस्थित नसतात. त्यावर विद्युत् व चुंबकीय क्षेत्रे लावली असता त्यामध्ये संवाहक विद्युत्प्रवाह मिळत नाही. याउलट धातू अथवा अर्धसंवाहक (ज्यंची विद्युत् संवाहकता धातू आणि निरोधक यांच्या दरम्यान असते असे पदार्थ) अथवा विद्युत् विच्छेद्य विद्राव (ज्यातील विरघळलेला पदार्थ विद्युत् भारित अणू, रेणू वा अणुगट या रूपात असल्याने त्यातून विद्युत् प्रवाह वाहू शकतो असा विद्राव) या पदार्थ माध्यमात विद्युत् प्रवाह वाहक मुक्त अवस्थेत असतात. अशा माध्यमावर विद्युत् क्षेत्र लावले असता त्यामुळे त्यामधील विद्युत् प्रवाह वाहक गतिमान होतात यामुळे माध्यमात संवाहक विद्युत् प्रवाह मिळतो. अशा परिस्थितीत विद्युत् प्रवाह घनता J चे मूल्य अशून्य असते. रेषीय माध्यमाकरिता (ज्याकरिता ओहम नियम लागू पडतो)
| J | = | σ E | . | . | . | . | . | . | . | . | (५) |
हे समीकरण सार्थ ठरते (येथे σ ही माध्यमाची विशिष्ट संवाहकता आहे). वरील समीकरणाशिवाय आणखी दोन समीकरणे साहाय्यक म्हणून मॅक्सवेल समीकरणांबरोबर वापरली जातात.
सर्वसामान्य माध्यमाकरिता ( उदा., लोहचुंबकीय वा लोहविद्युतीय पदार्थाकरिता ) B व H यांधील परस्परसंबंध अथवा D आणि E यांमधील संबंध रेषीय स्वरूपाचा असत नाही. एखाद्या माध्यमाकरिता ϵ व μ हे स्थिरांक सर्वत्र एकाच मूल्याचे असतील, तर ते माध्यम एकजिनसी आहे असे म्हणतात. एखाद्या माध्यमात या स्थिरांकांचे चलन स्थलानुसार दिशेवर अवलंबून नसेल, तर ते माध्यम समदिक् आहे असे म्हणतात. माध्यम एकजिनसी, समदिक् व रेषीय असेल तर B व H आणि D व E यांमधील संबंध
| B | = | μ H | . | . | . | . | . | . | . | . | (६) |
| D | = | ϵ E | . | . | . | . | . | . | . | . | (७) |
या सुलभ स्वरूपात दर्शविता येतो. मॅक्सवेल समीकरणांकरिता घटक समीकरणे म्हणून वरील समीकरणे उपयोगी पडतात.
विद्युत् व चुंबकीय क्षेत्रांसंबंधी प्रथम जे प्रयोग झाले त्यामुळे या दोन क्षेत्रांचा एकमेकांशी काही संबंध नसून त्यांचे कार्य एकमेकांपेक्षा सर्वस्वी भिन्न आहे, असा समज झाला होता. विद्युत् प्रवाहामुळे चुंबकीय क्षेत्र निर्माण करता येते असे एच्. सी. ओर्स्टेड यांनी १८२० मध्ये प्रथम प्रयोगाने दाखविले. विद्युत् प्रवाहाचे मूल्य व त्यामुळे निर्माण होणाऱ्या चुंबकीय क्षेत्राचे मूल्य व दिशा यांमधील संख्यात्मक परस्परसंबंध जे. बी. बायो व एफ्. साव्हार यांच्या प्रयोगाने, तर ए. एम्. अँपिअर यांच्या सैद्धांतिक संशोधनामुळे प्रस्थापित झाला ⟶ चुंबकत्व]. अँपिअर, फॅराडे व मॅक्सवेल यांच्यानंतरच्या कार्यावरून स्थिर विद्युत् भारांमुळे फक्त स्थिर विद्युत् स्थितिक क्षेत्र निर्माण होते आणि वरील विद्युत् भार गतिमान झाले, तर त्यांपासून चुंबकीय क्षेत्र निर्माण होते, असे माहीत झाले. याउलट फक्त कालपरिवर्ती चुंबकीय क्षेत्रामुळे विद्युत् क्षेत्राची निर्मिती करणे शक्य होते असे आढळले, वरील उदाहरणामध्ये एका क्षेत्राचे अस्तित्व विद्युत् भाराच्या गतीवर अवलंबून असते. सर्व गती सापेक्ष असल्यामुळे जर एखाद्या निरीक्षकाच्या सापेक्ष विद्युत् भाराला गती असेल किंवा विद्युत् भाराच्या सापेक्ष निरीक्षकाला गती असेल, तर अशा दोन्ही परिस्थितींत चुंबकीय क्षेत्र निर्माण होते. चुंबकीय क्षेत्र अशा रीतीने निरीक्षक सापेक्ष आहे असे कळते. कोणत्याही घटनेचे स्थल-काल एकमेकांच्या सापेक्ष गती असणाऱ्याण दोन निरीक्षकांना ज्याप्रमाणे [सापेक्षता सिद्धांतानुसार ⟶ सापेक्षता सिद्धांत] वेगवेगळे दिसते त्याचप्रमाणे एका निरीक्षकाला भासणारी E व B ही क्षेत्र मूल्ये दुसऱ्याला भासणाऱ्या E’ व B’ या मूल्यांपेक्षा भिन्न असतात. E, E’ व B, B’ यांमधील परस्परसंबंध लोरेन्ट्स रूपांतरण सूत्रांच्या [⟶ अवकाश-काल] साहाय्याने मिळविता येतो. E व H या क्षेत्रांमध्ये जरी वरील प्रकारची आंतरिक एकरूपता असली, तरी काही विशिष्ट परिस्थितीत (जेव्हा ती कालपरिवर्ती नसतात तेव्हा) विद्युत् स्थितिक व चुंबकीय स्थितिक अशी भिन्न क्षेत्रे गृहीत धरून त्यांच्या परिणामाचा स्वतंत्रपणे विचार करणे शक्य होते (या मुद्याच्या स्पष्टीकरणाकरिता पुढे पहा). ही क्षेत्रे जर कालपरिवर्ती असतील, तर असे विलगीकरण करता येत नाही, कारण विद्युत् व चुंबकीय क्षेत्रांमधील परस्परसंबंध समी. (१) व (२) यांमुळे निश्चित होत असतो. या कारणाकरिता सामान्यपणे विद्युत् चुंबकीय क्षेत्राचे संपूर्ण निर्देशन करण्याकरिता, E किंवा D, H किंवा B आणि J किंवा ρ या राशींची मूल्ये वा दिशा यांचे ज्ञान उपलब्ध असावे लागते.
मॅक्सवेल समीकरणांचा आधार व अर्थ : मॅक्सवेल यांचे पहिले समीकरण बायो व साव्हार नियम आणि अँपिअर नियम या दोहोंवर आधारित आहे. D कालपरिवर्ती नसेल, तर विद्युत् प्रवाह J मुळे चुंबकीय क्षेत्र H मिळते, असा याचा सुलभ अर्थ आहे. स्थिर विद्युत् प्रवाहापासून मिळणारे चुंबकीय क्षेत्र खाली दिलेल्या अँपिअर नियमापासून मिळते.
| Curl | H | = | J |
अँपिअर नियमाचे सूत्र मॅक्सवेल यांच्या दुसऱ्या समीकरणाशी सममित नाही. कालपरिवर्ती चुंबकीय क्षेत्रामुळे विद्युत् क्षेत्र निर्माण होते, हा निष्कर्ष फॅराडे यांनी प्रयोगाने काढला. याच न्यायाने कालपरिवर्ती विद्युत् क्षेत्रामुळे चुंबकीय क्षेत्र का निर्माण होऊ नये या विचाराने मॅक्सवेल यांनी
| Curl H | = | J | + | ∂(D) | … | … | … | … | (८) |
| ∂t |
हे समीकरण मांडले. याचा अर्थ सा होतो की, विद्युत् क्षेत्र E (व त्यामुळे D) याच्या मूल्यात कालानुसार बदल झाला, तर त्यामुळे ∂(D)/∂t या मूल्याची विद्युत् प्रवाह घनता निर्माण होते [कालपरिवर्ती E करिता J सुद्धा कालपरिवर्ती असणार, हे उघड आहे. J व ∂(D)/∂t या दोन सदिशांच्या दिशा (सदसत्किंमवा मिश्र संख्यांच्या आर्गा-आकडतीमध्ये ⟶ संख्या) एकरूप नसतात व त्याची सदिश बेरीज वरील दोन पदांनी दर्शविली आहे]. काही विद्युत् मंडलांत क्षणिक विद्युत् प्रवाह मिळतो व त्यामुळे काही भागात विद्युत् संचय होतो (उदा., धारित्राचे-विद्युत् भाराचा संचय करणाऱ्या साधनाचे-विद्युत् विसर्जन). अशा परिस्थितीत विद्युत् प्रवाह व विद्युत् भार यांना सातत्याची अट लावली असता ∂(D)/∂t हा विद्युत् प्रवाह घटक मिळतो, असे मॅक्सवेल यांनी दाखविले. निर्वात व निरोधक माध्यमांकरिता J » 0 व Curl H =∂(D)/∂t हे समीकरण मॅक्सवेल यांच्या पहिल्या समीकरणाशी सममित आहे वे कळते. ∂(D)/∂t या विद्युत् प्रवाह घटकाला मॅक्सवेल यांनी विद्युत् विस्थापनजन्य प्रवाह असे नाव दिले. निरोधकामधील विद्युत् भाराचे मर्यादित विस्थापन झाल्यामुळे हा विद्युत् प्रवाह निर्माण होतो असे प्रथम मानले जात असे. निर्वातामध्ये सुद्धा विद्युत् प्रवाह मिळत असल्यामुळे वरील स्पष्टीकरण सर्वव्यापी होऊ शकत नाही, हे उघड आहे. कोणत्याही सदिश F करिता div curl F = 0 असल्यामुळे मॅक्सवेल समीकरणापासून
| div | ( | J | + | ∂( D) | ) | = | 0 | … | … | (९) | |
| ∂t |
यामध्ये तिसऱ्या समीकरणाचा समावेश केल्यास
| Div J | + | ∂ρ | = | 0 | … | … | (१०) | ||
| ∂t |
यावरून विद्युत् भार अक्षय्यता नियमाचे [⟶ द्रव्य आणि ऊर्जा यांची अक्षय्यता] पालन करतो, असे दिसून येते. जर आविष्कार काल-अपरिवर्ती असेल, तर
| Div J | = | 0 | … | … | … | (११) |
वरील समीकरणावरून विद्युत् प्रवाह सातत्य नियम पाळतो, असे कळते. हा निष्कर्ष जी. आर्. किरखोफ यांच्या पहिल्या विद्युत् मंडल नियमाशी [⟶ एकदीश विद्युत् प्रवाह] एकरूप आहे, हे लक्षात घेण्याजोगते आहे.
मॅक्सवेल यांचे दुसरे समीकरण फॅराडे यांच्या विद्युत् चुंबकीय प्रवर्तन नियमावर (चुंबकीय क्षेत्राच्या तीव्रतेत बदल केल्यास विद्युत् प्रेरणा म्हणजे विद्युत् मंडलात प्रवाह वाहण्यास कारणीभूत होणारी प्रेरणा उत्पन्न होते या नियमावर) आधारित आहे. या समीकरणावरून हे स्पष्ट होते की, चुंबकीय क्षेत्र जर कालपरिवर्ती नसेल, तर त्यामुळे विद्युत् क्षेत्र (व विद्युत् मंडल पूर्ण असल्यास विद्युत् प्रवाह) निर्माण होणार नाही पण त्याबरोबर आजूबाजूला विद्युत् भार वितरण असेल, तर त्यामुळेही वेगळे विद्युत् क्षेत्र निर्माण होईल. सी. ए. कुलंब यांच्या नियमावरून (दोन विद्युत् भारांमधील प्रेरणा-आकर्षणाची वा प्रतिसारणाची –ही त्या भारांच्या गुणाकाराच्या सम प्रमाणात व त्यांतील अंतराच्या वर्गाच्या गुणाकाराच्या सम प्रमाणात व त्यांतील अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते) अशा विद्युत् क्षेत्रापासून मिळणाऱ्या curl E या राशीचे मूल्य शून्य असेल, असे दाखविता येते. अँपिअर सूत्राप्रमाणे काल-अपरिवर्ती विद्युत् प्रवाहामुळे सुद्धा चुंबकीय क्षेत्र निर्माण करता येते. याउलट स्थिर चुंबकीय क्षेत्राच्या द्वारे विद्युत् क्षेत्र अथवा विद्युत् प्रवाह निर्माण होत नाही. चुंबकीय क्षेत्रात जर बदल केला, तर त्यामुळे विद्युत् प्रवाह प्रवर्तित होतो पण तो क्षणिक असतो. अतिसंवाहक पदार्थामध्ये मात्र चुंबकीय क्षेत्रात बदल करून स्थिर असा प्रवर्तित विद्युत् प्रवाह मिळविता येतो [⟶ अतिसंवाहकता]. या आविष्काराचे विशदीकरण करण्याकरिता एफ्. लंडन यांनी मॅक्सवेल समीकरणांत काही बदल सुचविले आहेत.
चुंबकीय क्षेत्रात कालानुसार वाढ झाल्यामुळे विद्युत् क्षेत्र निर्माण होते या आविष्काराचा उपयोग करून डी. डब्ल्यू. कर्स्ट यांनी बीटाट्रॉन नावाचा इलेक्ट्रॉन वेगवर्धक [⟶ कणवेगवर्धक] तयार केला (१९४१). त्यापासून मिळालेल्या वेगवान इलेक्ट्रॉन झोताच्या साहाय्याने त्यांनी क्ष-किरण निर्माण केले. विद्युत् ऊर्जा निर्मितीकरिता सध्या वापरली जाणारी विद्युत् जनित्रे फॅराडे यांच्या मूलभूत शोधावरच आधारित असतात, हे सुपरिचित आहे.
कुलंब यांनी प्रयोग करून दोन विद्युत् भारांतील प्रेरणा त्यांमधील अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते, असे दाखविले. मॅक्सवेल यांचे तिसरे समीकरण या निष्कर्षाचे व्यापकीकरण आहे. क्षेत्र स्रोत धन विद्युत् भारापासून उगम पावतो असे मानले, तर हे समीकरण व स्रोताकरिता सातत्याची अट हे दोन समतुल्य आहेत, असे गणिताने दाखविता येते. एखाद्या बंदिस्त अवकाशात जर निरनिराळ्या ठिकाणी विद्युत् भार विखुरलेला असेल, तर त्या अवकाशाच्या सर्व पृष्ठभागापासून (लंबवर्ती मार्गे) बाहेर पडणारा विद्युत् विस्थापनाचा स्रोत हा अवकाशातील संकलित विद्युत् भाराएवढा असतो. या नियमाला के. एफ्. गौस यांचा नियम असेही म्हणतात.
मॅक्सवेल यांचे चौथे समीकरण चुंबकीय क्षेत्रासंबंधी आहे. ते चुंबकीय क्षेत्र स्रोताचे सातत्य दाखविते. विद्युत् आविष्कारामध्ये ऋण आणि धन विद्युत् भार ज्याप्रमाणे मुक्त स्थितीत उपलब्ध होऊ शकतात, त्याप्रमाणे चुंबकीय आविष्कारात मुक्त चुंबकीय ध्रुव सापडत नाहीत. त्यामुळे चुंबकीय क्षेत्राकरिता सर्व परिस्थितींत
Div μH = 0
चुंबकीय क्षेत्राच्या स्रोत रेषा अखंडित किंवा परिनलिकाकृती (लांबट नळीसारख्या व्यवस्थित गुंडाळलेल्या संवाहक तारेच्या वेटोळ्याच्या आकाराप्रमाणे) असतात. एखादे बंदिस्त अवकाश विचारात घेतल्यास त्यामध्ये असणाऱ्या सर्व ध्रुवांचे परिणामी मूल्य शून्य असते व त्यामुळे त्यामधून बाहेर पडणाऱ्या चुंबकीय स्त्रोताचे मूल्यही शून्य असते. त्यामुळे त्यामधून बाहेर पडणाऱ्या चुंबकीय स्त्रोताचे मूल्यही शून्य असते. चुंबकीय ध्रुवाला वेगळे अथवा स्वतंत्र अस्तित्व नसल्यामुळे या आविष्काराचे वर्णन करण्याकरिता प्राथमिक स्तरावर उपयोगात असलेल्या चुंबकीय उत्तर व दक्षिण ध्रुवांच्या संकल्पनेचा उपयोग करू नये, अशीच आधुनिक भूमिका आहे.
मॅक्सवेल समीकरणांचा अनुषंगाने खालील काही गोष्टी लक्षात घेण्याजोगत्या आहेत :
(१) कोणत्याहि सदिशाचा div curl हा शून्य मूल्याचा असतो. या गणितीय सिद्धांताचा उपयोग फेल्यास मॅक्सवेल समीकरणे सर्वस्वी स्वतंत्र नाहीत, असे दाखविता येते. उदा., curl E = – ∂(B)/∂t या समीकरणापासून विद्युत् भाराची अक्षय्यता आणि div व ∂/∂t या क्रिया क्रमनिरपेक्ष आहेत असे मानले, तर
div B = 0
हे समीकरण मिळविता येते. अशा प्रकारे समी. (३) व (४) ही समी. (१) व (२) पासून मिळविता येतात पण समी. (३) व (४) ही महत्त्वाची असल्यामुळे त्यांचा निर्देश व विचार स्वतंत्रपणे केला जातो.
(२) मॅक्सवेल समीकरणांतली क्षेत्रे काल-अपरिवर्ती आहेत असा निर्बंध त्यावंर घातला, तर समी. (१) व (२) अयुग्मित होतात व curl E = 0 अशा परिस्थितीत E व H यांमधील परस्परसंबंध तुटल्यामुळे E करिता अदिश वर्चस्[ ⟶ वर्चस् ] ϕ याचा उपयोग करता येतो.
| E | = | – grad ϕ | . . . | . . . | . . . | (१२) |
(grad या संज्ञेच्या स्पष्टीकरणासाठी ‘सदिश’ ही नोंद पहावी ).

लाप्लास व प्वासाँ समीकरणांचा उपयोग सर्व प्रकारच्या विद्युत् स्थितिक क्षेत्रांविषयीचे प्रश्न सोडविण्याकरिता केला जातो. E व H यांचे युग्मन तुटल्यामुळे त्यांच्या परिणामाचा स्वतंत्रपणे विचार करणे शक्य होते. अशा परिस्थितीत विद्युत् चुंबकीय क्षेत्राचे संपूर्ण निर्देशन करण्याकरिता E, D व H, B अशा चार सदिश राशींचे संपूर्ण ज्ञान आवश्यक होते. क्षेत्राच्या ऐवजी वर्चस् वापरले असता गणितीय रीत सोपी होते व अशा प्रकारे मिळविलेली समीकरणे गेज रूपांतरणा करिता [⟶ वर्चस्] निश्चल राहतात, असे दाखविता येईल.
द्रव्याच्या विद्युत् पार्यतेशारख्या विद्युत् गुणधर्मीची मीमांसा, इलेक्ट्रॉन बंदुकीमधून [इलेक्ट्रॉन उत्सर्जित करून त्यांचे संकेंद्रण करणाऱ्या विद्युत् अग्रांनी बनलेल्या रचनेमधून ⟶ ऋण किरण नलिका] उत्सर्जित होणाऱ्या इलेक्ट्रॉनांचा उड्डाण मार्ग, विद्युत् भार वाहकाकरिता प्रवेगक (वेगवर्धक) योजना, विद्युत् क्षेत्राद्वारे विद्युत् भार वाहक मार्गाचे विचलन करणाऱ्या प्रणाली, धारित्रासारख्या विद्युत् मंडल घटकाच्या मूल्याचे गणन, इलेक्ट्रॉनीय प्रयुक्तीमध्ये विद्युत् वर्चस् प्रवणतेचे गणन इ. प्रश्नांकरिता विद्युत् स्थितिक मीमांसेचा उपयोग केला जातो. या पद्धतीमध्ये चुंबकीय परिणामाचा विचार करण्याची आवश्यकता नसल्याने यास स्वतंत्र विद्युत् स्थितिक मीमांसा असे म्हणतात.
विद्युत् स्थितिक क्षेत्र मीमांसेसारखी गणितीय पद्धत वापरून चुंबकीय स्थितिक सिद्धांतांचे वरीलप्रमाणेच विशदीकरण करता येते. यामध्ये विद्युत् स्थितिक परिणामाचा विचार केला जात नसल्यामुळे यास स्वतंत्र चुंबकीय स्थितिक पद्धत असे म्हणता येते. याकरिता उपयुक्त अशी गणितीय पद्धत विद्युत् स्थितिकीकरिता वापरण्यात येणाऱ्या रीतीप्रमाणेच असते. चुंबकीय क्षेत्र व्यवहारात निर्माण करण्याकरिता लोहचुंबकीय द्रव्याचा उपयोग बहुतांशी केला जातो. या द्रव्याकरिता चुंबकीय पार्यतेचे मूल्य हे चुंबकीय प्रवर्तन मूल्यावर आणि इतरही काही गोष्टींवर अवलंबून राहत असल्यामुळे मॅक्सवेल चुंबकीय स्थितिक समीकरणे नैकरेषीय (द्वितीय अथवा अधिक घातींची) होतात. अशी समीकरणे सोडविण्याकरिता उपलब्ध गणितीय पद्धती अपुऱ्या पडतात. त्यांपासून निष्कर्ष मिळविण्याकरिता आसन्नीकरणे (अंदाजी मूल्ये मिळविण्याच्या क्रिया) करावी लागतात. काही मर्यादित बाबींकरिता ⇨ चुंबकीय मंडल पद्धतीसुद्धा वापरता येते. चुंबकीय स्थितिक क्षेत्र समीकरणाचा वापर करून विद्युत् चलित्र (मोटर), जनित्र, ⇨ अभिचालित्र (अगदी अल्प शक्तीचा उपयोग करून मोठ्या शक्तीच्या विद्युत् मंडलात पाहिजे तसा बदल घडवून आणणारे विद्युत् साधन), चिरचुंबकयुक्त चुंबकीय उद्ग्राहक (ध्वनितरंकांचे ग्रहण करून त्यांचे विद्युत् तरंगात रूपांतर करणारी प्रयुक्ती), ⇨ ऊर्जापरिवर्तकातील (एका प्रकारच्या ऊर्जेचे दुसऱ्या प्रकारच्या ऊर्जेत रूपांतर करणाऱ्याय साधनातील) तारवलय आणि संगणकातील (गणकयंत्रातील) स्मरण प्रयुक्ती यांसारख्या सर्व चुंबकीय प्रयुक्तींची मीमांसा करता येते.
(३) विद्युत् भाराचे मापन करण्याकरिता त्यामुळे उत्पन्न होणाऱ्या परिणामाचा उपयोग केला जातो. विश्रामी (गतिहीन) विद्युत् भाराचे मापन करण्याकरिता त्यापासून एका ठराविक अंतरावर ठेवलेल्या परिक्ष्य विद्युत् भारावर जी प्रेरणा मिळते तिचा उपयोग करतात. विद्युत् भार जर गतिमान असेल, तर त्याकरिता कुलंब किंवा गौस नियम किती प्रमाणात सार्थ असतो, हा प्रश्न उद्भवतो. प्रणाली जरी गतीमान झाली, तरी तीमधील विद्युत् भाराच्या मूल्यात फरक पडत नाही, असा निष्कर्ष काही प्रयोगांवरून काढता येतो. या परिस्थितीत गौस नियमसुद्धा सार्थ असतो, असे मानले जाते.
(४) वरील समीकरणात विद्युत् चुंबकीय क्षेत्र ज्यावर कार्य करतात ते माध्यम अखंडित आहे, असे गृहीत अभिप्रेत आहे. समीकरणांना अवकल स्वरूप देणे या गृहीताशिवाय शक्य होणार नाही. जर माध्यमात कोणत्याही स्थानी खंड असले किंवा त्याच्या गुणधर्मात अथवा त्यावरील क्षेत्रात तीव्र खंडित स्वरूपाचे बदल होत असतील, तर अशा ठिकाणी काही विशिष्ट सीमा अटींची पूर्तता व्हावा लागते, असे दाखविता येते.
(५) मॅक्सवेल यांनी विद्युत् चुंबकीय क्षेत्रे कालपरिवर्ती असतील, तर त्यांपासून काही परिस्थितीत विद्युत् चुंबकीय तरंग प्रेषित केले जातात, असे दाखविले. या तरंगाचा वेग प्रकाश वेग C एवढाच असतो व ते अवतरंग स्वरूपाचे (म्हणजे ज्यांत माध्यमाच्या कणांचे कंपन तरंग प्रसारणाच्या लंब दिशेत होते अशा स्वरूपाचे) असतात. प्रकाशामध्ये ध्रुवीकरण, परावर्तन, प्रणमन इ. आविष्कार [⟶ प्रकाशकी] ज्या नियमांनुसार होतात, बहुतांशी तेच नियम विद्युत् चुंबकीय तरगांकरिता लागू पडतात, असे सैद्धांतिक दृष्ट्या मॅक्सवेल व हाइन्रिपख हर्ट्झ यांनी दाखविले. हर्ट्झ यांनी प्रयोगाद्वारा त्याकरिता पडताळा मिळविला. या सर्व गोष्टींवरून प्रकाश हासुद्धा विद्युत् चुंबकीय तरंगरूपच आहे, हे स्पष्ट झाले. हर्ट्झ यांच्या प्रयोगानंतर गूल्येल्मो मार्कोनी यांनी अशा तरंगाद्वारे संदेशवहन करता येते असे दाखविले. त्यानंतर रेडिओ, रडार, सूक्ष्मतरंग इ. इलेक्ट्रॉनीय पद्धतीचा शोध लागून या तंत्रविद्येत जी झपाट्याने वाढ झाली ती सुपरिचित आहे.
(६) विद्युत् चुंबकीय क्षेत्रे प्रस्थापित करण्याकरिता ऊर्जा लागते. या क्षेत्रांकरिता ऊर्जा घनता ½ ϵE2 व ½ μH2 या सूत्रांनी मिळते. संपूर्ण विद्युत् चुंबकीय क्षेत्राची ऊर्जा मॅक्सवेल समीकरणांचा वापर करून मिळविता येते.
विद्युत् चुंबकीय क्षेत्राचे वर्चस् व क्षेत्र प्रदिशाद्वारे निर्देशन : विद्युत् क्षेत्र E व चुंबकीय स्त्रोत घनता B यांच्याऐवजी अदिश विद्युत् वर्चस् ϕ व सदिश वर्चस् A यांचा उपयोग केला असता गणितीय रीतीमध्ये सुलभता येते व मिळालेली समीकरणे गेज रूपांतरणाकरिता निश्चल अशा स्वरूपात मिळतात. A हे वर्चस् सदिश असल्यामुळे त्याचे Ax, Ay, Az असे देकार्तीय घटक असतात. वर्चस् व क्षेत्रे यांमधील संबंध खालील सूत्रांनी मिळतो.

अशी दोन तरंग समीकरणे मिळतात. यावरून दोलायमान हर्ट्झ द्विध्रुवाच्या प्रतिकृतीचा उपयोग करून विद्युत् चुंबकीय प्रारणाची (तरंगरूपी ऊर्जेची) प्रेषण क्रिया प्रत्यक्षात कशी घडते, याचे विशदीकरण देता येते [⟶ विद्युत् चुंबकीय प्रारण].
माध्यम समदिक् (अथवा एकजिनसी) नसल्यास मॅक्सवेल समीकरणे प्रदिशाच्या स्वरूपात [⟶ प्रदिश] दिली असता गणितीय दृष्ट्या सुलभ ठरते. विद्युत् क्षेत्राचे तीन घटक Ex, Ey, Ez आणि चुंबकीय क्षेत्राचे (येथे B वापरण्याचा प्रघात आहे) Bx, By, Bz तीन घटक मिळून विद्युत् चुंबकीय क्षेत्र प्रदिश (F) तयार होतो. या प्रदिशाचे घटक सापेक्षता सिद्धांताशी सुसंगत आहेत. हा प्रदिश प्रतिसममित आहे असे दिसून येते [⟶ विद्युत् गतिकी]. प्रदिश राशीचे स्वरूप कोणत्याही सहनिर्देशक पद्धतीकरिता निश्चल राहात असल्यामुळे लोरेन्ट्स रूपांतरणाकरिता मॅक्सवेल समीकरणे निश्चल राहतात, असा महत्त्वाचा निष्कर्ष मिळतो. या निष्कर्षाला सापेक्षता सिद्धांताचा पाया असेही मानले जाते.
मॅक्सवेल समीकरणात क्षेत्रामुळे निश्चित होणाऱ्या बिंदु विद्युत् भाराच्या गतिमार्गाचा प्रत्यक्ष उल्लेख मिळत नाही. ही उणीव लोरेन्ट्स यांच्या खाली दिलेल्या समीकरणाने दूर केली जाते.
F = q·E + q (v × B)
येथे v या वेगाने धावणाऱ्या q या बिंदू विद्युत् भारावर विद्युत् क्षेत्र E व चुंबकीय प्रवर्तन B यांमुळे निर्माण होणाऱ्या परिणामी प्रेरणेचे मूल्य मिळते. q हा विद्युत् भार खूप जास्त मूल्याच्या वेगाने जात असेल, तर अशा परिस्थितीत सापेक्षता परिणाम विचारात घ्यावे लागतात, कारण वरील समीकरण असापेक्षीय परिस्थितीकरिता सार्थ असते. याविषयीची अधिक माहिती ‘सापेक्षता सिद्धांत’ या नोंदीत दिलेली आहे. सूक्ष्म स्तरावरील विद्युत् भार गतीचे वर्णन करण्याकरिता (उदा., q हा अणूमधील इलेक्ट्रॉन असेल तर) विचारात घ्याव्या लागणाऱ्या पुंज परिणामाचे विवेचन ‘पुंज यामिकी’ या नोंदीमध्ये ‘पुंज विद्युत् गतिकी’ या शीर्षकाखाली दिलेले आहे.
अ व आ या दोन बिंदु विद्युत् भारांमध्ये मिळणारी प्रेरणा अ भाराने आ येथे निर्माण केलेले विद्युत् क्षेत्र व तेथील आ हा विद्युत् भार यांमध्ये प्रत्यक्षात कार्यान्वित होते, असे ⇨ क्षेत्र सिद्धांतावरून कळते [⟶ मूलकण]. निर्वातामध्ये कशालाच अस्तित्व नसल्यामुळे तेथे काहीच घडणे शक्य नाही या कल्पनेचा प्रभाव पडल्यामुळे क्षेत्रधारणेकरिता माध्यमाची आवश्यकता असते, असा निष्कर्ष काढण्यात आलेला होता. मॅक्सवेल समीकरणांवरून काही परिस्थितीत विद्युत् चुंबकीय ऊर्जेचे प्रसारण तरंगाच्या स्वरूपात होऊ शकते, हे स्पष्ट झाले. ध्वनितरंग आणि त्याच्या प्रसारणाला लागणारे माध्यम या दाखल्याचा उपयोग केल्यामुळे विद्युत् चुंबकीय तरंगाच्या प्रसारणाकरिता ‘ईथर’ [⟶ ईथर-२] नावाचे एक माध्यम गृहीत धरले जात होते. माध्यमाशिवाय तरंगांना अस्तित्व असू शकते ही कल्पनाच त्या काळच्या वैज्ञानिकाना असह्य वाटत होती.
मॅक्सवेल समीकरणांवरून विद्युत् भाराशिवाय विद्युत् क्षेत्र निर्माण होऊ शकते, हा काढण्यात आलेला निष्कर्ष आणि पृथ्वीच्या ईथरच्या सापेक्ष गती मोजण्याकरिता केलेल्या सर्व प्रयोगांची असफलता यांमुळे पदार्थ व विद्युत् भार यांच्याएवढेच क्षेत्रांना ‘अस्तित्व’ असते, ही संकल्पना आधुनिक भौतिकीमध्ये प्रचलित झाली आहे. ‘विमुक्त अवकाश’ ही कल्पना टाळण्याकरिता क्षेत्राचे ‘ईथर’ या कल्पित द्रायूमध्ये (वायु वा द्रवामध्ये) रूपांतरण करण्याची आवश्यकता आज वाटत नाही. रेडिओविज्ञानात ‘ईथर’ संज्ञेचा अजूनही काही वेळा उपयोग केला जातो पण येथे ‘ईथर’ म्हणजेच विद्युत् चुंबकीय क्षेत्र ही गोष्ट या संदर्भात लक्षात ठेवावयास पाहिजे.
एम. के. एस. एकक पद्धतीमध्ये ही संकल्पना जास्त सुस्पष्ट झालेली दिसते. कारण या पद्धतीत निर्वाताला काही विशिष्ट भौतिकी गुणधर्म (उदा., विद्युत् पार्यता) आहेत, असे मानून त्यांकरिता निश्चित स्थिरांक पण देण्यात आलेले आहेत.
रूढ भौतिकीतील अनेक सिद्धांत व मीमांसा (उदा., न्यूटन यांचे गतिकीशास्त्र) यांचे अस्तित्व आजच्या आधुनिक भौतिकीमध्ये आढळत नाही. मॅक्सवेल विद्युत् चुंबकीय समीकरणांचा या विधानाला एक महत्त्वाचा अपवाद म्हणून उल्लेख करता येतो. या समीकरणांत गणितीय सुलभतेसाठी थोडे किरकोळ फेरफार करून त्यांचा आधुनिक सैद्धांतिक भौतिकीत समावेश करण्यात आलेला आहे असे आढळते. [⟶ विद्युत् गतिकी].
संदर्भ : 1. Besancon, R. M., Ed., The Encyclopaedia of Physics, New York, 1966.
2. Condon, E. U.; Odishaw, H., Ed., Handbook of Physics, New York, 1967.
3. Corson, D. R.; Lorrain, P. Introduction to Electromagnetic Fields and Waves, San Francisco, 1962.
4. Cullwick, E. G. Fundamentals of Electromagnetism, London, 1944.
5. Purcell, E. M. Berkeley Physics Course Vol. II : Electricity and Magnetism, New York, 1965.
चिपळोणकर, व. त्रिं.