|
वरील सूत्रावरून |
कोज्या θ – ज्या θ ज्या θ कोज्या θ |
हा ⇨ निर्धारक मिळतो. |
त्याला रूपांतर निर्धारक म्हणतात व त्याचे मूल्य + १ असते.
अवकाशात आक्ष, आय, आझ आणि आक्ष’, आय’, आझ’ हे दोन जात्य कार्तीय संदर्भ-व्यूह असतील आणि आक्ष’, आय’ आझ’ हे अनुक्रमे आक्ष बरोबर a१, a२, a३, आय बरोबर β१, β२, β३ व आझ बरोबर g१, g२, g३ असे कोन करीत असतील, तर रूपांतर सुत्रे खालीलप्रमाणे असतात.
क्ष = क्ष’. कोज्या a१ + य’. कोज्या β१ + झ’. कोज्या g१,
य = क्ष’. कोज्या a२ + य’. कोज्या β२ + झ’. कोज्या g२,
झ = क्ष’. कोज्या a३ + य’. कोज्या β३ + झ’. कोज्या g३,
रूपांतर निर्धारक
|
कोज्या |
a१ |
कोज्या |
β१ |
कोज्या |
g१ |
|
|
|
|
कोज्या |
a२ |
कोज्या |
β२ |
कोज्या |
g२ |
= |
± |
१ |
|
कोज्या |
a३ |
कोज्या |
β३ |
कोज्या |
g३ |
|
|
|
हे सिद्ध करता येते. दोन्ही संदर्भ-व्यूह समदिग्वलित असतील, तर हे मूल्य + १ असते.
वरील रूपांतर सूत्रांचा दुसरा एक अर्थ लावता येतो. एकाच संदर्भ-व्यूहात (क्ष, य, झ) व (क्ष’, य’, झ‘) हे दोन बिंदूंचे सहनिर्देशक असतील, तर अवकाशातील बिंदूंमध्ये वरील सूत्रांनी एकासएक संगती लावता येते म्हणजेच अवकाशाचे पुन्हा अवकाशावरच चित्रण मिळते.
वरील सहनिर्देशक रूपांतर सुत्रे ही सहनिर्देशकामध्ये एक घातीय असल्याने कोणत्याही राशीचा घात सहनिर्देशक रूपांतराने बदलत नाही. दोन बिंदूंमधील अंतर : प१ व प२ या बिंदूंचे सहनिर्देशक दर्शविण्याकरिता १, २ हे पादांक वापरले आहेत. प्रतलावर कार्तीय सहनिर्देशक पद्धतीमध्ये प१, प२ ह्या अंतराकरिता खालील सूत्र मिळते (आ. २१):
(प१ प२)२ = (क्ष२–झ१)२ +य२–य१)२ + २ (क्ष२–क्ष१) (य२–य१). कोज्या ω.
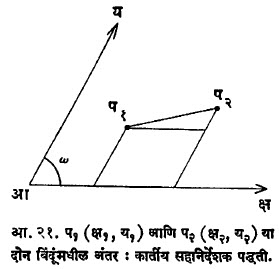
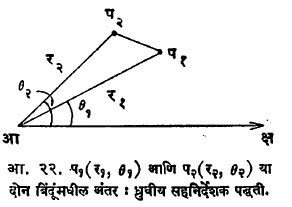
जात्य संदर्भ-व्यूह असेल, तर कोज्या ω = o ध्रुवीय सहनिर्देशक पद्धतीमध्ये खालील सूत्र मिळते (आ. २२) :
(प१ प२)२ = र१२+ र२२–२ र१ र२ . कोज्या (q२–q१) अवकाशामध्ये जात्य कार्तीय पद्धतीत (प१ प२)२ = (क्ष२–क्ष१)२+(य२–य१)२ + (झ२–झ१)२ असे सूत्र मिळते.
रेषेचा उतार व दोन रेषांमधील कोन : आक्ष, आय हा जात्य संदर्भ-व्यूह आहे. एखादी रेषा आक्ष बरोबर q कोन करीत असेल, तर स्प q याला त्या रेषेचा उतार म्हणतात. नेहमीच्या संकेताप्रमाणे अपसव्य परिभ्रमणाने मिळालेला कोन धन समजला जातो.
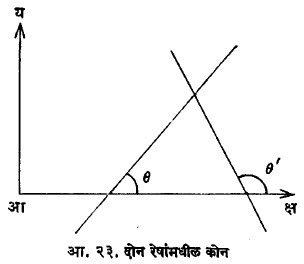
म= स्प q व म’= स्प q’ असे उतार असलेल्या दोन रेषा असतील, तर त्यांच्यामधील कोन (q’– q) हा खालील सूत्राने मिळतो (आ. २३) :
|
q’~q = स्प-१ |
( |
म’-म १+ म. म’ |
). |
या रेषा समांतर असतील, तर अर्थातच म = म’ आणि त्या लंब असतील तर म म’= -१.
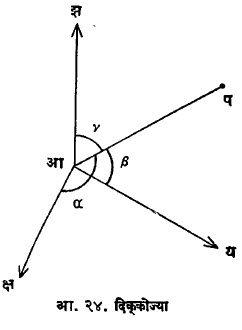
दिक्कोज्या : अवकाशामध्ये आप ही रेषा आक्ष, आय, आझ बरोबर α, β, γ असे कोन करीत असेल तर कोज्या α, कोज्या β, कोज्या g यांना त्या रेषेच्या दिक्कोज्या म्हणतात (आ. २४). त्यांचा परस्परसंबंध दाखविणारे सूत्र खालीलप्रमाणे आहे :
(कोज्या a)२+(कोज्या β)२+(कोज्या g)२ = १. (ब, भ, म) आणि (ब’, भ’, म’) या दिक्कोज्या असलेल्या दोन रेषांमधील कोन φ खालील सूत्राने मिळतो.
कोज्या φ= ब ब’+भ भ’ + म म’ त्या रेषा समांतर असल्यास ब = ब’, भ = भ’, म = म’ आणि लंब असल्यास बब’+ भ भ’+म म’=o.
रेषाखंड-विभाजक बिंदू : (क्ष१, य१, झ१) व (क्ष२, य२, झ२) हे अंत्यबिंदू असलेल्या रेषाखंडाला दिलेल्या गुणोत्तरामध्ये (म१ : म२) विभागणाऱ्या बिंदूचे सहनिर्देशक खालील सूत्रांनी मिळतात.
|
क्ष |
= |
म१ |
क्ष२ |
+ |
म२ |
क्ष१ |
, |
य |
= |
म१ |
य२ |
+ |
म२ |
य१ |
, |
झ |
= |
म१ |
झ२ |
+ |
म२ |
झ१ |
|
|
म१ |
+ |
म२ |
|
|
म१ |
+ |
म२ |
|
|
म१ |
+ |
म२ |
|
प्रतलीय वैश्लेषिक भूमिती : फ (क्ष, य) = ० या समीकरणाची ज्या बिंदूच्या सहनिर्देशकांनी सहज पूर्तता होते, त्या बिदूंचा संच म्हणजेच या समीकरणाने निदर्शित होणारा बिंदुपथ होय. उलटपक्षी चल (स्थानांतरण करणाऱ्या) बिंदूवर भूमितीय अटी लादल्या, तर येणारा बिंदुपथ हा एक वक्र होईल आणि या वक्रावरील प्रत्येक बिंदूचे सहनिर्देशक वक्राच्या समीकरणाची सहज पूर्तता करतील.
रेषा :संदर्भ-अक्ष आक्ष व आय यांची समीकरणे अनुक्रमे य = ० व क्ष = ० अशी होतील. क्ष = ग (स्थिरांक) आणि य = ग’ (स्थिरांक) या अनुक्रमे य – अक्षाला व क्ष – अक्षाला समांतर रेषा होतील.
रेषेच्या समीकरणाचे निरनिराळे प्रकार खाली दिल्याप्रमाणे असतात : (क्ष१, य१), (क्ष२, य२) या दोन बिंदूंतून जाणारी रेषा
|
क्ष – क्ष१ |
= |
य – य१ |
(दोन बिंदू प्रकार) …. (१) |
|
क्ष१ – क्ष२ |
य१ – य२ |
हे समीकरण खालील रूपातही मांडता येईल.
|
क्ष |
य |
१ |
= ० |
(निर्धारक प्रकार) |
……. |
(२) |
|
क्ष१ |
य१ |
१ |
||||
|
क्ष२ |
य२ |
१ |
वरील समीकरणावरून तीन बिंदू एकरेषीय असण्याची अट
|
क्ष१ |
य१ |
१ |
= ० |
अशी मांडता येईल. |
|
क्ष२ |
य२ |
१ |
||
|
क्ष३ |
य३ |
१ |
रेषा जर क्ष – अक्षावर व य – अक्षावर अनुक्रमे क आणि ख इतक्या लांब्याची खंड करीत असेल, तर तिचे समीकरण पुढीलप्रमाणे मिळते.
|
क्ष |
+ |
य |
= |
१ (खंड प्रकार) |
……. |
(३) |
|
क |
ख |
(क्ष१, य१) या बिंदूतून जाणारी व म उतार असेलेली रेषा खालील समीकरणाने मिळते.
य – य१= म (क्ष – क्ष१) (बिंदु-उतार प्रकार) . . . (४)
म उतार असलेली व य – अक्षावर ग इतक्या लांबीचा खंड करणारी रेषा खालील समीकरणाने मिळेल.
य = म क्ष + ग (उतार- खंड प्रकार) . . . . . . (५)
रेषेवर आदिबिंदूपासून काढलेला लंब प लांबीचा असेल व हा लंब क्ष – अक्षाशी a कोन करीत असेल, तर रेषेचे समीकरण खालीलप्रमाणे होईल.
क्ष. कोज्या a + य. ज्या a= प (लंब प्रकार) . . . . (६)
वरील सर्व समीकरणे एकघाती आहेत व याउलट कोणतेही एकघाती सीकरण हे रेषेचे समीकरण असते.
दिलेल्या बिंदूपासून रेषेवर काढलेल्या लंबाची लांबी रेषेच्या समीकरणाची वरील (६) या समीकरणाशी तुलना करून काढता येते.
कक्ष + खय + ग= ० या रेषेवर आदिबिंदूपासून काढलेला लंब
|
प |
= |
– ग |
या सूत्राने मिळतो. |
|
√ क२ + ख२ |
त्याच रेषेवर (क्ष१, य१) या बिंदूतून लंब टाकल्यास त्याची लांबी
|
कक्ष१ |
+ |
खय१ |
+ |
ग |
|
|
(क२ + ख२ ) १/२ |
|
||
या राशीने मिळते. त्याकरिता (क्ष१, य१) हा आदिबिंदू घेऊन रूपांतर सूत्रे वापरावीत.
कक्ष + खय + ग = ० व क’ क्ष +ख’ य’ + ग’= ० या दोन रेषांचा छेदनबिंदू ही दोन युगपत् समीकरणे सोडवून मिळतो.
वर्तुळ : वर्तुळाचा मध्यबिंदु (स, ह) असेल व त्रिज्या त असेल, तर दोन बिंदूंमधील अंतराच्या सूत्राचा उपयोग करून वर्तुळाचे समीकरण
(क्ष – स)२ + (य – ह) २ = त२ असे मिळेल.
क्ष२ + य२ + २ ट क्ष + २ छ य + ग = ० हे वर्तुळाचे सामान्य समीकरण होय. सामान्य समीकरण (क्ष + ट)२+(य + छ)२ = ट२ + छ२ – ग या स्वरुपात मांडल्यास वर्तुळाचा मध्य (- ट,- छ) व त्रिज्या √ ट२ + छ२ – ग आहे, हे स्पष्ट होईल. वर्तुळाचा मध्यबिंदू जर आदिबिंदू निवडला, तर वर्तुळाचे प्रमाणभूत समीकरण क्ष२ + य२ = त२असे मिळते.
शांकव : जात्य वृत्तीय शंकूचे निरनिराळ्या स्थितींतील प्रतलाने घेतलेले छेद या स्वरूपात हे वक्र प्रथम अभ्यासिले गेले पण प्रतलीय भूमितीमध्ये त्यांची व्याख्या अशी देतात :‘प्रतलावर ज्या बिंदुचे दिलेल्या स्थिर बिंदूपासूनचे (नाभिबिंदू) अंतर व दिलेल्या स्थिर रेषेपासूनचे (नियत रेषा) लंबांतर यांचे गुणोत्तर (विकेंद्रता) कायम (स्थिर) असते अशा बिंदूचा बिंदुपथ हा शांकव होय.’ (स, ह) हा नाभिबिंदू, ल क्ष + व य + श = o ही नियत रेषा व विकेंद्रता इ असेल, तर शांकवाचे समीकरण खालीलप्रमाणे होईल.
|
(क्ष – स)२ + (य – ह)२ = इ२ |
(ल क्ष + व य + श)२ |
|
ल२ + व२ |
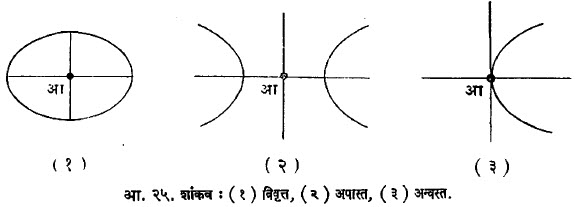
हे समीकरण कक्ष२ + २ जक्षय + खय२ + २ टक्ष + २ छय + ग =o या स्वरूपाचे आहे. म्हणजेच शांकवाचे समीकरण द्विघाती असते. शांकवाचे तीन मुख्य प्रकार आहेत :⇨ विवृत्त (दीर्घवर्तुळ विकेंद्रता इ < १ ), अपास्त (विकेंद्रता इ > १) आणि ⇨अन्वस्त (विकेंद्रता इ >१). ⇨ वर्तुळ हे विशिष्ट तऱ्हेचे विवृत्त व रेषायुग्म हे अपकृष्ट (सीमित रूपातील) शांकव मानता येईल. योग्य संदर्भ-व्यूह निवडून शांकवांची समीकरण सुलभ रूपात मिळू शकतात.
|
क्ष२ |
+ |
य२ |
= १ (विवृत्त), |
क्ष२ |
– |
य२ |
= १ (अपास्त), |
|
क२ |
ख२ |
क२ |
ख२ |
य२= ४ कक्ष (अन्वस्त) अशी या तीन शांकवांची प्रमाणभूत समीकरण आहेत (आ. २५).
आदिबिंदू बदलून व योग्य कोनीय परिभ्रमण करून कोणत्याही द्विघाती समीकरणाचे शांकवाच्या प्रमाणभूत समीकरणात रूपांतर करता येते म्हणून द्विघाती समीकरण शांकव निदर्शक असते, असे म्हणता येईल. सामान्य द्विघाती समीकरणात पाच स्वतंत्र प्रचल (विशिष्ट परिस्थितीत विशिष्ट स्थिर मूल्ये असणाऱ्या राशी) असतात, म्हणजेच पाच स्वतंत्र बिंदूंमधून एकच शांकव काढता येईल. शांकवाचे समीकरण कक्ष२ + २ जक्षय + खय२ + २ टक्ष + २ छय + ग = ० असल्यास खालीलप्रमाणे वर्गीकरण करता येते :
|
|
|
क |
ज |
ट |
|
|
∆ |
º |
ज |
ख |
छ |
घेऊन |
|
|
|
ट |
छ |
ग |
|
ज२ – कख< ० ∆≠ ० विवृत
ज२ – कख> ० ∆≠ ० अपास्त
ज२ – कख= ० ∆≠ ० अन्वस्त
|
∆ = ० असेल, तर ज२ – क ख |
£ > |
० |
असेल त्यानुसार दोन असत्, संपाती किंवा सत् रेषा मिळतील.
ज= ०, क = ख वर्तुळ.
गुणधर्म : अनंतस्थ बिंदू, अनंतस्थ रेषा, असत् बिंदू व असत् रेषा या संकल्पनांचा वापर केला, तर निरनिराळ्या शांकवांच्या गुणधर्मांत साधर्म्य पाहणे शक्य होते.
कोणतीही रेषा शांकवास दोन बिंदूमध्ये (सत् किंवा असत्) छेदते. कारण एक द्विघाती व दुसरे एकघाती अशी युगपत् समीकरणे
सोडविली, तर (क्ष, य) या युग्माची दोन मूल्ये मिळतात. हे दोन बिंदू सीमा स्थितीत एकमेकांशी जुळतात तेव्हा ती रेषा शांकवाची स्पर्शरेषा होते. दोन द्विघाती युगपत् समीकरणे (क्ष, य) ची चार मूल्ये देतात म्हणजेच दोन शांकव चार बिंदूंमध्ये (सत् किंवा असत्) छेदतात. दिलेल्या बिंदूपासून शांकवास दोन स्पर्श रेषा काढता येतात. हा बिंदू शांकवाच्या बाहेर असेल, तर स्पर्श रेषा सत् रेषा असतात, बिंदू शांकवावर असेल, तर त्या संपाती रेषा होतात आणि आत असेल, तर असत् रेषा असतात.
|
क्ष२ |
± |
य२ |
= |
१ |
|
क२ |
ख२ |
या शांकवांची आदिबिंदूमधून जाणारी प्रत्येक जीवा आदिबिंदूने दुभागली जाते म्हणून त्याला शांकवाचा केंद्रबिंदू म्हणतात. अन्वस्ताचा (य२ = ४ कक्ष) केंद्रबिंदू अनंतस्थ बिंदू असतो. विवृत व अपास्त यांना सकेंद्र शांकव म्हणतात.
|
सकेंद्र शांकवांना |
( |
क्ष२ क२ |
± |
य२ ख२ |
) |
= १ |
दोन सत् नाभिबिंदू ना, ना’ (± कइ, o) व दोन नियत रेषा
|
क्ष |
= |
± |
क |
|
इ |
असतात. अन्वस्तास (य२ = ४ कक्ष) एक नाभिबिंदू (क, ०) व एक नियत रेषा (क्ष =-क) असते. त्याचा दुसरा नाभिबिंदू अनंतस्थ बिंदू व दुसरी नियत रेषा अनंतस्थ रेषा असते. सकेंद्र शांकवांना केंद्रबिंदूमधून जाणारे दोन सममिती अक्ष असतात. अन्वस्तास एकच सममिती अक्ष असतो. शांकवाच्या नाभिबिंदूमधून काढलेल्या द्विगुण कोटिलंबास शांकवाचा नाभिलंब म्हणतात. प हा विवृत्तावरील कोणताही बिंदू आणि ना, ना’ नाभिबिंदू असतील, तर नाप + ना’ प = २ क दाखविता येते. हे सूत्र विवृत काढण्याकरिता बागेमध्ये माळी लोक वापरतात. शांकव जर अपास्त असेल, तर ना’ प~ नाप = २ क असे दाखविता येते.
विवृत हा परिसीमित वक्र आहे, तर अपास्त या शांकवाच्या दोन शाखा असून त्या अनंतापर्यंत पसरतात. अन्वस्ताची एकच शाखा असून ती अनंतापर्यंत पसरते. शांकवाला दोन अनंत स्पर्शिका (अनंतस्थ बिंदूतून काढलेल्या स्पर्शरेषा) असतात. विवृत्ताच्या अनंत स्पर्शिका असत् रेषा असतात, तर अपास्ताच्या अनंत स्पर्शिका सत् रेषा असतात. अन्वस्ताच्या दोन्हीही अनंत स्पर्शिका अनंतस्थ रेषेशी जुळतात. ज्या अपास्ताच्या अनंत स्पर्शिका परस्परांना लंब असतात, त्याला जात्य अपास्त म्हणतात.
शांकवांची प्रचलीय समीकरणे खालीलप्रमाणे आहेत :
क्ष = क. कोज्या q, य = क. ज्या q वर्तुळ
क्ष = क. कोज्या q, य = ख. ज्या q विवृत
क्ष = क. छे q , य = ख. स्पq अपास्त
क्ष = क. त२, य = २ क. त अन्वस्त
ध्रुवीय समीकरण : जात्य कार्तीय सहनिर्देशकामधील वक्राच्या कोणत्याही समीकरणात क्ष = र. कोज्या q, य = र. ज्या q अशी प्रतिष्ठापना केली, तर त्या वक्राचे (र, q) मधील ध्रुवीय समीकरण मिळते. क्ष कोज्या a+ य ज्या a= प या रेषेचे ध्रुवीय समीकरणर कोज्या (q – a) = प असे होईल. वर्तुळाच्या मध्यबिंदूचे ध्रुवीय सहनिर्देशक (r, a) असेल व त्रिज्या त असेल, तर वर्तुळाचे ध्रुवीय समीकरण र२ + r२ – २ र r. कोज्या (q–a ) त२ असे होईल. शांकवाचा नाभिबिंदू हा ध्रुवबिदू व त्यातून जाणारा अक्ष हा ध्रुवाक्ष निवडला, तर शांकवाचे ध्रुवीय समीकरण
|
ल |
= |
१ |
+ |
इ कोज्या q |
|
र |
अस मिळते.
|
[ |
ल |
= |
१ |
(नाभिलंब), |
इ |
= |
विकेंद्रता |
] |
|
२ |
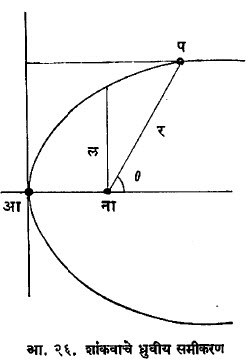
यामिकीमध्ये (वस्तूवर प्रेरणांची होणारी क्रिया व तीमुळे निर्माण होणारी गती यांचा अभ्यास करणाऱ्या शास्त्रामध्ये) ग्रह कक्षांच्या प्रश्नात हे समीकरण विशेष उपयोगी पडते.
वैश्लेषिक घ न भू मि ती :अवकाशात फ (क्ष,य,झ) = o हे पृष्ठाचे बैजिक निदर्शक असते [⟶ पृष्ठ]. अवकाशातील कोणताही वक्र दोन पृष्ठांचा छेद असल्याने हा वक्र दोन समीकरणांनी निश्चित होईल. खालील विवेचनात जात्य कार्तीय सहनिर्देशक वापरले आहेत.
प्रतल : एखाद्या प्रतलावर आदिबिंदूपासून टाकलेल्या लंबाची लांबी प असेल व तो अक्षांबरोबर a, b, g असे कोन करीत असेल, तर त्या प्रतलाचे समीकरण क्ष. कोज्या a+य. कोज्या b + झ. कोज्या g= प असे होईल. प्रतलाने अक्षांवर अनुक्रमे क, ख, ग इतक्या लांब्यांचे खंड केले असतील, तर त्याचे समीकरण
|
क्ष |
+ |
य |
+ |
झ |
= |
१ |
|
क |
ख |
ग |
असे होते. (क्ष१, य१, झ१), (क्ष२, य२, झ२) आणि (क्ष३, य३, झ३) या तीन बिदूंनी निश्चित केलेल्या प्रतलाचे समीकरण खालीलप्रमाणे मांडता येते :
|
क्ष |
य |
झ |
१ |
= ० |
|
क्ष१ |
य१ |
झ१ |
१ |
|
|
क्ष२ |
य२ |
झ२ |
१ |
|
|
क्ष३ |
य३ |
झ३ |
१ |
प्रतलीय भूमितीमध्ये रेपेचे समीकरण एकघाती असते, त्याचप्रमाणे अवकाशीय भूमितीमध्ये प्रतलाचे समीकरण एकघाती असते, हे वरील विवेचनातून दिसून येते. उलटपक्षी प्रत्येक एकघाती समीकरण हे प्रतलाचे निदर्शक असते, असे म्हणता येईल. आदिबिंदूपासून
कक्ष + खय + गझ + घ= o या प्रतलावर टाकलेल्या लंबाची लांबी
|
-घ |
या राशीने मिळते व (झ१, य१, झ१) |
|
√ क२ + ख२ + ग२ |
|
या बिंदूपासून टाकलेल्या लंबाची लांबी – |
कझ१ + खय१ + गझ१ + घ √ क२ + ख२ + ग२ |
या राशीने मिळते. प्रतलाला लंब असलेल्या रेपेच्या दिक्कोज्या
|
क |
, |
ख |
, |
ग |
असतात. |
|
√∑ क२ |
√∑ क२ |
√∑ क२ |
( ∑ क२ = क२ + ख२+ ग२). दोन प्रतलांमधील कोन त्यांना लंब असलेल्या रेषांमधील कोनाबरोबर असल्यामुळे कक्ष + खय + गझ + घ = ० आणि क’क्ष + ख’य + ग’झ + घ’=o या दोन प्रतलांमधील कोन पुढील सूत्राने मिळतो :
|
कोज्या f = |
कक’ + खख’ + गग’ √∑ क२ . √∑ क’२ |
अवकाशातील रेषा :अवकाशातील रेषा ही दोन प्रतलांचा छेद असल्यामुळे ती दोन एकघाती समीकरणांनी निश्चित होते. रेषा ही तीवरील एक बिंदू व दिशा यांनी निश्चित होत असल्यामुळे तिची समीकरणे खालीलप्रमाणेही मांडता येतात :
|
क्ष – क्ष१ |
= |
य – य१ |
= |
झ – झ१ |
यात (क्ष१, य१, झ१) |
|
ब |
भ |
म |
रेषेवरील एक बिंदू व ब, भ, म रेषेच्या दिक्कोज्या आहेत. ही रेषा कक्ष + खय + गझ + घ =o. अवकाशातील दोन रेषा समांतर असेल, तर कब + खभ + गम =o. अवकाशातील दोन रेषा प्रतलीय वा नैकप्रतलीय असतात. त्या नैकप्रतलीय असताना त्या दोन्ही ही रेषांना लंब असणारी रेषा त्यांच्यामधील लघुतम अंतर देते. रेषांची समीकरणे :
|
क्ष-क्ष१ |
= |
य-य१ |
= |
झ-झ१ |
|
क्ष-क्ष२ |
= |
य-य२ |
= |
झ-झ२ |
|
ब |
भ |
म |
ब’ |
भ’ |
म’ |
अशी असतील, तर त्यांच्यामधील लघुतम अंतर
|
क्ष१ – क्ष२ |
य१ – य२ |
झ१ – झ२ |
|
|
|
ब |
भ |
म |
¸√∑ (भम’ – भ’म)२ |
या सूत्राने मिळते. |
|
ब’ |
भ’ |
म’ |
|
|
रेषा प्रतलीय असताना त्यांच्यामधील लघूतम अंतर शून्य असते. म्हणजेच वरील सूत्रातील अंश शून्य असतो.
|
|
क्ष१ – क्ष२ |
य१ – य२ |
झ१ – झ२ |
|
|
|
|
ब |
भ |
म |
= ० |
ही दोन रेषा प्रतलीय असण्याकरिता अट होईल. |
|
|
ब’ |
भ’ |
म’ |
|
|
द्विघाती पृष्ठ (शांकवज) :कक्ष२ + खय२ + गझ२ + २ चझय + २ छझक्ष + २ जक्षय + २ टक्ष + २ ठय + २ डझ + ढ = o या समीकरणाने मिळणारा बिंदुपथ हा शांकवज असतो. अवकाशातील कोणतीही रेषा या शांकवजास दोन बिंदूंमध्ये छेदते. गोल हा द्विघाती शांकवजाचा नेहमीचा परिचयातील नमुना आहे. शांकवजाचा प्रतल छेद हा शांकव असतो. शांकवज गोल असेल, तर त्याचा प्रतल छेद वर्तुळ असतो. शांकवजाचे समांतर प्रकल छेद हे सरूप व समस्थित असे शांकव असतात. या शांकवांची केंद्रे एकरेषीय असतात व त्यारेषेला शांकवजाचा व्यास म्हणतात. शांकवजाचे व्यास या एकबिंदूगामी रेषा असतात व या बिंदूस शांकवजाचे केंद्र म्हणतात (केंद्रबिंदू काही वीळा अनंतस्थ बिंदूही असू शकेल). शांकवजाला एकमेकांस लंब असणारी तीन सममित प्रतले असतात व त्यांना शांकवजाची प्रमुख प्रतले म्हणतात. या प्रतलांच्या परस्पर छेद रेषा ही सममित अक्ष असतात, म्हणून त्यांना प्रमुख अक्ष म्हणतात.
शांकवजाच्या सामान्य समीकरणामध्ये नऊ स्वतंत्र प्रचल आढळतात. म्हणजेच सामान्यपणे नऊ बिंदूंमधून एकच शांकवज काढता येईल. शांकवजाचे केंद्र परिमित असेल, तर तीन प्रकारचे शांकवज संभवतात :
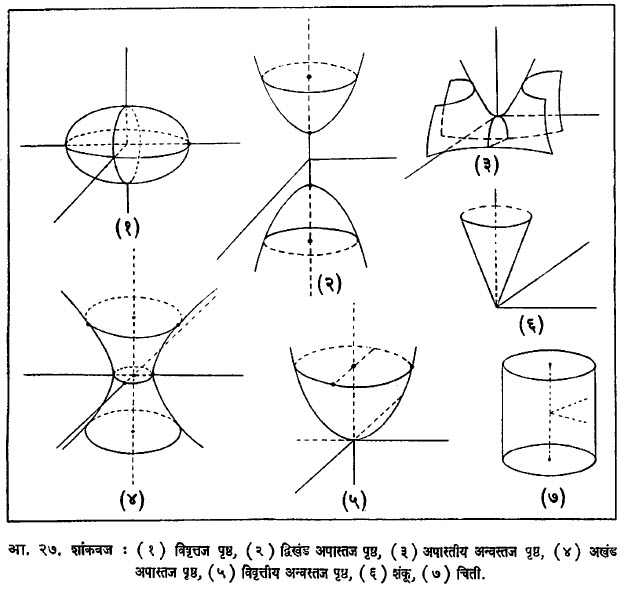
(१) विवृत्तज पृष्ठ (यामध्ये प्रमुख प्रतल छेद विवृत्त असतात), (२) अखंड अपास्तज पृष्ठ (यामध्ये एक प्रमुख प्रतल छेद विवृत्त व दोन अपास्त असतात), (३) द्विखंड अपास्तज पृष्ठ (यामध्ये एक प्रमुख प्रतल असत् विवृत्त व दोन अपास्त असतात).
शांकवजाचे केंद्र जर अनंतस्थ बिंदू असेल, तर तीनपैकी दोनच प्रमुख प्रतल छेद परिमित असतात. हे दोन्हीही प्रतल छेद अन्वस्त असतात. हा शांकवज विवृत्तीय अन्वस्तज पृष्ठ किंवा अपास्तीय अन्वस्तज पृष्ठ असतो. शांकवजाचे प्रमुख अक्ष शून्य लांबीचे असतील, तर तो शांकवज शंकू होतो व केंद्र जर अनंतस्थ बिंदू असेल तर तो शंकू चिती होतो.
शांकवजाचे प्रमुख अक्ष हे संदर्भ-अक्ष म्हणून निवडल्यास शांकवजांची खालील प्रमाणभूत समीकरणे मिळतात.
|
(१) |
क्ष२ |
+ |
य२ |
+ |
झ२ |
= १ |
विवृत्तज पृष्ठ |
|
|||
|
क२ |
ख२ |
ग२ |
|
||||||||
|
(२) |
क्ष२ |
+ |
य२ |
+ |
झ२ |
= १ |
अखंड अपास्तज पृष्ठ |
||||
|
क२ |
ख२ |
ग२ |
|||||||||
|
(३) |
क्ष२ |
+ |
य२ |
+ |
झ२ |
= १ |
द्विखंड अपास्तज पृष्ठ |
||||
|
क२ |
ख२ |
ग२ |
|||||||||
|
(४) |
क्ष२ |
+ |
य२ |
=ग झ |
विवृत्तीय अन्वस्तज पृष्ठ |
||||||
|
क२ |
ख२ |
||||||||||
|
(५) |
क्ष२ |
+ |
य२ |
=ग झ |
अपास्तीय अन्वस्तज पृष्ठ |
||||||
|
(६) |
क्ष२ |
+ |
य२ |
+ |
झ२ |
= त२ |
गोल |
|
|||
|
(७) |
क्ष२ |
+ |
य२ |
+ |
झ२ |
= ० |
शंकू |
|
|||
|
क२ |
ख२ |
ग२ |
|
||||||||
|
(८) |
क्ष२ |
+ |
य२ |
= १ |
चिती |
|
क२ |
ख२ |
वरील शांकवज एखाद्या जनक वक्राने रेखाटलेले (एखाद्या) रेषेभोवती-अक्षाभोवती-वक्र फिरविला असता तयार होणारे) पृष्ठ मानता येतात.
|
(१) |
क्ष२ |
+ |
य२ |
+ |
झ२ |
= १ |
विवृत्तज पृष्ठ |
|
क२ |
ख२ |
ग२ |
|
क्ष२ |
+ |
य२ |
= १ |
– |
प२ |
, झ = प |
|
क२ |
ख२ |
ग२ |
या वक्राने प ची मूल्ये – ग पासून + ग पर्यंत घेतली असता रेखाटली जाते.
|
(२) |
क्ष२ |
+ |
य२ |
= १ |
+ |
प२ |
, झ = प |
|
क२ |
ख२ |
ग२ |
हा अखंड अपास्तज पृष्ठाचा जनक वक्र म्हणता येईल.
|
(३) |
क्ष२ |
+ |
य२ |
+ |
प२ |
– १ |
, झ = प |
|
क२ |
ख२ |
ग२ |
हा द्विखंड अपास्तज पृष्ठाचा जनक वक्र होय.
|
(४) |
क्ष२ |
+ |
य२ |
= |
ग, प, झ |
= |
प |
|
क२ |
ख२ |
हे अनुक्रमे विवृत्तीय अन्वस्तज पृष्ठ व अपास्तीय अन्वस्तज पृष्ठ यांचे जनक वक्र होत.
शांकवजाचा प्रतल छेद दोनच दिशांना वर्तुळ असतो. यांना समांतर असणाऱ्या स्पर्श-प्रतलांच्या स्पर्शबिंदूंना शून्य-वृत्तके (शून्य त्रिज्या असलेली वर्तुळ) असे म्हणतात. शांकवजाचा नाभिबिंदू आणि नियम रेषा यांची व्याख्या अशी आहे : प हा जर शांकवजावरील कोणताही बिंदू घेतला, तर प चे नाभिबिंदूपासूनचे अंतर आणि प चे नियत रेषेपासून वर्तुळ छेदांना समांतर दिशेने मोजलेले अंतर यांचे गुणोत्तर कायम असते. ज्या शांकवावरील प्रत्येक बिंदू हा शांकवजाचा नाभिबिंदू असतो त्यास नाभीय शांकव म्हणतात. शांकवजास दोन सत् व एक असत् नाभीय शांकव असतात.
शांकवज हे रेषाजनित पृष्ठ आहे. शांकवजाच्या प्रत्येक बिंदूमधून दोन जनक रेषा जातात (सत् किंवा असत्) आणि या दोन रेषांनी निश्चित केलेले प्रतल हे शांकवजाचे स्पर्श-प्रतल असते. शांकवजावर दोन जनक रेषा प्रणाली असतात. एकाच प्रणालीतील दोन जनक रेषा एकमेकींस कधीच छेदत नाहीत पण एका प्रणालीतील रेषा दुसऱ्या
प्रणालीतील प्रत्येक रेषेस छेदते. एका प्रणालीच्या तीन रेषा दिल्यास शांकवज निश्चित होती. म्हणजे शांकवज हे तीन नैकप्रतलीय रेषांना छेदणाऱ्या रेषांनी रेखाटलेले पृष्ठ असे म्हणता येईल. शांकवजाची प्रमाणभूत समीकरणे घेतली, तर असे दिसून येते की, विवृत्तज पृष्ठ, द्विखंड अपास्तज पृष्ठ आण विवृत्तीय अन्वस्तज पृष्ठ यांच्या जनक रेषा या असत् रेषा आहेत परंतु
|
क्ष२ |
+ |
य२ |
– |
झ२ |
= |
१ |
|
क२ |
ख२ |
ग२ |
या अखंड अपास्तज पृष्ठाच्या जनक रेषा खालील समीकरणांनी मिळतील.
|
( |
क्ष |
– |
झ |
) |
= ट |
( |
१ – |
य |
) |
ट |
( |
क्ष |
+ |
झ |
) |
= |
( |
१ + |
य |
) |
|
क |
ग |
ख |
क |
ग |
ख |
ही एक प्रणाली आणि
|
( |
क्ष |
– |
झ |
) |
= ठ |
( |
१ + |
य |
) |
ठ |
( |
क्ष |
+ |
झ |
) |
= |
( |
१ – |
य |
) |
|
क |
ग |
ख |
क |
ग |
ख |
ही दुसरी प्रणाली. (येथे ट व ठ हे प्रचल आहेत).
|
क्ष२ |
– |
य२ |
= |
गझ |
|
क२ |
ख२ |
या अन्वस्तज पृष्ठाच्या जनक रेषा खालील समीकरणांनी मिळतात.
|
( |
क्ष |
+ |
य |
) |
= |
ट |
ट |
( |
क्ष |
– |
य |
) |
= |
ग झ |
|
क |
ख |
क |
ख |
ही एक प्रणाली व
|
( |
क्ष |
– |
य |
) |
= |
ठ |
ठ |
( |
क्ष |
+ |
य |
) |
= |
ग झ |
|
क |
ख |
क |
ख |
ही दुसरी प्रणाली.
शंकू आणि चिती हे विशिष्ट तऱ्हेचे रेषाजनित शांकवज आहेत. शंकूच्या सर्व जनक रेषा एकसंपाती असतात आणि चितीच्या जनक रेषा तिच्या मध्य अक्षास समांतर असतात. ही दोन पृष्ठे विकसनीय पृष्ठाची (जेपृष्ठ न ताणता अथवा आकुंचित न करता एखाद्या प्रतलावर विकसित करता येते म्हणजे पसरता येते अशा पृष्ठाची) उदाहरणे आहेत. [⟶ भ्रमण जन्य पृष्टे व घनाकृति].
बहुमितीय भूमिती आपल्या नेहमीच्या परिचयातील द्विमितीय व त्रिमितीय अवकाशातील संकल्पनांचा विस्तार करून बहुमितीय अवकाशातील भूमितीची मांडणी करण्यात येते. प्रथम चतुर्मितीय अवकाशाची मांडणी कशी केली जाते ते पुढील विवेचनात दर्शविले आहे.
चतुर्मितीय अवकाश : त्रिमितीय अवकाश सुपरिचित आहे. त्यातील कोणत्याही बिंदूचे स्थान निश्चित करण्यासाठी क्ष, य, झ अक्षांची मदत घेण्यात येते. आता अशी कल्पना करू की, क हा त्रिमितीय अवकाशात नसलेला असा आणखी एक अक्ष आहे (उदा., काल). या चार अक्षांनी चतुर्मितीय अवकाशातील कोणत्याही बिंदूची स्थान निश्चिती करता येईल. अर्थात प्रत्यक्ष आकृती काढून हे चार अक्ष किंवा चतुर्मितीय अवकाशातील बिंदू दाखविणे शक्य होणार
नाही, हे उघड आहे. त्रिमितीमध्ये क्ष = ०, झ = ० ही संदर्भ प्रतले असतात त्याच धर्तीवर चतुर्मितीमध्ये क्ष = ०, य = ०, झ = ०, क = ० अशी चार अधिप्रतले असतील. त्रिमितीमध्ये एखादा चल वस्तुकण क १ समयी (काली) (क्ष१, य१, झ१) या ठिकाणी असून क२ समयी (क्ष२, य२, झ२) या ठिकाणी असेल, तर हेच चतुर्मितीमध्ये (क्ष१, य१, झ१, क१) आणि (क्ष२, य२, झ२, क२) या दोन बिंदूंना जोडणाऱ्या वक्राने दाखविता येईल (अर्थात आकृती कल्पनेतच रेखाटावी लागेल). आपल्याला परिचित असलेला त्रिमितीय अवकाश हा अशा चतुर्मितीय अवकाशाचा उप-अवकाश होय, जसा द्विमितीय (एक प्रतलीय) अवकाश हा त्रिमितीय अवकाशाचा उप-अवकाश आहे. त्रिमितीय अवकाशात फ (क्ष, य, झ)=० या समीकरणाने एक पृष्ठ मिळते तसे चतुर्मिती अवकाशात फ (क्ष, य, झ, क)= ०, या समीकरणाने एक अधिपृष्ठ मिळेल. अ१, क्ष + अ२ य + अ३ झ + अ४ क + अ५ = ० अशा कोणत्याही एकघाती समीकरणाने अधिप्रतल मिळेल. दोन अधिपृष्ठे एका पृष्टात व दोन अधिप्रतले एका प्रतलात छेदतील, तीन अधिप्रतले एका रेषेत व चार अधिप्रतले एका बिंदूत छेदतील. ट या प्रचला पदांत मांडलेली क्ष = फ१ (ट),य = फ२ (ट), झ = फ२ (ट), क = फ४ (ट) ही समीकरणे चतुर्मितीमध्ये वक्र दर्शवितात. चार बिंदू किंवा एक प्रतल आणि एक बिंदू किंवा दोन नैकप्रतलीय रेषा यांनी एक अधिप्रतल निश्चित होते. बिंदूला रेषेवर एक मुक्तता मात्रा (स्थान निश्चितीसाठी लागणाऱ्या चलांची संख्या) असते. त्याला प्रतलावर दोन, अधिप्रतलावर तीन व अवकाशात (चतुर्मितीय) चार मुक्तता मात्रा असतात. रेषेला एक मिती, प्रतलाला दोन व अधिप्रतलाला तीन मिती असतात, असे म्हणतात.
प-मितीय अवकाश :वरील संकल्पनांचा विस्तार करून प-मितीय अवकाशाची मांडणी करता येते. बिंदू, रेषा, प्रतल, अधिप्रतल (किंवा ३-पुलीन),…, प-पुलीन हे अनुक्रमे एक, दोन, तीन, चार,…, (प + १) बिंदूंनी निश्चित केलेले प्रदेश आहेत आणि त्यांच्या मिती शून्य, एक, दोन, तीन,…, प आहेत. प-पुलीन सर्व बिंदू समावेशक आहे असे गृहीत मानले आहे. प-पुलिनाकरिता अप हे चिन्ह वापरतात. पुलिनास रेषीय अवकाश असेही म्हणतात. म-पुलीन निश्चित करण्याकरिता (म+१) बिंदू आवश्यक असतात आणि न-मितीय अवकाशात एक बिंदू निश्चित करण्याकरिता न अटी पुऱ्या व्हाव्या लागतात. म्हणून प-मितीय अवकाशात म-पुलीन निश्चित होण्याकरिता (म+१) (प-म) अटींची जरूरी भासते. म्हणजेच प-मितीय अवकाशातील म-पुलिनाच्या मुक्तता मात्रा (म+१) (प-म) असतात. याला म-पुलिनाचा स्थिरांक म्हणतात.
म > क असताना जर म-पुलीन आणि क-पुलीन यांना समान असणारा पुलीन र-पुलीन असेल, तर म-पुलीन आणि क-पुलीन यांची संपतन कोटी
|
र |
+ |
१ |
|
क |
+ |
१ |
आहे असे म्हणतात. अर्थात क-पुलीन म-पुलीनात समाविष्ट असेल, तर संपतन कोटी १ होईल व एकही बिंदू समान नसल्यास शून्य होईल. (प+१) बिंदूंनी तयार होणारी आकृती तसेच त्यांनी निश्चित केलेल्या रेषा, प्रतले वगैरे यांस प-मितीय समुच्चय म्हणतात व तो सप+१ या चिन्हाने दर्शवितात. यामध्ये रेषा, प्रतले,… वगैरे समुच्चयाच्या एक, दोन,… मितींच्या परिघी होत व बिंदू हे शिरोबिंदू होत. सप+१ ला र मितीच्या परिधी असतात.
|
( |
प+१ |
) |
|
र+१ |
४-पुलिनामध्ये दोन अधिप्रतले सर्वसाधारणपणे एका प्रतलात छेदतात. जर त्यांमध्ये एकही बिंदू समान नसेल, तर त्या अधिप्रतलांना समांतर अधिप्रतले म्हणतात. दोन अधिप्रतलांना छेदणारे तिसरे अधिप्रतल घेतल्यास दोन समांतर प्रतले मिळतात. दोन प्रतले एकाच अधिप्रतलात नसतील व त्यांना एकही बिंदू समान नसेल, तर ती प्रतले अर्धसमांतर आहेत असे म्हणतात. एखादा म-पुलीन व एखादा क-पुलीन (म ≥ क) जर एकाच (म + क – र)-पुलिनात समाविष्ट असतील (आणि म्हणून सर्वसाधारणपणे एका र-पुलिनात छेदताल) व त्यामध्ये एकही बिंदू समान नसेल, तर त्या पुलिनांना
|
र |
+ |
१ |
समांतर म्हणतात. |
|
क |
|||
संपूर्ण समांतरता कोणत्याही अवकाशात शक्य असते परंतु आंशिक समांतरतेकरिता काही किमान मितीचा अवकाश लागतो. जसे अर्ध समांतरतेकरिता ४-मितीय अवकाशाची जरूरी असते.
|
१ |
समांतरतेकरिता ६-मितीय अवकाशाची जरूरी असते. |
|
३ |
प-मितीय अवकाशात प्रतल व त्रिमितीय अवकाशातील समांतरभुज चौकोन किंवा समांतर पृष्ठक यांना सदृश आकृती म्हणजे (प – १) – पुलिनांच्या समांतर युग्मांनी बंधित असणारी आकृती होय.
प-मिती अवकाशात समांतर आणि लंब या संकल्पनांची मांडणी प-मितीय सदिशांचा [⟶ सदिश अवकाश] उपयोग करून खालीलप्रमाणे करता येईल.
क्ष = (क्ष१, क्ष२,….., क्षप) हा प-मितीय अवकाशातील सदिश होय. क्ष आणि य या दोन सदिशांमधील कोन खालील सूत्राने मिळेल.
|
कोज्या (क्ष, य) |
= |
क्ष . य |
|
lक्षl lयl |
अर्थातच
|
क्ष.य |
= |
प |
क्षरयर |
आणि |
lक्षl |
= |
प |
क्षर२ |
१/२ |
|
∑ |
∑ |
|
|||||||
|
र=१ |
र=१ |
|
म्हणून क्ष. य = ० असेल, तर क्ष व य लंब आहेत. जर य = द क्ष (द अदिश) तर क्ष व य समांतर आहेत असे म्हणता येईल. यावरून प-मितीय अवकाशात दोन रेषा समांतर आहेत किंवा लंब आहेत ही विधाने सार्थ आहेत, हे दिसून येईल.
आ बिंदूतून आक१, आक२…., आकप या कडा घेतल्या [कोणत्याही र कडा एकाच (र – १) –पुलिनात नाहीत हे गृहीत धरले आहे] आणि क१ मधून आक२, आक३, …., आकपयांनी निश्चित केलेल्या (प – १)–पुलिनात समांतर (प – १)-पुलीन घेतल्यास तो निसंदिग्धपणे निश्चित होईल. अशा तऱ्हेने क२, क३, ……, क प या सर्व बिंदूंतून (प – १)-पुलीन घेतल्यास आपल्याला २प (प – १) -पुलिनांनी बंधित आकृती मिळेल. या आकृतीला समांतर प्रदेश म्हणतात. कडा एकमेर्कीस लंब असतील, तर त्या आकृतीला आयताकारी समांतर प्रदेश म्हणतात. आ बिंदूतून एकमेकींस लंब अशा प रेषा घेतल्या आहेत. यांपैकी क रेषांनी एक क-पुलीन निश्चित होतो व उर्वरित रेषांनी (प – क) -पुलीन निश्चित होतो. यो दोन पुलिनांना संपूर्ण लंब पुलीन म्हणतात. एकाच ख-पुलिनाला संपूर्ण लंब असलेले सर्व क-पुलीन एकाच (क + ख)-पुलिनात समाविष्ट असतील, तर ते संपूर्ण समांतर असतात. जर दोन रेषीय अवकाश संपूर्ण लंब असतील, तर एका अवकाशातील प्रत्येक रेषीय उप-अवकाश दुसऱ्या अवकाशातील प्रत्येक रेषीय उप-अवकाशाला संपूर्ण लंब असतो.
प-मितीय प्रक्षेपीय भूमितीमध्ये क्ष बिंदू प + १ संख्यांच्या गुणोत्तरांनी निदर्शित केला जातो म्हणजेच क्ष२, क्ष१,…, क्षप या सहनिर्देशकांनी निदर्शित केला जातो. म्हणून त्याची मुक्तता मात्रा प असते. रेषा खालील समीकरणांनी निदर्शित होतेःr क्षर = ट क्ष’र + ठ क्षर’’, (र = ०, १, …., प) या ठिकाणी
|
ट |
प्रचल आहे. |
|
ठ |
क्ष’ व क्ष’’ हे दोन स्थिर बिंदू आहेत आणि ते ट = ० आणि ठ = ० यांनी मिळतात. तसेच r हा प्रमाणतेचा गुणक आहे. प्रतलाची समीकरणे खालीलप्रमाणे होतील :
r क्षर = ट क्षर’ + ठ क्षर ’’ +ड क्षर ’’’, (र = o, १, ……..,प) हे प्रतल क्ष’, क्ष’’, क्ष’’’ हे बिंदू समाविष्ट करील.
rक्षर = ट१ क्षर (१) + ट२ क्षर (२) +ट३ क्षर (३) +….+ टत क्षर (त), (र = o , १, …… प)
या समीकरणांनी एक त–पुलीन निदर्शित होईल. अधिप्रतलाचे समीकरण खालीलप्रमाणे मांडता येईल :
|
क्ष० क्ष१ ………….क्षप |
|
|
क्ष०(१) क्ष१(१)…………. क्षप(१) |
= ० |
|
……………………………….… |
|
|
क्ष०(प) क्ष१(प)……….क्षप(प) |
|
अधिप्रतलाचे समीकरण असेही होऊ शकेल :
|
प |
लर |
क्षर |
= |
० |
|
∑ |
||||
|
र=० |
|
क्ष०(१) |
… |
क्षप(१) |
|
… |
… |
…. |
|
क्ष०(प) |
… |
क्षप(प) |
हा आव्यूह प कोटीचा असेल, तर क्ष(१), क्ष(२),……., क्ष(प) हे प बिंदू रेषीय निरवलंबित असतील [⟶ आव्यूह सिद्धांत].
कoº (१,०,०,……०), क१ º (०,१,०,०,……,०), ……., कप º (०, ०,…..,१) या प + १ बिंदूंना संदर्भ बिंदू म्हणतात. या बिंदूंनी तयार होणाऱ्या समुच्चयाला मूल समुच्चय म्हणतात. क्षo= ०, क्ष१ =o,…., क्षप =o ही मूल अधिप्रलांची समीकरणे होत.
मानीय भूमितीमध्ये (आ आदिबिंदू व सर्व अक्ष एकमेकांस लंब) क बिंदूचे सहनिर्देशक (क्ष१,क्ष२,…….,क्षप) असल्यास क चे आदिबिंदूपासूनचे अंतर खालील सूत्राने मिळेल :
|
|
प |
|
|
आक२ = |
∑ |
क्षर२ |
|
|
र =१ |
|
तसेच क (क्ष१, क्ष२,……., क्षप) आणि ख (य१, य२,……,यप) या बिंदूंमधील अंतर
|
कख२ |
= |
प |
(क्षर-यर)२ |
|
∑ |
|||
|
र =१ |
या सूत्राने मिळेल.
आकर (र = १, २,…….,प) हे अक्ष असतील, तर कोन कर आक = qर यांना आक चे दिक् कोन व त्यांच्या कोज्यांना दिक्कोज्या म्हणतात व दिक्कोज्यांमधील संबंधांचे खालील सूत्र मिळते :
|
प |
(कोज्या qर)२= १ |
|
∑ |
|
|
र =१ |
आक’ रेषेच्या दिक्कोज्या कोज्या qर’ असतील, तर आक व आक’ यांच्यामधील कोनाकरिता (f) खीलील सूत्र तयार होईल :
|
|
प |
कोज्या qर. कोज्या qर ’ |
|
कोज्या f = |
∑ |
|
|
|
र =१ |
(प – १)–पुलिनाची दिक् स्थिती त्याला काढलेल्या लंबाने निश्चित होते व (प – १) –पुलिनाचे दिक् कोन म्हणजे त्याच्या लंबाचे दिक् कोन होत. आदिबिंदूतून काढलेला लंब जर ल लांबीचा असेल व त्याचे दिक् कोन qर असतील, तर त्या पुलिनाचे समीकरण खालीलप्रमाणे होईल.
|
प |
क्षर कोज्या qर = ल |
|
∑ |
|
|
र =१ |
रेषा प – १ ही (प – १) –पुलिनांनी निश्चित होते म्हणून ती प – १ रेषीय समीकरणांनी निदर्शित करता येते. रेषेची समीकरणे अशी होतील : क्ष२= बर + अ कोज्या qर येथे ब (ब१, ब२, ………, बप) रेषेवरील एक स्थिर बिंदू, अ हे ब आणि क्ष या बिंदूमधील अंतर, कोज्या qर रेषेच्या दिक्कोज्या आहेत. एका स्थिर बिंदूपासून समान अंतरावर असणाऱ्या बिंदूंचा बिंदूपथ म्हणजे (प – १) –मितीय अधिगोल होय. ब केंद्र आणि त त्रिज्या असलेल्या अधिगोलाचे समीकरण पुढीलप्रमाणे होईल.
|
प |
(क्ष२ – बर)२र =त२ |
|
∑ |
|
|
र =१ |
अप मधील म – पुलीन (प –१) –मितीय अधिगोलात (म –१).-मितीय अधिगोलास छेदील.
प्रतलावरील बहुभुजाकृतीला किंवा त्रिमितीमधील बहुपृष्ठाकाला सदृश प– मितीय अवकाशातील आकृती म्हणजे अधिप्रतलांनी तयार झालेली आकृती होय. अशा आकृतीला बहुप्रदेश म्हणतात. निकटवर्ती अधिप्रतले प्रत्येक (प –२) –मितीय परिधीमध्ये छेदतात. म किंवा त्याहून अधिक अधिप्रतले (प – म) –मितीय परिधीमध्ये छेदतात. प किंवा त्याहून अधिक अधिप्रतले ज्या बिंदूंमध्ये छेदतात त्या बिंदूंना बहुप्रदेशाचे कोन–बिंदू म्हणतात. सर्वांत साधा बहुप्रदेश म्हणजे समुच्चय सप + १ हा बहुप्रदेश प + अधिप्रतलांनी तयार होतो. हा बहुप्रदेश त्रिकोण किंवा चतुःपृष्ठक यांना सदृश असतो. तर ने र –मितीय परिधींची संख्या दर्शविली, तर पुढील सूत्र मिळते :
१- तo + त१ …….+ (-१)प तप-१ + (-१)प+१ = o ऑयलर यांच्या त्रिमितीय अवकाशातील सूत्राचा हा प – मितीय अवकाशातील विस्तार होय (त्रिमितीय अवकाशात तo त१ + त२ = २). जर बहुप्रदेश त्याच्या प्रत्येक (प – १) परिधीच्या एकाच बाजूला असेल, तर त्याला बहिर्वक्र बहुप्रदेश म्हणतात. जर बहुप्रदेश बहिर्वक्र असेल, तर त्याची प्रत्येक परिधी बहिर्वक्र असते.
वर्णनात्मक भूमिती
वर्णनात्मक भूमितीमध्ये अवकाशातील वस्तू प्रतलावरील आकृतीने कशा निदर्शित कराव्यात यासंबंधीच्या गणितीय व आलेखीय रीतींचा व तंत्रांचा अभ्यास करतात. चित्रकारही धन वस्तूंचे प्रतलावर चित्रण करतो पण वर्णनात्मक भूमितीमध्ये प्रतलचित्रण असे हवे की, त्यावरून त्या वस्तूची नीट कल्पना तर आली पाहिजेच, पण त्या वस्तूचे इतर वस्तूंमधील सापेक्ष स्थान, तिचा आकार, त्या वस्तूच्या निरनिराळ्या भागांचा एकमेकांशी संबंध असे सूक्ष्म प्रश्नही यथार्थ तऱ्हेने सोडवता आले पाहिजेत. वर्णनात्मक भूमिती ही सर्व तऱ्हेच्या वास्तुशिल्पीय व यांत्रिक आरेखनाचा सैद्धांतिक पाया आहे [⟶ आरेखन, अभियांत्रिकीय]. वास्तुरचनाकार व यंत्रज्ञ यांना वास्तूसंबंधीची यथार्थ कल्पना देण्याकरिता वास्तु-अभिकल्पकाचे (वास्तूचा आराखडा तयार करणाऱ्या तज्ञाचे) हे आरेखनशास्त्र हेच साधन आहे. या भूमितीला वास्तुशिल्पज्ञांचे भाषा असे यथार्थपणे म्हणतात.
या भूमितीमध्ये अवकाशातील वस्तूसंबंधीचा कोणताही प्रश्न घेतल्यास तो सोडविण्याचे तीन टप्पे आहेत : (१) अवकाशातील वस्तूचे प्रतलावर चित्रण, (२) या प्रतलावरील आकृतीद्वारे प्रश्नाचा अभ्यास करणे आणि (३) जो निष्कर्ष निघेल तो मूळ वस्तूशी संबंधित करून त्याचा योग्य अर्थ लावणे. हे साधण्याकरिता अशी एखादी निश्चित योजना हवी की, जिच्यामुळे अवकाशातील वस्तू व त्यांचे प्रतलचित्रण यांचे परस्परसंबंध निःसंदिग्धपणे प्रस्थापित झाले पाहिजेत. याकरिता जी योजना आज सर्वत्र उपयोगात आणली जाते. ती अठराव्या शतकाच्या शेवटी गास्पार माँझ या फ्रेंच गणितज्ञांनी शोधून काढली. माँझ हे फ्रेंच सरकारचे वास्तु-अभिकल्पक म्हणून काम करीत असताना त्यांच्याकडे एका संकल्पित किल्ल्याचा नकाशा तयार करण्याचे काम आले, हे काम बऱ्याच दीर्घ आकडेमोडीचे व म्हणून बरेच जिकिरीचे होते. माँझ यांनी या कामाकरिता एक आरेखन पद्धती शोधून काढली आणि तो नकाशा इतक्या थोड्या वेळात पूर्ण केला की, वरच्या अधिकाऱ्यांचा त्यावर विश्वासच बसेना. सुरुवातीला ही आरेखन पद्धत लष्करी गुप्तता म्हणून मानली गेली पण पुढे या आरेखन पद्धतीस १७९५ मध्ये प्रसिद्धी देण्यात आली.
घन वस्तूंचे प्रतलचित्रण करण्याचे साधन म्हणजे वस्तूंचा प्रतलावर प्रक्षेप घेणे. याकरिता वापरण्यात येणारे निरनिराळे प्रक्षेप प्रकार खाली दिले आहेत.
प्रक्षेपांचे प्रकार : लंबजन्य किंवा जात्य प्रक्षेप :अवकाशातील प या बिंदूपासून एखाद्या प्रतलावर काढलेला लंब जर प्रतलास प’ मध्ये छेदत असेल, तर प’ हा प चा त्या प्रतलावर लंबजन्य प्रक्षेप होतो (आ. २८). ज्या प्रतलावर प्रक्षेप घेतात त्यास प्रक्षेप-प्रतल व पप’ या रेषेस प्रक्षेपक असे म्हणतात. रेषेचा प्रक्षेप रेषाच असते.
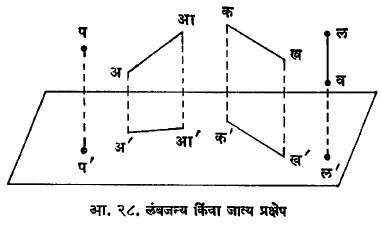
आ. २८ मध्ये अ ’आ’ हा अआ या रेषाखंडाचा प्रक्षेप आहे. रेषाखंड जर प्रक्षेपप्रतलास समांतर असेल, तर त्याचा प्रक्षेप रेषाखंडास समांतर व तितक्याच लांबीचा असेल (आ. २८ मध्ये कख = ।। क’ख’). रेषाखंड जर प्रक्षेप-प्रतलास लंब असेल, तर त्या रेषाखंडावरील प्रत्येक बिंदूचा प्रक्षेप लंबपादाशीच येईल (आ. २८ मध्ये लव या रेषाखंडाचा प्रक्षेप ल’ हा बिंदू होईल).
लंबजन्य प्रक्षेपामध्ये प्रक्षेपक किरण प्रक्षेप-प्रतलास लंब असतात म्हणजे ते एकमेकांस समांतर असतात. जेव्हा प्रक्षेपक किरण एकमेकांस समांतर पण प्रक्षेप-प्रतलास लंब नसतात, तेव्हा त्या प्रक्षेपणास तिर्यक् प्रक्षेपण म्हणतात. प्रक्षेपक किरण ज्या वेळी एकमेकांस समांतर असतात, त्या वेळी प्रक्षेप-आकृतीचे आकारमान हे वस्तू व प्रक्षेप-प्रतल यांमधील अंतरावर अवलंबून नसते.
शांकवीय किंवा यथादर्शन प्रक्षेप : ज्या प्रक्षेपणात प्रक्षेपक किरण एकसंपाती असतात त्याला शांकवीय प्रक्षेपण व या बिंदूस प्रक्षेप शिरोबिंदू अथवा दृष्टिबिंदू म्हणतात (आ.२९). छायाचित्र घेण्यामध्ये प्रक्षेप प्रकारचा उपयोग होतो. या प्रकारामध्ये प्रक्षेप-आकृतीचे आकारमान हे वस्तूच्या प्रक्षेप-प्रतल व दृष्टिबिंदू यांपासूनच्या अंतरावर अवलंबून असते.
यंत्रे, इमारती इत्यादींचे जे आरेखन करतात त्यामध्ये लंबजन्यप्रक्षेप प्रकारच वापरतात. वास्तुशिल्पज्ञ जे वास्तूचे आरेखन करतो ते दोन प्रकारचे असते. वास्तुरचनाकारांसाठी केलेल्या आरेखनामध्ये लंबजन्य प्रेक्षप प्रकार वापरतात, तर ग्राहकासाठी जे वास्तूचे चित्र काढलेले असते ते मात्र शांकवीय प्रक्षेप प्रकार वापरून काढलेले असते. खालील विवेचनामध्ये प्रक्षेप म्हणजे लंबजन्य प्रक्षेप असे समजावे. [⟶ यथादर्शन].
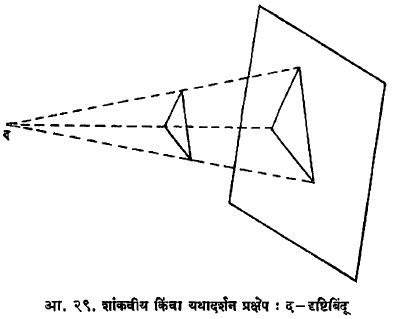
माँझ पद्धती :वस्तूचे प्रतलचित्रण करण्याची माँझ यांची पद्धती खाली दिली आहे. या पद्धतीमध्ये दोन किंवा अधिक प्रतलांवर प्रक्षेप घेण्यासाठी एक क्षैतिज प्रतल (आडवे प्रतल) व दुसरे ऊर्ध्व प्रतल (उभे प्रतल) अशी दोन प्रधान प्रतले निवडतात. या प्रतलांना अनुक्रमे क्ष-प्रतल व उ-प्रतल असे म्हणू. या प्रतलांची छेदरेषा भम हिला भूमिरेषा म्हणतात. ज्या वेळी तिसरे प्रक्षेप-प्रतल घ्यावे लागते त्या वेळी सामान्यतः ते या दोन प्रतलांना लंब असणारे प्रतल घेतात. या प्रक्षेप-प्रतलास पार्श्वचित्र प्रतल (प-प्रतल) म्हणतात. वस्तूच्या क्ष-प्रतलावरील प्रक्षेपास क्षैतिज प्रक्षेप, उ-प्रतलावरील प्रक्षेपास ऊर्ध्व प्रक्षेप किंवा उन्नत दर्शन आणि प-प्रतलावरील प्रक्षेपास पार्श्वदर्शन किंवा पार्श्वचित्र असे म्हणतात. क्ष-प्रतल व उ-प्रतल ही अपरिमित (अमर्यादपणे विस्तारलेली) प्रतले अवकाशांचे चार भाग (चतुष्क) करतात. आ. ३० मध्ये दाखविल्याप्रमाणे त्यांचा क्रम लावतात.
कोणत्याही वस्तूच्या रचनेचे भूमितीय घटक हे बिंदू, सरळ किंवा वक्र रेषा व पृष्ठे ही असतात. तेव्हा घटकांचे प्रतलचित्रण या पद्धतीमध्ये कसे करतात ते खाली दिले आहे.
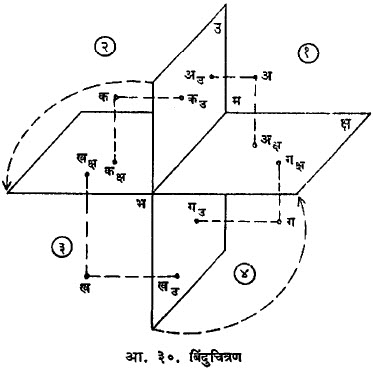
बिंदुचित्रण :अवकाशातील कोणताही बिंदू अ याचा क्ष-प्रक्षेप अक्ष आणि उ-प्रक्षेप अउ हे जर दिले, तर अ चे स्थान अवकाशात निश्चित होते. या पद्धतीमध्ये दोन प्रक्षेप-प्रतले जरी वापरली जात असली, तरी चित्रण शेवटी एकाच प्रतलावर करावयास हवे. म्हणून भूमिरेषा भम या अक्षाभोवती क्ष-प्रतलाचे ९०° तून परिभ्रमण करून ते उ-प्रतलाशी एकरूप करतात (आ.३०). परिभ्रमणाची दिशा अशी असेल की, २ व ४ हे चतुष्क त्यामुळे मिटले जातील. अ बिंदू व त्याचे प्रक्षेप अक्ष व अउ यांनी निश्चित केलेले प्रतल (अ, अक्ष, अउ) हे भूमिरेषा भम ला लंब असते. त्याचप्रमाणे ते प्रतल क्ष-प्रतल व उ-प्रतल यांसही लंब असते. क्ष-प्रतलाचे परिभ्रमण केल्यानंतर अक्ष आणि अउ यांना जोडणारी रेषा ही भम ला लंब असते. आकृतीमध्ये अ बिंदू पहिल्या चतुष्कात दाखविला आहे. दुसऱ्या, तिसऱ्या व चौथ्या चतुष्कांत दाखविलेल्या अनुक्रमे क, ख आणि ग या बिंदूंच्या बाबतीत अशाच प्रकारची विधाने करता येतील.
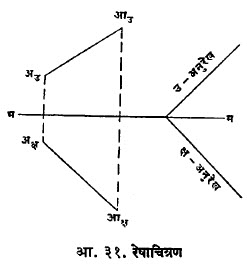
रेषाचित्रण :अवकाशातील अआ ही रेषा आरेखन फलकावर तिचा क्ष-प्रक्षेप अक्ष आक्ष व उ-प्रक्षेप अउ आउ या दोन रेषांनी दाखविली जाईल (आ.३१). एखादी पेन्सिल घेऊन ती जमीन व भिंत यांच्या संबंधांत खाली उल्लेखिलेल्या निरनिराळ्या स्थानांत धरल्यास खालील
विधानांतील सत्य सहज प्रत्ययास येईल : (१) अआ जर क्ष-प्रतल आणि उ-प्रतल या दोहांना समांतर असेल तर अक्ष आक्ष आणि अउ आउ या रेषा भम ला समांतर असतील. (२) अआ जर उ-प्रतलास फक्त समांतर असेल, तर अक्ष आक्ष ।। भम आणि अउ आउ = ।। अआ. (३) अआ जर उ-प्रतलास लंब असेल, तर तिचा उ-प्रक्षेप एक बिंदू होईस आणि अक्ष आक्ष भम ला लंब असेल.
प्रतलचित्रण : प्रतलावरील प्रत्येक बिंदूचा प्रक्षेप क्ष-किंवा उ-प्रतलावर घेतल्यास सामान्यतः (काही अपवाद सोडल्यास) सर्व प्रक्षेप-प्रतलच आच्छादिले जाईल. म्हणून प्रतल जेथे क्ष-प्रतलास व उ-प्रतलास छेदते त्या रेषा प्रतलचित्रणाकरिता उपयोगात आणतात. या रेषांना प्रतलाचा क्ष-अनुरेख व उ-अनुरेख म्हणतात. तीन प्रतलांच्या छेदरेषा या एकसंपाती किंवा समांतर असतात. म्हणून प्रतलाचे दोन अनुरेख भमला एकाच बिंदूत छेदतील (आ.३१) किंवा भम ला समांतर असतील. प्रतल जर भम या भूमिरेषेतून जात असेल, तर प्रतलाचा प-अनुरेख उपयोगी पडतो. जेव्हा क्ष-प्रतलाचे परिभ्रमण करून एक आरेखन फलक तयार होतो, त्यावर भूमिरेषेला एकाच बिंदूमध्ये छेदणाऱ्या किंवा तिला समांतर असणाऱ्या अशा दोन रेषा अवकाशातील एका प्रतलाचे क्ष-आणि उ-अनुरेख मानता येतील. हे दोन अनुरेख प्रतलाचे अवकाशातील स्थानही निश्चित करतात.
ज्या वेळी रेषा किंवा प्रतल हे क्ष-किंवा उ-प्रतलास समांतर स्थितीत असतात, त्या वेळी ते स्वाभाविक स्थितीत आहेत असे म्हणतात. वस्तू ज्या वेळी स्वाभाविक स्थितीत नसते, त्या वेळी तिच्या प्रतलचित्रणावरून वस्तूसंबंधीचे प्रश्न सोडविण्यात अडचणी येतात. यावर दोन तऱ्हेचे उपाय योजतात. पहिल्या पद्धतीमध्ये निरीक्षकाचेच स्थान असे बदलावयाचे की, नव्या स्थानापासून ती वस्तू स्वाभाविक स्थितीमध्ये दिसावी. याकरिता तिसरे सोयीचे प्रक्षेप-प्रतल घेऊन त्यावर वस्तूचे चित्रण करतात. दुसऱ्या पद्धतीमध्ये वस्तूचे परिभ्रमण करणे, तिच्या निरनिराळ्या भागांच्या छेदांचे चित्रण करणे वगैरे उपायांनी प्रश्न सोडविला जातो. या पद्धतीची कल्पना येण्याकरिता या भूमितीमधील एक साधा पण मूलभूत असा प्रश्न दोन्हीही पद्धतींनी कसा सोडविता येतो हे खाली दाखविले आहे :
प्रश्न : अवकाशातील दोन बिंदू अ, आ यांमधील यथार्थ अंतर काढणे.
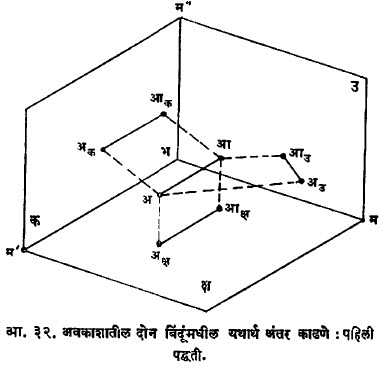
पहिली पद्धती : विश्लेषण : अआ ही रेषा क्ष-प्रतल किंवा उ-प्रतल यांना समांतर नाही असे समजू. क हे तिसरे प्रतल अआ ला समांतर व क्ष-प्रतलास लंब असे निवडले. त्यामुळे आ.३२ मध्ये दाखविल्याप्रमाणे अक आक = ।। अआ. उ.-आणि क – ही दोन्ही प्रतले क्ष-प्रतलास लंब असल्यामुळे अक व अउ यांची क्ष – प्रतलापासून उंची सारखी (= अअक्ष) आहे आणि त्याचप्रमाणे आक व अउ यांची क्ष-प्रतलापासून उंची सारखी (= अआक्ष) आहे. भम’ आणि भम” हे क-प्रतलाचे क्ष-आणि उ-अनुरेख आहेत. क-प्रतल व उ-प्रतल क्ष-प्रतलास लंब असल्यामुळे भम’ ^ भम. क-प्रतल हे (अआ, अक्ष आक्ष) या प्रतलास समांतर असल्यामुळे भम’ ।। अक्षआक्ष.
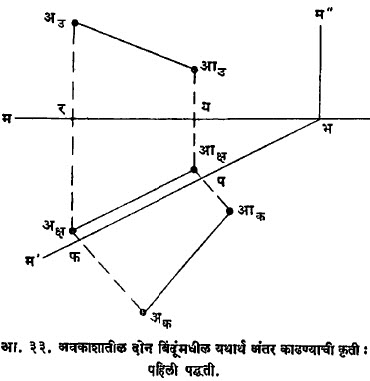
वरील सर्व मुद्दे लक्षात घेता आ. ३३ मध्ये दर्शविलेली आरेखन फलकावरील कृती सहज समजून येईल.
कृती : आ. ३३ मध्ये अक्ष आक्ष व अउ आउ हे अआ या रेषेचे क्ष व उ-प्रक्षेप आहेत. भम’ ही रेषा अक्ष आक्ष ला समांतर काढा व भम’’ ही भम ला लंब काढा. भम’व भम’’हे क-प्रतलाचे अनुरेख आहेत. अक्ष व आक्ष पासून भम’वर लंब टाकून ते अक व आक पर्यंत असे लांबवा की, फअक = रअउ आणि पआक = यआउ. अक व आक हे अ, आ चे क– प्रक्षेप झाले.
क-प्रतल हे अआ ला समांतर असल्यामुळे पुढील निष्कर्ष निघतात : (१) अक आक हे अ, आ मधील यथार्थ अंतर आहे. (२) अक आक व भम’ यांमधील कोन हा अआ आणि क्ष-प्रतल यांमधील यथार्थ कोन आहे (रेषा व प्रतल यांमधील कोन हा रेषा व तिचा प्रतलावरील प्रेक्षप यांमधील कोनाने मोजतात).
दुसरी पद्धती : विश्लेषण : आ. ३४ मध्ये अ, आ हे बिंदू व त्यांचे क्ष-प्रक्षेप अक्ष, आक्ष दाखविले आहेत. अअक्ष आक्ष आ या प्रतलीय आकृतीचे अक्ष आक्ष या अक्षाभोवती परिभ्रमण करून ते प्रतल क्ष-प्रतलाशी एकरूप केल्यावर, समजा अ, आ हे अ’, आ’या स्थानांवर आले. अ’ अक्ष आक्ष आ’ आणि अ’ अक्ष आक्ष आ’ या दोन आकृत्या एकरूप आहेत, हे उघड आहे. तेव्हा अ’ अक्ष^ अक्ष आक्ष, आ’ आ क्ष ^अक्ष आक्ष. शिवाय अ‘ अक्ष = अअक्ष = अ ची उंची, आ आक्ष = आआक्ष = आ ची उंची. अआ = अ’आ’ आणि अआ व अक्ष आक्ष यांमधील कोन = अ’ आ’व अक्ष आक्ष यांमधील कोन.
कृती : आ. ३५ मध्ये अआ चे क्ष-आणि उ-प्रक्षेप दाखविले आहेत. अक्ष आक्ष रेषेस अक्ष अ’ आणि आक्ष आ’या लंबरेषा काढून अक्ष अ’ = यअउ = अ ची उंची आणि आक्ष आ’= रआउ = आ ची उंची असे करावे.
विश्वेषणातील मुद्दे लक्षात घेता पुढील निष्कर्ष निघतात : (१) अ’ आ’हे अआ मधील यथार्थ अंतर आहे. (२) अ’ आ’व अक्ष आक्ष यांमधील कोन हा अआ व क्ष-प्रतल यांमधील यथार्थ कोन आहे.
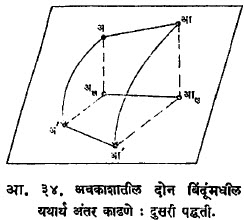
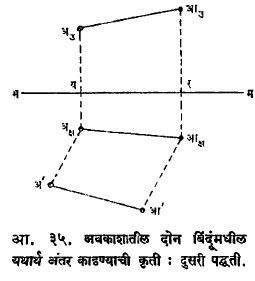
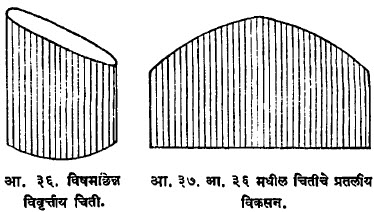
उपयोग :वर्णनात्मक भूमितीच्या पद्धती अवकाशातील पृष्ठांच्या अभ्यासासाठी उपयुक्त ठरतात. एखादा पत्रा घेऊन तो निरनिराळ्या तऱ्हेने वाकवून जी पृष्ठे तयार होतील, अशी विकसनीय पृष्ठांचे (उदा., शंकू, चिती) प्रतलीय विकसन करणे हा या भूमितीमधील एक महत्त्वाचा भाग आहे. आ. ३६ मध्ये विषमछिन्न (विषम छेद घेतलेली) विवृत्तीय चिती व आ. ३७ मध्ये तिचे प्रतलीय विकसन दाखविले आहे. या प्रतलीय विकसनावरून ते पृष्ठ तयार करण्याकरिता कशा आकाराचा पत्रा घ्यावा याची माहिती मिळते.
वर्णनात्मक भूमितीमध्ये वस्तूंचे निरनिराळ्या अवस्थेमधील प्रकाशित व अप्रकाशित भाग, एका वस्तूची दुसऱ्या वस्तूवर पडणारी छाया अशा तऱ्हेच्या प्रश्नांचाही अभ्यास होतो. प्रकाशकिरण हे अनंत अंतरापासून येतात असे समजल्यास ते एकमेकांना समांतर आहेत
आ. ३८. वस्तूचे प्रकाशित-अप्रकाशित भाग व छाया : (१) प्रकाशकिरण, (२) वस्तूचा प्रकाशित भाग, (३) वस्तूचा अप्रकाशित भाग, (४) छायाशंकू, (५) छाया.
असे मानता येते. आ. ३८ वरून या संबंधात वापरल्या जाणाऱ्या शब्दांचा अर्थ स्पष्ट होईल. [⟶ प्रकाशकी].
परिमित भूमिती
बिंदू व रेषा कोणत्याही भूमितीचे प्राकृतिक घटक असतात. ज्या भूमितीत यांची संख्या परिमित (मर्यादित, सांत) असते व त्यांच्या अन्योन्य संबंधाचा विचार करण्यात येतो अशा भूमितींना परिमित भूमिती असे म्हणतात. परिमित भूमितीची मूळ कल्पना व तिचा विस्तार प्रक्षेपीय भूमिती आणि क्षेत्र सिद्धांत [⟶ बीजगणित, अमूर्त] या दोन शाखांच्या द्वारे झालेला आहे. प्रक्षेपीय भूमितीमध्ये सत्, सदसत्, इ. विविध प्रकारची प्रक्षेप-प्रतले असू शकतात. कोणत्याही प्रतलास प्रक्षेप-प्रतल मानण्यासाठी त्या भूमितीतील कोणती गृहीतके या प्रतलावरील बिंदू व रेषा यांना लागू असतील याचा प्रथम निर्णय करावयास हवा. व्यापक प्रक्षेपीय भूमितीची गृहीतके खालीलप्रमाणे आहेत :
गृहीतक १: किमान एक रेषा असते.
” २: प्रत्येक रेषेवर किमान तीन बिंदू असतात.
” ३: सर्वच बिंदू एका रेषेवर नसतात.
” ४: दोन वेगवेगळे बिंदू एकाच रेषेवर असतात.
” ५: दोन वेगवेगळ्या रेषा एकाच बिंदूत मिळतात.
” ६: रेषेवरील एक सोडून इतर सर्व बिंदू व सत् संख्या
यांमध्ये क्रम न बदलणारी एकास-एक संगती असते. या मूळ गृहीतकांपैकी बिंदू व रेषा यांच्या अन्योन्य संबंधाविषयीची जी पहिली पाच गृहीतके आहेत, ती परिमित भूमितीत आवश्यक असतात परंतु विधान ६ मात्र वगळता येते. याऐवजी देझार्ग व ग्रीक गणितज्ञ पॅपस (इ. स. तिसरे-चौथे शतक) यांच्या प्रमेयांचाच (या प्रमेयांसंबंधी ‘प्रक्षेपीय भूमिती’ या भागात अधिक विवरण केलेले आहे तसेच ‘द्वित्व तत्त्व’ ही नोंदही पहावी) गृहीतके म्हणून समावेश करून यातून सिद्ध होणारे प्रतल निवडतात. या सात गृहीतकांच्या आधारे रेषेवरील एक विशिष्ट बिंदू – ¥ – सोडून उरलेल्या सर्व बिंदूंचा संच ‘क्षेत्र’ या नामाभिधानास पात्र होतो, हे सिद्ध करता येते. अर्थात त्याकरिता कोणत्याही दोन बिंदूंचा योग (बेरीज) व गुणाकार यांच्या या गृहीतकांच्या संदर्भात नव्या व्याख्या द्याव्या लागतात.
योग कृत्य :ल ही एक रेषा आहे. या रेषेवरील ¥ बिंदूतून जाणाऱ्या म व र या दोन वेगवेगळ्या रेषा आहेत. त्यांपैकी र रेषेवर.
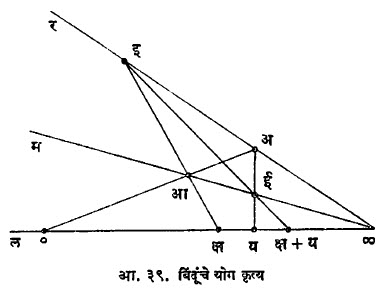
¥ खेरीज अ हा कोणताही बिंदू निवडा. क्ष व य हे दोन ल वरील कोणतेही बिंदू आहेत. आता क्ष व य यांची बेरीज क्ष + य यांचा संगत बिंदू पुढील रचनेने मिळतो : शून्य व अ बिंदू जोडा. ही रेषा म ला आ मध्ये छेदते. क्ष व आ जोडा. ही रेषा र ला इ मध्ये मिळते. यअ जोडा व ही रेषा म ला जिथे छेदते त्या बिंदूस ई म्हणा. इई जोडा व ही रेषा वाढवा. ती जेथे ल या रेषेला मिळते तो बिंदू क्ष + य म्हणा. या रचनेनुसार मिळणारा बिंदू अनन्य (एकमेव) असतो आणि तो क्षेत्र सिद्धांतातील बेरीज द्विमान कृत्यांसंबंधीच्या नियमांची पूर्तता करतो, असे सिद्ध करता येते [ हे नियम ‘ बीजगणित, अमूर्त’ या नोंदीत ‘पूर्णाकी प्रांत’ या उपशीर्षकाखाली दिलेले आहेत].
गुणाकार कृत्य : ल या रेषेवरील शून्य बिंदूमधून म रेषा व ¥ मधून र रेषा काढा. ल या रेषेवर कोणत्याही बिंदूस १ नाव द्या आणि क्ष व य असे दोन कोणतेही बिंदू निवडा. त्यांच्या गुणाकाराचा- क्षयचा-
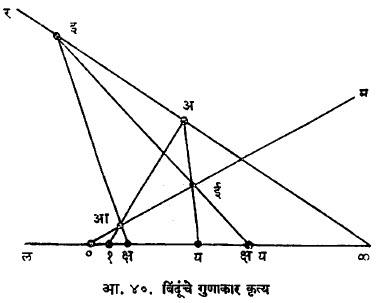
संगत बिंदू पुढील रचनेनुसार काढा : १ अ जोडा आणि ही रेषा म ला जिथे मिळते त्यास आ म्हणा. आक्ष जोडा आणि ही रेषा र ला मिळते तिथे इ नाव द्या. यअ जोडा आणि ही रेषा म ला जिथे मिळते त्यास ई नाव द्या. इई जोडून वाढविली असता ती ल रेषेस क्षय बिंदू मध्ये मिळते. अशा प्रकारे मिळणारा क्षय बिंदू अनन्य असतो आणि तो क्षेत्र सिद्धांतातील गुणाकार या द्विमान कृत्यासंबंधीच्या नियमांची पूर्तता करतो, असे सिद्ध करता येते [हे नियम ‘बीजगणित, अमूर्त’ या नोंदीत ‘पूर्णाकी प्रांत’ व ‘क्षेत्र’ या उपशीर्षकांखाली दिलेले आहेत].
क्षेत्र-भूमिती संबंध : रेषेवरील एक सोडून इतर सर्व बिंदूंचा संच म्हणजे क्षेत्र आहे व या क्षेत्रात योग व गुणाकार यांचा अर्थ काय हे वर पाहिले परंतु क्षेत्राच्या अनेकविध प्रकारांपैकी हे क्षेत्र कोणते असेल याचा मात्र यामध्ये निर्णय होत नाही. तेव्हा हे क्षेत्र जर आपण परिमित क्षेत्र घेतले, तर त्यामधून निर्माण होणाऱ्या परिमित प्रक्षेपप्रतलावरील भूमितीस परिमित भूमिती असे नाव आहे. प्रक्षेपीय भूमितीच्या गृहीतकानुसार प्रत्येक रेषेवर किमान तीन बिंदू असतात. जर एखाद्या रेषेवर असणाऱ्या बिंदूंची संख्या आपण न + १ मानली, तर त्या भूमितीतील प्रत्येक रेषेवर तेवढीच म्हणजे न + १ बिंदूसंख्या असते. या परिमित भूमितीस न – कोटी भूमिती म्हणतात. अआ ही एक रेषा या प्रतलावर घेऊ. समजा प हा या रेषेवर नसलेला एक बिंदू आहे. फ हा प्रतलावरील दुसरा कोणताही बिंदू असेल, तर पफ ही रेषा अआ ला एकाच बिंदूत छेदते. म्हणजे या प्रतलावरील प्रत्येक बिंदू हा प मधून काढलेल्या व अआ रेषेला छेदणाऱ्या एकाच सरळ रेषेवर आहे. यामुळे प्रतलावरील एकूण बिंदूसंख्या निश्चित करण्यास मदत होते. अआ रेषेवरील बिंदूंना प शी जोडणाऱ्या रेषांवरील बिंदूसंख्या म्हणजे आवश्यक ती संख्या होय. परिमित क्षेत्रातील घटकांची संख्या न असेल, तर प्रतलावरील प्रत्येक रेषेवर असणाऱ्या बिंदूंची संख्या न + १ येते आणि इतर प्रत्येक रेषेवर तेवढेच (म्हणजे न + १) बिंदू असतात. आता प मधून या न + १ बिंदूंना जोडणाऱ्या न + १ रेषा काढता येतील आणि प धरून यातील प्रत्येक रेषेवर न + १ बिंदू आहेत व प सोडून न बिंदू आहेत. म्हणून एकूण बिंदूसंख्या न (न + १) + ‘प’ बिंदू = न२ + न + १ अशी येते.
जर क ही एक अविभाज्य संख्या घेतली व ख हा कोणताही धन पूर्णांक घेतला, तर वरील पदावलीतील न चे मूल्य कख असते, हे एव्हारीस्त गाल्वा (१८११ – ३२) यांच्या परिमित क्षेत्रासंबंधीच्या सिद्धांतानुसार सिद्ध करता येते [⟶ बीजगणित, अमूर्त]. अशा तऱ्हेचे परिमित क्षेत्र (गाल्वा क्षेत्र) हे सुत्ररूपाने ग क्षे (कख) असे निदर्शित करतात आणि त्यानुसार उत्पन्न होणारी परिमित भूमिती जर द्विमितीय असेल, तर ती पभू (२, कख) अशी मांडण्याची पद्धत आहे. अर्थात या मांडणीतील मितीचा अंक कोणताही असू शकतो. तो जर म असेल, तर अशा भूमितीचे बीजगणितीकरण करताना बिंदूंचे समघाती सहनिर्देशक म + १ असतात. अर्थात द्विमितीय भूमितीमध्ये हे बिंदू समघाती सहनिर्देशक त्रयीत मांडता येतात. या परिमित भूमितीमध्ये देझार्ग प्रमेय ज्यांच्या बाबतीत गृहीत धरतात व ज्यांच्या बाबतीत वगळतात अशा ‘देझार्ग’ व ‘अ-देझार्ग’ अशा दोन जाती आहेत. न = क ख घटक असणाऱ्या प्रत्येक गाल्वा क्षेत्राशी–ग क्षे (कख) – संगत अशी न + १ बिंदू असणारी एकच परिमित भूमिती – प भू (२,कख) – असते आणि त्या भूमितीत देझार्ग प्रमेय सिद्ध करता येते.
सात बिंदूंची भूमिती :आपण जर क आणि ख यांना अनुक्रमे २ व १ ही किमान मूल्ये दिली, तर न = कख= २१ = २ आणि न २ + न + १ = ७ मिळतात. म्हणून प्रक्षेप–प्रतलातील लहानात लहान प्रतलात सात बिंदू असतात.⇨ द्वित्व तत्त्वानुसार त्यामध्ये रेषाही सातच असतात. जर हे सात बिंदू अ१, अ२, अ३, अ४, अ५, अ६, अ७ असे मानले, तर या सात रेषा खालील उभ्या ओळीत असणाऱ्या तीन बिंदूंनी तयार होतात.
|
अ१ |
अ२ |
अ३ |
अ४ |
अ५ |
अ६ |
अ७ |
|
अ२ |
अ३ |
अ४ |
अ५ |
अ६ |
अ७ |
अ१ |
|
अ४ |
अ५ |
अ६ |
अ७ |
अ१ |
अ२ |
अ३ |
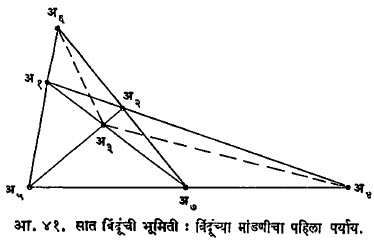
आ. ४१ व ४२ मध्ये या भूमितीतील बिंदूंच्या मांडणीचे दोन पर्याय दाखविले आहेत. यांतील बिंदूंचे सहनिर्देशक पुढीलप्रमाणे निश्चित करता येतात:
अ१ = (०,०,१), अ२ = (०, १, ०), अ३ = (०, १, १),
अ४ = (१, ०, ०), अ५ = (१, ०, १), अ६ = (१, १, ०),
अ७ = (१, १, १).
इतर कोटींच्या परिमित भूमिती : इ. स. १९०७ मध्ये ओ. व्हेब्लेन व जे. एच्. एम्. वेडरबर्न यांनी यांनी ९-कोटीच्या अ-देझार्ग प्रतलाची मांडणी केली. यामध्ये ९१ बिंदू व ९१ रेषा असतात. १९५७ मध्ये ह्यूझ या गणितज्ञांनी परिमित प्रतलांचे अपरिमित कुल असते व या अपरिमित कुलामध्ये ९-कोटीच्या प्रतलाचाही समावेश आहे असे दाखविले. १९४९ मध्ये ब्रुक व रायसर यांनी सिद्ध केलेल्या महत्त्वाच्या सिद्धांतानुसार जर न = १, २ (भाजक ४) (म्हणजे ४ ने न ला भागल्यास १ वा २ बाकी उरत असेल) व न चे मूल्य जर दोन पूर्णांकांच्या वर्गाच्या बेरजेच्या (म्हणजे न = क२ + ख२ क, ख पूर्णांक) रूपात मांडता येत असेल, तरच
न-कोटीचे परिमित प्रतल असू शकते. यानुसार ६, १४, २१, २२ या कोटीचे व अशा तऱ्हेच्या अनेक अपरिमित कोटींची प्रतले असूच शकत नाहीत, हे सिद्ध होते.
उपयोग : परिमित भूमितीचा उपयोग प्रामुख्याने सांख्यिकीमधील ⇨ प्रयोगांचा अभिकल्प या शाखेत होतो किंबहुना या उपयोगामुळेच परिमित भूमितीचा जास्त अभ्यास केला गेला. याविषयी संशोधन करण्यात आर्. सी. बोस, के. आर्. नायर व सी. आर्. राव या भारतीय सांख्यिकीविज्ञांनी विशेष पुढाकार घेतला.
‘संतुलित अपूर्ण खंड अभिकल्प’ तयार करण्यासाठी परिमित भूमिती फार उपयोगी पडते. या प्रकारच्या अभिकल्पांची जरूरी जेव्हा परिक्षण करावयाच्या उपचारांची संख्या मोठी असेल त्या वेळी भासते. एकाच खंडामध्ये सर्व उपचारांचा समावेश न करतासुद्धा जर अभिकल्पाचे उपयुक्ततेच्या दृष्टीने आवश्यक असलेले गुणधर्म टिकवायचे असतील, तर तो संतुलित ठेवावा लागतो. म्हणजेच कोणतीही उपचारांची जोडी एकत्र असलेले खंड ठराविक संख्येचे असावे लागतात (ही संख्या सर्वसाधारणपणे l या ग्रीक अक्षराने दर्शवितात). दिलेली उपचारांची संख्या, खंडांची संख्या, उपचारांची पुनरावृत्ती, खंडांचे आकारमान व l यांमुळे निश्चित होणारा संतुलित अपूर्ण खंड अभिकल्प नेहमीच तयार करणे शक्य होईल असे नाही. या शक्यतेचा संबंध आवश्यक त्या संख्येच्या बिंदूंची परिमित भूमिती अस्तित्वात असण्याशी आहे, कारण परिमित भूमितीवरून अभिकल्प तयार करण्यातील मुख्य पायरी एकेका बिंदूला एकेक उपचाराचे नाव देण्याची आहे. नंतर
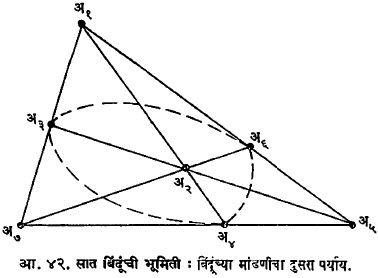
रेषा किंवा प्रतल यांना खंड म्हणून मानून अभिकल्प तयार करता येतो. उदा., आ. ४२ मध्ये दाखविलेल्या परिमित भूमितीवरून खालील अभिकल्प मिळू शकतो:
उपचार : अ१, अ२, अ३, अ४, अ५, अ६, अ७
खंड १ : अ१, अ३, अ७
खंड २ : अ१, अ२, अ४
खंड ३ : अ१, अ५, अ६
खंड ४ : अ२, अ३, अ५
खंड ५ : अ२, अ६, अ७
खंड ६ : अ३, अ४, अ६
खंड ७ : अ४, अ५, अ७
या अभिकल्पात खंडांची संख्या = ७, उपचारांची पुनरावृत्ती = ३, खंडाचे आकारमान = ३ व l= १
अयूक्लिडीय भूमिती
यूक्लिडीय भूमितीहून निराळ्या अशा कोणत्याही भूमितीस अयूक्लिडीय भूमिती असे म्हणता येईल पण ऐतिहासिक दृष्ट्या हे नाव दोन विशिष्ट भूमितींनाच दिले जाते. या भूमिती व यूक्लिडीय भूमिती यांमधील फरक मुख्यत्वेकरून समांतर रेषांसंबंधीच्या गृहीतकावर आधारित आहे. यूक्लिडीय भूमितीमध्ये समांतर रेषांसंबंधीचे पाचवे गृहीतक असे आहे:‘दोन सरळ रेषांना छेदणारी सरळ रेषा काढली असता ज्या बाजूच्या आंतरकोनांची बेरीज दोन काटकोनांपेक्षा कमी असेल त्या बाजूस त्या दोन रेषा वाढविल्या असता एकमेकींस छेदतात’. इतर गृहीतकांच्या तुलनेने हे गृहीतक स्वयंसिद्ध वाटत नाही. एकोणिसाव्या शतकापर्यंत हे गृहीतक इतर गृहीतकांच्या आधाराने सिद्ध करण्याचा प्रयत्न अनेक गणितज्ञांनी केला. या प्रयत्नांचा शेवट पूर्वीच्या प्रयत्नांतील उणिवा दाखविण्यात होत असे. शेवटी एकोणिसाव्या शतकात रशियन गणितज्ञ लोबाचेव्हस्की व हंगेरियन गणितज्ञ यानोश बोल्यॉई ह्यांनी केलेल्या संशोधनानंतर हे गृहीतक सिद्ध करणे शक्य नाही व याऐवजी दुसरे समांतर रेषा गृहीतक वापरले, तर यूक्लिडीय भूमिती इतकीच सुसंगत भूमिती निर्माण होऊ शकते, असे दिसून आले.
विकास : समांतर रेषा गृहीतक सिद्ध करण्याच्या प्रयत्नांमध्ये ज्यांनी अयूक्लिडीय भूमितीचा पाया तयार केला त्यांची उल्लेखनीय कामगिरी पुढीलप्रमाणे आहे : जेझुइट प्राध्यापक जी. साचेरी (१६६७ – १७३३) यांनी विचारात घेतलेली आकृती अशी : अआइई या चौकोनात ∠ अ =∠ आ = १ काटकोन अ ई = आ इ. ∠ इ =∠ ई. यूक्लि़ड यांचे पाचवे गृहीतक स्वीकारल्यास ∠ इ =∠ ई = १ काटकोन असे दाखविता येते. हे गृहीतक न मानल्यास हे कोन विशाल कोन किंवा लघुकोन असतील अशा तऱ्हेच्या दोन अनुमानांची शक्यता आहे. लघुकोन अनुमानावरून साचेरी यांनी अनेक प्रमेये सिद्ध केली. पुढे जे. एच् लँबर्ट (१७२८ – ७७) यांनी अशाच प्रकारची आकृती विचारात घेऊन लघुकोन अनुमानावर आधारित अशी प्रमेये असत् त्रिज्या असलेल्या गोलावर प्रस्थापित करता येतील, ही कल्पना मांडली. गौस (१७७७ – १८५५) यांनीही लघुकोन अनुमानावर आधारित भूमिती बरीच प्रगत केली व ही भूमिती यूक्लिडीय भूमिती इतकीच सुसंगत आहे, हा विचार प्रथम मांडला पण गौस यांच्यासारख्या मान्यवर गणितज्ञांनीही या क्रांतिकारक विचाराचे स्वागत कसे होईल या शंकेने त्यास प्रसिद्धी दिली नाही.
लोबाचेव्हस्की (१७९३ – १८५६) व बोल्यॉई (१८०२ – ६०) हे गणितज्ञ अयूक्लिडीय भूमितीचे जनके समजले जातात. अयूक्लिडीय भूमितीवरील पहिला निबंध प्रसिद्ध करण्याचे श्रेय लोबाचेव्हस्की यांना आहे. पुढच्याच वर्षी बोल्यॉई यांनी आपल्या वडिलांच्या [⟶ बोल्यॉई, फॉरकॉश]Tentamen या ग्रंथाच्या पुरवणीत ‘अवकाशाचे केवल विज्ञान’ या अर्थाच्या शीर्षकाखाली चोवीस पृष्ठांचा एक निबंध स्वतंत्रपणे प्रसिद्ध केला. या दोघांनीही साचेरी यांच्या लघुकोन अनुमानावर आधारित अशी भूमिती विकसित केली. अयूक्लिडीय भूमितीच्या विकासातील या पुढील महत्त्वाची पायरी म्हणजे १८५४ मध्ये रीमान(१८२६ – ६६) या जर्मन गणितज्ञांनी सादर केलेला निबंध. रीमान यांनी साचेरी यांच्या विशालकोन अनुमानावर आधारित अशी भूमिती एका विशिष्ट अवकाशात शक्य आहे, असे प्रतिपादिले. या विकासातील तिसऱ्या कालखंडाचे वैशिष्ट्य म्हणजे आर्थर केली (१८२१ – ९५) या गणितज्ञांनी या भूमितीच्या अभ्यासासाठी सुरू केलेला प्रक्षेपीय पद्धतीचा वापर हे होय. एका मूलभूत शांकवजाशी संबंधित अशा प्रक्षेपीय गुणधर्माचा अभ्यास केल्यास त्यात यूक्लिडीय व दोन तऱ्हेच्या अयूक्लिडीय त्रिमितीय भूमितीचा समावेश होतो. हा शांकबज सत् असेल तर लोबाचेव्हस्कीय भूमिती (अपास्तीय), असत् असेल तर रीमानीय भूमिती (विवृत्तीय) व अपकृष्ट असेल तर यूक्लिडीय भूमिती (अन्वस्तीय) मिळते. शांकवजाच्या ऐवजी शांकव घेऊन अशाच तऱ्हेच्या तीन द्विमितीय भूमिती मिळतील. फेलिक्स क्लाइन (१८४९ – १९२५) यांनी रीमानीय भूमितीचे दोन प्रकार शक्य आहेत, असे दाखविले (गोलीय व विवृत्तीय भूमिती). पुढे सोफुस ली (१८४२ – ९९) यांनी अवकाशात पूर्णपणे मुक्त असे स्थान परिवर्तन हे या चार प्रकारच्या अवकाशांतच शक्य आहे, असे प्रस्थापित केले.
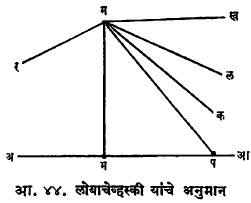
लोबाचेव्हस्कीय भूमिती : (अपास्तीय भूमिती). अआ या सरळ रेषेवर म ह्या बाहेरील बिंदूपासून मभ हा लंब काढला आहे (आ. ४४). प हा अआ या रेषेवरील एक बिंदू भ पासून दूर सरकू लागला, तर दोन शक्यता उद्भवतात. सरळ रेषा मर्यादित लांबीची असते असे गृहीत मानले, तर प हा बिंदू काही अंतर जाऊन परत मूळ स्थानावर येईल पण सरळ रेषा अनंतापर्यंत वाढविता येते असे मानल्यास भ आणि प यांमधील अंतर वाढत जाईल, म्हणजेच भप ⟶ ¥. प हा भ पासून दूर जात असता मप ही दिशायुक्त रेषा मल या विशिष्ट सीमान्त स्थानावर आल्यानंतर मल ही अआ ला संमांतर झाली असे म्हणता येईल. प हा बिंदू विरुद्ध दिशेने भ पासून दूर सरकू लागला, तर मप ही पुन्हा एकदा मर या सीमान्त स्थानावर आल्यानंतर मर ही आअ ला समांतर झाली, असे म्हणता येईल. या सीमान्त स्थानावरील रेषांचे वैशिष्ट्य असे की, या म मधून जाणाऱ्या सर्व दिशायुक्त रेषांचे दोन भाग पाडतात : भक सारख्या अआ ला छेदणाऱ्या व मख सारख्या अआ लान छेदणाऱ्या. यूक्लिडीय भूमितीमध्ये मल व मर या एकाच रेषेत असतात व ∠ भमल =∠ भमर = ९०° पण अपास्तीय भूमितीमधील गृहीत असे की, मल व मर या निरनिराळ्या दिशायुक्त रेषा आहेत, म्हणजेच एका बिंदूतून अआ ला दोन समांतर रेषा काढता येतात (मल ।। भआ, मर ।। भअ). ∠ भमल =∠ भमर हे सिद्ध करता येते. हा समांतर स्थिती कोन मभ (=p) या लंब अंतरावर अवलंबून असल्यामुळे तो Õ (p) या चिन्हाने दर्शवितात. जेव्हा p ⟶ ¥ तेव्हा Õ (p) ⟶ 0 आणि
|
जेव्हा p⟶ 0 तेव्हा Õ (p) ⟶ |
p |
. |
|
२ |
या भूमितीमधील काही प्रमेये पुढीलप्रमाणे आहेत : (१) दोन समांतर रेषांना जेव्हा तिसरी रेषा छेदते तेव्हा समांतर स्थितीच्या बाजूच्या दोन आंतरकोनांची बेरीज दोन काटकोनांपेक्षा कमी असते. (२) दोन समांतर रेषांमधील अंतर समांतर स्थितीच्या दिशेस कमी होत जाते व विरुद्ध दिशेस वाढत जाते. (३) त्रिकोणाच्या तीन कोनांची बेरीज दोन काटकोनांपेक्षा कमी असते. (४) समांतर स्थिती
|
कोन Õ (p) याचे मूल्य स्प |
Õ (p) |
= e– p/K |
|
२ |
या सूत्राने निश्चित होते. k यास अवकाशाचा स्थिरांक म्हणतात. e हा स्वाभाविक लॉगस्थिमाचा आधारांक आहे [⟶ इ (e)].
|
जर k→∞ तर e-p/k→ १ आणि ∏ (p) → |
p |
|
२ |
म्हणजे यूक्लिडीय अवकाश होतो. (५) अपास्तीय त्रिकोणमितीमधील काही सूत्रे खालीलप्रमाणे आहेत (का, खा, गा बाजूंच्या लांब्या क, ख, ग कोन):
|
ज्या |
(क) |
= |
ज्या |
(ख) |
= |
ज्या |
(ग) |
|
i= Ö-१ |
|
ज्या |
(iका) |
ज्या |
(iख) |
ज्या |
(iगा) |
|
|||
|
(K) |
(k) |
(k) |
|
|
कोज्या |
(iगा) |
= कोज्या |
(iका) |
कोज्या |
(iखा) |
|
(k) |
(k) |
(k) |
|
+ ज्या |
(iका) |
ज्या |
(iखा) |
कोज्या (ग). |
|
(k) |
(k) |
ज्या वेळी k→∞ अवकाश यूक्लि़डोय होतो व त्यामध्ये वरील सूत्राऐवजी खालील सूत्रे मिळतात :
|
ज्या (क) का |
= |
ज्या (ख) खा |
= |
ज्या (ग) गा |
(गा)२ = (का)२ + (खा)२ – २ (का) (खा). कोज्या (ग). यावरून एक निष्कर्ष निघतो की, k जर इतर राशींच्या मानाने फार मोठा असेल, तर अपास्तीय भूमिती स्थूलमानाने यूक्लिडीय होते.
रीमानीय (गोलीय व विवृत्तीय) भूमिती : या भूमितीमध्ये सरळ रेषा ही बंद व मर्यादित लांबीची असते, असे गृहीत आहे. त्यामुळे या भूमितीमध्ये समांतर रेषा नाहीत (आ.४५). कख या रेषेस ब, भ, म या ठिकाणी लंब रेषा काढल्यास त्या सर्व एकाच बिंदूतून जातात (अ किंवा अ’) व हे सर्व लंब एकाच लांबीचे असतात. अ हा कख चा ध्रुव व कख ही अ ची ध्रवीय रेषा असे म्हणतात. अ व
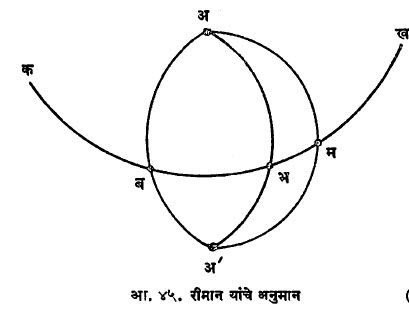
अ’ यांना प्रतिध्रुव बिंदू म्हणतात. प्रतिध्रुव बिंदू निरनिराळे बिंदू आहेत असे मानल्यास दोन रेषा दोन बिंदूमध्ये छेदतात व या दोन बिंदूमधील अंतर कोणत्याही रेषेवरून सारखेच असते. या भूमितीस गोलीय भूमिती म्हणतात. प्रतिध्रुव बिंदू हे एकरूप आहेत असे गृहीत धरल्यास विवृत्तीय भूमिती मिळते. या भूमितीत दोन रेषा एकाच बिंदूत छेदतात. या दोन्हीही भूमितींत सर्व रेषा सारख्याच लांबीच्या असतात. अब = ल असेल, तर गोलीय भूमितीत रेषेची लांबी ४ ल व विवृत्तीय भूमितीत ही लांबी २ ल येते. रीमानीय भूमितीमध्ये त्रिकोणाच्या कोनांची बेरीज २ काटकोनांपेक्षा जास्त येते. या भूमितीमधील त्रिकोणमितीची सूत्रे अपास्तीय भूमितीच्या सूत्रांमध्ये
|
iका K |
च्या ऐवजी |
का K |
असे बदल केल्यास मिळतील. |
|
१ |
p k= ल |
|
|
|
२ |
|
||
या सूत्राने निश्चित होतो. याही ठिकाणी जेव्हा k⟶¥ तेव्हा भूमिती यूक्लिडीय होते असे दाखविता येते.
अयूक्लिडीय भूमितीचे यूक्लिडीय निदर्शन :अनेक शतकांच्या परिचयामुळे यूक्लिडीय भूमिती हीच सत्य व नैसर्गिक आहे असे मानण्यात येते. यामुळे अयूक्लिडीय भूमितीची नीट कल्पना येण्याकरिता यूक्लिडीय भूमितीचे घटक घेऊन यूक्लिडीय अवकाशातच या भूमितीचे निदर्शन करणे उपयुक्त ठरते.
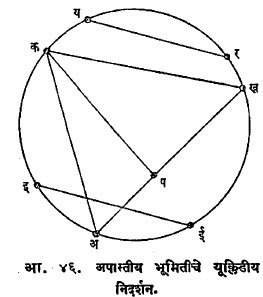
अपास्तीय भूमितीच्या निदर्शनाकरिता यूक्लिडीय प्रतलावर एक वर्तुळ घेऊन पुढे दिल्याप्रमाणे काही व्याख्या तयार करण्यात येतात. (आ. ४६): (१) अपास्तीय प्रतल म्हणजे वर्तुळाच्या आतील भाग. (२) अपास्तीयसरळ रेषा म्हणजे वर्तुळाची जीवा (उदा., कख). (३) समांतर सरळ रेषा म्हणजे ज्या जीवांचा छेदबिंदू परिघावर आहे अशा रेषा (उदा., अख व कख). (४) छेदणाऱ्या सरळ रेषा म्हणजे ज्या जीवांचे छेदबिंदू वर्तुळाच्या आत आहेत अशा जीवा (उदा., अख व इई).
(५) न छेदणाऱ्या रेषा म्हणजे ज्या जीवांचे छेदबिंदू वर्तुळावर बाहेर आहेत अशा जीवा (उदा., यर व इई).
या व्याख्यांवरून अपास्तीय भूमितीचे काही गुणधर्म आपण पडताळू शकतो. प सारख्या कोणत्याही बिंदूतीन कख सारख्या रेषेस पक आणि पख या दोन समांतर रेषा काढता येतात. प मधून जाणाऱ्या इतर रेषा कख ला छेदणाऱ्या किंवा न छेदणाऱ्या असतात.
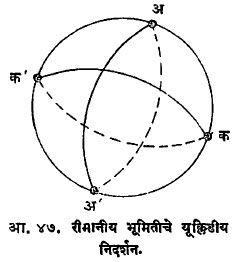
रीमानीय भूमितीच्या निदर्शनाकरिता अवकाशातील एक गोल घेऊन पुढे दिल्याप्रमाणे व्याख्या तयार करण्यात येतात. (आ. ४७): (१) रीमानीय प्रतल म्हणजे गोलाच्या पृष्ठभाग. (२) रीमानीय सरळ रेषा म्हणजे गोलावरील महावृत्त (गोलाच्या व्यासाइतकाच ज्याचा व्यास आहे असे वर्तुळ).
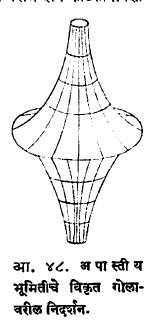
यावरून दिसून येईल की, रीमानीय प्रतलावर समांतर रेषा नाहीत. तसेच या भूमितीमध्ये त्रिकोणाच्या कोनांची बेरीज दोन काटकोनांपेक्षा जास्त असते. वरीलप्रमाणे अपास्तीय भूमितीचे निदर्शन विकृत गोलाच्या पृष्ठावर करता येते. या पृष्ठावरील अल्पांतरी वक्ररेषा या अपास्तीय सरळ रेषा घेऊन पृष्ठाच्या मर्यादित भागावर अपास्तीय भूमितीचे गुणधर्म दाखविता येतात (आ. ४८).
वरील निदर्शनांवरून एक गोष्ट स्पष्ट होते की, यूक्लिडीय भूमिती जर सुसंगत असेल, तर या अयूक्लिडीय भूमिती तितक्याच सुसंगत आहेत. ‘आपण राहतो त्या अवकाशाची भूमिती कोणती?’ हा या संबंधात एक सहज उद्भवणारा प्रश्न आहे पण या प्रश्नाचे एवढेच उत्तर देणे शक्य आहे की, विश्वाच्या तुलनेने लहान अशा क्षेत्राची भूमिती स्थूलमानाने यूक्लिडीय असते. विश्वाची भूमिती कदाचित अयूक्लिडीय असू शकेल.
प्रक्षेपीय भूमिती
भूमितीच्या अभ्यासाकडे तीन निरनिराळ्या दृष्टिकोनांतून पाहता येते. एक मानीय, दुसरा प्रक्षेपीय आणि तिसरा वैश्लेषिक. पहिल्या प्रकारच्या दृष्टिकोनातून ग्रीक गणितज्ञांनी अभ्यास केला व त्याच्याशी यूक्लि़ड यांचे नाव निगडित आहे. हा अभ्यास अंतर किंवा लांबी या मूलभूत संकल्पनेवर आधारित आहे. यूक्लिडीय भूमिती ही मानीय भूमिती आहे कारण तिच्यामध्ये प्रत्येक रेषाखंड किंवा कोन प्रमाणित लांबी किंवा प्रमाणित कोन यांच्या भाषेमध्ये दर्शविता येतो. तरी देखील यूक्लिडीय भूमितीमध्ये काही प्रमेये रेषांच्या एकसंपातितेविषयी किंवा बिंदूंच्या एकरेषीयतेविषयी मांडलेली असतात. पॅपस यांचे प्रमेय [⟶ द्वित्व तत्त्व] या प्रकारात मोडते. अशा प्रमेयांना प्रक्षेपीय प्रमेये म्हणून संबोधिले जात होते आणि ती युक्लिडीय भूमितीमध्येच मोडत.
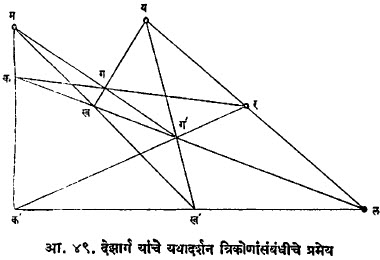
अशा प्रकारे प्रक्षेपीय भूमितीतील काही भाग प्राचीन काळीही माहीत होते असे आढळून येत असले, तरी तिचे खरे मूळ पंधराव्या व सोळाव्या शतकांतील चित्रकारांच्या (उदा., लिओनार्दो दा व्हींची, आलब्रेक्त ड्यूरर) त्रिमितीय वस्तूंचे द्विमितीमध्ये अचूक यथादर्शन मिळविण्याच्या पद्धतींत अधिक स्पष्टपणे दिसून येते [⟶ यथादर्शन]. सतराव्या शतकात मुख्यत्वे देझार्ग व थोड्या प्रमाणात पास्काल यांनी प्रक्षेपीय भूमितीची मुख्य प्रमेये प्रस्थापित केली आणि त्यांनी याकरिता मानीय भूमितीतील प्रमेयांचा पूर्णतः उपयोग केला. देझार्ग यांनी पुढील प्रमेय (याला ‘देझार्ग यांचे यथादर्शन त्रिकोणांसंबंधीचे प्रमेय’ म्हणतात) सिद्ध केले (आ. ४९).
D कखग व D क’ख’ग’ यांमध्ये कक’, खख’, गग’ जर म मध्ये एकसंपाती असतील, तर (खग, ख’ग’), (गक, ग’क’) व (कख, क’ख’) यांचे छेदबिंदू एकरेषीय असतात. या प्रमेयामध्ये मापनविषयक कल्पनांचा पूर्णपणे अभाव आहे, हे सहज लक्षात येते. आणखीही अशी काही प्रमेय या काळात मांडलेली आढळतात पण ही एका नवीन तऱ्हेच्या भूमितीचे भाग आहेत याची जाणीव एकोणिसावे
शतक उजाडेपर्यंत गणितज्ञांना झाली नाही. के.जे. एम्. फोन स्टाऊट यांनी १८४७ मध्ये Geometrie der Lage हा आपला ग्रंथ प्रसिद्ध केल्यानंतरच प्रक्षेपीय भूमिती ही यूक्लिडीय भूमितीमधील गृहीतकांपेक्षा निराळ्या गृहीतकांवर आधारित अशी शाखा बनली. तिच्यातील प्रमेये ‘अंतर’ या संकल्पनेवर अवलंबून नाहीत, असे दाखविण्यात आले. पुढे असेही दिसून आले की, प्रक्षेपीय भूमिती ही अधिक व्यापक असून तिच्यातील मर्यादित भागाशीच यूक्लिडीय भूमिती निगडित आहे. पाँस्ले यांनी १८२२ मध्ये व फेलिक्स क्लाइन यांनी १८७१ मध्ये लिहिलेल्या ग्रंथामुळेही प्रक्षेपीय भूमितीच्या विकासात फार मोठी मोलाची भर पडली.
प्रक्षेपीय रूपांतर :फ ही एक एकप्रतलीय आकृती आहे (आ.५०). म हा त्या प्रतलाच्या बाहेरील बिंदू आहे व P हे एक दुसरे प्रतल आहे. फ वरील बिंदू म ला जोडणाऱ्या रेषा P प्रतलाला छेदून त्यावर फ’ ही आकृती तयार होते. फ’ ही फ पासून प्रक्षेपणाने मिळालेली आकृती आहे. म याला प्रक्षेप केंद्र म्हणतात. अआ या रेषेचे प्रक्षेपण अ’आ’ यारेषेमध्ये होते. प हा अआ वरील बिंदू असेल, तर प’ हा अ’आ’ वर असला पाहिजे.
प्रक्षेपीय रूपांतर म्हणजे वर उल्लेखिलेल्या एक किंवा अधिक प्रक्रियांचे फलित होय. बिंदू व रेषा यांचे प्रक्षेपीय रूपांतर पुन्हा बिंदू
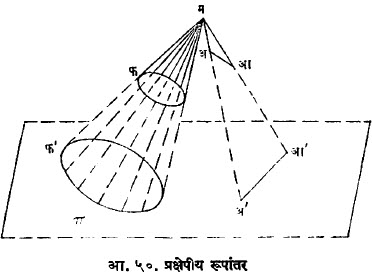
व रेषा यांमध्ये होते. बिंदूंची एकरेषीयता किंवा रेषांची एकसंपातिता हे गुणधर्म प्रक्षेपीय रूपांतरामध्ये अबाधित राहतात पण दोन बिंदूमधील अंतर किंवा दोन रेषांमधील कोन हे मात्र प्रक्षेपीय रूपांतरामध्ये अबाधित राहत नाहीत आणि म्हणूनच मापन कल्पनेला प्रक्षेपीय भूमितीमध्ये खरे स्थान नाही. बिंदू व रेषा हे प्रतलीय प्रक्षेपीय भूमितीचे मूलभूत घटक आहेत. वर्तुळाचे प्रक्षेपण पुन्हा वर्तुळामध्ये नेहमीच होऊ शकत नाही. म्हणून या भूमितीमध्ये मूळ घटकाचे स्थान त्याला मिळू शकणार नाही.
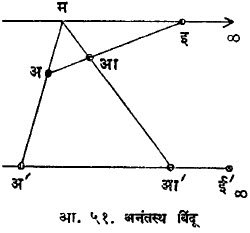
अनंतस्थ बिंदू व अनंतस्थ रेषा :यूक्लिडीय भूमितीमध्ये समांतर रेषांचा आपण सर्रास उपयोग करतो पण समांतर रेषा या प्रक्षेपणानंतर समांतर राहत नाहीत आणि त्यामुळे या संकल्पनेला प्रक्षेपीय भूमितीमध्ये स्थान नाही. शिवाय समांतर रेषांसंबंधीचा नेहमीचा दृष्टिकोन कायम ठेवला, तर अनेक प्रमेयांच्या व्यापकीकरणामध्ये अडचणी येतात. उदा., आ. ५१ मध्ये अआइ या एका रेषेवरील बिंदुंचे प्रक्षेप घेत असता, अ‘, आ‘ हे अ, आ चे प्रक्षेप झाले पण मइ ही अ‘ आ‘या रेषेस समांतर असेल, तर इ चा प्रक्षेप कोणता ? अशा तऱ्हेचे अपवाद टाळण्यासाठी अनंतस्थ बिंदू व अनंतस्थ रेषा या संकल्पनांचा उपयोग केला जातो. प्रत्येक रेषेवर एक अनंतस्थ बिंदू असतो व त्या रेषेला समांतर असणाऱ्या सर्व रेषा या बिंदूमध्ये येऊन मिळतात. आ. ५१ मध्ये इ चा प्रक्षेप इ‘¥ हा अनंतस्थ बिंदू होईल. प्रतलावरील सर्व अनंतस्थ बिंदू एकरेषीय असून या रेषेस प्रतलावरील अनंतस्थ रेषा म्हणतात. अवकाशातील सर्व अनंतस्थ रेषा मिळून अनंतस्थ प्रतल होते. या अनंतस्थ घटकांच्या योगाने बरीच प्रमेये अपवादाशिवाय मांडता येतात. उदा., ‘प्रतलावरील दोन रेषा एकमेकींना एका बिंदूत छेदतात’ किंवा ‘अवकाशातील दोन प्रतले एकमेकांना एका रेषेमध्ये छेदतात’.
द्वित्व तत्त्व : प्रक्षेपीय भूमितीमधील द्वित्व तत्त्व हे गणितामध्ये नेहमी वापरात असलेल्या संगतीचे एक उदाहरण म्हणता येईल. प्रतलावरील द्वित्व तत्त्वानुसार बिंदू आणि रेषा हे एकमेकांचे द्वैत घटक आहेत. एखाद्या प्रमेयामध्ये बिंदू व रेषा या शब्दांची अदलाबदल व त्यामुळे करावे लागणारे काही शाब्दिक बदल केल्यास द्वैत प्रमेय तयार होते.
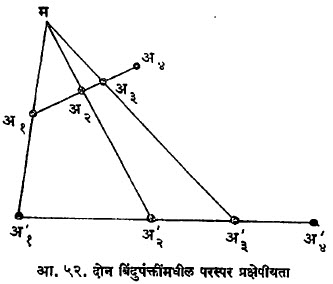
एकरेषीय बिंदूच्या संचाला बिंदुपंक्ती किंवा बिंदूमाला व एका बिंदूतून जाणाऱ्या प्रतलीय रेषांच्या संचाला शलाका किंवा रेखावली म्हणतात. तीन बिंदूंच्या दोन बिंदुपंक्ती या नेहमी प्रक्षेपीय असतात म्हणजेच एका किंवा अधिक प्रक्षेपणाने एकापासून दुसरी बिंदुपंक्ती मिळू शकते. दुसरे महत्त्वाचे प्रमेय म्हणजे दोन बिंदुपंक्तीमधील परस्पर प्रक्षेपीयता ही त्यांतील तीन बिंदु-युग्मांनी निश्चित होते. म्हणजे अ१, अ२, अ३ ही बिंदुपंक्ती अ’१ अ’२, अ’३ या बिंदुपंक्तीशी प्रक्षेपीय असेल, तर अ४ या संगत बिंदू अ’४ हा निश्चित होतो. द्वित्व तत्त्वानुसार शलाकांसंबंधीची द्वैत प्रमेये सहज रीत्या मांडता येतील. [⟶ द्वित्वतत्त्व].
प्रक्षेपणात अचल राहणारे गुणधर्म :अ’, आ’, इ’, ई’ जर अ, आ, इ, ई, या बिंदुपंक्तीचा प्रक्षेप असेल, तर सामान्यतः अआ ही लांबी किंवा अआ : आइ हे गुणोत्तर ही प्रक्षेपामध्ये अचल राहत नाही पण
|
अआ |
: |
आइ |
हे द्विगुणोत्तर (दोन गुणोत्तरांचे गुणोत्तर) प्रक्षेपणामध्ये अचल राहते. |
|
अई |
: |
ईइ |
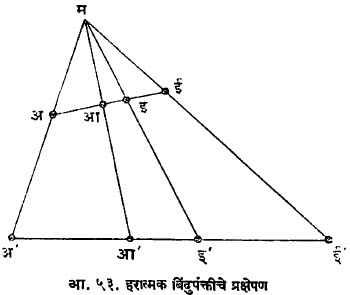
आ. ५३ वरून असे दिसून येईल की,
|
अआ : आई |
= |
^ |
^ |
= |
अ’ आ’: आ’ इ’ |
अआ: आइ |
= |
अआ. इई |
|
ज्या अमआ |
: ज्या आमइ |
|||||||
|
अई : ईइ |
^ |
^ |
अ’ ई’ : ई’ इ’ |
अई: ईइ |
अई. इआ |
|||
|
ज्या अमई |
: ज्या ईमइ |
हे द्विगुणोत्तर (अइ, आई) किंवा (अ आ इ ई) याने दर्शवितात. शलाकेचे द्विगुणोत्तर हे तिच्या किरणांना छेदणाऱ्या कोणत्याही छेदक रेषेवरील द्विगुणोत्तर म्हणजे म (अ आ इ ई) = (अ आ इ ई). जर (अ आ इ ई) = -१ असेल किंवा म (अ आ इ ई) = -१ असेल, तर अशा बिंदुपंक्तीला किंवा शलाकेला हरात्मक बिंदुपंक्ती किंवा हरात्मक शलाका असे म्हणतात. (अ आ इ ई) या द्विगुणोत्तरामध्ये ई हा बिंदू जर अनंतस्थ बिंदू असेल, तर
|
(अ आ इ ई) |
= |
अ आ . इ ई |
⟶ |
अ आ |
|
|
अ ई . इ आ |
इ आ |
|
कारण |
इ ई |
⟶ |
१ |
|
ई |
⟶ |
¥ |
|
अई |
म्हणजे कोणतेही गुणोत्तर त्या रेषेवरील अनंतस्थ बिंदू घेऊन द्विगुणोत्तराच्या रूपाने लिहिता येईल. दोन बिंदुपंक्ती जर समद्विगुणोत्तरीय असतील, म्हणजे (अ इ, आ ई) = (अ’ इ’, आ’ ई’) असेल, तर त्या प्रक्षेपीय असतात. दोन शलाकांसंबंधीही हे खरे आहे. द्विगुणोत्तर, हरात्मक बिंदुपंक्ती किंवा हरात्मक शलाका यांचे गुणधर्म यांना प्रक्षेपीय भूमितीमध्ये महत्त्वाचे स्थान आहे.
का, खा, गा या तीन रेषा जर एकसंपाती असतील, तर त्यांच्यामुळे एक क्रम निश्चित होतो. का खा गा हा क्रम गा खा का या क्रमाच्या विरूद्ध आहे. तसेच एका रेषेवर असलेल्या तीन बिंदूंचे क ख ग व ग ख क हे दोन विरूद्ध क्रम मांडता येतील व एकाच रेषेतून जाणाऱ्या तीन प्रतलांचा क्रम लावता येईल. प्रक्षेपीय भूमितीमध्ये क्रमवारता हा एक अचल राहणारा गुणधर्म आहे.
अखंडतेविषयीची पुढील विधान प्रक्षेपीय भूमितीमध्ये गृहीतक म्हणून घेतले जाते. एखाद्या रेषेवर बिंदूंचा क्रम लावला व त्यामध्ये क नंतर ख असेल आणि कख वरील बिंदू दोन वर्गांत असे विभागले की, (१) प्रत्येक बिंदू एका वर्गात समाविष्ट होतो व (२) एका वर्गातील बिंदू दुसऱ्या वर्गातील सर्व बिंदूंच्या पूर्वी येतात, तर ग हा एक असा बिंदू रेषेवर असतो की, ग पूर्वीचे सर्व बिंदू पहिल्या वर्गात पडतात व ग नंतरचे सर्व बिंदू दुसऱ्या वर्गात पडतात.
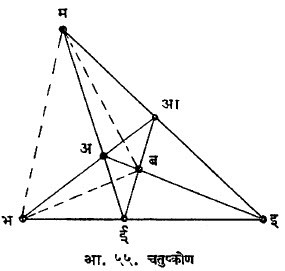
चतुर्भुज व चतुष्कोण : प्रतलीय प्रक्षेपीय भूमितीमध्ये चतुर्भुज आणि चतुष्कोण यांच्या गुणधर्मांचा अभ्यासही केला जातो. शिवाय
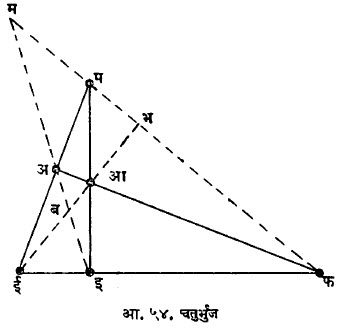
या दोन आकृती हे द्वित्व तत्त्वाचे एक चांगले उदाहरण आहे. या आकृतींचे वर्णन खालीलप्रमाणे करता येईल.
|
चतुर्भुज (आ. ५४) |
चतुष्कोण (आ. ५५) |
|
(१) चतुर्भुज ही चार रेषांनी तयार झालेली आकृती आहे (यांपैकी कोणत्याही तीन रेषा जोड्याजोड्यांनी सहा बिंदूंत मिळतात). याला ४ बाजू (अआ, आइ, इई, ईअ) व ६ कोनबिंदू असतात आणि म्हणून तीन संमुख कोनबिंदूंची युग्मे (अ, इ), (आ, ई), (प,फ) मिळतात.
(२) संमुख कोनबिंदूंना जोडणाऱ्या तीन कर्णरेषा अइ, आई, पफ यांनी बभम हा कर्ण-त्रिकोण तयार होतो.
(३) चतुर्भुजांची प्रत्येक कर्णरेषा ही इतर दोन कर्णरेषांनी हरात्मक द्विगुणोत्तरात छेदली जाते म्हणजे (अइ, बम) = (आई, बभ) = (पफ, भम) =-१. |
(१) चतुष्कोण ही चार बिंदूंनी तयार झालेली आकृती आहे (यांपैकी कोणतेही तीन बिंदू एकरेषीय नाहीत व हे बिंदू शक्य असलेल्या सर्व म्हणजे सहा रेषांनी जोडलेले आहेत). याला ४ कोनबिंदू (अ, आ, इ, ई,) व ६ बाजू असतात आणि म्हणून तीन संमुख बाजूंची युग्मे (अआ, इई), (अई, आइ), (अइ, आई) मिळतात.
(२) संमुख बाजूंचे तीन छेदबिंदू ब, भ, म, या तीन कर्णबिंदूंनी तयार झालेला त्रिकोण हा चतुष्कोणाचा कर्ण-त्रिकोण होतो.
(३) चतुष्कोणाच्या प्रत्येक कोनबिंदूपाशी तयार होणारी शलाका हरात्मक असते म्हणजे ब (अआ, भम) = भ (आइ, बभ) = म (इई, बभ) = – १. |
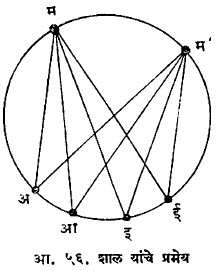
प्रक्षेपण व शांकव :शंकुच्छेद किंवा शांकव हे शंकूचे प्रतलीय छेद घेऊन मिळणारे वक्र आहेत. शांकवांचे प्रक्षेपण पुन्हा शांकवांतच होते त्यामुळे शांकवांच्या गुणधर्मांचा अभ्यास हा या भूमितीमधील महत्त्वाचा भाग आहे. वरील व्याख्येनुसार शांकव हा वर्तुळाचा प्रक्षेप असल्यामुळे वर्तुळाचे जे जे गुणधर्म प्रक्षेपणामध्ये अचल राहतात, ते सर्व शांकवांच्या बाबतीतही खरे असतात. यांपैकी एम्. शाल (१७९३ – १८८०) या फ्रेंच गणितज्ञांचे प्रमेय हे एक महत्त्वाचे प्रमेय आहे. अ, आ, इ, ई हे शांकवावरील चार बिंदू आहेत. म व म’ हे शांकवावरील कोणतेही दोन बिंदू घेतल्यास म (अ आ इ ई) = म’ (अ आ इ ई). या प्रमेयाचा व्यत्यासही खरा आहे (आ.५६).
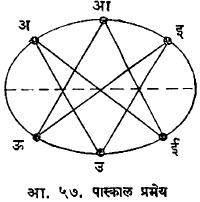
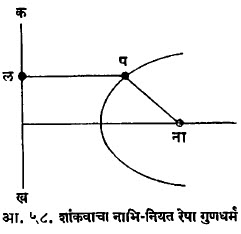
वरील प्रमेय वर्तुळाच्या बाबतीत सहज सिद्ध करता येते. द्विगुणोत्तर हे प्रक्षेपणामध्ये अचल राहत असल्यामुळे हे प्रमेय शांकवाच्या बाबतीतही खरे असले पाहिजे. या प्रमेयाच्या व्यत्यासाचा उपयोग शांकवाची व्याख्या करण्याकरिताही करतात. ‘दोन प्रक्षेपीय शलाकांच्या संगत किरणांचा छेदबिंदु-पथ हा शांकव असतो किंवा द्वित्व तत्त्वानुसार दोन प्रक्षेपीय बिंदुपंक्तींच्या संगत बिंदूंना जोडणाऱ्या रेषांच्या अन्वालोप (रेषा कुलातील प्रत्येक रेषेला स्पर्श करणारा वक्र) हा शांकव असतो’ अशी ही व्याख्या देता येईल. या व्याख्यांपासून शांकवाचे कोणतेही गुणधर्म प्रस्थापित करता येतात. यांपैकी प्रसिद्ध पास्काल प्रमेय पुढीलप्रमाणे आहे :‘अ, आ, इ, ई, उ, ऊ असे शांकवावरील ६ बिंदू घेतल्यास संमुख बाजूंचे छेदबिंदू एकरेषीय असतात’ (आ. ५७). शांकवाचा नाभि-नियत रेषा गुणधर्म हा एक दुसरा महत्त्वाचा गुणधर्म आहे. आ. ५८ मध्ये ना हा नाभिबिंदू व कख ही नियतरेषा आहे. प हा शांकवावरील कोणताही बिंदू असल्यास पना : पल हे गुणोत्तर अचल राहते (आ.५८). (‘वैश्लेषिक भूमिती’ या उपशीर्षकाखाली दिलेली शांकवांसंबंधीची माहितीही पहावी).
त्रिमितीय प्रक्षेपीय भूमिती : या भूमितीमध्ये बिंदू, रेषा व प्रतल मूलभूत घटक आहेत. बिंदू व प्रतल हे एकमेकांचे द्वैत घटक असून रेषा ही स्वद्वैतघटक आहे. कारण दोन बिंदूंना जोडणारी जशी रेषा तशीच ती दोन प्रतलांची छेदरेषाही असते. एकाच रेषेतून जाणाऱ्या प्रतल समूहास प्रतल-शलाका म्हणता येईल.
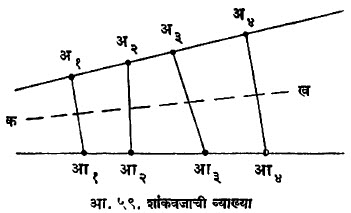
चार प्रतलांच्या शलाकेचे द्विगुणोत्तर म्हणजे त्यांना छेदणाऱ्या रेषेवरील चार बिंदूपंक्तींचे द्विगुणोत्तर होय. प्रतलीय प्रक्षेपीय भूमितीमध्ये शांकवांचे जे स्थान आहे ते येथे शांवजांचे आहे. शांकवजाची व्याख्या अशी देता येईल : अ१, अ२, अ३, अ४ आणि आ१, आ२, आ३, आ४ अशा दोन बिंदूपंक्ती वितल नैकप्रतलीय रेषांवर आहेत. त्या समद्विगुणोत्तरोय आहेत म्हणजेच (अ१ अ२ अ३ अ४) = (आ१ आ२ आ३ आ४). कख ही रेषा अ१ आ१, अ२ आ२, अ३ आ३ यांना छेदत असेल, तर ती अ४ आ४ हिलाही छेदते (आ. ५९). कख सारख्या जनक रेषांनी तयार झालेले पृष्ठ म्हणजे शांकवज होय.
वैश्लेषिक प्रक्षेपीय भूमिती :वरील विवेचनामध्ये जो दृष्टिकोन आहे त्यापेक्षा निराळ्या पद्धतीनेही या भूमितीचा अभ्यास करता येतो. वैश्लेषिक पद्धतीनुसार प्रतलावरील बिंदूंचे समघाती सहनिर्देशक(क्ष१, क्ष२, क्ष३) असे घेतात. बिंदू जर प-मितीय अवकाशात असेल, तर त्याचे समघाती सहनिर्देशक (क्ष०, क्ष१, क्ष२,…..,क्षप) असे होतील. बिंदूंचे प्रक्षेपीय रुपांतर (क्ष ⟶ क्ष’) खालील प्रकारच्या समीकरणाने होते.
|
क्ष’ल |
= |
प |
अरल क्षर |
|
∑ |
|||
|
र=० |
अशा सर्व प्रक्षेपीय रूपांतर समीकरणांचा प्रक्षेपीय गट [⟶ गट सिद्धांत] तयार होतो. या गटाचे वैशिष्ट्य असे की, दोन प्रक्षेपीय रूपांतर जर एकामागून एक केली, तर त्याचे फलित म्हणजे एक तिसरे प्रक्षेपीय रूपांतरच असेल. आकृत्यांचे जे गुणधर्म प्रक्षेपीय गटातील रूपांतरामध्ये अचल राहतात ते प्रक्षेपीय भूमितीचा अभ्यास विषय होतात. या गटाचे काही उपगट विचारात घेतल्यास, त्यांमधील रूपांतरांमध्ये जे गुणधर्म अचल राहतात, ते लक्षात घेता निरनिराळ्या भूमिती मिळतात. याची काही उदाहरणे अशी : जी प्रक्षेपीय रूपांतरे एखाद्या विशिष्ट रेषेस (अनंतस्थ रेषा) अचल ठेवतात, अशा उपगटापासून सजातीय भूमिती मिळते. यापुढे जाऊन वरील रेषेवरील दोन विशिष्ट बिंदू (वृत्तीय बिंदू) हेही अचल पाहिजेत अशी अट घातल्यास जो उपगट मिळतो त्यापासून यूक्लिडीय भूमिती मिळते. प्रतलावरील एखादा विशिष्ट शांकव अचल ठेवणाऱ्या रूपांतराच्या उपगटापासून अयुक्लिडीय भूमिती मिळतात. हा शांकव जर सत् असेल, तर अपास्तीय अयूक्लिडीय भूमिती आणि तो शांकव असत् असेल, तर विवृत्तीय अयूक्लिडीय भूमिती मिळते. नेहमीच्या अभ्यासातील बहुतेक भूमिती या प्रक्षेपीय भूमितीपासून काही विशेषीकरणाने मिळतात.
प्रक्षेपीय भूमितीच्या अभ्यासांची आणखी एक पद्धत म्हणजे प्रथम या भूमितीमधील गृहीतके मांडून त्यांपासून इतर प्रमेये सिद्ध करणे. या पद्धतीस स्वयंसिद्धकीय मूलक पद्धत म्हणता येईल.
अवकल भूमिती
अवकलनशास्त्राच्या [⟶ अवकलन व समाकलन] शोधामुळे गणितज्ञांना बिंदूच्या स्थानाबरोबर जे भूमितीय गुणधर्म बदलतात (उदा., वक्राच्या स्पर्शिकेची दिशा) त्यांचा अभ्यास करणे शक्य झाले. कारण अवकलज हा चल संख्येच्या बदलाचा दर मोजण्यास अगदी योग्य असे साधन आहे. आयझॅक न्यूटन (१६४२ – १७२७) व जी. डब्ल्यू. लायप्निट्स (१६४६ – १७१६) यांच्या काळात या भूमितीला सुरूवात झाली असे म्हणता येईल. या भूमितीच्या प्रगतीस ज्यांनी विशेष चालना दिली त्यांमध्ये माँझ (१७४६ – १८१८), गौस (१७७७ – १८५५), ऑयलर (१७०७ – ८६), जे.जी. दार्बू (१८४२ – १९१७) व एल. ब्यांगकी (१८५६ – १९२८) यांची नावे प्रसिद्ध आहेत.
या भूमितीचा अभ्यास विषय म्हणजे अवकाशातील वक्र [⟶ वक्र] व पृष्ठे. नेहमीचा अवकाश हा त्रिमितीय यूक्लिडीय अवकाश असल्याने स्थानांतर गती व परिभ्रमण गती यांमध्ये अचल राहणारे गुणधर्मच येथे विचारात घेतले जातात. खालील विवेचनामध्ये मापनाशी निगडित अशा गुणधर्मांचा विचार प्रामुख्याने केलेला आहे. म्हणजे ही मानीय अवकल भूमिती आहे व परिमाणाचे मापन यूक्लिडीय प्रमाणावर आधारित आहे.
अवकाशातील वक्र किंवा विषम वक्र :अवकाशातील कोणत्याही बिंदूचे (क्ष, य, झ) हे जात्य कार्तीय सहनिर्देशक असताना आदिबिंदू आ (०,०,०) आणि प (क्ष, य, झ) यांना जोडणारा सदिश
|
à |
= |
à |
= (क्ष, य, झ) |
|
आप |
र |
यास प चा स्थान सदिश असे म्हणतात. प (क्ष, य, झ) आणि क (क्ष+ d क्ष,य+ d य, झ+d झ) या दोन समीपस्थ बिंदूंमधील अंतर यूक्लिडीय प्रमाणानुसार खालील सूत्राने मिळते :
(d च२= (d क्ष)२ + (d य)२ + (d झ)२…….(१)
अवकाशातीत वक्र हा दोन पृष्ठांना छेद असल्यामुळे तो दोन समीकरणांनी फ (क्ष, य, झ) = o, फ (क्ष,य,झ) = o निश्चित होतो. परंतु वक्राची व्याख्या अशीही देता येते : बिंदूचे सहनिर्देशक हे एका प्रचलाची फलने असली, तर या बिंदूचा बिंदुपथ हा एक वक्र असतो. वक्राची प्रचलीय समीकरणे खालीलप्रमाणे देतात :
क्ष = फ१ (ट), य = फ२ (ट), झ = फ३ (ट) (ट प्रचल) किंवा र = (क्ष, य, झ) =[ फ१ (ट), फ२ (ट), फ३ (ट) ] ….(२) सूत्रे (१) व (२) वरून वक्राच्या क व ख या कोणत्याही दोन बिंदूंना जोडणाऱ्या चापाची लांबी च ही खालील सूत्राने मिळते :
|
च |
= |
ख |
√ |
dक्ष |
|
+ |
dय |
|
+ |
dझ२ |
|
.dट |
|
ò |
२ |
२ |
२ |
|||||||||
|
क |
dट |
|
dट |
|
dट |
|
|
= |
ख |
√ |
फ१२ (ट) + फ२२(ट) + फ३२(ट) .dट… (३) |
|
ò |
|||
|
क |
येथे फ१ (ट), फ२ (ट), फ३ (ट) ही एकदिक् व संतत फलने [⟶ फलन] आहेत व शिवाय त्यांचे अवकलजही संतत फलने आहेत, असे गृहीत धरले आहे. ज्या बिंदूत
|
d झ |
, |
d य |
, |
d झ |
|
d ट |
d ट |
d ट |
हे एकाच वेळी शून्य होतात त्यांना एकमात्र बिंदू व इतरांना नियमित बिंदू म्हणतात. अवकल भूमितीमध्ये नियमित बिंदूचे विचारात घेतात.
प (ट), क (ट+ δ ट) हे वक्रावरील दोन समीपस्थ बिंदू आहेत. जेव्हा क ⟶ प म्हणजेच δ ट ⟶ तेव्हा पक या रेषेची सीमावस्था ही वक्राची प बिंदूतील स्पर्शिका होय. या व्याख्येवरून वक्राला प्रत्येक बिंदूत स्पर्शिका असणे हा त्याचा अवकल गुणधर्म आहे हे स्पष्ट होते. पक ह्या सदिशास समांतर अशा एकक सदिशाचे घटक
|
( |
δ क्ष |
, |
δ य |
, |
δ झ |
) |
|
( |
δ क्ष |
, |
δ य |
, |
δ झ |
) |
|
√∑δ क्ष२ |
√∑δ क्ष२ |
√∑δ क्ष२ |
असे होतील.
जेव्हा क ⟶ प तेव्हा हा एकक सदिश स्पर्श सदिश होईल.
|
सीमा |
जीवा पक |
= |
१ म्हणून प बिंदूत एकक स्पर्श सदिश |
|
क ⟶ प |
चाप पक |
|
⟶ |
हा खाली दिल्याप्रमाणे निश्चित होईल. |
|
त |
|
à |
= |
( |
d क्ष |
, |
d य |
, |
d झ |
) |
= |
( |
क्ष’ य’ झ’ |
) |
. . . (४) |
|
त |
d च |
d च |
d च |
(क्ष, य, झ ही चाप च ची फलने आहेत असे वरील सूत्रात मानले आहे व ते नेहमीच शक्य होते).
प, क, ख या वक्रावरील तीन समीपस्थ बिंदूंनी निश्चित केलेले प्रतल जेव्हा क ⟶ प आणि ख ⟶ प तेव्हा सीमावस्थेत अधिस्पर्शी प्रतल होते असे म्हणतात. ह्या तीन बिंदूतून जाणार्या वर्तुळास सीमावस्थेत अधिस्पर्शी वर्तुळ म्हणतात. अधिस्पर्शी प्रतलावर
|
⟶ |
⟶ |
⟶ |
⟶ |
|
त आणी |
त+ d |
त हे सदिश असतात म्हणजेच |
त हे सदिश त्या प्रतलावर आहेत. |
म्हणून अधिस्पर्शी प्रतलाचे समीकरण खालीलप्रमाणे होईल.
|
क्ष – क्ष |
य – य |
झ – झ |
= ० |
|
क्ष’ |
य’ |
झ’ |
|
|
क्ष” |
य” |
य” |
अधिस्पर्शी प्रतलावर प मधून वक्राला लंब असणार्या रेषेला वक्राचा प्रधान अभिलंब म्हणतात.
|
à |
हा एकक प्रधान अभिलंब घेण्यास येतो. |
à |
हा एकक सदिश असल्यामुळे तो |
|
||||||||||
|
प्र |
त |
|
||||||||||||
|
à |
à |
हा सदिश अधिस्पर्शी प्रतलावर आहे. ह्यावरून खालील सूत्र मिळते. |
||||||||||||
|
त ला लंब आहे आणि |
त |
|||||||||||||
|
|
à |
= (क्ष”, य”, झ”) |
=k |
à |
… |
… |
(५) |
|
||||||
|
|
त’ |
प्र |
|
|||||||||||
वरील सूत्रात k ही अदिश राशी आहे. प बिंदू वक्रावरून फिरत असता
|
à |
या एकक स्पर्श सदिशाचा परिभ्रमण वेग |
à |
या सदिशाने मोजला जातो म्हणून |
|
त |
त’ |
|
à |
|
त’ यास वक्रता सदिश व या सदिशाचे परिमाण k यास वक्राची वक्रता म्हणतात. |
|
à |
à |
à |
|
त आणी |
त+ d |
त यांमधील कोन जर dq असेल, तर |
|
K |
= |
सीमा |
dq |
सूत्र (५) वरून k खालील सूत्रांवरून निश्चित होतो : |
|
d च → ० |
d च |
k२= (क्ष’’)२ + (य’’)२ + (झ’’)२ … … (६)
वक्रतेचा व्यस्तांक वक्रता त्रिज्या असते (⟶ वक्र).
|
|
K |
= |
1 |
(ρ-वक्रता त्रिज्या) |
|
r. |
अधिस्पर्शी प्रतलास प बिंदूत काढलेल्या लंबास वक्राचा अभिप्रलंब म्हणतात. एकक अभिप्रलंब सदिश
|
à |
ने दर्शवितात. प बिंदूतून जाणारे |
|
अ’ |
|
à |
à |
à |
या परस्पर लंब एकक सदिशांची एक त्रयी तयार होते. |
|
त |
प्र |
अ |
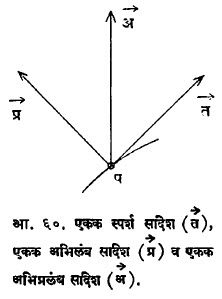
|
आ. ६०. एकक स्पर्श सदिश |
à |
एकक अभिलंब सदिश |
à |
व एकक अभिप्रलंब सदिश |
à |
|
त |
प्र |
अ |
(आ. ६०). यांच्या धन दिशा अशा घेतात की,
|
⟶ |
⟶ |
⟶ |
⟶ |
⟶ |
या परिभ्रमणाची दिशा ही संदर्भ-अक्ष |
|
||||
|
त |
प्र |
अ |
|
|||||||
|
⟶ |
⟶ |
⟶ |
⟶ |
|
यांच्या परिभ्रमण दिशेप्रमाणे होईल. |
|||||
|
आक्ष |
आय |
आझ |
||||||||
या त्रयीमुळे प बिंदूत तीन परस्परांस लंब अशी प्रतले मिळतात.
|
( |
à |
à |
) |
हे अधिस्पर्शी प्रतल, |
( |
à |
à |
) |
हे अभिलंब प्रतल आणि |
|
त |
प्र |
प्र |
अ |
|
( |
à |
à |
) |
हे चापकलन प्रतल असे म्हणतात. |
à |
हा एकक सदिश |
|
अ |
त |
अ |
|
( |
à |
à |
) |
या दोन्ही सदिशांना लंब असल्यामुळे सूत्रे (४) व (५) यांवरून खालील सूत्र मिळते : |
|
त |
प्र |
|
à |
= |
r(य’ झ’’- य’’ झ’, झ’ क्ष’’- झ’’ क्ष’, क्ष’ य’’- क्ष’’ य’) |
… (७) |
|
अ |
|
à |
à |
à |
|
अ हा एकक सदिश असल्यामुळे |
अ हा |
अ ला लंब आहे व सूत्र (५) वरून असे दाखविता येईल की, |
|
à |
à |
à |
à |
|
अ हा |
त लाही लंब आहे म्हणजे |
अ हा |
प्र ला समांतर असला पाहिजे. |
|
|
à |
= – ℸ |
à |
… … (८) |
|
अ |
प्र |
ℸ ही अदिश राशी अभिप्रलंबाचा बदल दर म्हणजेच अधिस्पर्शी प्रतलाचा बदल र मोजते. ℸ यास प बिंदूतील वक्राचे परिपीडन म्हणतात. सूत्रे (५) व (८) यांवरून आणि
|
à |
à |
|
प्र हा |
प्र ला लंब असल्यामुळे खालील सूत्र मिळते : |
|
|
à |
= ℸ |
à |
–k |
à |
… … (९) |
|
प्र’ |
अ |
त |
सूत्रे (५), (८) व (९) वापरून ℸ करिता खालील सूत्र तयार होईल :
|
|
क्ष’ य’ झ’ |
|
|
ℸ = ρ2 |
क्ष’’ य’’ झ’’ |
… … (१०) |
|
|
क्ष’’’ य’’’ झ’’’ |
|
सूत्रे (५), (८), (९) यांना जे. एफ्. फ्रेनेत आणि जे. ए. सेरेत या फ्रेंच गणितज्ञांच्या नावांवरून फ्रेनेत-सेरेत सूत्रे म्हणतात. ही सूत्रे
|
à |
à |
à |
यांचे अवकलज पुन्हा |
à |
à |
à |
मध्ये व्यक्त करतात. |
|
त, |
प्र, |
अ |
त |
प्र |
अ |
या सूत्रांच्या मदतीने पुढील मूलभूत सिद्धांत सिद्ध करता येतो :‘वक्राची वक्रता (k) व परिपीडन (ℸ) ही चापाची फलने या स्वरूपात दिली असता तो वक्र अवकाशातील त्याच्या स्थानाव्यतिरिक्त पूर्णपणे निश्चित होतो ’. वक्राच्या k= फ(च) आणि ℸ= व (च) या फलनदर्शक समीकरणांना अंगभूत समीकरणे म्हणतात, कारण ती सहनिर्देशक पद्धतीवर अवलंबून नाहीत. ℸ= ० हे समीकरण कोणत्याही प्रतलीय वक्राचा विशिष्ट गुणधर्म व्यक्त करते, कारण अशा वक्राच्या कोणत्याही बिंदूतील अधिस्पर्शी प्रतल हे ज्या प्रतलात वक्र आहे तेच प्रतल असते. त्याचप्रमाणे
|
K |
= |
स्थिरांक हा सर्पिल (आ. ६१) |
|
ℸ |
या वक्राचा विशिष्टगुणधर्म आहे. ज्या वेळी k व ℸ दोन्ही स्थिरांक असतात तेव्हा वृत्तीय सर्पिल मिळतो. दिलेल्या वक्राशी संबद्ध असे काही बिंदुपथ पुढीलप्रमाणे आहेत : (१) अधिस्पर्शी वर्तुळ-केंद्राचा बिंदुपथ, (२) अधिस्पर्शी
गोल केंद्राचा बिंदूपथ, (३) उद्वलित व अंतर्वलित (व या वक्राच्या स्पर्शिका व’ या वक्रास लंब असल्या, तर व हा व’ चा उद्वलित आणि व’ हा व चा अंतर्वलित असे म्हणतात).
पृष्ठ : अवकाशामध्ये फ (क्ष, य, झ) =o या समीकरणाने पृष्ठ निश्चित होते. खालील विवेचनामध्ये जास्त सोयीस्कर म्हणून क्ष = फ१ (ट, ठ), य = फ२ (ट, ठ), झ = फ३ (ट, ठ) …. (११) ही पृष्टाची प्रचल समीकरणे वापरली आहेत. फ१, फ२, फ३ ही (ट, ठ) ची फलने एकदिक्, संतत आणि जरूर तितक्या कोटीपर्यंत आंशिक अवकलनीय [⟶ अवकलन व समाकलन] आहेत, असे मानले आहे. (ट, ठ) या युग्माचा प्रत्येक मूल्याने पृष्ठावरील एक बिंदू मिळतो, म्हणून (ट, ठ) यास पृष्ठाचे वक्ररेषीय सहनिर्देशक म्हणतात. (ट, ठ) ⟶ (ड, ढ) असे सहनिर्देशक रूपांतर केल्यास
|
|
∂ट |
|
∂ट |
|
≠ o असले पाहिजे. |
|
∂ड |
|
∂ढ |
|||
|
|
|
|
|||
|
|
|
|
|||
|
∂ठ |
|
∂ठ |
|||
|
∂ड |
|
∂ढ |
|
à |
= |
à |
= (क्ष, य, झ) |
= |
à |
(ट, ठ) |
|
र |
र |
र |
हा जर पृष्ठावरील कोणत्याही बिंदूचा स्थान सदिश असेल, तर ज्या ठिकाणी
|
क्षट |
यट |
झट |
|
क्षठ |
यठ |
झठ |
या आव्यूहाची कोटी २ असेल ते नियमित बिंदू व जेथे ती २ पेक्षा कमी असेल ते एकमात्र बिंदू असे म्हणतात. खालील विवेचनात पृष्ठाच्या ज्या भागात सर्व बिंदू नियमित आहेत असेच भाग विचारात घेतले आहेत.
फ (ट, ठ) =o अशा समीकरणाने पृष्ठावरील एक वक्र निश्चित होतो कारण सूत्र (११) चा उपयोग करून क्ष, य, झ हे एका प्रचलाची फलने आहेत हे दाखविता येते. ट = क (स्थिरांक) आणि ठ = ख (स्थिरांक) या समीकरणांनी निश्चित होणाऱ्या वक्रांना पृष्ठावरील सहनिर्देशक वक्र म्हणतात. क आणि ख निरनिराळी मूल्ये
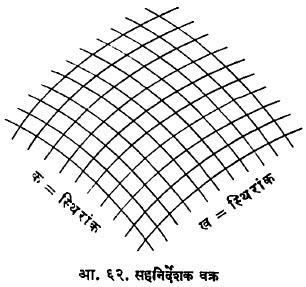
घेतील तसे पृष्ठ या सहनिर्देशक वक्रांच्या जाळ्याचे आच्छादिले जाईल (आ. ६२). प्रत्येक प्रणालीचा एक वक्र पृष्ठावरील बिंदूतून जाईल.
पहिले मूलभूत रूप :
|
प |
à |
आणि |
ब |
( |
à |
à |
) |
हे पृष्ठांवरील समीपस्थ बिंदू असल्यास |
|
र’ |
र + d |
र |
|
à |
= |
à |
dट |
+ |
à |
dठ. |
|
पब |
dरट |
रठ |
|
कंस पम =d च असेल, तर सीमा |
कंस |
पम |
= |
१ |
असल्यामुळे खालील सूत्र मिळते. |
|
जीवा |
पम |
|
(d च)२ |
= |
à |
= |
( |
à |
dट |
+ |
à |
dठ |
) |
२ |
|
(dर)२ |
रट |
रठ |
|
= क d ट२ + २ ख d ट d ठ + ग d ठ२… (१२)
क, ख आणि क ग – ख२ ही घन असतात. सूत्र (१२) मधील द्विघाती अवकल रूपास पृष्ठाचे पहिले मूलभूत रूप किंवा पृष्ठाचे मानीय असे म्हणतात. सहनिर्देशक वक्रांवर कंस लांबी d च =√ कdट आणि d च =√ ग d ठ अशी मिळेल. पृष्टाचे जे गुणधर्म केवळ त्याच्या मानीयावर अवलंबून असतात व जे अन्वालोपीय अवकाशावर अवलंबून नसताना त्यांना पृष्ठाचे अंगभूत गुणधर्म म्हणतात. पृष्ठावरील कोणत्याही वक्राची स्पर्शिका ही अर्थातच पृष्ठाचीही स्पर्शिका आहे.(d ट, d ठ) आणि (δ ट, δ ठ) या प बिंदूत दोन स्पर्शिका असल्यास त्यांच्यामधील कोन (q) खालील सूत्राने मिळतो.
|
कोज्याq = |
क |
dट |
. |
δट |
+ख |
( |
dट |
. |
δठ |
+ |
dठ |
. |
δट |
) |
|
dच |
δच |
dच |
δच |
dच |
δच |
|
+ ग |
dठ |
. |
δठ |
|
dच |
δच |
या दिशा जर सहनिर्देशक वक्राच्या दिशा असतील, तर
|
कोज्या q = |
ख |
|
√क ग |
म्हणजे सहनिर्देशक वक्र जात्य असण्यास ख =o ही अट आवश्यक व पुरेशी आहे.
गोलावर अक्षांश qव रेखांश fहे वक्ररेषीय सहनिर्देशक निवडल्यास गोलाची प्रचलीय समीकरणे खालीलप्रमाणे होतात.
क्ष= अ कोज्या q . कोज्या f, य = अ कोज्या q . ज्या f, झ= अ ज्या q.
गोलाचे मानीय dच२ = अ२ q२+अ२ (कोज्या q)२ df२ असे होईल. या ठिकाणी ख =o म्हणून अक्षांश-रेखांश वर्तुळे ही एकमेकांस जात्य आहेत.
|
|
à |
|
|
अभिलंब व स्वर्शप्रतल : पृष्ठाला प |
(र) |
या बिंदूत स्पर्श करणार्या सर्व रेषा एका प्रतलावर असतात व हे प्रतल
|
|
à |
à |
या दोन सदिशांनी निश्चित होईल. |
|
रट आणि |
रठ |
प बिंदूतील पृष्ठाच्या स्पर्शप्रतलाचे समीकरण खालीलप्रमाणे होईल.
|
क्ष – क्ष |
य – य |
झ – झ |
=o |
|
क्षट |
यट |
झट |
|
|
क्षठ |
यठ |
झठ |
![]()
![]()
प मध्ये स्पर्शप्रतलाला लंब असलेल्या रेषेला पृष्ठाचा अभिलंब म्हणतात.
|
à |
हा जर एकक अभिलंब सदिश असेल, तर |
|
ल |
|
à |
= |
( |
यटझठ-यठझट |
, |
झटक्षठ-क्षटझठ |
, |
क्षटयठ-यटक्षठ |
) |
|
ल |
[ ∑ कग – ख२] १/२ |
[∑ कग – ख२ ]१/२ |
[∑ क ग – ख२ ]१/२ |
|
त = |
à |
. |
à |
, |
थ = |
à ल |
. |
à |
, |
द = |
|
||||
|
ल |
रटट |
रठठ |
या अदिश राशी खालील विवेचनामध्ये महत्त्वाच्या आहेत.
अभिलंब वक्रता : समजा प बिंदूतील अभिलंबातून व (d ट, d ठ) या स्पर्शदिशेतून जाणारा पृष्ठाचा प्रतल छेद घेतला आहे. अभिलंबातून जाणाऱ्या छेदास अभिलंब छेद म्हणतात. या अभिलंब छेदाने आपल्याला पृष्ठावर असा एक वक्र मिळेल की, ज्याचा प बिंदूतील प्रधान अभिलंब हा पृष्टाचाही प बिंदूतील अभिलंब असेल. या अभिलंब छेद वक्राची वक्रता जर kल असेल, तर फ्रेनेत-सेरेत सूत्रान्वये
|
à |
= |
kल . |
à |
|
र’’ |
ल |
|
|
kल |
= |
à |
. |
à |
यावरून खालील महत्त्वाचे सूत्र मिळते. |
|
ल |
र |
|
Kल |
= |
त d ट२ |
+ |
२ थ dट dठ |
+ |
द dठ२ |
|
क d ट२ |
+ |
२ ख dट dठ |
+ |
ग dठ२ |
Kल यास पृष्ठाची (d ट, dठ) या दिशेची अभिलंब वक्रता म्हणतात. (d ट, d ठ) या स्पर्शदिशेतून जाणारा एक तिर्यक् प्रतल छेद घेतला व त्या वक्राची वक्रता K असली आणि या दोन छेदांमधील कोन qअसेल, तर मन्ये प्रमेय (जे. बी. एम्. सी. मन्ये द ला प्लेस या फ्रेंच गणितज्ञांच्या नावाने ओळखण्यात येणारे प्रमेय) खालील सूत्राने व्यक्त होते :
Kल=K कोज्या त dट२+२ थ d ट d ठ + द d ठ२ या द्विघाती अवकलरूपास पृष्ठांचे दुसरे मूलभूत रूप म्हणतात. हे मूलभूत रूप अन्वालोपीय अवकाशावर अवलंबित असल्यामुळे यापासून सिद्ध केलेले पृष्ठाचे गुणधर्म अंगभूत गुणधर्म मानता येणारे नाहीत.
|
प |
à |
, |
ब |
à |
+ |
d |
à |
|
(र) |
र |
र |
हे पृष्ठावरील दोन समीपस्थ बिंदू आहेत. प बिंदूतील स्पर्शप्रतलावर ब पासून काढलेल्या लंबाची लांबी (स) खालील सूत्राने मिळते.
|
स |
= |
à |
. |
à |
= |
१ |
(त d ट२ + २ थ d ट d ठ + द d ठ२) (वरच्या क्रमाची पदे गाळून). |
|
ल |
dर |
२ |
प शेजारील पृष्ठाचा भाग जर स्पर्शप्रतलाच्या एकाच बाजूस असेल, तर स चे चिन्ह कोणत्याही दिशेने सारखेच असेल. म्हणजे त द – थ२ >o अशा बिंदूस विवृत्तीय बिंदू म्हणतात. उदा., विवृत्तज पृष्ठावरील कोणताही बिंदू. याउलट प शेजारील पृष्ठाचा भाग स्पर्शप्रतलाच्याय दोन्ही बाजूंस असेल, तर स चे चिन्ह बदलेल. म्हणजे तद – थ२ <o अशा बिंदूस अपास्तीय बिंदू म्हणतात. उदा., अपास्तीय अन्वस्तज पृष्ठावरील कोणताही बिंदू. जर त द – थ२ =o असेल, तर तd ट२ +२ थ d ट d ठ + द d ठ२ हा पूर्ण वर्ग होईल व सचे चिन्ह एका दिशेव्यतिरिक्त नेहमी एकच राहील. या विशिष्ट दिशेने kल =o अशा बिंदूस अन्वस्तीय बिंदू म्हणतात. उदा., चितीवरील कोणताही बिंदू.
क, ख, ग, त, थ, द या सहा अदिश राशी पूर्णपणे स्वतंत्र नाहीत. त्यांना जोडणारी दोन समीकरण आहेत. त्यांना गौस-कोदातत्सी समीकरणे (गौस व इटालियन गणितज्ञ डी. कोदातत्सी यांच्या नावावरून) म्हणतात. पृष्ठासंबंधीचा मूलभूत सिद्धांत असा आहे : क, ख, ग, त, थ, द या राशी (ट, ठ) ची फलने या स्वरूपात दिली असता जेव्हा ती गौस-कोदातत्सी समीकरणांनी संबंधित असतात तेव्हा पृष्ठ त्याच्या अवकाशातील स्थानाव्यतिरिक्त पूर्णपणे निश्चित होते’.
प्रधान दिशा : प बिंदूत ज्या अनंत स्पर्शदिशा आहेत त्यांमध्ये दोन दिशा अशा आहेत की, ज्या दिशांना पृष्ठाची अभिलंब वक्रता kल हिचे मूल्य कमाल किंवा किमान होते.
|
kल |
= |
त |
d ट |
२ |
+ |
२ थ |
d ट |
+ |
द |
|
d ठ |
|
d ठ |
|||||||
|
क |
d ट |
२ |
+ |
२ ख |
d ट |
+ |
ग |
||
|
d ठ |
|
d ठ |
|
हे |
d ट |
चे फलन आहे. |
|
d ठ |
त्याच्या कमाल व किमान मूल्यांचा विचार केल्यास खालील अवकल समीकरण मिळते.
|
(क थ – ख त) |
d ट |
२ |
+ |
(क थ – ग त) |
d ट |
+ |
ख द – ग थ |
= ० |
|
d ठ |
|
d ठ |
हे समीकरण प्रत्येक बिंदूत दोन परस्पर लंब अशा पृष्ठांवरील दिशा निश्चित करते. या दिशांना प्रधान दिशा म्हणतात व ज्या वक्राची प्रत्येक बिंदूतील स्पर्शदिशा ही प्रधान दिशा असेल त्यास वक्रता रेषा म्हणतात. प्रत्येक बिंदूतून दोन वक्रता रेषा मिळतात. ज्या बिंदूत क : ख : ग = त : थ : द असेल त्या ठिकाणी प्रधान दिशा अनिश्चित असतील आणि या बिंदूतून कोणत्याही दिशेने अभिलंब वक्रता kल ही सारखीच असेल. अशा बिंदूंना शून्य वृत्तक म्हणतात. गोलावरील प्रत्येक बिंदू शून्य वृत्तक असतो.
पृष्ठावरील दोन समीपस्थ बिंदूंतून जर अभिलंब काढले, तर सर्व साधारपणे ते एकमेकांस छेदत नाहीत पण ते जर वक्रता रेषेवरील बिंदू असतील, तरच फक्त ते एकमेकांस छेदतात. यावरून प्रधान दिशेची व्याख्या अशीही देता येईलः ‘ज्या दिशेने पृष्ठाचे समीपस्थ अभिलंब एकमेकांस छेदतात तिला प्रधान दिशा म्हणतात’.
प्रधान वक्रता : पृष्ठाची प्रधान दिशांनी अभिलंब वक्रता जर k१, k२असेल, तर त्यांना प्रधान वक्रता म्हणतात. k १, k२या वक्रता रेषांच्या वक्रता नाहीत.
|
P१ |
= |
१ |
|
K१ |
व
|
P२ |
= |
२ |
|
K२ |
या प्रधान वक्रता त्रिज्या व प बिंदूतील अभिलंबावर म१, म२ हे बिंदू असे घेतले की, पम१ =p१, पम२ =p२, तर म१, म२ ही दोन वक्रता केंद्रे होतील. K१, k२ खालील समीकरणाने निश्चित होतात.
|
(क ग – ख२) |
K2 |
– |
(क द – २ ख थ + ग त) |
k |
+ |
(त द – थ२) |
= ० |
|
k |
= |
१ |
(k१ + k२) |
= |
क द – २ ख थ + ग त |
माध्य (सरासरी) वक्रता आणि |
|
२ |
२(क ग–ख२) |
|
k |
= |
k१ k२ |
= |
त द – थ२ |
|
क ग – ख२ |
यास गौसीय वक्रता किंवा पृष्ठाची समग्र वक्रता म्हणतात. प्रत्येक बिंदूत जर k=o असेल, तर पृष्ठात अल्पिष्ट पृष्ठ म्हणतात आणि प्रत्येक बिंदूत जर k=o असेल, तर त्यास विकसनीय पृष्ठ म्हणतात. क, ख, ग, त, थ, द यांना जोडणाऱ्या गौस-कोदातत्सी समीकरणांचा उपयोग करून त द – थ२ हे फक्त, क, ख, ग व त्यांचे अवकलज यांमध्ये व्यक्त करता येतात. म्हणजे पृष्ठाची समग्र वक्रता k ही पृष्ठाच्या अंगभूत गुणधर्मावरच फक्त अवलंबून आहे.
समग्र वक्रता k याची व्याख्या अशी देता येईल : स पृष्ठावर प बिंदूभोवती व या वक्राने मर्यादित असा प्र ही छोटासा भाग घेतला. एकक त्रिज्येचा एक गोल घेऊन त्याच्या केंद्रबिंदूमधून व वक्रावरील प्रत्येक बिंदूत पृष्ठाला अभिलंब असणाऱ्या दिशेला समांतर रेषा काढल्या असता व’ वक्र तयार होईल. जेव्हा
|
प्र ⟶ |
प |
तेव्हा |
व’ने बंधित क्षेत्रफळ |
|
व ने बंधित क्षेत्रफळ |
या गुणोत्तराची जी सीमावस्था होईल तिला स ची प बिंदूतील समग्र वक्रता म्हणतात.
पृष्ठावरील वक्रता रेषा सहनिर्देशक वक्र म्हणून निवडले, तर ख = o, थ = o या अटी पूर्ण होतील व प्रधान वक्रतांची मूल्ये
|
k१ |
= |
त |
(d ट = o या दिशेने), |
k२ |
= |
द |
(d ट = o या दिशेने) |
|
क |
ग |
अशी होतील.
प मधून d ठ = o या दिशेशी Y कोन करणारी दिशा घेतली व या दिशेने अभिलंब वक्रताkल असेल, तर
kल= k१कोज्या२ Y+ k२ ज्या२ Y
हे अभिलंब वक्रतेसंबंधीचे ऑयलर समिकरण झाले. प मधून दोन परस्पर लंब दिशा घेतल्या आणि त्या दिशांनी अभिलंब वक्रता kल, kल असतील, तर ऑयलर समीकरणावरून kल + kल = k१ + k२ हे पी. सी. एफ्. द्यूपँ या फ्रेंच गणितज्ञांच्या नावाने ओळखण्यात येणारे समीकरण मिळते.
अनंतवर्ती रेषा :पृष्ठावरील ज्या दिशेने अभिलंब वक्रता kल शून्य असते त्या दिशेस अनंतवर्ती दिशा म्हणतात. ज्या वक्राची प्रत्येक बिंदूतील स्पर्शदिशा ही अनंतवर्ती दिशा असते त्या वक्रास अनंतवर्ती रेषा म्हणतात. kल देणाऱ्या सूत्रावरून या रेषांचे अवकल समीकरण खालील प्रमाणे होईल : त d ट२ + २ थ d ट d ठ + द d ठ२ =o म्हणजे पृष्ठाच्या प्रत्येक बिंदूमधून दोन अनंतवर्ती रेषा काढता येतात. अर्थात जर त द – थ२ < ० असेल, तरच या रेषा सत् रेषा असतात. अनंतवर्ती रेषांचा विशेष गुणधर्म म्हणजे त्यांवरील बिंदूतील अधिस्पर्शी प्रतल हे पृष्टाचे त्या बिंदूतील स्पर्शप्रतल असते.
प आणि ब या पृष्ठांवरील समीपस्थ बिंदूंतील स्पर्शप्रतलांची छेदरेषा जर प र या दिशेने असेल, तर
|
à |
à |
या दोन दिशांना संयुग्म दिशा म्हणतात. |
|
पब आणि |
पर |
(d ट, d ठ) आणि (δ ट, δ ठ) या जर संयुग्म दिशा असतील, तर त d ट δ ठ + थ (d ट δ ठ + d ठ δ ट) + द d ठ δ ठ = ० यावरून प्रधान दिशा या संयुग्म दिशा आहेत आणि अनंतवर्ती दिशाही स्वसंयुग्म दिशा आहे, हे दिसून येईल. सहनिर्देशक वक्र दिशा जर संयुग्म दिशा असतील, तर थ = ०.
अल्पांतरी रेषा :पृष्ठावरील प्रत्येक बिंदूमधून व प्रत्येक दिशेने जाणारा असा एक वक्र असतो की, ज्याचा प्रधान अभिलंब हा पृष्ठाचाही अभिलंब असतो. या वक्रांना पृष्ठाच्या अल्पांतरी रेषा म्हणतात. कारण या रेषा पृष्ठावरील दोन बिंदूंमधील अल्पतम अंतर देतात आणि म्हणून प्रतलावरील सरळ रेषांना समधर्मी असे हे पृष्ठावरील वक्र आहेत. गोलावरील महावृत्ते ही त्यावरील अल्पांतरी रेषा आहेत. अल्पांतरी रेषांचे अवकल समीकरण हे क, ख, ग आणि त्यांचे अवकलज यांवर अवलंबून असते. म्हणजे हे पृष्ठांचे अंगभूत वक्र आहेत. वक्रता रेषा व अनंतवर्ती रेषा या मात्र अन्वालोपीय अवकाशावर अवलंबून असतात.
अल्पांसरीय वक्रता : प मधून जाणारा पृष्ठावरील व हा एक वक्र आहे.
|
à |
हा त्याचा एकक स्पर्शसदिश असल्यास |
à |
हा त्याचा वक्रता सदिश होईल. |
|
ट |
ट’ |
|
à |
हा पृष्ठाचा प बिंदूतील एकक अभिलंब सदिश व |
à |
हा पृष्ठाचा प बिंदूतील एकक अभिलंब सदिश व |
|
ल |
ट* |
|
à |
ला लंब घेतला आहे. प बिंदूत |
à à à टट*, ल या परस्पर लंब एकक सदिशांची त्रयी तयार होते. |
|
ट |
|
à |
à ल या दिशेचा वियोजित भाग हा अभिलंब वक्रता kल बरोबर असतो. |
|
ट’ चा |
|
à |
à ट* या दिशेचा वियोजित भाग kम असेल, तर |
|
ट’ चा |
|
à |
= |
à |
= |
à |
|
à |
|
|
d ट’ |
ट’ |
kलल |
+ |
kमट* |
यास त्या वक्राची अल्पांतरीय वक्रता म्हणतात. |
||
|
d च |
|
|
व हा वक्र जर अल्पांतरी रेषा असेल, तर
|
à |
à |
|
ट’ आणि |
ल एकाच दिशेने असतील म्हणजे kम= o होईल. |
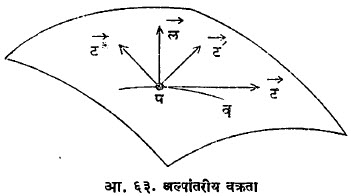
व जर अनंतवर्ती असेल, तर या दिशेने kल=o असते म्हणून व ची वक्रता ही व च्या अल्पांतरी वक्रतेबरोबर असते. kमफक्त क, ख, ग व त्याचे अवकलज आणि व हा वक्र यांवर अवलंबून असते म्हणजे kम पृष्ठाच्या अंगभूत गुणधर्मावर अवलंबून आहे.
चित्रण किंवा संगती :प (ट, ठ), प (ट, ठ) हे स आणि स या पृष्ठावरील बिंदू आहेत. ट = फ१, (ट, ठ), ठ = फ२ (ट, ठ) या समीकरणांनी स च्या काही भागाचे स वरील काही भागावर चित्रण निश्चित होईल. फ१, फ२ ही फलने एकदिक् आहेत. फ१ट फ२ट…. वगैरे अवकलज संतत फलने आहेत व
|
फ१ट |
फ१ठ |
≠ ० |
|
फ२ट |
फ२ठ |
![]()
![]()
ही अटही पूर्ण होते असे मानले आहे. वरील समीकरणांनी स वर (ट, ठ) ⟶ (ट, ठ) असे सहनिर्देशक रूपांतर केल्यास स आणि स यावरील ज्या बिंदूचे तेच सहनिर्देशक आहेत, ते संगत बिंदू होतील. दोन पृष्ठामधील चित्रणाचे पुढील प्रकार आहेत : (१) सममात्रीय चित्रण : यामध्ये लांबी स्थिर रहाते म्हणून सममात्रीय पृष्ठाचे अंगभूत गुणधर्म सारखेच असतात. (२) अनुरूपी चित्रण : यामध्ये कोन बदलत नाहीत. (३) अल्पांतरीय चित्रण : यामध्ये अल्पांतरी रेषा स्थिर रहातात. (४) समक्षेत्रीय चित्रण : यामध्ये क्षेत्रफळ अचल असते.
विशिष्ठ प्रकारची पृष्ठे :जे पृष्ठ चल रेषेने रेखाटले जाते त्यास रेषाजनित पृष्ठ म्हणतात. सर्वसाधारणणे अशा पृष्ठांच्या समीपस्थ जनक रेषा एकमेकींना छेदत नाहीत पण ज्या वेळी त्या छेदतात त्या वेळी विकसनीय पृष्ठ तयार होते. चिती व शंकू ही विकसनीय पृष्ठाची नेहमीची उदाहरणे आहेत. समग्र वक्रता K स्थिर असणारे पृष्ठ. विकसनीय पृष्ठावर K = o, K जर धन असेल, तर पृष्ठ गोल असतो व K जर ऋण असेल, तर पृष्ठ विकृत गोल असतो. शिवाय अल्पिष्ट पृष्ठ (k= o), समांतर पृष्ठ अशा निरनिराळ्या प्रकारच्या पृष्ठांचे गुणधर्म अवकल भूमितीत अभ्यासिले जातात.
वरील विवेचनामध्ये पृष्ठाच्या स्थानीय गुणधर्मांचा विचार केलेला आहे. पृष्ठाच्या मर्यादा, संबद्धता, संहतता वगैरे व्यापक गुणधर्मांचा अभ्यास ⇨ संस्थितिविज्ञानात केला जातो.
रीमानीय भूमिती
रीमान ह्या जर्मन गणितज्ञांनी दोन बिंदूंमधील अंतर देणारे सूत्र (मानीय) व्यापक करून त्यावर आधारित केलेली न-मितीय अवकाशाची अवकल भूमिती म्हणजेच रीमानीय भूमिती होय. ऐतिहासिक दृष्ट्या या भूमितीच्या अभ्यासाची सुरुवात १८५४ मध्ये गटिंगेन विद्यापीठात तत्त्वज्ञान शाखेच्या सभेपुढे रीमान यांनी वाचलेल्या निबंधाने झाली, असे म्हणता येईल. हा निबंध रिमान यांच्या मृत्यूनंतर १८६८ साली प्रसिद्ध झाला. गौस यांनी अवकाशातील पृष्ठाच्या भूमितीमध्ये जे निष्कर्ष काढले होते त्यांमधील बहुतेक संकल्पनांचे व्यापकीकरण करून त्या न-मितीय अवकाशाच्या भूमितीतही कशा प्रस्थापित करता येतील याचा विचार या निबंधात केलेला आहे. सुरूवातीच्या काळात या भूमितीच्या विकासाला हातभार लावणाऱ्या गणितज्ञांमध्ये एल्. व्यांगकी, ई. बेल्ट्रामी, सी. जी. रीत्वी, ई.बी. क्रिस्टोफेल, आय्. शूर, आर्. लिपशिट्झ यांची नावे महत्त्वाची आहेत. रीत्ची या इटालियन गणितज्ञांनी १८८७ मध्ये प्रदिश कलनशास्त्राच्या [⟶ प्रदिश] साहाय्याने या भूमितीच्या अभ्यासास सुसंबद्ध स्वरूप प्राप्त करून दिले.
अवकल भूमितीमध्ये जे गुणधर्म सहनिर्देशक रूपांतरामध्ये बदलत नाहीत अशा गुणधर्मांचा अभ्यास केला जातो. म्हणूनच जे गणितीय घटक वापरवयाचे तेही असेच सहनिर्देशक रूपांतरामध्ये बदलणार नाहीत असे असावयास पाहिजेत. याकरिता रीमानीय भूमितीमध्ये प्रदिश या गणितीय घटकाचा वापर केलेला आहे.
प्रदिश बीजगणित :कोणतेही न सत् स्वचल (क्षट) (ट = १, २,…, न) हे एका अखंड न-मितीय अवकाशातील बिंदूचे सहनिर्देशक मानता येतील. कारण या न स्वचलांच्या मूल्यांचा प्रत्येक संच हा या अवकाशातील एक बिंदू निश्चित करील. अशा न-मितीय अवकाशाला अ न हे चिन्ह वापरतात. ट, ठ,……. वगैरे अनुप्रत्ययांक (शिरांक व पादांक) नेहमी १, २,….. न अशी मूल्ये घेतात, असे खालील विवेचनात मानले आहे. फ ट (क्ष१, क्ष२,….., क्षन) ही न स्वचल फलने आहेत
|
म्हणजे |
∂ फट |
≠ ० |
आणि त्यांचे अवकलज संतत आहेत. |
|
∂ क्षठ |
क्ष’ट=फट (क्ष१, क्ष२, …..क्षन) ही न समीकरणे अन मध्ये (क्षट) या सहनिर्देशक पद्धतीचे (क्ष’ट) या पद्धतीमध्ये रूपांतर करणारी सूत्रे आहेत.
|
∂ फट |
≠ ० |
|
∂ क्षठ |
असल्यामुळे वरील समीकरणे सोडवून क्षट = मट(क्ष’१, क्ष’२,….., क्ष’न) या स्वरूपात मांडता येतील. प(क्षट) आणि ब (क्षट + d क्षट) असे अ न मधील दोन समीपस्थ बिंदू घेतल्यास (d क्षट) हे घटक पबची दिशा निश्चित करतात. हीच दिशा (क्ष’ट) या पद्धतीमध्ये (d क्ष’ट) या घटकांनी निश्चित होईल.
|
तसेचd क्ष’ट |
= |
∂ क्ष’ट |
d क्षठ |
|
|||
|
∂ क्षठ |
|
||||||
|
∂ क्ष’ट |
d क्षठ |
|
न |
∂ क्ष’ट |
d क्षठ |
||
|
= |
∑ |
||||||
|
∂ क्षठ |
|
ठ=१ |
∂ क्षठ |
||||
हा संकेत रूढ आहे व तो या विवेचनात वापरलेला आहे. याला संयुती संकेत म्हणतात.) (d क्षट) आणि d क्ष’ट) हे दोन सहनिर्देशक पद्धतींमधील एका प्रचलित सदिशाचे [⟶ प्रदिश] घटक आहेत. सर्वसाधारणपणे (कट) ही न फलने सहनिर्देशक रूपांतरामध्ये जेव्हा
|
क’ट |
= |
क’ठ |
∂ क्ष’ट |
|
∂ क्षठ |
अशी रूपांतरित होतात तेव्हा (कट) हे (क्षट) पद्धतीमध्ये एका प्रतिचल सदिशाचे घटक असतात. त्याचप्रमाणे (खट) ही न फलने
|
ख’ट |
= |
ख’ठ |
∂ क्षठ |
|
∂ क्ष’ट |
याप्रमाणे रुपांतरित झाली, तर ती एका सहचल सदिशाचे घटक असतात.
|
सामान्यपणे जेव्हा नत+पफलने |
( |
क |
ट१ ट२….ट त |
) |
सहनिर्दशक रूपांतरामध्ये |
|
ठ१ ठ२….ठथ |
|
क’ |
ट१ ट२….टत |
= |
क |
ड१ ड२….डत |
∂ क्ष’ट१ |
. |
∂ क्ष’ट२ |
…. …. |
∂ क्ष’ढ१ |
. |
∂ क्ष’ढ२ |
|
ठ१ ठ२….ठथ |
ढ१ ढ२….ढथ |
∂ क्षड१ |
∂ क्षड२ |
∂ क्ष’ठ१ |
∂ क्ष’ठ२ |
अशी रूपांतरित होतात, तेव्हा ती फलने त + थ कोटीच्या मिश्र प्रदिशाने घटक मानले जातात.
|
∂ क्ष’ट |
. |
∂ क्षड |
= |
ट |
क्रोनेकर डेल्टा : |
ट |
= |
= ०, ट ¹ ० |
|
∂ क्षड |
∂ क्ष’ठ |
dठ |
∂ठ |
= |
= १, ट = ० |
असल्यामुळे वरील समीकरणे खालीलप्रमाणे लिहिता येतील.
|
क |
ट१ ट२….टत |
= |
क’ |
ड१ ड२….डत |
∂ क्षट१ |
. |
∂ क्षट२ |
…. …. |
∂ क्ष’ढ१ |
. |
∂ क्ष’ढ२ |
|
ठ१ ठ२….ठथ |
ढ१ ढ२….ढथ |
∂ क्ष’ड१ |
∂ क्ष’ड२ |
∂ क्षठ१ |
|
∂ क्षठ२ |
सहचल किंवा प्रतिचल सदिश हे एक कोटीचे प्रदिश आहेत. तसेच फ (क्ष१, क्ष२, …..क्षन) हे फलन अदिश असल्यामुळे ते शून्य कोटीचा प्रदिश आहे, असे मानता येईल. प्रदिशाचे सममिती (क टठ = कठट) किंवा विषममिती (क टठ =–कठट) हे गुणधर्म सहनिर्देशक रूपांतरामध्ये स्थिर रहातात.
एकाच कोटीचा व एकाच प्रकारच्या प्रदिशांची बेरीज किंवा वजाबाकी केल्यास पुन्हा त्याच कोटीचा व त्याच प्रकारचा प्रदिश मिळतो ( उदा., क टठ + ख टठ = ग टठ).
त व थ कोटींच्या प्रदिशांचा बाह्म गुणाकरा केल्यास त + थ कोटींचा प्रदिश मिळतो. उदा., कटठ आणि ख ड, या प्रदिशांचा बाह्म गुणाकार कटठ ख ड हा मिश्र त्रिकोटीचा प्रदिश आहे. दोन प्रदिशांचा आंतर गुणाकार हा प्रथम त्यांच्या बाह्म गुणाकार घेऊन नंतर संकोचन क्रियेचा वापर करुन मिळतो. उदा., कटठ आणि खडढ या प्रदिशांचा बाह्य गुणाकार हा चतुर्थ कोटीचा प्रदिश कटठ खडढ हा आहे. यानंतर संकोचन क्रिया वापरून
|
क ट ठ ख ट ढ = क १ ठ ख १ ढ + क |
२ठ |
+ |
…….. |
+ क |
नठ |
|
२ढ |
नढ |
हा द्विकोटीचा प्रदिश कटठ आणि खडढ यांचा एक आंतर गुणाकार आहे. याप्रमाणे कटठ. खडट, कटठ. खठढ, कटठ. खडठ हेही त्यांचे आंतर गुणाकार होऊ शकतील.
फलनांचा एखादा समूह हा प्रदिशाचा घटक समूह आहे की काय हे ठरविण्यासाठी एक उपयुक्त अशी कसोटी आहे. कट हा कोणताही प्रतिचल सदिश आहे आणि कट खटतथ हा आंतर गुणाकार जर द्विकोटीचा सहचल प्रदिश असेल, तर खटतथ ही त्रिकोटीचा सहचल प्रदिश असला पाहिजे. एखाद्या प्रदिशाचे सर्व घटक जर एका सहनिर्देशक पद्धतीमध्ये शून्य असतील, तर ते दुसऱ्या कोणत्याही पद्धती मध्ये लोप पावतील. ही गोष्ट प्रदिशाच्य व्याख्येवरून स्पष्ट होते. याचा अर्थ असा होतो की, प्रदिश समीकरण हे सहनिर्देशक रूपांतरामध्ये स्थिर रहाते. याच कारणामुळे प्रदिशाचा भूमिती व भौतिकी यांमध्ये विशेष उपयोग होतो.
रीमान मानीय : वरील विवेचनामध्ये मापनावर आधारित अशा कोणत्याच गुणधर्मांचा विचार आलेली नाही कारण अशा गुणधर्मांना लागणारा पाया अन मध्ये तयार करावयास हवा. रीमान यांनी असे सुचविले की, (क्षट) आणि (क्षट + d क्षट) या दोन बिंदूंमधील अंतर d च हे मोजण्यासाठी d च२ = गटठ d क्षट d क्षठ या सूत्राचा उपयोग करावा. या सूत्रास रीमान मानीय आणि असे मानीय ज्या अन मघ्ये वापरले आहे त्यास रीमानीय अवकाश रहणतात. गटठ हा द्विकोटी समभित सहचल प्रदिश आहे |ग टठ| = ग≠ ०.गटठ d क्षट d क्षठहे रुप धनात्मक निश्चित रुप आहे असे सुलाभतेसाठी गृहीत धरतात पण हे आवश्यकच आहे असे नाही. ⇨ सापेक्षता सिद्धांतात ४–मितीय अवकाशात हे धनात्मक निश्चित रुप नसते .गटठ d क्षट d क्षठ = d च२ हा (d क्षट) ह्या प्रतिचल सदिशाच्या परि-माणाचा वर्ग आहे असे म्हणता येईल . (d क्षट) आणि (δ क्षट) असे एका बिदूमधून दोन सदिश घेतल, तर त्यांच्यामघील कोन qहा
|
कोज्या q= |
गटठ |
dक्षट |
. |
dक्षठ |
|
dच |
dच |
या सूत्राने निश्चित होतो.गटठ ही न२फलने रवालीलप्रमाणे व्याख्यात केली
|
गटठ = |
ग मधील गटठ चा सहअवयव |
|
[ग= । गटठ ।], |
|
ग |
तर की द्विकोटी सममित प्रतिचल प्रदिशाचे घटक असतात आणि
|
गटठ गठड |
= |
ड |
|
∂ट |
असे सूत्र मिळचे. गटठ व गटठ यांना रीमानीय अवकाशाचे मूलभूत संयुग्म प्रदिश म्हणतात. या मूलभूत प्रदिशांच्या साहाय्याने प्रदिशांचे अनुप्रत्ययांक वर-खाली करण्याची क्रिया केली जाते उदा
|
गटड |
ट |
= |
खडठ |
, |
गठड |
ट |
= खटड |
|
खठ |
खठ |
|
ट |
आणि खडठ |
|
खठ |
यांना सहप्रदिश म्हणतात. तसेच
|
ट |
व खटड |
|
खठ |
हे सगप्रदिश होतील.∫∫…∫प्रd क्ष१ d क्ष२….d क्षन हा समाकल सहनिर्देशक रूपांतरामध्ये ∫∫…∫प्रJd क्ष’१d क्ष’२….d क्ष’ न याप्रमाणे रुपांतरित होतो. प्र हा अन अवकाशाचा एक भाग आहे व
|
J = |
∂ क्षट |
|
∂ क्ष’ठ |
ग = । गटठ । हा निर्धारक ग’=J२ ग असा रूपांतरित होतो. म्हणून समाकल
∫∫…∫√ ग d क्ष१ d क्ष२……. d क्षनसहनिर्देशक रुपांतरामध्ये स्थिर रहातो. या समाकलाचे मूल्य हे प्र या प्रदेशाचे घनफळ होते.
सहचल अवकलज :पहिल्या व दुसऱ्या प्रकारची क्रिस्टोफेल चिन्हे या नावाने ओळखली जाणारी फलने खालीलप्रमाणे आहेत.
|
[ड, टठ]= |
१ |
( |
∂ गटड |
+ |
∂गठड |
– |
∂गटठ |
) |
|
|
२ |
∂ क्षठ |
∂क्षट |
∂क्षड |
, |
|
{ |
ड |
} |
= |
ग डढ [ ढ, ट ठ]. |
|
|
ट |
ठ |
||||
ही फलने प्रदिशाते घटक नाहीत हे त्यांच्या रूपांतर सूत्रावरून स्पष्ट होते. उदा., दुसऱ्या प्रकारचे चिन्ह खालीलप्रमाणे रूपांतरित होते.
|
{ |
ड |
} |
= |
{ |
त |
} |
|
|||||||||||||||
|
ट ठ
|
थ द |
|
(कट) किंवा (कट) या सदिशांचे अवकलज |
∂कट |
किंवा |
∂कट |
|
∂क्षठ |
∂क्षठ |
हे प्रदिश नाहीत, हे सहज समजून येईल परंतु
|
∂ कट |
– |
कड |
{ |
ड |
} |
= |
कट, ठ |
|
|
∂ क्षठ |
ट |
ठ |
||||||
आणि
|
∂ कट |
+ |
कड |
{ |
ट |
} |
= |
ट |
|
∂ क्षठ |
ड ठ |
क,ठ |
हे द्विकोटी प्रदिश असतात, असे दाखविता येते. क ट, ठआणि
|
क, |
ट |
|
ठ |
यांना त्या सदिशांचे सहचल अवकलज म्हणतात (स्वल्पविरामाने अवकलन दाखविले जाते).
|
क |
ट१ ट२…….. टत |
|
ठ१ ठ२…….. ठथ |
या मिश्र प्रदिशाचा सहचल अवकलज खालीलप्रमाणे मिळतो.
|
क |
ट१ ट२…….. टत |
ड = |
∂ |
क |
ट१ ट२…….. टत |
|
ठ१ ठ२…….. ठथ |
∂ क्षड |
ठ१ ठ२…….. ठथ |
|
+ क |
अ ट२…….. टत |
{ |
ट१ |
} |
+ … |
|
ठ१ ठ२…….. ठथ |
अ ड |
|
– क |
ट१ ट२…….. टत |
{ |
अ |
} |
… |
|
ठ१ ठ२…….. ठथ |
ठ१ ड |
|
तसेच ग ट ठ, ड =o, |
ट ठ |
= o, |
ट |
= o |
हे दाखविता येते. |
|
ग,ड |
δ ठ,ड |
जर अन मध्ये अशी सहनिर्देशक पद्धती असेल की, अन चे मानीय d=∑(d क्षट)२ असे असेल, तर अन हा सपाट अवकाश म्हणजेच न-मितीय यूक्लिडीय अवकाश होतो. मानीय असे रूपांतरित करणे शक्य नसल्यास अन हा वक्र अवकाश म्हणता येईल.
अन मधील ज्या बिंदूंचे सहनिर्देशक म प्रचलांची फलने असतील ते बिंदू म-मितीय उपावकाश निश्चित करतात. जर म = न – १, तर या उपावकाशास अधिपृष्ठ म्हणतात आणी म = १ असल्यास हा उपावकाश एक वक्र होतो. क्षट = फट (त) ही समीकरणे अन मधील एक वक्र करतात. या वक्रावरील दोन बिंदूंमधील अंतर च हे खालील सूत्राने मिळेल.
|
च = |
त१ |
√ गट ठ |
d क्षट |
. |
d क्षठ |
. |
d त |
|
ò |
|||||||
|
त० |
d त |
d त |
म्हणजे च हे त चे फलन आहे. म्हणजेच त च्याऐवजी च हा प्रचल कोणत्याही वक्राकरिता निवडता येईल. अन मधील विशेष महत्त्वाचे वक्र म्हणजे दोन बिंदूंमधील कमीत कमी अंतर देणाऱ्या अल्पांतरी रेषा. च हा प्रचल निवडल्यास
|
∂२ क्षट |
+ |
{ |
ट |
} |
|
|||||||
|
∂२ क्षठ |
ठ |
ड |
||||||||||
ही या रेषांची अवकल समीकरणे आहेत. यूक्लिडीय अवकाशात
|
∑ (d क्षट) २ असे मानीय असताना |
ट |
= ० म्हणजे |
|
|
ठ |
ड |
||
अल्पांतरी रेषांची समीकरणे क्षट = कट च + खट अशा स्वरूपाची होतील. म्हणून या रेषांना यूक्लिडीय अवकाशातील सरळ रेषा म्हणता येईल. रीमानीय अवकाशातील अल्पांतरी रेषा व यूक्लिडीय अवकाशातील सरळ रेषा या समानधर्मी आहेत. अन मधील प या बिंदूमधून जाणारे (d क्षट), (δ क्षट) हे सदिश घेतल्यास (त d क्षट + थ δ क्षट त, थ प्रचल) हे सदिश प मधून जाणारी एक शलाका तयार करतात. प मधून या दिशांना जाणाऱ्या अल्पांतरी रेषांनी एक अल्पांतरीय पृष्ठ तयार होते. या पृष्ठाची प बिंदूतील गौसीय वक्रता K ही अन या रीमानीय अवकाशाची (d क्षट) आणि (δ क्षट) यांनी निश्चित केलेल्या दिकस्थितीच्या बाजूने वक्रता, अशी रीमान यांनी व्याख्या केली. ही रीमानीय वक्रता खालील सूत्राने निश्चित होते.
|
K |
= |
Rटठडढd क्षट δ क्षठ d क्षड δ क्षढ |
|
|
(गडटढ गठढ-गटढ गठड) |
d क्षट δ क्षठd क्षड δ क्षढ |
||
Rटठडढ या चतुर्थ कोटीच्या प्रदिशास रीमान वक्रता प्रदिश म्हणतात. हा प्रदिश खालील सूत्राने निश्चित होतो.
|
Rटठडढ = गटद |
Rद |
|
ठडढ |
|
= गटद |
[ |
¶ |
{ |
द |
} |
– |
¶ |
{ |
द |
} |
|
¶ क्षड |
ठ ढ |
¶ क्षढ |
ठ ड |
|
+ { |
द |
} |
{ |
ध |
} |
– |
{ |
द |
} |
{ |
ध |
}] |
|
ध ड |
ठ ढ |
ध ढ |
ठ ड |
जर K=o असेल, तर अवकाश सपाट अवकाश होतो. रीमानीय अवकाश हा यूक्लिडीय अवकाश होण्यासाठी आवश्यक व पुरेशी अट Rटटडढ =o अशी आहे.
यूक्लिडीय अवकाशात सदिशांचे समांतरत्व हे दिशा-निरपेक्ष असते पण सामान्यपणे रीमानीय अवकाशात असे सदिश क्षेत्र अस्तित्वात नसते, म्हणून टी. लेअव्हि-चीव्हिता या गणितज्ञांनी खालील व्याख्या केली. क्षट=फट(च) हा एक वक्र आहे.
|
ट |
d क्षठ |
= |
d यट |
+ |
{ |
ट |
} |
यठ |
d क्षड |
= ० |
|
|
य,ठ |
d च |
d च |
ठ |
ड |
d च |
||||||
या अवकल समीकरणाची जी फले (यट) हे सदिश या वक्राच्या दिशेने समांतर आहेत असे मानावे. वरील अवकल समीकरणामध्ये
|
यट |
= |
d क्षट |
लिहिले, तर अल्पांतरी रेषेची अवकल समीकरणे मिळतात. |
|
d च |
म्हणून अल्पांतरी रेषा या स्वसमांतर रेषा आहेत असे म्हणता येईल. यूक्लिडीय अवकाशातील सरळ रेषांचाही हाच गुणधर्म आहे.
रीमानीय भूमितीमध्ये अन च्या उपावकाशांच्या अभ्यासाचाही समावेश होतो. उपावकाशाचे मानीय हे अन्वालोपी अवकाशाचे मानीय व उपावकाशाची समीकरणे यांनी निश्चित होते. उपावकाशातील अल्पांतरी रेषा, वक्रता रेषा, अनंतवर्ती रेषा यांचे गुणधर्म हे पृष्ठावरील समधर्मी रेषांच्या गुणधर्मांचे पुष्कळसे व्यापकीकरण आहे.
आइन्स्टाइन यांनी आपला व्यापक सापेक्षता सिद्धांत मांडताना ४ – मीतीय रीमानीय अवकाश विचारात घेतला आहे. या अवकाशातील सहनिर्देशक (क्ष, य, झ, ट) म्हणजे अवकाशातील स्थानदर्शक सहनिर्देशक (क्ष, य, झ) आणि कालदर्शक सहनिर्देशक ट या अवकाशाचे मानीय धनात्मक निश्चित रूप नाही. विश्वातील गुरुत्वाकर्षणामुळे हा अवकाश वक्र होतो. १९१६ मध्ये आइन्स्टाइन यांच्या व्यापक सापेक्षता सिद्धांतावरील निबंधाच्या प्रसिद्धीनंतर न-मितीय अवकाशाची अवकल भूमिती हा विषय भौतिकी व खगोलशास्त्र यांमध्येही उपयुक्त ठरेल असे दिसू लागले आणि यानंतर रीमानीय भूमितीच्या विकासास विशेष चालना मिळाली.
रीमानीय भूमितीच्या काही व्यापकीकरणांचा येथे उल्लेख केला आहे: न-मितीय अवकाशाची भूमिती मानीयावर आधारित न करता ती Γटठड अशा न३ फलनावर आधारित करावयाची. ही फलने क्रिस्टोफेल चिन्हे
|
{ |
ट |
} |
यांच्याप्रमाणे रूपांतरीत होतात. या फनांमुळे सहचल अवकलन क्रिया करता येते. |
|
|
ठ |
ड |
|||
अल्पांतरी रेषांना समधर्मी अशा रेषा या अवकाशात असतात. या भूमितीस सजातीय संबद्ध भूमिती म्हणतात. दुसऱ्या प्रकाराने झालेले व्यापकीकरण म्हणजे फन्सलर भूमिती. यामध्ये मानीय हे रीमानीय मानीयापेक्षाही व्यापक म्हणजे d च = फ(क्षट, d क्षट), [फ कोणतेही फलन] असे असते. सहचल अवकलन, समांतर सदिश वगैरे संकल्पना या भूमितीतही मांडता येतात.
बैजिक भूमिती
या भूमितीत एखाद्या योग्य सहनिर्देशक पद्धतीतील सहनिर्देशकांमधील बैजिक संबंधांवरून निर्धारित करता येईल अशा भूमितीय बिंदूपथांचा अभ्यास करण्यात येतो. अशा बैजिक संबंधात फक्त साध्या अंकगणितातील चार कृत्यांचा अंतर्भाव होतो. त्रिकोणमितीय, घातीय, लॉगरिथमीय वा इतर बीजातीत फलने [⟶ फलन], अनंत श्रेढी अथवा इतर सीमावर्ती प्रक्रिया यांचा या संबंधात समावेश होत नाही. उदा., प्रतलीय भूमितीतील बैजिक वक्राची व्याख्या फ (क्ष, य) =o यासारख्या समीकरणाने करता येईल (येथे फ ही क्ष, य सहनिर्देशकांतील बहुपदी आहे). सरळ रेषा, वर्तुळ व शांकव हे बैजिक वक्र होत. ज्या वक्रांची [उदा., त्रिकोणमितीतील ज्या फलनाचा वक्र, वृत्तज वक्र ⟶ वक्र] व्याख्या अशा प्रकारे करता येत नाही त्यांना बीजातीत वक्र म्हणतात आणि अशा वक्रांचा बैजिक भूमितीच्या अभ्यासात अंतर्भाव होत नाही. वक्रांमधील बैजिक व बीजातीत हा भेद प्रथम देकार्त यांनी सतराव्या शतकात केला.
प्रतलीय बैजिक वक्रांचे वर्गीकरण त्यांच्या समीकरणातील बहुपदीच्या घातावरून करता येते. वक्राचा घात हे वक्राशी संबंधित असलेले लक्षण भूमितीय असून तो सहनिर्देशकांच्या निवडीवर अवलंबन नाही. एक घाताचे प्रतलीय वक्र सरळ रेषा असतात. दोन घाताचे वक्र शांकव असतात. या गोष्टी प्येअर द फेर्मा यांना सतराव्या शतकात माहीत होत्या. यामुळे फेर्मा आणि देकार्त यांना बैजिक भूमितीचे संस्थापक म्हणता येईल.
अवकाशीय भूमितीत बैजिक पृष्ठ हा क्ष, य, झ या अवकाशीय सहनिर्देशकामधील फ (क्ष, य, झ) =o या एका समीकरणाने व्याख्या केलेला बिंदूपथ होय. येथे फ ही सहनिर्देशकांमधील बहुपदी असून तिचा घात हे पृष्ठाचे भूमितीय लक्षण आहे. प्रतलाच्या बाबतीत हा घात एक, तर द्विघाती पृष्ठाच्या (उदा., विवृत्तज पृष्ठ) बाबतीत तो दोन असतो, तथापि अवकाश वक्राची व्याख्या करण्यासाठी किमान दोन समीकरणे लागतात.
अधिक व्यापक दृष्टया, जर कोणत्याही जातीच्या भूमितीय घटक क्ष१, क्ष२, …,क्षन या सहनिर्देशकांनी अशा तऱ्हेने निर्धारित करता येत असेल की, क्ष१, क्ष२,….क्षन सहनिर्देशकांच्या प्रत्येक निवडीने त्या जातीचा फक्त एकच घटक निर्धारित होत असेल, तर
फ१ (क्ष१, …….,क्षन), …, फम (क्ष१,….,क्षन)…. (१) या प्रकारच्या कितीही समीकरणांनी त्या घटकांचा बैजिक बिंदूपथ निर्धारित होतो असे म्हणतात (यातील समीकरणाच्या डाव्या बाजू बहुपदी आहेत.) बैजिक बिंदूपथाला ‘प्रकार’ किंवा संवृत बैजिक संच [⟶ संच सिद्धांत] अशीही नावे आहेत.
जर (क्ष१, क्ष२,…., क्षन) हा (१) या समीकरण प्रणालीचा कोणताही निर्वाह (समीकरण प्रणाली सोडवून काढलेले उत्तर) असेल, तर तो प१ फ१+प२ फ२+…..पम फम = o (प१, प२, …,पम) या स्वेच्छ बहुपदी आहेत) या स्वरूपाच्या प्रत्येक समीकरणाचा निर्वाह होईल, हे स्पष्ट आहे. जर एखादे समीकरण असे असेल, की, ज्यात काही (सर्व नव्हे) सहनिर्देशकांचाच अंतर्भाव झालेला असेल, तर ते सर्व (एकूण) सहनिर्देशक निरवलंबी (स्वतंत्र) नाहीत असे म्हणतात. दिलेल्या बिंदुपथाच्या बाबतीत अधिकतम निरवलंबी असणाऱ्या सहनिर्देशकांच्या संख्येला त्या बिंदुपथाचे परिमाण म्हणतात. बैजिक वक्र हा एक परिमाणाचा बिंदुपथ आहे आणि बैजिक पृष्ठा हा दोन परिमाणाचा बिंदुपथ आहे. शून्य परिमाणाच्या बिंदुपथ हा ज्यांची संख्या परिमित आहे इतक्या बिंदूंचाच बनलेला असतो.
वैश्विक प्रांत :वैश्लेषिक भूमितीत सामान्यतः समीकरणांतील सहगुणक व चल हे संख्या (सत् वा सदसत्) आहेत, असे मानलेले असते. बहुपदी समीकरणे मांडताना ज्यांच्या घटकांचा सर्वसामान्य गुणधर्म असलेल्या बेरीज व गुणाकार या कृत्यांनी संयोग करता येतो असा केवळ एक प्रांत (घटकांचा संच) आवश्यक असतो. अशा प्रांताला वलय म्हणतात [⟶ बीजगणित, अमूर्त] तथापि बैजिक भूमितीत उद्भवणारे विशिष्ट प्रश्न सोडविण्यासाठी तीत सामान्यतः एकच अज्ञात राशी असलेल्या सर्व बैजिक समीकरणांचा निर्वाह मिळतो, असा प्रांत विचारात घेतला जातो. आधुनिक अमूर्त बीजगणिताच्या भाषेत त्याला ‘बैजिक दृष्ट्या संवृत असलेले क्षेत्र’ म्हणतात. या प्रांतात बैजिक दृष्ट्या निरवलंबी असलेल्या म्हणजे कोणत्याही बैजिक संबंधाची पूर्तता न करणाऱ्या घटकांची संख्याही स्वेच्छतः मोठी असते. अशा प्रांताला वैश्विक प्रांत म्हणतात.
सदसत् संख्यांचा (शुद्ध सत् व असत् संख्यांचाही समावेश असलेला) प्रांत हा वैश्विक प्रांत आहे. सत् संख्यांचे क्षेत्र हे बैजिक दृष्ट्या संवृत नसल्याने वरील अटींची पूर्वता करू शकत नाही. उदा., क्ष२ + १ =o या समीकरणाचा सत् संख्या क्षेत्रात निर्वाह मिळू शकत नाही. प्राथमिक बैजिक भूमितीतील मूलभूत तत्त्वांची व फलांची सुसूत्र उभारणी करण्यासाठी असत् सहनिर्देशक असलेल्या बिंदूंचा समावेश करण्याची आवश्यकता एकोणिसाव्या शतकाच्या सुरूवातीच्या दशकांत प्रथमतः जाणवली.
असंक्षेप्यता व परिमेयता : फ (क्ष, य) = o या समीकरणातील बहुपदी फ जर असंक्षेप्य असेल, म्हणजे ती तिच्या स्वतःच्या घातापेक्षा कमी घात असलेल्या दोन बहुपदींच्या गुणाकाराच्या रूपात मांडता येत नसेल, तर त्या समीकरणाने निदर्शित होणारा बैजिक प्रतलीय वक्र असंक्षेप्य आहे असे म्हणतात. जर ही बहुपदी अशा गुणाकाराच्यासमजा ख (क्ष, य). ग (क्ष, य) अशा-रूपात मांडता येत असेल तर दिलेला वक्र हा ख (क्ष, य) = o आणि ग (क्ष, य) = o या दोन समीकरणांनी निदर्शित होणाऱ्या वक्रांच्या संयोगाने मिळतो. व्यापक दृष्टया, एखादा बैजिक बिंदुपथ जर इतर दोन बैजिक बिंदुपथांचा संयोग नसेल, तर तो असंक्षेप्य आहे आसे म्हणतात. असंक्षेप्य बिंदुपथाला ‘प्रकार’ असेही म्हणतात.
असंक्षेप्य वक्राच्या बाबतीत जर क्ष आणि य हे ट या योग्य प्रचलाच्या परिमेय फलनांच्या [⟶ फलन] रूपात
क्ष = र (ट) आणि य = ल (ट)….. (२)
असे मांडता येत असतील, तर त्या वक्राला परिमेय वक्र म्हणतात. क क्ष + ख य + ग =o या समीकरणाने निदर्शित होणारी रेषा परिमेय आहे, कारण ती क्ष = ट या प्रचलाच्या रूपात खालीप्रमाणे मांडता येते.
|
य |
= |
– |
क |
ट |
– |
ग |
|
ख |
ख |
प्रत्येक शांकव हा परिमेय वक्र आहे. य२ – क्ष३ = o हा वक्रही परिमेय आहे, कारण क्ष = ट२ व य = ट३ असे घालून त्याचे प्रचलीकरण करता येते. याउलट य२ – क्ष३ – १ = o हा वक्र परिमेय नाही, असे दाखविता येते.
परिमेयतेची ही संकल्पना अठराव्या शतकात समाकलनशास्त्राच्या [⟶ अवकलन व समाकलन] विकासाच्या प्रथमावस्थेत मांडण्यात आली, कारण ती
∫म (क्ष, य) d क्ष…. …. (३)
यांसारख्या समाकलांच्या वर्गीकरणात मूलभूत महत्त्वाची आहे. येथे म हे (क्ष, य) चे परिमेय फलन असून य हे क्ष चे फ (क्ष, य) = o या समीकरणाने निदर्शित होणारे बैजिक फलन आहे. जर फ (क्ष, य) = o हा वक्र परिमेय असेल, तर (३) हा समाकल (२) या समीकरणांच्या साहाय्याने ट च्या परिमेय फलनाचा समाकल या रूपात मांडता येईल. यामुळे त्याचे परिमेय व लॉगरिथमीय फलनांनी समाकलन करता येईल.
जर फ (क्ष, य) = o हा वक्र परिमेय असेल, तर असे दाखविता येते की, (क्ष, य) चे परिमेय फलन (२) या समीकरणांतील ट प्रचलाच्या रूपात निवडता येईल. ट हा एखाद्या सरळ रेषेवरील बिंदूचा एक सहनिर्देशक घेता येत असल्याने वरील विधान पुढील प्रकारेही मांडता येईल : (२) ही समीकरणे आणि त्याचबरोबर ट हा (क्ष, य) च्या पदांत व्यक्त करणारे सूत्र यांनी फ (क्ष, य) = o हा वक्र व एक सरळ रेषा यांतील द्विपरिमेय संगतीची व्याख्या मिळते.
अधिक व्यापक दृष्ट्या, फ (क्ष, य) = o आणि भ (त, थ) = o यांनी निदर्शित केलेले अनुक्रमे व आणि स हे दोन वक्र विचारात घेता येतील. जर व च्या एका चल बिंदूचे सहनिर्देशक (क्ष, य) हे स च्या बिंदूच्या सहनिर्देशकांच्या (त, थ) पदांत
क्ष = र (त, थ), य = ल (त, थ) …..(४)
अशा परिमेय फलनांच्या रूपात मांडता येत असतील आणि त्याचबरोबर स च्या चल बिंदूचे सहनिर्देशक (त, थ) हे व च्या चल बिंदूच्या सहनिर्देशकांच्या (क्ष, य) पदांत
त = र’ (क्ष, य), थ = ल’ (क्ष, य) ….(५)
अशा परिमेय फलनांच्या रूपात व्यक्त करता येत असतील, तर (४) व (५) या समीकरणांनी व आणि स यांमधील द्विपरिमेय संगती निर्धारित होते, तसेच व आणि स हे द्विपरिमेयतः समतुल्य आहेत, असे म्हटले जाते. अशा प्रकारे परिमेय वक्र हा असा वक्र असतो की, तो एका सरळ रेषेशी द्विपरिमेयतः समतुल्य असतो.
समीकरणे (४) व (५) यांच्या साहाय्याने (३) या प्रकारचे समाकल (त, थ) च्या पदांत रुपांतरित करता येईल व त्याचप्रमाणे या उलटही रूपांतर करता येईल. अशा प्रकारे (३) या प्रकारच्या समाकलांच्या वर्गीकरणाच्या दृष्टीने पाहता द्विपरिमेयतः समतुल्य असलेल्या वक्रांची अदलाबदल करता येते. अशा प्रकारचा समाकल जर समाकलनाच्या सीमांच्या प्रत्येक निवडीसाठी सांत (परिमित) राहत असेल आणि चलांच्या समी. (४) या प्रकारच्या त्याच्या कोणत्याही रूपांतराच्या बाबातीतही हे सत्य असेल, तर त्या समाकलाला ‘पहिल्या जातीचा’ समाकल म्हणतात. ही व्याख्या समाकलन शास्त्रावर आधारित आहे असे वरकरणी वाटते तथापि ती पूर्णतः बैजिक असून अमूर्त बैजिक भूमितीतही ग्राह्य आहे. पहिल्या जातीचे नसलेले (३) या प्रकारचे समाकल ते कशा प्रकारे अनंत होतात त्यानुसार त्यांना दुसऱ्या वा तिसऱ्या प्रकारे समाकल म्हणतात.
वक्राचा जाती-अंक : वक्राचा घात ही द्विपरिमेय अचल राशी नाही म्हणजे द्विपरिमेयतः समतुल्य असलेल्या दोन वक्रांकरिता ती समान असण्याची आवश्यकता नाही. द्विपरिमेय समतुल्यतेच्या दृष्टीने बैजिक वक्रांचे वर्गीकरण करण्यासाठी प्रामुख्याने वक्राचा जाति-अंक लक्षात घेतला जातो. दिलेल्या वक्राशी संबंधित असलेल्या निरवलंबी समाकलांची अधिकतम संख्या म्हणजे त्या वक्राचा जाती-अंक अशी व्याख्या केली जाते. परिमेय वक्र हे असे वक्र असतात की, ज्यांचा जाति-अंक ० असतो. १ जाति-अंक असलेल्या वक्रांना विवृत्तीय म्हणतात कारण वैश्विक प्रांत सदसत् संख्याचे क्षेत्र असतो तेव्हा अशा वक्रांचे प्रचलीकरण विवृत्तीय फलनांनी [विवृत्तीय समाकलाच्या व्यस्त फलनाला विवृत्तीय फलन म्हणतात⟶ अवकलन व समाकलन] करता येते. जाति-अंकाची संकल्पना व बैजिक अवकलांच्या समाकलांशी संबंधित असलेली अत्यावश्यक फलिते १८५७ मध्ये रीमान यांनी एका निबंधात बीजातीत पद्धतींचा उपयोग करून दिलेली होती. यासंबंधीच्या बैजिक सिद्धता मागाहून मांडण्यात आल्या.
एकगुणित व बहुगुणित बिंदू :परिमेयता व द्विपरिमेय समतुल्यता, तसेच बैजिक अवकलांचे समाकल यांसंबंधीच्या संकल्पनांचा बैजिक पृष्ठांच्या आणि उच्चतर परिमाणांच्या प्रकारांच्या बाबतीत विस्तार करणे तत्त्वतः शक्य आहे तथापि बैजिक वक्रासंबंधीचा सिद्धांत पुष्कळसा पूर्णत्वास पोचलेला असला, तरी उच्चतर परिमाणाच्या वक्रांच्या बाबतीतील सिद्धांत फारसा विकसित झालेला नाही.
अवकलनशास्त्रानुसार फ (क्ष, य) =o या वक्रावरील (क, ख) या बिंदूपाशील स्पर्शिकेचे समीकरण खालीलप्रमाणे मिळते.
फ’क (क्ष – क) + फ’ख (य – ख) =o ….(६)
येथे फ’क व फ’ख हे सहगुणक म्हणजे (क, ख) या बिंदूपाशील फ च्या क्ष आणि य यांच्या सापेक्ष असलेल्या आंशिक अवकलजांची मूल्ये आहेत. याची नेहमीची सिद्धता सीमा प्रक्रियेवर अवलंबून आहे. बैजिक दृष्ट्या समी. (६) हे स्पर्शिकेची व्याख्या मानता येईल. बहुपदीच्या अवकलजांची व्याख्या अवकलनशास्त्रातील संबंधित नियमांनुसार मांडता येईल. जर (क, ख) बिंदूपाशी वरील दोन्ही सहगुणक नाहीसे (शून्य) होत असतील, तर स्पर्शिकेची अशी व्याख्या निरर्थक ठरेल. मग तो बिंदू बहुगुणित आहे असे म्हणतात, अन्यथा तो एकगुणित आहे असे म्हणतात. याचप्रमाणे बैजिक पृष्ठावर ज्या बिंदूपाशी स्पर्शप्रतलाचे सूत्र अर्थवाही राहत असेल त्याला एकगुणित व अन्यथा बहुगुणित म्हणतात. या व्याख्यांचा कोणत्याही मितीच्या अवकाशातील वक्र, पृष्टे व उच्चतर परिमाणांचे प्रकार यांच्याकरिता विस्तार करता येईल. एकगुणित बिंदूपाशी घात श्रेढींचा [⟶ श्रेढी] उपयोग करता येतो, मात्र त्यांच्या अभिसारितेसंबंधीचे सर्व प्रश्न बाजूला ठेवून केवळ स्वाभाविक अर्थबोधानेच त्यांचा उपयोग करणे आवश्यक आहे. बैजिक भूमिती एकगुणित बिंदूंच्या बाबतीत अधिक सुलभतेने विवरण करू शकते याचे हे एक प्रमुख कारण आहे.
आता मूलभूत प्रश्न असा उद्भवतो की, प्रत्येक बैजिक प्रकार बहुगुणित बिंदूविरहित प्रकारात द्विपरिमयेतः रूपांतरित करता येणे शक्य आहे का? उपयुक्ततेच्या दृष्टीने यात कोणत्या तरी सुयोग्य अर्थाने अनंतस्थ बिंदूंचाही समावेश करावा लागतो. अनंतस्थ बिंदूंचा अंतर्भाव रूढीप्रमाणे प्रक्षेपीय भूमितीच्या द्वारे करण्यात येतो. बैजिक वक्रांच्या बाबतीत वरील प्रश्नाला उत्तर असून ते मूलतः एकमेव असते आणि हे आता बैजिक वक्रांच्या सिद्धांताचे एक आवश्यक वैशिष्ट्य ठरलेले आहे. उच्चतर परिमाणांच्या बाबतीत सदसत् वैश्विक प्रांतासाठी तरी हा प्रश्न एच्. हीरोनाका यांनी १९६४ मध्ये सोडविलेला आहे. यामुळे पुढील प्रगतीचा मार्ग मोकळा झालेला असला, तरी उत्तर एकमेव असण्याच्या दृष्टीने याची उपयुक्तता वक्रांच्या बाबतीतील उत्तरापेक्षा कमी ठरते. ‘अभिलक्षण म (अविभाज्य संख्या) असलेल्या’[⟶ बीजगणित, अमूर्त] इतर वैश्चिक प्रांतांतच्या बाबतीत हा प्रश्न अद्यापही अनिर्णित आहे.
आणखी समस्या : बैजिक भूमितीतील आधुनिक पद्धतींचे स्थूलमानाने बैजिक व बीजातीत पद्धती असे वर्गीकरण करता येईल. बीजातीत पद्धतींत वैश्विक प्रांत हा सदसत् संख्यांचा असून त्यांत फलन सिद्धांत, संस्थितिविज्ञान व आंशिक अवकल समीकरण सिद्धांत [⟶अवकल समीकरणे] यांतील सर्व उपलब्ध साधनांचा व फलितांचा मुक्तपणे उपयोग केला जातो. या पद्धती म्हणजे वक्रांसंबंधीच्या रीमान यांच्या महत्त्वपूर्ण पद्धतींचे व्यापकीकरण होय. या पद्धतींचे सुपरिचित प्रवर्तक म्हणजे आंरी प्वँकारे, सी. ई. पीकर, सालोमन लेफशेट्स, डब्ल्यू. व्ही. डी. हॉज आणि अलीकडील काळातील के. कोडायरा व एच्. बी. ग्रिफिथ्स हे गणितज्ञ होत.
बैजिक पद्धती जरी काही वेळा कमी प्रभावी वाटत असल्या, तरी त्यांच्या बाबतीत वैश्विक प्रांतावर कोणतेही निर्बंध नसल्याने त्यांच्या उपयुक्ततेची व्याप्ती अधिक मोठी आहे. ⇨ संख्या सिद्धांतातील अनुप्रयोगांत हा त्यांचा गुणधर्म विशेष मौलिक ठरला आहे. यात गाल्वा क्षेत्रे [⟶ बीजगणित, अमूर्त] व ‘अभिलक्षण म असलेले’ वैश्विक प्रांत यांचा मूलभूत महत्त्वाचा भाग आहे.
पृष्ठ सिद्धांतात बैजिक पद्धती मुख्यत्वे सी. सेग्रे, जी. कास्तेलन्वाव्हो, फेदरीगो एन्रिक्स व फ्रांचेस्को सेव्हरी हे प्रतिनिधी असलेल्या इटालियन गणितज्ञांच्या गटाने विकसित केल्या आणि या विषयात १८९० – १९२५ या कालखंडात त्यांचा मोठा प्रभाव होता. या पद्धतींची व्याप्ती आता ‘अमूर्त प्रकार’ व ‘योजना’ (स्कीम्स) यांसारख्या नवींन संकल्पना आणि ‘समजातीय बीजगणित’ या नावाने ओळखण्यात येणाऱ्या अमूर्त बीजगणितातील शाखेचा उपयोग यांमुळे पुष्कळच वाढलेली आहे. फ्रेंच गणितज्ञ आलेक्सांद्र ग्रोथेद्येक यांनी मांडलेली आणि त्यांनी व त्यांच्या शिष्यगणाने अभ्यासिलेली ‘योजना’ ही संकल्पना विशेषत्वाने फलदायी ठरलेली आहे.
बैजिक भूमितीतील आधुनिक कालखंडाला आर्. एल्. व्हॅन डर वार्डेन, ऑस्कर झारिस्की व ए. व्हाइल यांच्या कार्यापासून सुरूवात झाली. व्हाइल यांच्या१९४७ मध्ये प्रसिद्ध झालेला फाउंडेशन्स ऑफ आल्जिब्राइक जॉमेट्री हा ग्रंथ विशेष महत्त्वाचा ठरला आहे. बैजिक गटांसंबंधीच्या आधुनिक सिद्धांताला सी. सी. शेव्हाली व व्हाइल यांच्यापासून प्रारंभ झाला आणि या विषयातील रोझेनलिश्ट, ए. बॉरेल व जे. पी. सेरे यांचे कार्य मूलभूत महत्त्वाचे आहे.
पहा : पृष्ठ प्रतल प्रदिश प्रस्थ, सामान्य फलनक विश्लेषण बिंदु भ्रमणजन्य पृष्ठे व घनाकृती रेषा वक्र शंकुच्छेद संस्थितिविज्ञान सदिश अवकाश.
संदर्भ :
1. Adler, I. A New Look at Geometry, London, 1966.
2. Auslander, L. Differential Geometry, New York, 1967.
3. Bell, E.T. Development of Mathematics, New York, 1945.
4. Bell, R. J.T. Co-ordinate Geometry of Three Dimensions, London, 1960.
5. Cajori, F.A History of Elementary Mathematics, London, 1961.
6. Coolidge, J.L. A History of Geometrical Methods, New York, 1963.
7. Coxeter, H.S.M. Non-Euclidean Geometry, New York, 1965.
8. Coxeter, H.S.M. Projective Geometry, NewYork, 1964.
9. Coxeter, H.S.M. The Real Projective Plane, Cambridge. 1955.
10. Cremona, L. Tr. Leudesdort, C. Elements for Projective Geometry, New York, 1960.
11. Earle, J.H. Descriptive Geometry, New York, 1971.
12. Eisenhart, L.P. Riemannian Geometry, Princeton, 1966,
13. Eisenhart, L. P. A Treatise on the Differential Geometry of Curves and Surfaces. New York, 1960.
14. Faulkner. T. E. Projective Geometry, Edinburgh, 1960,
15. Health. T. L. The Thirteen Books of Euclid’s Elements, Cambridge, 1925.
16. Heyting, A. Axiomatic Projective Geometry. Amsterdam, 1963.
17. Ince, E. L. Principles of Descriptive Geometry, London, 1933.
18. Krylov, N. and others Trans. Yankovsky, G. Desriptive Geometry, Moscow, 1968.
19. Lang, S. Introduction to Algebraic Geometry, New York, 1958.
20. Lefschetz, S. Algebraic Geometry, Princeton, 1923.
21. Macdonald, I. G. Algebraic Geometry: Introduction to Schemes, New York, 1968.
22. Pare. E. G. and others. Descriptive Geometry, New York, 1971.
23. Shanti Narayan, Analytical Solid Geometry, New Delhi 1973.Geometry, New Delhi 1973.
24. Smith, D. E. History of Mathematics, 2 Vols. New York, 1953.
25. Sommerville, D. M. Y. Analytical Geometry of Three Dimensions, Cambridge, 1959.
26. Sommerville, D. M. Y. The Elements of Non-Euclidean Geometry, New York, 1958.
27. Sommerville, D. M. Y. An Introduction to the Geometry of N-Dimensions, New York. 1958.
28. Spain, P. Analytical Conics, New York. 1957.
29. Struik. D. J. Concise History of Mathematics. New York, 1948.
30. Veblen, O. Young. J. W. Projective Geometry, 2 Vols.,New York, 1938 and 1946.
31. Watts, E. F, Rule. J. T. Descriptive Geometry, New York, 1946.
32. Weatherburn, C. E, Differential Geometry of Three Dimensions, Cambridge, 1956.
33. Weatherburn, C. E. An Introduction to Riemannian Geometry and the Tensor Calculus, Cambridge, 1963.
34. Weil, A. Foundations of Algebraic Geometry, Providence, 1962,
35. Whitehead, A. N. The Axioms of Descriptive Geometry, New York,1960.
36. Whitehead, A. N. The Axioms of Projective Geometry, Cambridge, 1960.
37. Wylie, C. R. Foundations of Geometry, New York, 1964.
आपटे, मधुमालती ओक, स. ज. इनामदार, चिं. शं.