महत्त्व मापन : रेषांची लांबी, पृष्ठांची क्षेत्रफळे व प्रस्थांची (घनाकृतींची) घनफळे मोजण्याच्या शास्त्रास महत्त्वमापनशास्त्र म्हणतात. या शाखेला सैद्धांतिक भूमितीची व्यवहारातील उपयोग असे म्हणता येईल. या शास्त्राची सुरुवात इतिहासपूर्व कालात झाली असे मानता येईल. समाज म्हणून मानवसमूह राहू लागल्यापासून त्याला महत्त्वमापनाची जरूरी भासू लागली असली पाहिजे. सामूहिक जीवनाच्या प्राथमिक अवस्थेमध्ये सुद्धा मानवाला निवाऱ्याची जागा बांधण्याकरिता लांबी मोजण्याची, शेतीचे वाटप करण्याकरिता क्षेत्र फळमापनाची व उत्पन्न केलेले धान्य मोजण्याकरिता घनफळमापनाची गरज भासली असणार. उत्खननामध्ये पुरातत्त्ववेत्यांना इ. स. पू. २०० च्या सुमारास मापनाची संकल्पना अस्तित्वात होती, असे आढळून आले आहे. बॅबिलोनीयन संस्कृतीमध्ये πचे [प्रतलावर काढलेल्या कोणत्याही वर्तुळाचा परिघ व त्याचा व्यास यांच्या गुणोत्तराचे ⟶ पाय्] मूल्य ३ असे वापरात होते, असे दिसून येते. ईजिप्तमध्ये इतिहासपूर्व कालात दिलेल्या कोणत्याही चौकोनी आकृतीचे क्षेत्रफळ मोजण्याचा प्रयत्न झाला होता. महत्त्वमापनशास्त्रात पुढील गोष्टींचा प्रामुख्याने अंतर्भाव होतो : (१) सरळ अथवा वक्र रेषांची लांबी, (२) सरळ रेषांनी किंवा वक्रांनी परिसीमित असलेल्या प्रतलातील किंवा अवकशातील पृष्ठांची क्षेत्रफळे, (३) प्रतलांनी किंवा पृष्ठांनी परिसीमित असलेल्या प्रस्थांची (उदा., चिती, शंकू, गोल वगैरे) घनफळे.
लांबीचे मापन : क्षेत्रफळ व घनफळ यांचे मापन लांबीच्या मापनावर अवलंबून आहे. लांबी मोजण्याकरिता एखादी विशिष्ट लांबी एकक म्हणून वापरण्यात येते जसे इंच, सेंटिमीटर, मैल, किलोमीटर वगैरे. पूर्वी वीत, हात, पुरुष. कोस ही परिमाणे पण वापरात होती [⟶ लांबी, क्षेत्रफळ व घनफळ यांची एकके]. एकक कोणते असावे हे त्या त्या प्रश्नावर अवलंबून असते. जसे घरबांधणीत किंवा कापड मोजण्याकरिता मीटर वापरतात, तर रेल्वेच्या लांबीकरिता किलोमीटर वापरतात. अर्थात एकक वापरात सुसंगती असली पाहिजे म्हणजे एका मितीकरता जे एकक वापरले असेल तेच एकक इतर मितींकरिता वापरले पाहिजे. लांबीचे मापन प्रत्यक्षपणे मीटरपट्टी, व्यासमापक इ. साधनांनी करतात किंवा काही वेळा अप्रत्यक्ष रीत्या ⇨त्रिकोणमितीचा वापर करून करतात. मितीचे मापन सेंटिमीटरमध्ये केले असता क्षेत्रफळाचे मापन चौरस सेंटिमीटरमध्ये (चौ. सेंमी.) व घनफळाचे मापन घन सेंटिमीटरमध्ये (घ. सेंमी.) करतात. वक्ररेषांच्या लांबीचे मापन अवकालनशास्त्राचा [⟶ अवकलन व समाकलन] उपयोग करून करतात. या क्रियेला रेखापन म्हणतात. रेखापनाकरिता पुढील सूत्र प्रसिद्ध आहे. वक्राचे समीकरण य = फ (क्ष) असेल तर [क, फ (क)] आणि [ख,फ (ख)] या बिंदूंमधील वक्राची लांबी
क∫ ख Ö१ + (dय)२ .dक्ष
dक्ष
या समाकलाने मिळते
जर वक्र क्ष = फ१ (ट) आणि य = फ२ (ट) या समीकरणांनी दिलेला असेल,
तर लांबी = ट∫ ट२ Ö [फ१‘ (ट)]२ + (फ२‘ (ट)]२ .dट
या सूत्राने मिळेल. अर्थात अवकाशातील वक्राकरिता
ट१∫ट२ Ö [फ१‘ (ट)]२ + (फ२ ‘ (ट)]२ + (फ३‘ (ट)]२ . dट
हा समाकल वापरतात. समाकलाचा उपयोग करून वर्तुळाचा परिघ २π गुणिले त्रिज्या या सूत्राने मिळतो. व्यवहारात π चे मूल्य ३.१४ किंवा २२/७ असे वापरण्यात येते (π चे मूल्य एक अपरिमेय संख्या आहे). वर्तुळाच्या कंसाची लांबी त्रिज्या गुणिले θ (θअरीयमानात मोजलेला संमुख कोन) या सूत्राने मिळते [कोन दोन प्रकारे मोजतात : अंशात किंवा अरीयमानात. एका काटकोनाचे ९० समान भाग केले असता एका भागास अंश म्हणतात. वर्तुळ त्रिज्येएवढ्या कंसासमोरील संमुख कोन म्हणजे एक अरीयमान होय ⟶ कोन]. वर्तुळाचे केंद्र माहीत नसल्यास किंवा आवाक्याच्या बाहेर असल्यास पुढील सूत्राने आसन्न (अंदाजी) मूल्य मिळविता येते.
कंसाची लांबी = ८/३ ल–१/३ सयेथे स जीवेची लांबी आणि ल कंसाचे टोक व कंसाच्या मध्य यांतील सरळ अंतर.
क्षेत्रफळाचे मापन : क्षेत्रफळाचे मापनात पायाभूत सूत्र म्हणजे आयताचे क्षेत्रफळ. हे क्षेत्रफळ (क्ष) आयताच्या लांबीच्या (ल) व रुंदीच्या (र) गुणाकाराने मिळते आणि ते सूत्ररुपात क्ष = ल×र असे मांडतात. (आ.१).
समांतरभुज चौकोनात पाया प व उंची उ यांच्या गुणाकाराने क्षेत्रफळ मिळते म्हणजे सूत्र क्ष = प× उ असे होईल. (आ. २).
त्रिकोण समांतरभुज चौकोनाच्या १/२ पट असतो (आ. ३ मधील तुटक रेषा पहा.) म्हणून त्रिकोणाचे क्षेत्रफळ १/२ प × उ या सूत्राने मिळेल. हेच क्षेत्रफळ त्रिकोणमितीचा वापर करून १/२ गा × खा × ज्या क या सूत्रानेही मिळते (ग व ख या कोनांसमोरील बाजूंची लांबी गा व खा यांनी दर्शविली आहे) किंवा ज्या सूत्राचा वापर करून ते
१ गा२ × ज्या ख × ज्या क
२ ज्या ग
या रुपातही मांडता येते. त्रिकोणाच्या प्रत्येक बाजूची लांबी माहीत असल्यास त्याचे क्षेत्रफळ
१Ö स (स−का) (स−खा) (स−गा) स = १
२ २ परिमिती या सूत्राने मिळते.
समलंब चौकोन एक आयत व दोन त्रिकोण यांची बेरीज असल्याकारणाने त्यांचे क्षेत्रफळ
१ उ × (का + खा)
२
या सूत्राने मिळते. (आ. ४).
बहुभुजाकृतीचे क्षेत्रफळ बहुभुजाकृतीचे त्रिकोणांत व समलंब चौकोनांच विभाजन करून मिळविता येईल.
बहुभुजाकृती समाभुज असेल, तर प्रत्येक बाजूसमोर परिवर्तुळ मध्यपाशी
२π
न कोन तयार होईल व बहुभुजाकृती क्षेत्रफळ
न ल२ कोस्पπ
४ न
या सूत्राने मिळेल. ल बाजूची लांबी व न बाजूंची संख्या (आ.५)
वर्तुळाचे क्षेत्रफळ क्ष = π त२ (त वर्तुळाची त्रिज्या) या सूत्राने मिळते. दोन त्रिज्या व कंस यांनी सीमित भागाला वर्तुळखंड म्हणतात. अशा वर्तुळखंडाचे क्षेत्रफळ
क्ष = १ त२ θ
२
( त त्रिज्या, θअरीयमानात संमुख कोन) या सूत्राने मिळते. जीवा व वर्तुळाचा कंस यांमधील भागाला वर्तुळ जीवाखंड म्हणतात. याचे क्षेत्रफळ पुढील सूत्राने मिळते : क्ष = त२ (α− ज्या αकोज्याα ) २ α= वर्तुळमध्याशी केलेला कोन. (आ.६).
याच क्षेत्रफळाचे आसन्न मूल्य पुढील सूत्राने मिळेल :
क्ष = उ × [२ स +८ल] उ
५ १५
जीवामध्य व कंसमध्य यांमधील अंतर, स जीवेची लांबी आणि ल कंसाच्या टोकापासून कंसमध्यापर्यंतचे सरळ अंतर.
वक्र, क्ष−अक्ष व दोन कोटी यांनी सीमित केलेल्या क्षेत्राचे क्षेत्रफळ पुढील सूत्राने मिळते. क ∫ख ।फ (क्ष)।dक्ष. (आ. ७ ). या सूत्राचा वापर करून विषृत्ताचे (लंबवर्तुळाचे) क्षेत्रफळ π अ ब असे मिळते (२ अ आणि २ ब विषृत्ताच्या अक्षांची लांबी).
⇨ अन्वस्ताच्या क्षेत्रफळाकरिता आर्किमिडीज यांचे सूत्र पुढीलप्रमाणे आहे : क्षेत्र अमप = २/३ क्षेत्र आयत क्षमपन अम अन्वस्ताचा अक्ष व अन शिरोबिंदूशी काढलेली स्पर्शिका. (आ. ८).
धुर्वीय सहनिर्देश पद्धतीमध्ये [⟶ भूमिती] क्षेत्रफळाकरिता सूत्र
१ α∫ β र२ dθ
असे आहे (येथे र हे त्रिज्यांतर असून वक्राच्या समीकरणावरून त्याचे च्या पदात मूल्य मांडता येते). (आ. ९).
समलंब नियम : जेव्हा क∫ख फ(क्ष) d क्ष या समकलाचे मूल्य काढणे शक्य नसेल किंवा ते मूल्य मिळविणे अवघड असेल तेव्हा समाकलाचे आसन्न मूल्य पुढील समलंब सूत्राने काढतात.[ क, ख] अंतरालाचे क्ष१, क्ष२……..,क्ष न-१ या बिंदूंनी समान भाग करून (क्ष०, य०), (क्ष१, य१),… … वगैरे बिंदू जोडून ते समलंब मिळतात. त्यांच्या क्षेत्रफळांची बेरीज म्हणजे समाकलाचे आसन्न मूल्य होय.
क∫ खफ (क्ष) d क्ष = ग[ १ य०+ य१+ …..+य न-१]
ग = क्षर − क्ष र-१. (आ.१०). [⟶ अवकलन व समाकलन].
सिंप्सन नियम : (टॉमस सिंप्सन या इंग्रज गणितज्ञांच्या नावावरून ओळखण्यात येणारा नियम). समलंब नियमामध्ये बिंदू सरळ रेषांनी जोडले आहेत, त्याऐवजी तीन पाठोपाठच्या बिंदूंतून एक अन्वस्त काढला असता अन्वस्त, दोन कोटी व क्ष−अक्ष या सीमित क्षेत्राचे क्षेत्रफळ काढता येईल. अशा तऱ्हेने मिळणाऱ्या क्षेत्रफळांची बेरीज म्हणजे आपणास पाहिजे असलेल्या क्षेत्रफळाचे आसन्न मूल्य होय. हे पुढील सूत्राने मांडता येते :
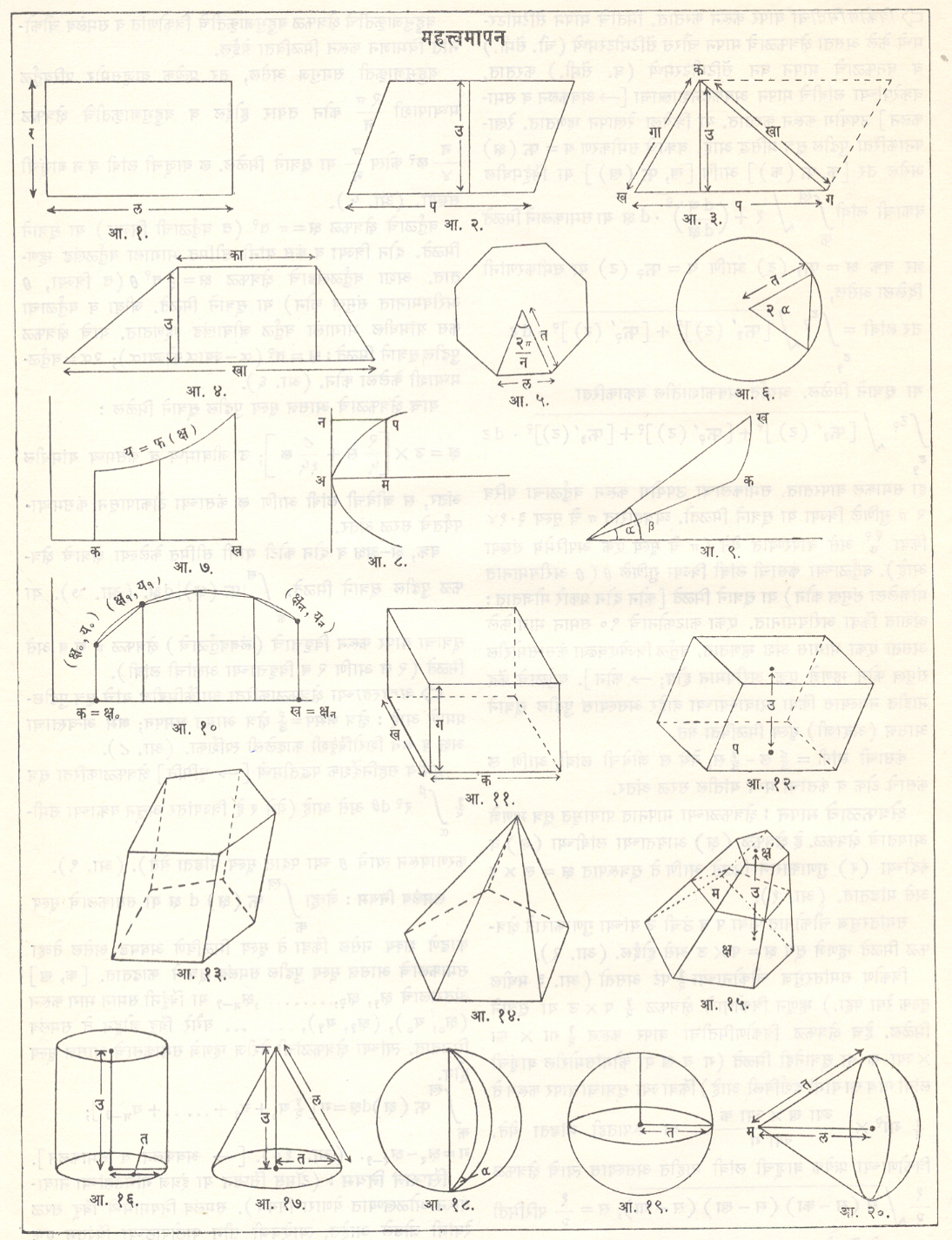
क∫खफ (क्ष) d क्ष = ग[य०+४य१+ २य२.+४य३+…… …+४य न-१+ यन ].
येथे [क, ख] या अंतरालाच्या भागांची संख्या सम असली पाहिजे. या नियमास सिंप्सन नियम म्हणतात.
घनफळाचे मापन : रोजच्या व्यवहारामध्ये निरनिराळ्या प्रस्थांच्या आकृती आढळून येतात. उदा., चेंडू गोल असतो, पाण्याचे पिंप चितीच्या आकाराचे असते, तर केरोसीनचे नसराळे शंकूच्या आकाराचे असते. या सर्व प्रस्थांची घनफळे काढण्याची पद्धत पुढील विवेचनात दिली आहे.
प्रस्थांमध्ये सर्वांत साधे व घनफळ मापनामध्ये पायाभूत प्रस्थ म्हणजे घनकल्प. घनकल्पाच्या कडा क, ख, ग लांबीच्या असल्यास घनफळ क×ख×ग या गुणाकाराने मिळते (आ. ११). त्याचे पृष्ठफळ २ (कख+खग+गक) या सूत्राने मिळेल. घन हा घनकल्पाचा विशिष्ट प्रकार असल्यामुळे त्याचे घनफळ क३ व पृष्ठफळ ६ क२ असे होईल ( क घनाच्या कडेची लांबी).
समांतरभुज प्रचिनाचे घनफळ पाया (प)×उंची (उ) या सूत्राने मिळते (आ. १२).
प्रचिनाचे घनफळही पाया×उंची या सूत्राने मिळते (आ. १३).
प्रसूचीचे घनफळ १/3 पाया × उंची या सूत्राने मिळते (आ. १४).
समच्छिन्न (पायाला समांतर असलेल्या प्रतलाने छेद घेतलेल्या) प्रसूचीच्या घनफळाकरिता पुढील सूत्र वापरतात :
घनफळ = १ उ [क्ष+क्ष‘+Öक्ष क्ष‘]
3 येथे उ ही उंची व क्ष आणि क्ष‘ही पाया व त्याला समांतर मुख यांची क्षेत्रफळे आहेत. म हे पाया व समांतर मुख यांच्या मध्यवर्ती छेदाचे क्षेत्रफळ असेल, तर घनफळाकरिता सूत्र १ उ (क्ष+क्ष‘ +४ म) ६ असे होईल. (आ. १५). चिती ही प्रचिनाची सीमा अवस्था आहे म्हणून तिचे घनफळ पाया × उंची या सूत्राने मिळेल म्हणजेच ते πत२उ याने मिळेल (त पायाची त्रिज्या व उ उंची) (आ. १६). चितीच्या वक्रपृष्ठाचे क्षेत्रफळ २π त२ उ या सूत्राने मिळेल. शंकूची आकृती ही प्रसूचीची सीमा अवस्था आहे म्हणून शंकूचे घनफळ १ πत२ उ ३ या सूत्राने मिळते (त तळाची त्रिज्या व उ उंची). शंकूच्या वक्रपृष्ठाचे क्षेत्रफळ πत ल किंवा πत Ö त२ +उ २ या सूत्राने मिळविता येईल. येथे ल ही उताराची लांबी आहे (आ. १७). गोलाचे घनफळ ४ πत३ ३ या सूत्राने मिळते व गोलाच्या पृष्ठाचे क्षेत्रफळ ४πत२ या सूत्राने मिळते (आ. १९). अर्धवर्तुळ आसाभोवती संपूर्ण फिरवून गोल तयार होतो हे उघड आहे. हेच अर्धवर्तुळ α कोनातून फिरविल्यावर जो कील तयार होतो त्याचे घनफळ २αत३ ३ असते (आ. १८). गोलमध्यापासून क आणि ख अंतरावर असणाऱ्या समांतर प्रतलांनी गोलाचा जो भाग कापला जातो त्याचे घनफळ π [त२ (क−ख) − १ (क३–ख३)] ३ या सूत्राने मिळते. प्रतल छेदांच्या त्रिज्या त‘ असतील व प्रतलांमधील अंतर न असेल, तर वरील घनफळाकरिता πन (३ त ‘२+ ३ त”२+ न२) ६ हेही सूत्र वापरता येते. गोलमध्यापासून ल अंतरावर प्रतलाने गोल छेदल्यास मिळणाऱ्या गोलाच्या टोपीचे क्षेत्रफळ २π त (त−ल) या सूत्राने मिळते. गोल दलाचे घनफळ पुढील सूत्राने मिळते : गोल दलाचे घनफळ = π (त–ल)२ (२त +ल). (आ. २०). ३ पहा : अवकलन व समाकलन प्रस्थ, सामान्य भूमिति. संदर्भ : 1. Hogben, L. T. Mathematics for the Million, New York, 1968. 2. Lopshits, A. M. Trans, Massalski J. Mills, C. Computation of Areas Oriented Figures, Boston, 1963. फडके, ना. ह. ओक, स. ज. “