ऊष्मीय प्रसरण : पदार्थाच्या रेणूंची गती त्याच्या तपमानावर अवलंबून असते. तपमान वाढवले असता रेणूंची गती वाढते त्यामुळे रेणू एकमेकांवर अधिक जोराने आपटतात व परतताना त्यांच्यातील अंतर वाढते. या कारणामुळे पदार्थाला उष्णता दिली असता त्याचे प्रसरण होते. उष्णतेच्या या परिणामाला ऊष्मीय प्रसरण म्हणतात.
प्रसरणाचे तीन प्रकार पाडले जातात : (१) लांबी प्रसरण, (२) क्षेत्रफळ प्रसरण आणि (३) घनफळ प्रसरण. घन पदार्थाचे प्रसरण ह्या तिन्ही प्रकारांनी होते, पण द्रवरूप व वायुरूप पदार्थाचे फक्त घनफळ (आयतन) प्रसरण होते.
प्रसरण गुणांक : निरनिराळ्या पदार्थांची प्रसरणक्षमता निरनिराळी असते. प्रसरण गुणांक पदार्थांची प्रसरणक्षणता दर्शवितो. वर उल्लेखिलेल्या तीन प्रकारच्या प्रसरणांच्या, प्रसरण गुणांकाच्या व्याख्या पुढीलप्रमाणे आहेत.
लांबी (रैखिक) प्रसरण गुणांक : मूळ ०० से तपमान व अकक लांबी असलेल्या पदार्थाचे तपमान १० से. ने वाढवले असता त्याच्या लांबीत होणाऱ्या वाढीला लांबी किंवा रैखिक प्रसरण गुणांक अ म्हणतात. यावरून ०० से. तपमान असताना पदार्थाची लांबी ल० असेल व तपमान त० से. ने वाढविल्यामुळे लांबी ल झाली असेल, तर सरासरी लांबी गुणांक अ काढता येतो. जसे
| अ = | ल – ल० | किंवा ल = ल० (१ + अ त) … (१) |
| ल० X त |
क्षेत्रफळ प्रसरण गुणांक : मूळ ०० से. तपमान व एकक क्षेत्रफळ असलेल्या पदार्थाचे तपमान १० से. ने वाढवले असता त्याच्या क्षत्रफळात होणार्या वाढीला क्षेत्रफळ प्रसरण गुणांक व म्हणतात. यावरून ०० से. तपमान असताना पदार्थाचे जर क्ष० क्षेत्रफळ असेल व तपमान त० से. ने वाढविल्यामुळे त्याचे क्षेत्रफळ जर क्ष झाले असेल, तर ब चे सरासरी मूल्य पुढीलप्रमाणे मिळते :
| ब = | क्ष – क्ष० | क्ष = क्ष० (१ + ब त) … (२) |
| क्ष० X त |
घनफळ प्रसरण गुणांक : मूळ ०० से. तपमान व एकक घनफळ असलेल्या पदार्थाचे तपमान १० से. ने वाढवले असता त्याच्या घनफळात होणार्या वाढीला घनफळ प्रसरण गुणांक क म्हमतात. ०० से. तपमानास पदार्थाचे घनफळ जर घ० असेल व त० से. तपमान केले असता जर त्याचे घनफळ घ झाले असेल, तर क चे सरासरी मूल्य पुढील प्रमाणे मिळते :
| क = | घ – घ० | घ = घ० (१ + क त) … (३) |
| घ० X त |
| काही घन व द्रव पदार्थांचे प्रसरण गुणांक | ||||
| घन पदार्थ | द्रव पदार्थ | |||
| पदार्थाचे नाव | लांबी गुणांक | पदार्थाचे नाव | घनफळ गुणांक | |
| ॲल्युमिनियम | ०.००००२५० | एथिल अल्कोहॉल | ०.००११० | |
| तांबे | ०.००००१६७ | ॲनिलीन | ०.०००८५ | |
| शिसे | ०.००००२९१ | बेंझीन | ०.००१२४ | |
| जस्त | ०.००००२६३ | ग्लिसरीन | ०.०००५३ | |
| पितळ | ०.००००१८९ | पारा | ०.०००१८ | |
| लोखंड (ओतीव) | ०.००००१०२ | पॅराफीन तेल | ०.०००९० | |
| पोलाद, घडीव लोखंड (सुमारे) | ०.००००१२० | टर्पेंटाइन | ०.०००९४ | |
| काच | ०.०००००८० | |||
घन पदार्थाची प्रसरणक्षमता तपमानाबरोबर फारशी बदलत नसल्याने व प्रसरण गुणांक फार अल्प असल्याने मूळ तपमान ०० से. ऐवजी प्रत्यक्ष असलेले तपमान धरले तरी विशेष फरक पडत नाही.
समदिक व असमदिक पदार्थ : सर्व प्रकारचे धातू व सैंधवासारखे काही नियमित स्फटिक समदिक असतात म्हणजे त्यांचे प्रसरण सर्व बाजूंनी सारखे होते. याउलट बहुतेक स्फटिक असमदिक असतात म्हणजे त्यांचे प्रसरण सर्व बाजूंनी सारखे होत नाही.
प्रसरण गुणांकांचा एकमेकांशी संबंध : हा संबंध पुढील सोप्या पद्धतीने काढता येतो. एकक लांबी, रुंदी व उंची असलेल्या घनाकृती पदार्थाचे तपमान १० से. ने वाढवल्यास पुढील समीकरणे मिळतात :
| ल = १ | (१ + अ X १) | = १ + अ | |
| क्ष = १ | (१ + ब X १) | = १ + ब | |
| घ = १ | (१ + क X १) | = १ + क | |
| यावरून | क्ष = ल२ = (१ + अ)२ = १ + २अ = १ + ब | ||
| घ = ल३ = (१ + अ)३ = १ + ३अ = १ + क | |||
येथे अ फार अल्प असल्याने अ२, अ३ असलेली पदे अत्यल्प व उपेक्षणीय होतात व म्हणून ती वगळली आहेत. यावरून ब = २अ आणि क = २अ असा संबंध मिळतो. म्हणजे क्षेत्रफळ प्रसरण गुणांक व घनफळ प्रसरण गुणांक लांबी प्रसरण गुणांकाच्या अनुक्रमे दुप्पट व तिप्पट असतात. यावरून पदार्थाचा कोणताही एक गुणांक मिळाला असता दुसरे दोन सहज काढता येतात.
समदिक पदार्थाचा लांबी प्रसरण गुणांक अ काढण्याची पद्धती : या पद्धतीचे तत्त्व पुढीलप्रमाणे आहे : पदार्थाची एक कांब एका बाष्पपेटीमध्ये ठेवावी. कांबीचे एक टोक पेटीबाहेर ठेवावे. या टोकाला एक गोलत्वमापक (गोलाची त्रिज्या किंवा अंतर मोजण्याचे उपकरण) बसवावा. गोलत्वमापकाने लांबीतील वाढ (ल – ल०) मिळते. एक तपमापक वापरून तपमानातील वाढ त मिळते. नंतर समी. (१) ने अ चे मूल्य मिळते.
लाप्लास व लव्हॉयझर यांनी लांबीतील बदल फार कमी असल्याने यांत्रिक तरफ वापरली. तरफेवर एक दूरदर्शक (दुर्बिण) बसवलेला असतो व तो एका मापकपट्टीवर केंद्रीभूत केलेलाअसतो. कांबीची लांबी बदलल्यामुळे तरफेची दिशा बदलते व त्यामुळे दूरदर्शकातून दिसणार्या पट्टीवरील नोंद बदलते. यावरून गणिताने अ काढता येतो. यांत्रिक तरफेऐवजी प्रकाशीय तरफ वापरल्यास जास्त फायदा होतो. यात कांबीवर एक आरसा बसविलेला असून त्यावरून परावर्तित झालेले एका मापपट्टीचे प्रतिबिंब एका स्थिर दूरदर्शकातून पाहून कांबीच्या लांबीतील बदल मोजता येतो.
‘ब्यूरो इंटरनॅशन डेस एट मेझर्स’ या संस्थेने अवलंबिलेली तौलनिक पद्धती सर्वमान्य झाली आहे. या पद्धतीत पदार्थाच्या एका पट्टीवर दोन रेखीव खुणा केलेल्या असतात. या पट्टीशेजारी तुलनेसाठी एक मानक मीटर पट्टी ठेवलेली असते. दोन्ही पट्ट्या निरनिराळ्या थाळ्यांत ठेवलेल्या असतात. मीटर पट्टीच्या थाळीचे तपमान कायम असते व पदार्थाच्या पट्टीच्या थाळीचे तपमान हवे तसे बदलता येते. तुलनेने लांबीतील बदल मोजण्यासाठी दोन सूक्ष्मदर्शक दोन्ही खुणांवर केंद्रिभूत केलेले असतात.
स्फटिकांचा लांबी प्रसरण गुणांक : स्फटिकाचे प्रसरण निरनिराळ्या दिशांना निरनिराळ्या प्रमाणांत होत असल्याने प्रसरणामुळे त्याच्या पृष्ठांमधील कोन बदलतात. प्रत्येक स्फटिकात एकमेकांशी काटकोन करणारे तीन अक्ष असतात. या अक्षांना समांतर असा जर स्फटिक कापला, तर मात्र उष्णतेमुळे पृष्ठांमधील कोन बदलत नाहीत. या अक्षांना प्रमुख अक्ष म्हणतात व या अक्षांच्या दिशेचे मोजलेल्या गुणांकास प्रमुख प्रसरण गुणांक म्हणतात.
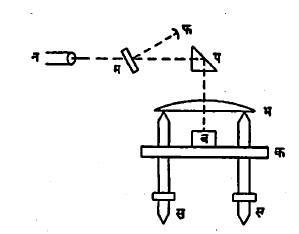
फीझो यांची व्यतिकरण पद्धती : दोन किंवा अधिक तरंगमालिका एकमेकींवर पडल्यास घडून येणाऱ्या आविष्कारास व्यतिकरण म्हणतात. अशा ठिकामी काळे-पांढरे (किंवा रंगीत) पट्टे वा वलये दिसतात. या पद्धतीत सु. १ सेंमी. जाडीची दोन्ही बाजू चकचकीत केलेली स्फटिकाची ब ही एक चकती क या धातूच्या चकचकीत तबकडीवर ठेवलेली असते (आ. १). ही तपकडी स मळसूत्रांवर ठेवलेली असते. मळमूत्रामुळे तबकडी क्षितिजसमांतर करता येते. मळसूत्रांवर भ हे अर्धगोल भिंग असते. फ या उगमस्थानातून प्रकाश निघून, तो म या अर्धपारदर्शक काचेपासून परावर्तित होऊन प या लोलकावर पडतो. येथून तो लंबरेषेत भ या भिंगावर पडतो. भिंगाच्या सपाट पृष्ठापासून काही प्रकाश परावर्तित होतो, तर काही प्रकाश स्फटिकाच्या वरील पृष्ठापासून परावर्तित होतो. दोन्ही परावर्तित होतो. दोन्ही परावर्तित प्रकाश किरण पूर्वीच्याच मार्गाने न या नेत्रभिंगावर (डोळ्याने ज्या भिंगातून निरीक्षण करावयाचे त्यावर) पडतात व व्यतिकरण होऊन न्यूटन वलये (सपाट पृष्ठभाग व बहिर्गोल भिंग यांच्या किंवा निरनिराळ्या वक्रतांच्या भिंगांच्या स्पर्शबिंदूभोवती व्यतिकरणामुळे दिसमारी व न्यूटन यांनी शोधून काढलेली वलये) निर्माण होतात. दोन वलयांमधील अंतर लां/२ असते (लां = प्रकाश तरंगाची लांबी) व ते सूक्ष्मदर्शकाने मोजता येते. उष्णतेमुळे स्फटिकाचे प्रसरण होऊन स्फटिक व भिंग यांच्यामधील हवेची जाडी बदलते व त्यामुळे व्यतिकरण वलये सरकतात. जर क्ष वलये सरकली तर क्ष लां/२ इतके प्रसरण झाले, असे समजावे. यातून मळसूत्रे व तबकडी यांचे प्रसरण वजा केले पाहिजे. ॲबे व पुलफ्रिच यांनी पुढे या पद्धतीत सुधारणा केल्या.
ग्रुनॅझेन यांचा नियम : पदार्थाचा लांबी प्रसरण गुणांक अ तसेच त्याची विशिष्ट उष्णता व हे तपमानाबरोबर बदलतात. तपमान कमी करता गेल्यास दोन्ही कमी होत जातात. ग्रुनॅझेन यांनी अति-नीच तपमानापर्यंत प्रयोग करून असे सिद्ध केले की. पदार्थाचा लांबी प्रसरण गुमांक व त्याची स्थिर घनफळाची विशिष्ट उष्णता यांचे गुणोत्तर (अ/व) कोणत्याही तपमानात कायम राहते.
द्रवांचे प्रसरण : उष्णतेमुळे द्रवांचे घनफळच बदलत असल्याने फक्त समीकरण (३) च त्यांना लागू पडते. घ = घ० (१ + क त); क = द्रवाचा घनफळ प्रसरण गुणांक, द्रवाचा प्रसरण गुणांक काढण्यामध्ये एक अडचण उद्भवते. द्रव धारण करणारा धारकही द्रवाबरोबरच प्रसरण पावत असल्याने द्रवाचे दिसून येणारे प्रसरण खरे नसून भासमान असतो. यामुळे द्रवाचे दोन प्रसरण गुणांक असतात. एक शुद्ध गुणांक क व दुसरा भासमान गुणांक कभ. धारकाचा गुणांक क = कभ + क‘. उष्णतेमुळे द्रवाचे घनफळ बदलत असल्यामुळे त्याची घनताही बदलते. समजा, ०० से. तपमान असताना द्रवाचे घनफळ घ० व घनता ग० आहे व तपमान त० से, केले असता घनफळ व घनता अनुक्रमे घत आणि गत होतात, मग द्रवाचे वस्तुमान जर म असेल, तर
| ग० = | म | आणि गत = | म |
| घ० | घत |
| ग० | = | घत | = | घ० (१ + क त) | = १ + क त … (४) |
| गत | घ० | घ० |
द्रवांचा प्रसरण गुणांक काढण्याच्या पद्धती : (१) जलस्थितिक पद्धती : यामध्ये एका घन पदार्थाचे हवेमधील वजन म आणि द्रवाचे तपमान त१ असताना द्रवामधील वजन म१ व पुन्हा द्रवाचे तपमान त२ असताना द्रवातले वजन म२ काढतात. वजनातील घट दोन्ही वेळा निरनिराळी येते (म३ = म – म१ आणि म४ = म – म२). यावरून समीकरण (४) वापरून द्रवाचा प्रसरण गुणांक पुढील समीकरण मिळतो :
| क = | म३ – म४ |
| म४ (त२ – त१) |
(२) डुलाँग व पेटिट यांची पद्धती : या पद्धतीत द्रव इंग्रजीतील U अक्षराच्या आकाराच्या काचेच्या नलिकेत असतो. नलिकेच्या एका बाजूचे तपमान ०० से. व दुसऱ्या बाजूचे बरेच अधिक म्हणजे त० से. ठेवलेले असते. जास्त तपमान असलेल्या बाजूंच्या द्रवाची घनता प्रसरणामुळे कमी होते त्यामुळे त्या बाजूच्या द्रवस्तांभाची उंची दुसऱ्या बाजूंच्या स्तंभापेक्षा जास्त होते. दोन्ही स्तंभांची उंची जर लत व ल० असेल आणि गुरुत्वप्रवेग जर प्र असेल, लत X गत X प्र = ल० X ग० X प्र हे समीकरण मिळते.
| ग० | = | घत | = | १ + क त या समीकरणाने क काढता येतो. संवहनामुळे दोन्ही बाजूंचे तपमान स्थिर रहात नाही हा या पद्धतीतील दोष आहे. |
| गत | ल० |
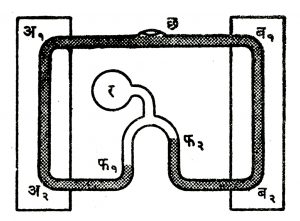
(३) रेनॉल्ट यांची पद्धती : वरील पद्धतीत सुधारणा करून रेनॉल्ट यांनी ती पाऱ्याचा प्रसरण गुणांक काढण्यासाठी वापरली. या पद्धतीत अ१अ२, ब१ब२ या लोखंडी नलिकेत पारा भरलेला असतो. ही नलिका फ१फ२ या काचेच्या वक्र नलिकेने र गोलाला जोडलेली असते. छ या छिद्रामुळे नलिकेवरील बाहेरील दाब वातावरणाच्या दाबाउतका असतो. अ१अ२ भोवती शीतपेटी (०० से.) व ब१ब२ भोवती उष्णपेटी (त० से.) असते. र मध्ये अधिक दाबाची हवा असते व तिचा दाब पाऱ्याच्या दोन्ही पातळ्यांवर (फ१ व फ२) सारखाच पडतो. दोन्ही पातळ्यांतील फरक ल मोजता येतो. प्रसरणारे वाढणारा पारा छ मधून बाहेर पडतो. यावरून डुलाँग व पेटिट यांच्या पद्धतीप्रमामेच प्रसरण गुणांक काढता येतो.
(४) भातापमापक पद्धती : प्रथम भारतापमापकाचे वजन करून ते ०० से. तपमानाच्या द्रवाने संपूर्ण भरावे व पुन्हा वजन करावे. या दोन वजनांतील फरक द्रवाच्या भाराइतका (म०) असतो. नंतर मापकाचे तपमान त० से. ने वाढवावे म्हणजे द्रव मापकापेक्षा जास्त प्रसरणक्षम असल्याने काही द्रव मापकातून बाहेर पडतो. पुन्हा वजन करून द्रवाचा भार (मत) काढावा. धारकाचे घनफळ ०० से. तपमानास घ० व त० से. तपमानास घत जर असेल व त्याचा प्रसरण गुणांक जर क असेल, तर पुढीलप्रमाणे गणित करून द्रवाचा प्रसरण गुणांक क काढता येईल.

| परंतु | म० | जवळजवळ १ असल्याने व क’ फार अल्प असल्याने क = कभ + क’ हे समीकरण मिळते. | ||||||||||
| मत | ||||||||||||
देशपांडे, अ. शा.