प्राक्षेपिकी : (बॅलिस्टिक्स). हाताने किंवा गोफण अथवा इतर तत्सम साधनाने फेकला (प्रक्षेपित केला) जाणारा दगड, धनुष्यातून सोडला जाणारा बाण, बंदुकीची गोळी, तोफगोळे व बाँब, क्षेपणास्त्रे यांसारख्या (सुयोग्य साधनाने) प्रक्षेपित केल्या जाणाऱ्या वस्तूंच्या म्हणजेच प्रक्षेप्यांच्या गतीचे व एकूण गुणधर्मांच्या अभ्यासाचे शास्त्र म्हणजेच प्राक्षेपिकी होय.
तसे पाहिले तर हे शास्त्र फार गुंतागुतीचे असून अद्याप पूर्णपणे विकसित झालेले नाही. रसायनशास्त्र, ⇨ऊष्मागतिकी, ⇨घन अवस्था भौतिकी, ⇨धातुविज्ञान, ⇨यामिकी, द्रायुगतिकी [⟶ द्रायुयामिकी], ⇨भूगणित, ⇨त्रिकोणमिती यांसारख्या अनेक शास्त्रशाखांतील तत्त्वांचा येथे उपयोग करावा लागतो.
इतिहास व विकास : लिओनार्दो दा व्हींची (१४५२-१५४९), गॅलिलीओ (१५६४-१६४२) व न्यूटन (१६४२-१७२७) यांनी या शास्त्राचा प्रारंभ केला. त्यानंतर स्विस गणितज्ञ लेनर्ड ऑयलर (१७००-८३) आणि फ्रेंच शास्त्रज्ञ पी. एस्. लाप्लास (१७४९-१८२७) आणि ए. एल्. लव्हॉयझर (१७४३-९४) यांनी त्यात महत्त्वाची भर घातली. आरंभीच्या काळात अचूक मारगिरी करणे हे केवळ अनुभवजन्य कौशल्यावरच अवलंबून होते परंतु त्यामागची शास्त्रीय तत्त्वे शोधून काढून ते नियमबद्ध करण्यासाठी शास्त्रज्ञांची धडपड होती.
प्रथम १३४६ मध्ये इंग्रजांनी क्रेसीच्या लढाईत तोफांचा उपयोग केला व तेव्हापासूनच खऱ्या अर्थाने प्राक्षेपिकीतील विविध समस्यांची जाणीव होऊ लागली. तोफेची नळी न फुटता गोळ्याला जास्तीत जास्त वेग कसा देता येईल, तोफेच्या नळीची झीज व वजन कसे कमी करावे, जास्त स्फोटक दारू कशी बनवावी, गोळ्याने लक्ष्याचा जास्तीत जास्त अचूक वेध कसा करता येईल, प्रत्यक्ष गोळा पडेल तेथे शत्रूची जास्तीत जास्त हानी व्हावी यासाठी काय केले पाहिजे यांसारखे विविध कूट प्रश्न हळूहळू पुढे येऊ लागले. त्यांची उत्तरे काढण्याच्या प्रयत्नातूनच प्राक्षेपिकी विकसित होत गेली.
सोळाव्या शतकाच्या मध्यापर्यंत, उडविलेल्या तोफगोळ्याचा मार्ग समद्विभुज त्रिकोणाच्या दोन बाजूंप्रमाणे असतो अशी कल्पना होती. पुढे गॅलिलीओ यांनी हा मार्ग वक्र [अन्वस्ताकार, पॅराबोलिक ⟶ अन्वस्त] असतो हे दाखविले. १७४२ मध्ये बेंजामिन रॉबिन्स या इंग्रज शास्त्रज्ञांनी गोळ्यांचा वेग मोजण्यासाठी ‘प्रक्षेपी लंबक’ हे उपकरण तयार करून या शास्त्राला प्रथम प्रयोगाची जोड दिली. त्याचा उपयोग करून १७९१ मध्ये चार्ल्स हटन यांनी असे शोधून काढले की, हवेमधून गोळा जसजसा पुढे जातो तसतशी त्याच्या वेगामध्ये मोठ्या प्रमाणावर घट होत जाते. गोळ्याच्या गतीवर गुरुत्वाकर्षणापेक्षाही हवेच्या विरोधाचा (कर्षण प्रेरणेचा) जास्त परिणाम होतो, हेही पुढे स्पष्ट झाले.
विभाग : प्राक्षेपिकीचे अंतर्गत, बाह्य व अंत्य असे तीन विभाग पडतात. अंतर्गत प्राक्षेपिकीत बंदुकीच्या वा तोफेच्या नळीत होणाऱ्या प्रक्षेप्य वस्तूच्या प्रवासाचा विचार करतात. तसेच दारूच्या ज्वलनामुळे उत्पन्न होणाऱ्या वायूचा दाब, तापमान व वायुदाबामुळे प्रक्षेप्याला मिळणारा वेग यांचाही विचार अंतर्गत प्राक्षेपिकीत होतो. प्रक्षेप्याला विवक्षित वेग देण्यासाठी लागणाऱ्या दारूचा प्रकार व वजन, बंदुकीच्या वा तोफेच्या नळीची लांबी, जाडी व एकंदर अंतर्गत रचना इ. गोष्टी निश्चित करण्यास अशा अभ्यासाचा मुख्यतः उपयोग होतो.
प्रक्षेप्याला विवक्षित दिशेने व विवक्षित वेगाने फेकल्यावर, लक्ष्य गाठीपर्यंत त्याच्या हवेतून, पाण्यातून अथवा अवकाशातून होणाऱ्या प्रवासाचा बाह्य प्राक्षेपिकीत समावेश होतो. लक्ष्यावर आदळण्याच्या वेळीचा प्रक्षेप्याचा वेग आणि त्याची दिशा, तसेच प्रक्षेप्याला लक्ष्य गाठण्यास लागणारा वेळ या गोष्टी ठरविण्यास या अभ्यासाचा मुख्यतः उपयोग होतो. याबरोबरच प्रत्येक क्षणी प्रक्षेप्याच्या वेगाची महत्ता व दिशा प्रक्षेप्याने त्या क्षणापर्यंत आक्रमिलेल्या पथाची लांबी, या इतर गोष्टींची माहितीही या अभ्यासामुळे मिळते. तसेच विवक्षित अंतरावर असलेले लक्ष्य गाठण्यास प्रक्षेप्याला कोणत्या दिशेने व किती वेगाने प्रक्षेपित करावे लागेल, हेही या अभ्यासावरून निश्चित करता येते.
विवक्षित वेगाने व विवक्षित दिशेने लक्ष्यावर आदळलेल्या वेगवेगळ्या प्रकारच्या प्रक्षेप्यांमुळे लक्ष्याच्या होणाऱ्या हानीचा विचार अंत्य प्राक्षेपिकीत होतो. अशा अभ्यासामुळे लक्ष्याची अपेक्षित हानी करण्यास कशा प्रकारचे प्रक्षेप्य वापरावे, हे निश्चित करता येते.
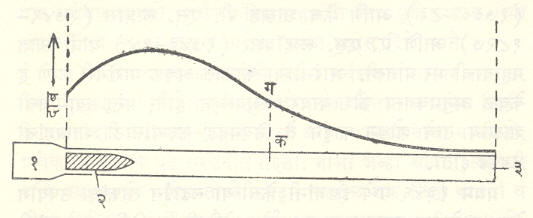
अंतर्गत प्राक्षेपिकी :वायुदाबातील बदल : बंदुकीचा चाप ओढल्यावर आतील दारूचा भडका उडून तिचे प्रचंड दाब व तापमान असणाऱ्या वायूंत एकदम रूपांतर झाले असते व अशा वायूंमुळे प्रक्षेप्य ताबडतोब पुढे सरकायला लागले असते व अशा वायूंमुळे प्रक्षेप्य ताबडतोब पुढे सरकायला लागले असते तर सुरुवातीपासूनच वायूचा दाब उत्तरोत्तर कमी होत होत, प्रक्षेप्य बंदुकीच्या नळीच्या टोकाशी येता क्षणी लघुतम झाला असता पण प्रत्यक्षात असे आढळते की, दारू पूर्ण जळायला थोडा वेळ लागत असल्यामुळे, तसेच बंदुकीच्या नळीतील काही रोधामुळे प्रक्षेप्य ताबडतोब पुढे सरकत नाही, म्हणून आतील वायूचा दाब चाप ओढल्याबरोबर महत्तम न होता, तदनंतर थोड्या वेळाने, प्रक्षेप्य नळीतून थोडे पुढे सरकल्यावर होतो. प्रक्षेप्याला गती देण्यासाठी दारूचा पुरेपूर उपयोग करावयाचा असेल, तर प्रक्षेप्य नळीत असेपर्यंत वायुदाब सतत स्थिर ठेवणे आवश्यक असते. असे करणे अनेक कारणांमुळे शक्य होत नाही, तरीपण बंदुकीची रचना करताना व गोळीचे वजन, आकार, तसेच दारूचे वजन, प्रकार, बंदुकीच्या नळीची लांबी, ज्वलन कोठीचे आकारमान इ. गोष्टी ठरविताना वरील आदर्श डोळ्यापुढे ठेवतात. बंदुकीच्या नळीची लांबी ठरविताना दोन परस्पर विरोधी गोष्टी विचारात घ्याव्या लागतात. जळालेल्या दारूचा पुरेपूर उपयोग करण्यासाठी नळीची लांबी जास्तीत जास्त घेणे आवश्यक असते, याउलट लांब नळीची बंदूक अवजड होते व त्यामुळे इकडून तिकडे नेण्यास गैरसोयीची होते. याखेरीज नळी फार लांब झाली, तर पुन्हा गोळीचा वेग कमी होतो.
बंदुकीच्या नळीतील वायुदाबातील बदल आ. १ मध्ये दर्शविले आहेत. आकृतीतील वक्र प्रत्यक्षात असणारा दाब दाखवितो. उदा., क या जागी प्रक्षेप्य असते त्या वेळेस वायूचा दाब कग इतका असतो.
बंदुकीचा प्रत्याघात कमी करणे : दारूच्या ज्वलनामुळे उत्पन्न झालेले वायू ज्याप्रमाणे प्रक्षेप्यास पुढे ढकलतात, त्याचप्रमाणे ते बंदुकीसही धक्का देऊन ती मागे सरकवतात. यालाच बंदुकीचा प्रत्याघात (किंवा प्रत्यागती) असे म्हणतात. प्रक्षेप्य नळीच्या बाहेर पडताच, त्याच्या पाठोपाठ नळीतील वायूही प्रक्षेप्याच्या जवळजवळ दुप्पट वेगाने बाहेर पडतात. त्यांचा उपयोग बंदुकीचा प्रत्याघात कमी करण्यासाठी प्रथम फ्रान्समधील श्नाइडर-क्रुसो या कंपनीने केला. यासाठी मुसगतिरोधक नावाचे साधन बंदुकीच्या वा तोफेच्या नळीच्या तोंडाशी बसविले. याच्यामुळे नळीच्या तोंडाजवळील वायूची वाहण्याची मूळची दिशा साधारणतः १२० ते १८० अंशांतून फिरविली जाते व त्यामुळे बंदुकीचा प्रत्याघात कमी होतो. तसेच नळीच्या आत तयार झालेल्या वायूपैकी काही अंश पाठीमागच्या बाजूने घालवून प्रत्याघाताचे जवळजवळ पूर्णपणे निराकरण करता येते.
रोध निर्माण करणाऱ्या गोष्टी : प्रसरणातील वायूंना नळीत पुढील रोध सहन करावे लागतात : (१) प्रक्षेप्याची निरुढी (जडत्व), (२) प्रक्षेप्य ढकलणारे तांब्याचे पट्टे व नळीचा पृष्ठभाग आणि प्रक्षेप्यास परिवलन गती देण्यासाठी नळीत असलेले आटे यांमधील घर्षण, (३) प्रक्षेप्याचे अग्र व नळीचे मुख यांमधील अवकाशातील हवेची निरुढी, नळीच्या मुखाचे आकारमान काहीही असले, तरी जर नळीची लांबी कमी असेल, तर हा तिसरा रोध दुर्लक्षिता येईल. नळीची लांबी जास्त असताना मात्र हा रोध दुर्लक्षण्याइतका थोडा नसतो. त्यातल्या त्यात नळीच्या मुखाजवळील प्रक्षेप्याची गती जर ध्वनिवेगापेक्षा जास्त असेल, तर हवेला नुसता प्रवेगच प्राप्त होतो असे नाही, तर ती संपीडितही होते (दाबलीही जाते). ह्या संपीडित हवेचा परिणाम एखाद्या दट्ट्यासारखा होतो आणि त्यामुळे गोळीचा मुखवेग (बंदुकीच्या नळीच्या बाहेर पडता क्षणीचा वेग) काढणे अवघड होते.
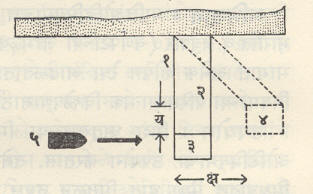
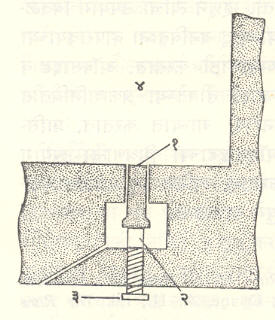
वायुदाब मोजण्याची साधने : सुरूवातीला यासाठी प्रक्षेपी लंबक हे एकमेव साधन उपलब्ध होते. याच्या साहाय्याने प्रक्षेप्याचा मुखवेग काढता येतो व त्यावरून नळीच्या आतील वायुदाबाचे अनुमान करता येते. या लंबकावर (आ. २) प्रक्षेप्य आपटून त्यात रुतते. त्यामुळे लंबक य इतक्या उंचीचा झोका घेतो व त्याचे क्ष इतके आडवे विस्थापन होते. झोक्याच्या या परिणामांवरून प्रक्षेप्याचा संवेग (वस्तुमान X वेग ही राशी) आणि अंती वेग काढता येतो. १७०७ मध्ये जे. डी. कासीनी यांनी ही पद्धती सुचविली. बेंजामिन रॉबिन्स यांनी ३० वर्षांनंतर तिचा वापर केला. या पद्धतीमध्ये नळीतील वायूच्या दाबाबाबतची मोजमापे अप्रत्यक्षपणेच करता येतात.
वायुदाब मोजण्याचे जास्त अचूक साधन म्हणजे ए. नोबेल यांचा दाबमापक. या साधनात वृत्तचितीच्या आकाराच्या तांब्याच्या बुचात वायूच्या दाबामुळे स्थायी विकृती निर्माण होते व तिच्यावरून वायूचा दाब काढता येतो. १९४० नंतर ⇨दाबविद्युत् परिणामाचा वापर करून ‘दाबविद्युत् दाबमापक’ बनविण्यात आला. यामध्ये तोरमल्लीच्या (टुर्मलिनाच्या) एका चकतीवर वायुदाब पडू देतात व या चकतीत दाबाच्या प्रमाणात विद्युत् चालक प्रेरणा (विद्युत् मंडलात प्रवाह वाहण्यास कारणीभूत होणारी प्रेरणा) निर्माण होते. तिच्या मोजमापावरून दाब काढता येतो. याशिवाय प्रतिविकृतिमापकांचाही [⟶ पदार्थांचे बल] वापर केला जातो.
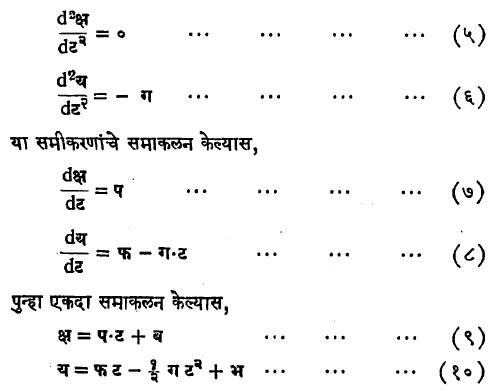
वायुदाबासंबंधी मूलभूत समीकरणे : दारूच्या ज्वलनामुळे उत्पन्न झालेल्या वायूचे तापमान जवळजवळ स्थिर असते व ते दारूच्या रासायनिक घटकांवर मुख्यतः अवलंबून असते. याउलट आतील वायूचे वस्तुमान, दाब व त्यामुळे प्रक्षेप्यास मिळालेला प्रवेग ही क्षणोक्षणी बदलत असतात आणि ती काढण्यासाठी ज्वलन समीकरण, ऊर्जा समीकरण व गती समीकरण यांचा उपयोग करतात.
ज्वलन समीकरण : जळत असलेल्या दारूपासून वायू निर्माण होण्याची त्वरा ही दारूच्या दाण्यांच्या जळणाऱ्या पृष्ठभागाच्या क्षेत्रफळाच्या प्रमाणात असते. हे दाणे जळताना मूळच्या पृष्ठभागाला समांतर असे आत आत जळत जातात. दारु जळायला लागल्यापासून ट सेकंदांनंतर जळणाऱ्या पृष्ठभागाचे मूळच्या पृष्ठभागापासूनचे अंतर य असेल, तर य, ट व वायूचा दाब दा यांमधील संबंध ज्वलन समीकरणाने पुढे दिल्याप्रमाणे दाखवितात.
| dय | = अ (य)·दाक … … (१) |
| dट |
येथे क हा स्थिरांक असून त्याचे मूल्य १ च्या आसपास असते. अ हा स्थिरांक असून त्याचे मूल्य दारूच्या प्रकारावर अवलंबून असते. (य) या फलनाचे (गणितीय संबंधदर्शक पदावलीचे) मूल्य दारूच्या दाण्यांच्या आकारावर अवलंबून असते. आकारावरून या समीकरणाच्या आधारे, जळायला सुरुवात झाल्यापासून ट सेकंदात किती स्फोटक जळाले ते समाकलनाने [⟶ अवकलन व समाकलन] काढता येते व दारुची घनता ठाऊक असल्यामुळे, त्यावरून जळालेल्या दारूचे वस्तुमान माहीत होते.
ऊर्जा समीकरण : दारूच्या ज्वलनापासून निर्माण झालेल्या ऊर्जेमुळे किती वायुदाब निर्माण होतो ते या समीकरणावरून कळते. हे समीकरण व्हॅन डर व्हाल्स यांच्या खालील समीकरणाच्या आधारे काढतात.
| (दा + | ब | ) (स-ल) = र·त … … (२) |
| स२ |
येथे दा = वायूचा दाब, स = वायूचे विशिष्ट घनफळ (एकक वस्तुमानाच्या वायूचे घनफळ), ब आणि ल = स्थिरांक, र = वायूचा विश्वस्थिरांक व त = वायूचे तापमान होय. ज्वलन कोठीचे घनफळ आ असेल व ट सेकंदात जळालेल्या दारूचे वस्तुमान व असेल, तर त्याक्षणी वायूचे विशिष्ट घनफळ आ/व इतके होते. तसेच तज हे दारुचे ज्वलन तापमान असेल, तर र·तज = फ ह्या स्थिरांकास दारूचा विशिष्ट दाब म्हणतात. ब/स२ हे पद सामान्यतः दा च्या मानाने लहान असते.
| समी. (२) मध्ये | ब | = ०, त=तज, तसेच स = | आ | लिहून |
| स२ | व |
| दा | ( | आ | – ल | ) | = फ … … (३) |
| व |
असे समीकरण मिळते व याचा उपयोग वायुदाब काढण्यासाठी होतो.
बंदुकीची अथवा तोफेची नळी तापते व त्यासाठी काही ऊर्जा खर्च होते, त्याचप्रमाणे प्रक्षेप्याच्या बाजूने काही वायू बाहेर जात असल्यास त्यामुळेही प्रक्षेप्याला मिळणारी गती काहीशी कमी होते. या दोन्ही गोष्टींची दखल घ्यावी लागते.
गती समीकरण : ट सेकंदांत म वस्तुमानाच्या प्रक्षेप्याचे बंदुकीच्या नळीत क्ष इतके स्थलांतर झाले असे मानू. वायुदाब प्रक्षेप्याच्या क्षे इतक्या क्षेत्रफळाच्या पृष्ठाभागावर असेल, तर न्यूटन यांच्या गतिविषयक दुसऱ्या नियमाप्रमाणे
| म | d२ क्ष | = दा·क्षे … … (४) |
| dट२ |
| ( | dक्ष२ | = प्रक्षेप्याचा प्रवेग | ). | या समीकरणावरून समाकलनाने प्रक्षेप्याचा वेग |
| dट | ||||
| dक्ष | तसेच क्ष ही दोन्ही काढता येतात. | |||
| dट | ||||
वरील तिन्ही समीकरणांत क्ष, दा आणि य हे एकमेकांशी संबद्ध असून कोणत्याही क्षणी त्यांची मूल्ये काढण्यासाठी किचकट गणित करावे लागते. तथापि स्थूलमानाने ती कशी काढतात याचा वर निर्देश केला आहे. वरील समीकरणांच्या साहाय्याने प्रक्षेप्याचा मुखवेग काढता येतो.
बाह्य प्राक्षेपिकी : बंदुकीच्या किंवा तोफेच्या मुखातून बाहेर पडून लक्ष्यावर पोहोचेपर्यंतचा प्रक्षेप्याचा गतिमार्ग किंवा क्षेपपथ वेग व प्रवेग यांची (वेगवेगळ्या बिंदूंवरील) मूल्ये व दिशा, योग्य मार्गापासून विचलन करणाऱ्या त्याच्यावर लागू होणाऱ्या प्रेरणा, त्याचा पल्ला व उड्डाण काल इ. गोष्टींचा ऊहापोह या भागात होतो. विशिष्ट ठिकाणापासून प्रक्षेप्य प्रक्षेपित केल्यावर ते बरोबर इष्ट लक्ष्यावरच जाऊन पोहोचण्यासाठी काय केले पाहिजे, ते या विवेचनावरून समजते.
न्यूटन यांच्या गतिविषयक पहिल्या नियमानुसार तोफेतून एकदा सुटल्यानंतर प्रक्षेप्य एका सरळ रेषेत जात राहिले पाहिजे परंतु त्यांच्या गतिमार्गात त्याच्यावर परिणाम करणाऱ्या विविध प्रेरणा त्याच्यावर लागू होतात, त्यामुळे त्याचे विचलन होते. या विचलनकारक प्रेरणा पुढीलप्रमाणे : (१) पृथ्वीच्या गुरुत्वाकर्षणाची प्रेरणा (सूर्य-चंद्राचे गुरुत्वाकर्षण दुर्लक्षणीय असते), (२) वाऱ्याचा परिणाम, (३) हवेमुळे उत्पन्न होणारी (कर्षण) प्रेरणा व परिबले (एखाद्या बिंदूभोवती क्रिया करणारी प्रेरणा व तिच्या क्रियारेषेपासूनचे त्या बिंदूचे लंबातर यांच्या गुणाकाराने निर्देशित होणाऱ्या राशीला परिबल असे म्हणतात), (४) ⇨कोरिऑलिस परिणाम. हे सर्व परिणाम लक्षात घेऊन प्रक्षेप्याची गती समीकरणे मांडल्यास ती सोडविणे अशक्यप्राय होते. समीकरणे सोपी करण्यासाठी योग्य परिस्थितीत वरीलपैकी काही परिणाम दुर्लक्षणीय मानतात व समीकरणे सोडवितात, मग अशा तऱ्हेने मिळणाऱ्या उत्तरात, आंरभी दुर्लक्षणीय मानलेल्या परिणामांसाठी योग्य त्या दुसऱ्या करून मिळणाऱ्या उत्तरानुसार तोफांच्या भडिमाराचा रोख ठरविता येतो.
निर्वात आसन्नीकरण : वरील परिणामांतील सर्वांत जटिल म्हणजे हवेचा परिणाम होय. तो हवेच्या घनतेनुसार बदलतो, त्याचप्रमाणे तो प्रक्षेप्याच्या वेगावरही अवलंबून असतो, प्रक्षेप्य संपूर्ण निर्वातातून जाते असे मानल्यास हे परिणाम विचारात घेणे जरूर राहत नाही. अशा विचार पद्धतीला निर्वात आसन्नीकरण असे म्हणतात. प्रक्षेप्याचा पल्ला अल्प असल्यास (उदा., बंदुकीची गोळी) कोरिऑलिस परिणामही दुर्लक्षणीय ठरतो.
गुरुत्वाकर्षण : प्रक्षेप्याचे वस्तुमान म असल्यास पृथ्वीच्या गुरुत्वाकर्षणामुळे त्याच्यावर म·ग [ग = गुरुत्वीय प्रवेग ⟶ गुरुत्वाकर्षण] या मूल्याची प्रेरणा लागू होते व तिची दिशा पृथ्वीच्या मध्याकडे असते. आंतरखंडीय क्षेपणास्त्रे [⟶ क्षेपणास्त्रे] भूष्ठापासून खूप उंचीवर जातात, तेथे ग चे मूल्य कमी होते. त्याचप्रमाणे पृथ्वी हा एकविध (सर्वत्र एकसारखा) गोल नसल्यामुळे अशा क्षेपणास्त्राच्या मार्गात जागोजागी ग चे मूल्य व दिशा बदलतात. हे परिणाम लक्षात घेऊन मांडलेली समीकरणे सोडविणे फार अवघड होते परंतु प्रक्षेप्याचा पल्ला फार नसल्यास त्याची भूपृष्ठापासूनची उंची अल्प असते. मग ग स्थिर मूल्यी व नेहमी अधोदिश मानता येते. त्याचप्रमाणे पृथ्वीचे पृष्ठही सपाट मानता येते. तोफेच्या मुखाशी आदिबिंदू घेऊन क्ष-अक्ष क्षितिज समांतर व य-अक्ष उदग्र (उभ्या दिशेत) घेऊन, ट या काली प्रक्षेप्याचे सहनिर्देशक क्ष आणि य घेतल्यास न्यूटन यांच्या दुसऱ्या गतिनियमानुसार पुढील गती समीकरणे मांडता येतात.
अशी समीकरणे येतात. येथे प, फ, ब आणि भ हे समाकलनामुळे आलेले स्थिरांक असून त्यांची मूल्ये प्रक्षेप्याच्या मूळच्या स्थितीवरून व वेगावरून काढतात. येथे सामान्यतः दोन महत्त्वाचे प्रकार संभवतात. एक तर प्रक्षेप्य काही उंचीवरून क्षितिजसमांतर प्रक्षेपित केले जाते (विमानातून टाकलेला बाँब हे याचे प्रत्यक्ष उदाहरण आहे आ. ४ पहा) किंवा प्रक्षेप्य जमिनीवरून क्षितिजाशी काही कोन करून प्रक्षेपिले जाते (उदा.,
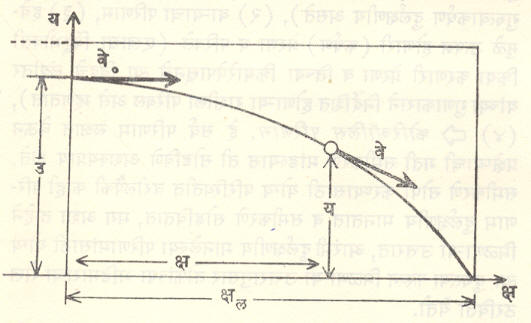
तोफगोळा किंवा अग्निबाण). पहिल्या प्रक्षेप्याची मूळची जमिनीपासूनची उंची उ असेल व क्षितिजसमांतर वेग वे० असेल, तर ट = ० असताना क्ष = ०, य = उ.तसेच
| dक्ष | = वे० आणि | dय | = ० होते. |
| dट | dट |
यांचा उपयोग करून व मागील समीकरणांवरून पुढील समीकरणे मिळतात.
त्यास प्रक्षेप्याचा ‘उड्डाणकाल’ म्हणतात. ट= टल समी. (१३) मध्ये घालून, क्षल = वे० √२उ/ग हा प्रक्षेप्याचा पल्ला मिळतो. तसेच ट= टल समी. (११) व (१२) मध्ये घालून प्रक्षेप्याचा पल्ला गाठतानाचा क्ष आणि य अक्षांस समांतर असे वेगघटक निघतात. त्यावरून प्रक्षेप्याचा वेग व त्याची दिशा काढता येते.
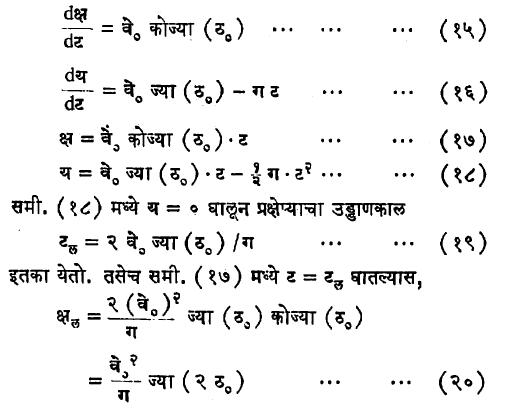
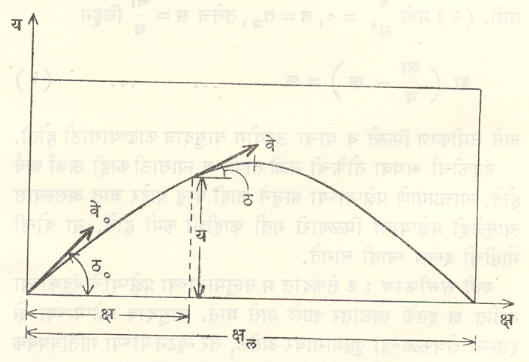
प्रक्षेप्य जर जमिनीवरून क्षैतिज रेषेशी ठ० अंशाचा कोन करून वे० या वेगाने प्रक्षेपित केले, तर ट = ० असताना, य = क्ष = ०,
| dक्ष | = वे० कोज्या (ठ०) आणि | dय | = वे० ज्या (ठ०) |
| dट | dट |
यांचा समी. (७), (८), (९) व (१०) यांत उपयोग करून प, फ, ब, आणि भ या स्थिरांकाची मूल्ये काढतात व त्यांवरून पुढील समीकरणे येतात.
हा प्रक्षेप्याचा पल्ला येतो (आ. ५). जर ठ१ आणि ठ२ या दोघांची बेरीज ९०° असेल, तर ठ१ आणि ठ२ असे क्षैतिज रेषेशी कोन करून एकाच वेगाने प्रक्षेपित केलेल्या दोन प्रक्षेप्यांचा पल्ला एकच असतो, असे समी. (२०) वरून समजून येते (आ. ६). तसेच दिलेल्या वेगाने प्रक्षेपित केलेले प्रक्षेप्य क्षितिजाशी ४५° कोन करून प्रक्षेपित केल्यास महत्तम पल्ला गाठते हेही समी. (२०) वरून कळून येते [कारण ज्या (२ठ०) चे महत्तम मूल्य १ असून, ते २ठ० = ९०° असताना होते]. समी (१३) व (१४) मधून, तसेच समी. (१७) व (१८) मधून ट चा निरास केल्यास
य = उ –१/२ग क्ष२/वे०२ … … (२१)
आणि
य = क्ष·स्प (ठ०) – ग क्ष२/२ वे०२ कोज्या२ (ठ०) … (२२)
अशी समीकरणे येतात व त्यांवरून प्रक्षेप्याचा गतिमार्ग अन्वस्त आहे असे ठरते. समी. (२२) वरून अन्वस्ताचा शिरोबिंदू काढता येतो व प्रक्षेप्य जास्तीत जास्त किती उंचीवर पोहोचते ते समजते. एकाच प्रारंभीच्या वेगाने (वे०) प्रक्षेपित केलेल्या प्रक्षेप्याचा प्रक्षेपण कोन बदलल्यास त्याच्यामुळे प्रक्षेप्याचा गतिमार्ग व पल्ला यांमध्ये कसे फरक पडतात ते आ. ६ मध्ये दाखविले आहे. वेगवेगळ्या अंतरांवरील लक्ष्यावर तोफांचा भडिमार करताना प्रक्षेपण कोन बदलून इष्ट पल्ला मिळविता येतो.
![आ. ६. प्रक्षेपण कोन बदलाचा गतिमार्गावर व पल्ल्यावर होणारा परिणाम : (१) अल्प (ठ१) प्रक्षेपण कोनासाठी, (२) प्रक्षेपण कोन = ४५° [कमाल पल्ला], (३) प्रक्षेपण कोन = ९०° - ठ१ [पल्ला (१) इतकाच].](/images/stories/Khand%2010%20Interal%20Images/P%20-%20621%20%20%20-%20%201.jpg) हवेचा परिणाम : वातावरणातून प्रक्षेप्य पुढे जात असताना हवेच्या त्याच्यावर होणाऱ्या परिणामांचे तीन प्रकार करता येतात (पाण्यातून जाणाऱ्या प्रक्षेप्यावरही पाण्याचे असेच परिणाम होतात). ते म्हणजे (१) उत्थापक प्रेरणा, (२) प्रक्षेप्याला फिरवू पाहणारे परिबल, (३) कर्षण प्रेरणा.
हवेचा परिणाम : वातावरणातून प्रक्षेप्य पुढे जात असताना हवेच्या त्याच्यावर होणाऱ्या परिणामांचे तीन प्रकार करता येतात (पाण्यातून जाणाऱ्या प्रक्षेप्यावरही पाण्याचे असेच परिणाम होतात). ते म्हणजे (१) उत्थापक प्रेरणा, (२) प्रक्षेप्याला फिरवू पाहणारे परिबल, (३) कर्षण प्रेरणा.
उत्थापक प्रेरणा : प्रक्षेप्याच्या पृष्ठभागावरील वायुगतिकीय दाबाच्या वितरणामुळे ही प्रेरणा उत्पन्न होते. तिच्यामुळे प्रक्षेप्य आपल्या मार्गापासून वर किंवा खाली ढकलले जाते. या प्रेरणेचे मूल्य (उ) पुढील समीकरणाने दिले जाते.
उ = घ व्या२ वे२ (कउ)·ज्या(ड) … … (२३)
येथे घ = हवेची घनता, व्या = प्रक्षेप्याच्या लंबछेदाचा व्यास, वे = त्याचा वेग, ड = प्रक्षेप्याचा अक्ष व त्याच्या वेगाची दिशा यांमधील कोन. कठ हा एक ‘परिमाणरहित अंक’ असून त्याला उत्थापक गुणांक (KL) असे म्हणतात. वेगवेगळ्या परिस्थितीत त्याची मूल्ये प्रयोगाने काढावी लागतात.
परिबल : वायुगतिकीय परिणामांमुळेच परिबल निर्माण होते. त्याच्यामुळे प्रक्षेप्याची प्रवृत्ती कोलांट्या घेत पुढे जाण्याची होते. पुढील समीकरणावरून त्याचे मूल्य (प) काढता येते.
प = घ व्या३वे२(कप).ज्या (ड).कोज्या (ड) … (२४)
(कप) हाही परिमाणरहित अंक असून त्याला परिबल गुणांक ( KM) असे म्हणतात. त्याचेही मूल्य प्रयोगानेच काढावे लागते आणि ते परिस्थितीनुसार बदलते.
कर्षण प्रेरणा : या प्रेरणेमुळे प्रक्षेप्याच्या गतीला रोध होत असून तिचे तीन घटक असतात : (१) प्रक्षेप्य पुढे जात असता त्याच्या पुढची हवा दाबली जाते म्हणून तिचा दाब वाढतो. या दाबामुळे पहिला घटक उत्पन्न होतो. हा कमी करण्यासाठी प्रक्षेप्याच्या पुढील भागाला निमुळता आकार दिला जातो. (२) प्रक्षेप्याच्या बाजूंच्या हवेशी होणाऱ्या घर्षणामुळे दुसरा घटक निर्माण होत असून तो कमी करण्यासाठी या बाजू अगदी गुळगुळीत करतात. (३) प्रक्षेप्याच्या मागे हवेत उत्पन्न होणाऱ्या संक्षोभामुळे तिसरा घटक कार्यवाहीत येतो व तो कमी करण्यासाठी प्रक्षेप्याचा मागील भागही काहीसा निमुळता केला जातो. निष्पन्न कर्षण प्रेरणेचे मूल्य (क) पुढील सूत्राने दिले जाते.
क = घ व्या२ वे२ (कग) … … … (२५)
येथे (कग) हा कर्षण गुणांक असून तो प्रक्षेप्याचा वेग व ध्वनिवेग यांच्या गुणोत्तरावर [म्हणजे एर्न्स्ट माख या शास्त्रज्ञांच्या नावाने ओळखण्यात येणाऱ्या ‘माख अंका’वर ⟶ माख अंक) अवलंबून असतो. त्यातल्या त्यात प्रक्षेप्याचा वेग ध्वनिवेगाच्या जवळ असल्यास, (कग) मध्ये फारच फरक पडतो. कर्षण गुणांकाचे मूल्य माख अंकाबरोबर कसे बदलते हे आ. ७ मध्ये दाखविले आहे. हवेची घनता व तापमान उंचीबरोबर बदलत असल्याने कर्षण व कर्षण गुणांक ही दोन्ही उंचीबरोबर बदलतात.
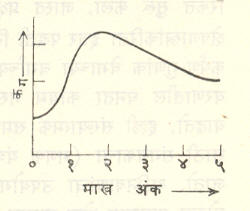
या कर्षणामुळे प्रक्षेप्य त्याच्या निर्वातातील पल्ल्याच्या अलीकडे पडते व पडताना त्याने क्षितिजाशी केलेला कोन वाढतो. (कग) चे मूल्य निरनिराळ्या तापमानाला व घनतेला काढून त्याचे कोष्टक तयार करतात. कर्षण असताना गती समीकरणे पुढे दिल्याप्रमाणे होतात.
वरील समी. (२६) व (२७) मध्ये (क) हा क्ष, य आणि ट यांचे फलन असल्याने ही समीकरणे सोडविणे अवघड जाते.
आसन्नता पद्धती : जर प्रक्षेपण कोन कमी असेल व प्रक्षेप्याचा वेग खूप कमी असून ते जड असेल, तर निर्वातातील प्रक्षेपणाकरिता काढलेली समीकरणे (१५) व (१६) वापरता येतात आणि उत्तरे काढता येतात.
डिडिऑन-बेर्नुली पद्धती : प्रक्षेपण कोन जर २०° पेक्षा कमी असेल आणि वेग अंदाजे २४० मी./से. पेक्षा कमी असेल (येथे कर्षण वेगाच्या वर्गाच्या प्रमाणात बदलते), तर समीकरण सोडवीत असताना, काही विशिष्ट ठिकाणी छेदक ठ हा स्थिरांक मानल्यास, समीकरणातील चल वेगळे करता येतात व समीकरणांचे निर्वाह (उत्तरे) अचूक मिळविता येतात.
ओटो-लार्डिलॉन पद्धती : कमी वेगाने व जास्त प्रक्षेपण कोनाने जाणाऱ्या क्षेपणास्त्रांसाठी या पद्धतीचा उपयोग केला जातो. गती समीकरणांचा निर्वाह संख्यात्मक समाकलन पद्धतीचा [⟶ संख्यात्मक विश्लेषण] वापर करून काढतात व त्यांची कोष्टके बनविली जातात.
क्षेपणास्त्रांच्या गतिमार्गाबाबतची गणितकृत्ये करण्याच्या पद्धती : पहिल्या महायुद्धापर्यंत क्षेपणास्त्रे १५° ते २०° प्रक्षेपण कोन करून सोडीत (प्रक्षेपण कोन = ठ०). त्या वेळी सिॲकी यांच्या पद्धतीने गणितकृत्ये केली जात. जास्त वेगाने, पण कमी प्रक्षेपण कोनाने सोडलेल्या क्षेपणास्त्रांसाठी ही पद्धती अचूक उत्तरे देते. प्रक्षेपणाबाबतची सर्व माहिती याद्वारे कळू शकते. प्रक्षेपण कोन अंदाजे १५° असून गतिमार्गावरील वातावरणाची घनता कायम राहते, असे या पद्धतीत गृहीत धरलेले असते.
दुसऱ्या महायुद्धामध्ये जास्त पल्ला साधण्यासाठी क्षेपणास्त्रे जास्त कोन करून प्रक्षेपित करण्याची जरूरी भासू लागली. ज्योतिषशास्त्रात बराच काळ वापरात असलेल्या आसन्न संख्यात्मक समाकलन पद्धतीचा वापर याबाबतीत एफ्. मौल्टन व त्यांच्या सहकाऱ्यांनी अमेरिकेत सुरु केला. जास्त प्रक्षेपण कोन व जास्त वेग असलेल्या क्षेपणास्त्रांकरिता इतर पद्धती तितक्याशा उपयोगी पडत नाहीत. येथे कर्षण गुणांक वेगाच्या वर्गाच्या प्रमाणात बदलत नसल्याने व वातावरणातील घनता कायम नसल्याने, गणितकृत्यातील किचकटपणा वाढतो. हल्ली संख्यात्मक समाकलन पद्धतीतील गणितकृत्ये करण्यासाठी संगणकाचा (गणक यंत्राचा) मोठ्या प्रमाणावर वापर केला जातो. अग्निबाणांचा उपयोग सुरू झाल्यावर या पद्धतीचा वापर मोठ्या प्रमाणात होऊ लागला.
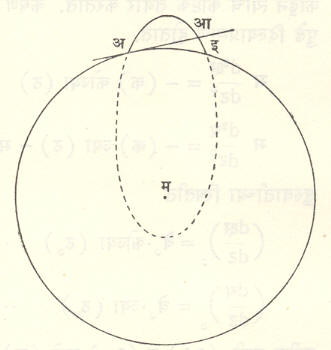
पृथ्वीच्या वक्रतेचा परिणाम : आतापर्यंतच्या विवेचनात प्रक्षेप्याच्या पल्ल्यामध्ये पृथ्वीचा पृष्ठभाग सपाट असून गुरुत्वाकर्षणाचे मूल्य वा दिशा बदलत नाही, अशी कल्पना केलेली होती. पल्ला वाढल्यानंतर ही गृहीते टिकू शकत नाहीत म्हणून याबाबतींत विश्लेषणाची पद्धती बदलणे आवश्यक ठरते. गुरुत्वाकर्षण भूमध्यापासून अंतराच्या वर्गाच्या व्यस्त प्रमाणात बदलत असून त्याची दिशा नेहमी पृथ्वीच्या मध्याकडे असते व त्यामुळे गतिमार्गावर प्रक्षेप्य पुढे सरकत असताना गुरुत्वाकर्षणाची दिशा बदलत जाते, हे ध्यानात घ्यावयास हवे. पृथ्वीच्या पृष्ठभागाच्या वक्रतेमुळे क्षेपणास्त्राचा पल्ला वाढतो. आ. ८ मध्ये तो अआ ऐवजी अइ झालेला आहे. अआ ही पृथ्वीस प्रक्षेपण स्थान अ या ठिकाणी काढलेली स्पर्शरेषा आहे. पृथ्वी स्थिर आहे अशी कल्पना केल्यास गतिमार्ग पृथ्वीमध्य हा ज्याची एक नाभी आहे असे विवृत्त (दीर्घवर्तुळ) असेल. ७,६२० मी./से. यापेक्षा कमी वेग असलेल्या प्रक्षेप्यांचे गतिमार्ग भूपृष्ठाला छेदू शकतात.
कोरिऑलिस परिणाम : आतापर्यंतच्या विवेचनात पृथ्वीचे अक्षीय परिभ्रमण लक्षात घेतलेले नाही. विशिष्ट ठिकाणी तोफेतून गोळा सुटतो तेव्हा त्याला प्रक्षेपणाने मिळणाऱ्या वेगाखेरीज पृथ्वीच्या अक्षीय परिभ्रमणानेही काही वेग प्राप्त होतो परंतु तोफेपासून अलग झाल्यावर गोळा पृथ्वीच्या परिभ्रमणात सहभागी होत नाही. त्यामुळे त्याच्यावर एक प्रेरणा लागू होते व गोळा पृथ्वीवर प्रत्यक्ष जेथे जाऊन पडतो तो बिंदू व पृथ्वी स्थिर असती, तर तो गोळा जेथे पडला असता तो बिंदू यांमध्ये काही अंतर पडते, हे अंतर गोळ्याचा वेग, दिशा व पल्ला त्याचप्रमाणे प्रक्षेपण स्थानाचे रेखांश व पृथ्वीच्या परिभ्रमणाचा कोनीय वेग यांवर अवलंबून असते. या परिणामाला ‘कोरिऑलिस परिणाम’ असे म्हणतात. विशेषतः दूर पल्ल्याच्या लक्ष्यावर अचूक मारगिरी करण्यासाठी हा परिणाम विचारात घ्यावा लागतो. [⟶ कोरिऑलिस परिणाम].
स्थिरीकरण : प्रक्षेप्याच्या वेगाची दिशा त्याच्या अक्षाला नेहमी समांतर राहील अशी योजना करून प्रक्षेप्य आपल्या नियोजित मार्गापासून ढळू न देण्याच्या क्रियेला स्थिरीकरण असे म्हणतात. या स्थितीत प्रक्षेप्याला हवेचा रोध किमान होतो. पल्ला जास्तीत जास्त व त्याचा माराही जास्तीत जास्त अचूक होतो.
पक्ष : बाणांच्या मागील टोकाला पिसे लावलेली असतात त्याचप्रमाणे उखळी तोफांचे गोळे किंवा विमानातून टाकावयाचे बाँब यांच्या मागील टोकावर धातूची पाती बसविलेली असतात, त्यांना पक्ष असे म्हणतात. त्यांच्यावरील वायुगतिकीय प्रेरणांमुळे प्रक्षेप्याचे स्थिरीकरण होते. ज्या प्रक्षेप्यांना आपल्या अक्षाभोवती परिवलन गती दिलेली नसते त्यांच्या स्थिरीकरणासाठी ही पद्धत वापरतात.
परिवलन स्थिरीकरण : तोफांच्या किंवा लष्करी बंदुकांच्या नळ्यांना आतून आटे पाडलेले असतात. त्यामुळे त्यांतून प्रक्षेप्य पुढे सरकताना त्याला आपल्या अक्षाभोवती परिवलन गती दिली जाते. त्यामुळे प्रक्षेप्याला ⇨घूर्णीचे गुण प्राप्त होऊन त्याच्या अक्षाची दिशा अचल राहते व त्यामुळे मारा जास्त अचूक होतो परंतु हे परिवलन फार जोरदार झाल्यास, गतिमार्गाच्या शिरोबिंदूवरून प्रक्षेप्य नीटपणे वळू शकत नाही व अचूकता कमी होते. परिवलन होणाऱ्या प्रक्षेप्याच्या गती समीकरणात परिवलनामुळे उत्पन्न होणाऱ्या परिबलांकरिता आणखी काही पदे घालावी लागतात व त्यामुळे त्याचा निर्वाह काढणे अधिकच कठीण होते. [⟶ दारूगोळा बंदूक व रायफल].
लक्ष्यवेध यंत्रणा : वर उल्लेखिलेल्या प्रक्षेप्यांच्या गतिमार्गांचा उपयोग पुढीलप्रमाणे केला जातो, प्रथम लक्ष्याचे तोफेपासून किंवा बंदुकीपासूनचे अंतर ⇨परासमापकाच्या साहाय्याने (किंवा इतर उपायाने) अजमावण्यात येते. प्रक्षेप्य सरळ क्षैतिज दिशेने सोडल्यास एवढ्या अंतरावर गुरुत्वाकर्षणामुळे त्या रेषेपासून ते किती खाली ढळते ते काढता येते आणि त्याचे निराकरण होईल इतपत बंदुकीची (वा तोफेची) नळी वर कलवून गोळी सोडण्यात येते. यासाठी बंदुकीवर (किंवा तोफेवर) एक यंत्रणा असते, तिच्या साहाय्याने लक्ष्याच्या अंतरानुरूप बंदुकीच्या नळीला योग्य तो कल देता येतो. या यंत्रणेला लक्ष्यवेध यंत्रणा असे म्हणतात. या यंत्रणेवरील अंशांकन (अंशदर्शक खुणा करण्याची क्रिया) नळीतून सुटताना प्रक्षेप्याला एक विशिष्ट वेग प्राप्त होईल असे मानून केलेले असते. अंतर्गत प्राक्षेपिकीत म्हटल्याप्रमाणे हा ‘मुखवेग’ काडतुसात किती दारू भरली, तिच्या ज्वलनाची त्वरा किती होती, प्रक्षेप्याला नळीतून जाताना किती रोध झाला अशा घटकांवर अवलंबून असते. विशिष्ट शस्त्राच्या बाबतीत हे सर्व घटक सर्व गोळ्यांना अगदी समान मूल्यांचे असतील असे होत नाही. त्यामुळे त्या शस्त्रातून विशिष्ट लक्ष्यावर अगदी यंत्राच्या साहाय्याने जरी गोळ्या झाडल्या, तरी त्या एकाच बिंदूवर पडत नाहीत, तर एका विशिष्ट क्षेत्रफळात त्यांचे यदृच्छ वितरण झालेले आढळते, याला परिक्षेपण असे म्हणतात. हे परिक्षेपण शक्य तितके कमी करण्यासाठी शस्त्रे व दारूगोळा यांच्या निर्मितीत काय दक्षता घ्याव्यात हे शोधून काढण्यासाठी शास्त्रज्ञांचे प्रयत्न चालू असतात.
प्रयोगांची जोड : बाह्य प्राक्षेपिकीसंबंधीच्या संशोधनासाठी दोन प्रकारच्या प्रायोगिक पद्धती वापरतात. एका पद्धतीत प्रक्षेप्य (किंवा त्याची प्रतिकृती) एका लांब बोगद्यात स्थिर ठेवून त्याच्याभोवती विविध वेगांचे वायू प्रवाह सोडतात व त्यामुळे प्रक्षेप्यावर लागू होणाऱ्या विविध वायुगतिकीय प्रेरणा व परिबले यांचे योग्य उपकरणांच्या साहाय्याने मापन करतात, या पद्धतीला वातविकार पद्धती असे म्हणतात [⟶ वातविवर].
दुसऱ्या पद्धतीत एका लांब बोगद्यात (लांबी ३ ते ३०० मी. पर्यंत) प्रत्यक्ष गोळी झाडली जाते. मग शीघ्रगती कॅमेऱ्यांच्या [⟶ छायाचित्रण] साहाय्याने त्या गोळीची वेगवेगळ्या अंतरांवर छायाचित्रे घेतली जातात. या छायाचित्रांवरून गोळीचा गतिमार्ग, वेगवेगळ्या बिंदूंच्या ठिकाणी तिचा वेग व दिशा निश्चित करता येतात.
अंत्य प्राक्षेपिकी : प्रक्षेप्यामुळे लक्ष्याच्या होणाऱ्या हानीचा विचार अंत्य प्राक्षेपिकीत केला जातो. यामुळे आपण पाठविलेली प्रक्षेप्ये अधिकाधिक परिणामी कशी होतील व शत्रूने पाठविलेल्या प्रक्षेप्यांपासून आपले जास्तीत जास्त संरक्षण कसे करता येईल, हे ठरविता येते. क्ष-किरण छायाचित्रण व शीघ्रगती छायाचित्रण यांचा शोध लागल्यानंतरही दुसऱ्या महायुद्धापर्यंत अंत्य प्राक्षेपिकीची विशेष प्रगती झाली नव्हती. लक्ष्य वेगवेगळ्या प्रकारचे असते व त्यात मुख्यतः शत्रुपक्षाचे सैन्य, त्याची शस्त्रास्त्रे, दारूगोळा, वाहतुकीची साधने इत्यादींचा समावेश होतो. या विविध प्रकारच्या लक्ष्यांची प्रक्षेप्यामुळे होणारी हानी निरनिराळ्या कारणांनीच व निरनिराळ्या प्रकारची होते. वेगवान प्रक्षेप्यांच्या केवळ धक्क्याने माणसे मरतात व जखमी होतात, तसेच वाहनाची मोडतोड होते. प्रक्षेप्यात असलेल्या दारूगोळ्याचा स्फोट होऊन प्रक्षेप्याची लहान मोठी शकले होतात व ती प्रचंड वेगाने इतस्ततः पसरतात. या शकलांमुळेही वरीलप्रमाणेच हानी होते. प्रक्षेप्य अणुबाँबच्या वर्गातील असेल, तर अणुकेंद्रीय भंजनामुळे (अणुकेंद्राचे तुकडे झाल्यामुळे) उत्पन्न झालेल्या प्रचंड उष्णतेमुळे, आघात तरंगांमुळे व किरणोत्सार्गमुळे (भेदक किरण वा कण बाहेर पडल्यामुळे) लक्ष्याची विविध प्रकारची हानी होते [⟶ अणुबाँब] यांपैकी शकलीकरणामुळे होणाऱ्या हानीचा विचार खाली थोड्या विस्ताराने केला आहे.
शकलीकरण : प्रक्षेप्यातील धातूच्या पातळ आवरणातील दारूच्या स्फोटामुळे आवरणाची शकले उडतात. या शकलांचे आकारमान, वेग व वितरण यांवर लक्ष्याची हानी अवलंबून असते. दारूच्या स्फोटामुळे निर्माण झालेल्या शक्तींपैकी फक्त ४०% शक्ती शकले उडविण्यात उपयोगा पडते, उरलेली ६०% धातूचे आवरण प्रसरण पावण्यात, तसेच स्फोटामुळे उत्पन्न होणाऱ्या आघात तरंगांत खर्ची पडते.
शकलांचे आकारमान व सुरुवातीचा वेग ही धातूच्या आवरणाचे वस्तुमान व आतील दारूचे वस्तुमान यांवर मुख्यतः अवलंबून असतात. शकले पृष्ठभागास लंब अशा दिशेने उडतात. क्षेपणास्त्र उडत असतानाच स्फोट झाल्यास, स्फोटामुळे मिळणारी प्रेरणा व क्षेपणास्त्राच्या वेगामुळे प्राप्त होणारा संवेग यांच्यामुळे शकलांना प्रक्षेप्याच्या दिशेने जास्त वेग प्राप्त होतो. स्फोट झाल्यावर लहान मोठी शकले आजूबाजूला कशा प्रकाराने व किती दूरवर पसरतात, ते प्रयोग करून ठरवितात. कारण यावरून प्रक्षेप्याच्या स्फोटामुळे लक्ष्याच्या संभवनीय हानीचा अंदाज करता येता. या हानीचे परिणाम शकले किती दूरवर व किती जोराचा आघात करतात, तसेच शकले मृदू पोलादाच्या किती जाडीतून आत जाऊ शकतात, यांवरून मापतात.
स्फोट : दारूचा स्फोट झाल्यानंतर निर्माण झालेले वायू उफाळून येऊन सभोवतालची हवा दाबली जाते. यातूनच आघात तरंग निर्माण होतात. अतिशय कमी निरूढीमुळे (जडत्वामुळे) वायू लवकर थंडावतात व त्यांचा वेगही खूप कमी होतो. आघात तरंगांच्या सुस्पष्ट मुखास आघात मुख म्हणतात. या मुखात सुरुवातीस हवेचा दाब आजूबाजूच्या वातावरणाच्या दाबापेक्षा कितीतरी पटींनी अधिक असतो. या स्थितीस आघात तरंगाचा धन पट्टा म्हणतात नंतर थोड्या वेळाने व थोड्या अंतरावर मुखातील दाब भोवतालच्या हवेच्या दाबापेक्षा पुष्कळच कमी होतो, यास आघात तरंगाचा ऋण पट्टा म्हणतात. आघात तरंगाची तीव्रता आघात मुखातील धन पट्ट्याच्या वेळचा महत्तम दाब व तो टिकण्याचा काळ यांवरून ठरवितात. आघात तंरगांमुळे लक्ष्याची हानी होण्यास धन पट्ट्यातील महत्तम दाब एका विशिष्ट मूल्यापेक्षा अधिक, तसेच तो टिकण्याचा कालही एका विशिष्ट मूल्यापेक्षा अधिक असावा लागतो.
भेदन : रणगाड्याचे चिलखत किंवा संरक्षक निवाऱ्याचे काँक्रीट याचा भेद करून आतील सामग्रीची किंवा सैनिकांची हानी करण्यासाठी प्रक्षेप्याकडून या संरक्षक आवरणाचा भेद केला जाणे आवश्यक असते. यासाठी एक पद्धत म्हणजे उच्च वेगाच्या खास चिलखत भेदी गोळ्यांचा वापर करणे. या गोळ्याचे अग्र पोलाद किंवा टंगस्टन कार्बाइड यासारख्या अती कठिण पदार्थाचे केलेले असते. कित्येकदा गोळा चिलखतातून संपूर्णपणे आरपार जाऊ शकत नाही. अशा वेळी प्रक्षेप्याच्या आघातामुळे चिलखत काहीसे आत दबते. मग चिलखतामध्ये आघातामुळे निर्माण झालेल्या- आघात तरंगांच्या दाबामुळे चिलखताच्या आतील भागाचा टवका उडून आत प्रक्षेपित होऊ शकतो. याला हॉपकिन्स परिणाम असे म्हणतात.
गोळा रणगाड्याच्या चिलखतावर आपटल्याबरोबर त्यातील दारूचा स्फोट व्हावा अशी रचना करता येते. या दारूला सुयोग्य आकार देऊन तयार केलेल्या गोळ्याने चिलखताचे भेदन करता येते. [⟶ दारूगोळा].
प्राक्षेपिकीच्या तत्त्वावर चालणाऱ्या इतर यंत्रणा : दुसऱ्या महायुद्धाच्या अखेरीनंतर इतर अनेक क्षेत्रांत स्फोटकांचा व प्राक्षेपिकीच्या तत्त्वांचा उपयोग होऊ लागला आहे. उदा., विमान बिघडल्यास विमानातून वैमानिकाला दूर फेकणारी यंत्रणा, विमानातून बाँब व अग्निबाण सोडणाऱ्या यंत्रणा, मोटारीला अपघात झाल्यास आत बसणाऱ्याच्या समोर आपोआप फुगविल्या जाणाऱ्या हवाई उश्या इत्यादींमध्ये प्राक्षेपिकीच्या तत्त्वांचा उपयोग केला जातो.
पहा : तोफ व तोफखाना दारूगोळा बाँब रॉकेट क्षेपणास्त्रे.
संदर्भ: 1. Bliss G. A. Mathematics for Exterior Ballistics, New York, 1944.
2. Corner, J. Theory of the Interior Ballistics of Guns, New York, 1950.
3. Devis, J. L. Jr. Follin, J. W. Jr. Blitzer, L. Exterior Ballistics of Rockets, Princeton, 1958.
4. Mcshane, E. J. Kelley, J. L. Reno, F. V. Exterior Ballistics, Denever, 1953.
फाटक, मो. पुं.; पुरोहित, वा. ल.