घर्षण : घर्षण हा भौतिक आविष्कार रोजच्या जीवनक्रमात पदोपदी जाणवतो. घर्षणामुळे निर्माण होणारी प्रेरणा ही एकमेकांना स्पर्श करणाऱ्या दोन पृष्ठभागांच्या सापेक्ष गतीला विरोध करते. अशा प्रकारे घर्षण हे वस्तूच्या गतीला अडथळा निर्माण करीत असते. तरीपण घर्षण आवश्यक आहे. जगात घर्षण अजिबात नसून चालणार नाही. त्याच्या अभावी आपणास चालणेही अशक्य होईल घर्षणामुळेच आपण रस्त्यावरून सहज चालू शकतो. पण निसरड्यावर किंवा गुळगुळीत फरशीवर (जिचे घर्षण फारच कमी आहे) चालणे अवघड होते. शास्त्रज्ञ निरनिराळ्या उपायांनी यंत्रांतील घर्षण कमी करण्याचे प्रयत्न करीत आहेत. गोल चाकाचा उगम हा त्यापैकीच एक होय. कारण परिघर्षण (एखादा पदार्थ पृष्ठभागावरून स्वतःभोवती फिरत जाताना होणारे घर्षण) हे सर्वांत कमी गतिविरोधक असते. मोटारीमध्ये निरनिराळ्या भागांच्या घर्षणामुळे २०% शक्तीची हानी होते. तसेच घर्षणामुळे यंत्रांच्या निरनिराळ्या भागांचीही झीज होत असते.
घर्षणाचे नियम : प्रयोगावरून घर्षणासंबंधी पुढील नियम प्रस्थापित झालेले आहेत.
(१) घर्षण प्रेरणा ही स्वसमायोजी (स्वतः जुळवून घेणारी) प्रेरणा आहे. वस्तूला सरकविण्याकरिता लावलेली प्रेरणा वाढविली असता घर्षण प्रेरणादेखील काही मर्यादेपर्यंत वाढत राहते. घर्षण प्रेरणा आणि लावलेली प्रेरणा यांच्या दिशा परस्परांविरुद्ध असतात. वस्तू सरकण्याच्या बेतात असताना घर्षण प्रेरणा महत्तम होते व ह्या महत्तम घर्षण प्रेरणेस सीमांत घर्षण असे म्हणतात आणि त्याचे मूल्य निरनिराळ्या पृष्ठभागांच्या जोड्यांकरिता निरनिराळे असते.
(२) दोन वस्तूंमधील सीमांत घर्षण व त्या वस्तूंच्या स्पर्शबिंदूशी होणारी प्रलंब (काटकोनात असणारी) प्रतिक्रिया यांचे गुणोत्तर हे एक स्थिरांक असते. जर र ही प्रलंब प्रतिक्रिया असेल आणि स हे दोन पृष्ठभागांतील सीमांत घर्षण असेल, तर
स α र किंवा स/र = घ
घ ह्या स्थिरांकास घर्षणांक असे म्हणतात.
(३) घर्षणांक हा स्पर्श होणाऱ्या पृष्ठभागाच्या क्षेत्रफळावर अवलंबून नसतो.
(४) घर्षण प्रेरणा ही दोन पृष्ठभागांच्या सापेक्ष गतीवर अवलंबून नसते.
वरील नियम लिओनार्दो दा व्हींची ह्यांनी प्रयोगावरून काढलेले असून ते फ्रेंच अभियंते गीयोग आमाँताँ यांनी १६९९ साली प्रतिपादन केले. ते पुढे कुलंब यांनी पडताळून पाहिले व त्यांनी स्थितिक घर्षण (वस्तू गतिमान होण्याच्या क्षणी असणारी घर्षण प्रेरणा) आणि गतिज घर्षण (गती मिळाल्यावर ती कायम ठेवण्याकरिता लागणारी प्रेरणा) ह्यांमधील फरक स्पष्ट केला व घर्षण हे दोन पदार्थांच्या कोरड्या कडक पृष्ठभागांच्या एकत्र येण्याने निर्माण होते असे प्रतिपादन केले.
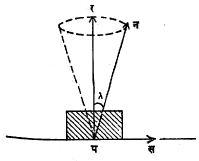घर्षण कोन : संस्पर्श (एकमेकांस स्पर्श करीत असलेल्या) स्थितीत आणि सीमांत घर्षण असताना दोन खडबडीत वस्तूंच्या प स्पर्शबिंदूशी होणाऱ्या निष्पन्न प्रेरणेने प्रलंब प्रतिक्रियेशी केलेल्या कोनाला घर्षण कोन असे म्हणतात. हा कोन साधारणतः λ या अक्षराने दाखवितात. असे सिद्ध करता येते की, घ = स्प λ (स्प = त्रिकोणमितीय स्पर्शक गुणोत्तर). वरील सूत्रावरून असे स्पष्ट होते की, प्रलंब प्रतिक्रिया र आणि घर्षण प्रेरणा स ह्यांची निष्पन्न प्रेरणा न ही एका शंकूच्या पृष्ठभागावर असते व त्या शंकूचा अर्ध उदग्र कोन हा λ असतो (आ. १). ह्या शंकूस घर्षण शंकू असे म्हणतात. एखाद्या पदार्थावर बाहेरून लावलेल्या प्रेरणेची दिशादर्शक रेषा जर ह्या शंकूच्या आत असेल, तर ती प्रेरणा कितीही मोठी असली, तरी ती वस्तू सरकू शकणार नाही. कारण त्या प्रेरणेचा पृष्ठभागाशी समांतर असणारा घटक हा स ह्या सीमांत घर्षणापेक्षा कमी असतो. संस्पर्श स्थितीत असलेल्या दोन खडबडीत वस्तूंचा केवळ स्पर्शबिंदू असताना हा शंकू तयार होऊ शकतो.
समजा, क्षैतिज (क्षितिज समांतर) ऱेषेशी क्ष कोन करणाऱ्या) व पृष्ठभाग खडबडीत असलेल्या एका उतरणीवर ठेवलेला म वस्तुमान असलेला एक ठोकळा, खाली घसरण्याच्या बेतात आहे (आ. २). ग हा गुरुत्व प्रवेग (दर सेकंदास होणारा वेग बदल) आहे. ठोकळा खालच्या दिशेने घसरण्याच्या बेतात आहे, म्हणून तो समतोल स्थितीत आहे. ठोकळ्याच्या वजनाचे दोन घटक पाडले असता एक घटक (म·ग·ज्या क्ष) हा उतरणीच्या पृष्ठभागाशी समांतर व दुसरा घटक (म·ग·कोज्या क्ष) हा त्याला लंब असतो. जर घ हा त्या दोन पृष्ठभागांचा घर्षणांक असेल, तर घर्षण प्रेरणा
स = घ.म.ग. कोज्या क्ष
इतकी असते. ठोकळ्याच्या समतोल स्थितीमध्ये
म.ग. ज्या क्ष = घ.म.ग कोज्या क्ष
म्हणून घ = स्प क्ष
परंतु घ = स्प λ
म्हणून क्ष = λ
निष्कर्ष असा की, जर क्ष > λ, तर वस्तू खाली सरकेल आणि जर क्ष < λ, तर वस्तू खाली सरकणार नाही.
एखाद्या उतरणीच्या समतल रेषेशी असणाऱ्या ह्या महत्तम कोनास (क्ष = λ) अभिशयन कोन (ज्या कोनापर्यंत पदार्थ स्थिर असतो असा कोन) असे म्हणतात. ह्या वेळेस वस्तू उतरणीवरून खाली घसरण्याच्या बेतात असते.
स्पर्शित क्षेत्रफळ : इलेक्ट्रॉन सूक्ष्मदर्शकाच्या साहाय्याने जर एखाद्या गुळगुळीत पृष्ठभागाचे निरीक्षण केले, तर तो पृष्ठभाग उंचसखल असा दिसतो आणि ती उंची किंवा खोली १० ते १०० अणू इतकी असते. तसेच एकावर एक ठेवलेल्या व डोळ्यास जवळजवळ चिकटल्यासारख्या दिसणाऱ्या दोन पृष्ठभागांतील विद्युत् संवाहकतेचे मापन केल्यास असे दिसते की, एकमेकांना खरोखरीच स्पर्श करणाऱ्या भागांचे क्षेत्रफळ फारच कमी असते व ते वस्तूच्या वजनावर अवलंबून असते. गुळगुळीत केलेले पोलादाचे दोन पृष्ठाभाग एकमेकांवर ठेवल्यास खरोखरीच स्पर्श करणाऱ्या पृष्ठभागांचे क्षेत्रफळ हे भासमान स्पर्श करणाऱ्या क्षेत्रफळाच्या १/१०००० इतक्याहूनही कमी असते. ह्यावरून स्पष्ट होते की, ज्यात खरोखर स्पर्श होतो असे क्षेत्रफळ भासमान क्षेत्रफळावर अवलंबून नसते परंतु वस्तूच्या वजनावर अवलंबून असते आणि वजन वाढले असता स्पर्शित क्षेत्रफळही वाढते. पृष्ठभागाचे फारच थोडे क्षेत्रफळ स्पर्श करीत असल्यामुळे स्पर्शबिंदूपाशी निर्माण होणारा दाब प्रचंड असतो आणि कितीही कठीण धातू असल्यास ती स्पर्शबिंदूपाशी लवचिक बनते व झिजते. यामुळे वस्तूचे वजन तोलण्याइतके स्पर्शित क्षेत्रफळ तयार होते.
स्पर्श होणारे क्षेत्रफळ = वजन/शरण दाब
(शरण दाब म्हणजे पदार्थ आपल्या मूळ स्थितीला येऊ शकेल इतपत दिलेला कमाल मर्यादेचा दाब).
वरील विवेचनावरून घर्षणाच्या काही नियमांचे स्पष्टीकरण खालीलप्रमाणे करता येईल. (१) स्पर्शित क्षेत्रफळ हे भासमान क्षेत्रफळावर अवलंबून नसते म्हणजेच घर्षणसुद्धा भासमान क्षेत्रफळावर अवलंबून नसते. (२) स्पर्शित क्षेत्रफळ हे वस्तूच्या वजनाच्या सम प्रमाणात असते म्हणजेच घर्षणसुद्धा वस्तूच्या वजनाच्या सम प्रमाणात असते.
घर्षणाची उत्पत्ती : निरनिराळ्या प्रयोगांनी असे दिसून आले आहे की, घर्षण हे एकमेकांशी सापेक्ष गती असलेल्या व एकावर एक असलेल्या पृष्ठभागांमधील आसंजनामुळे (स्पर्श करणारी दोन पृष्ठे एकमेकांना धरून राहण्यामुळे) निर्माण होते आणि ते घर्षण कर्तरण (जी प्रेरणा एखाद्या प्रतलास लावल्यास ते प्रतल लगतच्या प्रतलावरून सरकते अशा प्रेरणेमुळे होणारी क्रिया) करण्याकरिता लागणारी प्रेरणा दर्शविते. तसेच एखाद्या पृष्ठभागावरील उंच-सखल भाग हा मऊ पृष्ठभागातून जोराने मार्ग काढतो व त्यामुळे घर्षण वाढते. तुलनात्मक रीतीने पाहता यात कर्तरण जास्त असते म्हणून
घर्षण = कर्तरण मूल्य X स्पर्श करणारे क्षेत्रफळ
पृष्ठभागाचे होणारे कर्तरण हे पृष्ठभागाची झीज करण्यास कारणीभूत होते. जर दोन पृष्ठभाग एकमेकांवर नुसते सरकत राहिले, तर पृष्ठाभागाची झीज फारच कमी प्रमाणात झाली असती, पण असे फारच थोड्या ठिकाणी होते, कारण स्पर्श होणाऱ्या पृष्ठांच्या आसंजनामुळे सरकणे अशक्य होते. दोन पृष्ठभागांचे कर्तरण होताना एका पृष्ठभागाचा अतिलहान कण अलग होऊन तो दुसऱ्या पृष्ठभागाशी जोडला जातो. हे अलग होणारे कण फारच लहान असले, तरी एक पृष्ठभाग किरणोत्सर्गी (भेदक किरण वा कण बाहेर टाकणारा) करून घर्षणानंतर दुसऱ्या पृष्ठभागाची तपासणी करून त्यांचा शोध घेता येतो. यंत्रात सुद्धा अशा प्रकारे अलग होणारे कण त्या यंत्रात वापरण्यात येत असलेल्या वंगणात जमा झालेले आढळून येतात व त्यावरून यंत्रांच्या भागांची होणारी झीज कळते.
अधातूंचे घर्षण : वरील विवेचन फक्त धातूंच्या पृष्ठभागांसंबंधी केलेले आहे. तथापि अधातूंच्या घर्षणालाही ते लागू पडते त्याचप्रमाणे घर्षणाचे नियमही त्यांस लागू होतात. प्लॅस्टिक ह्या अधातवीय पदार्थाचा घर्षणांक ०·३ ते ०·६ इतका आहे. परंतु टेफ्लॉन या नावाने प्रसिद्ध असलेल्या पदार्थाच्या घर्षणांकाचे मूल्य ०·०५ ते ०·१ इतके कमी आहे. जर मऊ रबराचा ठोकळा घेतला, तर त्याचे स्पर्शित क्षेत्रफळ हे वजनाच्या सम प्रमाणात नसते म्हणून रबराचा किंवा त्यासारख्या पदार्थाचा घर्षणांक स्थिर नसतो व तो वजन वाढविल्यास कमी होतो. प्रयोगाने असे स्पष्ट झाले आहे की, घर्षणांक α (वजन)-१/२ रबरातील घर्षणाचा बराचसा भाग तो पदार्थ विकृत झाल्यामुळे त्याच्या अंतर्गत स्थितिस्थापकतेच्या मंदायन (विकृतावस्थेतून मूळ स्थितीत परत येण्यास लागणाऱ्या विलंबामुळे होणाऱ्या) ऱ्हासामुळे निर्माण होतो. बर्फाच्या (घर्षणांक ०·०२) दोन तुकड्यांचे एकमेकांवर होणारे घर्षण हे फारच कमी असते व ह्याचे कारण त्या दोन तुकड्यांमध्ये असलेला पाण्याचा पातळ थर हा थर दाबाचा परिणाम म्हणून वितळबिंदूत होणाऱ्या फरकामुळे निर्माण होतो व ही गोष्ट बर्फावरून घसरण्याच्या लांब लाकडी फळीच्या बाबतीत फार महत्त्वाची आहे.
पृष्ठभागावरील पातळ पापुद्र्याचा परिणाम : वरील विवेचनात असे गृहीत धरले आहे की, पदार्थाचे पृष्ठभाग स्वच्छ आहेत परंतु सर्वसाधारणपणे कोणत्याही पृष्ठभागाशी हवेचा संपर्क आल्यास त्या पृष्ठभागावर ऑक्साइडमिश्रित पातळ पापुद्रा तयार होतो. ह्या पापुद्याची जाडी ५, ६ रेणूंच्या जाडी इतकी जरी लहान असली व म्हणून डोळ्यास दृश्यमान होत नसली, तरी घर्षणावर तिचा फार परिणाम होतो, कारण त्यामुळे दोन पृष्ठभाग एकमेकांशी ज्या बिंदूत स्पर्शित होतात, तेथील आसंजक प्रेरणा कमी होते. अशा प्रकारच्या पापुद्र्यापासून पृष्ठभाग मुक्त करणे केवळ अशक्य आहे. परंतु जर हा पापुद्रा पूर्णपणे काढून पृष्ठभाग निर्वात भांड्यात ठेवले, तर घर्षण इतके प्रचंड वाढते की, दोन्ही पृष्ठभाग एकमेकांवर सरकू शकत नाहीत. अशा वेळेस जर थोडी हवा किंवा पृष्ठभाग दूषित करणारा एखादा पदार्थ भांड्यात जाऊ दिला, तर घर्षण नेहमी इतके होते. अधातवीय पृष्ठभागांवरही वरीलप्रमाणेच परिणाम होतो.
तापमान व घर्षण : दोन पृष्ठभागांचे घर्षण जर जोराने होत असेल, तर त्यामुळे त्यांच्या तापमानामध्ये वाढ होते, ही महत्त्वाची गोष्ट ध्यानात घ्यावयास हवी. घर्षणाविरुद्ध केलेल्या कार्याचे उष्णतेमध्ये रूपांतर होते व ह्यामुळे स्पर्शबिंदूंचे तापमान वाढते. जरी ही वाढ लक्षात घेण्यासारखी नसली व पृष्ठभाग थंड वाटत असला, तरी ही गोष्ट प्रयोगाने सिद्ध झालेली आहे. दोन निराळ्या धातूंच्या पृष्ठभागांत तपयुग्म (दोन भिन्न धातूंच्या तारांचे सांधे भिन्न तापमानात ठेवल्यामुळे उत्पन्न होणारा विद्युत् दाब मोजण्याचे एक साधन) वापरून पृष्ठभागांतील स्पर्शबिंदूमध्ये उष्णता फरकामुळे निर्माण होणारी विद्युत् चालक प्रेरणा (विद्युत् प्रवाह वाहण्यास कारणीभूत होणारी प्रेरणा) मोजली असता ही गोष्ट सिद्ध होते. अशा बिंदूपाशी जरी तापमान जवळजवळ १,०००० से. इतके असले, तरी हे तापमान क्षणिक असते. ह्या बिंदूंना उष्ण बिंदू असे म्हणतात. अर्थात हे तापमान त्या धातूच्या वितळबिंदूपेक्षा जास्त राहू शकत नाही, हे उघड आहे. हे तापमान वस्तूच्या वजनावर, घर्षणाच्या त्वरेवर, धातूच्या औष्णिक संवाहकतेवर व धातूच्या वितळबिंदूवर अवलंबून असते. वरील प्रकारामुळे धातू मृदू होणे किंवा वितळणे ह्यासारखे प्रकार होऊन पृष्ठभागाची झीज होते. वितळलेल्या धातूच्या दोन पृष्ठभागांमध्ये तयार झालेला पापुद्रा घर्षण कमी करतो. वंगण वापरताना ही गोष्ट लक्षात घेणे जरूर आहे, कारण तापमानातील वाढीमुळे वंगाणाचे कार्य असफल होते.
परिघर्षण : परिघर्षणाचे दोन प्रकार आहेत. ज्यावेळेस रेल्वे एंजिनाला गती देणारे चाक रुळावरून न घसरता गोल फिरते त्यावेळेस प्रेरणा परिबल (प्रेरणा व तिचे ज्याभोवती पदार्थ फिरतो त्या बिंदूपासूनचे
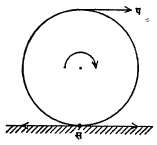
अंतर यांचा गुणाकार) त्या चाकावर कार्य करीत असते. चाक व रूळ या दोहोंत परस्पर स्पर्श एका सरळ रेषेत होतो. आ. ३ मध्ये दाखविलेला दोघांचा स्पर्शबिंदू स या रेषेवरील आहे. या बिंदूपाशी दोन समान पण विरुद्ध दिशा असलेल्या प्रेरणा उद्‌भवतात. प ही स्पर्शरेषेच्या दिशेने असलेली प्रेरणा आहे. स बिंदूवर असणारी उजव्या दिशेची प्रेरणा ही त्याविरुद्ध दिशेला असलेल्या घर्षण प्रेरणेमुळे समतोलित होते आणि त्यामुळे स्पर्शबिंदू स्थिर राहतो परंतु असमतोलित प्रेरणा प चाकास स या स्पर्शबिंदूभोवती फिरविण्यास कारणीभूत होते. चाक फिरत असताना होणाऱ्या प्रत्येक स्पर्शबिंदूस हीच गोष्ट लागू पडते. ज्यावेळेस रूळ फार गुळगुळीत होतात त्यावेळेस घर्षण प्रेरणा फार कमी होते व अशा प्रसंगी चाक पुढे न सरकता त्याच ठिकाणी आपल्या अक्षाभोवती वर्तुळाकार फिरते. अशा प्रसंगी रूळावर वाळू टाकून घर्षण प्रेरणा वाढवितात. जेव्हा एखादे दृढ चाक घट्ट अशा क्षैतिज पृष्ठभागावरून स्वतःच्या अक्षाभोवती न घसरता फिरते, तेव्हा त्या दोघांचा स्पर्श मागे सांगितल्याप्रमाणे एका सरळ रेषेवर घडतो. जर चाकाचे वजन व पृष्ठभागाची प्रतिक्रिया याव्यतिरिक्त इतर कोणतीही प्रेरणा त्या चाकावर लागू नसेल तर या दोन प्रेरणा (वजन व प्रतिक्रिया) लंबरेषेत विरुद्ध दिशांस असल्याने घर्षण प्रेरणा खरे म्हणजे उद्‌भवू नये. म्हणजे तत्त्वतः चाकास फिरण्याची गती एकदा मिळाल्यानंतर ते एकसारखे फिरतच रहावयास हवे. प्रत्यक्षात मात्र असे आढळते की, चाकास फिरते ठेवण्यासाठी प्रेरणा न लावल्यास त्याचे फिरणे कमी होत होत अखेर थांबते. याचा अर्थ असा की, चाकाच्या फिरण्यास विरोध उत्पन्न होतो. हा विरोध होण्याचे कारण असे की, चाक व पृष्ठभाग हे दोन्ही थोड्या फार प्रमाणात विकृत होतात व म्हणून त्यांचा स्पर्श सरळ रेषेवर न होता काही क्षेत्रफळावर होतो. पदार्थ अधिक दृढ असतील तर स्पर्शांचे क्षेत्रफळ कमी होईल इतकेच, पण या विकृतिजन्य स्थितिस्थापक प्रेरणेमुळेच चाकाच्या फिरण्यास विरोध म्हणजे परिघर्षण निर्माण होते.
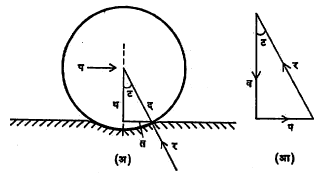
पृष्ठभागावरून चाक फिरत असताना स्पर्शित क्षेत्रफळाच्या पुढील भागात त्याच्या मागच्या भागाच्या मानाने दाब अधिक असतो व पुढील भागातील क्षेत्रफळही मागच्या मानाने अधिक असते. या दाबातील फरकामुळे आ. ४ मध्ये दाखविल्याप्रमाणे प्रलंबाशी मागच्या अंगाने ट कोन करणारी निष्पन्न प्रतिक्रिया र निर्माण होते व तिचा क्षैतिज घटक गतीस विरोध करतो. आ. ४ (आ) वरून
प – र . ज्या ट = ० र. कोज्या ट – व = ०
साहजिकच गती चालू रहावी म्हणून हा विरोध दूर करण्यासाठी चालक प्रेरणा प लावावी लागते. आ. ४ (अ) वरून स्पष्ट दिसते की,
प = व . स्प ट = व. त/थ
(त, थ, द या आ. ४ (अ) मधील त्रिकोणाच्या बाजू आहेत)
व हे चाकाचे वजन आहे. बहुतेक सर्व पदार्थांच्या बाबतीत ट फार लहान असल्याने थ ऐवजी द लिहिण्यास हरकत नाही व म्हणून
प = व . त/द
या समीकरणात त यास परिघर्षणांक म्हणतात व तो एक लांबी दर्शवीत असल्याने त्यास परिघर्षणाची भुजा म्हणणे अधिक योग्य होईल.
वरील दोन्ही प्रकारांत चाकाचे थोड्या फार प्रमाणात होणारे घसरणे पण विचारात घ्यावयास हवे. परंतु डी. टेबर यांनी असे दाखवून दिले की, घर्षणाच्या तुलनेने घसरणे फारच कमी असते. परिघर्षणात पृष्ठभागाचे पापुद्रे निघतात, तर अधिघर्षणात (सरकत जाण्याच्या गतीला विरोध करणाऱ्या प्रेरणेत) पृष्ठभागाचे उंच-सखल भाग कापले जातात. पापुद्रे कापण्यासाठी फारच कमी कार्य करावे लागते म्हणूनच वंगणामुळे अधिघर्षण जरी पुष्कळ कमी होत असले, तरी परिघर्षणावर त्याचा फारच कमी परिणाम होतो.
वंगणाचे कार्य : दोन पृष्ठभाग एकमेकांवर घासले जात असताना घर्षण निर्माण होते आणि हे घर्षण पृष्ठभागांच्या गतीला विरोध करते. अशा वेळेस दोन पृष्ठाभागांमध्ये वंगणाचा थर ठेवल्यास वंगण दोन प्रकारचे कार्य करते. (१) गतीला होणारा विरोध कमी करणे आणि (२) पृष्ठभाग एकमेकांपासून दूर ठेवले जात असल्यामुळे पृष्ठभागांची झीज कमी करणे [ → वंगण].
वंगणामुळे निरनिराळ्या पृष्ठभागांच्या घर्षणांकामध्ये कसकसा बदल होतो ते कोष्टक क्र. १ वरून स्पष्ट होईल. काही विशेष पदार्थांच्या जोड्यांनुसार घर्षणांक व घर्षण कोन कोष्टक क्र. २ मध्ये दिले आहेत.
|
कोष्टक क्र.१. वंगणामुळे निरनिराळ्या पृष्ठभागांच्या घर्षणांकांत होणारा बदल. |
||
|
पृष्ठभागाची स्थिती |
घर्षणांक |
|
|
अभिसीमा |
सरासरी |
|
|
वंगणविरहित पृष्ठभाग |
०·१ ते ०.४ |
०·१६० |
|
अंशतः वंगण दिलेले पृष्ठभाग |
०·०१ ते ०·१० |
०·०३० |
|
आदर्श वंगण दिलेले पृष्ठभाग |
०·००२ ते ०·०१ |
०·००६ |
|
गोलक धारवा (बॉल बेअरिंग) वापरून |
०·००१ ते ०.००३ |
०·००२ |
|
लाटणी धारवा (रोलर बेअरिंग) वापरून |
०·००२ ते ०·००७ |
०·००५ |
कोणताही पदार्थ अनेक रेणूंचा बनलेला असतो. ह्या रेणूंमधील अंतर अल्प असल्यास त्यांची परस्परांवरील आकर्षण प्रेरणा जास्त असते आणि अंतर जास्त असल्यास ही प्रेरणा कमी असते. र हे अंतर प्रभावी समजल्यास र त्रिज्येचा गोल एका अ रेणूभोवती काढला असता ह्या गोलातील सर्व रेणूंवर अ ह्या रेणूचे आकर्षण घडेल. र चे मूल्य १ ते ३ X १०-८ सेंमी. इतके अल्प असते. या अंतरातील रेणुरेणूंमध्ये आसक्ती फार मोठी असते. ह्या आसक्ती प्रेरणेचा प्रत्यय ज्यावेळेस दोन पृष्ठभाग एकमेकांपासून १ ते ३ X १०-८ सेंमी. या
|
कोष्टक क्र. २. काही पदार्थांच्या जोड्यांनुसार घर्षणांक व घर्षण कोन |
|||
|
पदार्थ व त्याच्या पृष्ठभागाची स्थिती |
घर्षणांक |
घर्षण कोन |
|
|
लाकडावर लाकूड |
कोरडे |
०·२५ ते ०·५ |
१४° ते २६·५° |
|
लाकडावर लाकूड |
ओलसर |
०·०४ ते ०.२ |
२° ते ११·५° |
|
धातूवर धातू |
कोरडी |
०·१५ ते ०·२ |
८·५° ते ११·५° |
|
धातूवर धातू |
ओली |
०·३ |
१६·५° |
|
चामड्यावर धातू |
कोरडी |
०.५६ |
२९·५° |
|
चामड्यावर धातू |
ओली |
०·३६ |
२०·०° |
|
चामड्यावर धातू |
तेलकट |
०·१५ |
८·५° |
अंतरावर असतात त्यावेळेस येतो. ही आसक्ती सिद्ध करण्याकरिता केलेला प्रयोग पुढीलप्रमाणे आहे. पृष्ठभाग चकचकीत व गुळगुळीत असलेला तांब्याचा एक घन (घनाकृती) घेऊन त्यावर तसाच दुसरा घन ठेवला असता हे दोन्ही घन त्यांच्या स्पर्श होणाऱ्या पृष्ठभागातील रेणूंमध्ये असलेल्या नैसर्गिक आकर्षणामुळे एकमेकांना घट्ट चिकटतात व वरचा घन उचलला असता खालचा घन पण उचलला जातो. अशा रीतीने जवळजवळ ११ घन एकमेकांना चिकटले असता वरचा घन उचलल्यावर खालचे दहाही घन उचलले जातात.
दोन पृष्ठभागांतील घर्षणाचा विचार करीत असताना त्यावरील प्रेरणांचा विचार केल्यास असे म्हणता येईल की, घर्षणामध्ये पृष्ठभागांच्या खडबडीतपणामुळे एका पृष्ठभागातील रेणूंच्या प्रभावी अंतरापलीकडे दुसऱ्या पृष्ठभागाचे रेणू असतात. तसेच पृष्ठभागाने शोषण केलेल्या दूषित पदार्थाचे थरही ह्या प्रभावी अंतरापेक्षा जास्त जाडीचे असतात आणि हे थर काढणे जवळजवळ अशक्य असते. या सर्व गोष्टींमुळे आसंजन प्रेरणा प्रभावी होत नाही. पण पृष्ठभाग गुळगुळीत केल्याने ही आसंजन प्रेरणा प्रभावी झाल्यास होणारा फायदा म्हणजे ह्या प्रेरणेमुळे वंगणाचा पापुद्रा पृष्ठभागाकडून आकर्षिला जातो व घट्ट धरून ठेवला जातो. घर्षणामुळे दोन पृष्ठभागांवर विरुद्ध जातीचे विद्युत् भार (धन व ऋण) निर्माण होतात व त्यांच्यात असलेल्या आकर्षण प्रेरणेचाही विचार घर्षणाचा अभ्यास करताना केला पाहिजे, असे काही शास्त्रज्ञांचे मत आहे.
घर्षण हे सर्व प्रकारच्या यंत्रांत व सान्निध्यात येणाऱ्या विविध प्रकारच्या पृष्ठभागांत आढळत असल्यामुळे घर्षणाचा अभ्यास आणि पर्यायाने ते कमी करण्याकरिता वंगणांचा अभ्यास करणे अत्यंत महत्त्वाचे आहे. या दृष्टीने ब्रिटनमध्ये एक संशोधन केंद्र (नॅशनल सेंटर ऑफ ट्रायबॉलॉजी) स्थापन करण्यात आलेले असून विविध पदार्थांसंबंधी व यांत्रिक प्रक्रियांसंबंधी तेथे घर्षणविज्ञानाच्या दृष्टीने संशोधन करण्यात येत आहे.
संदर्भ : 1. Dunken, J. Starling, S. G. A Textbook of Physics, London, 1957.
2. American Institute of Physics Handbook, New York, 1967.
घन, प. द.
“