उष्णतेचा यांत्रिक तुल्यांक : यांत्रिक कार्य व त्यापासून निर्माण होणारी उष्णता यांच्या गुणोत्तराला उष्णतेचा यांत्रिक तुल्यांक म्हणतात. उष्णता म्हणजे एक न दिसणारा द्रवरूप पदार्थ (ऊष्मद्रव, कॅलरिक) आहे अशी समजूत अठराव्या शतकापर्यंत दृढमूल होती. हा द्रव अणु-रेणूंच्या मधील जागेत असतो. पदार्थ उष्ण होणे म्हणजे हा द्रव वाढणे व थंड होणे म्हणजे द्रव कमी होणे होय. उष्णतेमुळे पदार्थाचे वजन वाढत नसल्याने हा द्रव वजनरहित असला पाहिजे. हा द्रव अतिशय लवचिक, सर्वव्यापी, नष्ट न होणारा व कोणत्याही पद्धतीने तयार होऊ न शकणारा आहे, अशा प्रकारच्या समजुती त्यावेळी होत्या.
या कल्पनेला पहिला धक्का उंकाट रम्फर्ड यांनी दिला. बंदुकीच्या कारखान्यात काम करत असताना त्यांना असे दिसून आले की, बंदुकीच्या नळीला भोक पाडताना प्रचंड उष्णता निर्माण होते. भोक पाडताना बाहेर पडणार्या लोखंडाच्या भाराशी निर्माण होणार्या उष्णतेचा काहीही संबंध दिसून आला नाही. उलट भोक पाडण्याच्या यंत्राच्या गतीशी उष्णतेचा संबंध आढळून आला. यावरून ऊष्मद्रव सिद्धांत खोटा असावा, असे मत त्यांनी व्यक्त केले.
यानंतर १७९९ मध्ये सर हंफ्री डेव्ही यांनी बर्फाचे दोन तुकडे एकमेकांवर घासले, तर पाणी निर्माण होते असे दाखवून दिले. बर्फापेक्षा पाण्यात जास्त उष्णता असते हे सर्वमान्यच होते. तेव्हा पाणी निर्माण होण्यासाठी लागणारी जादा उष्णता आली कोठून हे ऊष्मद्रव सिद्धांताचा पाठपुरावा करणार्याना सांगता आले नाही.
रम्फर्ड व डेव्ही यांच्या या संशोधनाचे महत्त्व त्यावेळी फारसे कुणाला वाटले नाही. परंतु पुढे जूल यांनी उष्णता ही प्रकाश, विद्युत् वगैरेंप्रमाणे एक ऊर्जेचा आविष्कार आहे, द्रव पदार्थ नाही, असे सिद्ध केले आणि यांत्रिक कार्य व त्यापासून निर्माण होणारी उष्णता यांचा अन्योन्यसंबंध दर्शविणारा नियम प्रसिद्ध केला. या त्यांच्या सिद्धांताला सर्वमान्यता मिळाली. या नियमाप्रमाणे यांत्रिक कार्य (य) व त्यापासून निर्माण होणारी उष्णता (उ) यांचे गुणोत्तर (य/उ) स्थिरांक (जे) असते.
य/उ = जे; य = जे × उ … … (१)
या स्थिरांकाला उष्णतेचा यांत्रिक तुल्यांक (सममूल्य) म्हणतात. यांत्रिक तुल्यांक काढण्याच्या विविध पद्धती खाली दिल्या आहेत.
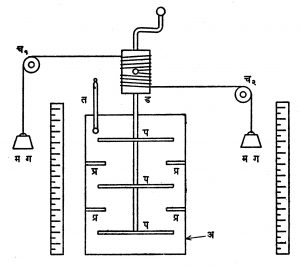
(१) जूल यांची पद्धती : आ. १ मध्ये दाखविल्याप्रमाणे अ हा एक उष्मतामापक असून त्यात पाणी असते. प या अनेक पात्यांची क्षेपणी पाण्यात फिरवली असता पाणी ढवळून निघते. पाणी चांगले ढवळले जावे म्हणून प्र हे लहान पातीवजा तुकडे मापकाला कायमचे जोडलेले असतात. क्षेपणीचा अक्ष ड या दंडगोलाला एका काढता-घालता येणार्या खुंटीच्या साहाय्याने जोडलेला असतो. दंडगोलाभोवती दोन दोर्या गुंडाळलेल्या असून त्या च१ व च२ या कप्प्यांवरून नेलेल्या असतात. त्यांच्या टोकांना म ग ही समान वजने जोडलेली असतात. त हा तपमापक आहे.
प्रथम उष्णतामापकाचे तपमान त१ पाहून नंतर म ग ही वजने जोडावीत. गुरुत्वाकर्षणाने वजने खाली येतात त्यामुळे दंडगोल व त्याबरोबर क्षेपणी फिरते. यामुळे पाणी ढवळले जाऊन त्याचे तपमान वाढते. ही वाढ अत्यल्प असल्याने हाच प्रयोग अनेकदा (न वेळा) करवा लागतो. प्रत्येक खेपेला दोरी दंडगोलाभोवती गुंडाळताना क्षेपणीची खुंटी काढून ठेवावी नाहीतर क्षेपणी उलटी फिरेल, तसेच वजने पुन्हा मूळ ठिकाणी परत जोडावीत व मग प्रयोग करावा. शेवटी मापकाचे तपमान त२ घ्यावे. समजा, प्रत्येक वेळी वजने ल अंतर खाली आली, मापकाचे जल सममूल्य (मापकाचा भार × त्याची विशिष्ट उष्णता) ज आहे व त्यातील पाण्याचा भार म१ आहे. यावरून पुढील समीकरणाने जे चे मूल्य मिळते.
| जे = | २ न × म × ग × ल | अर्ग/कॅलरी |
| (म१ + ज) (त२ – त१) |
या पद्धतीत पुढील दोष आहेत : (१) वजने जमिनिला टेकतात त्यावेळी त्यांना गतिज ऊर्जा असते, (२) कप्पीवरील घर्षणामुळे काही ऊर्जा फुकट जाते, (३) तपमान अतिशय सावकाश वाढत असल्याने (सु. o·६° से. / तास) प्रारणाने बरीच उष्णता फुकट जाते. या सर्वांबद्दल दुरुस्ती करणे आवश्यक आहे.
हे दोष काढून टाकण्यासाठी रोलंड यांनी पुढील सुधारणा केल्या : (१) क्षेपणी जोराने फिरविण्यासाठी छोटे बाष्प एंजिन वापरले. (२) क्षेपणाचा वेग असा ठेवला की वजने स्थिर रहावीत. त्यामुळे दंडगोलाचा व्यास जर ड असेल, तर म × ग × ड हे प्रेरणायुग्म (सारख्या व समांतर पण विरुद्ध प्रेरणांची जोडी) परिबल (युग्मापैकी एका प्रेरणेचा व युग्मातील लंब अंतराचा गुणाकार) निर्माण होते. (३) न भ्रमणसंख्या यांत्रिक गणकाने मोजली. या सुधारणांमुळे तपमान जलद वाढू शकले (४५० से./तास) या पद्धतीत पुढील समीकरणाने जे चे मूल्य मिळते.
| जे = | २π × न × म × ग × ड | अर्ग/कॅलरी |
| (म१ + ज) (त२ – त१) |
निरनिराळ्या तपमानांस प्रयोग केल्यावर असे दिसून आले की, तपमान वाढीबरोबर जे चे मूल्य पद्धतशीरपणे थोडे थोडे कमी होते. याचे कारण म्हणजे तपमानाबरोबर पाण्याची विशिष्ट उष्णता बदलते. सर्वसाधारणपणे जे चे मूल्य ४·१८ × १०७ अर्ग/कॅलरी इतके दिसून आले.
लॅबी आणि हरकस यांची पद्धती : विद्युत् पद्धतींनी काढलेल्या जे च्या मूल्याचा अचूकपणा विद्युत् चुंबकीय एककांच्या अचूकपणावर अवलंबून असतो. हा प्रयोग लॅबी व हरकस यांनी यांत्रिक तंत्र वापरून जे चे अचूक मूल्य काढले. या पद्धतीत वापरलेल्या उपकरणाचे वर्णन खालीलप्रमाणे आहे (आ. २).

घूर्णक : (क). हा एक विद्युत् चुंबक अ-अ असून तो एका बिडाच्या चौकटीत गोलक धारवे (बॉल बेअरिंग) वापरून बसवलेला असतो. ही चौकट एका काँक्रीटच्या बैठकीवर बसवलेली असते. चुंबकाचा अक्ष प्रथम उदग्र (उभ्या दिशेत) करावा लागतो. नाहीतर चुंबक फिरताना त्याच्या मधोमध असलेल्या स्थाणुकावर (स्थिर भागावर) स्थ तो धडकण्याचा संभव असतो. एक अश्वशक्तीच्या विद्युत् मोटरने चुंबक स्थिर गतीने फिरता ठेवलेला असतो. फ हे चक्र मोटरीचा पट्टा बसविण्यासाठी आहे.
स्थाणुक : (ग). हे नळकांड्याच्या आकाराचे असून त्याची रचना विद्युत् मोटरीतील धात्रासारखी (संवाहक तारा बसविलेल्या भागासारखी, आर्मेचरसारखी) असते. यात तांब्याच्या नळ्या (आकृतीतील ‘ख‘ भाग पहावा) वापरलेल्या असतात. हे नळकांडेही दोन पोलादी गोलक धारव्यांना जोडलेले असते. धारव्यांची आतील अस्तनी एका परिपीडन (पीळ घालणारे प्रेरणायुग्म निर्माण करणार्या) चक्राला व ते दोन्ही एका परिपीडन तारेला जोडलेले असतात. तारेच्या वरील भागास पुष्कळ समायोजन केलेले असते. परिपीडन चक्र सु. २० सेंमी. व्यासाचे असून ते तांबे व ॲल्युमिनियम यांच्या मिश्रधातूपासून बनवलेले असते. चक्रावरून दोन टंगस्टन तारा दोन कप्प्यांवरून नेऊन त्यांना सारखी वजने जोडलेली असतात. कप्प्या गारेच्या दगडाच्या तीक्ष्ण धारेवर आधारित असतात. स्थाणुकाच स्थिर-प्रवाह उष्णतामापकासारखा उपयोग होतो. स्थाणुकामधून एक पन्हळ नेलेली असून त्यातून पाण्याचा स्थिर प्रवाह सोडलेला असतो. त१ व त२ ही प्लॅटिनमाची रोध तपमापके पाणी जाताना व बाहेर पडताना त्याचे तपमान नोंदतIत.
चुंबक स्थिर वेगाने फिरत ठेवल्यामुळे प्रेरणायुग्म निर्माण होऊन ते स्थाणुक फिरवण्याचा प्रयत्न करते. परिणामतः परिपीडन तार व स्थाणुकाला जोडलेल्या वजनामुळे प्रेरणायुग्म निर्माण होऊन ते पहिल्या युग्माला समतोलित करते व स्थाणुक स्थिर रहाते. स्थाणुकामधील तांब्याच्या नलिकांत विद्युत् प्रवाह निर्माण होऊन त्या तापतात व त्यामुळे पन्हळातून वाहणार्या पाण्याचे तपमान वाढते. या पद्धतीचे तत्त्व रोलंड यांच्या पद्धतीप्रमाणेच असल्याने गणित व समीकरणे त्यात पद्धतीप्रमाणे आहेत.
या पद्धतीतील दोष व त्यावरील उपाय : (१) तपमापकांच्या नलिकातून थोडी उष्णता बाहेर जाते, याकरिता या नलिका निर्वात नलिकांत बंदिस्त ठेवतात. (२) स्थाणुकाच्या वरील झाकणातून थोडी उष्णता बाहेर पडते. म्हणून प्रयोगखोलीचे तपमान स्थाणुकाएवढेच ठेवल्यास हा दोष टाळता येतो. (३) स्थाणुकाच्या बाजूंनी उष्णता बाहेर पडते. याकरिता स्थाणुक एका निर्वात केलेल्या काचेच्या नळकांड्यात ठेवल्यास उष्णतेची हानी होत नाही.
लॅबी व हरकस यांनी १५० से. तपमानास जे चे मूल्य ४·१८६० × १०७ अर्ग / कॅलरी इतके काढले.
चौधरी व कोठारी यांनी स्थिर चुंबक क्षेत्राऐवजी फिरते चुंबक क्षेत्र वापरून या पद्धतीत सुधारणा करण्याचा प्रयत्न केला आहे.
विद्युत् पद्धती : जे चे मूल्य विद्युत् पद्धतीने प्रथम जूल यांनी काढले. त्यामध्ये कॅलेंडर व बार्न्झ, लॅबी वगैरेंनी सुधारणा केल्या. ऑस्बर्न, स्टिमसन आणि गिनिंग्ज यांनी ब्यूरो ऑफ स्टँडर्स, वॉशिंग्टन येथे जे चे मूल्य काढण्याकरिता जी विद्युत् पद्धती वापरली ती अचूक समजली जाते. त्यांनी जूल यांचीच पद्धती सुधारून वापरली.
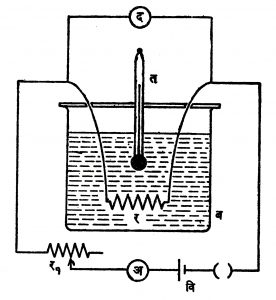
जूल पद्धती : आ. ३ मध्ये दाखविल्याप्रमाणे तारेचे वेटोळे र हे वि या विद्युत् घटाला जोडलेले आहे. विद्युत् प्रवाहाचे नियंत्रण र१ हा रोध करतो व प्रवाहाचे मापन अ हा अँपिअरमापक करतो. र ही तार ब या उष्णतामापकामधून गेलेली आहे. द हा व्होल्टमापक आहे व त हा तापमापक आहे. समजा विद्युत् प्रवाह प्र अँपिअर आहे व दाब द व्होल्ट आहे, ट सेकंद वेळ प्रवाह चालू ठेवला असता तपमानातील फरक त२ – त१ इतका होतो. उष्णतामापकातील पाण्याचे वस्तुमान म ग्रॅम आहे व मापकाचे जल सममूल्य ज आहे. मग जूल यांच्या सिद्धांताप्रमाणे विद्युत् ऊर्जा = जे (उष्णतामापक व त्यातील पाणी यांना मिळालेली उष्णता).
द × प्र × ट = जे (म + ज) (त२ – त१)
यावरून जे चे मूल्य मिळते. या पद्धतीतील प्रमुख दोष म्हणजे (१) प्रारणाने (तरंगरूपी ऊर्जेच्या रूपाने) बाहेर पडणारी उष्णता आणि (२) अशुद्धी निर्माण करणारे पाण्यात विरघळलेले पदार्थ व वायू.
हे दोष नाहीसे करण्यासाठी ऑस्बर्न, स्टिमसन व गिनिंग्ज यांनी पुढील सुधारणा केल्या : प्रारणाने उष्णता बाहेर पडू नये म्हणून उष्णतामापक दुसर्या एका उष्णतामापकाइतकेच तपमान असलेल्या भांड्यात ठेवला. शिवाय खोलीचे तपमानही मापकाच्या तपमानाइतकेच ठेवले, यामुळे प्रारणाचा दोष संपूर्णपणे नाहीसा झाला. अशुद्धीचा दोष टाळण्यासाठी त्यांनी पाणी ऊर्ध्वपातित करून (पाण्याची वाफ करून व ती थंड करून) घेतले त्यामुळे त्यातील इतर द्रव्ये दूर झाली. नंतर पुन्हा एकदा पाणी ऊर्ध्वपातित केल्याने त्यात विरघळलेले वायू दूर झाले. बाकीचा प्रयोग जूल यांच्या वरील पद्धतीनेच करावयाचा असतो. निरनिराळ्या तपमानांस प्रयोग करून त्यांनी पाण्याची विशिष्ट उष्णता, बाष्पीभवनाची उष्णता वगैरे ०० से. पासून वाफबिंदूपर्यंत काढली. जे चे त्यांनी काढलेले मूल्य १५० से. तपमानास जे = ४·१८५० ± ०·०००४ आंतरराष्ट्रीय जूल / कॅलरी असे आहे.
‘जे’चे अतिसंभाव्य मूल्य : येथे जे च्या १५० से. तपमानास काढलेल्या मूल्यांचा विचार केलेला आहे. लॅबी आणि हरकस यांनी यांत्रिक पद्धतीने जे चे मूल्य जे = ४·१८५२ ± ०·०००७ निरपेक्ष जूल / कॅलरी, काढले यात दर्शविलेली संभाव्य चूक बर्ग यांनी काढली.
येगर आणि स्टाइनवेर यांनी काढलेल्या (विद्युत् पद्धतीने) जे च्या मूल्यातही बर्ग यांनी दुरुस्ती केली. हे मूल्य असे आहे :
जे = ४·१८३२ ± ०·०००९ आंतरराष्ट्रीय जूल / कॅलरी. ऑस्बर्न, स्टिमसन आणि गिनिंग्ज यांच्या पद्धतीने जे चे मूल्य
जे = ४·१८५० ± ०·०००४ आंतरराष्ट्रीय जूल / कॅलरी असे येते. जे चे अलीकडील सर्वमान्य मूल्य ४·१८५५ ± ०·०००४ जूल / कॅलरी (१५० से.) इतके आहे. यावरून यांत्रिक व विद्युत् पद्धतींनी काढलेले जे चे मूल्य एकमेकांशी अगदी मिळतेजुळते असल्याचे दिसून येते व ही गोष्ट विद्युत् पद्धतीचा अचूकपणा दर्शविते.
संदर्भ : 1. Noakes, G. R. A Textbook of Heat, London, 1960.
2. Saha, M. N.; Srivastava, B. N. A Treatise on Heat, Allahabad and Calcutta, 1965.
देशपांडे, अ. शा.