चुंबकीय द्रवगतिकी

चुंबकीय द्रवगतिकी : (मॅग्नेटो-हायड्रोडायनॅमिक्स, MHD). द्रवरूप किंवा वायुरूप पदार्थाच्या विद्युत् भारित कणांच्या चुंबकीय क्षेत्रामधील गतीच्या शास्त्राला अत्यंत व्यापक अर्थाने चुंबकीय द्रवगतिकी असे म्हणतात. केव्हा केव्हा वायुरूप पदार्थांच्या बाबतीत चुंबकीय वायुगतिकी ही विशेष संज्ञा वापरली जाते. या दृष्टीने प्रस्तुत विषयाला चुंबकीय द्रायुगतिकी हे नाव अधिक समर्पक होईल.

या विषयाच्या अभ्यासाला प्रथम मायकेल फॅराडे (१७९१ – १८३७) यांनी सुरुवात केली. आरंभीच्या प्रयोगांत पारा किंवा वितळविलेला सोडियम यासारख्या द्रवरूप धातूंचा उपयोग करीत, परंतु सध्या प्रामुख्याने वायूंबद्दलच संशोधन चालू आहे.

विश्वोत्पत्तिशास्त्र, चुंबकीय वादळे, ध्रुवीय प्रकाश (ध्रुवीय प्रदेशांत आढळणारा विविध रंगी आविष्कार), व्हॅन ॲलन प्रारण पट्ट [→ प्रारण पट्ट], आयनांबराद्वारे (पृथ्वीपासून सु. ८० ते ३०० किमी. उंचीमधील विद्युत् संवाहक हवेच्या थराद्वारे) रेडिओ तरंगाचे प्रसारण, अति-उष्ण आयनद्रायूची चुंबकीय क्षेत्रजन्य साठवण [→ आयनद्रायु भौतिकी], अणुकेंद्रीय संघटनाद्वारे (दोन अणूंचा संयोग होऊन) निर्माण होणाऱ्या प्रचंड ऊर्जेचा औद्योगिक उपयोग, अणुऊर्जेवर चालणारी अवकाशयाने, चुंबकीय द्रवगतिकीय पद्धतीने विद्युत् निर्मिती, चुंबकीय द्रवगतिकीय धारवा (यंत्रातील फिरता दंड योग्य स्थितीत राहण्यासाठी दिलेला आधार), दाबमापक आणि पंप यांसारखी साधने इ. विविध वैज्ञानिक व तांत्रिक चुंबकीय द्रवगतिकीच्या तत्त्वांचा उपयोग करण्यात येत आहे. यामुळे या विषयाच्या अभ्यासाला हल्ली फार महत्त्व प्राप्त झाले आहे.

द्रायूंच्या (वायू व द्रव या प्रवाही पदार्थांच्या) प्रवाहाला द्रायुगतिकीचे नियम लागू होतात [→ द्रायुयामिकी], पण द्रायूत विद्युत् भारित कण असल्यास त्यांची गती विद्युत् गतिकीच्या सिद्धांतांनुसार असते. तेव्हा चुंबकीय द्रवगतिकीचे नियम हे द्रायुगतिकी व विद्युत् गतिकी यांचे नियम व त्या नियमांचे अन्योन्य परिणाम यांवरून सिद्ध होतील, हे उघड आहे.

वायुकणावर गुरुत्त्वाकर्षणाची प्रेरणाही लागू होत असल्याने तिचाही परिणाम लक्षात घेणे जरूर आहे. परंतु सर्वसामान्य प्रयोगात ही प्रेरणा तुलनात्मक दृष्टीने फार दुर्बल असते. तेव्हा ती दुर्लक्षणीय मानून गतिविषयक समीकरणे सुलभ करता येतात. परंतु सूर्य किंवा इतर प्रचंड ताऱ्यांच्या अंतर्भागात गुरुत्वाकर्षण खूपच प्रभावी होते, तेथे ही प्रेरणा विचारात घेऊन निष्पन्न होणारी समीकरणे वापरावी लागतात.

सर्वसामान्य दाबाखाली व सर्वसामान्य तापमानाला वायूंचे कण बव्हंशी निर्भारित असतात. पण तापमान उच्च (५,०००^° से. किंवा अधिक) असल्यास वायुकणांची औष्णिक गती खूपच जोरदार होते. मग त्या कणांच्या टकरींमुळे त्यांच्या अणूतील (एक वा अधिक) इलेक्ट्रॉन अणूपासून फुटून निघतात. म्हणजेच वायूमध्ये आयन (विद्युत् भारित कण) निर्माण होतात व त्यामुळे वायू विद्युत् संवाहक (ज्यामधून विद्युत् प्रवाह सुलभपणे जाऊ शकतो असे) बनतात. अशा आयनयुक्त वायूला आयनद्रायू असे म्हणतात. अशा आयनद्रायूच्या गतीचा अभ्यास हाच प्रस्तूत नोंदीचा विषय आहे.

मूलभूत संकल्पना : आयनद्रायूमधील कणांची संख्या फार प्रचंड असते. प्रत्येक कणावर लागू होणाऱ्या प्रेरणांच्या महत्ता सामान्यतः वेगळ्याच असणार. प्रत्येक कणावरील प्रेरणा लक्षात घेऊन त्याचे गतिविषयक समीकरण मांडता येईल व अशा सर्व समीकरणांच्या साहाय्याने त्या द्रायूची गती अगदी तपशीलवारपणे निश्चित करता येईल. या पद्धतीला सूक्ष्ममानीय पद्धती असे म्हणतात. या पद्धतीने प्रत्येक कणाची गती बिनचूकपणाने ज्ञात होऊ शकते. पण एकूण समीकरणांची संख्या इतकी प्रचंड होईल की, ती सोडविणे अव्यवहार्य व अशक्यप्रायही आहे. तेव्हा काही प्रमाणात बिनचूकपणाचा त्याग करून द्रायूतील कणांच्या गतीचा सरासरीने विचार करणे, हाच व्यवहार्य व उपयुक्त मार्ग स्वीकारावा लागतो. याकरिता एकूण द्रायू छोट्या छोट्या विभागांत (कोशिकांत) विभागला आहे, अशी कल्पना करू. या कोशिकांचे आकारमान इतके लहान असावे की, त्यांत द्रायूची घनता सर्वत्र समान आहे असे मानता यावे. पण आकारमान फारच लहानही नसावे, ते इतपत मोठे असावे की, त्यातील कणांच्या गतिविषयक राशींमधील अनियत वधघट सरासरीने पाहता उपेक्षणीय ठरावी. अशा सुयोग्य आकारमानाच्या कोशिकांची निवड बहुधा करता येते. वैयक्तिक कणाऐवजी या कोशिकांच्या गतीचा विचार करणे यालाच स्थूलमानीय दृष्टिकोन म्हणतात.

अशा प्रत्येक कोशिकेची वस्तुमान घनता (कोशिकेतील एकूण कणांचे वस्तुमान भागिले कोशिकेचे आकारमान) ρ व कोशिकेतील कणांचा सरासरी वेग u हा विचारात घ्यावयाचा असतो. हा सरासरी वेग कोणत्याही एका कणाच्या वेगाहून खूपच वेगळा असू शकतो. उदा., वाहत्या पाण्यात बुचाचा तुकडा तरंगत असेल, तर त्या तुकड्याचा वेग हा पाण्याच्या रेणूंच्या सरासरी वेगाइतका असेल, परंतु प्रत्येक रेणूचा वेग त्याहून खूपच जास्त असतो. ⇨द्रव्यांच्या गत्यात्मक सिद्धांतानुसार रेणूचा यदृच्छ वेग सु. ३०० मी. /से. इतका असेल. तापमान वाढले की हा यदृच्छ वेगही वाढतो आणि दाबही वाढतो. मग रेणूंच्या होणाऱ्या टकरांमध्ये ते परस्परांवर जास्त जोरदार प्रेरणा लागू करू लागतात. त्यामुळे या दाबातील फेरबदलाला विशेष महत्त्व येते.

प्राथमिक समीकरणाची सिद्धता : अशी कल्पना करा की, एका विशिष्ट कोशिकेतील कणांना १,  २, ३,…, i,…असे क्रमांक दिले. त्यांपैकी कोणताही i क्रमांकाचा कण विचारात घ्या. त्याचे वस्तुमान m_i आहे व त्याच्यावरील निष्पन्न प्रेरणा (लागू होणाऱ्या सर्व प्रेरणांची सदिश बेरीज म्हणजे महत्ता व दिशा लक्षात घेऊन केलेली बेरीज) f_i आहे असे समजू. मग न्यूटन यांच्या दुसऱ्या गतिविषयक नियमानुसार या कणाचा प्रवेग a_i हा,  

या समीकरणाने दिला जाईल. कणावर लागू होणाऱ्या प्रेरणा चार प्रकारच्या असतील. (१) दाबजन्य, (२) गुरुत्वीय व कण विद्युत् भारित असेल तर, (३) विद्युत् क्षेत्रजन्य व (४) चुंबकीय क्षेत्रजन्य. चुंबकीय क्षेत्रजन्य प्रेरणा फक्त गतिमान विद्युत् भारावरच लागू होऊ शकते. कणावरील विद्युत् भार q व त्याचा वेग u असून त्याच्या भोवतीच्या विद्युत् क्षेत्राची तीव्रता E व चुंबकीय क्षेत्राची तीव्रता B असल्यास त्याच्यावरील विद्युत् चुंबकीय प्रेरणा f ही

f = q ( E + u X B) … … … (२)

या सदिश समीकरणाने दिली जाते. [येथे u × B हा u व B या सदिशांचा फुली गुणाकार असल्याने त्याची दिशा u व B या दोघांनाही लंब असते, → सदिश]. या प्रेरणेला लोरेन्ट्‌स प्रेरणा असे म्हणतात.

स्थूलमानीय पद्धतीने विचार करता u ऐवजी कोशिकेतील कणांचा सरासरी वेग u हा विचारात घ्यावा लागेल. कोशिकेतील कणांवरील सरासरी प्रेरणा आणि सरासरी प्रवेग u यांना जोडणारे समीकरण (गुरुत्वाकर्षण दुर्लक्षणीय मानल्यास)

ù = ( ¹/_ρ )(δ p + σ E + j  X B) … (३)

असे येईल. येथे δp ही कोशिकेच्या दोन बाजूंवरील दाबांमधील फरकामुळे उत्पन्न होणारी प्रेरणा आहे व σ  ही कोशिकेतील विद्युत् भार घनता (कोशिकेतील एकूण विद्युत् भार भागिले कोशिकेचे आकारमान) व j ही कोशिकेतील विद्युत् प्रवाह घनता (विद्युत् भारित कणांच्या गतींमुळे कोशिकेतून जाणारा विद्युत् प्रवाह भागिले कोशिकेच्या लंब काटछेदाचे क्षेत्रफळ) होय. जरूर तर या समीकरणात उजव्या बाजूला गुरुत्वीय प्रेरणा व्यक्त करणारे जादा पद घालता येईल. हे समीकरण म्हणजे चुंबकीय द्रवगतिकीतील प्राथमिक समीकरण होय. विशिष्ट परिस्थितीत हे समीकरण यापेक्षाही सोपे करता येते.

काही आसन्नीकरणे : (१) अनेकदा प्रयोगात घेतलेल्या वायूचे तीव्र आयनीकरण झालेले असते. त्यामुळे तो चांगला विद्युत् संवाहक बनतो. मग अल्प तीव्रतेच्या विद्युत् क्षेत्रामुळेही वायूमध्ये जोरदार विद्युत् प्रवाह सुरू होऊन त्यामुळे विद्युत् क्षेत्र निर्माण करणाऱ्या विद्युत् भारांचे निराकरण होते. अशा तऱ्हेने विद्युत् भार घनतेचे मान अत्यंत अल्प होते. त्यामुळे अशा परिस्थितीत विद्युत् क्षेत्रजन्य प्रेरणा दुर्लक्षणीय मानता येते.

(२) आयनीकरण तीव्र असल्यास त्याला आदर्श विद्युत् संवाहक मानता येईल (आसन्नीकरणाने). अशा परिस्थितीत वायूच्या प्रवाहाबरोबर त्याच्या भोवतीच्या चुंबकीय क्षेत्ररेषाही त्याच वेगाने पुढे जातात. (हे गणिताने सिद्ध करता येते).

आयनद्रायुगतिकीशी संबंधित आविष्कार : (१) आयनद्रायूचे स्वनिर्मित आकुंचन, (२) अणुकेंद्रीय संघटन विक्रियेने ऊर्जा निर्माण करण्याच्या साधनात उपयोगात आणली जाणारी चुंबकीय कोष (स्टेलेरेटर) योजना, (३) आयनद्रायूतील आयनांची गती, (४) चुंबकीय दर्पण योजना, (५) आयनद्रायूमधील आंदोलने, या आविष्कारांसंबंधीचे विवेचन ‘आयनद्रायू भौतिकी’ या नोंदीत पहावे. या आविष्कारांच्या बाबतीत काही जादा विवेचन पुढे दिले आहे.

अणुकेंद्रीय संघटनाच्या विक्रियेपासून औद्योगिक उपयोगासाठी ऊर्जा मिळविण्याचे प्रयत्न सध्या चालू आहेत. ही पद्धत लाभदायी होण्यासाठी हायड्रोजनाच्या दोन समस्थानिकांचे (एकच अणुक्रमांक पण भिन्न अणुभार असलेल्या त्याच मूलद्रव्याच्या प्रकारांचे) अणू एक कोटी अंश से. या तापमानाला पुरेसा वेळ ठेवणे आवश्यक असते. परंतु इतका अतितप्त द्रायू कोणत्या प्रकारच्या पात्रात ठेवावयाचा ही मुख्य अडचण आहे. त्यासाठी चुंबकीय परिरोध (अडकवून ठेवण्याच्या) पद्धतीचा उपयोग करणे योग्य दिसते. या पद्धतीत अतितप्त द्रायू जणू काही चुंबकीय क्षेत्ररेषांनी बनलेल्या (काल्पनिक) पात्रात साठविला जातो. अशा दोन साठवणांचे विवेचन ‘आयनद्रायू भौतिकी’ या नोंदीत दिलेले आहेच.

अशा सर्व साधनांत एक अडचण उभी राहते ती ही की, साठवणांतील द्रायूच्या अंगभूत अस्थिरतेमुळे द्रायू फारच अल्प काळपर्यंत (१०^-३ से. ते १०^-६ से.) एकत्रित राहतो. हा काळ वाढवावयाचा म्हणजे द्रायूची अस्थिरता कमी केली पाहिजे. यासाठी अनेक प्रकल्प हाती घेतले गेले. यामधील सामान्य तत्त्व म्हणजे परिरोधित द्रायूभोवतालच्या चुंबकीय रेषांना जास्त उपयुक्त आकार देणे, हे होय. या नव्या प्रकल्पात रशियन शास्त्रज्ञांनी बनविलेले टोकामॅक हे साठविण्याचे साधन जास्त उपयुक्त ठरावे अशी कल्पना आहे आणि म्हणून त्याची कार्यक्षमता वाढविण्याच्या दृष्टीने प्रयोग सुरू आहेत.

चुंबकीय द्रायुतरंग : चुंबकीय द्रायुतरंग हे अल्प परमप्रसराचे (कणाचे मूळ स्थितीपासून होणारे कमाल स्थानांतरण) असतील, तर त्यांचे तीन प्रकार असतात. अवतरंग (ज्या तरंगात आंदोलने तरंगगतीला लंब असतात), अनुतरंग (ज्यात आंदोलने तरंगगतीला समांतर असतात) व व्यावर्तन (पिळाकार) तरंग हे ते प्रकार होत.

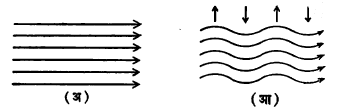या तरंगांची यंत्रणा सुलभतेने समजावी यासाठी दोन कल्पनांचा उपयोग करतात. एक म्हणजे संपूर्णपणे विद्युत‌् संवाहक द्रायूच्या कणांचे विस्थापन केल्यास त्यांच्याबरोबर संबंधित चुंबकीय क्षेत्ररेषांचेही त्याच दिशेने व त्याच मानाने विस्थापन होते. दुसरी कल्पना म्हणजे चुंबकीय क्षेत्ररेषांची (ताणलेल्या रबराच्या पट्टीप्रमाणे) आकुंचन पावून आपली लांबी कमी करण्याची प्रवृत्ती असते. त्याचबरोबर या रेषा आपल्या शेजारच्या रेषांवर लंबदिशेने दाब देत असतात. या कल्पनांच्या साहाय्याने अवतरंगांचे स्पष्टीकरण पुढीलप्रमाणे देता येईल. समजा की, आ. १ (अ) मध्ये दाखविल्याप्रमाणे आयनद्रायूमधील चुंबकीय क्षेत्ररेषा आडव्या आहेत व द्रायुकणांच्या उभ्या स्तरांना एकाआड एक वर व खाली अशी विस्थापने दिली. मग द्रायुकणाबरोबर क्षेत्ररेषांचेही तसेच विस्थापन होऊन त्यांचा आकार आ. १ (आ) मध्ये दाखविल्याप्रमाणे होतील. यामुळे छेडलेल्या तारेप्रमाणे क्षेत्ररेषा आंदोलने करू लागतील. त्यानुसार शेजारचे द्रायुकणही आंदोलने करू लागून द्रायूमध्ये क्षेत्ररेषांच्या दिशेने प्रसारित होणारा अवतरंग उत्पन्न होईल. या तरंगांची कंप्रता (दर सेकंदास होणाऱ्या आंदोलनांची संख्या) f व तरंगलांबी (दोन लागोपाठच्या सारख्याच स्थितीतील कणांमधील अंतर) λ असेल तर 

येथे ρ वस्तुमान घनता व B चुंबकीय क्षेत्राची तीव्रता होय.

आ. २ (अ) मध्ये दाखविल्याप्रमाणे क्षेत्ररेषा उभ्या व समांतर असून द्रायूचे एकाआड एक उभे स्तर अनुक्रमे परस्परांजवळ व परस्परांपासून दूर नेले तर त्यामुळे चुंबकीय क्षेत्ररेषांचेही तसेच विस्थापन होऊन त्यांचा आकृतिबंध आ.२ (आ) प्रमाणे बनेल. त्या रेषा परत पूर्व स्थळी येण्याचा प्रयत्न करतील व आपल्याबरोबर तेथील द्रायूकणांनाही त्याच दिशेने खेचतील. अशा तऱ्हेने द्रायूत (आडव्या दिशेने) आंदोलने निर्माण होऊन त्या दिशेने अनुतरंग प्रसारित होईल.

तरंगांचे विविध प्रकार : चुंबकीय क्षेत्रात आयनद्रायुकणांची गती भोवतालच्या विद्युत् चुंबकीय क्षेत्रांशी निगडित झालेली असते. त्यामुळे त्यात नेहमीपेक्षा काही वेगळ्या प्रकारचे तरंग प्रस्थापित होऊ शकतात. चढत्या कंप्रतेनुसार या तरंगांचे स्थूलमानाने चार टप्पे मानता येतात.

(१) पहिला किमान कंप्रतेचा टप्पा म्हणजे आयनद्रायुकणांच्या परस्परांमधील टकरींची (सरासरी) कंप्रता. (२) द्रायूतील आयनांची सायक्लोट्रॉन कंप्रता  आयनांचा विद्युत् भार आणि M-वस्तुमान) हा दुसरा टप्पा. (३) इलेक्ट्रॉनांची सायक्लोट्रॉन कंप्रता  इलेक्ट्रॉनाचा विद्युत भार आणि m – वस्तुमान). (४) आयनद्रायूमधील इलेक्ट्रॉनांच्या नैसर्गिक आंदोलनांची कंप्रता  = सु. ५ X १०^१० हर्ट्‌झ ( n — द्रायूच्या प्रतिएकक घनफळातील इलेक्ट्रॉन संख्या). (आयनांची सायक्लोट्रॉन कंप्रता आणि इलेक्ट्रॉनांची सायक्लोट्रॉन कंप्रता यांचे स्पष्टीकरण पुढील परिच्छेदात दिले आहे).

पहिल्या टप्प्यापेक्षा कमी कंप्रतेच्या तरंगांचे आयनद्रायूतील प्रसारण हे पूर्णपणे ध्वनितरंगांच्या वायूतील प्रसारणासारखेच होते. आयनद्रायूची घनता जास्त असून तापमान कमी असेल, तर त्यात असे तरंग संभवतात. या दोन टप्प्यांमधील कंप्रतांचे तरंग आल्फव्हेन तरंग म्हणून ओळखले जातात. हे तरंग म्हणजे चुंबकीय द्रायुगतिकीचे एक खास वैशिष्ट्य आहे. वर सांगितल्याप्रमाणे चुंबकीय क्षेत्ररेषांची छेडलेल्या तारेसारखी जी आंदोलने होतात त्यामुळे द्रायूत हे तरंग निर्माण होतात. ते चुंबकीय क्षेत्ररेषांच्या दिशेनेच जातात.

आयन आणि इलेक्ट्रॉन सायक्लोट्रॉन तरंग : तरंगाची कंप्रता पहिल्या टप्प्यापासून दुसऱ्या टप्प्यापर्यंत वाढवीत गेल्यास, आल्फव्हेन तरंगांचे दोन वृत्तध्रुवित (ज्यामध्ये द्रवाचे कण तरंगांच्या प्रसारणाच्या दिशेभोवती वर्तुळाकार फिरत असतात) तरंगांमध्ये द्विभंजन होते. एका तरंगांतील वर्तुळाकार गती आयनाच्या गतीच्या दिशेप्रमाणे व दुसऱ्यातील त्याच्या विरुद्ध दिशेने असते. यांतील पहिल्या तरंगांना आयन सायक्लोट्रॉन तरंग व दुसऱ्याला इलेक्ट्रॉन सायक्लोट्रॉन तरंग असे म्हणतात. पहिल्याची कंप्रता f_i पेक्षा कमी असते. रेडिओमध्ये कित्येकदा आयनांवरातील प्रक्रियांमुळे शिटीसारखे आवाज येतात. त्यांचे स्पष्टीकरण इलेक्ट्रॉन सायक्लोट्रॉन तरंगावरून देता येते.

विद्युत चुंबकीय तरंग : आयनद्रायूमधून विद्युत् चुंबकीय तरंगांच्या होणाऱ्या प्रसारणाबद्दल ‘आयनद्रायू भौतिकी ’ आणि ‘आयनांबर’ या नोंदी पहाव्या.

पृथ्वीचे चुंबकत्व : पृथ्वीच्या चुंबकीय क्षेत्राची उपपत्ती ही अद्याप न सुटलेली समस्या आहे. चुंबकीय द्रायुगतिकीनुसार दिलेली उपपत्ती सध्या सामान्यपणे मान्य झालेली आहे. पृथ्वीच्या अंतर्भागात १,८०० किमी. च्या खाली द्रवरूप लोह व निकेल या धातू आहेत. त्यांतील अनेक अणूंचे आयनीकरण झालेले आहे. त्यांच्या संनयन प्रवाहामुळे (द्रवातील उष्ण भाग वर येऊन त्याची जागा थंड भागाने घेतल्यामुळे निर्माण होणाऱ्या प्रवाहामुळे) विद्युत् प्रवाह तयार होतात व त्यामुळे चुंबकीय क्षेत्र निर्माण होते. या चुंबकीय क्षेत्रामुळे स्वयं-उत्तेजित जनित्राप्रमाणे (यांत्रिक ऊर्जेचे विद्युत् ऊर्जेत रूपांतर करणाऱ्या यंत्राप्रमाणे) विद्युत् प्रवाह चालू राहतो व त्यामुळे पृथ्वीचे चुंबकीय क्षेत्र प्रस्थापित होते. हे विद्युत् प्रवाह चालू राहण्यासाठी आवश्यक ती ऊर्जा पृथ्वीच्या वलनापासून व पृथ्वीच्या अंतर्भागातील किरणोत्सर्गी (आपोआप भेदक किरण बाहेर टाकणाऱ्या) मूलद्रव्यांमुळे निर्माण होणाऱ्या उष्णतेतून मिळते. या आयनद्रायूतील आवर्तांमुळे पृथ्वीच्या चुंबकीय क्षेत्रात आढळून येणारे स्थानिक स्वरूपाचे फेरफार निर्माण होतात.

चुंबकीय वादळे आणि त्यांच्याशी निगडित आविष्कार : सूर्यापासून प्रोटॉनांचा (हायड्रोजनाच्या विदलित म्हणजे इलेक्ट्रॉन अलग झालेल्या अणूंचा) प्रवाह बाहेर पडत असतो. त्याला सौरवात असे म्हणतात. केव्हा केव्हा हा प्रवाह फारच जोरदार होतो व त्याबरोबर सूर्याशी संबद्ध चुंबकीय क्षेत्रही पृथ्वीकडे प्रसारित होते. यामुळे पृथ्वीच्या चुंबकीय क्षेत्रात अचानक मोठे बदल झालेले अनुभवाला येतात. यांनाच चुंबकीय वादळे असे म्हणतात. या प्रोटॉन प्रवाहांचे कित्येकदा फार दूरगामी परिणाम होतात. उदा., ध्रुवीय प्रकाश जास्त तेजस्वी होतात. दूर अंतरावरील रेडिओ संदेश खंडित होतात. या प्रोटॉन प्रवाहामुळे दूरध्वनीच्या तारांत विद्युत् प्रवाह प्रवर्तित होऊन दूरध्वनी संदेशसुद्धा ऐकू येईनासे होतात. त्याचप्रकारे विद्युत् ऊर्जावाहकात प्रवर्तित झालेल्या विद्युत् प्रवाहांमुळे वीजपुरवठासुद्धा केव्हा केव्हा खंडित होतो. हे सर्व परिणाम चुंबकीय द्रायुगतिकीच्या साहाय्याने समजू शकतात.

त्याचप्रमाणे चुंबकीय वादळाबरोबरच केव्हा केव्हा विश्वकिरणांची (बाह्य अवकाशातून येणाऱ्या अतिशय भेदक किरणांची) तीव्रता एकदम कमी झालेली आढळते. याला ‘फॉरबुश परिणाम’ असे म्हणतात. विश्वकिरणांची तीव्रता नेहमीच विषुववृत्तावर कमी असून ती ध्रुवांकडे वाढत जाते. त्याचप्रमाणे पश्चिमेकडून पृथ्वीकडे येणाऱ्या विश्वकिरणांची तीव्रता पूर्वेकडून येणाऱ्या विश्वकिरणांपेक्षा २०% जास्त असते. हे सर्व आयनद्रायुगतिकीचेच आविष्कार होत.

व्हॅन ॲलन प्रारण पट्ट : आयनद्रायुगतिकीनुसार विशिष्ट ऊर्जेचे विद्युत् भारित कण विशिष्ट तीव्रतेच्या चुंबकीय क्षेत्रात जणू काही अडकून बसतात. व्हॅन ॲलन व त्यांच्या सहकाऱ्यांनी असे दाखवून दिले की, विषुववृत्तावर पृथ्वीच्या पृष्ठभागापासून सरासरी ४,००० किमी. उंचीवर १ ते १०० Mev ऊर्जेचे प्रोटॉन (Mev म्हणजे दशलक्ष इलेक्ट्रॉन व्होल्ट इलेक्ट्रॉन व्होल्ट हे ऊर्जेचे एकक असून ते १·६०२०३ X १०^-१२ अर्ग बरोबर आहे) व सरासरी २०,००० किमी. उंचीवर १ ते १० Mev ऊर्जेचे प्रोटॉन अडकून त्यांची पृथ्वीभोवती वलये बनलेली आहेत. [→ प्रारण पट्ट] .

विश्वकिरणांची ऊर्जा : विश्वकिरणांतर्गत कणांना इतकी प्रचंड ऊर्जा प्राप्त होण्याची यंत्रणा अद्याप नीट समजलेली नाही. याबद्दल फेर्मी यांनी एक उपपत्ती सुचविली आहे. प्रकाशवेगाशी तुलनीय वेगाने जाणाऱ्या विद्युत् भारित कणांचे जेव्हा गतिमान चुंबकीय ‘आरशा’ वरून परावर्तन होते तेव्हा त्या कणांची ऊर्जा वाढते हे चुंबकीय द्रवगतिकीवरून सिद्ध करता येते. आंतरतारकीय अवकाशात गतिमान आयनांचे मेघ व त्यांच्याशी संलग्न चुंबकीय क्षेत्रे विखुरलेली आहेत. ही क्षेत्रे गतिमान चुंबकीय आरशाप्रमाणे कार्य करतात. प्रारंभीचे (कमी ऊर्जेचे) विश्वकिरण कण पृथ्वीवर येईतो अशा आरशावरून अनेकदा परावर्तन पावतात व अशा प्रत्येक परावर्तनात त्यांची ऊर्जा वाढता वाढता शेवटी ती फार प्रचंड होते [→ विश्वकिरण].

विश्वोत्पत्तिशास्त्र व चुंबकीय द्रवगतिकी : कोनीय संवेगाच्या अक्षय्यतेचा नियम (वलन करणाऱ्या वस्तूचे निरूढी परिबल – म्हणजे कोनीय प्रवेगाला होणाऱ्या विरोधाचे माप — गुणिले तिचा कोनीय वेग ही राशी बाह्य परिबलाच्या अभावी कमी वा जास्त होऊ शकत नाही) सर्व वस्तूंना लागू पडतो तसाच दीर्घिकांनाही (परस्परांशी संबद्ध अशा ताऱ्यांच्या प्रचंड समुदायालाही, उदा., आपल्या आकाशगंगेलाही) लागू पडतो. आकाशात दिसणाऱ्या दीर्घिकांचा हल्लीचा कोनीय संवेग निश्चित करता येतो. त्यावरून गणित करता या दीर्घिकांचा आरंभीच्या अवस्थेतील कोनीय संवेग हल्लीपेक्षा सु. ५ अब्जपट जास्त असला पाहिजे असे दिसून येते. म्हणजेच ह्या दीर्घिका निर्माण झाल्यापासून आतापर्यंत त्यांच्या कोनीय संवेगात फार प्रचंड घट झालेली आहे. या घटीची मीमांसा चुंबकीय द्रवगतिकीनुसार पुढीलप्रमाणे करता येते. दीर्घिकेतील एखादा तारा चुंबकीय वायुमेघात जन्माला आला असेल, तर त्याच्या वलनावर भोवतीच्या चुंबकीय क्षेत्राचे गतिविरोधकासारखे कार्य होते आणि त्यामुळे वलन गती व म्हणून कोनीय संवेग कमी होत जातो [→ विश्वोत्पत्तिशास्त्र].

चुंबकीय द्रवगतिकीचे काही उपयोग : (१) चुंबकीय द्रवगतिकिय जनित्र : तप्त वायूच्या गतिज ऊर्जेचे एकदम विद्युत् ऊर्जेत रूपांतर करण्याचे हे अभिनव साधन आहे. अद्याप याचा पूर्ण विकास झालेला नसला, तरी त्याच्यासंबंधी जोरदार संशोधन चालू आहे.

प्रचलित पद्धतीच्या जनित्रापेक्षा यामध्ये अनेक फायदे आहेत. मुख्य म्हणजे यात कोठलेच फिरते किंवा हालते भाग नसल्याने घर्षण व त्यामुळे होणारी झीज हे प्रश्नच उत्पन्न होत नाहीत. यात कोठलाही तप्तवायू (उदा., जेट एंजिनातून बाहेर पडणारा वायू) वापरता येतो किंवा थंड वायू कोणत्याही प्रकारच्या इंधनाने अथवा अणुकेंद्रीय विक्रियेने तापवून वापरता येतो. नेहमीचे वायू सु. ३,०००^° से. तापमानाला पुरेसे विद्युत्‌ संवाहक होतात. परंतु वायूत अल्प प्रमाणात (सु. १ टक्का) सोडियम वा पोटॅशियमाची वाफ मिसळल्यास सु. १,०००^° ते २,०००° से. तापमानाचा वायू सुद्धा चालू शकतो.

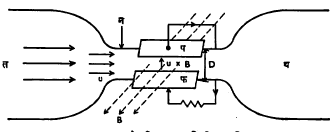आ. ३ मध्ये अशा जनित्राच्या रचनेची रूपरेषा दाखविली आहे. तप्त वायू उच्च तापमानाला व उच्च दाबात त या पोकळीमध्ये असून तो न या नलिकेने थ या नीच दाब असलेल्या पोकळीमध्ये जाऊ लागतो. यामुळे न मध्ये u या वेगाचा वायुप्रवाह चालू होतो. या प्रवाहाच्या लंबदिशेने B तीव्रतेचे (सु. १०,००० गौस) चुंबकीय क्षेत्र लावल्यास B आणि u या दोहोंना लंबदिशेने कार्य करणारी u × B ही प्रेरणा वायूतील आयनावर लागू होते. त्यामुळे धन व ऋण आयन परस्परांना विरुद्ध दिशेने सरकू लागून नळीत दोन्ही बाजूंना ठेवलेल्या प आणि फ या विद्युत् संवाहकाकडे जातात आणि प व फ यांच्यामध्ये V = D&lt u × B&gt व्होल्ट इतका विद्युत् दाब निर्माण होतो. प व फ कोणत्याही विद्युत् उपकरणाला जोडल्यास त्यातून विद्युत् प्रवाह चालू होतो. (येथे D हे प व फ यांमधील अंतर व &lt u × B&gt हे u × B चे सरासरी मूल्य होय). या जनित्राचा अंतर्गत विद्युत् रोध फारच अल्प असल्याने त्याला जोडावयाच्या साधनाचा बाह्य रोधही शक्य तितका कमी असणे इष्ट असते. यासाठी अतिसंवाहक [ कित्येक धातूंचा विद्युत् रोध सु. ४^° के. या अतिनीच तापमानाला शून्यप्राय होतो व ती धातू मग अतिसंवाहक झाली असे म्हणतात, →  अतिसंवाहकता ] पदार्थ वापरणे फायदेशीर होते.

वर वर्णन केलेले जनित्र एकदिश (एकाच दिशेने वाहणारा) विद्युत् प्रवाह देते. पण चुंबकीय क्षेत्र प्रत्यावर्ती (दिशा एकसारखी उलट सुलट होणारे) असल्यास प्रत्यावर्ती विद्युत् प्रवाह मिळतो.

या प्रकारच्या जनित्रांचा अद्याप पूर्ण विकास झालेला नाही. परंतु त्या दृष्टीने जोरात प्रयत्न चालू आहेत. अमेरिकेच्या संयुक्त संस्थानांतील ॲडव्हान्स्ड रिसर्च प्रॉजेक्ट एजन्सी या संस्थेने व विमानदलाने सहकार्य करून ३२,००० किवॉ. शक्तीचे एक जनित्र चालू केलेले आहे.

या जनित्राच्या बाबतीत दोन मुख्य अडचणींचे निराकरण करणे जरूर आहे. (१) उच्च तापमानाला टिकाव धरतील अशा धातूंच्या पट्ट्या व त्या बसविण्यासाठी उच्च तापमानातही तग धरू शकणारे विद्युत् निरोधक पदार्थ विकसित करणे जरूर आहे. (२) जनित्राचा अत्यंत कमी अंतर्गत रोध ही सुद्धा एक अडचणच आहे.

(२) चुंबकीय द्रवगतिकीय प्रवाहमापक : वरील रचनेत प व फ यांना एक व्होल्टमापक (विद्युत् दाब मोजणारे उपकरण) जोडून विद्युत् दाबाचे (V चे) मापन करता येईल. परंतु वरील सूत्रानुसार V α u. तेव्हा V वरून u चे मान काढता येईल. या पद्धतीच्या प्रवाहमापकाला विद्युत् चुंबकीय प्रवाहमापक असेही म्हणतात. सध्या असा प्रवाहमापक केशनलिकेतून (अतिशय बारीक व्यासाच्या नलिकेतून) जाणारा रक्ताचा प्रवाह व द्रवरूप धातूंचे प्रवाह मोजण्यासाठी वापरला जात आहे.

(३) चुंबकीय द्रवगतिकीय पंप : एखादा विद्युत् संवाहक द्रायू u या वेगाने B या u ला लंब असलेल्या चुंबकीय क्षेत्रातून वाहत असेल आणि त्या u व B ला लंब असे E हे विद्युत् क्षेत्र तेथे असेल, तर त्या द्रायूतून जाणाऱ्या विद्युत् प्रवाहाची घनता j = k (E + u × B ) या समीकरणाने दिली जाते (K = द्रायूची संवाहकता) व त्यामुळे द्रायूवर f = j × B ही प्रेरणा कार्य करू लागते. पुरेशी जोरदार असल्यास ही प्रेरणा द्रायूला दाबाच्या विरुद्ध दिशेनेही रेटू शकते. म्हणजेच तिचा उपयोग पंपासारखा होऊ शकतो. या तत्त्वावर कार्य करणाऱ्या पंपाला विद्युत् चुंबकीय पंप असेही म्हणतात. काही अणुभट्ट्यांतील उष्णता बाहेर काढून घेण्यासाठी त्यांच्यामधून द्रवरूप सोडियम धातू खेळविलेली असते. त्यासाठी या पंपाचा उपयोग करतात.

(४) चुंबकीय द्रवगतिकीय प्रचालन : रॉकेटाचे प्रचालन (पुढे जाण्याची क्रिया) त्याच्या पाठीमागून फार वेगाने बाहेर पडणाऱ्या वायूच्या प्रतिक्रियेमुळे होते. या वायूत मोठ्या प्रमाणात आयन असल्यास त्याला सुयोग्य दिशांनी विद्युत् आणि चुंबकीय क्षेत्रे (E व B) लावल्यास त्या वायूवर वरीलप्रमाणे f = j × B ही प्रेरणा कार्य करील. या प्रेरणेची प्रतिक्रिया रॉकेटाला पुढे रेटेल. अशा प्रकारच्या प्रचालनाला विद्युत् चुंबकीय प्रचालन असे म्हणतात. या प्रचालनाच्या पद्धतीत पुन्हा अनेक प्रकार आहेत. परंतु हा सर्व भाग अद्याप प्रायोगिक अवस्थेत आहे [→ रॉकेट विद्युत् चुंबकीय प्रचालन].

संदर्भ : 1. Alfven, H. Cosmical Electrodynamics, Oxford, 1950.

           2. Hughes, W. F. Young, F. J. Electromagnetodynamics of Fluids, New York, 1966.

           3. Lichnerowicz, A. Relativistic Hydrodynamics and Magnetohydrodynamics, New York, 1967.

           4. Pai, S. Ι . Magnetogasdynamics, and Plasma Dynamics, Englewood Cliffs, N. J., 1962.

           5. Rosa, R. J. Magnetohydrodynamic Energy Conversion, New York, 1968.

           6. Spitzer, L. Physics of Fully Ionised Gases, New York, 1956.

           7. Thompson, W. B. An Introduction to Plasma Physics, Oxford, 1962.

पाटणकर, भा. वि. घुणकीकर, ज. तु.

“