गणितातील अनिर्वाहित प्रश्न : ज्या प्रश्नांना (किंवा कूटांना) उत्तर मिळालेले नाही किंवा खूप काळापर्यंत उत्तरे मिळालेली नव्हती अशा प्रश्नांना येथे अनिर्वाहित असे म्हटले आहे. पुढील प्रश्न गणितामध्ये फार पुरातन काळापासून अनुत्तरित किंवा अनिर्वाहित राहिल्याने त्यांना ऐतिहासिक महत्त्व आहे.
कंपास व सरळ पट्टी ह्या दोनच उपकरणांच्या साह्याने पुढील तीन रचना करणे : (१) घनाची दुप्पट करणे, म्हणजे दिलेल्या घनाच्या दुप्पट घनफळ असेल अशा घनाची बाजू रचणे. (२) कोनाचे त्रिभाजन. (३) वर्तुळाचे चौरसीकरण. हे प्रश्न अठराव्या शतकापर्यत अनिर्वाहित गणले जात होते. परंतु आता मात्र ते अनिर्वाहित राहिलेले नाहीत. इटालियन गणितज्ञ रूफफीनी (१७६५–१८२२), नॉर्वेजियन गणितज्ञ आबेल (१८०२–२९) आणि फ्रेंच गणितज्ञ गाल्वा (१८११–३२) ह्यांनी बीजगणितात केलेल्या संशोधनानंतर ह्या रचना अशक्य असल्याचे प्रस्थापित झाले आहे.
कंपास व सरळ पट्टी यांच्या साहाय्याने करता येणाऱ्या मूलभूत रचना अशा : (१) दिलेले दोन बिंदू सरळ रेषेने जोडणे, (२) दिलेला मध्य व दिलेली त्रिज्या घेऊन वर्तुळ काढणे, (३) दिलेल्या दोन रेषांचा छेदनबिंदु (असल्यास) काढणे, (४) दिलेल्या दोन वर्तुळांचे छेदनबिंदू (असल्यास) काढणे आणि (५) दिलेले वर्तुळ व दिलेली रेषा यांचे छेदनबिंदू (असल्यास) काढणे.
संख्यांची रचना : दिलेले रेषाखंड आणि वरील दोन उपकरणे ह्यांच्या साह्याने पुढील संख्यांच्या (म्हणजेच तेवढी लांबी असणाऱ्या रेषाखंडाच्या) रचना करता येतात. (१) दोन संख्यांची बेरीज, (२) दोन संख्यांची वजाबाकी, (३) दोन संख्यांचा गुणाकार आणि (४) दोन संख्यांचा भागाकार (छेद ≠ ०).
जर एक एकक लांबीपासून आरंभ केला तर आपल्याला सर्व परिमेय संख्यांची (ज्या संख्या दोन पूर्णाकांच्या गुणोत्तराच्या स्वरूपात मांडता येतात अशा संख्यांची) रचना करता येईल. परिमेय संख्यांचे एक ‘क्षेत्र’ असते [→ बीजगणित, अमूर्त].
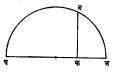
आता क्षे हे संख्यांचे कोणतेही एक क्षेत्र घेऊ. क ही क्षे मधील कोणत्याही संख्येची रचना करता येत असेल तर ह्या संख्येचीही रचना करता येते. एका रेषेवर प, फ आणि भ हे बिंदु असे घ्या की पफ = क, फभ = १. पभ हा व्यास घेऊन एक वर्तुळ काढा. पभ ला फ मधून काढलेला लंब वर्तुळास ब मध्ये मिळत असेल तर फब =
हे शालेय भूमितीच्या आधारे सिद्ध करत येईल.
दिलेल्या रेषाखंडांपासून (म्हणजे त्यांच्या लांबीपासून) जर क्षे हे क्षेत्र मिळत असेल तर क्षे मधील सर्व संख्यांच्या रचना तर करता येतातच, पण क ही क्षे मधील एकविशिष्ट संख्या घेतली तर त + थ (त आणि थ, क्षे मधील) अशा प्रकारच्या संख्यांचीही रचना करता येते.त्यांपासून पुन्हा त्यांची बेरीज, वजाबाकी, गुणाकार व भागाकार (छेद ≠ ०) अशा संख्यांची रचनाही करता येते. पण त + थ
ह्या संख्यांपासून वरील चार क्रियांनी मिळणाऱ्या संख्यांचेही क्षेत्र बनते. हे क्षे’ ने दर्शवू. क्षे’ ला क्षे चे अतिदिष्ट (विस्तारित) क्षेत्र म्हणतात आणि क्षे ला क्षे’ चे उपक्षेत्र म्हणतात. क्षे ला
जोडून क्षे’ मिळाले असेही म्हणतात [→ बीजगणित, अमूर्त].
ही संख्या क्ष२–क = ० ह्या समीकरणाचे एक बीज आहे.
दिलेल्या रेषाखंडांपासून ह्याप्रमाणे प्रत्येक वेळा सारख्या संख्या जोडून अतिदेश (विस्तार) करीत मिळणाऱ्या सर्व संख्यांची रचना कंपास व सरळ पट्टी ह्या उपकरणांच्या साह्याने करता येते. म्हणजे जर एकक लांबी दिली असेल, तर त्यांपासून (म्हणजे परिमेय संख्यांपासून) आपल्याला
अशा प्रकारच्या सत् संख्यांच्या (परिमेय व अपरिमेय संख्यांच्या) रचना करता येतात. ह्याउलट कंपास व सरळ पट्टी यांच्या साह्याने केवळ अशाच प्रकारच्या संख्यांच्या रचना करता येतात. इतर कोणत्याही संख्यांची रचना करता येत नाही, असे सिद्ध करता येईल.
सिद्धता : कंपास व सरळ पट्टी यांच्या साह्याने मिळणारे नवीन बिंदू म्हणजे दोन रेषांचे छेदनबिंदू किंवा एक रेषा आणि एक वर्तुळ यांचे छेदनबिंदू किंवा दोन वर्तुळाचे छेदनबिंदू. यांत रेषांची आणि वर्तुळांची बैजिक समीकरणे म्हणजेच त्यांतील सहगुणक माहिती आहेत असे गृहीत धरले आहे. त्यावरून छेदनबिंदूंचे सहगुणक काढावयाचे आहेत. दोन रेषांची समीकरणे खालीलप्रमाणे आहेत असे समजू.
क१ क्ष + ख१ य + ग१ = ०
क२ क्ष + ख२ य + ग२ = ०
ही समीकरणे सोडविताना अंकगणितातील चार क्रियांचाच उपयोग करावा लागत असल्याने छेदनबिंदूंचे सहगुणक क१, ख१ इत्यादी संख्यांच्या क्षेत्रातच (क्षे) असणार म्हणजे ते रचता येतातच. एक रेषा आणि एक वर्तुळ यांची समीकरणे पुढीलप्रमाणे मानू :
क क्ष + ख य + ग = ०
क्ष२ +य२ +२ प क्ष +२ फ य +ब = ०
यातील य चा निरास करून मिळणाऱ्या समीकरणाचे सहगुणक दिलेल्या सहगुणकांच्या क्षेत्रातच राहतील. कारण पहिल्या चार क्रियांचाच त्यांत अंतर्भाव आहे. य चा निरास करून पुढील समीकरण मिळते असे मानू :
म्हणजे क्ष ची मूल्ये क्षे राहणार हे सिध्द होते. दोन वर्तुळांची समीकरणे खालीलप्रमाणे आहेत असे मानू :
क्ष२ + य२ + २ प१क्ष + २ फ१य + ब१= ०
क्ष२ + य२ + २ प२क्ष + २ फ२य + ब२= ०
ह्या दोन वर्तुळांचे छेदनबिंदू म्हणजेच पहिले (किंवा दुसरे)वर्तुळ आणि
२ (प१ – प२) क्ष + २ (फ१ – फ२ ) य + (ब१ – ब२ ) = ०
ह्या त्यांच्या समाईक जीवेचे छेदनबिंदू होत.
म्हणून कंपास व सरळ पट्टी ह्यांच्या साहाय्याने वर वर्णन केलेल्या संख्यांच्याच रचना करता येतात हे सिध्द झाले.
काही संख्या दिल्या असता त्यांपासून मिळणारे क्षेत्र किंवा त्याला जोडून मिळणारे क्षेत्र, पुन्हा त्यापासून ह्याच पध्दतीने मिळणारे क्षेत्र, अशा सर्व क्षेत्रांतील संख्यांच्या रचना करता येतात. यावरून ‘एखादी संख्या दिलेल्या संख्यांपासून मिळणाऱ्या क्षेत्रातील संख्या ज्याचे सहगुणक असतील व ज्याचा घात २प (प पूर्णांक) अशा प्रकारचा असेल अशा समीकरणाचे बीज असेल तर आणि तरच ती संख्या कंपास व सरळ पट्टी यांच्या साह्याने रचता येते’, हे प्रमेय मिळते.
कंपास व सरळ पट्टी यांच्या साहाय्याने करावयाच्या रचनांची अशक्यता : वरील प्रमेयाच्या साहाय्याने सुरुवातीस उल्लेखिलेल्या तिन्ही रचना अशक्य असल्याचे प्रस्थापित करता येईल.
(१) घनाची दुप्पट करणे : दिलेल्या घनाची बाजू एक एकक असेल तर त्याचे घनफळ १ होईल. मग ज्याचे घनफळ २ असेल अशा घनाची बाजू एकक येईल. पण
ही संख्या क्ष३ – २ = ० ह्या समीकरणाचे मूळ आहे आणि त्या समीकरणाचे सहगुणक परिमेय संख्याक्षेत्रातील (म्हणजेच १ ह्या संख्येपासून मिळणाऱ्या क्षेत्रातील) आहेत. त्याचा घात ३ असल्याने वरील प्रमेयानुसार
ची रचना अशक्य ठरते.
(२) कोनाचे त्रिभाजन : दिलेला कोन र मानू. कोन दिला असेल तर त्याच्या कोज्याची रचना करता येतेच. कोज्या र = श मानू. जर र/३ कोनाची रचना करता आली तर कोज्या (र/३) ह्या संख्येची रचनाही करता येईल. हे अशक्य असल्याचे दाखवू.
कोज्या र = ४ कोज्या३ (र/३) – ३ कोज्या (र/३) म्हणजे कोज्या (र/३) ही संख्या ४ क्ष३ -३ क्ष –श = ० ह्या समीकरणाचे बीज आहे. पण वरील प्रमेयानुसार क्ष ची रचना अशक्य आहे.
(३) वर्तुळाचे चौरसीकरण : एक एककापासून (किंवा परिमेय संख्यांपासून) आरंभ करून ज्या संख्या रचता येतात त्या सर्व संख्या बैजिक असतात, हे उघड आहे. त त्रिज्येच्या वर्तुळाचा समक्षेत्र चौरस काढावयाचा म्हणजे त्याचे क्षेत्रफळ πत२ असले पाहिजे. त = १ मानू म्हणजे त्या चौरसाचे क्षेत्रफळ π असले पाहिजे. म्हणजे चौरसाची बाजू असली पाहिजे. जर
ची रचना करता आली तर π चीही रचना करता येईल. पण πही संख्या बैजिक नसून बीजातीत (परिमेय संख्या सहगुणक असलेल्या कोणत्याही समीकरणाचे बीज नसलेली) आहे असे लिंडेमान यांनी १८८२ मध्ये दाखविले.
इतर अनिर्वाहित प्रश्न : वरील तीन अनिर्वाहित प्रश्नांशिवाय गणितात इतरही काही अनिर्वाहित प्रश्न असून त्यांची माहिती खाली दिली आहे.
(४) वर्तुळात सुसम सप्तभुज अंतर्लिखित करणे : हेही अशक्य असल्याचे वरील प्रमेयाने दाखविता येते. वर्तुळाची त्रिज्या १ आणि आरंभबिंदू मध्य घेऊन वर्तुळ काढू. सप्तभुजाचे शिरोबिंदू ज्ञ ह्या सदसत् संख्येने दर्शविल्यास ज्ञ७ = १ मिळेल. ज्ञ = क्ष + i य, (i = मानू. जर ज्ञ हे बिंदू रचता आले तर क्ष आणि य हे त्यांचे सहगुणकही रचता येतील. ज्ञ७ -१ = (ज्ञ-१) (ज्ञ६ + ज्ञ५ +….+ ज्ञ +१)म्हणून ज्ञ६ + ज्ञ५ + ….. + ज्ञ +१ = ० हे समीकरण सोडवणे आवश्यक आहे. ज्ञ३ने भागून ज्ञ३ + ज्ञ२ +….. +१/ज्ञ२+१/ज्ञ३= 0 मिळेल. ते (ज्ञ + १/ज्ञ)३ +(ज्ञ + १/ज्ञ)२ -२(ज्ञ + १/ज्ञ)-१ = ० असे मांडता येईल. १/ज्ञ = क्ष – i य म्हणून ज्ञ + १/ज्ञ = २ क्ष म्हणून वरील समीकरण ८ क्ष३ + ४ क्ष२ – ४ क्ष – १ = ०. पण याचा घात ३ आहे. म्हणून क्ष ची रचना अशक्य. म्हणून ज्ञ ची रचना अशक्य म्हणजेच सुसम सप्तभुज अंतर्लिखित करता येणे अशक्य .
कोणते बहुभुज अंतर्लिखित करता येतात याचे संपूर्ण उत्तर गौस यांनी दिले आहे. जर (सुसम) प–भुज अंतर्लिखित करावयाचा असेल तर प = २स किंवा आविभाज्य फेर्मा संख्या [ +१ ह्या प्रकारची → अविभाज्य संख्या] असली पाहिजे किंवा या संख्यांच्या गुणाकाराइतकी असली पाहिजे. हे आणि केवळ हेच प-भुज अंतर्लिखित करता येतात. ३, ४, ६, ८, १२, १६, बाजूंचे बहुभुज अंतर्लिखित करण्याकरिता शालेय भूमितीचे ज्ञान पुरेसे आहे. ५, १० आणि १५ बाजूंचा बहुभुज अंतर्लिखित करण्याकरिता ⇨सुवर्ण छेद माहिती पाहिजे. १७ बाजूंचा अंतर्लिखित करण्याची पध्दत बर्नार्ड आणि चाइल्ड यांनी दिली आहे.
मात्र कंपास आणि सरळ पट्टी यांच्या साहाय्याने करण्यास अशक्य असलेल्या काही रचना इतर उपकरणांच्या साहाय्याने करता येतात.
(५) वर्ग समीकरण, घन समीकरण व चतुर्घात समीकरण यांची बीजे करणीरूपात (एक वा अधिक अपरिमेय संख्यांच्या बेरजेच्या रूपात) व्यक्त करणे जसे शक्य झाले होते तसे पंचघात समीकरण आबेल यांच्या काळापर्यंत शक्य झालेले नव्हते. तोवर शोधून काढलेली उत्तरे चुकीची होती. रूफफीनी आणि आबेल यांनी ‘सर्वसाधारण पंचघात समीकरणाची बीजे करणीरूपात व्यक्त करणे शक्य नसल्याचे’ दाखवून दिले.
(६) गोल्डबाख यांचा कयास : ‘२ सोडून इतर प्रत्येक सम संख्या दोन अविभाज्य संख्यांच्या बेरजेच्या रूपात व्यक्त करता येते’ असा कयास गोल्डबाख यांनी ऑयलर यांना १७४२ साली लिहिलेल्या पत्रात व्यक्त केला होता. उदाहरणे ४ = २ + २, ६ = ३ + ३, …, १६ = १३ + ३, …, १०० = ९७ + ३ . ह्या प्रमेयाची सिध्दता १९३१ पर्यत संपूर्णत: अशक्य भासत होती. पण १९३१ मध्ये श्निरेलमान ह्या रशियन गणितज्ञांनी असे सिध्द केले की, कोणत्याही धन पूर्णाक ३,००,००० किंवा कमी अविभाज्य संख्यांच्या बेरजेच्या रूपात व्यक्त करता येतात. त्यानंतर व्होनग्राडॉव्ह ह्या रशियन गणितज्ञांनी, हार्डी, लिट्लवुड आणि प्रख्यात भारतीय गणितज्ञ रामानुजन् यांच्या रीतीचा उपयोग करून ही संख्या ४ वर आणली. मात्र गोल्डबाख यांच्या कयासाचे संपूर्ण उत्तर अद्याप उपलब्ध नाही.
(७) जुळ्या अविभाज्य संख्या : ज्यांच्यातील फरक २ आहे अशा अविभाज्य संख्यांना जुळ्या अविभाज्य संख्या म्हणतात. ‘जुळ्या अविभाज्य संख्या असंख्य आहेत’ हे प्रमेयसुध्दा अजून अनिर्वाहित आहेत.
(८) नकाशा रंगविणे : पृथ्वीच्या पाठीवरचे निरनिराळे प्रदेश दर्शविणारा नकाशा रंगविण्याकरिता एकूण किती वेगवेगळे रंग लागतील? अर्थात शेजारच्या दोन प्रदेशांना तोच रंग येऊ नये ही अट स्वाभाविक आहे. ह्या प्रश्नाचेही संपूर्ण उत्तर अद्याप सापडलेले नाही [→ संस्थितिविज्ञान].
(९) फेर्मा यांचे शेवटचे प्रमेय : क्षस + यस = झस यात स ⩾ ३ असेल, तर ह्या समीकरणाची उत्तरे परिमेय संख्या वापरून काढणे शक्य नाही. ह्या प्रश्नाचा निर्वाहही (उत्तरही) अद्याप संपूर्णत: मिळालेला नाही. मात्र स च्या काही विशिष्ट प्रकारच्या मूल्यांकरिता याचा निर्वाह मिळालेला आहे. [→ बेर्नुली संख्या].
वरील प्रश्न हा ⇨संख्या सिध्दांतामधील आहे. संख्या सिध्दांतात असे अनिर्वाहित प्रश्न बरेच आहेत. खरे म्हणजे गणिताचा जसजसा विकास होत आहे तसतसे प्रश्न सुटण्याबरोबर अनिर्वाहित प्रश्नांची भरच पडत चालली आहे.
संदर्भ : 1. Bernard, S. Child, J. M. Higher Algebra, London, 1960.
2. Courant, R. Robbins, H. What is Mathematics?, New York, 1961.
राईलकर, म. रा.
“