डॉप्लर परिणाम : डॉप्लर (१८०३ – ५३) या ऑस्ट्रियन भौतिकीविज्ञांनी १८४२ साली असे दाखवून दिले की, तरंगगतीच्या उगम व ते तरंग ग्रहण करणाऱ्या निरीक्षकास, परस्पर सापेक्ष वेगामुळे तरंगांच्या कंप्रतेत (प्रती सेकंदात होणाऱ्या कंपनांच्या संख्येत) किंवा तरंगलांबीत (तरंगातील लगतच्या दोन सारख्या स्थितींतील अंतराच्या लांबीत) फरक पडतो, असे भासते. या आविष्काराला डॉप्लर परिणाम म्हणतात.
वे = कंत … … … (१)
येथे वे = तरंग वेग, कं= कंप्रता, त = तरंगलांबी.
कं कंप्रता मूल्याचा बिंदूरूप ध्वनि-उगम (उ) स्थिर असलेल्या श्र या श्रोत्याकडे वेउ या वेगाने जात आहे असे मानू. एका सेकंदात उगम उ पासून उ’ येथे गेला असल्यास कं ध्वनितरंग वे मीटर (ध्वनीने तोडलेल्या) अंतरात मावण्याच्या ऐवजी उगमाच्या वेगामुळे ते आता वे—वेउ मीटर या कमी अंतरात मावतात यांचा परिणाम म्हणून पूर्वीची तरंगलांबी त आता कमी झाली असे वाटते. नवीन तरंगलांबी त१ अशी दर्शविली, तर
|
त१= |
वे—वेउ |
|
कं |
असे तिचे मूल्य येईल. पण ध्वनीचा वेग वे हाच असल्यामुळे ध्वनीचा वेग भागिले नवीन तरंगलांबी बरोबर नवीन कंप्रता या सूत्राप्रमाणे भासमान कंप्रता
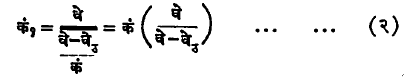
काढता येते. (२) वरून कं१ > कं आहे हे स्पष्ट दिसते. ध्वनीचा उगम श्रोत्याकडे जाण्याऐवजी तो त्याच्यापासून दूर जात असेल, तर
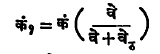
होईल. या वेळी कं१ > कं असते. थोडक्यात ध्वनि-उगम श्रोत्याला जोडणाऱ्या रेषेत वेउ या वेगाने त्याच्याकडे किंवा त्याच्यापासून दूर जात असेल, तर भासमान कंप्रता पुढील समीकरणाने मिळेल.
या उलट ध्वनि-उगम स्थिर असून श्रोताच ध्वनि-उगमाकडे वेश या वेगाने जात आहे असे समजले, तर तरंगलांबी त मध्ये आता भासमान फरक पडत नाही पण श्रोताच उगमाकडे वेगाने जात असल्यामुळे तो प्रती सेकंद जास्त तरंग ऐकतो (पकडतो किंवा त्याच्या कानावर जादा तरंग आदळतात), म्हणून भासमान कंप्रता जास्त वाटते. ही जादा तरंगाची संख्या, श्रोत्याचा वेग वेश व मूळ तरंगलांबी त यांच्या भागाकाराने मिळते. मूळ कंप्रता कं अधिक जादा तरंगांची संख्या मिळून भासमान कंप्रता
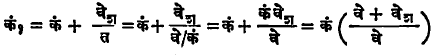
या समीकरणाने मिळते. श्रोता उगमाकडे जाण्याऐवजी तेवढ्याच वेगाने पण त्याच्यापासून दूर जात असेल, तर वेश / त इतके तरंग तो प्रती सेकंदाला कमी ऐकेल. थोडक्यात श्रोता उगमाकडे वा त्यांपासून त्याच रेषेत दूर जात असेल, तर भासमान कंप्रता पुढील समीकरणाने मिळते.
निरीक्षकाच्या जवळून वेगाने जाणाऱ्या रेल्वे एंजिनाच्या शिटीचा आवाज प्रथम चढा (जास्त कंप्रतेचा) व नंतर एंजिन दूर जात असताना (कमी कंप्रतेचा) वाटतो. याचे कारण निरीक्षकात व एंजिनात असणाऱ्या सापेक्ष वेगामुळे कंप्रतेत चढ-उतार होत असतो हे डॉप्लर परिणामाचे नेहमी अनुभवाला येणारे उदाहरण आहे.
वरील विवेचनात श्रोत्यापासून ध्वनि-उगमाचे जवळ वा दूर जाणे किंवा उगमापासून श्रोत्याने जवळ वा दूर जाणे यात त्यांच्या सापेक्ष वेगामुळे कंप्रतेत बदल होतो, हे दाखविले आहे. तसाच आणखी एका प्रकारानेही कंप्रतेत बदल झालेला वाटतो. ध्वनी वाहून नेणाऱ्या माध्यमाला जर उगम व श्रोता यांना जोडणाऱ्या दिशेत उलट-सुलट वेग आहे असे मानले, तर कंप्रतेत कमीजास्त बदल होतो. हे सर्व परिणाम लागू होत असताना कंप्रता कं१ खालील समीकरणे मिळते.
यात वेम माध्यमाचा वेग. येथे श्रोत्याकडून उगमाकडे जाणाऱ्या दिशेस धन चिन्ह (+) आहे असे समजले आहे त्याचप्रमाणे वेश व वेउ यांना वरील व्याख्येप्रमाणे धन चिन्ह समजून उलट दिशेस ऋण चिन्ह असते, असे मानले आहे.
प्रकाशतरंगांच्या बाबतीतही डॉप्लर परिणाम होऊ होऊ शकतो पण ध्वनि तरंगांच्या बाबतीत वर्णिलेल्या परिणामापेक्षा तो काहीसा वेगळा असतो. कारण प्रकाशतरंगाच्या कंप्रतेतील बदल, प्रकाश-उगम निरीक्षकाकडे (किंवा प्रकाशतरंग ग्रहण करणाऱ्या उपकरणाकडे) जावो किंवा निरीक्षक प्रकाश-उगमाकडे जावो, परिणाम एकाच प्रकारचा भासतो. तसेच प्रकाश वाहन नेणाऱ्या माध्यमाच्या वेगावर हा परिणाम (ध्वनितरंगाप्रमाणे) अवलंबून नसतो. प्रकाशीय डॉप्लर परिणाम प्रकाश-उगम व निरीक्षक एकमेकांस लंब दिशेत जात असले, तरी अनुभवास येतो तसा ध्वनितरंगांच्या बाबतीत तो आढळत नाही.
पृथ्वीपासून वेगाने दूर जाणाऱ्या ताऱ्यापासून आलेल्या प्रकाशाची तरंगलांबी वाढते म्हणजे कंप्रता कमी होते. त्यामुळे प्रकाशाचा रंग तांबूस दिसतो किंवा वर्णपटातील वर्णरेषा तांबड्या बाजूकडे सरकलेल्या आढळतात. या उलट पृथ्वीकडे वेगाने येणाऱ्या ताऱ्याच्या प्रकाशाची तरंगलांबी कमी होते म्हणजेच कंप्रता वाढते व प्रकाशाचा रंग निळसर दिसतो. ए. फीझो या फ्रेंच भौतिकीविज्ञांनी १८४८ साली प्रकाशीय डॉप्लर परिणाम वर्णरेषेच्या स्थलांतरामुळे आढळणे शक्य आहे, असे प्रथम प्रसिद्ध केले. वर्णपटातील वर्णरेषेचे स्थलांतर तारा व पृथ्वी यांतील सापेक्ष वेग आणि तरंगलांबी या दोघांच्या गुणाकाराशी सम प्रमाणात असते.
प्रकाशीय डॉप्लर परिणामामुळे ताऱ्यांचे अरीय (तारा व निरीक्षक यांना जोडणाऱ्या रेषेतील) वेग, एकमेकांच्या अगदी जवळ असलेल्या तारकायुग्मांच्या कक्षांचे मापन, सूर्याचे स्वतःभोवतीचे परिभ्रमण, शनीभोवती असणाऱ्या भिन्नभिन्न कड्यांचा वेग इत्यादींबाबत पुष्कळ संशोधन करता आले आहे [→ तारा]. अत्यंत दूर असलेल्या दीर्घिकेच्या (अनेक ताऱ्यांच्या बनलेल्या प्रचंड समूहाच्या) वर्णपटातील रेषांचे तांबड्या बाजूकडे झालेले स्थलांतर डॉप्लर परिणामामुळे होते असे मानले, तर विश्व प्रसरण पावत आहे. असा निष्कर्ष निघतो.
प्रकाश-उगमातील अणु-रेणूंच्या ऊष्मीय गतीमुळे डॉप्लर परिणाम होऊन वर्णरेषांची रुंदी वाढते. ⇨ मॉसबावर परिणामाच्या प्रयोगात डॉप्लर परिणामाचा उपयोग केला जातो. सोनार [→ सोनार व सोफार] या उपकरणाच्या साहाय्याने पाणबुडीचे स्थान निश्चित करताना डॉप्लर परिणामाचा उपयोग करतात. ⇨ रडारच्या साहाय्याने डॉप्लर परिणामाचा उपयोग करून उडणाऱ्या विमानाला आपला पृथ्वीसापेक्ष वेग अचूकपणे काढता येतो. त्याचप्रमाणे रडार-डॉप्लर परिणामाच्या साहाय्याने वेगमर्यादा ओलांडणाऱ्या मोटारींचा पोलिसांना मागोवा घेता येतो. पी. डी. रडार या साधनात डॉप्लर परिणामाचा उपयोग केलेला असून त्याच्या साहाय्याने शत्रू सैन्याची हालचाल समजून येते. त्याचप्रमाणे त्याच्या साहाय्याने विस्तृत क्षेत्रावरील पर्जन्यवृष्टीचे मापन करता येते व पुराबद्दल आगाऊ सूचना देता येते. क्षेपणास्त्रे व त्यांचा नाश करणारी प्रतिक्षेपणास्त्रे ही दोन्ही डॉप्लर परिणामाचा उपयोग करतात.
संदर्भ : 1. Ghosh, S. N. Deb, S. Sound for Degree Students, Calcutta, 1963.
2. Jenkins, F. A. White, H. E. Fundamentals of Optics, New York, 1957.
3. Wood, R. W. Physical Optics, New York, 1959.
जोशी, वि. भि.
“