संस्थिति विज्ञान : (टोपॉलॉजी). (अ) संस्थितिविज्ञान ही गणिताची एक आधुनिक शाखा आहे. ताणणे, आकसणे, पिरगळणे यांसारख्या क्रिया केल्या असता एखादया आकृतीचे जे गुणधर्म निश्चल राहतात त्या गुणधर्मांचा अभ्यास या शाखेत केला जातो. रबराच्या एखादया पृष्ठावर त्रिकोण काढला तर तो पृष्ठ ताणून त्रिकोणाचा गोल तयार करता येतो. तो पृष्ठभाग दाबून त्रिकोणाच्या कोनांची मापे बदलता येतात. पृष्ठभाग वाकवून त्रिकोणाच्या सरळ बाजू वाकविता येतात. पण यापैकी काहीही केले तरी आकृतीच्या आतला बिंदू बाहेर येणार नाही वा बाहेरचा बिंदू आत जाणार नाही. म्हणजे ‘बिंदूचे त्रिकोणाच्या आत असणे’ हा गुणधर्म वरील कियांच्या सापेक्ष निश्चल आहे. या गुणधर्माला सांस्थितिक गुणधर्म असे म्हणतात. या उदाहरणावरून असे दिसून येते की, आकृतीच्या आकाराला किंवा आकारमानाला या विज्ञानात महत्त्व नसून बिंदूच्या सापेक्षस्थितीला महत्त्व आहे. म्हणून या विज्ञानाला पूर्वी स्थितिविज्ञान (ॲनॅलिसिस सायटस) असे म्हणत असत.
वरील वर्णनात ताणणे, आकसणे, पिरगळणे या क्रिया मान्य केल्या पण तुकडे करणे, भोक पाडणे, कापणे या क्रिया मान्य केल्या नाहीत. यावरून मूळ आकृतीत जे बदल करणे या शाखेला अपेक्षित आहे त्यांचा अंदाज येतो. हे बदल ‘संततेच्या कक्षेत आले पाहिजेत. यातील संततता ही संकल्पना क्रमाक्रमाने स्पष्ट होत जाईल. त्याचा अर्थ असा की, आकृतीतील जे बिंदू परस्परांच्या निकट आहेत ते बिंदू पृष्ठभागावर अभिप्रेत क्रिया केली असता निकटच राहिले पाहिजेत.
संस्थितिविज्ञानाचा अभ्यास करताना संच सिद्धांतातील अनेक कल्पनांचा – विशेषतः फलन, संततता, संचावरील क्रिया यांचा – उपयोग करावा लागतो. [⟶ संच सिद्धांत].
(आ) ऐतिहासिक दृष्टया संस्थितिविज्ञानाला ⇨ रने देकार्त (१५९६-१६५०) यांनी १६४० मध्ये बहुपृष्ठाकृतीच्या शिरोबिंदूंची संख्या, कडांची संख्या व पृष्ठांची संख्या यांच्यातील संबंधाचे पुढीलप्रमाणे सूत्र मांडले : (शिरोबिंदूंची संख्या – कडांची संख्या + पृष्ठांची संख्या) = २. ⇨ लेनर्ड ऑयलर (१७०७-८३) यांनी या सूत्राची एक सिद्धता १७५२ साली दिली. अधिक व्यापक दृष्टिकोनातून या प्रश्नाचा विचार करून या बद्दलची एक नवी उपपत्ती ⇨ झ्यूल आंरी प्वँकारे (१८५४- १९१२) यांनी मांडली.
ऑयलर यांनी ‘ क्योनिग्जबर्गमधील पुलांचा प्रश्न ’ (याची माहिती पुढे आली आहे) सोडवून संस्थितिविज्ञान या शाखेतील दुसऱ्या विभागाला सुरूवात केली. याच विभागात ⇨ कार्ल फीडि्नख गौस (१७७७ – १८५५) व पी. जी. टेट (१८३१-१९०१) यांनी महत्त्वाचे संशोधन केले.
ए. एफ्. मोबियस (१७९०-१८६८) यांनी ‘ चार रंगांचा प्रश्न ’ पहिल्यांदा मांडला व त्याचा अधिक विचार ⇨ ऑगस्ट द मॉर्गन (१८०६-७१) व ⇨ आर्थर केली (१८२१-९५) यांनी केला. ⇨ गेओर्क कँटर (१८४५ – १९१८) यांनीही गणिताच्या या शाखेत महत्त्वाची भर घातली. (इ) संस्थितिविज्ञानाचे तीन ढोबळ विभाग पडतात.
(१) समचयात्मक संस्थितिविज्ञान : या विभागात भौमितिक आकाराचे लहान भाग पाडून त्यांची पुन्हा जुळणी करून नवीन आकार बनविणे, या प्रक्रियेचा अभ्यास केला जातो. (२) बैजिक संस्थिति-विज्ञान : या शाखेत दिलेल्या संस्थिति-अवकाशाचा अभ्यास त्या अवकाशाशी सुयोग्य अशी बैजिक रचना जोडून तिच्या साहाय्याने केला जातो. (३) बिंदु-संच संस्थितिविज्ञान : यात संस्थितिविज्ञानातील खुला संच, बंद संच, पुंज बिंदू इ. संकल्पनांचा वापर करून संचांची व्यवस्था लावण्याचा प्रयत्न केला जातो.
संस्थितिविज्ञानाचे दुसऱ्या पद्धतीने निराळे विभागही पाडता येतात. येथे वर्गीकरणाची एकमात्र पद्धत दिली आहे. विषय जसजसा विस्तार पावतो तसतसे नवे विभाग अस्तित्वात येतात.
महत्त्वाच्या संकल्पना : (अ) संस्थितिविज्ञानातील पहिली मूलभूत कल्पना संस्थिति-अवकाश ही होय. ‘ क्ष ’ हा विश्वसंच आहे व त्यातील उपसंचांच्या समूहाला (त्याला ‘ स ’ हे चिन्ह वापरू) संस्थिती असे म्हणतात. ‘ स ’ या समूहाचे घटक असणाऱ्या संचांना खुले संच असे म्हणतात. हे संच पुढील अटींची पूर्तता करतात:(१)‘ क्ष ’ हा विश्वसंच आणि ϕ हा रिक्त संच ‘ स ’ मध्ये आहे. (२) अ आणि ब हे संच स चे घटक असतील तर अ ∩ब हाही ‘ स ’ चा घटक असला पाहिजे. (३) { ख} हा ‘ स ’ मधील अगणित संचांचा एक वर्ग घेतला तर∪α खα हा संयोगाने मिळणारा संचही ‘ स ’ मध्ये असला पाहिजे. (क्ष, स) या कमित जोडीला संस्थिति-अवकाश असे म्हणतात.
(आ) (क्ष१, स१) आणि (क्ष२, स२) असे दोन संस्थिति-अवकाश आहेत. फ : क्ष१⟶ क्ष२ हे असे फलन आहे की, ते एकास-एक आणि आच्छादक या पद्धतीने क्ष१ मधील बिंदूंशी क्ष२ मधील बिंदू जोडते. त्यामुळे फ-१ : क्ष२⟶ क्ष१ हे उलट फलनही मिळू शकते. जर फ आणि फ-१ ही दोन्ही फलने संतत असतील तर (क्ष१, स१) आणि (क्ष२, स२) हे संस्थिति-अवकाश संस्थितीय दृष्टया तुल्य आहेत आणि फ हे दोन्हींमधील सामियरूपण आहे, असे म्हणतात.
या दोन्ही संचांचे बीज कळण्यासाठी फ हे फलन संतत आहे, म्हणजे काय ते पाहिले पाहिजे. फ : क्ष१⟶ क्ष२ हे फलन संतत होण्यासाठी पुढील अट पूर्ण झाली पाहिजे : स२ मधील ‘ अ ’ हा संच घ्या. याचाच अर्थ ‘अ ’ हा खुला संच आहे. फ-१(अ) ही ‘ अ ’ या संचाची क्ष१ मधील पूर्वप्रतिमा आहे. ही पूर्वप्रतिमा (क्ष१, स१) या संस्थिति-अवकाशातील खुला संच असेल, म्हणजेच फ-१ (अ) हा स१ या समूहात असेल, तर फ हे फलन संतत आहे असे म्हणतात. संतततेची ही व्याख्या संतततेच्या इतर व्याख्यांशी तार्किक दृष्टया समान आहे, असे दाखविता येते.
आता ‘ संस्थितीय तुल्यता ’ या संज्ञेचे मर्म समजून येईल. (क्ष१, स१) हा संस्थिति-अवकाश दिला व फ : क्ष१⟶क्ष२ हे सामियरूपण दिले की, क्ष२ मधील सर्व खुले संच म्हणजेच स२ ही संस्थिती मिळते. त्याचप्रमाणे (क्ष२, स२) हा संस्थिति-अवकाश दिला तर फ-१ या फलनाच्या साहाय्याने क्ष१ मधील सर्व खुले संच म्हणजेच स1 ही संस्थिती मिळते.
(क्ष१, स१) मधील संचाचे जे गुणधर्म कोणत्याही तुल्य संस्थिति- अवकाशात तसेच आढळतात, त्यांना संस्थितीय गुणधर्म असे म्हणतात व त्यांचा अभ्यास संस्थितिविज्ञानात होतो.
(इ) (क्ष, स) हा संस्थिति-अवकाश आहे. प हा बिंदू आहे. अ हा संच प या बिंदूचा परिसर होण्यासाठी खालील अट पूर्ण झाली पाहिजे: ब हा असा खुला संच मिळाला पाहिजे की, प ϵ ब ⊂ अ असे झाल्यावर अ हा प चा परिसर आहे असे म्हणतात.
प हा बिंदू आहे आणि य हा संच आहे. जर प चा कोणताही परिसर अ याच्यात य च्या अ पेक्षा निराळ्या अशा एका तरी बिंदूंचा समावेश होत असेल, म्हणजेच अ ∩ य मध्ये प खेरीज निराळा बिंदू असेल, तर प ला य चा पुंजबिंदू असे म्हणतात. य च्या पुंजबिंदूंचा संच य‘ या चिन्हाने दाखवितात.
जर य’ ⊂ य असे असेल, तर य ला बंद संच असे म्हणतात. य ∪य‘ = य या संचाला य या संचाची बंदिस्ती असे म्हणतात.
(ई) (क्ष१, स१) या संस्थिति-अवकाशात अ१ आणि अ२ हे अरिक्त संच असे आहेत की, अ१∩अ२= ϕ आणि अ१∩ अ२= ϕ. अशा वेळी अ = अ१ ∪ अ२ या संचाला खंडित संच असे म्हणतात. जर अ हा संच खंडित नसेल तर त्याला अखंड संच असे म्हणतात.
संचाची अखंडता हा संस्थितीय गुणधर्म आहे. म्हणजे (क्ष२, स२) हा (क्ष१, स१) शी तुल्य असा संस्थिति-अवकाश असेल आणि फ हे दोहोंमधील सामियरूपण असेल, तर फ(अ) हा संचही (क्ष२, स२) मध्ये अखंड असतो.
(उ) (क्ष१, स१) हा संस्थिति-अवकाश आहे. आ हा खुल्या संचांचा समूह आहे. यातील प्रातिनिधिक खुला संच पα या चिन्हाने दाखविला आहे. अ हा असा संच आहे की, अ ⊂∪α पα , तर आ ला अ चे खुले आच्छादन असे म्हणतात.
समजा, अ हा संच असा आहे की, आ हे त्याचे कोणतेही खुले आच्छादन घेतले असता आ मधील खुल्या संचांचा असा सांत समूह मिळू शकतो की, तो सांत समूहही अ चे आच्छादन होतो. अशा स्थितीत ‘ अ ’ ला आटोपशीर संच असे म्हणतात.
आटोपशीरपणा हाही संस्थितीय गुणधर्म आहे.
बैजिक संस्थितिविज्ञान : (अ) पुढील प्रतलीय आकृती पहा. आ. १ (अ) व (आ) यांना छिद्रे नाहीत. आ. १ (इ) हिला एक छिद्र तर आ. १ (ई) हिला दोन छिद्रे आहेत. त्यामुळे आ. १ (अ) मधील कोणताही बंद वक्र आपल्याला आकसत नेत एका बिंदूत ओढविता येतो. तीच गोष्ट आ. १ (आ) मधील बंद वकाची आहे. म्हणून आ. १ (अ) व (आ) या संस्थितीय दृष्टिकोनातून सारख्या आहेत.
आ. १ (इ) मधील छिद्राला वेढणारा जो बंद वक्र असेल तो आकसवून एका बिंदूत आणता येणार नाही. त्यामुळे आ. १ (इ) मधील बंद वकांचे दोन वर्ग होतील. (१) आकसवून बिंदूंत आणता येतील असे वक्र आणि (२) असे न करता येईल असे वक्र. मात्र आ. १ (इ) मधील ही आकृती पफ या रेषेवर छेदली तर ती छिद्रशून्य होऊन आ. १ (अ) व (आ) यांच्याशी संस्थितीय दृष्टया तुल्य होईल.
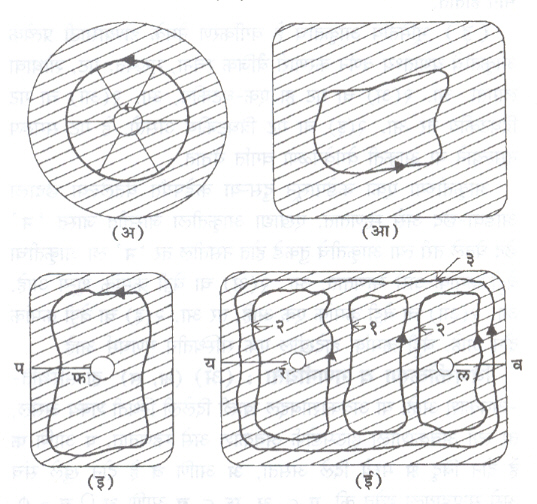आ. १ (ई) मध्ये बंद वकांचे तीन प्रकार होतील कोणत्याच छिद्राला न वेढणारे बंद वक्र, एका छिद्राला वेढणारे बंद वक्र व दोन्ही छिद्रांना वेढणारे बंद वक्र. आकृती यर या रेषेवर कापली तर ती आ. १ (इ) शी संस्थितीय दृष्टया तुल्य होईल आणि यर व लव या दोन रेषांवर छेदली तर आ. १ (अ) शी संस्थितीय दृष्टया तुल्य होईल.
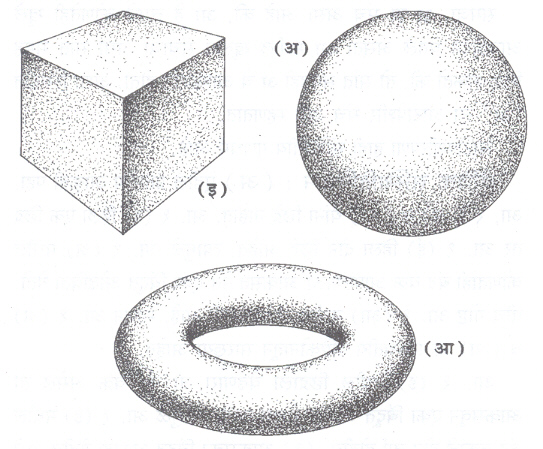
(आ) एक गोल व एक वृत्तजवलय घ्या. त्यांच्या आकृत्यासंस्थितीय दृष्टया तुल्य आहेत का ? त्या तुल्य नाहीत याचे एक गमक असे आहे. गोलावर कोणताही बंद वक्र घेतला, तर तो गोलाचे दोन भाग करतो. तशी स्थिती वृत्तजवलयाच्या बाबतीत होत नाही. वृत्तजवलयावर बंद वक्र काढला असता त्याचे दोन भाग होत नाहीत. त्याचे दोन तुकडे करण्यासाठी दोन बंद वक्र काढावे लागतात. याउलट घन व गोल हे संस्थितीय दृष्टया तुल्य आहेत. कारण घनावर कोणताही बंद वक्र असल्यास घनाचे दोन भाग होतात.
(इ) भूमितीय आकृतींचे हे वर्गीकरण नेमके होण्यासाठी प्रत्येक आकृतीचे यथातथ्य वर्णन करणारी बैजिक रचना, मुख्यतः गट शोधावा लागतो. आ. २ (अ) चा गट हा एक-घटकीय, आ. २ (आ) चा गट द्विघटकीय तर आ. २ (इ) चा गट त्रिघटकीय असतो. हे गट समरूप नसल्याने या आकृती वेगवेगळ्या वर्गात येतात.
आकृतीच्या एका कडेपासून दुसऱ्या कडेपर्यंत घेतलेल्या छेदाला आडवा-छेद असे म्हणतात. एखादया आकृतीला जास्तीत जास्त ‘ न ’ छेद घेतले तरी त्या आकृतीचे तुकडे होत नसतील तर ‘ न ’ ला आकृतीचा बेट्टी क्रमांक असे म्हणतात. आ. २ (अ) चा बेट्टी क्रमांक शून्य आहे. आ. २ (आ) चा बेट्टी क्रमांक एक आहे, तर आ. २ (इ) चा बेट्टी क्रमांक दोन आहे. बेट्टी क्रमांक हादेखील एक संस्थितीय गुणधर्म आहे.
विभक्तीकरण व गणनीयता : (अ) (क्ष, स) हा संस्थिति- अवकाश आहे. या अवकाशाबद्दल खाली दिलेली स्थिती शक्य असेल, तर त्या अवकाशाला हाउसडोर्फ अवकाश असे म्हणतात. प आणि फ हे दोन बिंदू क्ष मध्ये दिले असता, अ आणि ब हे दोन खुले संच असे सापडायला हवेत की, प ϵ अ, फ ϵ ब आणि अ ∩ ब = ϕ. या स्थितीला हाउसडोर्फ गुणधर्म असे म्हणतात. हा विभक्तता दाखविणारा गुणधर्म आहे.
समजा, प हा बिंदू आणि अ हा बंद संच असे आहेत की, प ∉ अ अशा वेळी य आणि र हे खुले संच असे शोधून काढता येतात की, प ϵ य, फ ϵ र आणि य ∩ र =ϕ, तर (क्ष, स) या संस्थिति-अवकाशाच्या ठिकाणी रेखीवता हा गुणधर्म आहे असे म्हणतात. रेखीवता हाही विभक्ततादर्शक गुणधर्म आहे.
समजा, (क्ष, स) हा संस्थिति-अवकाश आहे. त्यात अ आणि ब हे बंद संच असे आहेत की, अ ∩ ब =ϕ. अशा स्थितीत य आणि र हे असे खुले संच शोधून काढता येत असतील की, अ⊂य, ब⊂र आणि य ∩ र = ϕ तर (क्ष, स) हा संस्थिति-अवकाश नियमित आहे, असे म्हणतात.
नियमितता, रेखीवता, हाउसडोर्फ हे सर्व गुणधर्म विभक्तीकरण या सदरातील गुणधर्म असून ते संस्थितीय गुणधर्म आहेत.
(आ) (क्ष, स) हा संस्थिति-अवकाश आहे. यातील प्रत्येक बिंदू प याला गणनीय संख्येत परिसर असतील, तर हा संस्थिति-अवकाश गणनीयतेचा पहिला नियम पाळतो, असे म्हणता येईल. उदा., संख्या रेषेवरील प्रत्येक ‘ प ’ या बिंदूशी दिलेल्या धन पूर्णांक ‘ न ’ याच्या इतक्या त्रिज्येचा खुला अंतराल घेता येऊ शकतो. म्हणून संख्या रेषा हा संस्थिति-अवकाश गणनीयतेचा पहिला नियम पाळतो.
(क्ष, स) हा संस्थिति-अवकाश आहे. ‘ स ’ हा खुल्या संचांचा समूह आहे. समजा, ट हा स चा असा उपसमूह आहे की, स मधला अ हा संच दिला असता ट मध्ये ब हा असा उपसंच मिळविता येऊ शकतो की, ब ⊂ अ. अशा वेळी ट ला (क्ष, स) या संस्थिति-अवकाशाचा आधार असे म्हणतात. संपूर्ण समूह ‘ स ’ हा (क्ष, स) यांचा आधार असतोच. आता (क्ष, स) या संस्थिति-अवकाशाला जर गणनीय आधार शोधून काढता येऊ शकतो, तर (क्ष, स) हा संस्थिति-अवकाश गणनीयतेचा दुसरा नियम पाळतो असे म्हणतात.
(इ) क्ष हा एक संच घ्या. त्यातील बिंदूंच्या क्रमित जोड्यांचा क्ष × क्ष हा संच तयार करा. अशा प्रत्येक (प, फ) या जोडीशी d (प, फ) ही न-ऋण संख्या अशा रीतीने जुळवा की, ही जुळणी पुढील नियमांची पूर्तता करील : (१) d (प, फ) = d (फ, प). (२) d (प, फ) = 0 जर आणि जरच फ = प. (३) जर प, फ, ब हे कोणतेही तीन बिंदू असतील,
तर (प, फ) ≤ d (प, ब) + d (ब, फ).
अशा स्थितीत (क्ष, d) या जोडीला मानीय अवकाश असे म्हणतात. या मानीय अवकाशात आपल्याला खुल्या संचाची संकल्पना खालील रीतीने बसविता येते. समजा, प हा बिंदू आहे व ϵ > 0 अशी संख्या आहे, तर uϵ(प) = { ब l d (प, ब) < ϵ}. या संचाला प चा ϵ -त्रिज्येचा परिसर असे म्हणतात. आता अ या संचाला खुला संच म्हणावयाचे असेल, तर त्याने पुढील अटींची पूर्तता केली पाहिजे : (१) प ϵ अ असेल, तर ϵ > 0 असा शोधता आला पाहिजे की, uϵ (प) ⊂ अ. (२) क्ष मध्ये खुल्या संचाची संकल्पना d या ‘ माना ’च्या सिद्घ झाल्यानंतर (क्ष, d) या मानीय अवकाशाकडे संस्थिति-अवकाश म्हणूनही पाहता येते.
(ई) आता पुढील प्रश्न निर्माण होतो. (क्ष, स) हा संस्थितिय-अवकाश दिला असता d हा मानीय शोधून काढता येईल का, की ज्यामुळे (क्ष, d) हा मानीय अवकाश आणि (क्ष, स) हा संस्थिति-अवकाश एकच होतील.
(क्ष, स) या संस्थिति-अवकाशाला त्याच्या ठिकाणी पुढील गुणधर्म असेल तर विभक्तीकरणीय अवकाश असे म्हणतात. तो गुणधर्म असा : क्ष मध्ये असा एक गणनीय संच आहे की, क्ष मधील प्रत्येक खुला संच या गणनीय संचाशी अरिक्त छेद घेतो.
आता वरील प्रश्नाचे उत्तर पुढील प्रमेयातून मिळते : (क्ष, स) हा विभक्तीकरणीय, रेखीवता आणि हाउसडोर्फ गुणधर्म असणारा संस्थिति- अवकाश आहे. तो अवकाश होण्यासाठी त्याने गणनीयतेचा दुसरा नियम पाळणे पुरेसे व आवश्यक आहे.
मूलभूत प्रश्न :(अ) गणित शाखेची वाढ काही प्रश्नांच्या सोडवणुकीचा विचार करताना होत असते. संस्थितिविज्ञानाची वाढ अशीच काही प्रश्नांचा मागोवा घेताना झाली आहे. त्यातील काही प्रश्नांची चर्चा अशी : एखादया प्रतलावर एक बंद वक्र काढला तर त्यामुळे वक्राचा आतील भाग व बाहेरील भाग असे प्रतलाचे दोन भाग होतात. हा प्रतल रबराचा असेल आणि त्यामुळे तो आकसून टाकला, ताणला, पिरगळला तरी प्रतलाचे दोन भाग झाले आहेत ते तसेच राहतात. हा अनुभव प्रमेयाच्या स्वरूपात मांडून सिद्ध करण्याचा प्रयत्न केला तर सिद्धता फार अवघड जाते, कारण जो वक्र समोर असेल तो फार गुंतागुंतीचा असू शकतो. ⇨ कामीय झॉर्दां (१८३८-१९२२) या गणितज्ञांनी हे प्रमेय प्रथम मांडले. त्यांची समाधानकारक सिद्धता ⇨ ऑझ्‌वाल्ड व्हेब्लेन (१८८०- १९६०) या शास्त्रज्ञांनी १९०५ साली दिली.
(आ) एक वर्तुळ त्याच्या आतल्या भागासकट घेऊन या प्रदेशाला ‘ प्र ’ असे नाव दिले असता समजा, फ : प्र ⟶ प्र असे एक संतत फलन आहे. आता प्रश्न असा आहे की, ‘ प्र ’ या प्रदेशात ‘ प ’ हा असा एक बिंदू असेल का, की ज्याच्या बाबत फ (प) = प अशी स्थिती येईल?
याचे व्यावहारिक उदाहरण असे घेता येईल : एका परातीत जोंधळे घेतले व ते रोळून परातीत पसरले, तर जोंधळ्याचा एक तरी दाणा परातीतील आपल्या मूळच्या जागीच पडला पाहिजे. हे प्रमेय ⇨ ल्यूइटझेन एखबेर्ट्‌स यान ब्रौवर या गणितज्ञांनी मांडून सिद्ध केले.
(इ) १८५२ साली एका नकाशाकाराला असे जाणवले की, शेजारच्या देशांना तोच रंग दयायचा नाही हा नियम पाळून कोणताही नकाशा रंगावयला चारपेक्षा जास्त रंग लागत नाहीत, हे प्रमेय सिद्ध करण्याचे अनेक प्रयत्न झाले. पाच रंग पुरेसे होतात, हे प्रमेय सिद्ध झाले होते, पण त्यापेक्षा कमी रंग पुरत नाहीत, हे सिद्ध करता येत नव्हते. १९७६ साली केनेथ आप्पेल व वुल्फगँग हाकिन या दोन गणितज्ञांनी चार रंग पुरेसे व आवश्यक आहेत, हे प्रमेय संगणकाच्या साहाय्याने सिद्ध केले.
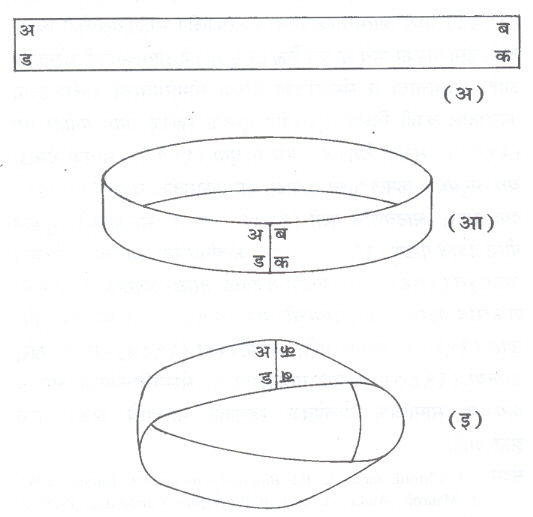
(ई) सामान्यतः पृष्ठाला दोन बाजू असतात. परंतु, ज्याला एकच बाजू आहे असेही पृष्ठ अस्तित्वात आहेत. त्यांपैकी एक म्हणजे मोबियस पट्टा (आ. ३). मोबियस यांनी १८५८ साली हा पट्टा शोधून काढला. अबकड अशी आयताकृती पट्टी घ्या. जर अब व कड या कडा ‘अ ’ टोक व ‘ब ’ टोक आणि ‘क ’ टोक व ‘ड ’ टोक अशा रीतीने जोडल्या तर एक बंद पट्टा तयार होईल. या पट्ट्याला दोन बाजू असतात. बाहेरच्या बाजूने फिरणारी मुंगी कड न ओलांडता आतल्या बाजूस जाऊ शकणार नाही. उलट अब व कड या कडा अ टोक व क टोक आणि ब टोक व ड टोक असा वेढा देऊन चिकटविल्या तर मोबियस पट्टा तयार होतो. जर मुंगी या पट्टयावर एका बिंदूपासून एका दिशेने चालू लागली,तर ती मूळ बिंदूशी ‘ खाली डोके वर पाय ’ अशा अवस्थेत परत येईल, किंवा कात्रीने हा पट्टा आडवा कापला असता त्याचे दोन तुकडे होणार नाहीत.
पहा : गट सिद्धांत भूमिति संच सिद्धांत.
संदर्भ : 1. Armstrong, M. A. : Basic Topology, 1983.
2. Blackett, D. W.: Elementary Topology, 1982.
3. Nagata, J. : Modern Gen eral Topology, 1985.
4. Porteous, I. R. Topological Geometry, Cambridge, 1981.
भावे, श्री. मा.