विभिन्नवर्धन

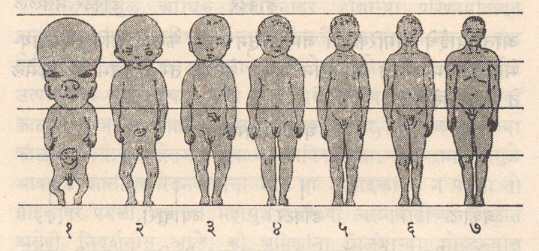
विभिन्नवर्धन : वर्धन, प्रजोत्पादन व संवेदनक्षमता या सजीवांच्या तीन महत्त्वाच्या गुणधर्मांपैकी वध्रन (वाढ) हा एक मुख्य गुणधर्म होय. प्राण्याच्या शरीरामध्ये आणि अवयवांमध्ये नियत काळात होणाऱ्या बदलास वर्धन म्हणता येईल. प्राण्याचे वय वाढत असता त्याचे वजन, आकारमान, अवयवांची लांबी आदि नियमित बदलतराहतात. वर्धन बदल घन असतो. वाढ अप्रतिहत चालू न राहता प्रौढत्व प्राप्त झाल्यावर (वयात आल्यावर) ती स्थिर होते व विशिष्ट मर्यादेनंतर प्राण्याची वाढ थांबते. वय वाढत असता कधी कधी अवयव लहान होतात वा नष्ट होतात (उदा., स्तनी प्राण्यांमधील यौवनलोपी ग्रंथी). प्राण्यांच्या वर्धनाचा अभ्यास गणिती पद्धतीने करता येतो. प्राण्याच्या एकाच अवयवातील कालबद्ध बदल हो मूलभूत मापन करण्यायोग्य गुण होय. एकाच प्राण्याच्या शरीरातील दोन अवयवांची तुलनात्मक वाढ व त्यांचे एकूण शरीराच्या वाढीशी प्रमाण आणि आकारमानात होणारे बदल हे प्राण्यांच्या वर्धनाचे परिमाणात्मक, अभ्यासण्याजोगे गुणधर्म आहेत.

प्राण्याच्या वर्धनाचा अभ्यास करत असता एका अवयवाच्या एकूण वाढीचा शरीराच्या वाढीच्या प्रमाणाशी तुलनात्मक अभ्यास करण्याची गणिती पद्धत जे.एम्. इक्सली यांची रूढ केली. प्राण्यांची वाढ विशिष्ट मर्यादेपर्यंतच होते. ही होत असताना त्या प्राण्याची एकूण वाढ व त्याच्याच एका अवयवाची वाढ यांचे प्रमाण बराच काळ स्थिर असते (उदा., सांबराच्या शरीराची एकूण वाढ व त्याच्या शिंगाची वाढ यांचे प्रमाण बराच काळ स्थिर असते), यास ‘विभिन्नवर्धन’ असे म्हणतात. खालील सूत्राने ते दाखवता येईल. 

d log y / d log x

      y = bx^α

log y = log b + α  lox x

किंवा K_gy /K_gx = α

येथे K_gy वK_gx हे दोन भौमितिक वर्धन प्रमाणα हा गुणक किंवा स्थिरांक होय. α स्थिरांक, गुणोत्तर विशिष्ट प्रसंगी कायम (स्थिर) असतो, असे गृहीत धरले आहे. जर निश्चित काल α हा स्थिर असेल, तर xy या मितीमधील परस्परसंबंध खालील सूत्राने दाखवता येईल. 

y= bx ^α

 या सूत्रास विभिन्नवर्धन सूत्र असे म्हणतात. यासूत्रातील x व y या मिती आहेत, तर α हे भौमितिक प्रमाणांच्या वाढींचे गुणोत्तर होय आणि b हा विचारार्थ असलेल्या अवयवाचा स्थिरांक होय. b या स्थिरांकाला स्पष्ट असा गणिती अर्थ आहे. b हा yची किंमत x ^α = १ किंवा ज्या वेळी x ^α ची किंमत १ असते त्या वेळी y चेx शी असलेले प्रमाण म्हणजेच स्थिरांक b होय. या सूत्राचा जीवशास्त्रीय उपयोग बराचसा अस्पष्ट व अनिश्चित आहे. यामुळे काही वेळा यास पूर्णवाढ स्थिरांक असे म्हणतात.

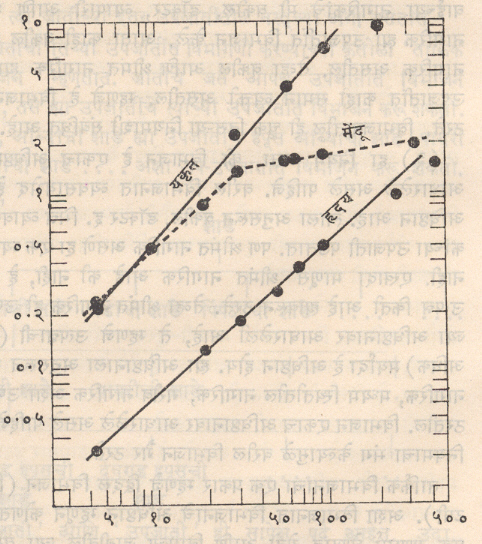
xy मधील हा संबंध एकाच प्राण्याच्या अवयव मितीस एका वेळीच लागू पडेल. भौमितिक वाढीपेक्षा वाढींच्या परस्परसंबंधासच हे सूत्र लागू पडते, असे निरीक्षणांती दिसून आले आहे. याचे कारण असे असावे की, विभिन्नवर्धन सूत्रαस्थिर असता लागू पडते तथापि भौमितिक वाढ आलेखासाठी वाढींचे प्रमाणाच कायम असावे लागते. K_gy आणि K_gx हे वाढ होत असता बऱ्याच प्रमाणात बदलतील व यामुळे भौमितिक वर्णनात्मक प्रमाण निकामी ठरते. K_gy आणि K_gx यांच्या किंमती कायम राहिल्या, तरच विभिन्नवर्धन सूत्र लागू पडेल. याशिवाय K च्या बदलत्या किंमतीमुळे बऱ्याच प्रसंगी ज्या वेळी भौमितिक व अंकगणितीय आलेख लागू पडत नाहीत, त्या वेळी विभिन्नवर्धन सूत्र लागू पडेल. गणिती वा जीवशास्त्रीय अंदाजापेक्षा पूर्वअनुभवसिद्ध प्रसंगांनी α अंदाजे कायम राहील. इतर भौमितिक व गणिती सूत्राप्रमाणेच विभिन्नवर्धन सूत्राचा प्राण्यांच्या वाढीच्या वर्णनासाठी उपयोग होतो. विशिष्ट तपशीलामध्ये हे सूत्र कसे लागू पडते, यावरच या सूत्राची उपयोगिता ठरते. α या स्थिरांकाला विभिन्नवर्धन गुणोत्तर वा स्थिरांक असे म्हणतात. त्याला वाढीचे गुणोत्तर असेही संबोधतात आणि सामान्यतः ते K या अक्षराने दर्शवितात व त्याचा असाच उपयोग करतात. K = 1.

जर K = 1 आणि दोन मितींचे भौमितिक वाढ गुणोत्तर कायम असेल, तर α = १ y = bx y/x = b. दोन मितींच्या आकारांचे गुणोत्तर जर स्थिर असेल, तर त्या मिती ‘सममात्रीय’, ‘समरूपतेने’ वा ‘समदिकपाताने’ वाढतात, असे म्हणता येईल. याउलट जर या साध्या सहसा न घडणाऱ्या परिस्थितींपेक्षा ज्या मितींचे गुणोत्तर सारखे बदलत असते, अशांना त्या विभिन्नवर्धनाने, विभिन्नरूपाने वा विभिन्नमितीने व विभिन्नदिशेने वाढत आहेत, असे म्हणतात. x/y ज्यांचे गुणोत्तर सारखे बदलते, तथापि गुणोत्तराचे प्रमाण कायम आहे, म्हणजे K_gx/ K_gy हे कायम आहे. ज्यांचे गुणोत्तर बदलते अशा मितींचे प्रमाण खालील सूत्राने दाखविता येईल. 

y = bx^α

अशा मिती विभिन्नवर्धन दर्शवितात आणि α हा स्थिरांक विभिन्नवर्धन स्थिरांक असतो. या पद्धतीचा उपयोग प्राण्यांच्या वर्धनाचा अभ्यास करताना होतो. 

कुलकर्णी, र.ग.

“