विद्युत् चुंबकीय क्षेत्र सिद्धांत :वस्तूमधील विद्युत् चुंबकीय आंतरक्रिया विशद करण्यासाठी हा सिद्धांत उपयुक्त आहे. या सिद्धांतान्वये ज्या दोन (अगर अधिक) वस्तूंमध्ये आंतरक्रिया होत असते, त्यांपैकी कोणतीही एक वस्तू अवकाशात स्वतःभोवती विद्युत् चुंबकीय क्षेत्र निर्माण करते व त्या क्षेत्राची दुसऱ्या वस्तूवर आंतरक्रिया होते. आंतरक्रिया करणाऱ्या वस्तू स्थिर अगर गतिशील असू शकतात. वस्तू गतिशील असल्यास आणि आंतरक्रियेचा वेग परिमित असल्यास क्षेत्र सिद्धांताला भौतिक व गणिती सत्यता प्रदान करणे उपयुक्त ठरते.
क्षेत्र सिद्धांतापूर्वी स्थिर वस्तूंमधील आंतरक्रिया ‘दीर्घ अंतरावरून होणारी क्रिया’ म्हणून ओळखली जात असे. त्याचप्रमाणे गतिशील वस्तूंबाबतही ‘विलंबित’ आणि ‘प्रगत’ प्रत्यक्ष आंतरक्रियांचा अवलंब करता येतो परंतु क्षेत्र सिद्धांताची उपयुक्तता आता मान्य झाली आहे.
| विद्युत् चुंबकीय क्षेत्र | आणि | या सदिश राशींचे मिळून बनलेले असते. यांतील |
| राशी विद्युत् क्षेत्र व | राशी चुंबकीय क्षेत्र दर्शविते. |
ही क्षेत्रे परस्परावलंबी असून दोहोंचे मिळून पूर्ण क्षेत्रे होते. सदिश क्षेत्राच्या अभिव्यक्तीसाठी अवकाशातील प्रत्येक बिंदूपाशी क्षेत्रदिशा, मूल्य व कालानुसार त्यात होणारा बदल स्पष्ट करणे आवश्यक असते.
| च्या पूर्ण अभिव्यक्तीसाठी | (स्त्रोत घनता) आणि |
| (परिसंचरण घनता) माहीत असणे आवश्यक ठरते |
. ⇨मॅक्सवेल विद्युत् चुंबकीय समीकरणांतून ही मूल्ये स्पष्ट केली जातात. त्यामुळेच मॅक्सवेल विद्युत् चुंबकीय समीकरणे ‘क्षेत्र समीकरणे’ म्हणून ओळखली जातात.
पोकळीमधील किंवा मुक्त अवकाशातील स्थिर माध्यमासाठी ही समीकरणे खालीलप्रमाणे लिहितात. यामध्ये मुक्त अवकाशात
| आणि | चे उद्गम म्हणून ρtrue ही विद्युत् भार घनता आणि |
ही विद्युत भार घनता असून विद्युत् आणि चुंबकीय ध्रुवक द्रव्य आहे, असे गृहीत धरलेले असते.
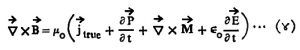 |
वरील समीकरणांबरोबर पुढील घटक समीकरणांचा अंतर्भाव करता येतो.
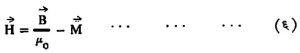 |
या अंतर्भावानंतर मॅक्सवेल विद्युत् चुंबकीय समीकरणे पुढीलप्रमाणे लिहिता येतात.
स्थिर विद्युत् क्षेत्र : स्थिर विद्युत् आणि स्थिर विद्युत् प्रवाह (चुंबकत्व) या बाबतींत वरील मॅक्सवेल समीकरणांचे (७) व (९) आणि (८) व (१०) असे दोन स्वतंत्र भाग करता येतात. यांपैकी पहिला स्थिर विद्युत् साठी व दुसरा स्थिर विद्युत् प्रवाह यासाठी आहे. स्थिर परिस्थितीत
इतकी असते. r चे मूल्य ज्याप्रमाणे बदलेल त्याप्रमाणे E (r) चे मूल्य बदलते. त्याची दिशा बिंदूपासून अरीय (त्रिज्यीय) मार्गाने दूर जाणारी असते. येथे ∊० ही माध्यमाची विद्युत् पार्यता आहे. हे क्षेत्र सभोवतालच्या अवकाशात बाहेरच्या (म्हणजे त्या विद्युत् भारापासून दुरच्या) दिशेत पसरलेले असते. तसेच या अवकाशातील दुसऱ्या विद्युत् भारावर कार्य करणारी प्रेरणा ही विद्युत् क्षेत्र व दुसरा विद्युत् भार यांच्यातील थेट आंतरक्रिया असते. असा विचार करणे सोईचे असते. अशा प्रकारे दुसऱ्या विद्युत् भारावर होणाऱ्या अशा परिणामावरुन विद्युत् क्षेत्र आहे की नाही, ते ओळखू येते.
विद्युत् क्षेत्रात प्रविष्ट होणाऱ्या दुसऱ्या विद्युत् भारित वस्तूवर विद्युत् प्रेरणा कार्य करते. त्यामुळे वस्तूतील विद्युत् भारांच्या रचनेत बदल होणे शक्य असते. उदा., सजातीय विद्युत् भाराच्या वस्तू एक मेकींना दूर लोटतात. तर विजातीय विद्युत् भारांच्या वस्तू एकमेकींकडे आकर्षित होतात.
स्थिर विद्युत् क्षेत्राची ऊर्जा घनता निश्चित करताना ज्या मुक्त विद्युत् भार समूहामुळे विद्युत् क्षेत्र निर्माण झाले आहे, तो समूह तयार करण्यासाठी अनंत अंतरावरुन थोडा थोडा विद्युत् भार समूहापर्यंत आणण्यासाठी करावे लागणारे कार्य विचारात घेतले जाते. अशा प्रकारे पोकळीतील
|
स्थिर क्षेत्राबरोबर |
(ε0E2/2) |
इतकी ऊर्जा घनता संबद्ध असते. |
पोकळीमध्ये विद्युत् अपारक (निरोधक पदार्थ) असल्यास क्षेत्राची ऊर्जा घनता
|
इतकी असते. मात्र यासाठी |
आणि |
| आणि | विद्युत् अपारक स्थिरांकाने (k) संबंधित असू शकतात. [⟶विद्युत् अपारक पदार्थ]. |
कोणत्याही बिंदूजवळची विद्युत् क्षेत्राची तीव्रता (E) म्हणजे त्या बिंदूपाशी ठेवलेल्या एकक धन चाचणी विद्युत् भारामागे (q) कार्यरत असणारी प्रेरणा (F) होय म्हणजे E = F/q. हिलाच विद्युत् क्षेत्राचे बल किंवा केवळ विद्युत् क्षेत्र असेही म्हणतात. चाचणी किंवा दुसरा विद्युत् भार दुप्पट असल्यास निष्पन्न प्रेरणा दुप्पट होईल परंतु विद्युत् क्षेत्र ज्यात मोजले जाते तो भागाकार वा निर्देशांक हा कोरणत्याही विशिष्ट बिंदूपाशी तोच राहतो. विद्युत् क्षेत्राची तीव्रता उद्गम (मूळ) विद्युत् भारावर अवलंबून असते, चाचणी विद्युत् भारावर नव्हे. चाचणी विद्युत् भार पुरेसा लहान असून त्यामुळे विद्युत् क्षेत्रात होणारा बदल नगण्य असतो, असे गृहीत धरतात. नेमकेपणे सागायचे झाल्यास स्वतःचे विद्युत् क्षेत्र असलेला चाचणी विद्युत् भार विद्युत् क्षेत्रात प्रविष्ट झाल्याने किंचित बदल होतो. तथापि असा बदल होण्याआधीच असणारी एकक धन विद्युत् भारामागील प्रेरणा म्हणजे विद्युत् क्षेत्र असे मानावे लागेल.
ऋण विद्युत् भारावर कार्यरत होणाऱ्या विद्युतीय प्रेरणेची दिशा ही धन विद्युत् भारावरील विद्युतीय प्रेरणेच्या दिशेच्या विरुद्ध असते. विद्युत् क्षेत्राला परिमाण व दिशा दोन्ही असतात. म्हणजे ही ⇨ सदिश राशी आहे. त्यामुळे एखाद्या धन विद्युत् भारावरील या प्रेरणेची दिशा ही त्या विद्युत् क्षेत्राची दिशा आहे, असे यदृच्छपणे मानतात. धन विद्युत् भार एकमेकांचे प्रतिसारण (दूर लोटण्याची क्रिया) करतात. त्यामुळे सुट्या धन विद्युत् भाराभोवतीचे विद्युत् क्षेत्र हे बाहेरच्या अरीय दिशांनी असते. म्हणून जेव्हा विद्युत् क्षेत्र हे प्रेरणा रेषा किंवा क्षेत्र रेषा या काल्पनिक रेषांनी रेखाटले जाते, तेव्हा या रेषा धन विद्युत् भारांपासून सुरू होऊन ऋण विद्युत् भारावर संपतील अशा तऱ्हेने काढतात. एखादा छोटा धन विद्युत् भार विद्युत् क्षेत्रात ठेवल्यास तो जो मार्ग अनुसरेल, तो मार्ग या रेषांनी दर्शविला जातो. क्षेत्र रेषेला एखाद्या बिंदूवर काढलेली स्पर्शिका ही तेथील विद्युत् क्षेत्राची दिशा दर्शविते. जेथे क्षेत्र रेषा एकमेकींलगत म्हणजे दाट असतात तेथील विद्युत् क्षेत्राची तीव्रता ही जेथे त्या एकमेकींपासून दूर म्हणजे विरळ असतात तेथील विद्युत् क्षेत्राच्या तीव्रतेपेक्षा जास्त असते. एखाद्या उद्गम विद्युत् भाराभोवतीच्या विद्युत् क्षेत्राचे परिमाण हे त्या विद्युत् भाराचे अवकाशातील वितरण कसे झाले आहे यावर अवलंबून असते. जवळजवळ एका बिंदूतच एकवटलेल्या विद्युत् भाराच्या संदर्भात विद्युत् क्षेत्र हे त्या भाराच्या मूल्यावर अवलंबून असते. तसेच ते तो बिंदू व उद्गम विद्युत् भाराचा मध्य यांच्यातील अरीय दिशेतील अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते आणि ते माध्यमाच्या स्वरुपावरही अवलंबून असते. (समीकरण ११ पहा). निर्वातामधील विद्युत् क्षेत्राचे मूल्य हे द्रव्यरुप माध्यमातील त्याच्या मूल्याहून नेहमीच जास्त असते. एखाद्या बिंदूजवळच्या विद्युत् भारावर विद्युत् क्षेत्राचा काय परिणाम होईल, हे निश्चित करण्यासाठी केवळ विद्युत् क्षेत्राचे मूल्य व दिशा माहीत असणे आवश्यक असते मग विद्युत् क्षेत्र कशामुळे निर्माण झाले आहे, ते माहीत नसले तरी चालते.
दर एकक क्षेत्रफळामागील प्रेरणा हे विद्युत् क्षेत्राचे परिमाण आहे. मी. –किग्रॅ. –से. किंवा एसआय पध्दतींतील विद्युत् क्षेत्राचे एकक न्यूटन/कुलंब असे असून व्होल्ट/मी. हे याच्याशी एकक आहे. सेंमी.- ग्रॅ.-से. पद्धतीत डाइन/विद्युत् स्थितिक एकक या एककात विद्युत् क्षेत्र देतात आणि स्टॅटव्होल्ट/सेंमी. हे त्याच्याशी समतुल्य एकक आहे.
स्थिर विद्युत् प्रवाहातील आंतरक्रिया : विद्युत् भारांच्या प्रवाहाचा विचार करताना साधारणपणे फक्त विद्युत् क्षेत्राचा विचार पुरेसा होत नाही. विद्युत् प्रवाहाबरोबर चुंबकीय क्षेत्र असते व त्याचाही विचार करावा लागतो परंतु विद्युत् प्रवाह स्थिर असेल अगर कालानुसार बदलण्याची कंप्रता (दर सेकंदास होणाऱ्या आवर्तनांची संख्या) कमी असेल (म्हणजेच हळूहळू बदलत असेल), तर चुंबकीय परिणाम खूप कमी असल्याने या बाबतीत फक्त प्रवाहाशी निगडित विद्युत् क्षेत्र विचारात घेतले तरी चालते. म्हणजेच अशा परिस्थितीत विद्युत् प्रवाह फक्त उपयोजित विद्युत् क्षेत्रावर अवलंबून असतो, असे गृहीत धरता येते. प्रवाह घनता
|
आहे असे मानल्यास पुढील अखंडता समीकरण लागू पडते, |
येथे p ही प्रवाह वाहत असलेल्या माध्यमातील विद्युत् भार घनता आहे. प्रवाहाचा सिध्दांत विद्युत् क्षेत्राशी जोडण्यासाठी
हे समीकरण आहे परंतू स्थिर प्रवाह वहात असताना ऊर्जेचा ऱ्हास होत असल्याने व ही ऊर्जा
| या स्थिर विद्युत् क्षेत्रातून मिळू शकत नसल्याने, |
या स्थिर विद्युत् क्षेत्रातून मिळू शकत नसल्याने, स्थिर प्रवाह वाहण्यासाठी विद्युत् चालक प्रेरणेची (मंडलातून विद्युत् प्रवाह वाहण्यास कारणीभूत होणाऱ्या प्रेरणेची वि. चा. प्रे. ची) गरज असते. म्हणून समीकरण (१३) पुढीलप्रमाणे लिहावे लागते.
येथे σ ही सुवाहकाची संवाहकता (रोधाचा व्यस्तांक) असून तो म्हो/मी. मध्ये मोजतात.
विद्युत् चालक प्रेरणेचा (ε) व परिभ्रमणशील विद्युत् क्षेत्र,
| चा संबंध पुढील समीकरणाने मांडता येतो. |
सुवाहकातील प्रवाह स्थिर असल्यास (कालानुसार मूल्य बदलत नसल्यास)
येथे a हे सुवाहकाचे लंबच्छेद क्षेत्रफळ आहे. समी. (१६) चा उपयोग करून समी. (१५) पुढीलप्रमाणे लिहिता येते.
येथे R हा सुवाहकाचा रोध असून समी. (१७) हा ओहम नियम व्यक्त करतो. वि. चा. प्रे. ( ε) व्होल्टमध्ये मोजतात आणि
| वि. चा. प्रे. ने निर्माण केलेले विद्युत् क्षेत्र आहे. समी. (१४) वरुन असे दिसते की, |
|
प्रवाह शून्यअसताना |
म्हणजेच, खंडित मंडलाच्या दोन बिंदूतील विद्युत् वर्चस् (विद्युतीय स्थिती) वि.चा. प्रे इतके असते. |
ज्याप्रमाणे मुक्त विद्युत् भार विद्युत् क्षेत्रात ठेवल्यावर त्यावर विद्युत् प्रेरणा कार्य करु लागते, त्याचप्रमाणे विद्युत् भार चुंबकीय क्षेत्रात गतिमान असेल, तर त्यावर चुंबकीय प्रेरणा कार्य करु लागते. या दृष्टीने दोन्ही क्षेत्रांत साम्य आहे. चुंबकीय प्रेरणेचे समीकरण खाली दिले आहे.
| येथे | चुंबकीय क्षेत्रात (याला चुंबकीय प्रवर्तन असेही नाव आहे) q विद्युत् भार | ||
| गतीने फिरत आहे. | आणि | यांच्यात सदिश गुणाकार होत असल्याने ह्याचे | |||||
मूल्य या राशीमधील कोनाच्या ‘ज्या’ या त्रिकोणमितीय राशीच्या प्रमाणात बदलते. उदा.,
| आणि | काटकोनात असताना प्रेरणा महत्तम असते व समांतर असताना शून्य असते | ||||
| चुंबकीय क्षेत्राप्रमाणेच | चुंबकीय स्त्रोत (Φm) महत्त्वाचा आहे. चुंबकीय रेषेच्या लंबरूप प्रतलात एक बंद वेटोळे आहे |
अशी कल्पना केल्यास वेटोळ्याचे क्षेत्रफळ (s) गुणिले चुंबकीय क्षेत्र तीव्रता (B) म्हणजे चुंबकीय स्रोत
(स्त्रोत वेबरमध्ये मोजतात).
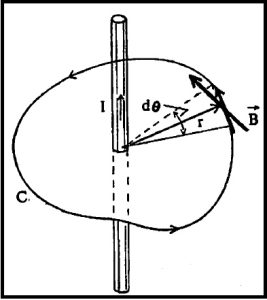
ओर्स्टेड यांनी सिद्ध केल्याप्रमाणे विद्युत् प्रवाह हा चुंबकीय क्षेत्राचा उद्गम आहे. त्यामुळे प्रत्येक विद्युत् मंडलाशी निगडीत असे चुंबकीय क्षेत्र असते. अर्थात शेजारील दोन मंडलांमध्ये आंतरक्रिया होऊन त्यांच्यात आकर्षण अगर प्रतिसारण निर्माण होते. मंडलातील प्रवाह एकमेकांस समांतर असतील तर प्रतिसारण आणि विरुध्द दिशेने असतील तर आकर्षण असते. याचा उपयोग पुष्कळ प्रकारच्या साधनांतून करण्यात आला आहे. स्थिर विद्युत् प्रवाह आणि त्याच्याशी निगडीत असलेले चुंबकीय क्षेत्र यांच्या संबंधातील अँपिअर नियम महत्त्वाचा आहे. आकृतीतील संवाहकातून I विद्युत् प्रवाह वहात आहे. त्याच्याशी निगडीत चुंबकीय क्षेत्र संवाहकाला लंबरुप प्रतलात वर्तुळाकार दिशेने असते. या क्षेत्राचे रेखा समाकल [⟶ अवकलन व समाकलन] हे µo गुणिले संवाहकातील प्रवाह याबरोबर असते.
याला विद्युत् मंडलाबाबतचा अँपिअर नियम असे नाव आहे. हा नियम पुष्कळ दृष्टींनी विद्युत् क्षेत्रातील गौस नियमासारखा आहे व त्यासारखाच महत्त्वाचा आहे.
|
समी. (१४) मध्ये |
क्षेत्राची निर्मिती सुवाहकाच्या मंडलात विद्युत् घट |
क्षेत्राची निर्मिती सुवाहकाच्या मंडलात विद्युत् घट उपयोजित करून करण्यात आली. कालानुसार शीघ्र गतीने बदलणारे चुंबकीय क्षेत्र देखील
|
क्षेत्र निर्माण करु शकते. |
| स्थिर विद्युत् क्षेत्र | स्थितिरक्षक असते. याउलट बदलत्या चुंबकीय क्षेत्राला क्षेत्राला अस्थितिरक्षक विद्युत् क्षेत्र |
याचा अर्थ मंडलातील वि. चा. प्रे. ओहम नियमान्वये जितकी असायला हवी त्यापेक्षा [-(dΦm)/dt] तक्या मूल्याने जास्त असते. मॅक्सवेल यांच्या लक्षात आले की, फॅराडे नियम स्वयंभू असून त्याचे महत्त्व जास्त व्यापक आहे. त्याचप्रमाणे पोकळीतील विद्युत् क्षेत्राचा बदलत्या चुंबकीय क्षेत्राशी संबंध विशद करणारा हा भौतिक नियम असला पाहिजे. यावरुन त्यांनी वरील नियम गणितीय पध्दतीत अवकल समी. (९) प्रमाणे मांडला.
अशा प्रकारे निरनिराळ्या प्रयोगांतून आढळलेल्या निष्कर्षांचे व्यापकीकरण गणितीय समीकरणांद्वारा मॅक्सवेल विद्युत् चुंबकीय समीकरणांमधून व्यक्त होते. यामुळे मॅक्सवेल समीकरणे प्रमाणित करता येत नाहीत, परंतु त्यांच्या उपयोजनातून सत्यापन पडताळता येते. आज पर्यंत विस्तृत प्रमाणावर झालेल्या प्रयोगांतून असे सिध्द झाले आहे. की, मॅक्सवेल विद्युत्क चुंबकीय समीकरणे जवळजवळ सर्व स्थूलमानीय परिस्थितींमध्ये लागू पडतात. व समान्यपणे त्यांचा उपयोग मार्गदर्शक तत्त्वांप्रमाणे केला जातो.
मॅक्सवेल विद्युत् चुंबकीय समीकरणांचे महत्त्वाचे उपयोजन विद्युत् चुंबकीय तरंग समीकरणे मिळविण्यासाठी होते. विद्युत् भारविरहित, संवाहक अगर असंवाहक, एकजिनसी, रैखिक माध्यमामधील विद्युत् चुंबकीय क्षेत्राचे नियमन ही समीकरणे करतात. यांच्या अभ्यासातून निरनिराळ्या परिस्थितींत भिन्न कंप्रतांच्या विद्युत् चुंबकीय तरंगांचे प्रेषण कसे होते ते समजते. त्याचप्रमाणे त्यांचे परावर्तन, प्रणमन यांची अभिलक्षणे स्पष्ट होतात. या समीकरणांवरुन हे अवतरंग असून त्यांतील
| क्षेत्रे व प्रेषण दिशा परस्परांस लंबरुप असतात व पोकळीमध्ये त्यांचे प्रेषण ‘c’ या प्रकाश वेगाने होते, हे समजते. |
विद्युत् चुंबकीय प्रारणाची (तरंगरुपी ऊर्जेची) अभिलक्षणे समजून घेण्यासाठी आणि त्यांच्या प्रसारण, प्रकीर्णन, अपस्करण इ. गुणधर्णांच्या अभ्यासात मॅक्सवेल विद्युत् चुंबकीय समीकरणांचा उपयोग करावा लागतो. प्रारण ऊत्सर्जनात विद्युत् चुंबकीय क्षेत्र हे उद्गम विद्युत् भार व विद्युत् प्रवाह यांपासून अलग होते. उदा., विद्युत् द्विअग्र आंदोलकापासून होणारे प्रारण उत्सर्जन तसेच रेडिओ व दूरचित्रवाणी प्रेषण हे प्रारण विद्युत् चुंबकीय तरंगाच्या रूपात असते.
| आणि | यांच्या सदिश गुणाकाराला (म्हणजे | ला) पॉयंटिंग सदिश असे नाव आहे. |
या राशीचे बंदिस्त क्षेत्रफळावरील समाकल घेतल्यास क्षेत्रफळातून प्रतिसेकंद बाहेर जाणारी प्रारण ऊर्जा मिळते.
पहा : मॅक्सवेल विद्युत् चुंबकीय समीकरणे विद्युत्.
संदर्भ : 1 Halliday, D. Resnick, R. Fundamentals of Physics, New York, 1981.
2. Purcell, E. M. Electrictity and Magnetism, 1984
आगाशे, वसंत वा.; कोळेकर, शं. वा.

