वर्तुळ : वर्तुळ म्हणजे प्रतलातील एक वक्र असून तो शांकव कुलातील [⟶ शंकुच्छेद] आहे. त्याच्यावरील प्रत्येक बिंदू एका विशिष्ट बिंदूपासून ठराविक अंतरावर असतो. या विशिष्ट बिंदूस वर्तुळमध्य किंवा वर्तुळकेंद्र म्हणतात व ठराविक अंतरास त्रिज्या म्हणतात.
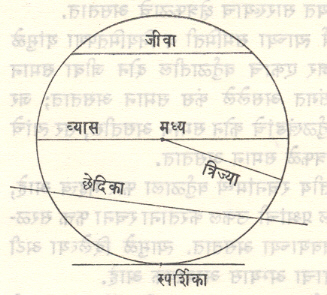वर्तुळाशी संबंधित रेषा: वर्तुळावरील कोणतेही दोन बिंदू जोडणाऱ्या रेषेस जीवा म्हणतात. जीवा वर्तुळमध्यातून जात असल्यास तिला वर्तुळाचा व्यास म्हणतात. वर्तुळास दोन बिंदूंत छेदणाऱ्या रेषेस छेदिका म्हणतात. क व ख वर्तुळावरील दोन बिंदू असून बिंदू ख वर्तुळावरून क च्या जवळ सरकतो तेव्हा कख च्या सीमावस्येस स्पर्शिका म्हणतात. वर्तुळाला व स्पर्शिकेला एकच बिंदू समाईक असतो. (आ. १).
वर्तुळाचा कंस: (आ. २). वर्तुळावरील कोणत्याही दोन बिंदूंमधील वर्तुळाच्या भागास कंस म्हणतात. हे दोन बिंदू व्यासाची टोके असल्यास त्या कंसाला अर्धवर्तुळ म्हणतात. वर्तुळाची लांबी म्हणजे वर्तुळाचा परिघ होय. 
वर्तुळावरील कोणतेही दोन बिंदू व्यासाची टोके नसल्यास वर्तुळ परिघाचे दोन भाग पडतात एक लघू कंस (कगख) व दुसरा विशाल कंस (कपख). कंसाची टोके कंसावरील कोणत्याही बिंदूस जोडली असता तयार होणाऱ्या कोनास परिघ कोन (∠ कपख) म्हणतात. कंसाची टोके वर्तुळमध्यास जोडली असता तयार होणाऱ्या कोनास मध्यकोन (∠ कमख) म्हणतात. जीवा आणि तिने छेदलेला कंस यांमध्ये बंदिस्त असलेल्या वर्तुळाच्या भागास वर्तुळ जीवा खंड (कगख) म्हणतात. तसेच दोन त्रिज्या आणि त्यांनी छेदलेला कंस यांमध्ये बंदिस्त असलेल्या भागास वर्तुळखंड (मकगख) म्हणतात.
वर्तुळाचे गुणधर्म : पुढील प्रमेये वर्तुळाचे गुणधर्म स्पष्ट करतात. (१) वर्तुळमध्यापासून जीवेवर टाकलेला लंब जीवेचे दोन सारखे भाग करतो. यावरून कोणत्याही तीन बिंदूंतून एक आणि एकच वर्तुळ काढता येते, हे सिद्ध करता येते.
(२) वर्तुळातील कोणत्याही कंसासमोरील परिघ कोन हा त्याच कंसासमोरील मध्यकोनाच्या निम्मा असतो (उदा., आ. २ मधील ∠कपख = १/२ ∠ कमख). त्यामुळे एकाच कंसातील सर्व परिघ कोन समान असतात. अर्धवर्तुळातील कोणत्याही बिंदूजवळ तयार होणारा परिघ कोन काटकोन असतो.
(३) चक्रीय चौकोनात (ज्याचे सर्व शिरोबिंदू एकाच वर्तुळावर आहेत अशा चौकोनात) समोरासमोरील कोनांची बेरीज दोन काटकोन असते. जर प्रतलातील चौकोनाच्या संमुख कोनांच्या जोड्यांपैकी कोणत्याही जोडीची बेरीज दोन काटकोन असेल, तर चौकोनाच्या चारी शिरोबिंदूंमधून जाणारे वर्तुळ काढता येते.
(४) एका बिंदूत काढलेल्या स्पर्शिका व जीवा यांमधील कोन विरुद्ध कंसातील कोनाबरोबर असतो.
(५) स्पर्शिका व स्पर्शबिंदूतून काढलेली त्रिज्या यांमधील कोन काटकोन असतो. यावरून दिलेला बिंदू वर्तुळमध्य आणि दिलेली रेषा स्पर्शिका म्हणून असेल असे फक्त एकच वर्तुळ काढता येणे शक्य असते.
(६) दोन जीवा छेदत असल्यास छेदनबिंदूने पडलेल्या जीवांच्या भागांनी तयार होणारे आयत सारख्याच क्षेत्रफळाचे असतात.
वर्तुळाचे अनेक गुणधर्म त्याच्या सममिती व नियमितपणा यांमुळे सरळ मिळतात उदा., जर एकाच वर्तुळातील दोन जीवा समान असतील, तर त्यांच्याशी संगत असलेले कंस समान असतात जर एकाच वर्तुळातील दोन वर्तुळखंडांचे कोन समान असतील, तर त्यांचे कंस व त्यांची समाविष्ट क्षेत्रफळे समान असतात.
वर्तुळ रचना : भूमितीय रचनांमध्ये वर्तुळाला फार महत्त्व आहे, कारण परंपरेने भूमितीमधील प्रश्नांची उकल करताना रचना फक्त सरळपट्टी व कंपास यांनीच करावयाच्या असतात. त्यामुळे दिलेल्या अटी पूर्ण करणारी वर्तुळे काढण्याचा अभ्यास आवश्यक आहे.
तीन बिंदूंतून जाणारे वर्तुळ : क, ख, ग या तीन बिंदूंतून जाणारे वर्तुळ पुढील रचनेने मिळते. कख व खग यांचे लंबदुभाजक म मध्ये मिळत असतील, तर म हा पाहिजे असलेल्या वर्तुळाचा मध्य असतो आणि मक = मख = मग ही त्रिज्या असते. या वर्तुळाला त्रिकोण कखग चे परिवर्तुळ म्हणतात.
तीन रेषांना स्पर्श करणारे वर्तुळ : ∆ कखग च्या तिन्ही बाजूंना स्पर्श करणारे वर्तुळ पुढीलप्रमाणे मिळेल. ∠ क आणि ∠ ख यांचे दुभाजक न मध्ये मिळत असल्यास न हा वर्तुळमध्य होईल व न पासून बाजूवर टाकलेला लंब ही त्रिज्या होईल. या वर्तुळाला अंतर्लिखित वर्तुळ म्हणतात. दोन बिंदूंतून जाणारे व दिलेल्या रेषेला स्पर्श करणारे वर्तुळ काढता येते. तसेच दिलेल्या जीवेवर दिलेला कोन असणारा वर्तुळकंस काढता येतो. दिलेल्या तीन वर्तुळांना स्पर्श करणारे वर्तुळ काढणे हा प्रश्न ‘ॲपोलोनियस समस्या’ म्हणून प्रसिद्ध आहे. दोन बिंदूंतून जाणाऱ्या वर्तुळाचा मध्य हा त्या बिंदूंना जोडणाऱ्या रेषेच्या लंबदुभाजकावर असतो आणि दोन रेषांना स्पर्श करणाऱ्या वर्तुळाचा मध्य त्या रेषांनी तयार होणाऱ्या कोनाच्या दुभाजकावर असतो. एखादा बिंदू दिलेल्या अटी पूर्ण करून फिरत असता काही वेळा त्याचा बिंदुपथ वर्तुळ असतो. जसे त्रिकोणाचा पाया स्थिर असून उरलेल्या दोन बाजूंचे गुणोत्तर अचल असेल, तर शिरोबिंदूचा बिंदुपथ एक वर्तुळ असते. या वर्तुळाला ‘ ॲपोलोनियस वर्तुळ ’ म्हणतात.
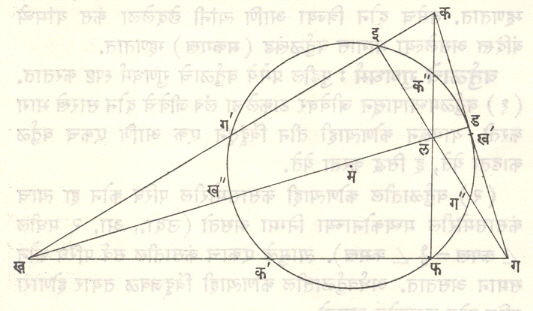
नऊ बिंदू वर्तुळ: (आ. ३). त्रिकोणाशी संबंधित असलेले हे महत्वाचे वर्तुळ पुढील नऊ बिंदूंमधून जाते : (१) ∆ कखग मधील खग, गक व कख या बाजूंचे अनुक्रमे क’, ख’ आणि ग’ हे मध्यबिंदू, (२) कोनबिंदू व लंबसंपात बिंदू जोडणाऱ्या खल, गल व कल या रेषांचे अनुक्रमे ख”, ग” व क” हे मध्यबिंदू, (३) शिरोबिंदूंतून समोरच्या बाजूंवर टाकलेल्या लंबांचे ड, इ व फ हे पादबिंदू.
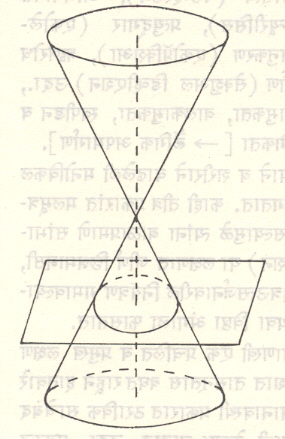वैश्लेषिक भूमितीच्या पद्धती : वर्तुळ हा एक ⇨ शंकुच्छेद आहे. वृत्तशंकूच्या (वर्तुळाकृती पाया असलेल्या शंकूच्या) अक्षाला लंब असलेल्या पण शिरोबिंदूतून न जाणाऱ्या प्रतलाने वृत्तशंकूचा छेद घेतल्यास मिळणारा छेदवक्र वर्तुळ असते (आ. ४).
जात्य देकार्तीय सहनिर्देशक पद्धतीमध्ये (‘भूमिति’ या नोंदीतील ‘वैश्लेषिक भूमिती’ हा भाग पहावा) (क, ख) हा वर्तुळमध्य आणि र ही त्रिज्या लांबी असल्यास वर्तुळाचे प्रमाणभूत समीकरण पुढीलप्रमाणे मिळते.
(क्ष-क)२ + (य-ख)२ = र२ ……. (१)
वर्तुळमध्य हा आदिबिंदूच्या ठिकाणी असल्यास क = ख = ° होऊन वर्तुळाचे समीकरण क्ष२ + य२ = र२ असे रूपांतरित होते.
जर क्ष अक्ष व त्रिज्या यांतील कोन θ असेल, तर क्ष = र कोज्या θ आणि य = र ज्या θ अशी समीकरणे मिळतात. यांना वर्तुळाची प्रचलीय समीकरणे (प्रचल θ) किंवा एकाच चलातील समीकरणे म्हणतात. क्ष व य यांची ही मूल्ये क्ष२ + य२ = र२ या वर्तुळ समीकरणाची पूर्तता करतात, हे सहज दिसून येईल. वर्तुळाचे व्यापक समीकरण पुढीलप्रमाणे असते (आ. ५).
क्ष२ + य२ + २ तक्ष + २ थ य + द = o ……. …… (२)
येथे त, थ आणि द हे स्थिरांक आहेत. याचे प्रमाणभूत समीकरण (क्ष + त)२ + (य + थ)२ = त२ + थ२ – द असे मांडता येते. या वर्तुळाचा मध्य [ -त, -थ ] आणि त्रिज्या √त२+थ२-द असते. दिलेल्या तीन बिंदूंतून वर्तुळ जात असेल, तर या बिंदूंच्या सहनिर्देशकांची मूल्ये समी. (२) मधील क्ष व य करिता घातली असता तीन समीकरणे मिळतात आणि त्यांवरून त, थ व द या स्थिरांकांची मूल्ये काढता येतात. जर बिंदू वर्तुळाबाहेर असेल, तर समी. (२) ची डावी बाजू शून्याबरोबर नसते.
समी. (२) ने निदर्शित केलेल्या वर्तुळाला (क्ष१ , य१) या बिंदूत स्पर्शिका काढल्यास तिचे समीकरण पुढीलप्रमाणे मिळते.
क्ष क्ष१ + य य१ + त (क्ष+क्ष१) + थ (य+य१) + द = o …… (३)
(क्ष१, य१) बिंदू वर्तुळावर नसल्यास समी. (३) हे (क्ष१, य१) या बिंदूची ध्रुवीय रेषा निर्देशित करते.
(क्ष१, य१) या बिंदूपासून वर्तुळाला काढलेल्या स्पर्शिकेची लांबी √क्ष१२+य१२+२त क्ष१+२ थ य १+द असते. यावरून दोन वर्तुळांना (क्ष, य) पासून काढलेल्या स्पर्शिका समान असल्यास √— क्ष२+य२+२त क्ष+२थ य+द = √क्ष२+य२+२ त’क्ष+२थ य+द हे समीकरण मिळते. म्हणून (क्ष, य) चा बिंदुपथ २ (त-त’) क्ष + २ (थ- थ’) य + द – द’ = o ही रेषा मिळते. या रेषेला दोन वर्तुळांचा समस्पर्शिका अक्ष म्हणतात.
ध्रुवीय सहनिर्देशक पद्धतीने वर्तुळाचे समीकरण : (स१, θ१), हा वर्तुळमध्य आणि र ही त्रिज्या असल्यास र२= स२ + स१२ – २ सस१ कोज्या ( θ–θ१) असे वर्तुळाचे व्यापक समीकरण मिळते. जर वर्तुळमध्य [ ०, ०० ] या ठिकाणी असेल, तर स= र असे समीकरण मिळते.
वर्तुळाशी संबंधित महत्त्वमापन : प्रतलावर काढलेल्या सर्व वर्तुळांच्या बाबतीत परिघ आणि व्यास यांच्या लांबींचे गुणोत्तर एकच (कायम) असते. हे गुणोत्तर नेहमी π (= ३.१४१५९२६५ आठ दशांश स्थळांपर्यंत) या चिन्हाने दर्शविले जाते [⟶ पाय् (π)]. π करिता स्थूल आसन्न (अंदाजी) मूल्य २२/७ वापरण्यात येते. जर वर्तुळाचा व्यास ड आणि त्रिज्या र असेल, तर परिघाची लांबी = π ड किंवा २ π र असते.
हिपार्कस (इ. स. पू. १२६ मृत्यू) यांनी राशिचक्राच्या खाल्डियन विभाजनावर आधारित वर्तुळाचे ३६० अंशांमध्ये विभाजन केले. त्रिज्येच्या लांबीइतक्या कंसाने आंतरित केलेला मध्यकोन म्हणजे १ अरीयमान किंवा १ रेडियन (= ५७.२९५७८०) होय. अशा प्रकारे ३६०० चे २ π रेडियन होतात.
वर्तुळाच्या कंसाची लांबी जरी प्रत्यक्ष मिळविता येत नसली, तरी कंस तर त्रिज्येच्या मानाने लहान असेल, तर त्याच्या लांबीचे आसन्नमूल्य काढण्याकरिता पुढील पद्धत उपयोगी पडते (आ. ६) : कख ही जीवा ग पर्यंत अशी वाढवा की, खग = १/२ कख. ग मध्य घेऊन कग त्रिज्येचे वर्तुळ काढा. हे वर्तुळ ख बिंदूतील स्पर्शिकेला प मध्ये मिळत असल्यास खप रेषेची लांबी म्हणजे कसख कंसाच्या लांबीचे आसन्नमूल्य असते. परिघाच्या १/४ भागाकरिता या पद्धतीने काढलेल्या लांबीमध्ये ३०० मध्ये १ भाग एवढी त्रुटी येते. परिघाच्या १/३६ भागामध्ये ही त्रुटी दहा लाखामध्ये एक एवढी असते.
समजा स ही कख कंसाची लांबी, त ही कख जीवेची लांबी आणि थ हे कंसाच्या मध्यापासून जीवेपर्यंतचे अंतर आहे. कमख वर्तुळखंडाच्या क्षेत्रफळाचे आकृतीमध्ये दाखविल्याप्रमाणे विभाजन करून अनेक लहान त्रिकोणांची बेरीज केली असता असे अनुमान करता येते की, वर्तुळखंडाचे क्षेत्रफळ = १/२ र·स म्हणून संपूर्ण वर्तुळाचे क्षेत्रफळ = १/२ र X २ π र = π र२ येते.
कंपास व अंशांकन (लांबीचे अंश दाखविणाऱ्या खुणा) न केलेली सरळपट्टी यांच्या साहाय्याने वर्तुळाच्या परिघाच्या लांबीची रेषा काढणे किंवा वर्तुळाएवढे क्षेत्रफळ असलेला चौरस रचणे हा प्रश्न अठराव्या शतकापर्यंत अनिर्वाहित म्हणून गणला जात होता. र त्रिज्येच्या वर्तुळाचा समक्षेत्र चौरस काढावयाचा म्हणजे त्याचे क्षेत्रफळ π र२ असले पाहिजे. र = १ मानल्यास त्या चौरसाचे क्षेत्रफळ π असले पाहिजे म्हणजे चौरसाची बाजू √π असली पाहिजे परंतु π ही संख्या बैजिक नसून बीजातीत (परिमेय संख्या सहगुणक असलेल्या कोणत्याही समीकरणाची बीज नसलेली) असल्याचे सी. एल्. फर्दिनांद लिंडेमान (१८५२ – १९३९) यांनी १८८२ मध्ये दाखविले. म्हणून वर्तुळाचे चौरसीकरण ही रचना अशक्य असल्याचे सिद्ध झाले.
पहा : गणितातील अनिर्वाहित प्रश्न पाय् (π) भूमिति वक्र शंकुच्छेद.
ओक, स. ज. सूर्यवंशी, वि. ल.
“