रेणवीय भौतिकी : रेणूंच्या भौतिकीय गुणधर्मांचा अभ्यास या विषयात करण्यात येतो. अलग अणूंपेक्षा रेणूंच्या भौतिकीय व रासायनिक गुणधर्मांत फार मोठी विविधता आढळून येते. घटक अणूंशी तुलना करता रेणवीय संरचनेची असलेली मोठी जटिलता हे या विविधतेचे मुख्य कारण आहे. रेणू कंप पावू शकत असल्याने त्यांच्या अंगी जादा ऊर्जा प्रकार संभवतात म्हणजे त्यांची घटक अणुकेंद्रे त्यांच्या समतोल स्थितीच्या भोवती आंदोलित होतात व अडथळा नसेल तेव्हा त्यांचे परिभ्रमणही होते. या प्रकारांमुळे अणूंशी तुलना करता रेणूंना अधिक वर्णपटविज्ञानीय गुणधर्म प्राप्त होतात [⟶ वर्णपटविज्ञान]. दृश्य, अवरक्त व सूक्ष्मतरंग या विभागांतील रेणवीय वर्णपटविज्ञान हे रेणवीय संरचना ओळखण्याचे व समजण्याचे भौतिकीय रसायनशास्त्राचे एक अत्यंत समर्थ साधन बनलेले आहे [⟶ रेणवीय संरचना].
रेणवीय भौतिकी हा अलग रेणूंच्या गुणधर्मांच्या अभ्यासाचा विषय आहे, तर रेणवीय विक्रियांचा अधिक व्यापक अभ्यास भौतिकीय रसायनशास्त्राच्या कक्षेत येतो. या गुणधर्मात वर्णपटविज्ञानाच्या विस्तीर्ण क्षेत्राखेरीज इलेक्ट्रॉन आकर्षण (रेणवीय ऋण विद्युत् भारित आयन तयार होण्यासाठी) ध्रुवीयता (बाह्य विद्युत् क्षेत्रांमुळे विविध सममिती अक्षांवर रेणू विकृत होण्याची शक्यता) चुंबकीय व विद्युत् अनेकध्रुवी परिबले (यांचा विद्युत् भाराच्या वितरणांशी संबंध लावता येतो) इतर अणूंशी, रेणूंशी व आयनांशी (विद्युत् भारित अणू, रेणू व अणुगट यांच्याशी) होणाऱ्या रेणूंच्या परस्परक्रिया इत्यादींचा समावेश होतो.
संघनन (वायूचे द्रवात रूपांतर होणे), ⇨पृष्ठताण, वायूंचे विसरण (रेणू परस्परांत मिसळणे), स्फटिकीय व अस्फटिकीय घन पदार्थ तयार होणे यांसारख्या विविध आविष्कारांना आंतररेणवीय प्रेरणा जबाबदार असतात. अशा प्रकारे रेणूची संरचना त्यांची सममिती व आकार निश्चित करण्याच्या पद्धती, दिष्ट संयुजा [⟶ संयुजा], त्याची ध्रुवीयता, त्याच्या परिभ्रमण कंपन व इलेक्ट्रॉनीय ऊर्जा अवस्था इत्यादींचा रेणवीय भौतिकीत अंतर्भाव केला जातो. वरील आविष्कारांचे योग्य विशदीकरण करण्यासाठी ⇨पुंजयामिकीचा मोठ्या प्रमाणात उपयोग करावा लागतो.
द्रव्याच्या स्थूल भौतिकीय गुणधर्मांचे विवेचन त्यामधील सूक्ष्म घटक रेणूंच्या गुणधर्मांनुसार करण्याचा प्रयत्न भौतिकीमध्ये केला जातो. कोणत्याही पदार्थाचे विशिष्ट रासायनिक गुणधर्म दाखविणारा त्या पदार्थातील सर्वांत सूक्ष्म कण किंवा मुक्त अवस्थेत मिळू शकणारा कोणत्याही पदार्थाचा सर्वांत लहान घटककण म्हणजे रेणू, असे रेणूचे वर्णन करता येते. विविध प्रक्रियांच्या साहाय्याने रेणूचे विभाजन त्याच्या घटकांत करता येते. यावरून एक किंवा त्यापेक्षा अधिक अणू एकत्र येऊन संलग्न झाल असता त्यापासून रेणू तयार होतो हे कळते. उदा., दोन हायड्रोजन अणू व एक ऑक्सिजन अणू यांच्या संयोगाने पाण्याचा रेणू निर्माण होतो. रेणूमध्ये असणाऱ्या अणूंच्या संख्या निरनिराळ्या असू शकतात. हीलियम, निऑन, आर्गॉन यांसारख्या मूलद्रव्यांच्या रेणूमध्ये फक्त एकच अणू असतो. हायड्रोजन रेणूमध्ये हायड्रोजनाचे दोन अणू असतात, तर प्रथिनासारख्या पदार्थाच्या रेणूमध्ये कित्येक हजार अणू असतात. काही वेळा अनेक लहान रेणू एकत्र येऊन एक मोठा जटिल असा बहुवारिक रेणू निर्माण करतात [⟶ बहुवारिकीकरण]. आधुनिक काळात सर्वत्र उपलब्ध असलेला पॉलिथीन हा पदार्थ एक बहुवारिक आहे. अशाच प्रकारची परिस्थिती स्फटिक स्वरूपात असणाऱ्या घन अवस्थेतील पदार्थाच्या रेणूमध्ये मिळते. स्फटिकातील सर्व अणू एका विशिष्ट आकृतिबंधात जालकाच्या स्वरूपात प्रस्थापित होतात, असे आढळते.
पदार्थाच्या तीन सामूहिक अवस्था : वायू अवस्थेमध्ये पदार्थाची घनता सगळ्यात कमी असते. या अवस्थेत कोणत्याही दोन रेणूंमधील सरासरी अंतर इतके जास्त असते की, त्यांचा एकमेकांवर प्रत्यक्ष यदृच्छरीत्या आघात होईतोपर्यंत त्यांमधील आकर्षणी प्रेरणेचे प्रमाण नगण्य असते. प्रयोगाने आढळणारे वायूचे सर्व गुणधर्म संख्यात्मक वायूच्या गत्यात्मक सिद्धांताच्या साहाय्याने [⟶ द्रव्याचा गत्यात्मक सिद्धांत] स्वरूपात विशद करता येतात. वायूच्या रेणूंच्या इतस्ततः गतीमुळे तो ज्या पात्रात ठेवलेला असेल त्याच्या भिंतीवर होणाऱ्या त्यांचा प्रत्यक्ष आघातांमुळे दाब निर्माण होतो, तर वायूमधील उष्णता संचयाचे प्रमाण त्यामधील रेणूंच्या सरासरी इतस्ततः गतिज ऊर्जा व आंतरिक ऊर्जा यांमुळे निश्चित होते, असे दाखविता येते. हायड्रोजन (H2) किंवा पाणी (H2O) हे रेणू संपूर्णपणे दृढ नसून त्यांमधील घटक अणू एकमेकांच्या सापेक्ष अल्प प्रमाणाच्या कंपन क्रिया पूर्ण करू शकतात, असे आढळते. या क्रियेमध्ये अणूचे त्याच्या मूळ स्थानापासून होणारे प्रत्यक्ष विचलन अल्प प्रमाणाचे असले, तरी तदनुरूप कंप्रता (दर सेकंदात होणाऱ्या कंपनांची संख्या) मात्र उच्च मूल्याची असते. याशिवाय संपर्ण रेणूला परिभ्रमण गती असू शकते, त्यामधील घटक अणुकेंद्रांना व इलेक्ट्रॉनांना परिवलन गतीसुद्धा असते, असे प्रयोगाने कळते. रेणूची गतीज ऊर्जा ही विचलन गती, परिभ्रमण गती, कंपन गती व परिवलन गती या चार प्रकारे उद्भवते. यांपैकी शेवटल्या तीन ऊर्जा प्रकारांनी मिळून रेणूंची आंतरिक ऊर्जा होते.
द्रव पदार्थातील रेणूंसाठी वायूप्रमाणेच अवकाशात नियुक्त अशी स्थाने नसतात. त्यामुळे त्यामधील रेणू द्रवाच्या एका भागातून दुसऱ्या भागाकडे सुलभपणे जाऊ शकतात (विसरण क्रिया) द्रवामधील कोणत्याही रेणूच्या सभोवताली इतर रेणू इतक्या जवळजवळ अंतरावर दाटीने उपस्थित असतात की, द्रवामध्ये रेणूंनी प्रत्यक्षपणे न व्यापलेल्या अशा घनफळाचे प्रमाण अगदी कमी असते. द्रवावर बाहेरून दाब लावला असता संपीडनाचे (संकोचनाचे) प्रमाण अत्यल्प का असते व लावलेला दाब सर्व दिशांत सारखा का संक्रामित केला जातो याचे विशदीकरण वरील वस्तुस्थितीवरून मिळते. द्रव रेणूच्या बाष्पीभवन क्रियेचा अभ्यास केल्यास असे दिसून येते की, बाष्पीभवन होणाऱ्या रेणूवर द्रवातील इतर रेणूंमुळे होणारी आकर्षणी प्रेरणा महत्त्वाची असते. रेणू जर द्रवाच्या खूप आत असेल, तर त्यावर द्रवातील इतर रेणूंमुळे उद्भवणारी आकर्षणी प्रेरणा शून्य मूल्याची असते, असे सममिती तत्त्वाचा उपयोग करून दाखविता येते. द्रवाच्या पृष्ठभागाजवळ असणाऱ्या रेणूकरिता मात्र ही परिस्थिती असत नाही. तेथील रेणूवर एक परिणामी प्रेरणा मिळते आणि रेणूला द्रवाच्या आत ओढून घेण्याकडे तिची प्रवृत्ती असते. या परिणामी प्रेरणेमुळे द्रवाच्या पृष्ठभागांवर पृष्ठताण मिळतो. क्ष-किरण विवर्तन पद्धतीचा [⟶ क्ष-किरण] उपयोग करून द्रवामधील रेणूंना सुद्धा स्फटिकातील रेणूंप्रमाणे एक अस्पष्ट आकृतिबंधानुसार अवकाश वितरण असते, असे दाखविता येते. घन अवस्थेतील पदार्थांमध्ये मात्र त्यांमधील रेणू हे जास्त नियमबद्ध रीतीने जालकाच्या स्वरूपात प्रस्थापित केलेले असतात. त्यामुळे घन पदार्थांतील रेणूसाठी कंपन, परिभ्रमण वा परिवलन या प्रकारच्या गती असू शकतात. स्फटिक जालकामधील आपले मूळचे स्थान सोडून विसरण क्रियेच्या द्वारे दुसऱ्या एखाद्या जागी जाणे घन पदार्थांतील रेणूला क्वचित प्रसंगीच शक्य होते. जालकातील रेणूच्या परिस्थितीचे वरील चित्रीकरण सार्थ आहे असे क्ष-किरण विश्लेषणाद्वारे दाखविता येते. पदार्थाच्या अवस्थेमध्ये जरी बदल झाला, तरी त्याच्या रेणूच्या आकारमानात, संरचनेत अथवा स्वरूपात विशेष असा फरक पडत नाही, असे प्रयोगाने कळते. उदा., वायुरूप आयोडीन रेणू (I2) च्या घटक अणूंमधील अंतर = २·६५ (१ म्हणजे अँगस्ट्रॉम = १०−८ सेंमी.] एवढे असते, तर घन अवस्थेतील याच रेणूंकरिता हे अंतर २·७० Åएवढे होते. अवरक्त (दृश्य वर्णपटातील तांबड्या रंगाच्या अलीकडील) किरणांच्या साहाय्याने बेंझीन रेणूचे विश्लेषण केल्यास बेंझीन वलयाच्या आकृतिबंधात अवस्थेतील बदलामुळे काही फरक पडत नाही, असे दाखविता येते.
आंतररेणवीय प्रेरणा व त्यांचे स्वरूप : विद्युत् भारित रेणूचा अपवाद सोडल्यास बहुतेक सर्व रेणू इतर रेणूंना आकर्षित करतात. रेणूंमधील अंतर जर एका ठराविक मर्यादेपेक्षा कमी झाले, तर या आकर्षणी प्रेरणेचे प्रतिसारक प्रेरणेत रूपांतर होते, असे प्रयोगाद्वारे आढळते. कोणत्याही दोन रेणूंमधील अंतर त्यांच्या व्हॅन डर व्हाल्स त्रिज्यांच्या (लगतच्या रेणूंमधील दोन अणू जास्तीत जास्त किती जवळ येऊ शकतात त्या अंतराच्या निम्म्या अंतराला जे. डी. व्हॅन डर व्हाल्स या डच शास्त्रज्ञांच्या नावावरून व्हॅन डर व्हाल्स त्रिज्या म्हणतात). बेरजेएवढे झाले असता त्यामधील प्रेरणा सामान्यपणे प्रतिसारक स्वरूपाची होऊ लागते, असे म्हणता येते. रेणूच्या व्हॅन डर व्हाल्स त्रिज्येचे मूल्य प्रयोगाद्वारे काढता येते. उदा., आयोडीन रेणूमधील दोन एकरूप अणूंकरिता ही त्रिज्या १·७७ Åएवढी आहे. या रेणूमधील घटक अणूंचे परस्परांपासूनचे प्रत्यक्ष अंतर १·३३ Åएवढे आहे असे आढळते. आयोडीन रेणूमधील अणूंना एकत्र बांधून ठेवणारी प्रेरणा व रेणु-रेणूमध्ये सामान्यपणे मिळणारी आकर्षणी प्रेरणा, या दोन प्रेरणा निरनिराळ्या विक्रियांद्वारे उद्भवत असाव्यात असा अंदाज वरील वस्तुस्थितीवरून बांधता येतो.

रेणु-रेणूमधील आकर्षणी प्रेरणा अनेक कारणांमुळे निर्माण होत असते. जर रेणूंना शाश्वत अथवा कायम स्वरूपाचे विद्युत् द्विध्रुवी परिबल (विद्युत् भार आणि त्याचा स्थान सदिश यांच्या गुणाकाराची येथे रेणूतील सर्व विद्युत् भारांकरिता घेतलेली सदिश बेरीज) असेल, तर त्यामुळे त्यांमध्ये परिणामी आकर्षणी प्रेरणा मिळते. आ. १ मध्ये अ व आ असे दोन रेणू दाखविले आहेत. या रेणूंना शाश्वत अथवा कायम स्वरूपाची विद्युत् परिबले आहेत असे मानले आहे. त्यांवरील विद्युत् भाराचा विन्यास पण आकृतीत दाखविला आहे. जर हे रेणू एकमेकांच्या सापेक्ष असममित अवस्थत असतील, तर त्यांच्या वरील विद्युत् भारामुळे त्यांमध्ये परिणामी आकर्षणी प्रेरणा निर्माण होईल, असे दाखविता येते. वरील मीमांसा रूढ भौतिकीप्रमाणे दिली आहे. पुंजयामिकीचा उपयोग करून एफ्. लंडन यांनी प्रथम रेणूमध्ये एक तिसऱ्या प्रकारची सुद्धा अपस्करण आकर्षणी प्रेरणा मिळते. असे दाखविले. रेणूच्या घटक अणूंमधील अंतर सामान्यपणे १०−८ सेंमी. या प्रमाणाचे असते, तर त्याचे विच्छेदन करण्याकरिता १−५ eV एवढी ऊर्जा पुरवावी लागते. यावरून रेणूमधील प्रेरणेचा पल्ला व तिचे मूल्य यांविषयीचा अंदाज करणे शक्य होते.
रेणुनिर्मिती व संयुजा : जेव्हा अणू एकमेकांच्या जवळ येऊन संलग्न होतात तेव्हा त्यांपासून रेणू निर्माण कसा होतो, हे विशद करण्याकरिता ⇨संयुजा ही संकल्पना पुढे आली. आधुनिक दृष्टिकोनाप्रमाणे ⇨आवर्त सारणीमधील (इलेक्ट्रॉन रचनेनुसार केलेल्या मूलद्रव्यांच्या कोष्टकरूप मांडणीमधील) मूलद्रव्यांचा अणूच्या संरचनेचा अभ्यास केल्यास असे आढळते की, संयुजांबंधाचे स्वरूप सामान्यपणे अणूच्या सर्वांत बाहेरच्या कवचात असणाऱ्या इलेक्ट्रॉनांच्या कृतीवर अथवा त्यांच्या संख्येवर अवलंबून असते. अणूचे संयुजा इलेक्ट्रॉन कवच पूर्णपणे भरण्याकरिता लागणाऱ्या इलेक्ट्रॉनांच्या संख्येपेक्षा कमी इलेक्ट्रॉन जर कवचामध्ये असले, तर दुसऱ्या अणूच्या बरोबर देवघेव करून ही संख्या पुरी करण्याकडे प्रत्येक अणूची प्रवृत्ती असते. उदा., सोडियमाच्या सर्वांत बाहेरच्या म्हणजे संयुजा इलेक्ट्रॉन कवचात फक्त एकच इलेक्ट्रॉन असतो. त्यामुळे तो गमावून सोडियम अणूला स्थिर स्थितीकडे जाता येते. याउलट क्लोरिनाच्या संयुजा कवचात सात इलेक्ट्रॉन असल्यामुळे दुसऱ्या अणूकडून आणखी एक इलेक्ट्रॉन हस्तगत करून स्थैर्याकरिता सागणारी इलेक्ट्रॉनांची आठ ही संख्या पुरी करता येते. त्यामुळे सोडियम व क्लोरीन अणू जर एकमेकांच्या जवळ आले, तर सोडियमामधील एक इलेक्ट्रॉन क्लोरिनाकडे वर्ग केला जातो. उरलेल्या दोन अणूंवर विरुद्ध चिन्हाचे विद्युत् भार झाल्यामुळे त्यांमधील विद्युत् स्थितिक आकर्षणामुळे ते एकत्रित येऊन NaCl हा रेणू निर्माण करतात. याप्रकारे होणाऱ्या बंधाला विद्युत् संयुजी किंवा आयनी बंध म्हणतात. या विक्रियेमधील पहिल्या टप्प्यात अणूमध्ये इलेक्ट्रॉनाची देवघेव होऊन दोन अणूंचे आयनांमध्ये प्रथम रूपांतर होते. याउलट जर दोन क्लोरीन अणू एकमेकांजवळ आले, तर त्यापैकी प्रत्येकाला एक इलेक्ट्रॉन हस्तगत करण्याची आवश्यकता असल्यामुळे, प्रत्येक अणूमधील एकेक इलेक्ट्रॉन समाईक रीतीने वापरला जातो. या क्रियेमुळे अणूवरील मूळ विद्युत् भारात कोणताही फरक पडत नाही. इलेक्ट्रॉनांची परस्पर देवाणघेवाण झाल्यामुळे घटक अणूंमध्ये मात्र विनिमय आकर्षणी प्रेरणा निर्माण होऊन त्यामुळे रेणूची निर्मिती होते. हे आकर्षण विद्युत् स्थितिक स्वरूपाचे असत नाही. इलेक्ट्रॉन विनिमय क्रियेमुळे निर्माण झालेल्या विनिमय प्रेरणेचे विशदीकरण पुंजयामिकीचा उपयोग केल्यानंतरच करता येतो. अशा बंधाला सहसंयुजी बंध असे म्हणतात. याशिवाय इतर कारणांमुळे सुद्धा बंध निर्माण होऊ शकतो. दोन निकट अणूंमध्ये चार किंवा सहा समाईक इलेक्ट्रॉन असतील, तर त्यामुळे अनुक्रमे द्विबंध व त्रिबंध निर्माण होतात, असे दाखविता येते. वर वर्णन केलेले रासायनिक बंध निर्मितीच्या प्रकारांचे विशदीकरण हे सुलभीकृत रीतीने दिलेले आहे.
काही रेणू एकमेकांजवळ आणले असता त्यांमध्ये असणाऱ्या प्रेरणेमुळे अनेक प्रकारांच्या रासायनिक विक्रिया घडून येतात. या विक्रया मुख्यत्वे करून तीन प्रकारच्या असतात : (१) समघटकीकरण : या प्रकारामध्ये संयुगाच्या रासायनिक सूत्रात फरक पडत नाही. त्यामधील घटक अणूंच्या बंधामध्ये पुनर्विन्यास (पुन्हा मांडणी) झाल्यामुळे संयुगाच्या गुणधर्मांत बदल घडून येतो. अमोनियम सायनेटाचे यूरियामध्ये रूपांतर ही या प्रकारची एक महत्त्वाची अशी विक्रिया फ्रीड्रिख व्हलर यांनी जर्मनीमध्ये १८२८ साली संशोधिली, [⟶ समघटकीकरण]. (२) प्रतिष्ठापन विक्रिया : हिच्यात रेणूमधील काही घटक अणूंऐवजी फक्त दुसरे अणू, रेणू अथवा अणुगट प्रस्थापित केले जातात. निओपॅटेन (C5H12) या रेणूच्या मिथिल गटामधील (CH3−) हायड्रोजन अणूंच्याऐवजी इतर अणू किंवा अणुगट यांची प्रस्थापना केल्यास या प्रकारची विक्रिया घडून येते. जर R = (CH3)3 C− धरले तर या विक्रियेत खाली दर्शविलेले बदल मिळतात.
RCH3 → RCH2Cl → RCH2MgCl → RCH2CO2H → RCH2NH2.
(३) समावेशक विक्रिया : या तिसऱ्या प्रकारामध्ये रेणूमधील मूळ घटकांमध्ये अतिरिक्त अणूंचा समावेश केला जातो. उदा., एथिलिनाचे एथेनामध्ये [(C2H4) → (C2H6)].
रेणूविषयीचे संपूर्ण ज्ञान होण्याकरिता पुढील माहिती असणे आवश्यक असते : (१) रेणूकरिता मूलद्रव्य प्रमाणदर्शी सूत्र उदा., पाण्याकरिता H2O असे मूलद्रव्य प्रमाणदर्शी सूत्र देता येते. (२) समतोल अवस्थेत घटक अणूंचे सरासरी अवकाश वितरण. (३) गतिकीय अवस्था. दुसऱ्या प्रकारची माहिती प्राथमिक स्तरावर भूमितीय परिभाषेचा उपयोग करून देता येते. उदा., कार्बन टेट्राक्लोराइड हा रेणू रेखीव चतुष्फलक आकारचा आहे, त्यामध्ये चार क्लोरीन अणू चार टोकांस असून कार्बन अणू त्याच्या मध्यभागी आहे, असे वर्णन करता येते. कार्बन टेट्राक्लोराइडामध्ये चारही बंधांची लांबी एकसारखी असून तिचे प्रमाण १·७७ Åएवढे असते, तर त्यांमधील कोन १०९०२८¢एवढा आहे, असे नमूद केल्यास ही माहिती निश्चित स्वरूपाची होते. सामान्यपणे रेणूंच्या संरचनेमधील सममितीचे प्रमाण जेवढे कमी प्रतीचे त्या प्रमाणात त्याविषयीचे ज्ञान निश्चित करण्याकरिता लागणाऱ्या स्वतंत्र प्रचलांची (विशिष्ट परिस्थितीत अचल राहणाऱ्या राशींची) संख्या जास्त होते. रेणूमध्ये असणारी सममिती व रेणूमधील आंतरिक परिमाणे यांबद्दलचे ज्ञान वर्णपटविज्ञान, इलेक्ट्रॉन वा न्यूट्रॉन अथवा क्ष-किरण विवर्तन इ. प्रयोगांद्वारे मिळविता येते. रेणूची गतिकीय अवस्था ही त्यामधील अणू वा अणुकेंद्रे यांचे कंपन व परिभ्रमण, त्यांमधील इलेक्ट्रॉनांच्या अक्षीय व परिवलन गती यासंबंधीच्या प्रचलांवरून निश्चित होते. रेणवीय वर्णपटविज्ञान, द्विध्रुवी परिबल, रेणवीय शलाका इ. पद्धतींचा उपयोग करून या प्रचलांची मूल्ये निश्चित केली जातात.
रेणवीय आकार व आकारमान : रेणूचे निरपेक्ष द्रव्यमान व त्याचे आकारमान यांचे मापन करण्याकरिता विशेष संवेदनशील अशा भौतिकीय मापन पद्धतीचा उपयोग करावा लागतो. भौतिकीमधील निरनिराळ्या शाखांमधील प्रयोगांद्वारे बहुसंख्य रेणू काही अँगस्ट्रॉम त्रिज्या असणाऱ्या गोलकाप्रमाणे कार्य करतात, असे कळते. बहुतेक सर्व रेणूंची द्रव्यमानमूल्ये १०−२३ ते १०−२० ग्रॅ. या मर्यादेत आढळतात. प्रथिनांसारखे असे काही रेणू आहेत की, इलेक्ट्रॉन सूक्ष्मदर्शकाच्या साहाय्याने त्यांचे प्रत्यक्ष निरीक्षणही करता येते.
घटक अणूंची वा रेणूंची संख्या व आकारमान यांवर त्यांपासून निर्माण झालेल्या रेणूचे आकारमान साहजिकच अवलंबून असते. द्वि-आणवीय रेणू हा प्रकार सर्वांत वर्णन करण्यास सोपा आहे. प्रत्येक अणू गोलीय आकाराचा असून त्याला एक ठराविक (व्हॅन डर व्हाल्स) कार्यकारी त्रिज्या असते, असे मानता येते. रेणूमधील दोन अणू एकमेकांस जेथे प्रत्यक्ष स्पर्श करतात तेथील त्या दोघांचेही पृष्ठभाग मात्र थोडेफार सपाट होतात. त्यांमधील समतोल स्थितीमधले अंतर Re याने दर्शविले, तर Re मूल्य (r1 + r2) पेक्षा नेहमीच कमी असते (r1, r2 = दोन अणूंच्या व्हॅन डर व्हाल्स त्रिज्या). हायड्रोजन रेणू (H3) करिता r1 = r2 = १·२ Å, तर Re = ०·७४ Å या मूल्याची असते. रेणूचा आकार त्यामधील अणूच्या विन्यासावर सुद्धा काही प्रमाणात अवलंबून असतो. उदा., पाण्याच्या रेणूमध्ये H, O, H हे तीन अणू दोन रेषीय बंधांनी एकमेकांशी जोडले गेले असून त्यांमध्ये १०५ अंशांचा कोन असतो.
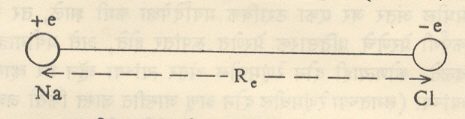
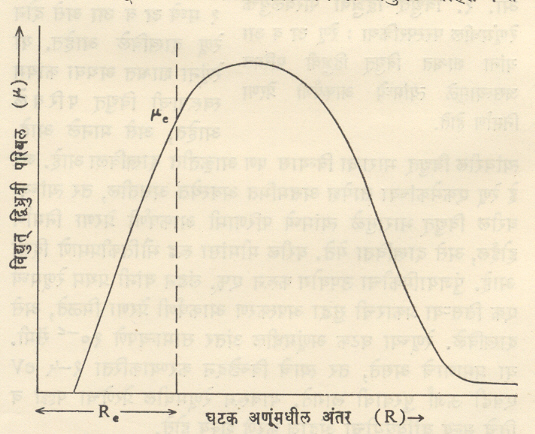
विध्रुत् द्विध्रुवी परिबल : बऱ्याच रेणूंना विद्युत् द्विध्रुवी परिबल (वि. द्वि. प.) असते. अणूमध्ये पुंजयामिकीप्रमाणे मिळणारे इलेक्ट्रॉन वितरण हे अणुकेंद्राभोवती सममित रीतीने पसरलेले आहे. वितरणाचे विद्युत् केंद्र व (धन विद्युत् भारित) अणुकेंद्र यांची स्थाने एकच असतात. त्यामुळे अणूला कायम स्वरूपाचे शून्य मूल्याचे वि. द्वि. प. असते. रेणूमध्ये परस्परक्रियेमुळे ही सममिती भंग पावते व त्यामुळे वि. द्वि. प. निर्माण होते. या परिणामाचे वर्णन Nacl या द्वि आणवीय रेणूच्या संदर्भात करणे सुलभ ठरते. Nacl मधील रासायनिक बंध आयनी प्रकारचा आहे त्यामुळे त्यामधील विद्युत् भार विन्यास आ. २ मध्ये दाखविल्याप्रमाणे असतो. या परिस्थितीकरिता वि. द्वि. प. = µ = eRe इलेक्ट्रॉनावरचा विद्युत् भार = e = ४·८ X १०−१० विद्युत् स्थितिक एकक. सामान्यपणे Re ≈१ Åअसल्यामुळे µ≈४·८ × १०−१८ विद्युत् स्थितिक एकक ४·८ ≈ D (डेबाय एकक). जेव्हा रेणू कंप पावतो तेव्हा वि. द्वि. प. चे मूल्य बदलते. हा बदल आ. ३ मध्ये दाखविला आहे. आकृतीमध्ये Re = घटक अणूंमधील समतोल अवस्थेत असणारे अंतर, µe = समतोल अवस्थेतील वि. द्वि. प. चे मूल्य.
वरील वर्णनात खालील गृहीते मानली आहेत : (१) रेणूतील विद्युत् भार बिंदुरूपात असतात. (२) रेणूमधील फक्त बंधक इलेक्ट्रॉनामुळे वि. द्वि. प. निर्माण होते. प्रत्यक्षात रेणूच्या घटक अणूंमधील इतर इलेक्ट्रॉनसुद्धा याकरिता साहाय्यभूत होतात. सहसंयुजी बंधाकरिता सुद्धा या प्रकारचा परिणाम कमीजास्त प्रमाणात घडून येतो. H2, N2, CO2 यांसारख्या रेणूंमध्ये एक प्रकारची इलेक्ट्रॉन स्थानच्युती होते असे दिसून येते पण ही स्थानच्युती इतक्या सममित प्रकारे होते की, त्यामुळे वि. द्वि. प. निर्माण होत नाही. रेणूच्या वि. द्वि. प. चे अचूक गणन पुंजयामिकीचा उपयोग करून करता येते पण विवध प्रकारच्या रेणूंच्या वि. द्वि. प. चे प्रयोगाद्वारे मापन करून त्यांचा परस्परसंबंध रेणूच्या ज्ञात संरचनेशी जोडणे हे जास्त सोपे ठरते.
विशिष्ट रासायनिक बंध, अणुगट इत्यादींमुळे मिळणारे परिबल हे सदिश (महत्ता व दिशा हे दोन्ही असलेली राशी) असते. कोणत्याही जटिल रेणूमध्ये कोणकोणते घटक बंध वा अणुगट आहेत व ते संरचनेत कोणत्या जागी कसे प्रस्थापित केले आहेत हे जर प्रयोगाने माहीत झाले, तर या प्रत्येक घटकाकरिता असणारे विशिष्ट सदिश परिबल विचारात घेऊन त्यावरून समग्र रेणूकरिता परिणामी परिबलाचे गणन करणे अवघड नसते. अशा प्रकारे गणन केलेले परिबलाचे मूल्य पुरेशा अचूक रीतीने प्रयोगांनी मिळालेल्या मूल्याशी एकरूप आढळते. उदा., बेंझिनामध्ये एका हायड्रोजनाच्या बदली एक क्लोरीन अणू बसविला, तर त्यामुळे निर्माण होणाऱ्या क्लोरोबेंझीन रेणूमध्ये १·७०D या मूल्याचे वि. द्वि. प. निर्माण होते, असे या पद्धतीने दाखविता येते. हे परिबल C–Cl या बंधामुळे निर्माण होते, असे सिद्ध करता येते. याच तत्त्वाचा उपयोग केला असता ऑर्थो, मेटा व पॅरा डायक्लोरोबेंझीन (C6H4Cl3) करिता अनुक्रमे २·९४, १·७० आणि ०D या मूल्यांची वि. द्वि. प. असली पाहिजेत, असे कळते. प्रयोगाने या संयुगांकरिता २·५३, १·६७ व ०D एवढी मूल्ये मिळतात.
रेणवीय ध्रुवीयता : वर वर्णन केलेले शाश्वत स्वरूपाचे वि. द्वि. प. काही रेणूंनाच असते. याउलट बाह्य क्षेत्र लावले असता रेणूमधील अंतर्गत इलेक्ट्रॉन एका बाजूस विचलित होतात, तर त्यांमधील धन विद्युत् भारवाही अणुकेंद्रे त्याच्या बरोबर विरुद्ध दिशेत ढकलली जातात. यामुळे रेणूमध्ये प्रवर्तित प्रकारचे अल्प वि. द्वि. प. निर्माण होते. ही क्रिया सर्व रेणूंमध्ये घडून येते. या क्रियेस ध्रुवीकरण असे म्हणतात. भिन्न रेणूंमध्ये ध्रुवीकरणाचे प्रमाण निरनिराळे असते व त्याचे मापन रेणवीय ध्रुवीयता या राशीच्या साहाय्याने केले जाते. एकक बलाचे बाह्य विद्युत् क्षेत्र लावले असता प्रत्येक रेणूमध्ये अशा प्रकारे निर्माण होणाऱ्या प्रवर्तित वि. द्वि. प. च्या मूल्यास रेणवीय ध्रुवीयता म्हणतात. रेणूमधील घटकांमध्ये असणाऱ्या प्रत्येक रासायनिक बंधाकरिता एक विशिष्ट मूल्याची ध्रुवीयता नियुक्त करून यावरून समग्र रेणूकरिता परिणामी ध्रुवीयतेचे गणन करता येते. पदार्थावर जर E मूल्याचे विद्युत् क्षेत्र बाहेरून लावले, तर यामुळे रेणूला प्रवर्तित वि. द्वि. प. µप्राप्त होते, हे परिबल विद्युत् क्षेत्राच्या रेषीय प्रमाणात बदलत असल्यामुळे µ = µ E असे सूत्र मांडता येते. या सूत्रात ∝ = रेणूची ध्रुवीयता आहे. एक विद्युत् स्थितिक एकक मूल्याच्या क्षेत्राकरिता या परिबलाचे प्रमाण सामान्यतः १०−२३ विद्युत् स्थितिक एकक किंवा १०−५ D एवढे असते (१ D = १०−१८ स्थिर विद्युत् एकक). या परिबलाची दिशा ही सामान्यपणे क्षेत्राच्या दिशेपेक्षा भिन्न असू शकते, असे आढळते. हा परिणामसुद्धा समदिक् नसतो म्हणजे ध्रुवीयतेचे मूल्य निरनिराळ्या दिशांत भिन्न असू शकते.
रेणू व प्रकाश प्रारण (तरंगरूपी ऊर्जा) यांमधील परस्परक्रियेचे स्वरूप रेणवीय परिबलाच्या मूल्यावरून ठरते, हे लक्षात ठेवण्याजोगते आहे. रेणूद्वारे प्रकाशाचे उत्सर्जन, शोषण व प्रकीर्णन (विखुरणे) या परस्परक्रिया होत असतात. या सर्वात परिणाम रेणूच्या परिबलावरून निश्चित होत असते.
विद्युत् अपार्यता स्थिरांक : ध्रुवीयता व वि. द्वि. प. यांमध्ये घनिष्ठ संबंध असतो. पदार्थाचे विद्युत् गुणधर्म रेणूच्या वि. द्वि. प. मुळे (कायम अथवा प्रवर्तित) निश्चित होतात. विद्युत् क्षेत्रामध्ये ⇨विद्युत् अपारक पदार्थ आणला असता त्यामध्ये घट होते. क्षेत्रात होणारी ही घट दोन प्रकारे होऊ शकते. पहिला परिणाम विकृती ध्रुवीकरणामुळे निर्माण होतो. उपयोजित F या विद्युत् क्षेत्रामुळे रेणूमधील अंतर्गत इलेक्ट्रॉन वितरणावर परिणाम घडून त्यामुळे रेणूला वि. द्वि. प. µ m प्राप्त होते. येथे m = µpF आणि µp = रेणूची ध्रुवीयता असून m याचे मूल्य पदार्थाच्या तापमानावर अवलंबून नसते. आता जर पदार्थांमधील रेणूंना शाश्वत स्वरूपाचेही वि. द्वि. प. असेल, तर उपयोजित क्षेत्रामुळे प्रत्येक रेणूवर त्यामुळे एक प्रेरणा कार्यान्वित होऊन रेणूच्या सदिश द्विध्रुवी परिबलाच्या दिशा क्षेत्रदिशेशी समांतर करण्याचा ती प्रयत्न करते. याउलट ऊष्मीय हालचालीमुळे रेणूंचे एकमेकांबरोबर जे परस्पर आघात होतात, त्यांमुळे या परिबलाच्या दिशांची मांडणी इतस्ततः करण्याकडे प्रवृत्ती असते. पदार्थामध्ये प्रत्यक्षात जी मांडणी अस्तित्वात येते ती या वरील दोन विरुद्ध स्पर्धक क्रियांचाच परिपोष असते. परिणामी प्रत्येक रेणूला विद्युत् क्षेत्र दिशेत एक सरासरी मूल्याचे परिबल मिळते. या परिणामामुळे प्रत्येक रेणूची दिकविन्यास ध्रुवीयता खालील सूत्राने मिळते असे दाखविता येते.
|
∝० |
= |
µ2 |
… … … (१) |
|
3kT |
येथे µ = रेणूचे शाश्वत वि. द्वि. प., k = बोल्टसमान स्थिरांक (एल्. वोल्टसमान या भौतिकीविज्ञांच्या नावावरून ओळखण्यात येणारा स्थिरांक), T = पदार्थाचे तापमान. या परिस्थितीत पदार्थाची रेणुभारात्मक ध्रुवीयता (प्रती ग्रॅम – मोल) खालीलप्रमाणे मिळते.
|
Pm |
= |
4 π N० |
( |
∝P |
+ |
µ 2 |
) |
… … (२) |
|
3 |
3kT |
येथे N० = ॲव्हागाड्रो स्थिरांक (आमेडेओ अँव्होगाड्रो या भौतिकीविज्ञांच्या नावाने ओळखण्यात येणारी, पदार्थांच्या ग्रॅम रेणुभारातील रेणूंची संख्या). वायू व अध्रुवीय (ज्यात शाश्वत वि. द्वि. प. नाही अशा) विद्रावकामधील (विरघळणाऱ्या द्रवातील) विरल विद्राव यांकरिता खाली दिलेले आर्. जे. ई. क्लॉसियस व ओ. एफ. मसोती यांचे सूत्र मिळते.
|
Pm = ( |
∊−1 ∊+2 |
) |
m d |
= |
4πN० 3 |
( |
∝P + |
µ2 3kT |
) |
… … (3) |
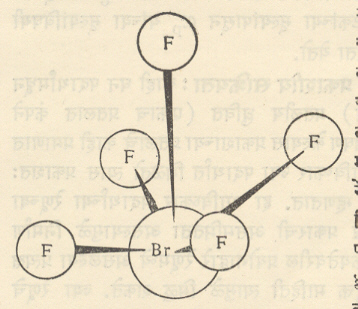 येथे (∊= विद्युत् अपार्यता स्थिरांक [→ विद्युत् अपारक पदार्थ], m = पदार्थाचा रेणुभार, d = पदार्थाची घनता, ∝P व µ यांची मूल्ये प्रयोगाने काढण्याकरिता सामान्यपणे दोन पद्धती वापरल्या जातात. या दोन्ही पद्धतींत विद्युत् अपार्यतेचे मापन करून त्यापासून रेणुभारात्मक ध्रुवीयता मिळविली जाते. पहिल्या पद्धतीत ध्रुवीयतेचे (Pm) तापमानाबरोबरचे चलन प्रयोगाने मोजले जाते. या प्रदत्तापासून (माहितीपासून) वरील सूत्राचा (BrF5) वि. द्वि. प. १·५२ D एवढे आहे, असे दिसून आले आहे. या वि. द्वि. प. मुळे त्याच्या रेणूच्या संभाव्य सममितीवर निर्बंध पडतात. आ. ४ मध्ये दाखविलेली फक्त संरचना प्रदत्ताशी सुसंगत आहे, असे दाखविता येते.
येथे (∊= विद्युत् अपार्यता स्थिरांक [→ विद्युत् अपारक पदार्थ], m = पदार्थाचा रेणुभार, d = पदार्थाची घनता, ∝P व µ यांची मूल्ये प्रयोगाने काढण्याकरिता सामान्यपणे दोन पद्धती वापरल्या जातात. या दोन्ही पद्धतींत विद्युत् अपार्यतेचे मापन करून त्यापासून रेणुभारात्मक ध्रुवीयता मिळविली जाते. पहिल्या पद्धतीत ध्रुवीयतेचे (Pm) तापमानाबरोबरचे चलन प्रयोगाने मोजले जाते. या प्रदत्तापासून (माहितीपासून) वरील सूत्राचा (BrF5) वि. द्वि. प. १·५२ D एवढे आहे, असे दिसून आले आहे. या वि. द्वि. प. मुळे त्याच्या रेणूच्या संभाव्य सममितीवर निर्बंध पडतात. आ. ४ मध्ये दाखविलेली फक्त संरचना प्रदत्ताशी सुसंगत आहे, असे दाखविता येते.
प्रयोगात वापरलेल्या तापमानाच्या मर्यादेत सगळ्याच पदार्थांना स्थैर्य असतेच असे नाही. त्यामुळे प्रयोगाद्वारे µ व Pm यांची मूल्ये काढण्याकरता दुसरी पर्यायी पद्धत वापरतात. या पद्धतीकरिता वापरलेल्या मीमांसेत विकृती ध्रुवीयता (Pm) ∝ यामध्ये (Pm)e व (Pm)A हे अनुक्रमे इलेक्ट्रॉन व अणू यांच्या विचलनामुळे दोन घटक निर्माण होतात, असे मानले जाते. त्यामुळे समग्र रेणुभारात्मक ध्रुवीयता
Pm=(Pm)e +(Pm)A + Po … … (४)
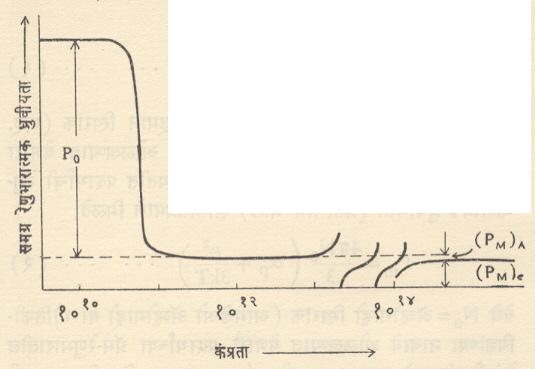 या स्वरूपात मांडता येते (Po = दिक्विन्यास ध्रुवीयता घटक). या तीन ध्रुवीयता घटकांशी संबंधित असलेल्या निरूढीची (जडत्वाची) मूल्ये भिन्न असल्यामुळे त्यांचा प्रत्यावर्ती (दर सेकंदास अनेक वेळा दिशा व मूल्य उलटसुलट होणाऱ्या) विद्युत् क्षेत्राकरिता मिळणारा प्रतिसाद निरनिराळा होतो म्हणून तिचे विद्युत् क्षेत्र कंप्रतेबरोबरच चलन प्रयोगाद्वारे मिळविल्यास, त्यापासून या तीन घटकांचे परिणाम एकमेकांपासून वेगळे करणे किंवा त्यांची मूल्ये निश्चित करणे शक्य होते. आ. ५ वरून वरील वर्णन स्पष्ट होते.
या स्वरूपात मांडता येते (Po = दिक्विन्यास ध्रुवीयता घटक). या तीन ध्रुवीयता घटकांशी संबंधित असलेल्या निरूढीची (जडत्वाची) मूल्ये भिन्न असल्यामुळे त्यांचा प्रत्यावर्ती (दर सेकंदास अनेक वेळा दिशा व मूल्य उलटसुलट होणाऱ्या) विद्युत् क्षेत्राकरिता मिळणारा प्रतिसाद निरनिराळा होतो म्हणून तिचे विद्युत् क्षेत्र कंप्रतेबरोबरच चलन प्रयोगाद्वारे मिळविल्यास, त्यापासून या तीन घटकांचे परिणाम एकमेकांपासून वेगळे करणे किंवा त्यांची मूल्ये निश्चित करणे शक्य होते. आ. ५ वरून वरील वर्णन स्पष्ट होते.
क्षेत्राची कंप्रता वाढवीत गेल्यास एका ठराविक कंप्रता मर्यादेनंतर रेणूच्या परिबलाचा दिक्विन्यास होत नाही आणि त्यामुळे Pm मधील Po या घटकाचा लोप होतो. कंप्रतेमध्ये आणखी वाढ केल्यास [(Pm)A] हा घटक लोप पावतो. अतिउच्च कंप्रतेकरिता फक्त [(Pm)e] हा घटकच शिल्लक राहतो. अशा प्रकारे [(Pm)e], [(Pm)A] व Po या घटकांचे मापन करता येते. Po च्या मूल्यावरून µव इतर घटकांच्या मूल्यापासून µP यांच्या मूल्यांविषयी संख्यात्मक अंदाज करता येतो.
रेणू सममिती व प्रकाशीय सक्रियता : काही घन पदार्थांमधून (किंवा विद्रावांमधून) प्रतलीय ध्रुवित (एकाच प्रतलात कंपने होणाऱ्या) प्रकाशाचे प्रेषण केल्यास प्रकाशाच्या प्रतलाचे काही प्रमाणात परिभ्रमण होते, हा आविष्कार ज्या पदार्थात मिळतो त्यास प्रकाशतः सक्रिय पदार्थ असे म्हणतात. हा आविष्कार पदार्थांच्या रेणूच्या संरचनेत एक विशिष्ट प्रकारची असममितता असल्यामुळे निर्माण होतो. प्रकाशीय सक्रियतेवरील प्रयोगाद्वारे रेणूमध्ये असलेल्या प्रत्यक्ष सममितीविषयी उपयुक्त माहिती त्यामुळे मिळू शकते. ज्या रेणूचे आरशामधील प्रतिबिंब मूळ रेणूवर अध्यारोपित करता येत नाही अशा रेणूकरिता प्रकाशीय सक्रियता मिळते. आरशातील प्रतिबिंबात पार्श्विक पर्यसन होत असल्यामुळे असा पर्यसनाने ज्या रेणूच्या संरचनेत बदल झालेला दिसतो अशाच रेणूकरिता हा आविष्कार अनुभवास येतो. या आविष्काराची मीमांसा करताना पदार्थावरील पृथक् रेणूचे दिक्विन्यास काहीही असले, तरी सबंध समूह एक मोठा रेणू असे समजून या समूहाच्या गुणधर्माचे वर्णन केले जाते. या मोठ्या समतुल्य रेणूचे गुणधर्म एकरूप असतात, असे या ठिकाणी समजले जाते. एका मध्यवर्ती कार्बन अणूभोवती असलेल्या चतुष्फलकाच्या चार टोकांशी ज्यामध्ये (परस्परांपासून) भिन्न असे चार प्रकारांचे अणू किंवा अणुगट आहेत असा रेणू हे या प्रकारच्या रेणूचे सर्वांत सोपे असे उदाहरण आहे. [⟶ त्रिमितीय रसायनशास्त्र ध्रुवणमिति ].
रेणवीय संरचना संशोधना पद्धती : काही काळापूर्वी रेणवीय संरचनेविषयीचे अंदाज मुख्यत्वेकरून पदार्थाचे स्थूलमानीय गुणधर्म (उदा., विद्युत् अपार्यता स्थिरांक, विद्युत् द्विध्रुवी परिबल) किंवा संयुगांच्या रासायनिक विक्रिया यांच्यावरच आधारलेले असत. वर्णपटविज्ञान व विवर्तन (क्ष-किरण व इलेक्ट्रॉन यांच्याद्वारे) ही आधुनिक तंत्रे वापरली असता रेणवीय संरचनेविषयी जास्त तपशीलवार असे ज्ञान होते. रेणवीय संरचनेविषयी माहिती मिळविण्याकरिता ज्या अनेक संवेदनशील व अचूक अशा पद्धती अलीकडे उपलब्ध झाल्या आहेत. त्यांपैकी महत्त्वाच्या पद्धतीचे वर्णन खाली दिले आहे.
इलेक्ट्रॉन विवर्तन : एकसमान गतिज ऊर्जा असलेल्या इलेक्ट्रॉनांची शलाका पदार्थांच्या रेणूमधून गेली असता तिचे विवर्तन (मार्गातील अडथळ्याच्या कडेवरून जाताना दिशाबदल होणे) होते. इलेक्ट्रॉन शलाकेकरिता पदार्थामधून भेदून जाण्याची क्षमता कमी असल्यामुळे ही पद्धत बहुतांशी वायूंच्या रेणूंचे संशोधन करण्याकरिताच उपयोगी पडते. वायू अवस्थेमध्ये रेणूंमधील सरासरी अंतर खूप असल्यामुळे रेणूमधील अणूंच्या अंतर्गत विन्यासामुळे विवर्तनाचा आकृतिबंध निश्चित होत असतो. या पद्धतीमध्ये एक विशिष्ट रेणवीय संरचना गृहीत धरून निरनिराळ्या दिशांत मिळणाऱ्या विवर्तनीय इलेक्ट्रॉनांच्या तीव्रतेचे (म्हणजेच त्यांच्या संख्येचे) गणन केले जाते. गणित करून मिळालेल्या संख्येची प्रयोगान्ती मिळालेल्या संख्येशी तुलना करून गृहीत धरलेल्या रेणवीय संरचनेच्या प्रतिकृतीच्या यथार्थतेविषयी अंदाज घेतला जातो.
क्ष-किरण व न्यूट्रॉन विवर्तन : सामान्यपणे टक्केवारीने विचार केल्यास पदार्थामध्ये होणाऱ्या क्ष किरणांच्या विवर्तनाचे प्रमाण इलेक्ट्रॉन विवर्तनापेक्षा पुष्कळच कमी असते. त्यामुळे क्ष-किरण पदार्थाच्या आत खोल अंतरापर्यंत प्रवेश करू शकतात. घनअवस्थी स्फटिक जालकामधील रेणूच्या (अणूंच्या) विन्यासाचा अभ्यास क्ष-किरण विवर्तनामुळे सहज करता येतो.
स्फटिकाच्या एकक कोशाचा आकार व स्वरूप यांमुळे क्ष-किरण विवर्तन महत्तम मूल्यांचा भूमितीय आकृतिबंध निश्चित होत असतो. क्ष-किरण विवर्तन छायाचित्रामध्ये महत्तम मूल्य स्थाने ठिपक्यांनी निर्देशित केली जातात. विवर्तन महत्तम मूल्याची तीव्रता या कोशात असणाऱ्या अणूंची संख्या, त्यांचे स्वरूप व वितरण यांवर अवलंबून राहते (आ. ६).
चुकतमापत पद्धतीचा उपयोग करून प्रयोगाने मिळालेल्या विवर्तन आकृतिबंधाची तुलना वाजवी गृहितांवर आधारलेल्या व गणितीय रीत्या मिळालेल्या आकृतिबंधाची करून रेणवीय संरचना निश्चित करता येते.
क्ष-किरण विवर्तनामुळे रेणूमधील भिन्न ठिकाणी असणाऱ्या इलेक्ट्रॉन घनतेविषयीचे ज्ञान मिळते. आधुनिक भौतिकीप्रमाणे रेणूमधील इलेक्ट्रॉनांचे निर्देशन एक प्रकारचा ऋण विद्युत् भार मेघ अशा स्वरूपात करण्यात येते. रेणूच्या निरनिराळ्या भागांतील वा मेघाची घनता क्ष-किरण विवर्तनापासून मिळू शकते.
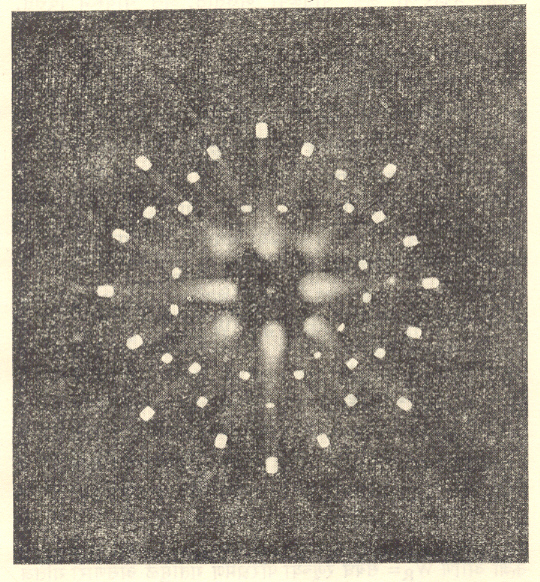
क्ष-किरण विवर्तन प्रयोगांवरून रेणूकरिता इलेक्ट्रॉन घनता वितरण काढण्याच्या पद्धतीत अनेक टप्पे असतात. कोणत्याही एका विवक्षित दिशेत विवर्तित होणाऱ्या क्ष-किरण शलाकेला एक विशेषक तीव्रता (अथवा परमप्रसर म्हणजे स्थिर स्थितीपासून असणारे महत्तम स्थलांतर) असते व त्यामधील प्रारणाच्या कलेस (एखाद्या संदर्भाच्या सापेक्ष असणाऱ्या अवस्थेस) एक विशिष्ट मूल्य असते. प्रयोगाने फक्त तीव्रतेबद्दलचा अचूक व निश्चित असा प्रदत्त मिळतो. निरनिराळ्या दिशांतील कलेचे मूल्य निश्चित करण्याकरिता (१) सममिती मीमांसा, (२) सांख्यिकीय (संख्याशास्त्रीय) पद्धती, (३) ज्ञात अणूच्याबाबतीतील प्रारंभिक मूल्ये इ. गोष्टींचा उपयोग करण्यात येतो. भिन्न दिशांत विवर्तन पावणाऱ्या क्ष-किरण शलाकेकरिता योग्य असे कलासंबंध प्रस्थापित करता आले, तर त्यांपासून त्रिमितीय इलेक्ट्रॉन घनता नकाशे मिळविता येतात. अशा रीतीने रेणूची संरचना निश्चित करता येते. विसापेक्षा जास्त घटक अणुसंख्या असणाऱ्या रेणूची वरील प्रकारे संरचना निश्चित करणे, संगणकाच्या शोधापूर्वी शक्य नव्हते. संगणकाच्या साहाय्याने आधुनिक काळात शंभर घटक अणुसंख्या असणाऱ्या रेणूच्या एकाकी स्फटिकावर प्रयोग करून त्याची संरचना अगदी सुलभपणे निर्धारित करता येते.
डी. हॉजकिन व त्यांचे सहाध्यायी यांनी वर वर्णन केलेली रीत वापरून ब१२ जीवनसत्वाची संरचना निश्चित केली. या शोधाबद्दल त्यांना १९६४ सालचे नोबेल पारितोषिक देण्यात आले. जे. सी. केंड्र्यू व माक्स पेरूट्झ यांना मायोग्लोबिन व हीमोग्लोबिन (रक्तारुण) या प्रथिनांची संरचना शोधून काढल्याबद्दल १९६२ सालचे नोबेल पारितोषिक मिळाले. एम्. एच्. एफ्. विल्फिन्झ यांनी क्ष-किरण विवर्तन पद्धतीचा उपयोग करून डीएनएच्या (डीऑक्सिरिबोन्यूक्लिइक अम्लाच्या) रेणूविषयी केलेल्या अभ्यासामुळे त्याची रेणवीय संरचना निश्चित करण्यास मदत झाली. [⟶ क्ष-किरण स्फटिकविज्ञान].
क्ष-किरण विवर्तन पद्धत ही वायूकरिता इलेक्ट्रॉन विवर्तन पद्धतीपेक्षा जास्त अचूक आहे, असे समजतात. दुसऱ्या महायुद्धकाळापासून क्ष-किरणांऐवजी न्यूट्रॉन शलाकेचा उपयोग विवर्तन अभ्यासाकरिता करण्यात येऊ लागला. हिचा उपयोग हायड्रोजन व त्यासारखे इतर हलके अणू यांवरील प्रयोगांकरिता केला जातो, कारण सर्व भारांच्या अणूंद्वारे न्यूट्रॉनाचे सारख्याच प्रमाणात विवर्तन होते, असे आढळते.
द्रव्यमान वर्णपटविज्ञान : या भंजक (ज्यात नमुन्याच्या पदार्थाचा अंशतः नाश करावा लागतो अशा) विश्लेषण पद्धतीत द्रव्यमान वर्णपटमापकामध्येच इलेक्ट्रॉनांचा भडिमार करून नमुन्यामधील संयुगाचे प्रथम त्याच्या घटक मूलकांत (म्हणजे अणू किंवा अणुगटांत) विभाजन केले जाते. त्यानंतर द्रव्यमान वर्णपटमापकात उपलब्ध झालेल्या सर्व मूलक घटकांचे व्यक्तिशः द्रव्यमान व त्यांची विपुलता यांचे मापनकेले जाते. अनुमान व प्रायोगिक पडताळा या क्रियांचा अनुक्रमे उपयोग करून संयुगाच्या संरचनेविषयी अंदाज करणे शक्य होते. या पद्धतीत विश्लेषणाकरिता आवश्यक अशा नमुनाद्रव्यांचे द्रव्यमान काही मिग्रॅ. एवढे कमी असल्यामुळे ही मापन पद्धती सोयीस्कर ठरते. [⟶ द्रव्यमान वर्णपटविज्ञान].
क्ष-किरण अनुस्फुरण विश्लेषण : घन व द्रव पदार्थांच्या विश्लेषणासाठी मोठ्या प्रमाणात उपयुक्त ठरलेल्या या अभंजक पद्धतीकरिता नमुनाद्रव्य स्फटिक स्वरूपातच पाहिजे अशी अट सुद्धा असत नाही. नमुनाद्रव्यावर उच्च तीव्रतेचे क्ष-किरण टाकले असता त्यामधील घटक अणू त्याच्या विशिष्ट वर्णपट रेषा उत्सर्जित करतात. उत्सर्जित क्ष-किरण वर्णपट रेषांचे एका स्फटिक चकतीपासून विवर्तन करून त्यांचे तरंगलांबीनुसार विश्लेषण केले जाते. उत्सर्जित क्ष-किरणाच्या तरंगलांबीच्या विशिष्ट मूल्यावरून नमुन्यातील अणूची ओळख करून घेतली जाते. घटक अणूंची विपुलता किंवा संहती या रेषांच्या तीव्रतेवरून निश्चित करता येते. या पद्धतीचा उपयोग करून पदार्थामधील मूलकाची ओळख मात्र करून घेता येत नाही. ही पद्धत प्रकाशीय विश्लेषण पद्धतीइतकी संवेदनशील नसली, तरी तिच्या साहाय्याने काही मिलिग्रॅम द्रव्यमानाच्या नमुन्यामधील १०−६ ग्रॅमएवढे सूक्ष्म द्रव्यमान असणाऱ्या घटकाचा शोध घेता येतो. शंभर टक्के संहती असणाऱ्या घटकद्रव्याकरिता सुद्धा हा पद्धतीचा उपयोग करता येतो, हे या पद्धतीचे वैशिष्ट्ये आहे. प्रकाशीय विश्लेषण पद्धतीची कमाल वापर मर्यादा फक्त वीस टक्के संहतीपर्यंत असते.
अणुकेंद्रीय चुंबकीय अनुस्पंदन : काही अणुकेंद्रांना परिणामी परिवलन गती असते. ज्या अणुकेंद्रांचा कोनीय संवेग [⟶ यामिकी ] शून्य मूल्याचा नसतो, अशी अणुकेंद्रे एखाद्या सूक्ष्म चुंबकाप्रमाणे कार्य करतात. त्यांवर बाहेरून चुंबकीय क्षेत्र लावले असता ⇨पुंजसिद्धांताप्रमाणे हे चुंबक बाह्य क्षेत्राच्या सापेक्ष काही ठराविक दिशांतच राहू शकतात. वरील भिन्न पण ठराविक दिशांत विस्थापन केलेल्या अणुकेंद्रीय चुंबकांच्या ऊर्जा निरनिराळ्या निश्चित मूल्याच्या असतात. या भिन्न मूल्यांच्या ऊर्जा पातळ्यांना (पीटर झीमान या भौतिकीविज्ञांच्या नावावरून) झीमान ऊर्जा पातळ्या असे म्हणतात. अणुकेंद्र विचलित करून त्यास नवीन दिशेत वळविण्याकरिता त्याला ऊर्जा पुरवावी लागते. ही ऊर्जा बहुधा रेडिओ कंप्रता पट्ट्यातील (१० किलोहट्र्झ ते १०० गिगॅहट्र्झ) असते. रेडिओ कंप्रता प्रारणाचे अणुकेंद्राद्वारे होणारे शोषण हे पुंज सिद्धांतानुसार होत असल्यामुळे अणुकेंद्रीय चुंबकाच्या दोन ऊर्जा पातळ्यांच्या मूल्यांनुसार एका ठराविक कंप्रतेच्या रेडिओ प्रारणाच्या शोषणाने ही क्रिया घडून येऊ शकते. त्यामुळे या परिणामाला अनुस्पंदन परिणाम असे म्हटले जाते. उच्च विभेदनक्षमता असणारी तंत्रे१/२परिवलन पुंजांक [परिवलनांक ⟶ पुंजयामिकी ] असणाऱ्या अणुकेंद्रांच्या बाबतीतच उपलब्ध आहेत. यामध्ये H2, C13, F13, P31या अणुकेंद्रांचा मुख्यत्वेकरून समावेश होतो.
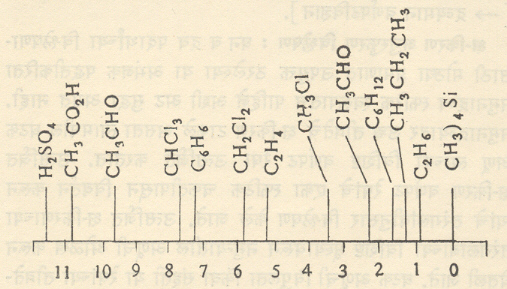
अणुकेंद्राच्या झीमान ऊर्जा पातळ्यांमधील फरक हा बाह्य चुंबकीय क्षेत्राच्या मूल्यावर सरळ अवलंबून असतो. ज्या रेडिओ कंप्रतेकरिता अनुस्पंदन मिळते व ज्या कंप्रतेकरिता पुंजीय शोषण होऊन अणुकेंद्रीय चुंबकाचे एका ऊर्जा पातळीपासून जास्त ऊर्जेच्या पातळीमध्ये संक्रमण होते, त्या रेडिओ कंप्रतेचे मूल्य बाह्य चुंबकीय क्षेत्र मूल्य बदलून बदलता येते. चुंबकीय क्षेत्र व अनुस्पंदन रेडिओ कंप्रता यांमधील वरील विशिष्ट संबंधामुळे अणुकेंद्रीय चुंबकीय अनुस्पंदनाद्वारे रेणवीय संरचनेचा शोध घेता येतो. सर्व एकरूप अणुकेंद्राकरिता (उदा., प्रोटॉन) बाह्य चुंबकीय क्षेत्र व अनुस्पंदन रेडिओ कंप्रता यांमधील संबंध एकाच सूत्राने दर्शविला जावा अशी अपेक्षा असली, तरी ही अपेक्षा काटेकोरपणे पूर्णहोत नाही. कार्बनी संयुगामध्ये हायड्रोजन अणुकेंद्र (म्हणजेच प्रोटॉन) हे निरनिराळ्या संख्येत, इतर अणूंच्या बरोबर विविध प्रकारच्या गटांत आढळते. उदा., ॲसिटिक अम्लामध्ये (CH3CO2H) ते दोन निरनिराळ्या गटांशी संलग्न असते. प्रत्येक गटातील प्रोटॉन संख्या हीसुद्धा भिन्न असते. C6H0 मध्ये प्रोटॉनाची रासायनिक परिस्थिती निराळी असते. पदार्थावर (सामान्यपणे विद्रावाच्या स्वरूपात) चुंबकीय क्षेत्र बाहेरून लावले असता, त्याचा परिणाम निरीक्षणाखालील प्रोटॉनापुरताच सीमित न राहता, तो त्याच्या रासायनिक परिसरातील सर्व अणूंवर व त्यांमधील इलेक्ट्रॉनांवर सुद्धा होतो. क्षेत्रामुळे इलेक्ट्रॉन गतीत जो बदल होतो, त्यामुळे त्यांच्या आसपासच्या अवकाशात चुंबकीय परिणाम निर्माण होत असल्यामुळे प्रोटॉनावर प्रत्यक्ष कार्य करीत असलेल्या चुंबकीय क्षेत्राच्या मूल्यात फरक पडतो. याचा अर्थ असा होतो की, एकाच रेडिओ कंप्रतेकरिता प्रोटॉन अनुस्पंदन मिळविण्याकरिता निरनिराळ्या परिसरांतील प्रोटॉनांकरिता विभिन्न मूल्याची चुंबकीय क्षेत्र मूल्ये आवश्यक होतात. याउलट संयुगामधील प्रोटॉनाची अनुस्पंदन कंप्रता प्रयोगशाळेत मोजली असता त्यापासून प्रोटॉनाच्या संयुगामधील परिस्थितीबद्दल सविस्तर आणि महत्त्वाची अशी माहिती मिळू शकते. या कार्याकरिता प्रोटॉनयुक्त असे एक विशिष्ट रसायन प्रमाणभूत धरतात. प्रमाणभूत रसायन व निरीक्षणाखालील संयुग यांमधील प्रोटॉन अनुस्पंदन कंप्रता मूल्ये मोजली जातात.आ. ७ मध्ये काही प्रातिनिधिक संयुगांकरिता मिळालेली रासायनिक बदलाची (म्हणजे कंप्रतेत मिळणाऱ्या बदलाची) मूल्ये दिली आहेत.
वरील मापनाकरिता टेट्रामिथिलसिलेन (CH3)4 Si हे द्रव्य प्रमाणभूत म्हणून धरले आहे. आकृतीवरून प्रोटॉन चुंबकीय अनुस्पंदन प्रयोगापासून संयुगातील प्रोटॉनाच्या रासायनिक परिस्थितीबद्दल (प्रोटॉन संख्या व संलग्न परिसर गट) महत्त्वाची माहिती कशी मिळविता येते, हे लक्षात येते.
रेणवीय वर्णपटविज्ञान : रेणवीय ऊर्जा पातळ्या व वर्णपट : वर्णपटविज्ञानाचा उपयोग करून रेणूच्या ऊर्जा पातळ्या अथवा अवस्था, त्यांची आंतरिक संरचना, घटक अणूंमधील प्रेरणेचे स्वरूप, त्यांमधील बंध व त्याचे प्रकार अशा अनेक बाबींविषयी चांगली माहिती मिळते. रेणूने उत्सर्जित केलेल्या वर्णपटांचा अभ्यास केल्यास, त्यांमध्ये दोन विभाग असतात असे आढळते : (१) पट्टयुक्त वर्णपट व (२) अखंडित वर्णपट. यांपैकी पट्टयुक्त वर्णपट अनेक पृथक् पट्टांपासून तयार झालेला असतो असे आढळते. यामधील प्रत्येक पृथक् पट्टाची एका बाजूची सीमा अथवा कड विशेषेकरून स्पष्ट असतात. या सीमेस पट्टशीर्ष असे म्हणतात. निरनिराळ्या रेणूंकरिता पट्टशीर्षांचे वर्णपटावरील स्थान अलग व निश्चित असल्यामुळे पट्टशीर्षाच्या तरंगलांबीवरून रेणूची ओळख पूर्ण करून घेता येते. उच्च विभेदनक्षमता असलेल्या वर्णपटमापकाच्या साहाय्याने या पट्टाचे निरीक्षण केले असता हे पट्ट अखंडित नसून जवळजवळ असलेल्या असंख्य वर्णपट रेषांमुळे बनले आहेत असे आढळते. रेणूला अखंडित व पृथक् अशा दोन्ही प्रकारच्या ऊर्जा पातळ्या असतात, असे यावरून दिसते. हायड्रोजन रेणूचा अखंडित वर्णपट या दुसऱ्या प्रकारच्या उत्सर्जनाचे एक चांगले उदाहरण आहे.
रेणू जर वायुरूप असेल, तर त्याच्या पृथक् ऊर्जा पातळ्या सुस्पष्ट व रेखीव असतात. घन किंवा द्रव अवस्थेमधील पदार्थाच्या रेणूंमध्ये परस्परक्रिया होत असल्यामुळे ऊर्जा पातळ्यांचे रेखीव स्वरूप नष्ट होते व त्या अस्पष्ट अथवा पुसटलेल्या बनतात. खालील वर्णनात विवेचनाच्या सोईकरिता रेणू वायू अवस्थेत आहेत, ते द्वि-आणवीय आहेत व त्यांच्या पृथक् ऊर्जा पातळ्या अथवा अवस्था एकाकी आहेत, अशी गृहिते स्वीकारलेली आहेत. येथे इलेक्ट्रॉन परिवलन गतीमुळे मिळणारी रेणवीय ऊर्जा पण विचारात घेतलेली नाही. पुंजयामिकीप्रमाणे कोणत्याही रेणूची एकंदर ऊर्जा W खालील पृथक् घटकांच्या स्वरूपात मांडता येते.
W = WT + We + Wv + WR … … … (५)
वरील समीकरणात WT ही उष्णतेमुळे रेणूजवळ असणारी यादृच्छिक स्वरूपाची स्थानांतरण गतिज ऊर्जा दाखविली आहे पण तिचा परिणाम वर्णपटावर अत्यंत कमी प्रमाणात होतो व त्यामुळे ती नगण्य समजतात. We = इलेक्ट्रॉनीय स्वरूपात असणारा रेणू ऊर्जा अंश, Wv = रेणूमधील दोन अणू गुरुत्वमध्याभोवती करू शकणाऱ्या कंपनांमुळे उद्भवणारी ऊर्जा आणि WR = सबंध रेणूच्या परिभ्रमण गतीमुळे असणारी गतिज ऊर्जा. द्वि-आणवीय रेणू डंबेलच्या आकाराचा आहे असे समजले, तर Wv व WR या दोन्ही गतींची कल्पना करणे शक्य होईल. टोकाशी असलेले अणू जेव्हा एकमेकांजवळ किंवा दूर होत कंपने करतात तेव्हा या कंपनांची ऊर्जा Wv असे मानले आहे. द्वि आणवीय डंबेल आपल्या अक्षाभोवती परिभ्रमण करू शकते या क्रियेमुळे WR ही ऊर्जा निर्माण होते. यांपैकी We व Wv मिळून रेणूची आंतरिक ऊर्जा बनते, तर WT व WR या ऊर्जा यामिकीय स्वरूपाच्या असतात. यांपैकी WT या ऊर्जेचा वर्णपटावर नगण्य परिणाम होत असल्याने ती यापुढील विवेचनात विचारात घेतलेली नाही. ज्या अवस्थेत रेणूची ऊर्जा सर्वांत कमी मूल्याची (W” = We” + Wv” + WR”) असते ती रेणूची निम्न स्थिती होय. रेणूला जर त्यावर प्रारण (पुरेशा ऊर्जेचे) टाकून ऊर्जा पुरविली, तर तो त्याचे एका ठराविक मापातच शोषण करू शकतो. ऊर्जा शोषणामुळे वरील तिन्ही ऊर्जा घटकांत फरक (म्हणजे वाढ) होऊन त्यांची नवी मूल्ये We’, Wv’, WR’ एवढी झाली असे समजले, तर या नव्या अवस्थेत रेणू काही क्षण उत्तेजित अवस्थेत राहतो. नंतर तो परत आपल्या मूळच्या (W”) या निम्न अवस्थेत उस्फूर्तपणे येतो. या घटनेत अतिरिक्त ऊर्जा, प्रारणाच्या स्वरूपात उत्सर्जित केली जाते. प्रारण कंप्रता जर v असेल, तर कंप्रतेचे मूल्य खालील सूत्राने मिळते.
hν = (We’−We”) + (Wv’−Wv”) + (WR ’−WR”) … (६)
येथे h हा प्लांक स्थिरांक (माक्स प्लांक या भौतिकीविज्ञांच्या नावाने ओळखण्यात येणारा स्थिरांक) आहे. बहुतेक सर्व रेणूंकरिता पहिल्या पदाचे मूल्य १.·०९ eV तर दुसऱ्या व तिसऱ्या पदांची अनुक्रमे ≈१·०९ eV व ≈०·००५ eV या प्रमाणांची असतात. याचा अर्थ असा होतो की, फक्त परिभ्रमण ऊर्जा पातळ्यांमध्येच बदल झाला, तर त्यामुळे उत्सर्जित होणाऱ्या प्रारणाची कंप्रता सूक्ष्मतरंग विभागात (१−१०० गिगॅहर्ट्झ) असते. रेणूच्या कंपन ऊर्जेत फक्त फरक पडला, तर त्यामुळे उद्भवणारे प्रारण अवरक्त अथवा अतिअवरक्त प्रकारचे असते. मात्र अवरक्त प्रारण रेणूवर टाकले असता त्यामुळे कंपन व परिभ्रमण या दोन्ही प्रकारांच्या ऊर्जा पातळ्या उत्तेजित होऊ शकतात. रेणूच्या इलेक्ट्रॉनीय ऊर्जा पातळीमध्ये फक्त फरक केला, तर त्यामुळे दृश्य व जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगाच्या पलीकडील) कंप्रतेचे प्रारण उत्सर्जित केले जाते. रेणूच्या इलेक्ट्रॉनीय ऊर्जा पातळ्या उत्तेजित करण्याकरिता लागणारी किमान ऊर्जा (म्हणजेच कंप्रता, कारण प्रारण ऊर्जा = hν) निरनिराळ्या संयुगांकरिता त्यांच्या आंतरिक संरचनेनुसार भिन्न मूल्याची असते. ज्या पदार्थ रेणूकरिता ही किमान कंप्रता उच्च जंबुपार विभागात पडते असे पदार्थ सामान्य सूर्यप्रकाशात रंगहीन दिसतात. या कंप्रतेचे मूल्य दृश्य वर्णपट सीमेत पडत असेल, तर ते रंगीत दिसतात. संयुगामध्ये असणाऱ्या एकांतरित (एकाआड एक) द्विबंधाची संख्या व संयुगाचा दृश्य रंग यांचा निकट संबंध आहे, असे दाखविता येते. संयुगातील द्विबंध एकांतरित प्रकारचे आहेत की विलग प्रकारचे याविषयीचा अंदाज अशा प्रकारे पदार्थाच्या रंगावरून करता येतो.
रेणूच्या उत्सर्जन व शोषण वर्णपटांच्या अभ्यासावरून रेणूसंबंधीच्या पुढील गोष्टींविषयी माहिती मिळते : (१) आंतर-अणुकेंद्रीय अंतर, (२) रेणू विघटन ऊर्जा, (३) प्रेरणा स्थिरांक, (४) रेणूचे निरूढी परिबल, (५) रेणूमधील समस्थानिक अणूंचे (अणुक्रमांक तोच पण भिन्न अणुभार असलेल्या त्याच मूलद्रव्याच्या प्रकारांच्या अणूंचे) सापेक्ष द्रव्यमान, (६) अणुकेंद्रीय परिवलन व त्याकरिता सार्थ असणारी फेमी-डिरॅक किंवा बोस-आइन्स्टाइन सांख्यिकी [⟶ सांख्यिकीय भौतिकी].
निरूढी परिबल : द्वि-आणवीय रेणूला जर विद्युत् द्विध्रुवी परिबल असेल, तरच तो शुद्ध परिभ्रमण वर्णपट उत्सर्जित किंवा शोषण करू शकतो. परिभ्रमण करणारा द्विध्रुव प्रारणाच्या विद्युत् क्षेत्राबरोबर परस्परक्रिया करून त्याच्याबरोबर ऊर्जा-विनिमय करतो. जेव्हा शुद्ध परिभ्रमण वर्णपट मिळतो तेव्हा रेणूच्या कंपन व इलेक्ट्रॉनीय ऊर्जा पातळ्या उत्तेजित होत नाहीत. अशा परिस्थितीत मिळणारा परिभ्रमण वर्णपट एकसारख्या अंतरावर असलेल्या अनेक वर्णपट रेषांमुळे बनलेला असतो, असे आढळते. रेणू हा दृढ धूर्णकाप्रमाणे कार्य करतो असे मानून पुंजयामिकीप्रमाणे त्याचे विश्लेषण केले, तर दोन समीपस्थ वर्णपट रेषांमधील कंप्रता फरक (d) खालील सूत्राने दिला जातो, असे दाखविता येते.
|
dν = |
2h 8π2I |
= 2B० … (७) |
येथे I = रेणूच्या गुरुत्वमाध्यमातून आंतर-आणवीय अक्षाला लंब असणाऱ्या अक्षाभोवती रेणूचे निरूढी परिबल, h = प्लांक स्थिरांक, द्वि-आणवीय रेणूकरिता
|
I = |
m1 m2 m1 + m2 |
.re2 … … … (८) |
येथे m1, m2 घटक अणूंची द्रव्यमाने दर्शवितात, तर re = आंतरआणवीय अंतर अथवा बंधलांबी. वर्णपटमापकाच्या साहाय्याने रेणूकरिता dν मोजले असता त्यावरून I व re या राशींच्या मूल्यांचे गणन करता येते.
फारसे बदल न करता वरील मीमांसा त्रि-आणवीय व इतर रेषीय रेणूंकरिता वापरता येते. जर OCS यासारखा रेषीय रेणू विचारात घेतला, तर या रेणूला एकच निरूढी परिबल असले, तरी त्याकरिता O−C व C−S अशा दोन निराळ्या मूल्यांच्या बंधलांब्या असतात. यांची मूल्ये काढण्याकरिता समी. (६) पुरे पडत नाही. आणखी प्रदत्त मिळविण्याकरिता समस्थानिक प्रतिष्ठापन विक्रियेचा उपयोग करतात. OCS रेणूमध्ये S32च्याऐवजी S34 या समस्थानिक अणूची प्रतिष्ठापना करून परत त्याच्या वर्णपटाचे संशोधन केले जाते. अशा विक्रियेमध्ये बंधलांबीची मूल्ये बदलत नाहीत हे गृहीत धरले असता, या सर्व प्रदत्तावरून O−C व C−S या बंधलांब्यांची मूल्ये काढता येतात. कोष्टक क्र. १ मध्ये सूक्ष्मतरंग शोषण वर्षपटद्वारा अशा प्रकारे निर्धारित केलेली मूल्ये दाखविली आहेत.
कोष्टक क्र. १. सूक्ष्मतरंग शोषण वर्णपटापासून द्वि-आणवीय/रेषीय रेणूकरिता बंधलांबी मूल्ये.
|
रेणू |
बंध |
बंधलांबी (Å) |
|
कार्बन मोनॉक्साइड CO |
C=O |
१·१२ |
|
सोडियम क्लोराइड NaCl |
Na=Cl |
२·३६ |
|
सायनोजेन क्लोराइड ClCN |
C-Cl |
१·६३ |
|
CºN |
१·१६ |
प्रत्यक्षात रेणू जेव्हा परिभ्रमण करू लागतो तेव्हा त्यामुळे केंद्रोत्सारी प्रेरणा (केंद्रापासून दूर ढकलणारी प्रेरणा) अस्तित्वात येते. यामुळे अणूंमधील अंतरामध्ये वाढ होण्याकडे प्रवृत्ती राहते.
सामान्य बहु-आणवीय रेणूकरिता एकमेकांशी लंब कोन करणाऱ्या अशा तीन विशिष्ट दिशा निश्चित करता येतात. या दिशांना प्रधान अक्ष असे म्हणतात. अशा रेणूंना वरील तीन दिशांभोवती तीन भिन्न अशी निरूढी परिबले असू शकतात. या तीन परिबलांच्या परस्पर संबंधांनुसार रेणूकरिता पुढील सममिती प्रकार आढळतात : तिन्ही परिबले एकाच मूल्याची असतील, तर रेणूची सममिती गोलीय घूर्णक प्रकाराची दोन परिबल मूल्ये एकसमान असतील, तर रेणू सममितीय घूर्णक प्रकाराचा आणि तिन्ही परिबल मूल्ये भिन्न असतील, तर रेणू असममितीय घूर्णक प्रकाराचा म्हणतात. निसर्गात मिळणारे बहुसंख्य रेणू असममितीय घूर्णक प्रकारचे असतात.
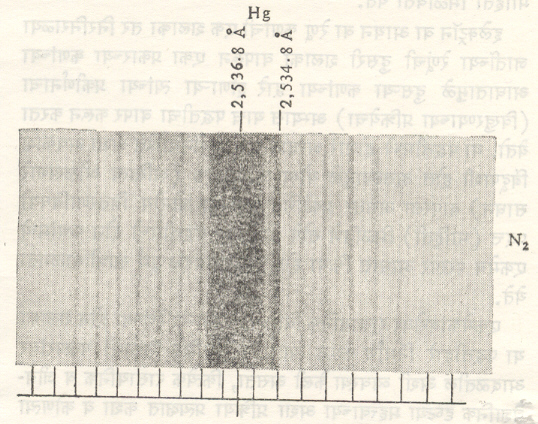
रामन वर्णपट : शून्य द्विध्रुवी परिबल असणाऱ्या H2, HD, D2, N2 यांसारख्या रेणूंच्या बाबतीत शुद्ध परिभ्रमण वर्णपट मिळत नाहीत, याचा उल्लेख मागे आलाच आहे. अशा रेणूंकरिता परिभ्रमण रामन वर्णपट मिळू शकतो. त्यापासून रेणूचे निरूढी परिबल इ. राशी गणन करून काढता येतात. [⟶ रामन परिणाम].
एकवर्णी प्रकाश रेणूवर टाकला असता, अणुकेंद्राभोवती असलेल्या इलेक्ट्रॉनांच्या वितरणामध्ये बदल होतो व त्यामुळे आपाती प्रकाशाचे प्रकीर्णन (विखुरणे) होते. या आविष्काराकरिता रॅली यांनी रूढ भौतिकीनुसार जी मीमांसा दिली आहे, त्याप्रमाणे प्रकीर्णित प्रकाशाची तरंगलांबी बदल नाही पण याच परिणामाचे पुंजयामिकीप्रमाणे विश्लेषण केले, तर ज्यामध्ये तरंगलांबीमध्ये बदल होत असतो अशा प्रकारचे दुसरेही प्रकीर्णन होते, असे दाखविता येते. ν० कंप्रतेचा प्रकाश परिभ्रमण स्थिरांक B असलेल्या द्वि-आणवीय रेणूवर पडला, तर नव्या मीमांसेप्रमाणे ν0 कंप्रता (प्रकीर्णन स्वरूपात रॅली मीमांसेनुरूप) तर मिळतेच पण त्याच्या एका बाजूस कमी तीव्रतेच्या ν0 + 6B, ν0 + 10B, ……. इ. कंप्रतांच्या प्रतिस्टोक्स वर्णपट रेषा, तर दुसऱ्या बाजूस v0 – 6B, v0 – 10B,……. इ. कंप्रतांच्या वर्णपट रेषांना प्रतिस्टोक्स रेषा (किंवा रामन रेषा), तर कमी कंप्रतामूल्याच्या रेषांना स्टोक्स रेषा असे म्हणतात [⟶ रामन परिणाम]. या रेषांचे मापन करून B चे मूल्य काढणे सोपे होते. रेणूचा अवरक्त वर्णपट व रामन वर्णपट यांपासून अनुक्रमे मिळणारी माहिती एकरूपनसते. कारण या दोन प्रकारच्या संक्रमणामध्ये दोन विभिन्न असे निवड नियम पाळले जात असतात. या दोन पद्धतींमुळे मिळणाऱ्या प्रदत्ताचा तुलनात्मक अभ्यास केला असता (मिथेन, बेंझीन यांसारख्या) लहान पण सममित स्वरूपाच्या रेणवीय संरचनेविषयी सूक्ष्म व अचूक ज्ञान मिळविता येते. अवरक्त व रामन वर्णपटविज्ञानाचा उपयोग निरनिराळ्या प्रकारच्या रासायनिक संयुगाचे गुणात्मक विश्लेषण अथवा ओळख पूर्ती करून घेण्यासाठी मोठ्या प्रमाणात केला जातो.
रेणूवर बाहेरून विद्युत् स्थितिक क्षेत्र लावले असता विद्युत् द्विध्रुवी परिबलयुक्त रेणूच्या परिभ्रमण ऊर्जा पातळ्यांत व त्यांच्या संख्येत फरक पडतो, असे दाखविता येते. या परिणामामुळे प्रत्येक मूळ परिभ्रमण वर्णपट रेषेचे विभाजन होऊन त्यामध्ये सूक्ष्म संरचना दिसू लागते. या आविष्कारास जे. स्टार्क या भौतिकीविज्ञांच्या नावावरून स्टार्क परिणाम असे म्हणतात. परिभ्रमण वर्णपट रेषेच्या या प्रकार होणाऱ्या विभाजनाचा अभ्यास केल्यास त्यापासून रेणवीय विद्युत् द्विध्रुवी परिबलाच्या मूल्याचेही मापन करता येते. अशा प्रकारे निश्चित केलेली काही मूल्ये कोष्ट क्र. २ मध्ये दिली आहेत.
कोष्टक क्र. २. वर्णपट प्रदत्तापासून निश्चित केलेली रेणवीय विद्युत् द्वि-ध्रुवी परिबलांची मूल्ये
|
रेणू |
वि. द्वि. प. (डेबाय एकक) |
|
OCS |
०·७१० |
|
N2O |
०·१६६ |
|
NH3 |
१·४७० |
|
CH3CI |
१·८७० |
रेणू कंपन वर्णपट : रेणूच्या कंपन वर्णपटाचा अभ्यास केल्यास त्यावरून त्याच्या घटक अणूंमध्ये असणाऱ्या बंधाच्या सामर्थ्याविषयी अनुमान करता येते. रेणूमधील दोन घटक अणू जर त्यांच्या द्रव्यमान मध्याभोवतील सरल हरात्मक आंदोलने [⟶ सरल हरात्मक गति] करत असतील, तर
|
.. |
|
|
μx = |
− kx …. …. …… (९) |
हे समीकरण मिळते.
|
यांमध्ये μ = |
m1 m2 |
|
m1 + m2 |
संक्षिप्त द्रव्यमान, m1 व m2 घटक अणूंची द्रव्यमाने, k = बंध प्रेरणा स्थिरांक (दोन अणूंमधील आकर्षणामुळे निर्माण झालेली प्रेरणा). अणूची कंपन कंप्रता νo खालील सूत्राने मिळते.
|
νo = |
1 |
√ |
k |
… … … (१०) |
|
2π |
μ |
पुंजयामिकीप्रमाणे कंपन पावणारा द्वि आणवीय रेणू हा हरात्मक आंदोलकाप्रमाणे आंदोलने करतो असे मानले, तर अशा आंदोलकाला काही ठराविक पृथक् ऊर्जा मूल्येच अनुज्ञात असतात [⟶ पुंजयामिकी]. ही मूल्ये
|
Ev = |
(v + |
1 |
) |
h |
√ |
k |
… … (११) |
|
2 |
2π |
m |
या सूत्राने मिळतात. येथे v = कंपन पुंजांक असून त्याची मूल्ये v = 0, 1, 2, 3 ……. अशी असतात.
वरील मीमांसा, रेणूची कंपने जर पूर्णपणे हरात्मक स्वरूपाची असतील, तरच यथार्थ ठरते. प्रत्यक्षात रेणू कंपने हरात्मक नसतात. जर रेणू कंपन ऊर्जा कमी मूल्याची असेल (म्हणजे त्याच्या गतीचे वर्णन लहान मूल्याच्या पुंजकाने देता येत असेल), तर त्याचे कार्य आसन्नपणे (जवळजवळ) हरात्मक प्रकारासारखे असते. अशा परिस्थितीत खालील आसन्न सूत्रे वापरले तरी चालते.
|
Ev ≈hcwe = |
( |
+ |
1 |
) |
… … (१२) |
|
2 |
|
येथे we = |
1 |
. |
1 |
√ |
k |
|
c |
2π |
m |
समी. (१२) वरून असे दिसते की, रेणूच्या निम्नतम अवस्थेत त्याची कंपन ऊर्जा शून्य नसून तिचे मूल्य 1/2 we एवढे राहते. या ऊर्जामूल्याला शून्यबिंदू ऊर्जा असे म्हणतात. निरनिराळ्या रेणू कंपन ऊर्जा मूल्यांमध्ये (v = 0, 1, 2, 3,……) hc weएवढा सारखाच फरक असतो, असा आणखी एक निष्कर्ष समी. (१२) वरून मिळतो. प्रत्यक्षात v मध्ये वाढ झाली असता अनुक्रमिक ऊर्जा पातळ्यांमधील अंतर कमी होत जाते, असे दिसते. रेणू कंपनात जो अहरात्मक भाग आहे त्यामुळे हा परिणाम मिळतो असे दाखविता येते. v पुंजांकाच्या उच्च मूल्यांकरिता खालील सुधारित सूत्र जास्त योग्य ठरते.
|
Ev = hc we [(v+ |
1 |
) – xe |
(v + |
1 |
) 2 ] … (१३) |
|
2 |
2 |
येथे Xe हा हरात्मक रेणू स्थिरांक असून Xe < < 1. काही निवडक द्वि आणवीय रेणूंकरिता मिळालेली बंध प्रेरणा स्थिरांक मूल्ये कोष्टक क्र. ३ मध्ये दिली आहेत.
बंध प्रेरणा स्थिरांक हा दोन घटक अणूंमधील आकर्षणी प्रेरणेचे अथवा बंध सामर्थ्याचे निर्देशन करतो. या स्थिरांकाचे मूल्य जेवढे जास्त, तेवढे अणूंमधील बंधसामर्थ्य जास्त असते तसे म्हणता येते. कोष्टक क्र. ३ मध्ये दिलेल्या मूल्यांवरून या विधानाचा पडताळा मिळू शकतो.
कोष्टक क्र. ३. काही निवडक द्वि – आणवीय रेणूंकरिता बंध प्ररणा स्थिरांक (k)
|
रेणू |
K (डाइन प्रती सेंमी.) ×१०५ |
|
H2 |
५·२ |
|
CO |
१८·७ |
|
NaCI |
१·२ |
|
KCI |
०·८ |
वरील मीमांसा अचूक नाही कारण प्रत्यक्षात रेणूचे कंपन संपूर्णपणे हरात्मक स्वरूपाचे नसते. निराळ्या शब्दात हेच सांगावयाचे झाल्यास घटक अणूंमधील आकर्षणी प्रेरणा (८) या सरल सूत्राप्रमाणे मिळत नाही.
रासायनिक बंधाकरिता स्थितिज ऊर्जा फलन : रेणूचे कंपन हरात्मक स्वरूपाचे आहे असे समजल्यास आंतर आणवीय अंतर करिता असणारी त्याची स्थितिज ऊर्जा खालील सूत्रानुसार मिळते.
|
V = |
1 |
k |
( |
r – re |
) 2 |
… … (१४) |
|
2 |
समतोल स्थितीमधील रेणुबंधलांबीपासून होणारे विचलन (r – re) या पदाने दाखविले आहे. पुंजयामिकीचा उपयोग करून स्थितिज ऊर्जेचे चलन फक्त H2 रेणूकरिताच काढण्यात आलेले आहे.
रेणूमधील स्थितिज ऊर्जेच्या चलनाकरिता पी. एम्. मोर्स यांनी खालील अनुभवजन्य गणितीय सूत्र सुचविले आहे.
Vq = De (1 – e−ßq)2 …. ….. …. (१५)
येथे De = बंध वियोजन ऊर्जा, q = r – re, re = बंधलांबी व ß = रेणू स्थिरांक. वर्णपटीय प्रदत्तावरून रेणूकरिता De व ßयांची मूल्ये काढता येतात.
रेणूच्या इलेक्ट्रॉनीय, कंपन व परिभ्रमण ऊर्जा पातळ्यांत बदल झाला, तर मिळणाऱ्या वर्णपटाचे विशदीकरण वरील संकल्पनांच्या साहाय्याने पुढे केले आहे.
रेणवीय परिभ्रमण व अणुकेंद्रीय परिवलन : वर वर्णन केलेल्या रेणूच्या दृढ घूर्णक प्रतिकृतीमध्ये फक्त रेणूच्या कोनीय संवेगाचाच विचार केला होता. काही रेणूंमधील अणुकेंद्रांना परिवलन गती असते आणि रेणूच्या कोनीय संवेगात त्यामुळे पडणारी भर लक्षात घेणे आवश्यक होते. रेणवीय कोनीय संवेगाचे मूल्य J पुंजांकामुळे खालील सूत्रानुसार ठरते.
|
रेणवीय कोनीय संवेग = √J (J + 1) . |
h |
… … (१६) |
|
2π |
त्याप्रमाणेच अणुकेंद्रीय संवेगाचेही पुंजीकरण केले असता त्याकरिता तसेच खालील सूत्र मिळते
|
अणुकेंद्रीय संवेग = √I (I + 1) . |
h |
… … (१७) |
|
2π |
जर या दोन संवेगांमध्ये युग्मन असले, तर त्याकरिता समग्र परिणामी कोनीय संवेगाचे परत पुंजीकरण करावे लागते. याकरिता F हा नवा पुंजांक वापरतात. अशा परिस्थितीत
|
समग्र रेणवीय कोनीय संवेग = √F (F + 1). |
h |
… … (१८) |
|
2π |
याकरिता निवड नियम ∆F = 0, ± 1 असे असतात. या परिणामामुळे रेणूच्या मूळ परिभ्रमण ऊर्जा पातळ्यांत फरक पडतो उदा., DCN रेणूमध्ये J = 1 या एका पातळीचे F = 0, 2, 1 असे सूक्ष्म फरकाने विभाजन होते, त्यामुळे रेणूच्या परिभ्रमण वर्णपट रेषांतही सूक्ष्म रचना आढळून येते.
H2 व N2 यांसारख्या सम अणुकेंद्रीय रेणूच्या आनुक्रमिक परिभ्रमण वर्णपट रेषांच्या तीव्रतेत लक्षणीय बदल आढळतो. याच्याही स्पष्टीकरणाकरिता अणुकेंद्रीय परिवलनाचा उपयोग करावा लागतो. जर अणुकेंद्रांना बोस आइन्स्टाइन सांख्यिकी लागू असेल, तर त्यांमधील विषम परिभ्रमण रेषांची (J–विषम) तीव्रता नगण्य असते. याउलट अणुकेंद्राकरिता फेर्मी –डिरॅक सांख्यिकी यथार्थ ठरत असेल, तर त्याकरिता सम J रेषांची तीव्रता नगण्य असते, असे दाखविता येते. पदार्थाच्या नमुन्यामध्ये समस्थानिक अणूंचे मिश्रण असते. उदा., HCl35, HCl37 अशा पदार्थाच्या कंपन परिभ्रमण वर्णपट रेषांमध्ये सूक्ष्म विभाजन मिळते. समस्थानिक अणुकेंद्रांची द्रव्यमाने व त्यांची सापेक्ष विपुलता मूल्ये यांविषयीचे तपशीलवार ज्ञान रेणवीय वर्णपट रेषांच्या अभ्यासावरून मिळविता येते.
रेणवीय वर्णपटाचे विशदीकरण : मागे वर्णन केल्याप्रमाणे रेणवीय वर्णपटांत तीन मुख्य प्रकार आढळतात : (१) शुद्ध परिभ्रमण वर्णपट, (२) कंपन परिभ्रमण वर्णपट आणि (३) इलेक्ट्रॉनीय कंपन परिभ्रमण वर्णपट.
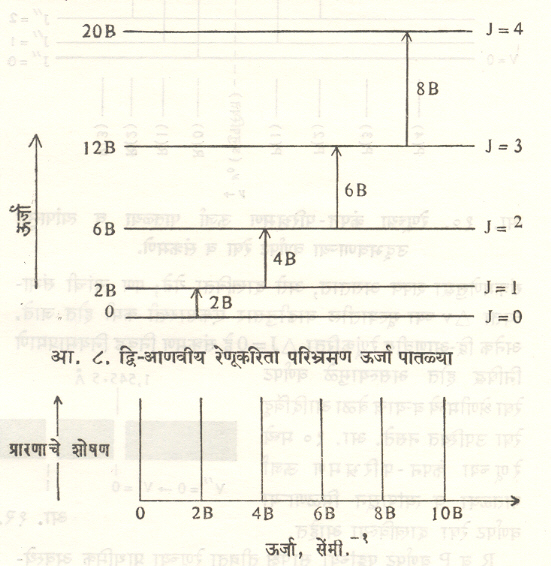
(१)शुद्ध परिभ्रमण वर्णपट : रेणूच्या फक्त परिभ्रमण ऊर्जेत जर फरक पडला (अथवा त्याच्या ऊर्जा पातळीकरिता फक्त J हा पुंजांक बदलला), तर त्याकरिता पुढील निवड नियम यथार्थ असतात : जर रेणवीय वि. द्वि. प. = 0, तर ∆J = 0 म्हणजे संक्रमण शक्य होत नाही. जर रेणूकरिता वि. द्वि. प. 0, तर त्याकरिता निवड नियम ∆J = + 1, हा बंधनकारक असतो. ∆J = + 1 करिता रेणूची ऊर्जा वाढत असल्यामुळे या परिस्थितीत शोषण विक्रिया घडून येते. ∆J = – 1 करिता रेणू ऊर्जा उत्सर्जित करतो. HCl सारख्या असममित रेणूला वि. द्वि. प. असते व त्यामुळे या रेणूकरिता शुद्ध परिभ्रमण वर्णपट मिळतो. अशा रेणूकरिता परिभ्रमण ऊर्जा पातळ्यांसाठी खालील सूत्र मिळते.
|
ER = |
h2 |
. J (J + 1) … … (१९) |
|
π82I |
यामधील वर्णपट रेषा कंप्रता खालील सूत्राने मिळतात :
|
hν = |
h2 |
[ |
J’ (J’ + 1) |
– |
J”( J” + 1 ) |
] |
… (२०) |
|
8π2 |
I’ |
I” |
यामध्ये J’ = उत्तेजित रेणू ऊर्जा पातळी पुंजांक व J” = निम्न ऊर्जा पातळी पुंजांक आहे. परिभ्रमण गतीमुळे निरूढी परिबलात होणारा थोडा फरक नगण्य मानला, तर
|
hν ≈ |
h2 |
(J² + I) = 2 B (J² + I) … … (२१) |
|
8π2I2 |
असे सूत्र मिळते. वर्णपट रेषेची तीव्रता पुढील गोष्टींवर अवलंबून असते : (१) वि. द्वि. प. चे re अंतराकरिता असणारे मूल्य, (२) निम्म ऊर्जा पातळीमधील रेणूंची समष्टी, (३) शोषण वर्णपटाकरिता ν चे मूल्य, तर उत्सर्जन वर्णपटाकरिता ν4 चे मूल्य.
आ. ८ मध्ये द्विआणवीय रेणूकरिता ऊर्जा पातळ्या व आ. ९ मध्ये त्यापासून मिळणाऱ्या शुद्ध परिभ्रमण वर्णपट रेषा दाखविल्या आहेत.
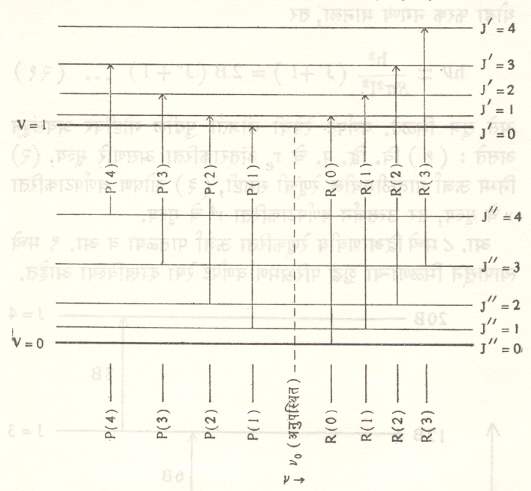
 (२) कंपन परिभ्रमण वर्णपट : रेणूची निम्न ऊर्जा अवस्था v²व J²या अनुक्रमे कंपन व परिभ्रमण पुंजांकांच्या द्वारे आणि उत्तेजित अवस्था v²व J²या पुंजांकांच्या द्वारे निर्देशित केल्या, तर त्यांपासून उत्सर्जित वा शोषित होणाऱ्या वर्णपट रेषेची कंप्रता खालील सूत्राने मिळते.
(२) कंपन परिभ्रमण वर्णपट : रेणूची निम्न ऊर्जा अवस्था v²व J²या अनुक्रमे कंपन व परिभ्रमण पुंजांकांच्या द्वारे आणि उत्तेजित अवस्था v²व J²या पुंजांकांच्या द्वारे निर्देशित केल्या, तर त्यांपासून उत्सर्जित वा शोषित होणाऱ्या वर्णपट रेषेची कंप्रता खालील सूत्राने मिळते.
hν = νo (v’, v”) + B’J’ (J’ + 1) – B”J” (J” + 1) … … (२२)
निरूढी परिबलाचे मूल्य रेणूच्या इलेक्ट्रॉनीय, कंपन (म्हणजे पुंजांक v) व परिभ्रमण (म्हणजे पुंजांक J) अवस्थांवर अवलंबून असल्यामुळे B या स्थिरांकाची मूल्ये B’ व B” या भिन्न चिन्ह मूल्यांनी दाखविली आहेत. रेणूच्या परिभ्रमण ऊर्जेत फरक न होता रेणू v² = 0 या निम्नतम कंपन पातळीपासून v² = 1 या पातळीला उत्तेजित केला गेला, तर या संक्रमणापासून νoया एकाच कंप्रतेची अशी वर्णपट रेषा मिळेल असे दिसते. आता याबरोबरच J याच्या मूल्यात सुद्धा बदल झाला, तर νo या रेषेच्या दोन्ही बाजूंस अनेक परिभ्रमण रेषांनी बनलेले पट्ट दिसतील, असे दाखविता येते. νoया रेषेला पट्टाचा आदिबिंदू असे म्हणतात. νo पासून उच्च कंप्रता बाजूस असलेल्या वर्णपट पट्टास R किंवा धन शाखा म्हणतात. यामधील रेषांकरिता J’ = J” + 1 या सूत्राने मिळतो. νo च्या दुसऱ्या बाजूस असलेल्या पट्टास P किंवा ऋण शाखा अशी संज्ञा दिली आहे (यातील रेषेकरिता J’ = J” – 1).
हरात्मक आंदोलनाकरिता v करिता निवड नियम ∆v ± 1 असा मिळतो. अहरात्मक आंदोलनाकरिता ∆v = 1, 2, 3,… अशी संक्रमणेसुद्धा शक्य असतात, असे दाखविता येते पण त्यांची संभाव्यता ∆v च्या मूल्यातील वाढीनुसार एकसारखी कमी होत जाते. अनेक द्वि आणवीय रेणूंकरिता ∆J = 0 हे संक्रमण निवड नियमाप्रमाणे निषिद्ध होत असल्यामुळे वर्णपट रेषा श्रेणीमध्ये बऱ्याच वेळा आदिबिंदू रेषा उपस्थित नसते. आ. १०. मध्ये रेणूच्या कंपन परिभ्रमण ऊर्जा पातळ्या व त्यांपासून मिळणाऱ्या वर्णपट रेषा दाखविल्या आहेत.
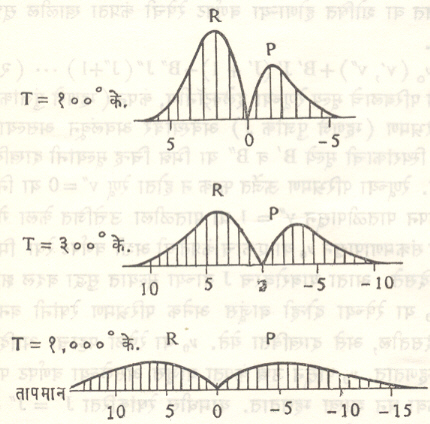
 R व P वर्णपट पट्टांच्या सापेक्ष तीव्रता रेणूच्या प्राथमिक अवस्थेमधील परिभ्रमण ऊर्जा वितरणावर अवलंबून असते. हे ऊर्जा वितरण मॅक्सवेल बोल्टसमान ऊर्जा वितरण नियमानुसार होत असते. आ. ११ मध्ये R व P वर्णपट पट्टांच्या तीव्रतेत तापमानानुसार (T०के.) होणारे बदल दाखविले आहेत.
R व P वर्णपट पट्टांच्या सापेक्ष तीव्रता रेणूच्या प्राथमिक अवस्थेमधील परिभ्रमण ऊर्जा वितरणावर अवलंबून असते. हे ऊर्जा वितरण मॅक्सवेल बोल्टसमान ऊर्जा वितरण नियमानुसार होत असते. आ. ११ मध्ये R व P वर्णपट पट्टांच्या तीव्रतेत तापमानानुसार (T०के.) होणारे बदल दाखविले आहेत.
या आकृतीच्या सुलभतेकरिता B’ = B” असे गृहीत धरले आहे. मागे वर्णन केल्याप्रमाणे रेणूच्या कंपन परिभ्रमण वर्णपट पट्टातील घटक वर्णपट, रेषांमधील अंतर, वाढत्या कंप्रतेनुसार कमी होत जाते व त्या एका ठराविक कंप्रता सीमेपर्यंत येऊन थांबल्यासारख्या दिसतात. या कंप्रता सीमेच्या पलीकडील उच्च कंप्रता भागाकरिता आपाती प्रकाश ऊर्जेचे शोषण अखंडित स्वरूपाचे होते. कंप्रता सीमेपेक्षा कमी कंप्रतांकरिता ते पृथक् व विवेचक स्वरूपाचे असते, हे लक्षात घेण्यासारखे आहे.
या कंप्रता सीमेपाशी रेणूचे विच्छेदन होते असे दाखविता येते. कंप्रता सीमेच्या मूल्यावरून आवश्यक अशा विच्छेदन ऊर्जेचे मूल्य काढता येते प्रकाश ऊर्जा शोषणामुळे असा प्रकारे मुक्त केलेले अणू निरनिराळ्या उत्तेजित अवस्थांत जाऊ शकत असल्यामुळे असे निश्चित केलेले ऊर्जा मूल्य हे ऊष्मारासायनिक पद्धतीने काढलेल्या विच्छेदन मूल्याशी एकरूप असत नाही. अर्थात या दोन मूल्यांमध्ये निश्चितपणे निकटचा संबंध असतो.
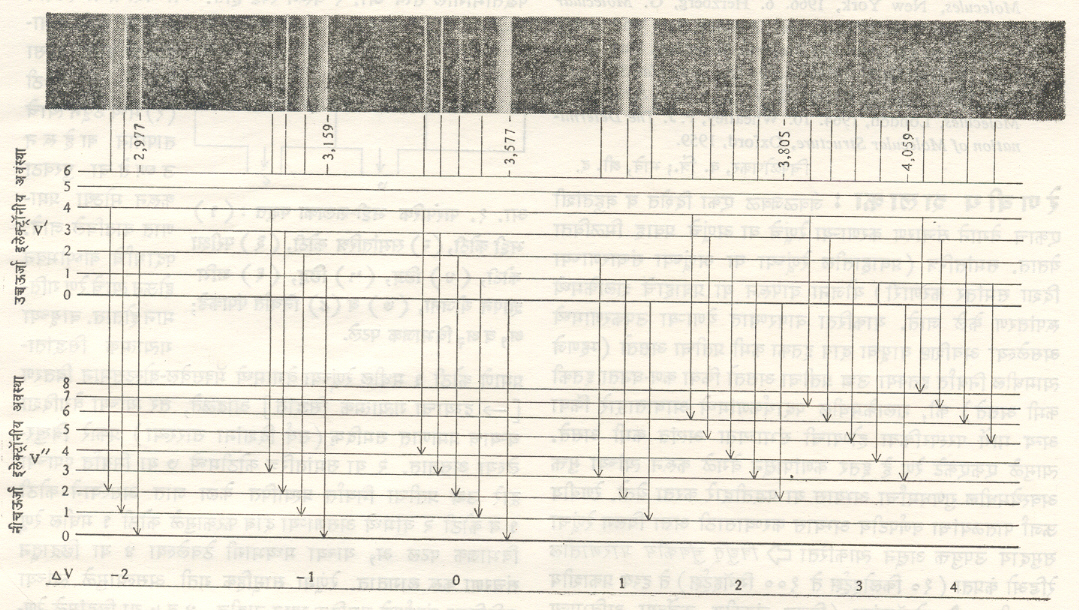
(३) इलेक्ट्रॉनीय वर्णपट : हा रेणवीय वर्णपटाचे सर्वसामान्य स्वरूप निर्देशित करतो, असे म्हणता येते. अणूप्रमाणेच रेणूमध्ये सुद्धा इलेक्ट्रॉनांना निरनिराळ्या ऊर्जा पातळ्या असतात. इलेक्ट्रॉनीय संक्रमणाप्रमाणे निरनिराळ्या ऊर्जा पातळ्या असतात. इलेक्ट्रॉनीय संक्रमणामध्ये रेणूच्या इतर प्रकारच्या ऊर्जातही बदल होत असल्यामुळे वर्णपटामध्ये एका रेषेऐवजी पट्टांच्या श्रेणी मिळतात. त्यांतील प्रत्येक पट्ट रेणूच्या कंपन ऊर्जेत झालेल्या बदलामुळे निर्माण होत असल्यामुळे त्याच्याशी v” व v’ या कंपन पुंजांकांची ठराविक मूल्ये निगडित असतात.
![]()
पट्टातील सूक्ष्म संरचना परिभ्रमण ऊर्जेतील झालेल्या बदलामुळे मिळते. इलेक्ट्रॉनीय अवस्थेत बदल झाला असता, रेणूमधील आणवीय अंतर व निरूढी परिबल विशेषक कंप्रता νo यांच्या मूल्यांत फरक पडत असल्यामुळे पट्टातील परिभ्रमण वर्णपट रेषा समांतर नसतात. त्यांमधील अंतर कमी होत जाते. अंती त्या पट्टाच्या उच्च कंप्रता किंवा निम्न कंप्रता परिसीमेवर (पट्टशीर्षावर) एकवटतात. जर B’–B” धन मूल्याचे असेल, तर वर्णपट रेषा उच्च कंप्रता परिसीमेवर एकत्रित होतात. जर B’ –B” ऋण मूल्याचे असेल, तर याउलट परिस्थिती मिळते. इलेक्ट्रॉनीय संक्रमणाकरिता सामान्य सूत्र खालील स्वरूप धारण करते.
|
hn |
= (Ee’ – Ee”) + (Ev’ – Ev”) + (Er’ – Er”) |
|
= h (ne + nv + nr) |
|
|
= h (nev + nr) … (२३) |
वरील सूत्रात Ee’, Ev’, Er’ उत्तेजित अवस्थेकरिता अनुक्रमे इलेक्ट्रॉनीय, कंपन आणि परिभ्रमण ऊर्जा दाखवितात. Ee²इ. राशी प्राथमिक अवस्थेकरिता असणारी त्यांची मूल्ये दर्शवितात. प्रयोगात आढळणारे विविध पट्ट νoपेक्षा कमी किंवा जास्त कंप्रतेचे असू शकतात कारण νoयाला धन किंवा ऋण मूल्ये असू शकतात. प्रत्येक पट्टात R आणि P शाखांच्या स्वरूपात परिभ्रमण रेषा मिळतात. इलेक्ट्रॉनीय पट्टांचे मूल्य मुख्यत्वेकरून त्यांच्या कंपन ऊर्जा पातळीवरून निश्चित होत असल्यामुळे पुढील विवेचन त्यांच्याच संदर्भात केले आहे.
इलेक्ट्रॉनीय ऊर्जा संक्रमणाध्ये पुढील विशेष गोष्टी आढळतात : (१) एकाच इलेक्ट्रॉनीय ऊर्जा पातळीमधील दोन कंप्रता उपपातळ्यांमध्ये संक्रमण होते, तेव्हा ∆v = ± 1 ही निवड अट लागू असते पण जेव्हा दोन निरनिराळ्या इलेक्ट्रॉनीय पातळ्यांमधील दोन कंप्रता पातळ्यांमध्ये संक्रमण होते, तेव्हा त्याकरिता हे बंधन रहात नाही. फ्रांक-काँडन तत्त्वानुसार (जेम्स फ्रांक व ई. यू. काँडन यांनी मांडलेल्या या तत्त्वाचे सविस्तर विवेचन पुढे दिले आहे) येणारे निर्बंध मात्र त्यावर पडतात. (२) दोन इलेक्ट्रॉनीय पातळ्यांकरिता स्थितिज ऊर्जा वक्र निरनिराळ्या प्रकारचे असतात आणि त्यामुळे या दोन्ही प्रकारच्या स्थितींकरिता re, I व k यांची मूल्ये वेगळी असतात. (३) इलेक्ट्रॉनीय पट्टाची सापेक्ष तीव्रता पुढील गोष्टींवर अवलंबून असते : (अ) प्राथमिक अवस्थेत कंपन ऊर्जेचे रेणूंमध्ये असणारे वितरण, (आ) कोणत्याही एका मूळ ऊर्जा पातळीपासून निरनिराळ्या अंतिम पातळ्यांमध्ये संक्रमण होण्याची संभाव्यता अथवा संक्रमण संभाव्यता. (४) कोणत्याही एका इलेक्ट्रॉनीय पट्टातील सूक्ष्म रचना परिभ्रमणातील बदलामुळे मिळते. याकरिता निवड नियम ∆J = 0, ± 1 हा असतो. (५) स्थितिज ऊर्जा वक्राचे स्वरूप इलेक्ट्रॉनीय स्थितीवर म्हणजे रेणूमधील त्यांच्या मांडणीवर अवलंबून असते. काही इलेक्ट्रॉनीय स्थितींकरिता घटक अणूंमधील प्रेरणा आकर्षणी स्वरूपाची असेल, तर त्याच दोन अणूंकरिता निराळ्या इलेक्ट्रॉनीय मांडणीकरिता तिचे स्वरूप बदलून ती प्रतिसारक प्रकारची होऊ शकते. (६) द्वि-आणवीय इलेक्ट्रॉनीय वर्णपटाचा अभ्यास त्याचे उत्सर्जन चालू असताना केला जातो. या प्रकारच्या प्रयोगात पदार्थाचे तापमान उच्च प्रतीचे असल्यामुळे अनेक उच्च ऊर्जा पातळ्यांची समष्टी चांगल्या प्रतीची असते. त्यामुळे त्याच्या इलेक्ट्रॉनीय वर्णपटात विविध उत्तेजित पातळ्यांपासून अनेक नीच ऊर्जा पातळ्यांपर्यंतच्या संक्रमणांचा समावेश झालेला आढळतो. एकाच उत्तेजित पातळीपासून (v’) निरनिराळ्या नीच ऊर्जा पातळ्यांमध्ये संक्रमण झाल्यामुळे जो वर्णपट रेषा समूह मिळतो, त्यास v v’− श्रेणी असे म्हणतात. (७) बहु-आणवीय रेणूच्या इलेक्ट्रॉनीय वर्णपटाचे संशोधन बहुशः नीच तापमानाकरिता मिळालेल्या त्यांच्या शोषण वर्णपटाद्वारे करतात. या परिस्थितीत v” = 0 या प्राथमिक पातळीत असणाऱ्या रेणूंची संख्या फार मोठी असते. शोषण वर्णपटात v” = 0 या एकाच पातळीपासून (शून्यापासून मोठ्या मूल्यापर्यंत) निरनिराळ्या v’ मूल्यापर्यंतच्या संक्रमाणांपासून मिळालेली एक वर्णपट रेषा श्रेणी (v’− श्रेणी) मिळते.
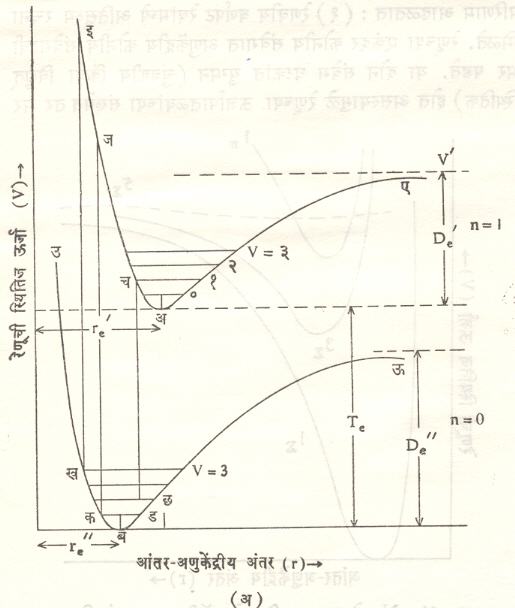
फ्रांक काँडन तत्व : पुंजयामिकीचा उपयोग करून या तत्वाचे विशदीकरण करता येते. माक्स बोर्न व जे. आर्. ओपेनहायमर यांची आसन्नीकरण (खऱ्या मूल्याच्या जवळात जवळचे मूल्य काढण्याची) पद्धत वापरून रेणूच्या विविध इलेक्ट्रॉनीय अवस्थांकरिता संक्रमण संभाव्यता मूल्ये निश्चित करता येतात. या विवेचनाकरिता परिभ्रमण ऊर्जेतील बदलामुळे होणारे सूक्ष्म परिणाम विचारात घेतलेले नाहीत. आ. १३ (अ) मध्ये व या ठिकाणी दाखविलेल्या रेणूत दोन्ही घटक निम्नतम ऊर्जा अवस्थेत आहेत, असे दाखविले आहे. याकरिता आंतर अणुकेंद्रीय अंतर re²असून विच्छेदन ऊर्जा De²एवढी आहे. अ येथे रेणूमधील एक अणू निम्नतम, तर दुसरा उत्तेजित इलेक्ट्रॉनीय अवस्थेत आहे, असे मानले जाते. या अवस्थेकरिता इलेक्ट्रॉन उत्तेजन ऊर्जा Te असून आंतर अणुकेंद्रीय अंतर re², तर विच्छेदन ऊर्जा De²एवढी आहे. कोठी तापमानाकरिता बहुतेक सर्व रेणू व या अवस्थेत असतात. या अवस्थेत त्याची समग्र ऊर्जा निमनतम मूल्याची असून कंपन ऊर्जा Ev²एवढी असते, त्यामुळे रेणू कड या रेषेवर कंपन आंदोलने करतो. तो जेव्हा या रेषेवरील क व ड या परिवर्तन बिंदूंवर असतो, तेव्हा त्याची गतिज ऊर्जा शून्य, तर कंपन स्थितिज ऊर्जा महत्तम असते. N = 0, v = 0 या प्रागतिक अवस्थेपासून संक्रमणे सुरू होतात, हे उघड आहे. संक्रमणामध्ये संवेग अक्षय राहिला पाहिजे व परिवर्तन बिंदू निर्देशित केलेल्या अवस्थेत रेणू सगळ्यात जास्त काळ घालवितो.

या गोष्टी विचारात घेता प्राथमिक पातळीच्या परिवर्तन बिंदूपासून उत्तेजित पातळीच्या परिवर्तन बिंदूपर्यंत संक्रमण होण्याची संभाव्यता सगळ्यात जास्त राहील, असा निष्कर्ष काढता येतो. (पुंज सिद्धांताप्रमाणे आंदोलन रेषेच्या मध्यभागापासून संक्रमण होण्याची संभाव्यता सगळ्यात जास्त असते, तर संक्रमणे परिवर्तन बिंदूपासून होतात हा निष्कर्ष रूढ भौतिकीप्रमाणे मिळतो. दुसरा निष्कर्ष गृहीत धरल्यास अंतिम विवेचनात विशेष बदल होत नाही, अस दाखविता येते). जर re² < < re’ [आ. १३ (अ)] तर कड पातळीपासून ज पर्यंत संक्रमण होईल. ज हा बिंदू ए पेक्षा जास्त उंचीवर असल्यामुळे वरच्यास्थितीत गेलेला रेणू एक आंदोलन (मार्ग–इजचअए) पूर्ण करून विच्छेदन पावेल. याच तत्त्वानुसार छ पातळी ते च हे संक्रमण बहुसंभाव्य होईल. जर re ≈ re’ [आ. १३ (आ)] याकरिता काढलेले वक्र पाहिले, तर त्यापासून अल्प कंपन ऊर्जा प्राथमिक पातळीपासून (vv ≈ 0) कमी कंपन ऊर्जा पातळ्यांपर्यंत (v’≈ 0) उत्तेजित अवस्थेत संक्रमण होईल.
जर re² > re’ असेल, तर re² = re’ या प्रकाराप्रमाणेच निष्कर्ष निघतात.
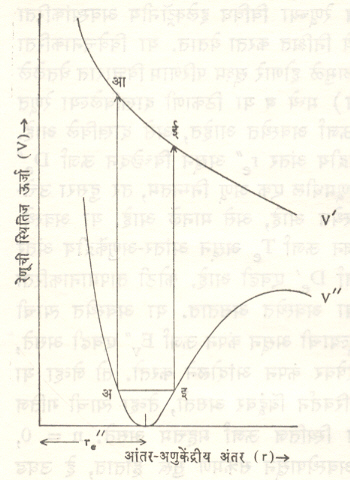 आ. १४ मध्ये एक इलेक्ट्रॉनीय संक्रमण प्रकार दाखविला आहे. यामध्ये अंतिम अवस्था प्रतिसारक स्वरूपाची आहे. यामधील अंतिम बिंदू स्थितिज ऊर्जा वक्राच्या डाव्या विभागावर V’ पेक्षा जास्त उंचीवर असल्यामुळे शोषणानंतर रेणूचे विच्छेदन होते. या क्रियेमध्ये एका लघुतम कंप्रतेपेक्षा जास्त कंप्रतेच्या सर्व प्रकाशतरंगाचे शोषण होते. मागील दोन प्रकारांमध्ये हे शोषण काही पृथक् विवेचक मूल्यांच्या प्रकाशतरंगाकरिताच घडून येते. शोषण क्रियेत मिळणाऱ्या अशा प्रकारच्या संततीयाची लघुतम सीमा प्रयोगाने मिळविली असता त्यापासून De’ या बंधविच्छेदन ऊर्जेचे गणन करता येते.
आ. १४ मध्ये एक इलेक्ट्रॉनीय संक्रमण प्रकार दाखविला आहे. यामध्ये अंतिम अवस्था प्रतिसारक स्वरूपाची आहे. यामधील अंतिम बिंदू स्थितिज ऊर्जा वक्राच्या डाव्या विभागावर V’ पेक्षा जास्त उंचीवर असल्यामुळे शोषणानंतर रेणूचे विच्छेदन होते. या क्रियेमध्ये एका लघुतम कंप्रतेपेक्षा जास्त कंप्रतेच्या सर्व प्रकाशतरंगाचे शोषण होते. मागील दोन प्रकारांमध्ये हे शोषण काही पृथक् विवेचक मूल्यांच्या प्रकाशतरंगाकरिताच घडून येते. शोषण क्रियेत मिळणाऱ्या अशा प्रकारच्या संततीयाची लघुतम सीमा प्रयोगाने मिळविली असता त्यापासून De’ या बंधविच्छेदन ऊर्जेचे गणन करता येते.
रेणवीय ऊर्जा अवस्था व परिवलन : आतापर्यंतच्या विवेचनात इलेक्ट्रॉन परिवलन गतीचे परिणाम विचारात घेतले गेले नाहीत. रेणूमधील इलेक्ट्रॉनाच्या परिवलनामुळे रेणूमध्ये परिवलन-परिवलन किंवा परिवलन-कक्षीय प्रकारच्या परस्परक्रिया अस्तित्वात येतात. यामुळे रेणूच्या ऊर्जेमध्ये पडणाऱ्या सरळ फरकाचे मूल्य महत्त्वाचे असत नाही. त्यामुळे रेणवीय वर्णपट रेषांना बहुघटकी संरचना मिळते. त्याबरोबरच संक्रमण निवड नियमावर काही निर्बंध येतात. इलेक्ट्रॉन परिवलनामुळे दोन घटक अणूंमधील परस्परक्रियेवर सुद्धा मोठ्या प्रमाणात परिणाम होतो. रेणूमधील प्रत्येक इलेक्ट्रॉन प्रणालीमधील त्याच्या नियुक्त जागी प्रस्थापित करीत जात आहोत अशी कल्पना केली, तर त्यामुळे अणूंमधील बंधाच्या सामर्थ्यात वाढ किंवा घट होत जाते. ज्या इलेक्ट्रॉनामुळे घटक अणूंमधील आकर्षणी प्रेरणेत वृद्धी होते त्यास बंधक इलेक्ट्रॉन म्हणतात. ज्या इलेक्ट्रॉनामुळे या प्रेरणेत घट होते त्यास प्रतिबंधक इलेक्ट्रॉन अशी संज्ञा दिली जाते. परिवलन परिणाम विचारात घेऊन रेणवीय अवस्था कशा निर्देशित केल्या जात याचे प्राथमिक विवेचन द्वि-आणवीय रेणूच्या संदर्भात पुढे दिले आहे. द्वि-आणवीय रेणूमधील इलेक्ट्रॉनावर जे आंतरिक विद्युत् स्थितिक क्षेत्र कार्य करते त्यास x या अणुकेंद्रे जोडणाऱ्या रेषेभोवती सममिती असते. हे क्षेत्र अणुकेंद्रावरील धन विद्युत् भार व इलेक्ट्रॉनांचे ऋण विद्युत् भार वितरण यांमुळे निर्माण झालेले असते. कक्षीय गतीमुळे रेणूमधील सर्व इलेक्ट्रॉनांचा L* हा जर सदिश कोनीय संवेग असेल, तर आंतरिक विद्युत् स्थितिक क्षेत्रामुळे या सदिशाला परांचन गती येते. ही गती इतकी जलद असते की, तीमुळे तिच्या x दिशेतील घटकालाच निश्चित मूल्य असते. ∧ या पुंजांकाच्या साह्याने कोनीय संवेग घटकाचे पुंजीकरण केले जाते. येथे ∧ = 0, 1, 2, 3, …., L. तदनुरूप रेणवीय अवस्थांकरिता ∑, π, ∆, Φअशी चिन्हे वापरली जातात. रेणूमधील सर्व इलेक्ट्रॉनांच्या परिवलनाचा परिणामी सदिश S* असेल, तर x या दिशेतील त्याच्या घटकांची मूल्ये पुंजीकरण क्रियेनंतर ∑ या चिन्हाने दाखविली जातात. ∆ ∧ = 0, + 1 व ∆s = 0 हे यामधील संक्रमणाकरिता निवड नियम असतात.
|∑| = +s, s – 1, s – 2,……., −s.
l ∆ + ∑ l या संकलित कोनीय संवेगाला Ω म्हणतात. ∆ ∑यांच्यामधील युग्मनामुळे Ω या राशीला पुंजीकरण
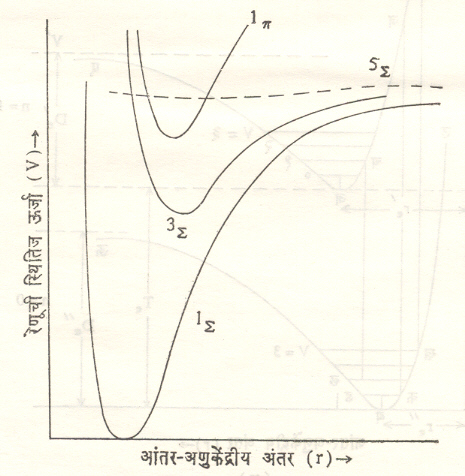
नियम लावून पूर्णांक किंवा अर्धपूर्णांक मूल्य असते, असे दाखविता येते. कोणत्याही रेणवीय अवस्थेचे बहुगुणनत्व 2s + 1 या सूत्राने मिळते. N2 रेणूच्या काही इलेक्ट्रॉनीय अवस्थांकरिता स्थितिज ऊर्जा वक्र आ. १५ मध्ये दाखविले आहेत. N2 रेणूच्या उत्सर्जन वर्णपटाच्या काही इलेक्ट्रॉनीय अवस्था आ. १६ मध्ये दाखविल्या आहेत.
अणुकेंद्रीय परिवलन : बहुतेक अणुकेंद्रांना परिवलन संवेग असतो तो I या पुंजांकाने निर्देशित केला जातो. परिवलनाचे मूल्य Iħया सूत्राने मिळते (ħ = h/2π). प्रोटॉनाला±१/२ परिवलन असते. त्यामुळे हायड्रोजन रेणूमध्ये एकत्रित येणाऱ्या प्रोटॉनांच्या परिवलनाकरिता दोन सापेक्ष दिकविन्यास शक्य असतात. ऑर्थोहायड्रोजन रेणूमध्ये केंद्रीय परिवलने समांतर असतात. याकरिता विषम (J) परिभ्रमण अवस्था अतिसंभाव्य असतात. पॅराहायड्रोजनामध्ये परिवलने प्रतिसमांतर असतात. त्याकरिता सम (J) परिभ्रमण अवस्था अतिसंभाव्य असतात.
अणुकेंद्रीय परिवलन गती लक्षात घेता रेणवीय वर्णपटामध्ये पुढील परिणाम आढळतात : (१) रेणवीय वर्णपट रेषांमध्ये अतिसूक्ष्म रचना मिळते. रेणूच्या एकंदर कोनीय संवेगात अणुकेंद्रीय कोनीय संवेगाची भर पडते. या दोन संवेग घटकांत युग्मन (चुंबकीय किंवा विद्युत् स्थितिक) होत असल्यामुळे रेणूच्या ऊर्जापातळ्यांच्या संस्थेत तर भर पडतेच पण त्यामुळेच अतिसूक्ष्म ऊर्जा फरक आढळतो. इलेक्ट्रॉनीय वर्णपटात त्यामुळे पडणारा फरक प्रयोगाने मापनकरण्याइतका मोठ्या मूल्याचा नसतो. कमी कंप्रतेच्या शुद्ध परिभ्रमण वर्णपटामध्ये (किंवा रामन वर्णपटात) या प्रकारच्या अतिसूक्ष्म रचनेचा शोध घेणे शक्य होते. (२) अणुकेंद्रीय परिवलन संवेग विचारात
घेतला असता, तर त्यामुळे संक्रमण निवड नियमामध्ये थोडा फरक पडतो. जी संक्रमणे पूर्वी संपूर्णपणे निषिद्ध होती ती यामुळे पुष्कळ कमी प्रमाणात का होईना अनुज्ञान होतात. प्रत्यक्ष रेणवीय वर्णपटामध्ये त्यामुळे एकामागून येणाऱ्या अनुक्रमी रेणूंचे दोन विभाग पडतात. एका विभागातील रेषा उच्च तीव्रतेच्या असतात, तर दुसऱ्या अल्प तीव्रतेच्या असतात. या दोन प्रकारच्या रेषांच्या तीव्रतेच्या गुणोत्तरावरून रेणूच्या पराणामी अणुकेंद्रीय परिवलन संवेगाचे मूल्य काढता येते. रेषांच्या तीव्रतेत आढळणारा प्रत्यावर्ती फरक हा आ. १७ वरून स्पष्ट होईल. (३) अणुकेंद्रीय परिवलन मूल्यावरून त्याकरिता यथार्थ असणारी सांख्यिकीय पद्धती निश्चित करता येते. अणुकेंद्राचा परिणामी परिवलन संवेग पुंजांक जर अपूर्णांक असेल, तर ते अणुकेंद्र फेर्मी−डिरॅफ सांख्यिकी व तो जर पूर्णांक किंवा शून्य मूल्याचा असेल, तर अणुकेंद्र बोस-आइनस्टाइन सांख्यिकीचे पालन करते.
रेणवीय शलाका : वायुरूप पदार्थामध्ये रेणवीय वर्णपटाचे जेव्हा निरीक्षण केले जाते तेव्हा त्यामधील वायू कण एकमेकांच्या खूप जवळ येत असतात व त्यांचे परस्परांबरोबर आघातही होत असतात. या प्रक्रियेत कणांमध्ये परस्परक्रिया होऊन त्यामुळे त्यांच्या ऊर्जा पातळ्यांत (आणि म्हणून वर्णपट रेषेच्या कंप्रतेत) सूक्ष्म असा बदल घडून येतो.
 अशा परिस्थितीत मिळणारा वर्णपट हा मुक्त एकेरी रेणूचा अथवा अणूचा वर्णपट असत नाही. रेणवीय शलाका पद्धतीत शलाका कणाची घनफळ घनता इतकी कमी असते की, त्यांमध्ये परस्पर आघात होण्याची संभाव्यता नगण्य असते. या पद्धतीचा उपयोग करून रेणू किंवा अणू यांच्या शलाका मिळतात. येथील वर्णन फक्त रेणूंच्या संदर्भात केले असले, तरी योग्य बदलाने ते अणूंकरिताही यथार्थ आहे. रेणवीय शलाका पद्धतीमध्ये एकेरी रेणूचा वर्णपट मिळू शकतो. फोटॉनाचा (शोषण क्रियेद्वारे) एषणी (मापन करण्यासाठी उपयोगात आणावयाची प्रयुक्ती) म्हणून उपयोग करून या पद्धतीद्वारे रेणवीय ऊर्जा पातळ्यांचे अचूकपणे मापन करता येते. रेडिओ कंप्रता दृश्य कंप्रतेच्या वर्णपट रेषांशी संबंधित सर्व ऊर्जा पातळ्यांचा अशा प्रकारे शोध घेता येतो. रेणवीय शलाका पद्धतीचा उपयोग करून रेणवीय वर्णपट रेषांच्या सूक्ष्म व अतिसूक्ष्म रचना, रेणूंच्या संरचना व त्यांमध्ये घडणाऱ्या विक्रिया या सर्वांचा अभ्यास करता येतो. हिचा उपयोग रेणवीय परस्पर आघातांद्वारे होणाऱ्या रासायनिक व जैव प्रक्रिया आणि विक्रिया यांविषयीचे ज्ञान करून घेण्याकरिता केला जातो [⟶ रेणवीय शलाका].
अशा परिस्थितीत मिळणारा वर्णपट हा मुक्त एकेरी रेणूचा अथवा अणूचा वर्णपट असत नाही. रेणवीय शलाका पद्धतीत शलाका कणाची घनफळ घनता इतकी कमी असते की, त्यांमध्ये परस्पर आघात होण्याची संभाव्यता नगण्य असते. या पद्धतीचा उपयोग करून रेणू किंवा अणू यांच्या शलाका मिळतात. येथील वर्णन फक्त रेणूंच्या संदर्भात केले असले, तरी योग्य बदलाने ते अणूंकरिताही यथार्थ आहे. रेणवीय शलाका पद्धतीमध्ये एकेरी रेणूचा वर्णपट मिळू शकतो. फोटॉनाचा (शोषण क्रियेद्वारे) एषणी (मापन करण्यासाठी उपयोगात आणावयाची प्रयुक्ती) म्हणून उपयोग करून या पद्धतीद्वारे रेणवीय ऊर्जा पातळ्यांचे अचूकपणे मापन करता येते. रेडिओ कंप्रता दृश्य कंप्रतेच्या वर्णपट रेषांशी संबंधित सर्व ऊर्जा पातळ्यांचा अशा प्रकारे शोध घेता येतो. रेणवीय शलाका पद्धतीचा उपयोग करून रेणवीय वर्णपट रेषांच्या सूक्ष्म व अतिसूक्ष्म रचना, रेणूंच्या संरचना व त्यांमध्ये घडणाऱ्या विक्रिया या सर्वांचा अभ्यास करता येतो. हिचा उपयोग रेणवीय परस्पर आघातांद्वारे होणाऱ्या रासायनिक व जैव प्रक्रिया आणि विक्रिया यांविषयीचे ज्ञान करून घेण्याकरिता केला जातो [⟶ रेणवीय शलाका].
संदर्भ : 1. Barrow, G. M. Introduction to Molecular Spectroscopy, New York, 1962.
2. Brand, J. C. D. Speakman, J. C. Molecular Structure, London, 1964.
3. Dixon, R. N. Spectroscopy and Structure, London, 1965.
4. Dunford, H. B. Elements of Diatomic Molecular Spectra, Reading, Mass, 1968.
5. Herzberg, G. Molecular Spectra and Molecular Structure, 2 Vols. New York, 1962.
7. Herzberg, G. Spectra of Diatomic Molecules, New York, 1961.
8. King, G. W. Spectroscopy and Molecules, New York, 1964.
9. Linnet, J. W. Electronic Structure of Molecules, London, 1964.
10. Wheatley, P. J. The Determination of Molecular Structure, Oxford, 1959.
चिपळोणकर, व. त्रिं. भावे, श्री. द.
“