यथादर्शन

यथादर्शन :  चराचर विश्वातील वस्तूंचे दर्शन ज्या रीतीने व्हावयाचे, जसे व्हावयाचे, त्याविषयीच्या शास्त्राला ‘यथादर्शन’ (पर्स्पेक्टिव्ह) असे म्हणतात. या वस्तू आपणास कशा दिसाव्यात, याविषयीचे नियमन निसर्गानेच करून ठेवलेले आहे. उदा., दूरच्या वस्तू लहान आणि जवळच्या मोठ्या दिसतात. रेल्वेचे पक्के समांतर रूळ दूर कुठेतरी, क्षितिजाजवळ, एका बिंदूत विलीन झाल्यासारखे भासतात (आ. ८). विजेच्या खांबांची दूरवर पोहोचलेली रांग पाहताना हे खांब उत्तरोत्तर लहान होत, शेवटी एका बिंदूत विलय पावल्यासारखे भासतात (आ. ७). जवळच्या डोंगरकपारी राकट, विक्राळ दिसतात दुरून तेच डोंगर ‘साजरे’ दिसतात. ही या नियमनाचीच किमया असते. या किमयेशिवाय वस्तूंचे दर्शन शक्यच नसते.

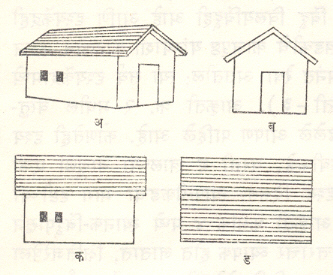
वस्तूंना भौमितिक परिमाणे असतात. लांबी, रुंदी, जाडी या परिमाणांशिवाय वस्तूंना व्याप्ती आणि अस्तित्व मिळणे शक्य नसते. घन भूमितीमध्ये या परिमाणांचा विचार केला जातो. अशा वेळी वस्तूचे समोरून, डाव्या बाजूकडून, उजव्या बाजूकडून, मागच्या बाजूकडून तसेच वरून आणि तळाखालून सुद्धा दिसणारे नकाशे तयार केले जातात. आकृती क्र. १ मध्ये ‘अ’ ही आकृती आ. १ आपणाला घर म्हणून दिसते. ती समोरून पाहिल्यास ‘ब’ मधल्यासारखी, बाजूने पाहिल्यास ‘क’ मधल्यासारखी व वरून ‘ड’ मधल्यासारखी दिसेल. पण तिचा घरपणा डोळ्यांनी अनुभवता येण्यासाठी ‘अ’ मधल्यासारख्या आकृत्यांचाच उपयोग होऊ शकतो. ‘ब, क, ड’ सारख्या भौमितिक आकृत्या हा दृश्यानुभव देण्यास असमर्थ आहेत. घराचे मोजमाप, परिमाणे देणे, त्याविषयी संपूर्ण भौतिक, वस्तुनिष्ठ माहिती पुरविणे हे कार्य भौमितिक आकृत्यांमधून करता येते. पण घरपणाचा ‘चाक्षुष’ अनुभव त्यातून साध्य होणे अशक्य. हे कार्य यथादर्शनातूनच सिद्ध होत असते. मानवी दर्शनाविषयीची ही वस्तुस्थिती आहे. मानवनिर्मित कॅमेराही याला अपवाद नाही. कारण मानवी नेत्र आणि कॅमेरा या दोहोंत विलक्षण साम्य आहे. दोन्ही ठिकाणी भिंगातून प्रकाशकिरण आत घेऊन केंद्रित केले जातात आणि या केंद्रस्थानी प्रतिबिंब साकार होते. फरक इतकाच की, मानव दोन डोळ्यांनी पाहतो आणि त्यातून उपलब्ध होणाऱ्या दोन वेगळ्या बिंबांचे संयोजन मज्जासंस्थेकडून केले जाते. भूमिती ही जशी गणिताची एक शाखा आहे, तद्वतच यथादर्शन हे वस्तूंचे दर्शन काटेकोर गणिती नियमांनी आकारित करून दाखविणारे गणिती अंगाचे शास्त्र आहे. 

पश्चिमी प्रबोधनकाळात या यथादर्शनीय नियमनाकडे कलावंतांचे लक्ष प्रथमच वेधले गेले आणि हे नियम शोधून शास्त्र म्हणून त्याचा पाया घातला गेला. ग्रीक संस्कृती आणि तत्त्वज्ञान यांची पार्श्वभूमी त्यासाठी पोषक ठरली. प्रकाशाचा प्रवास हा सरळ रेषेतच होत असतो, याचे ज्ञान ग्रीक भौमितीय तत्त्वज्ञ आणि कलावंत यांना झालेले होते. यूक्लिड, पायथॅगोरस यांसारख्या तत्त्वज्ञांनी या ज्ञानशाखेचा पाया घालून दिला होता. झीनॉक्राटीझ आणि पॉलिक्लीटस यांनी दृश्यकलांच्या अंगाने त्याचा विचार केला होता. प्लेटो या तत्त्वज्ञाला अनुकृतिशील (इमिटेटिव्ह) चित्र-शिल्पकलांऐवजी या भौमितिक आकारातच सौंदर्य दिसले होते. कारण प्लेटोला ज्या मूलभूत सत्त्वकल्पांचा (आयडियाज) ध्यास लागला होता, ते सत्त्वकल्प त्याला दृश्यविश्वातील वस्तूंमध्ये त्रिकोण, चौकोन, घन, शंकू, दंड, गोल इ. भौमितिक आकारांत भावत होते. प्लेटोच्या मताप्रमाणे सत्त्वांचा वेध फक्त तत्त्वज्ञच घेऊ शकतो आणि उपरिनिर्दिष्ट तत्त्वज्ञांनीच भूमितीशास्त्राचा पाया घातला होता. शिवाय सर्व वस्तूमात्राच्या ठायी हे दृश्य सत्त्वकल्प उपस्थित असतात. याविषयी शंका वाटण्याचे काहीही कारण आजही नाही. वस्तूमधील सत्त्वांकडे दुर्लक्ष करून वस्तूंची, म्हणजे प्लेटोच्या भाषेत, भासमानांची (ॲपीअरन्सेस) अनुकृती करणे, प्लेटोला निषिद्ध वाटले होते. ॲरिस्टॉटलने अनुकृतिशील कलेची बाजू मांडताना दृश्यकलांवर विशेष भाष्य केले नाही. पण त्याच्या तत्त्वज्ञानव्यूहामधून दृश्यकलांना नवी स्फूर्ती मिळाली. निसर्ग स्वयंपूर्ण आहे. प्लेटो कल्पितो, त्याप्रमाणे सत्त्वे ही या विश्वापलीकडील कुठल्यातरी गूढ जगात निवास करीत नसतात, ती या निसर्गातच ओतप्रोत भरलेली आहेत. म्हणून निसर्ग हा सत्त्वांप्रमाणे स्वयंसत्य, स्वयंशिव आणि स्वयंसुंदर असतो, ही ॲरिस्टॉटलच्या धर्तीची विचारसरणी हे प्रबोधनकालीन शास्त्रे आणि कला यांच्या विकासामागील प्रबळ प्रेरणास्थान ठरले. निसर्ग जर स्वयंसत्य, शिव आणि सुंदर असेल, तर त्याच्या अचूक अनुकृतीमधून या तिन्हींची सिद्धी निश्चितच होणार. म्हणून प्रबोधनकालीन कलावंत अशा अचूक अनुकृतीच्या ईर्षेने झपाटला गेला. प्रकाश हे निसर्गाचे अंग. वस्तूकडून प्रकाशाला अवरोध होत असताना छाया उपलब्ध होते, म्हणून तीही निसर्गाचेच अंग. या छायाप्रकाशाचा वेध घेण्याचे प्रयत्न हिरीरीने झाले. यथादर्शनीय नियमन हेही निसर्गप्राप्त, निसर्गांग आणि निसर्गकार्य आहे, म्हणून त्याचा पायाशुद्ध अभ्यास करून अनुकृती सर्वांगपरिपूर्ण करण्याचे हरप्रयत्न झाले. निसर्गातील प्रत्यक्ष वस्तूंना भासमाने म्हणून वास्तवतेच्या संदर्भात प्लेटोने त्यांना दुसऱ्या क्रमांकाचे स्थान दिले होते. त्यांची अनुकृती करण्याच्या प्रयत्नात सत्त्वकल्पांकडे दुर्लक्ष होण्याचा प्रमाद घडतो, सत्त्वकल्प फक्त तत्त्वज्ञवृत्तीनेच आकलन होऊ शकतात, असे प्लेटोचे म्हणणे होते. यथादर्शनकारांनी या भासमानामागील गणित उलगडून दाखविले, त्यामागे प्लेटोप्रणीत तत्त्वज्ञवृत्ती जागृत होती, असे दिसून येते.

यथादर्शनाचा शास्त्रीय पाया घालण्याचे कार्य फिलिप्पो ब्रूनेल्लेस्की (१३७७-१४४६) आणि ⇨लेओन बात्तीस्ता आल्बेर्ती (१४०४-७२) या दोन विचारवंतांनी केले. हे दोघेही प्रामुख्याने वास्तुकार होते. ब्रूनेल्लेस्कीने एक लक्षणीय प्रयोग केला. यथादर्शनीय नियमानुसार त्याने एक देखावा चित्रित केला. आकाशाचा साक्षात प्रत्यय यावा, म्हणून त्याने ते चंदेरी रंगाने रंगविले. या चित्रफलकाच्या केंद्रस्थानी त्याने एक बारीक (सहजी लक्षात न येणारे) छिद्र ठेवले. प्रेक्षकाने हे चित्र प्रत्यक्षात पहावयाचे नव्हते तर चित्राच्या मागे उभे राहून छिद्राला डोळा लावून आरपार पहावयाचे होते. चित्राच्या बरोबर समोर भिंतीला आरसा लावलेली असून तो चित्राच्याच पातळीवर चित्राला समांतर होता. छिद्रातून आरपार पहाताना आरसा किंवा भिंत यांची जाणीव न होता चित्राचे प्रतिबिंबच फक्त दिसावे, अशी मांडणी केली होती. पण आपण हे चित्र पहात आहोत, असे वाटण्याऐवजी साक्षात निसर्गदृश्यच पहात आहोत, असा भास प्रेक्षकाला होत असे. यथादर्शनीय नियमांच्या अचूक आविष्कारातून निसर्गाचा साक्षात अनुभव देण्याइतकी परमोच्च अनुकृती निष्पन्न होते, हे या प्रयोगातून सिद्ध झाले.

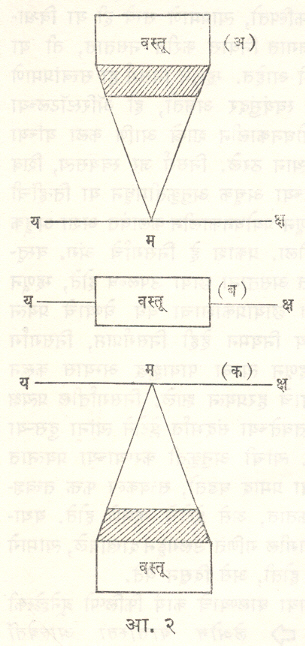एखादी घन वस्तू भूपृष्ठाशी लंबरेषेत सरळ उभी ठेवली असताना विविध अवस्थांमध्ये ती कशी दिसेल, ते आकृती क्रमांक २ मध्ये दाखविले आहे. यातील ‘य-क्ष’ ही क्षितिजरेषा आहे. आकृती ‘अ’ मध्ये वस्तुघन क्षितिजरेषेच्या बराच वर ठेवला आहे. क्षितिजरेषा नेहमी प्रेक्षकाच्या नेत्रपातळीत (आय लेव्हल) असते. त्याअर्थी हा वस्तुघन नेत्रपातळीच्या वर आहे. आकृती ‘ब’ मध्ये तो क्षितिजरेषेच्या म्हणजे नेत्रपातळीच्या ठिकाणी आहे. ‘क’ मध्ये तो नेत्रपातळीच्या म्हणजे क्षितिजाच्या खाली आहे. या तिन्ही उदाहरणांत या घनाचे प्रेक्षकाकडील पृष्ठ प्रेक्षकाला समांतर आहे. म्हणून ते पृष्ठ प्रेक्षकाला सातत्याने दिसेल. मात्र वस्तुघनाची उजवीकडील किंवा डावीकडील पृष्ठे दिसणार नाहीत. पलीकडील पृष्ठ दिसणे हे अर्थातच अशक्य असते. पण विशिष्ट परिस्थितीत वरचे किंवा खालचे पृष्ठ दिसू शकेल. वस्तुघन नेत्रपातळीच्या वरती असेल (आकृती अ) तर खालचे तळपृष्ठ दिसेल. तो नेत्रपातळीच्या खाली असेल (आकृती क) तर वस्तुघनाचे वरचे पृष्ठ दिसेल. आकृती ‘ब’ मध्ये वस्तुघन आ. २ नेत्रपातळीच्या ठिकाणी असल्याने वरचे पृष्ठ किंवा तळपृष्ठही दिसणार नाही. फक्त प्रेक्षकसमांतर पृष्ठ तेवढे दिसेल. वस्तुघनाच्या सहा पृष्ठांपैकी एकच पृष्ठ दिसण्याची ही परम प्रतिबंधक यथादर्शनीय अवस्था म्हणता येईल. आकृती ‘अ’ आणि ‘क’मध्ये वस्तुघनाच्या क्षितिजाकडे जाणाऱ्या, समांतर रेषा ‘म’ या बिंदूमध्ये विलय पावलेल्या दिसतात. म्हणून त्याला ‘विलयबिंदू’ (व्हॅनिशिंग पॉइंट) अशी संज्ञा आहे. आकृती ‘ब’ मधील विलयबिंदू प्रत्यक्षात असूनही दिसत नाही. या यथादर्शनीय अवस्थेत वस्तुपृष्ठांच्या क्षितिजाकडे जाणाऱ्या रेषाच फक्त विलय पावतात. म्हणून एकच विलयबिंदू प्राप्त होतो. आल्बेर्तीने याला ‘एकबिंदू यथादर्शन’ (वन पॉइंट पर्स्पेक्टिव्ह) अशी संज्ञा वापरली. त्याऐवजी आज ‘समांतर यथादर्थन’ (पॅरलल पर्स्पेक्टिव्ह) अशी संज्ञा वापरली जाते. कारण यात वस्तुघनाची प्रेक्षकाकडील बाजू प्रेक्षकसमांतर असते. या उदाहरणातील वस्तुघन अगदी साधा, प्राथमिक असून त्याची प्रेक्षकाच्या संदर्भातील अवस्थाही अगदी प्राथमिक म्हणजे प्रेक्षकसमांतर आहे. पण असे नेहमीच होत नाही. प्रेक्षक संदर्भात वस्तूच्या अवस्था याहून वेगळ्या असू शकतात. त्यांचा विचार करताना वस्तु-प्रेक्षक संबंधातील मूलभूत यथादर्शनीय घटकांचा किंवा तत्त्वांचा विचार करणे आवश्यक असते.

प्रेक्षक काचेच्या खिडकीजवळ उभा असून बाहेरील दृश्य पाहत आहे, अशी कल्पना करू. खिडकीच्या काचेचे पृष्ठ त्याच्या खांद्यांना,आ. ३कपाळाला, म्हणजेच त्याच्या दोन डोळ्यांना जोडणाऱ्या रेषेला समांतर असेल. त्याच्या नासिकेचे मूळ हा त्याच्या नेत्ररेषेचा मध्य आहे. खिडकीसमोर त्याने आपले जे स्थान निश्चित केले आहे, त्याचाही हा मध्यबिंदू आहे. यथादर्शनीय परिभाषेत प्रेक्षकाच्या या स्थानाला ‘स्थानक-बिंदू’ (स्टेशन पॉइंट) म्हणतात. या बिंदूपासून नाकासमोर सरळ निघणारी रेषा क्षितिजरेषेला ज्या बिंदूमध्ये मिळते, तो आपल्या दृश्याचा मध्यबिंदू असेल. याला ‘दृश्यकेंद्र’ (सेंटर ऑफ व्हिजन) अशी संज्ञा आहे (आकृती-३). आकृती क्र. २ मध्ये दिसणारा ‘म’ हा बिंदू विलयबिंदूही आहे आणि दृश्यकेंद्रही आहे. प्रेक्षकपृष्ठ आणि खिडकीचे काचपृष्ठ यांच्याशी काटकोन करून क्षितिजाकडे जाणाऱ्या अनंत रेषा असतील त्या सर्व दृश्यकेंद्रामध्ये विलय पावतील (आकृती-३). आकृती क्र. २ मधील वस्तुघनाच्या संदर्भात हेच घडलेले आपण पाहिले आहे. कोणतेही दृश्य पाहताना उजवीकडे, डावीकडे वरती व खालच्या बाजूला एका विशिष्ट मर्यादेपर्यंतचेच दृश्य दिसते. त्यापलीकडचा भाग दृष्टीच्या आवाक्यात येत नाही.

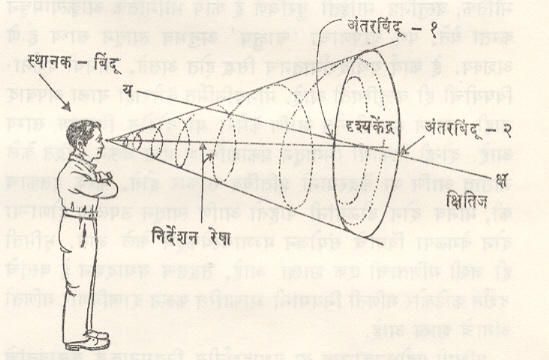
आकृती क्रमांक ४ मध्ये स्थानक-बिंदूपासून सूक्ष्म वर्तुळे सुरू होऊन उत्तरोत्तर व्यापक होत जातात, क्षितिजरेषेला भिडतात. स्थानक-बिंदूपासून क्षितिजरेषेवरील दृश्यकेंद्रापर्यंत एक रेषा जाते. आपण ज्या दिशेकडे पाहत असतो, तिचा अचूक निर्देश या रेषेने होतो. तिला ‘निर्देशन रेषा’ (डायरेक्टिंग लाइन) अशी संज्ञा आहे. स्थानक-बिंदूपासून क्षितिजापर्यंत जाणाऱ्या वर्तुळांचा एकआ. ४शंकू तयार होतो. याला ‘दृश्यशंकू’ (कोन ऑफ व्हिजन) अशी संज्ञा आहे. या शंकूच्या बाहेरील विश्वाचे दर्शन (मान आजूबाजूला वळविल्याशिवाय) आपणास होऊ शकत नाही. स्थानक-बिंदूजवळ असणारा या शंकूचा कोन साधारणतः साठ अंशांचा असतो. याला ‘दृश्यकोन’ (अँगल ऑफ व्हिजन) असे म्हणतात. कॅमेऱ्यातून पाहताना कॅमेऱ्याच्या भिंगानुसार, म्हणजे केंद्रांतरानुसार हा कोन बदलत जाईल. तो केंद्रांतराच्या व्यस्त प्रमाणात असेल. शंकूचे शेवटचे वर्तुळ क्षितिजरेषेवर येते. या वर्तुळाचा परिघ क्षितिजरेषेला दोन ठिकाणी छेद देतो. या बिंदूंच्या पलीकडील दृश्य आपणास दिसत नाही. या अर्थाने त्यांना ‘अंतरबिंदू’ (डिस्टंट पॉइंट्स) अशी संज्ञा आहे.

या उदाहरणातील खिडकीचे काचपृष्ठ पारदर्शक आहे. भिंतीसारखे किंवा चित्रफलकासारखे अपारदर्शक नाही. भिंतीवर रंगविलेल्या चित्रालासुद्धा खिडकीसारखी चौकट असते. पण तीतून बाहेरचे दृश्य प्रत्यक्षात दिसत नाही. त्याऐवजी भिंतीचा रंग किंवा चित्रात रंगविलेले आकार दिसतात. आता अशी कल्पना करू की, खिडकीच्या पारदर्शक काचेतून दिसणारे बाहेरचे दृश्य काचपृष्ठावरच येऊन स्थिरावले आहे. यामुळे असे होईल की, खिडकीतून आरपार बाहेर पाहताना अनुभवाला येणारी प्रत्यक्षातील, दृश्य घटना मानसिक पातळीवरआ. ५बदलून घेतली जाईल. खिडकीतून दिसणारे दृश्य, ही तिची अवस्था मागे पडून काचेला भिडलेले दृश्य-चित्र, अशी अवस्था आता तिला प्राप्त होईल. भिंतीवरील खऱ्या चित्राच्या बाबतीत याच्या बरोबर उलटी प्रक्रिया स्वीकारावयाची म्हणजे भिंतीचा जो पृष्ठभाग चित्र म्हणून रंगविला आहे, तेवढ्या भागापुरते भिंतीच्या अस्तित्वाचे भान विरून गेले आहे. त्यामुळे अपारदर्शक असूनही रंगविण्याच्या प्रक्रियेत भिंत जणू काचेच्या पृष्ठासारखी पारदर्शक होऊन त्या पृष्ठावर बाहेरील दृश्याची स्थापना झाली आहे. अर्थातच, खिडकीतून आरपार पाहताना बाह्यविश्वाचे जसे दर्शन घडते, तसेच दर्शन चित्रचौकटीतून घडते आहे. काचेच्या पृष्ठासारख्या बनलेल्या या चित्रित पृष्ठाला ‘चित्रपृष्ठ’ (पिक्चर प्लेन) अशी संज्ञा आहे. हे पृष्ठ खालपर्यंत वाढवीत नेल्यास भूपृष्ठाला ते ज्या ठिकाणी मिळेल त्या ठिकाणी एक रेषा मिळेल. तिला ‘भूपृष्ठरेषा’ किंवा ‘भूरेषा’ (ग्राऊंड लाइन) अशी संज्ञा आहे, (भूपृष्ठाला ‘ग्राऊंड प्लेन’ अशी इंग्रजी संज्ञा आहे). कल्पनेच्या पातळीवर हे चित्रपृष्ठ पारदर्शक असून ते सतत प्रेक्षकसमांतर असते. अर्थात प्रेक्षक आणि दृश्यविश्व यांच्यामध्ये ते उभे असते. चित्रचौकट ही जणू खिडकी असून तिच्यातून दिसणारे पलीकडील विश्व म्हणजे चित्र, अशी चित्राची व्याख्या प्रबोधनकाळात सिद्ध झाली त्यामागे निसर्गाची अचूक अनुकृती करणे, हा उद्देश होता.

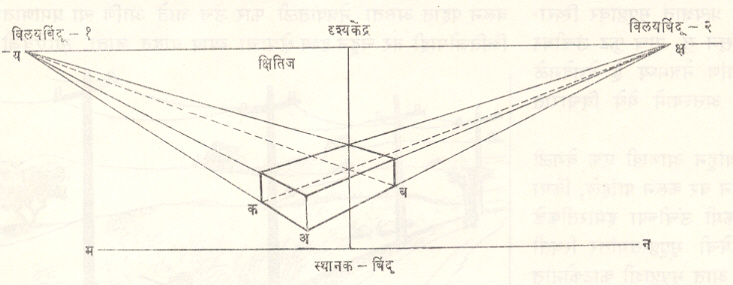
आकृती क्रमांक दोनमधील विलय पावणारी पृष्ठे भूपृष्ठाशी काटकोनात आहेत. यातील प्रेक्षकाकडचे पृष्ठ प्रेक्षकसमांतर म्हणजेच चित्रपृष्ठाला समांतर आहे. पण ते नेहमीच समांतर असेल असे नाही. हे पृष्ठ चित्रपृष्ठाशी कोन करून उभे असल्यास कोणती परिस्थिती उद्‌भवेल ते आकृती क्रमांक पाचमध्ये दाखविले आहे. यातील ‘य-क्ष’ ही क्षितिजरेषा असून ‘म-न’ ही भूरेषा म्हणजे चित्रपृष्ठाची पायाभूत रेषा आहे. वस्तुघन आता स्थानक-बिंदूच्या किंवा निर्देशनरेषेच्या म्हणजे प्रेक्षकाच्या डावीकडे आहे. कधीकधी संपूर्ण वस्तू अशी एका बाजूला असेल, तर कधी या आकृतीत दाखविल्याप्रमाणे चित्रपृष्ठाला जवळ असलेला ‘अ’ हा बिंदू डावीकडे किंवा उजवीकडे असेल. या उदाहरणात ‘अ-ब’ ही वस्तुघनाची रेषा चित्रपृष्ठाशी म्हणजे ‘म-न’ या भूरेषेशी सु. तीस अंशांचा कोन करून आहे. त्यामुळे ‘अ-ब’ आणि तिला समांतर असणाऱ्या सर्व रेषा उजवीकडील विलयबिंदू क्रमांक दोनमध्ये विलय पावतील. आणि ‘अ-क’ आणि तिच्या समांतर रेषा डावीकडे विलयबिंदू क्रमांक एकमध्ये विलय पावतील. या अवस्थेत वस्तूच्या चार उभ्या पृष्ठांपैकी दोन पृष्ठे प्रेक्षकाला दिसतात. वस्तू नेत्रपातळीच्या खाली असेल, तर वरचेही पृष्ठ दिसले. ती नेत्रपातळीच्या वर असेल, तर तळपृष्ठ दिसेल. ती नेत्रपातळीतच असेल, तर वरचे किंवा खालचे यांपैकी कोणतेही पृष्ठ दिसणार नाही. म्हणजे या अवस्थेत वस्तुघनाची जास्तीत जास्त तीन पृष्ठे दिसू शकतात. आकृती क्रमांक २ मध्ये दृश्यकेंद्र हाच विलयबिंदूही होता. कारण वस्तूचे एक पृष्ठ प्रेक्षकाला म्हणजेच चित्रपृष्ठाला समांतर होते. ती स्थिती बदलून आकृती क्रमांक पाचमध्ये वस्तूचे ‘अ-ब’ हे पृष्ठ चित्रपृष्ठाला कोन करून उभे आहे. त्यामुळे दोन वेगळेच विलयबिंदू प्राप्त झाले. आल्बेर्तीने या स्थितीला ‘द्विबिंदू यथादर्शन’ (टू पॉइंट-पर्स्पेक्टिव्ह) अशी संज्ञा वापरली. आज त्यासाठी ‘कोनीय यथादर्शन’ (अँग्युलर पर्स्पेक्टिव्ह) अशी संज्ञा वापरली जाते. या उदाहरणात समजुतीच्याआ. ६सोयीसाठी स्थानक-बिंदू म्हणजेच प्रेक्षकाचा नेत्रमध्य असे गृहित धरले आहे. प्रेक्षकाच्या शीर्षावरील एखाद्या उंच ठिकाणच्या बिंदूतून आपण खाली प्रेक्षकाकडे पाहिले, तर त्याचा नेत्रमध्य आणि त्याचे स्थान निश्चित करणारा पावलांचा मध्य हे एकाच बिंदूत दिसतील. या अर्थाने या उदाहरणातील ही अवस्था यथायोग्य आहे. पण प्रेक्षकाच्या बाजूला उभे राहून आपण पाहिले, तर त्याचे पाय प्रत्यक्षात भूपृष्ठावर स्थिरावलेले असून त्याची नेत्रपातळी भूपृष्ठापासून सु. पाच फुट उंचीवर असेल. म्हणजे प्रत्यक्षात स्थानक-बिंदू आणि नेत्रमध्य हे वेगवेगळे होतात. ही स्थिती अधिक गुंतागुंतीची असल्याने येथे विचारात घेतलेली नाही.

या दोन प्रकारच्या यथादर्शनीय अवस्थांहून आणखी एक वेगळी अवस्था शक्य आहे. उंच इमारतींकडे मान वर करून पाहिले, किंवा उंचच उंच इमारतीवरून भोवतालच्या कमी उंचीच्या इमारतींकडे पाहिले, की आपल्या दृष्टीच्या निर्देशनरेषेची भूपृष्ठ-समांतर स्थिती नाहीशी होते. अर्थात आपले चित्रपृष्ठही आत भूपृष्ठाशी काटकोनात उभे न राहता तिरकस (इन्क्लाइन्ड किंवा ऑब्लिक) होते. त्यामुळे आधीच्या उदाहरणांप्रमाणे पाहिलेल्या वस्तुघनाच्या उभ्या, म्हणजे भूपृष्ठाशी लंबरेषेत असणाऱ्या रेषा पूर्वीप्रमाणे चित्रपृष्ठाला समांतर राहणार नाहीत. चित्रपृष्ठाशी त्यांचा तीरोभाव (ऑब्लिकनेस) निर्माण होईल. इमारतीकडे रस्त्यावरून, म्हणजे खालून वर पाहिले असता या उभ्या रेषाही आकाशात कुठल्यातरी बिंदूमध्ये विलय पावू लागतील आणि वरून खाली पाहिले असता खालच्या बाजूला कुठल्यातरी बिंदूमध्ये विलय पावताना भासतील. हे आकृती क्रमांक ६ वरून दिसून येईल. या यथादर्शनीय अवस्थेला आल्बेर्तीने ‘त्रिबिंदू यथादर्शन’ (थ्री पॉइंट-पर्स्पेक्टिव्ह) अशी संज्ञा वापरली. आज त्यासाठी ‘तीरोभावी यथादर्शन’ (ऑब्लिक पर्स्पेक्टिव्ह) अशी संज्ञा रूढ आहे.

आतापर्यंतच्या विवेचनावरून पाहता नियमित घनवस्तूच्या सहा पृष्ठांपैकी जास्तीत जास्त तीनच पृष्ठे प्रेक्षकाला दिसू शकतात, असे निश्चित विधान सिद्ध होते. या त्रोटक विवेचनात वस्तूचा अत्यंत साधा विनागुंतागुंतीचा घन विचारात घेतला आहे. शिवाय तो प्रत्येक वेळी भूपृष्ठाशी लंबरेषेतच उभा असल्याचे गृहित धरले आहे. पीसाच्या मनोऱ्यासारखा तो तिरकस असल्यास यथादर्शनीय विरूपीकरण (डिस्टॉर्शन) वेगळ्या प्रकारे होईल. हे सर्व विवेचन वस्तूंच्या फक्त रेषात्मक वर्तनेविषयीचे आहे. यात रंगाचा विचार केलेला नाही. प्रत्यक्ष दृश्यविश्वात वातावरण हा घटक प्रभावी असतो. त्याचा वस्तूच्या रंगावर परिणाम होऊन यथादर्शनीय विरूपीकरण होत असते. वस्तूचे प्रेक्षकापासूनचे अंतर वाढत जाते, त्या प्रमाणात वातावरणाचा पडदा दाट व धुकट होत जातो. त्यामुळे जवळच्या वस्तूचे मूळ रंग अधिक स्पष्ट व तीव्र दिसतात. दूरच्या वस्तूंचे रंग धुकट दिसतात. रंगविषयक परिभाषेप्रमाणे पाहता त्यांच्या छटा (टिंट्स) बनतात. या वातावरणावर आकाशाच्या निळेपणाचाही प्रभाव असतो. त्यामुळे दूरच्या वस्तू धुकट निळसर दिसतात. दूरचे डोंगर यामुळेच सुंदर ‘साजरे’ भासतात. निसर्गचित्रकाराला या वातावरणीय यथादर्शनाचा (एअरिअल पर्स्पेक्टिव्ह) बारकाईने विचार करावा लागतो. कॅमेऱ्यातून मिळणाऱ्या चित्रातूनही याचा प्रत्यय येतो. वातावरणीय प्रभावाचा विचार न करता साध्य झालेल्या यथादर्शनीय आकृतीला ‘रेषात्मक यथादर्शन’ (लिनिअर पर्स्पेक्टिव्ह) अशी संज्ञा आहे.

वास्तुकाराला यथादर्शनीय गणिताचा फार उपयोग होतो. त्याने कल्पिलेल्या वास्तूचे प्रत्यक्षातील दर्शन कसे असेल, याची यजमानाला कल्पना देण्याचे कार्य यथादर्शनामुळे होते. प्रबोधनकाळापासून आजवरच्या वास्तववादी चित्रकला-शिक्षणात यथादर्शनीय गणित हा एक महत्त्वाचा विषय असतो. हे गणित कागदावर सोडविताना प्रथम वस्तूची सर्व बाजूंची मापे निश्चित करून घ्यावी लागतात. वस्तू प्रत्यक्षात फार मोठ्या असतात. त्यांचे चित्रण कागदात सामावले जाण्यासाठी तुलनात्मक प्रमाण (स्केल) ठरवावे लागते. भूरेषेपासून प्रेक्षकाची नेत्रपातळी किती उंचीवर आहे, तेही आधी ठरवून त्याप्रमाणे क्षितिजरेषा निश्चित करावी लागते. उदा., आपण उंच डोंगरावरून पहात असता नेत्रपातळी फार उंच जाते आणि त्या प्रमाणात क्षितिजरेषाही वर चढून दृश्य क्षेत्राचा व्याप वाढत जातो. त्याऐवजीआ. ७. विजेचे खांब मैदानात बसलेला किंवा झोपलेला प्रेक्षक क्षितिजपातळीला फार जवळ असल्याने अशा वेळी क्षितिजरेषा अगदी खाली उतरते. स्थानक-बिंदू आणि दृश्यकेंद्र यांना जोडणारी निर्देशनरेषा काढून त्यासंदर्भात वस्तूचे डावीकडील अथवा उजवीकडील स्थान निश्चित करून घ्यावे लागते. या पूर्वनिश्चित गोष्टींच्या (डेटा) आधारावर ती ती वस्तू प्रेक्षकाच्या त्या त्या स्थानावरून कशी दिसेल, ते गणिताने अचूक दाखविता येते.

चित्रपट क्षेत्रामध्येही यथादर्शनीय गणिताचा अर्थपूर्ण उपयोग होऊ शकतो. पश्चिमी देशांत असे यथादर्शनीय गणितकार हे कलादिग्दर्शक, छायादिग्दर्शक आणि दिग्दर्शक यांच्या समवेत काम करीत असतात. कलादिग्दर्शकाने कल्पिलेले आणि धावते रेखाटलेले नेपथ्य अचूकपणे तसेच्या तसे कॅमेऱ्यातून दिसावयाचे असेल, तर त्या नेपथ्याची मोजमापे नेमकी किती ठरवावयाची, कॅमेरा कोणत्या ठिकाणी किती उंचीवर लावावयाचा, याविषयी गणिती अचूकपणे तो सूचना देतो. कधीकधी तर कलादिग्दर्शकाच्या कल्पनेतही नसलेली एखादी जागा हुडकून काढून तेथे कॅमेरा लावून चित्रण केले असता ते अधिक परिणामकारक कसे होऊ शकते, हे तो दाखवून देतो. मुंबईच्या ‘रॅमनॉर्ड रिसर्च लॅबोरेटरी’मध्ये ही अभ्यासशाखा प्रायोगिक अवस्थेत तीसेक वर्षांपूर्वी सुरू झाली आणि बंद पडली.

भारतीय चित्रकलेमध्ये यथादर्शनाचा पश्चिमी पद्धतीने काटेकोर उपयोग केलेला दिसत नाही. कारण निसर्गाची अचूक अनुकृती हे ध्येय भारतीय कलावंतांनी स्वीकारलेले नव्हते. एकोणिसाव्या शतकातील भारतीय प्रबोधनात पश्चिमी प्रबोधनकालीन आदर्शांचा स्वीकार कलाशिक्षणातही झाल्याने तदनंतरच्या वास्तववादी भारतीय कलेमध्ये मात्र यथादर्शनाचा अभ्यास हिरिरीने केला गेला. परंपरागत भारतीय कलावंतांना यथादर्शनीय विरूपीकरणाची काहीएक जाण होती, असे दिसून येते आणि याचा प्रत्यय विशेषतः ⇨लघुचित्रणातून येतो. मात्र चित्राच्या समग्र रचनात्मक आकृतीमध्ये हे यथादर्शनीय विरूपीकरण लयबद्ध रीतीने एकजीव व्हावे, अशा प्रमाणात त्याचा मर्यादित स्वीकार केला गेला. पश्चिमी आधुनिकांनी प्रबोधनकालीन कलाविषयक आदर्शांचा त्याग केल्यामुळे कलेतील यथादर्शनीय अभ्यासाचे महत्त्व त्यानंतर कमी झाले. तरीही जोर्जो दी कीरीको (१८८८-१९७८), पॉल नॅश (१८८९-१९४६) यांसारख्या आधुनिक कलावंतांनी वातावरण, अभिव्यक्ती आणि आकृतिबंध यांसाठी यथादर्शनाचा कल्पकतेने उपयोग केला.

साहित्यसमीक्षेत कधीकधी ‘पर्स्पेक्टिव्ह’ या संज्ञेचा लाक्षणिक अर्थाने वापर केला जातो, तेव्हा तिचा अचूक अर्थ स्वीकारलेला असतोच, असे नसते. याउलट एडवर्ड बुलो आणि गॅसेट या सौंदर्यशास्त्रवेत्त्यांनी यथादर्शनशास्त्राचा प्रत्यक्ष उल्लेख केलेला नसूनही त्यांच्या विचाराला यथादर्शनीय आकलनाचा भक्कम पाया आहे. बुलोने मांडलेल्या ‘मानसिक अंतर’ (सायकिक डिस्टन्स) या संकल्पनेत यथादर्शनीय दूरत्वाचीच तर्कशुद्ध मांडणी केलेली आहे. बंदरातील धुक्याचे उदाहरण त्याने स्पष्टीकरणासाठी घेतले आहे. वातावरणात धुके नसताना नौकादिकांचे आपणापासून असलेले अंतर जेवढे दिसते, त्याहून ते धुक्याच्या वातावरणात अधिक भासते आणि त्यामुळे संपूर्ण दृश्य आस्वाद्य होते. काहीसे तसे अंतर निर्माता आणि आस्वादक यांच्या मनांमध्ये निष्पन्न झाल्याशिवाय कलानिर्मिती आणि आस्वाद अशक्य असतो, असे बुलोचे म्हणणे आहे. या लेखामध्ये पूर्वभागात घेतलेले काचेच्या खिडकीचे उदाहरणच नेमके गॅसेटने आपल्या स्पष्टीकरणासाठी घेतले आहे. व्यवहारी जीवनात खिडकीच्या काचेपलीकडील प्रत्यक्ष वस्तूंकडे माणूस पहात असतो, तद्वतच कलाकृतींत चित्रित झालेल्या प्रत्यक्ष जीवनामध्ये तो रस घेतो, कलाकृती म्हणून त्याकडे पहात नाही. कलाकृतीकडे आस्वादकाच्या वृत्तीने पहावयाचे असेल, तर खिडकीच्या काचेवर अवधान ठेवले असता बाहेरच्या प्रत्यक्षातील दृश्य घटनांचे जसे अवस्थान्तर होते, तसे जीवनानुभवाच्या बाबतीतही घडले पाहिजे. खिडकीतून दिसणारे तेच दृश्य आता काचेवर स्थिरावले आहे, अशा काल्पनिक मानसिक पातळीवरून पाहिले असता व्यावहारिक आस्था बाद होऊन आपण त्या दृश्य घटनेचे मनन करू शकतो. कलानिर्मिती आणि आस्वाद यांमध्ये असेच मानसिक अवस्थान्तर आवश्यक असते. या प्रक्रियेला गॅसेटने ‘अवमानवीकरण’ (डीह्युमनायझेशन) असे म्हटले आहे.आ. ८. रेल्वेचे रूळभारतीय सौंदर्यशास्त्रातील साधारणीकरण आणि त्या अनुषंगाने येणाऱ्या अलौकिकता या संज्ञांच्या मागेही अशाच प्रकारची वैचारिक भूमिका आहे, असे दाखवून देता येईल.

संदर्भ: 1. Ballinger, Louise Bowen, Perspective : Space and Design, New York, 1969.

2. Dennis, H. J. Elementary Perspective, London, 1957.

3. Gill, Robert W. Basic Perspective, London, 1974.

4. Gill, Robert W. Creative Perspective, London, 1975.

5. Watson, Ernest W. How to Use Creative Perspective, New York, 1967.

कदम, संभाजी.

“