भ्रमणजन्य पृष्ठे व घनाकृति : एखादा प्रतलीय वक्र (ज्याचे सर्व बिंदू एकाच प्रतलात आहेत असा वक्र) त्याच प्रतलातील एका रेषेभोवती फिरविला असता एक पृष्ठ तयार होते, त्यालाच भ्रमणजन्य पृष्ठ म्हणतात. जनक वक हा एकच चाप असेल किंवा काही रेषा खंड जोडून तयार झालेला असेल. एखादे प्रतलीय क्षेत्र त्याच प्रतलातील रेषेभोवती फिरविले असता भ्रमणजन्य घनाकृती (किंवा प्रस्थ) मिळते. भ्रमणजन्य घनाकृतीची सीमा ही एक भ्रमणजन्य पृष्ठ असते. ज्या रेषेभोवती वक्र किंवा क्षेत्र फिरविण्यात येते, त्या रेषेला भ्रमणाचा अक्ष म्हणतात.
नेहमीच्या यूक्लिडीय भूमितीच्या अभ्यासामध्ये वृत्तचिती (दंडगोल), शंकू व गोल हे शब्द भ्रमणजन्य घनाकृतीकरिता वापरलेले असतात आणि आनुषंगिक भ्रमणजन्य पृष्ठाकरिता वृत्ताचित्याकृती, शंक्वाकृती व गोलीय आकृती असे शब्द वापरतात परंतु वैश्लेषिक भूमितीमध्ये आणि आधुनिक परिभाषेमध्ये वृत्तचिती, शंकू व गोल हे शब्द पृष्ठांकरिता वापरलेले आढळतात. (‘भूमिति’ या नोंदीतील ‘वैश्लेषिक भूमिती’ हा भाग पहावा).
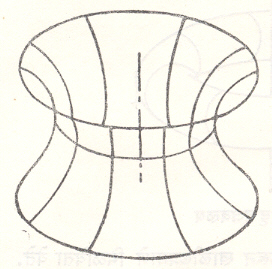वृत्तचिती ही एक सरळ रेषा तिला समांतर असलेल्या दुसऱ्या रेषेभोवती फिरवून तयार होते. शंकू हा एक सरळ रेषा तिला छेदणाऱ्या अक्षाभोवती फिरवून तयार होतो. विवृत्त (लंबवर्तुळ) त्याच्या अक्षाभोवती फिरविले असता तयार होणाऱ्या पृष्ठाला विवृत्ती गोल (किंवा गोलाभ) म्हणतात. ⇨अन्वस्त आणि ⇨अपास्त हे वक्र त्यांच्या अक्षाभोवती फिरविले असता अनुक्रमे अन्वस्तज पृष्ठ व अपास्तज पृष्ठ मिळतात. रज्जुवक्र व मालावलित हे वक्र [⟶ वक्र] त्यांच्या अक्षाभोवती फिरवून मिळणारी पृष्ठे लक्षणीय आहेत. साबणाच्या पाण्याचे तारेच्या दोन समांतर वर्तुळांत जोडणारे पटल पृष्ठताणामुळे (द्रवाच्या पृष्ठाचे क्षेत्रफळ कमीत कमी करण्याची प्रवृत्ती असणाऱ्या प्रेरणेमुळे) जो आकार धारण करतो, तो रज्जुवक्रज पृष्ठाचा एक भाग असतो. मालावलित वक्रज पृष्ठाचे वैशिष्ट्य म्हणजे या पृष्ठाची वक्रता एक ऋण स्थिरांक असते. त्यामुळे या पृष्ठावरील भूमिती अयूक्लिडीय असते.
पॅपस (इ. स. तिसरे-चौथे शतक) या ग्रीक भूमितिविज्ञांची भ्रमणजन्य पृष्ठे व घनाकृती यांविषयीची पुढील दोन प्रमेये प्रसिद्ध आहेत :
(१) संयोगित प्रतलीय क्षेत्र (ज्यात कोणत्याही दोन बिंदूंना जोडणारा एक अखंड मार्ग असून तो त्या क्षेत्राच्या सीमेबाहेर जात नाही असे प्रतलीय क्षेत्र) त्याला न छेदणाऱ्या अक्षाभोवती फिरवून निर्माण होणाऱ्या घनाकृतीचे घनफळ हे त्या क्षेत्राचे क्षेत्रफळ आणि त्या क्षेत्राच्या ⇨गुरुत्वमध्याने रेखाटलेल्या वक्राची लांवी यांच्या गुणाकाराबरोबर असते.
(२) भ्रमणजन्य पृष्ठाचे क्षेत्रफळ हे जनक वक्राची लांबी व त्याच्या गुरुत्वमध्याने रेखाटलेल्या वक्राची लांवी त्यांच्या गुणाकाराबरोबर असते.
संयोगित प्रतलीय क्षेत्र व वक्राचा चाप यांचे गुरुत्वमध्य खालील सूत्रांनी मिळतात.
(अ)क्ष Δ =∫∫ क्ष dक्ष dय
य Δ =∫∫ य dक्ष dय
[येथे Δ = प्रतलीय क्षेत्राचे क्षेत्रफळ आणि (क्ष, य)= गुरुत्वमध्याचे सहनिर्देशक].(आ) क्ष= ∫ क्ष dल
य=∫ यdल
[येथे ल=चापाची लांबी आणि (क्ष,य)=गुरुत्वमध्याचे सहनिर्देशक].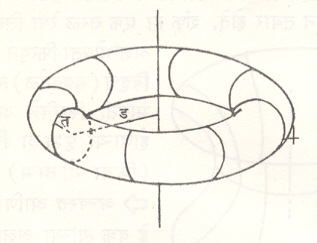
क्ष-अक्षाच्या संपूर्णतया वरच्या बाजूस असलेल्या क्षेत्राने व चापाने क्ष-अक्षाभोवती फिरल्यावर तयार होणाऱ्या घनाकृती व पृष्ठे यांच्या घनफळाकरिता व क्षेत्रफळाकरिता खालील सूत्रे उपयोगी पडतील.
(इ) घनफळ = २ π∫∫ य dक्ष dय
क्षेत्रफळ = २π∫ य dल
उदा., त त्रिज्या असलेले वर्तुळ त्याचा प्रतलात वर्तुळ केंद्रापासून ड अंतरावर असलेल्या रेषेभोवती फिरविल्यावर निर्माण होणाऱ्या घनाकृतीचे (याला वृत्तजवलय म्हणतात, आ. २) घनफळ व पृष्ठाचे क्षेत्रफळ पॅपस प्रमेयांचा उपयोग करून खालीलप्रमाणे मिळविता येते.
घनफळ = २πड (π त२) २ π २त२.ड
क्षेत्रफळ = २πड (२ π त) ४ π २त.ड
ओक, स. ज.
“