अंक : संख्यादर्शक चिन्हांना किंवा अक्षरांना ‘अंक’ म्हणतात. मोजण्याची. आवश्यकता मानवाला त्याच्या प्रारंभापासून स्वाभाविकपणेच भासली असावी. मानवजातीच्या बाल्यावस्थेत प्रत्येक मानवाला मी एक व हा दुसरा एवढे साधे ज्ञान असणार यात वाद नाही. म्हणजे दोन अंक मोजण्याइतपत त्याची प्रगती उपजतच असणार. त्याच्या पुढची पायरी म्हणजे त्याच्याजवळ असलेल्या वस्तूंची मोजदाद करावयास तो हळूहळू शिकला असेल. प्राथमिक अवस्थेमध्ये हाताची बोटे, गारगोट्या, झाडाची पाने, काठ्या यांचा उपयोग मोजण्यासाठी मानव करीत असे. जगातील बहुतेक जमाती प्राथमिक अवस्थेमध्ये सामान्यपणे अशाच तऱ्हेने अंकनिर्देश करीत असत. मानवास लेखनकला अवगत झाल्यावर तो एकेक अक्षराचा अंकासाठी उपयोग करू लागला. अशा तऱ्हेची पद्धती ॲरेमाइक, हिब्रू, खरोष्ठी, ब्राह्मी आणि ग्रीक लिपींत दिसून येते.
मानवाने अंकाचा शोध लावला त्या वेळेस तो अंकांचे उच्चार कसे करीत असणार याविषयी गूढ वाटणे साहजिक आहे. वेदकालापासून सर्व ज्ञान एका पिढीपासून दुसऱ्या पिढीस मौखिक पद्धतीने शतकानुशतके दिले गेल्यामुळे भारतात अंकांचे उच्चार कोणते होते हे स्पष्ट होते ते म्हणजे एक, द्वि, त्रि, चतुर्, पंचन्, षष्, सप्तन्, अष्टन्, नवन् आणि दशन् हे होत. या संस्कृत उच्चारांवरून पुढे मराठीत एक, दोन, तीन वगैरे संज्ञा अपभ्रष्ट स्वरूपात रूढ झाल्या.
ईजिप्त : लेखनकलेचे सर्वांत प्रचीन नमुने ईजिप्तमध्ये सापडतात तसेच अंकलेखनाचे नमुनेही (इ.स.पू.सु. ३४००) तेथेच सापडतात. तेथे एक ते नऊ ह्या अंकांसाठी उभ्या दंडांची योजना केलेली आढळते. ही रीत ⇨हायरोग्लिफिक लिपि-पद्धतीचा एक भाग आहे. दहा, शंभर, हजार ह्या संख्यांसाठी मात्र तेथे वेगळी चिन्हे वापरलेली आढळतात. लाखाकरिता बेडकाचे व दहा लाखाकरिता आश्चर्याचे बाहू पसरलेल्या मानवाचे चित्र काढले जाई. यानंतरच्या काळात ईजिप्तमध्ये हिअरेटिक अंक (इ.स.पू.सु. १२ वे शतक) आणि त्यापासून पुढे डेमॉटिक अंक (इ.स.पू.सु. ७ वे ते ३ रे शतक) उपयोगात आणले गेले. हिअरेटिक आणि डेमॉटिक अंकांतील फरक काटेकोरपणे दाखविणे कठिण असले, तरी हिअरेटिक अंकांपासून डेमॉटिक अंक विकसित झाले असावेत असे दिसते. जलद लेखनासाठी वरील दोन्ही पद्धती मूळ हायरोग्लिफिक पद्धतीपासून निघाल्या असाव्यात. हायरोग्लिफिक पध्दतीपेक्षा हिअरेटिक पद्धतीत अधिक चिन्हे असल्याने तीत लहानमोठ्या संख्या अधिक संक्षिप्तपणे दर्शविणे सोयीचे होते. हिअरेटिक अंकपद्धतीत आधी मोठ्या मूल्यांची चिन्हे आणि त्यानंतरत्यापुढे (उजवीकडे) कमी मूल्यांची चिन्हे लिहिली जात (पहा : तक्ता क्र.१).
बॅबिलोनिया : बॅबिलोनियामध्ये सुमेरियन लोकांच्या (इ.स.पू.सु. ३०००) लेखनात ![]() हे चिन्ह एका आकड्याकरिता वापरीत व हे
हे चिन्ह एका आकड्याकरिता वापरीत व हे ![]() चिन्ह दहाकरिता वापरीत. साठ आणि सहाशेकरिता अनुक्रमे
चिन्ह दहाकरिता वापरीत. साठ आणि सहाशेकरिता अनुक्रमे ![]() ,
, ![]() अशी चिन्हे वापरीत. यावरून
अशी चिन्हे वापरीत. यावरून ![]() = १०,
= १०,![]() = २०,
= २०, ![]() = ३० अशा प्रकारे संख्या लिहिल्या जात. ओल्या मातीच्या विटांवर विशिष्ट प्रकाराच्या काठीच्या टोकाने दाबून वरील प्रकाराच्या आकृत्या काढीत व त्या विटा भाजून ठेवीत. अशा प्रकाराच्या अनेक विटा सापडल्या आहेत. ही लेखनपद्धती⇨क्यूनिफॉर्म लिपि-पद्धती म्हणून ओळखली जाते. शंभर
= ३० अशा प्रकारे संख्या लिहिल्या जात. ओल्या मातीच्या विटांवर विशिष्ट प्रकाराच्या काठीच्या टोकाने दाबून वरील प्रकाराच्या आकृत्या काढीत व त्या विटा भाजून ठेवीत. अशा प्रकाराच्या अनेक विटा सापडल्या आहेत. ही लेखनपद्धती⇨क्यूनिफॉर्म लिपि-पद्धती म्हणून ओळखली जाते. शंभर ![]() असे लिहित तर कधीकधी
असे लिहित तर कधीकधी ![]() असेहीलिहित. या दोहोंपैकी दुसरा प्रकार तर्कशुद्ध वाटतो. तथापि एकावर दहा लिहून शंभर कसे होतात? एकावर दहा लिहून जर शंभर होतात तर
असेहीलिहित. या दोहोंपैकी दुसरा प्रकार तर्कशुद्ध वाटतो. तथापि एकावर दहा लिहून शंभर कसे होतात? एकावर दहा लिहून जर शंभर होतात तर ![]() असे लिहून २०० कसे? येथे तर विसावर शंभर लिहून दोनशे दाखविले आहेत आणि ते तितकेसे सुसंगत नाही. यावरून ही संख्या दर्शविण्याची पद्धती सदोष होती हे उघड आहे.
असे लिहून २०० कसे? येथे तर विसावर शंभर लिहून दोनशे दाखविले आहेत आणि ते तितकेसे सुसंगत नाही. यावरून ही संख्या दर्शविण्याची पद्धती सदोष होती हे उघड आहे.
बगदाद येथे सापडलेल्या दोन जुन्या तक्तयांवरून असे आढळून येते, की बॅबिलोनियामध्ये षष्टिकमानपद्धती रूढ असावी. यावरून तेथे संख्येतील स्थानमूल्याचे महत्त्व ज्ञात असावे असे वाटते. त्यांतील एका तत्त्क्यावर एकापासून साठापर्यंतचे वर्ग लिहिलेले आहेत. सातानंतरच्या संख्यांचे वर्ग साठापेक्षा मोठे असल्याकारणाने आठाचा वर्ग![]() = (६०+४), नवाचा वर्ग
= (६०+४), नवाचा वर्ग ![]() = (६०+२१) इ. चिन्हांनी दर्शविले आहेत. या पद्धतीत साठापर्यंतच्या संख्या लिहिणेही बरेच त्रासाचे आहे. एकूणपन्नास लिहावयाचे झाल्यास एकूण तेरा चिन्हे लिहावी लागतात, तर एकूणसाठाकरिता चौदा चिन्हे लागतात.
= (६०+२१) इ. चिन्हांनी दर्शविले आहेत. या पद्धतीत साठापर्यंतच्या संख्या लिहिणेही बरेच त्रासाचे आहे. एकूणपन्नास लिहावयाचे झाल्यास एकूण तेरा चिन्हे लिहावी लागतात, तर एकूणसाठाकरिता चौदा चिन्हे लागतात.
उदा., ५९=![]() = १०X५+९. ही पद्धती तितकीशी सुटसुटीत नाही हे स्पष्ट आहे (पहा : तक्ता क्र. १)
= १०X५+९. ही पद्धती तितकीशी सुटसुटीत नाही हे स्पष्ट आहे (पहा : तक्ता क्र. १)
ग्रीक : प्राचीन ग्रीसमध्ये अंकलेखनाच्या दोन पद्धती रूढ होत्या. (१) ॲटिक किंवा हेरोडायानिक आणि (२) आयोनियन किंवा ॲलेक्झांड्रियन किंवा अक्षरांकित. पहिलीचा काल इ.स.पू.सु. ६ वे शतक असून या पद्धतीतील कोरीव लेख अथेन्स येथे सापडले आहेत. मूलतः ही दशमानपद्धती होती तथापि पाच ह्या अंकालाही तीत विशेष महत्त्व असल्याचे दिसते. ह्या अंकपद्धतीत एक ते चारापर्यंतचे अंक अनुक्रमे एक ते चार उभे दंड एकापुढे एक लिहून दर्शवीत असत. पाचासाठी मात्र 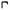 , दहासाठी Δ, विसासाठी ΔΔ, पन्नासासाठी
, दहासाठी Δ, विसासाठी ΔΔ, पन्नासासाठी  , साठासाठी
, साठासाठी  , शंभरासाठी H, दोनशेसाठी HH, पाचशेसाठी
, शंभरासाठी H, दोनशेसाठी HH, पाचशेसाठी 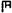 , वगैरे चिन्हांचा वापर केला जाई (पहा : तक्ता क्र. १).
, वगैरे चिन्हांचा वापर केला जाई (पहा : तक्ता क्र. १).
तक्ता क्र. १ : जगातील काही महत्त्वाच्या अंकलेखनपद्धती

दुसऱ्या म्हणजे आयोनियन पद्धतीत अंकांसाठी ⇨ग्रीक लिपीतील अक्षरांचा वापर केला जाई. ही पद्धतीही मूलतः दशमानच होती. तिच्यातील अंक येणेप्रमाणे : A=१, B=२, 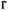 = ३ इ. तसेच I = १०, K = २०, P = १००, Φ = ५००,
= ३ इ. तसेच I = १०, K = २०, P = १००, Φ = ५००, 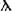 = ९०० वगैरे. बारासाठी IB (म्हणजे दहा व दोन) असे चिन्ह वापरीत. या चिन्हांची उलटापालट करता येत नसे कारण बाराच्या उलट एकवीस होतात आणि एकविससाठी विसाचे K हे चिन्ह आणि एकासाठी A म्हणून KA ही चिन्हे वापरावी लागत. शून्याची कल्पना त्या वेळी नसल्याकारणाने विसासाठी आणखी एक चिन्ह वापरणे क्रमप्राप्त होतो. याप्रमाणेच ३०, ४०, १०० वगैरेंसाठी वेगवेगळी अक्षरे वापरली जात. ग्रीक वर्णमालेतील मूळ चोवीस अक्षरे आणि बाहेरून घेतलेली F, Q आणि
= ९०० वगैरे. बारासाठी IB (म्हणजे दहा व दोन) असे चिन्ह वापरीत. या चिन्हांची उलटापालट करता येत नसे कारण बाराच्या उलट एकवीस होतात आणि एकविससाठी विसाचे K हे चिन्ह आणि एकासाठी A म्हणून KA ही चिन्हे वापरावी लागत. शून्याची कल्पना त्या वेळी नसल्याकारणाने विसासाठी आणखी एक चिन्ह वापरणे क्रमप्राप्त होतो. याप्रमाणेच ३०, ४०, १०० वगैरेंसाठी वेगवेगळी अक्षरे वापरली जात. ग्रीक वर्णमालेतील मूळ चोवीस अक्षरे आणि बाहेरून घेतलेली F, Q आणि 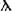 ही तीन अक्षरे, अशा एकूण सत्तावीस अक्षरांच्या मदतीनेही फार मोठ्या संख्या दर्शविणे सोयीचे नाही (पहा : तक्ता क्र. १). आरंभी मोठ्या (कॅपिटल) लिपीतील अक्षरे वापरण्याचा प्रघात होता नंतर मात्र त्यांऐवजी लहान (स्मॉल) लिपीतील अक्षरे वापरात आली.
ही तीन अक्षरे, अशा एकूण सत्तावीस अक्षरांच्या मदतीनेही फार मोठ्या संख्या दर्शविणे सोयीचे नाही (पहा : तक्ता क्र. १). आरंभी मोठ्या (कॅपिटल) लिपीतील अक्षरे वापरण्याचा प्रघात होता नंतर मात्र त्यांऐवजी लहान (स्मॉल) लिपीतील अक्षरे वापरात आली.
चीन : प्राचीन काळात (इ.स.पू.सु. ५४०) चीनमध्ये तसेच जपानमध्येही टेबलावर उभे व आडवे दंड ठेवून त्यांचा गणितकृत्यांसाठी उपयोग केला जाई. एक ते पाच हे अंक अनुक्रमे एक ते पाच उभ्या दंडांनी दर्शविले जात. एक ते चार ह्या उभ्या दंडांच्या डोक्यांवर प्रत्येकी एकेक आडवा दंड ठेवला म्हणजे सहा, सात, आठ व नऊ हे अंक तयार होत. दहासाठी एक आडवा दंड, विसासाठी दोन, पन्नासासाठी पाच दंड देण्यात येत. साठासाठी एक उभा दंड व त्याच्या खाली एक आडवा दंड (म्हणजे ![]() ) जोडलेला असे. त्याचप्रमाणे शंभर ते पाचशेसाठीही उभे दंडच वापरीत परंतु त्यांचे स्थान अगदी डावीकडे असे (पहा : तक्ता क्र. १).
) जोडलेला असे. त्याचप्रमाणे शंभर ते पाचशेसाठीही उभे दंडच वापरीत परंतु त्यांचे स्थान अगदी डावीकडे असे (पहा : तक्ता क्र. १).
चीनमध्ये अंकलेखनाची दुसरीही एक पद्धती ह्याच काळाच्या सुमारास रूढ होती. या पद्धतीत पहिल्या नऊ अंकांसाठी नऊ वेगवेगळ्या चिन्हांचा वापर करण्यात येई. तसेच यांव्यतिरिक्त दहाच्या पहिल्या अकरा घातांसाठी वेगवेगळी चिन्हे वापरली जात. एक ते तीन अंकांकरिता कमीअधिक लांबीचे अनुक्रमे एक ते तीन दंड, दहासाठी एक उभा व आडवा दंड छेद देऊन ( ), शंभराकरिता
), शंभराकरिता  हे चिन्ह वगैरे (पहा : तक्ता क्र. १). वरील चिन्हांच्या साहाय्याने गुणाकाराच्या व बेरजेच्या नियमांचा वापर करून १०१२ (एकावर बारा शून्ये) पर्यंत कोणतीही संख्या दर्शविता येते.
हे चिन्ह वगैरे (पहा : तक्ता क्र. १). वरील चिन्हांच्या साहाय्याने गुणाकाराच्या व बेरजेच्या नियमांचा वापर करून १०१२ (एकावर बारा शून्ये) पर्यंत कोणतीही संख्या दर्शविता येते.
रोमन : (इ.स.पू.सु. ७ वे शतक). रोमन लोक एक ते चार अंकांकरिता I, II, III, IIII ही चिन्हे वापरीत व पाचाकरिता V हे चिन्ह वापरीत. सहा, सात, आठ या संख्या पाच अधिक एक, पाच अधिक दोन, पाच अधिक तीन, म्हणून VI = ६, VII = ७, VIII = ८ अशा लिहीत व दहाकरिता X हे चिन्ह वापरीत.चार लिहिताना चारउभी चिन्हे काढणे कालापहारी वाटल्यामुळेपाचाच्या आधीI हे चिन्ह वापरून म्हणजे ५ – १ = ४ = IV असे लिहिण्याचा प्रघात पडला व त्याच न्यायाने IX = ९. यानंतर L = ५०, C = १००, D = ५००, M = १,००० ही चिन्हे वापरण्यात येत असत. ह्या पद्धतीप्रमाणे ३८ ही संख्या लिहावयास सात चिन्हे लिहावी लागतात (XXXVIII=३८). L च्या पूर्वी I म्हणजे IL याचा अर्थ ४० घ्यावयाचा ५० – १ = ४९ नव्हे. गुणाकार करतानाI ने गुणिल्यास मूळ संख्या येते. V गुणिले V = XXV V गुणिले X म्हणजे LV गुणिले L म्हणजे CCL. या नियमांवरून दोन आकड्यांच्या संख्यांचा गुणाकारदेखील एक जिकिरीचे काम होते असे दिसते. यामुळे ही अंकपद्धती दैनंदिन व्यवहाराकरिता रूढ होऊ शकली नाही. तथापि रोमन अंकांचा थोडाफार वापर अद्यापही घड्याळाच्या तबकडीवरील आकडे, परिच्छेद-क्रमांक इत्यादींसाठी केला जातो (पहा : तक्ता क्र. १).
हिब्रू : इ.स. दुसऱ्या शतकाच्या सुमारास हिब्रूंनी ग्रीकांच्या पद्धतीसारखीच, ⇨हिब्रू लिपीतील बावीस अक्षरांचा वापर करून अंक दर्शविण्याची पद्धती उपयोगात आणली. या पद्धतीत पहिले नऊ पूर्णांक दर्शविण्यासाठी नऊ अक्षरे आणि आणखी नऊ अक्षरांनी दहाचे पहिले नऊ गुणक दर्शविले जात. शेवटची अक्षरे शंभराच्या पटी दर्शवीत. ह्या पद्धतीत शंभराच्या पटी फक्त चारशेपर्यंतच्या दर्शविणे शक्य होते. यापुढील शंभराच्या पटी दर्शविण्यासाठी वरील अक्षरांचाच वापर संयोगाने केला जाई. उदा., ९०० साठी ४००, ४०० आणि १०० यांच्या अक्षरचिन्हांचा वापर केला जाई. या आडचणीतून मार्ग काढण्यासाठी पुढे पाचशेहून अधिक शंभराच्या पटी दर्शविण्यासाठी त्यांनी नवीन अक्षरचिन्हे विकसित केली (पहा : तक्ता क्र. १).
मध्य अमेरिका (माया) : यूरोपीयन अंकपद्धतींपेक्षा सर्वस्वी वेगळी अशी अंकपद्धती मध्य अमेरिकेतील माया संस्कृतीत (इ.स.सु. ३ रे-४ थे शतक) वापरात असल्याचे सोळाव्या शतकात काही संशोधकांना आढळून आले. ही पद्धती वीस ह्या मूलांकावर आधारलेली आहे. तीत दहाऐवजी पाच हा उपमूलांक आहे. हीच तत्त्वे बॅबिलोनियामध्येही अनुसरलेली आढळतात. मायापद्धतीत एक बिंदू एकासाठी तसेच दोन, तीन, चार यांसाठी प्रत्येकी एकापुढे एक असे दोन, तीन, चार बिंदू अनुक्रमे वापरले जात. पाचासाठी आडवा दंड, दाहासाठी दोन आडवे समांतर दंड आणि पंधरासाठी तीन समांतर आडवे दंड वापरीत. विसासाठी  असे एक चिन्ह वापरून स्थानमूल्याच्या तत्त्वानुसार त्यावर एक बिंदू दिला जाई (
असे एक चिन्ह वापरून स्थानमूल्याच्या तत्त्वानुसार त्यावर एक बिंदू दिला जाई ( ). ह्या पद्धतीत संख्यांतील अंकचिन्हे उभ्या स्तंभात दर्शविली जात त्यातील सर्वांत वरचे चिन्ह सर्वोच्च मूल्याचे निदर्शक असे आणि सर्वांत खालचे चिन्ह एकाच्या पटी व याच्या वरील चिन्ह विसाच्या पटी दर्शवी. परंतु त्यावरचे चिन्ह मात्र चारशेच्या पटींऐवजी ३६० च्या पटी दर्शवी.
). ह्या पद्धतीत संख्यांतील अंकचिन्हे उभ्या स्तंभात दर्शविली जात त्यातील सर्वांत वरचे चिन्ह सर्वोच्च मूल्याचे निदर्शक असे आणि सर्वांत खालचे चिन्ह एकाच्या पटी व याच्या वरील चिन्ह विसाच्या पटी दर्शवी. परंतु त्यावरचे चिन्ह मात्र चारशेच्या पटींऐवजी ३६० च्या पटी दर्शवी.
उदा., ६,७८९ ही संख्या या पद्धतीत
 अशी लिहिली जाई. म्हणजे
अशी लिहिली जाई. म्हणजे
(३ x ५ + ३) x (३६०) + ३ x ५ x (२०) + (५ + ४) = ६,७८९ (पहा : तक्ता क्र. १).
अरबी पद्धती : पाश्चात्य जगात रूढ असलेली आधुनिक दशमान अंकपद्धती ‘अरबी पद्धती’ म्हणून संबोधिली जाते. तथापि ‘हिंदु-अरबी’ या नावाने ओळखणे अधिक बरोबर होईल. कारण मूलतः ही पद्धती भारतीय असून तेथून ती अरबांनी स्वीकारली असे आढळून येते. इ.स. १०१० पर्यंत अरबस्तानात संख्या दर्शविण्यासाठी हजार, शतक, दशक व सुटे यांचा वापर करीत असत. आरबांनी ही पद्धती इराणी लोकांजवळून हस्तगत केली असेही दिसून येते. इराणातदेखील वरील पद्धती फार उशीरा रूढ झाली. फिर्दौसी याने शाहनामा ग्रंथाचा लेखनकाल हिजरी कालगणनेत ‘पंज-हश्ताद बार’ म्हणजे ऐंशीच्या पाचपट म्हणजे ४०० हिजरी (इ.स. १०२२) असा दिला आहे.
गुरशास्प-नामा ग्रंथाचा लेखनकाल असदी याने चार शतके पन्नास व आठ म्हणजे ४५८ हिजरी (इ.स. १०८०) असा दिलेला आढळतो. ही भारतीय जुनी पद्धती होय. दशमानावर आधारलेली भारतीय नवीन संख्यांकनपद्धती अल्-ख्वारिज्मी याने प्रथमच अरबी भाषेत सांगितली. ७७२ च्या सुमारास भारतातील गणितज्ञ व ज्योतिषविशारदांना सन्मानाने बगदाद येथे बोलवून त्यांच्याजवळील ज्ञानभांडार अरबीत भाषांतरित केले गेले. अल्-फजारी याने सिंद-हिंद या नावाचा गणितविषयक ग्रंथ भारतीय गणितग्रंथांच्या आधारे अरबीत लिहिला. या ग्रंथवरूनच अल्-ख्वारिज्मी याने ज्योतिषविषयक सारण्या सु. ८२५ मध्ये तयार केल्या. त्याने अंकासाठी गुबार (म्हणजे धूळ) पद्धतीचे अंक वापरून हिंदूंच्या दशमानपद्धतीची अरबांना ओळख करून दिली. तथापि तेथे दशमानपद्धती संपूर्णतया रूढ व्हावयास दहावे शतक उजाडावे लागले. मध्यंतरीच्या काळात तेथे त्यांची अक्षरांकित पद्धती (प्रामुख्याने ज्योतिषशास्त्रात) आणि जुनी हिंदुपद्धती ह्या दोन्ही प्रचलित होत्या. या पद्धतीत शून्यासाठी हिंदुपद्धतीच्या पोकळ वर्तुळाऐवजी भरीव टिंबाचा वापर करण्यात येत असे. ⇨अरबी लिपी उजवीकडून डावीकडे लिहिण्याची पद्धत असली, तरी संख्या मात्र डावीकडून उजवीकडे म्हणजे हिंदुपद्धतीप्रमाणेच लिहीत. (पहा : तक्ता क्र १.)
फार्सी साहित्यात ‘अबजद’ नावाची अक्षरांना मूल्ये प्रदान करून कालोल्लेख करण्याची पद्धती तेराव्या शतकात रूढ झाली. ती भारतीय संपर्काने अथवा रोमन लोकांकडून घेतलेली असावी. अबजदपद्धतीचा उपलब्ध असलेला सर्वप्रथम उल्लेख ६५६ हिजरी म्हणजे इ.स. १२७८ चा आहे. अरबी साहित्यिकांनी या पद्धतीचा फारसा अवलंब केल्याचे आढळत नाही तथापि नंतरच्या काळात क्वचित प्रसंगी तो केलेला आढळतो. भारतीय फार्सी साहित्यात अबजदपद्धतीचा उपयोग मात्र प्राचुर्याने आहे. अमीर खुसरौ (१२५३-१३२५) याने या पद्धतीचा प्रथम अवलंब केल्याचे आढळते. भारतीय फार्सी शिलालेखांतून अबजदपद्धतीचा उपयोग चौदाव्या शतकाच्या उत्तरार्धात सुरू झाला.
स्पेन व पश्चिम यूरोप : दहाव्या शतकात पोप दुसरा सिल्व्हेस्टर (मूळ नाव झेर्बेअर) याने हिंदू अंकपद्धतीचा पश्चिम युरोपात प्रसार केला. बगदाद येथे विद्वानांना जेव्हा आश्रय मिळेनासा झाला तेव्हा ते स्पेनमध्ये गेले. त्यांत रबीबेन इझ्रा (बारावे शतक) हा होता. त्याचा अंकगणितावरील एक ग्रंथ तेथे आहे. त्यात त्याने हिंदूंचे अंकगणित शून्याच्या वापरामुळे कसे सोयीचे झाले आहे हे साधार दाखविलेले आहे. ह्या ग्रंथात हिंदुपद्धतीतील फक्त शून्य घेण्यात आले आहे आणि बाकी नऊ अंकांसाठी हिब्रू अक्षरे वापरलेली आहेत. यावेळीच युरोपात शून्याचा वापर रूढ झाला. यानंतर सॅम्युएल बेन अब्बास (?- ११७४) याने अल्-तब्सीरा नावाचा अंकगणितावर ग्रंथ लिहिला. त्यात मात्र त्याने हिंदुपद्धतीच्या आकडयांचा वापर कटाक्षाने सर्वत्र केलेला आढळतो. बारव्या शतकात सेव्हिलचा जॉन याने अल्-ख्वारिज्मी याच्या अरबी ग्रंथाचे लॅटिनमध्ये डी न्यूमेरो इंडोरम् नावाने भाषांतर केले लॅटिन ही यूरोपात अभिजात भाषा मानली जात असल्याकारणाने स्वाभाविकपणे ह्या ग्रंथामुळे हिंदुपद्धतीचा परिचय सर्व यूरोपला झाला.
दशमानपद्धतीचा पुरेपूर प्रचार मात्र इटालियन गणितज्ञ लेओनार्दो फीबोनात्वी याच्यामुळे तेराव्या शतकात झाला. त्याच्या Liber Abaci (१२०२) या ग्रंथात हिंदु-अरबी पद्धतीने संख्या कशा लिहाव्यात व त्या कशा वाचाव्यात हे त्याने विस्ताराने सांगितले आहे. अशा प्रकारे हिंदु-अरबी दशमानपद्धती आधुनिक यूरोपीय जगात रूढ व स्थिर झाली.
सायमन स्टेव्हाइन (१५४८-१६२०) या डच गणितज्ञाने अपूर्णांक दर्शविण्यासाठी हिंदु-अरबी पद्धतीचा प्रथम वापर केला. यानंतर सतराव्या शतकाच्या आरंभी संख्येतील पूर्णांकी व अपूर्णांकी भाग वेगवेगळे दाखविण्यासाठी सध्याच्या दशांशचिन्हाचा वापर सुरू झाला आणि या वेळी अंकलेखनाची प्रचलित पद्धती परिपूर्णतेस पोचली. असे असले तरी अलीकडच्या काळातही पाश्चात्य देशांत काही किरकोळ भेद आढळतात. कित्येकदा एकच संज्ञा भिन्न संख्या दर्शविताना आढळते. उदा., ‘बिलियन’ ही संज्ञा अमेरिका व फ्रन्समध्ये ‘वन थाउजंड मिलियन’ म्हणजे १०९ (= १,०००,०००,०००) ही संख्या दर्शविते तर इंग्लंड व जर्मनीत तिचा अर्थ ‘मिलियन मिलियन’ म्हणजे
१०१२ (= १,०००,०००,०००,०००) हा होतो.
ज्योतिषशास्त्रात दूरस्थ ताऱ्यांचे अंतर दर्शविण्यासाठी फार मोठ्या संख्या वापराव्या लागतात आणि त्या लिहिणे फार गैरसोयीचे आहे. शास्त्रज्ञांनी प्रकाशवर्षाचे एकक मानून अथवा दहाच्या घातांत संख्या दर्शविण्याचा प्रघात पाडून ही अडचण सोडविली आहे.
भारत : वेदांची परंपरा ही लिखित नसून मौखिक आहे. वेदकाळातील यज्ञसंस्थेतून अंक जन्माला आले.अग्नीला आहुती देताना भारतीयांनी जयघोषात पहिल्या पूर्णांकाचा उच्चार केला असणार. नाभानेदिष्टाने केलेल्या सावर्णी राजाच्या स्तुतीत एक सहस्र गाई दान केल्याचा उल्लेख आहे: “सहस्र मे ददतो अष्टकर्ण्य:” (ऋ. १०.६७.७). या ठिकाणी ‘अष्टकर्ण्य गाय’ म्हणजे ‘जिच्या कानावर आठाच्या आकड्याचे चिन्ह आहे अशी गाय’ असा अर्थ होतो. आपल्या गाई ओळखता याव्यात म्हणून गाईच्या कानावर विशिष्ट खुणा करण्याचा त्या काळी प्रघात होता असे दिसते. वसिष्ठाच्या गाई ‘स्थूणाकर्ण्य:’ म्हणून ओळखल्या जात. स्थूण म्हणजे स्तंभ (जात्याचा खुंटा अगर मुसळ), यावरून एकाचा आकडा स्तंभासारखा लिहिला जात असावा, असा एक विचार येतो. पण याशिवाय इतर अंक कसे लिहीत याविषयीचा वेदकालीन कोणताही पुरावा उपलब्ध नसल्यामुळे याबद्दल नि:संदिग्ध विधान करता येत नाही. तथापि निदान आठ अंक त्या काळी लिहीत असावेत असे दिसते. भारतातील अंकांचा सर्वांत प्राचीन पुरावा ऋग्वेदामध्ये आढळून येतो.
तिस्त्रो द्यावःसवितुर्द्वा उपस्थां एका यमस्य
भुवने विराषाट् ।।ऋ. १.३५.६
अष्टौ व्यख्यत्ककुभःपृथिव्यास्त्रीधन्वयोजना
सप्त सिंधून् ।।ऋ. १.३५.८
सहस्रशीर्ष: पुरूषःसहस्त्राक्ष: सहस्रपात्।
स भूमिं विश्वतो वृत्वात्यतिष्ठद्दशाङ्गुलम्।।ऋ. १०.९०.१
या ऋचांवरून ऋग्वेदकालात केवळ तीन, सात, आठ इ. लहान संख्याच होत्या असे नाही, तर हजारापर्यंत अंकमोजणी होऊ शकत होती, असे दिसून येते. शुक्लयजुर्वेद संहितेमध्ये एक, दश, शत, सहस्र, अयुत, नियुत, प्रयुत, अर्बुद, न्यर्बुद, समुद्र, मध्य, अंत, परार्ध यांपर्यंत स्थानमूल्ये दिलेली आहेत. हेच अंक तैत्तिरीय संहिता, मैत्रायणी आणि काठक संहितांमध्येही आढळतात. ⇨भास्कराचार्यांनी (१११४-८५) लीलावती ह्या आपल्या प्रसिद्ध ग्रंथात स्थानमूल्यांसंबंधीचे पुढील दोन श्लोक दिलेले आहेत :
एकदशशतसहस्त्रायुतलक्षप्रयुतकोठ्य:क्रमशः।
अर्बुदमब्जं खर्वनिखर्वमहापद्मशङ्कवस्तस्त्मात्।।
जलधिश्चान्त्यं मध्यं परार्धमिति दशगुणोत्तरं संज्ञाः।
संख्याया:स्थानानां व्यवहारार्थ कृताःपूर्वैः।।
ललितविस्तर ह्या बौद्ध ग्रंथात गौतम आणि अर्जुन यांच्या संवादात ‘कोटि’ हा अंकवाचक शब्द आलेला आहे. शिलालेखातील आणि वाङ्मयातील अंकाबाबतच्या पुराव्यांवरून त्याच्या उत्पत्तीविषयी कुठलाही निश्चित सिद्धांत मांडणे कठीण आहे. तैत्तिरीय संहितेत युग्म आणि अयुग्म हे शब्द सम आणि विषम संख्यांकरिता वापरलेले असून दोन, चार, पाच, व दहा यांचे पाढे दिलेले आहेत. अंक कसे लिहीत याविषयीची दृष्टिगोचर असा कोणताही दाखला मिळत नाही. पण श्रवणगोचर पुराव्यावरून आपणास असे आढळून येते, की वाजसनेयी व तैत्तिरीय संहितांत दहा आकडे व दहाच्या १०१२ पर्यंतच्या सर्व पटींची नामाभिधाने दिलेली आहेत. एवढया मोठ्या संख्या कोणत्या कसल्या प्रकारच्या चिन्हांनी दर्शवीत, हे आपणास समजणे शक्य नाही. पण त्या काळी ह्या संख्या दर्शविण्याची पद्धत प्रचारात असल्याशिवाय त्यांची नावे देण्याचे प्रयोजन नव्हते असे दिसते. पण दहाच्या पटींवरूनच दशमान पद्धती अस्तित्वात आली, असे अनुमान करण्यास हरकत नाही. संख्या सांगताना ‘अंकानां वामतो गति:’ ही पद्धती अवलंबिलेली असल्याकारणाने वरील विधानास पुष्टी मिळते.
भारतवर्षात अंकलेखनाची पद्धत केव्हापासून सुरू झाली हे नक्की सांगता येत नाही. अशोकाच्या सिद्धपूर, सहस्त्राम आणि रूपनाथ येथील शिलालेखांत २००, ५० आणि ६ हे अंक आढळून येतात. दक्षिणेकडे नाणेघाटातील, सातवाहन-सम्राज्ञी नागनिका (इ.स.पू. २ रे शतक) हिच्या लेखात १, २, ४, ६, ७, ९, २०००० वगैरे संख्याही आलेल्या आहेत.
ही चिन्हे येणेप्रमाणे:

तसेच नासिकजवळील पांडव लेण्यातील शिलालेखात (इ.स. १ ले किंवा २ रे शतक) संपूर्ण १ ते १० पर्यंतच्या अंकांची चिन्हे आढळतात. ती पुढीलप्रमाणे:

शिलालेखातील पुरावा जास्त विश्वसनीय असला, तरी तो नंतरचा आहे.
जेम्स प्रिन्सेप यांनी १८३८ मध्ये अंक म्हणजे त्यांच्या सूचक शब्दांचे प्रथमाक्षर आहे असे प्रतिपादन केले. भगवानलाल इंद्रजी यांच्या मते पहिल्या तीन अंकांशिवाय बाकी सर्व अंक अक्षराने दर्शविले जात. ती अक्षरे कालानुरूप लिपीप्रमाणे असल्यामुळे लिपीमध्ये आणि देशविशेषांत फरक पडला असेल, तर अंकलेखनातही फरक पडलेला आढळून येतो. पन्नास आणि साठ या अंकांची चिन्हे अनुनासिक आणि जिव्हामूलीयाच्या खुणा असल्यामुळे अंकलेखनपद्धती भारतीय पंडितांनी निर्माण केली, असे भगवानलाल इंद्रजी यांनी प्रतिपादन केले. हे मत ए. सी. बर्नेल यांना पटले नाही. त्यांच्या मते ब्राह्मी लिपी फिनिशियन (बॅबिलोनीयन) लिपीपासून निर्माण झाली आणि अंक ईजिप्तच्या डेमॉटिक अंकांतून उत्पन्न झाले. अशोकाच्या लेखांतील अंकांची उत्पत्ती डेमॉटिक लिपीपासून झाली आणि त्यांचा विकास भारतात झाला. बेली यांच्या मतानुसार भारतीय अंक ईजिप्तमधील हायरोग्लिफिक अंकापासून उत्पन्न झाले. १८९६ मध्ये जी. ब्यूलर यांनी हे म्हणणे खोडून काढले. अशोकाच्या शिलालेखांत जे अंक आढळतात त्यांवरून भारतात तत्पूर्वी अंकलेखनाची कला निश्चितपणे अस्तित्वात होती असे दिसते. ब्यूलर यांच्यामते हायरोग्लिफिक लिपीतील अंकांचा क्रम भारतीय अंकांपेक्षा फार भिन्न आहे. हायरोग्लिफिक लिपीमध्ये एकापासून नवापर्यंतचे आकडे उभ्या दंडांनी दर्शविले जात. एकाचा आकडा नऊ वेळा लिहिला तर नऊ हा आकडा होतो. दहाचे चिन्ह दोन वेळा लिहिले, तर २० हा आकडा होतो. तिसासाठी दहाचे चिन्ह तीन वेळा, साठासाठी सहा वेळा लिहिले जाई. दोनशेचा आकडा लिहिण्यासाठी शंभराचा आकडा दोन वेळा लिहित. याप्रमाणे हजार, दहा हजार आणि लक्ष या संख्या लिहिल्या जात. ईजिप्शियन आणि भारतीय अंकलेखनात वीस चिन्हे असल्यामुळे भारतीय अंक हायरोग्लिफिकवरून घेतले असावेत, असा तर्क आहे. असे असले तरी त्यांमध्ये केवळ नऊ चिन्हांमध्येच किंचित साम्य आहे. भारतातील अंकलेखनाची पद्धती इतकी स्वतंत्र आहे, की तिचे मूळ परदेशी असले तरी ते ओळखणे अतिशय अवघड आहे.
वि. १ – ४
भारतीय अक्षरांकपद्धती : भारतीय कोरीव लेखांत सर्वसामान्यपणे आलेले अंक खालीलप्रमाणे आहेत. तथापि या अंकांसाठी प्रचलित देवनागरी वर्णमालेतील जी अक्षरे दिलेली आहेत ती ह्या कोरीव लेखांच्या काळी आजच्या देवनागरी वर्णमालेप्रमाणे नव्हती, तर ती ब्राह्मीजन्य होती, हे उघड आहे.
एक, दोन आणि तीन या अंकांना एक, दोन आणि तीन असे आडवे दंड आहेत. जे. एफ्. फ्लीट यांनी ते ऱ्हस्व, दीर्घ आणि प्लुत (अतिदीर्घ उच्चार) उ असल्याचे प्रतिपादन केले आहे.
चार ह्या अंकासाठी क, प्क,ङ्क,ण्क ही अक्षरे आढळतात.
पाचासाठी तृ हे अक्षर असले तरी ऋकार लावण्यात मात्र निश्चितपणा दिसून येत नाही. तृा, तु, नु, न, ना, हु, ह्र ही अक्षरेही कधीकधी लेखांतून आढळतात.
सहा या अंकाबद्दल ज, स, फ्र, फ्रा, फ, फा या अक्षरांची योजना केलेली दिसते.
सातासाठी ग्र किंवा गु, ग ही अक्षरे येतात.
आठासाठी ह्र हे अक्षर असले तरी रफार मात्र अनिश्चितपणे काढलेला दिसून येतो. शिवाय ह, हा, ह्रा, पु ही अक्षरेही आढळून येतात.
नऊ या अंकासाठी ओ आणि कधीकधी औ हे अक्षर आलेले आहे.
दहा या संख्येसाठी ठू हे अक्षर कोरीव लेखांत आढळते. ठ या अक्षरातील वर्तुळातूनच ठू हे अक्षर तयार झाले. र्य, ळ, ख, लृ या अक्षरांचाही दहासाठी उपयोग केलेला आढळून येतो.
विसासाठी ठ, थ, था ह्या अक्षरांची योजना दिसून येते.
तिसासाठी ल हे अक्षर काढीत.
चाळीस या अंकासाठी हस्तलिखितांमधून प्त हे अक्षर असले, तरी शिलालेख आणि ताम्रपटांतून स, त ही अक्षरे आलेली दिसतात.
पन्नासासाठी अर्धचंद्राकृती, उजवीकडे तोंड करून डावीकडे अथवा उजवीकडे वळलेली काढीत.
साठासाठी पु हे अक्षर विविध आकारांनी दर्शवीत.
सत्तर ह्या संख्येसाठी पू किंवा प्रा ही अक्षरे निरनिराळया पद्धतींनी काढलेली आढळून येतात.
ऐंशी ही संख्या दर्शविण्यासाठी उपध्मानियाच्या ![]() लंबवर्तुळात उभा दंड काढलेला आढळून येतो.
लंबवर्तुळात उभा दंड काढलेला आढळून येतो.
नव्वद या संख्येसाठी उपघ्मानियाच्या लंबवर्तुळात बेरजेच्या चिन्हासारखे चिन्ह काढलेले आढळते.
शंभर या आकड्यासाठी सु हे अक्षर आलेले असून, सातव्या-आठव्या शतकांतील नेपाळातील लेखांत त्यासाठी अ हे अक्षर आलेले आहे. देशविभाग आणि कालमानानुसार यामध्ये निरनिराळे फरक होत गेलेले आहेत. शंभराच्या खुणेला एक आणि दोन आडवे दंड लावले म्हणजे अनुक्रमे दोनशे आणि तीनशे या संख्या होतात.
चारशेसाठी शंभराची आणि चाराची खूण, पाचशेसाठी शंभराची आणि पाचाची खूण, हजाराच्या खूणेसाठी रो किंवा चु ही अक्षरे काढण्यात येत असत. दोन हजार आणि तीन हजार यांसाठी धु या अक्षराला अनुक्रमे एक आणि दोन आडवे दंड काढलेले दिसून येतात. चार हजारासाठी रो + कि किंवा धु + कि सहा हजारासाठी रो + फ्र सात हजारासाठी धु + प्त आठ हजारासाठी धु + ह्र दहा हजारासाठी रो + ठू वीस हजारासाठी रो + ठ अशा तऱ्हेची अक्षरयोजना केलेली आढळून येते.
कोरीव लेखांतील अंक आणि हस्तलिखितांतील अंक यांमध्ये पुष्कळ वेळा फरक आढळतो. प्राचीन हस्तलिखितांमध्ये खालीलप्रमाणे अंकसूचक अक्षरे दिलेली आहेत :
हस्तलिखितांमध्ये १, २, ३ या अंकांसाठी ए, द्वि, त्रि, स्व, स्ति, श्री, ओं, न, म: ही अक्षरे आढळतात. ती मांगल्यसूचक असल्यामुळे पहिल्या तीन आकड्यांची निदर्शक आहेत. एकाच आकड्यासाठी हस्तलिखितांमधून निरनिराळी अक्षरे आलेली आहेत. वीस हा आकडा प्रथम थ प्रमाणे काढीत आणि नंतर घ प्रमाणे काढू लागले. पुढे पुढे ह्या आकड्यासाठी घ ह्या अक्षराऐवजी प्व आणि प ही अक्षरे प्रचारात आली. अशा तऱ्हेने

बाकीच्याही अंकांत बदल झाले. प्राचीन शिलालेखांत आणि दानपत्रांत अंक एका ओळीत लिहीत असत. परंतु हस्तलिखितांमध्ये अंक एकाखाली एक लिहीत असत. अशा तऱ्हेने अंक पाटण, खंबायत, उदयपूर येथील हस्तलिखितांतून सापडतात (पहा : तक्ता क्र. २, २ अ व २ आ).
स्थानमूल्याप्रमाणे केलेले अंकलेखन उत्तर व दक्षिण भारतात आठव्या शतकाच्या शेवटच्या पादात प्रथम आढळते. विद्वानांच्या मते शक ६१६ ही दशमानपद्धतीतील संख्या देवेंद्रवर्मन याच्या सिद्धांतम् ताम्रपटात आलेली आहे. तसेच कंबोडीयात दशमानपद्धतीने कालोल्लेख असलेले शक ५२६ आणि शक ५४६ चे संस्कृत शिलालेख उपलब्ध आहेत. शिवाय वराहमिहिराने अनेक संख्या ‘अंकानां वामतो गतिः’ या पद्धतीने आपल्या पंचसिद्धांतिका (५०५) ग्रंथात मांडलेल्या असून या पद्धतीत दशमानपद्धतीतील स्थानमूल्यांकन अभिप्रेत आहे. असे असले तरी दहाव्या शतकापर्यंत प्राचीन पद्धतीनेच अंकलेखन करीत असत. परंतु त्यानंतर मात्र स्थानमूल्याप्रमाणेच अंकलेखन सर्रास सुरू झाले.
अंकलेखनामध्ये शून्याची योजना कधीपासून झाली, हे सांगणे अवघड आहे. वराहमिहिराच्या पंचसिद्धांतिकेत शून्याविषयीचा उल्लेख पुष्कळ ठिकाणी आला आहे. वराहमिहिराचा समकालीन जिनभद्रगणी (५२९-५८९) हा २,२४,४०,००,००,००० या संख्येचे वर्णन बावीस चव्वेचाळीस आठ शून्ये असे करतो. उमास्वातीच्या तत्वाधिगमसूत्रांवर टीका करताना सहाव्या शतकात होऊन गेलेला सिद्धसेनगणी असे सांगतो, की ३५,३४,४०,००,००,००० या संख्येच्या वर्गमूळात चार शून्ये येतात व ते वर्गमूळ १८,८०,००० इतके येते. शून्याकरिता वापरलेले व सध्या प्रचलित असलेले वर्तुळाकार चिन्ह भोजदेवाच्या ग्वाल्हेरच्या शिलालेखात (८७०) कोरलेले आढळते. त्यानंतर मात्र या चिन्हाचा शून्याकरिता सर्रास वापर केलेला दिसतो. आठव्या शतकात भारतामध्ये दशगुणोत्तर अंकक्रमाचा उपयोग कोरीव लेखांत केला आहे. नवव्या शतकात अल् ख्वारिज्मी याने अरबी भाषेत या अंकपद्धतीचे विवेचन केले आहे. बाराव्या शतकात ही पद्धती सर्व यूरोपभर रूढ झाली. १ ते ९ पर्यंतचे आकडे लिहिल्यानंतर काढलेल्या शून्यामुळे अंकाच्या किंमतीमध्ये दसपटीचा फरक पडतो. ज्योतिषग्रंथांमध्ये या पद्धतीचा अवलंब केलेला आढळून येतो. वराहमिहिराने आपल्या पंचसिद्धांतिका या ग्रंथामध्ये अंकांचा स्थानमूल्याप्रमाणे निर्देश केलेला आहे. त्यावरून वराहमिहिरापूर्वीदेखील ही पद्धती अस्तित्वात होती यात शंका नाही. होर्नले यांच्या मते तिचा शोध इसवी सनाच्या आरंभी किंवा तत्पूर्वीही भारतात लागला असावा.
तक्ता क्र. २ : ब्राह्मी व ब्राह्मीजन्य लिपींतील १ ते ९ पर्यंतच्या अंकांचा विकास (इ.स.पू. ३ रे ते इ.स. ४ थे शतक)
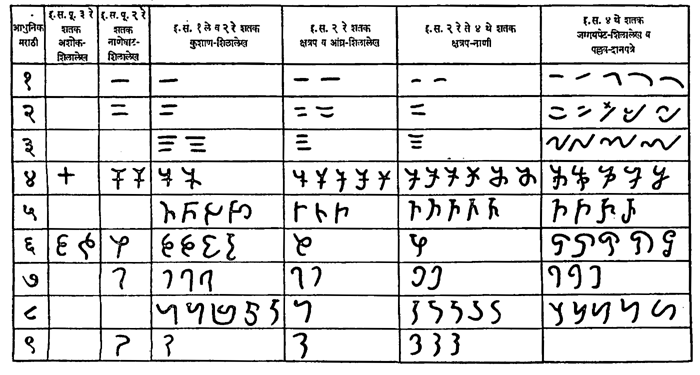
तक्ता क्र. २ अ : ब्राह्मी व ब्राह्मीजन्य लिपींतील १ ते ९ पर्यंतच्या अंकांचा विकास (इ.स. ४ थे ते ९ वे शतक)
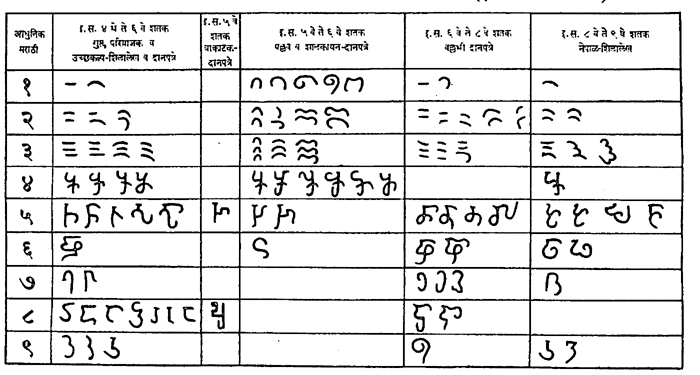
तक्ता क्र. २ आ : ब्राह्मी, ब्राह्मीजन्य व खरोष्ठी लिपींतील १ ते ९ पर्यंतच्या अंकांचा विकासक्रम
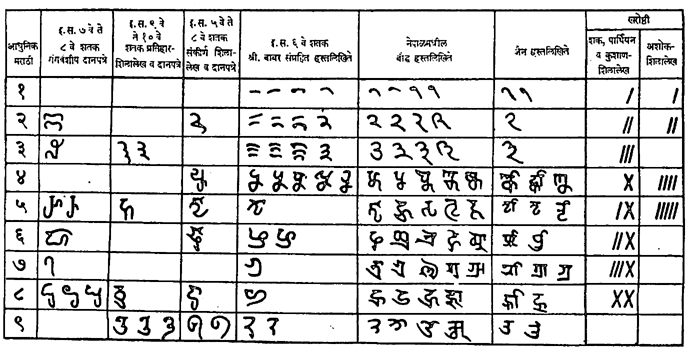
भारतीय शब्दांकपद्धती : स्थानमूल्याप्रमाणे अंकनिर्देश केलेला असला, तरी शब्दांनी अंक लिहिण्याची पद्धतीही ज्योतिष आणि गणित ग्रंथांत दिसून येते. पुढे पुढे संख्या संक्षिप्त रूपाने आणि सांकेतिक शब्दांनी सूचित करण्याची पद्धती रूढ झाली. निरनिराळ्या अंकांसाठी रूढ असलेले शब्द खाली दिलेले आहेत:
० = शून्य, ख, गगन, आकाश आणि आकाशवाचक शब्द.
उदा., व्योम, अंतरिक्ष, नभ, पूर्ण, रंध्र इ.
१ = आदि, शशि, इंदु, विधु, चंद्र आणि चंद्राची नावे पृथ्वी आणि पृथ्वीची नावे शिवाय पितामह, नायक, तनु इ.
२ = यम, यमल, अाश्विन्, नासत्य, कर्ण, नेत्र, ओष्ठ, जानु, बाहु, युगल, कुटुंब, रविचंद्रौ इ.
३ = राम, गुण, त्रिगुण, लोक, त्रिजगत्, त्रिनेत्र इ.
४ = वेद, आश्रम, वर्ण, युग, बंधु, दिशा इ.
५ = बाण, शर, पांडव, महाभूत, तत्त्व, इंद्रिय, रत्न इ.
६ = रस, अंग, काय, ऋतु, दर्शन, तर्क इ.
७ = पर्वतवाचक शब्द. उदा., गिरी, वार, स्वर, धातु, अश्व, तुरग इ.
८ = वसु, अहि, नाग, अनुष्टुभ इ.
९ = अंक, नंद, द्वार इ.
१० = दिश्, दिशा, अंगुलि इ.
११ = रूद्र, ईश्वर इ. महादेवाची नावे.
१२ = आदित्य वगैरे सूर्याची नावे, मास, राशि इ.
१३ = विश्वेदेवा, काम अतिजगति, अघोष इ.
१४ = मनु, विद्या, इंद्र इ.
१५ = तिथी, पक्ष इ.
१६ = नृप, कला इ.
१७ = अत्यष्टि
१८ = धृति
१९ = अतिधृति
२० = नख, कृति इ.
२१ = उत्कृति इ.
२२ = कृति, जाति इ.
२३ = विकृति.
२४ = गायत्री इ.
२५ = तत्त्व
२७ = नक्षत्र इ.
३२ = दंत इ.
३३ = देव इ.
४० = नरक
४८ = जगती
४९ = तान
अशा तऱ्हेने अंक सूचित करण्याची पद्धती शतपथ आणि तैत्तिरीय ब्राह्मणां मध्ये दिसून येते. चारासाठी कृत हा शब्द वापरला आहे कात्यायन आणि लाटयायन श्रौतसूत्रांमध्ये चोवीस या आकड्यासाठी गायत्री, अठ्ठेचाळीस या आकडयासाठी जगती हे शब्द योजले आहेत. वेदांगज्योतिष या ग्रंथात १, ४, ८, १२, २७ यांसाठी अनुक्रमे रूप, अय, गुण, युग आणि भसमूह हे शब्द आलेले आहेत. वराहमिहिराच्या पंचसिद्धांतिका आणि ब्रह्मगुप्ताच्या ब्रह्मस्फुटसिद्धांत या ग्रंथांतून आणि ताम्रपटांतून शब्दांनी अंक सूचित केले आहेत.
शब्दांनी अंक सूचित करण्याची पद्धती लोकप्रिय झाल्यावर शब्दांचा संक्षेप करण्याची पद्धती अस्तित्वात आली. शब्दांच्या जागी अक्षरे आली. पाचव्या शतकामध्ये पहिल्या आर्यभटाने आपल्या आर्यसिद्धांत (४९९) या ग्रंथात अंकांसाठी खलील अक्षरे उपयोगात आणली आहेत :
क् = १ ख् =२ ग्=३ घ् = ४ ङ् = ५
च् = ६ छ् = ७ ज् =८ झ् = ९ त्र् = १०
ट् = ११ ठ् = १२ ड् = १३ ढ् = १४ ण् = १५
त् = १६ थ् = १७ द् = १८ ध् = १९ न् = २०
प् = २१ फ = २२ ब् = २३ भ् = २४ म् = २५
य् = ३० र् = ४० ल् = ५० व् = ६० श् = ७०
ष् = ८० स् = ९० ह् = १००
अ = १, इ = १००, उ = १०,०००, ऋ = १०,००,०००,
लृ = १०,००,००,०००, ए = १०,००,००,००,०००,
ओ = १०,००,००,००,००,००,०००,
औ = १०,००,००,००,००,००,००,०००,
या अंकलेखनाच्या पद्धतीत स्वरांमध्ये ऱ्हस्व-दीर्घ भेद नाहीत. व्यंजनांमध्ये जो स्वर असेल त्या ठिकाणी व्यंजनसूचक अंकाला स्वरसूचक अंकाने गुणावे. उदा., ङि. (ङ्+इ) या अक्षराने मूल्य ५ X १०० = ५०० होते.
दुसऱ्या आर्यभटाने ११ व्या शतकात आपल्या ग्रंथामध्ये अंकांचे आणि दर्शक अक्षरांचे खालील कोष्टक दिले आहे :
| १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ | १० |
| क् | ख् | ग् | घ् | ङ् | च् | छ् | ज् | झ् | ञ् |
| ट् | ठ् | ड् | ढ् | ण् | त् | थ् | द् | ध् | न् |
| प् | फ् | ब् | भ् | म् | |||||
| य् | र् | ल् | व् | श् | ष् | स् | ह् | ळ् |
एका व्यंजनाने एकाच अंकाचा निर्देश केलेला आहे. असा पद्धतीने अंक शिलालेख आणि दानपत्रांतून आलेले दिसून येतात. परंतु ‘अंकांना वामतो गतिः’ या नियमानुसार पहिल्या अक्षराने एकम् स्थान दुसऱ्या अक्षराने दहम् स्थान आणि तिसऱ्या अक्षराने शतम् स्थान दर्शविले जाते. अक्षराने अंक सूचित करण्याची पद्धती पणिनीच्या व्याकरणातही आढळून येते. सूत्र १.३.११ वरून असे कळते, की अष्टाध्यायीत अधिकारव्याप्ती स्वरियुक्त वर्णाने दाखविली जात असे आणि ते वर्ण शिवसूत्रांतील क्रमानुसार संख्या दर्शवीत असत. उदा. अ = १, इ = २, उ = ३ इत्यादि.
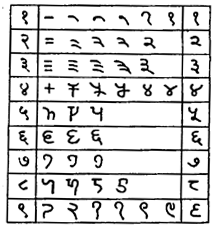
आधुनिक भारतीय अंक : सध्या भारताच्या भिन्न प्रदेशांत वेगवेगळ्या लिपी प्रचलित आहेत. या लिपीमधील अंकचिन्हांतही तफावत आढळते. तथापि या सर्व लिपी ⇨ब्राह्मी आणि त्यापासून ⇨नागरी या लिपींतून उद्गम पावल्या असल्याकारणाने त्यांच्यातील परस्परसंबंध दर्शविणे तसे सोपे आहे. अंकचिन्हेही अशीच मूळ ब्राह्मी-नागरीतून विकसित झाली परंतु देश व कालमानानुसार त्यांतील काही चिन्हांत फार मोठा फरक होत गेला (पहा तक्ता क्र.३) एवढे मात्र निश्चित, की या प्रादेशिक लिपी प्रचारात येण्यापूर्वीच शून्याची कल्पना व स्थानमूल्याच्या तत्वाचे महत्व भारतीयांना माहीत होते. वर्तमान प्रादेशिक लिपींमध्ये प्रचलित असलेले १ ते ९ पर्यंतचे अंक तक्ता क्र ४ मध्ये दर्शविले आहेत.
विविध मूलांकपद्धती : कोणतीही गणना करण्यासाठी दोनादोनाचे, पाचापाचाचे, दहादहाचे वगैरे गट पाडून ती गणना करणे सोयीचे ठरते. ह्या दोन, पाच, दहा वगैरे प्रत्येक गटातील संख्येस त्या ‘अंकपद्धतीचामूलांक’ म्हतात.प्राचीन काळापासून निरनिराळया मूलांकांवर आधारलेल्या अंक पद्धती जगाच्या निरनिराळ्या भागात प्रचलित आहेत. मोजण्याकरिता हातांच्या पायांच्या बोटांचा उपयोग करण्याच्या पद्धतीवरून पुढे ५, १० व २० या मूलांकांचा वापर प्रचारात आला असावा. कान, हात,डोळे,पाय यांच्या दोन संख्येवरून दोन हा मूलांक, तर हाताच्या बोटांवरील पेऱ्यांच्या संख्येवरून ३ व १२ हे मूलांक वापरात आले असावेत. अंदमान, मलाक्का,ऑस्ट्रेलिया येथील काही वन्य जमातींत दोन हा मूलांक घेण्याची पद्धती आढळते. कॅलिफोर्नियातील काही रेड इंडियन जमातीत चार हा मूलांक वापरतात, तर वायव्य आफ्रिकेतील काही जमातीत सहा मूलांक प्रचारात आहे. दक्षिण अमेरिकेतील आरावाक भाषासमूहातील एका भाषेत पाच हा मूलांक घेतात. मध्य अमेरिका (माया संस्कृती), आफ्रिकेतील गिनी देश व हिमालयाशी भिडलेल्या तिबेट-चीनच्या सरहद्दीवरील प्रदेशात वीस हा मूलांक घेण्याची प्रथा होती. आणखी एक प्रचारात आलेली पद्धती म्हणजे द्वादशमान पद्धती होय. पण ही पद्धती सर्वांत जुनी असणे संभवत नाही. कारण बाराचे अवयव १, २, ३, ४, ६ व १२ असू शकतात व त्यामुळे अवयव पाडण्याचे ज्ञान अवगत झाल्यावरच द्वादशमानपद्धती वापरण्याची कल्पना मानवाला सुचली असावी. पण या सर्व पद्धती कालांतराने मागे पडल्या व फक्त दशमानपद्धतीचा वापर रूढ झाला. तथापि अलीकडे ⇨ संगणकात द्विमानपद्धतीचा उपयोग फायदेशीर असल्याचे आढळून आल्यापासून, इतर काही मूलांक (उदा, ३, ७, ८ इ.) घेऊन गणितकृत्ये सोपी होतील की काय, याचा विचार होत आहे.
सतराव्या शतकात लायप्रिट्स या जर्मन गणितज्ञांनी द्विमानपद्धतीचा विकास केला. तथापि १९४० च्या सुमारास संगणकाचा विकास होईपर्यंत या पद्धतीचा व्यवहारात उपयोग होऊ शकला नाही. हल्ली अनेक इलेक्ट्रॉनीय संगणकांत द्विमानपद्धती वापरतात. द्विमानपद्धतीतील अंक विद्युतमंडलाच्या स्वरूपात दर्शविणे सोपे असते. ० हा अंक खुल्या स्विचने (म्हणजे बंद दिवा) आणि १ हा अंक बंद स्विचने (म्हणजे चालू दिवा) दर्शविणे शक्य असते. द्विमानपद्धतीचा इतर ठिकाणीही उपयोग करणे शक्य असल्याचे आढळून आले आहे. उदा., बिंदू व रेघ यांनी दर्शविण्यात येणारी मॉर्स सांकेतिक लिपी, वीज-धारित्र-संचातील भारित व निर्भारित धारित्रे इ.
अंकांचा उपयोग करून गणना करणे व निरनिराळ्या संख्यांना नावे देणे यांकरिता तत्वत: कोणत्याही मूलांकाचा उपयोग करणे शक्य आहे. अशा कोणत्याही अंकपद्धतीत उपयोगात आणिलेल्या अंकांची संख्या ही मूलांकाबरोबर असते. उदा., द्विमानपद्धती ० व १ हे दोन अंक असतात, तर पंचमानपद्धतीत ०, १, २, ३, ४ हे पाच अंक असतात. अर्थात येथे ०, १, २ इ. चिन्हेच वापरणे आवश्यक आहे असे नाही. द्वादशमानपद्धतीत १० व ११ या अंकांना निराळी चिन्हेच देणे आवश्यक होईल कारण द्वादशमानपद्धतीतील १० व ११ या चिन्हांचा अर्थ आणि दशमान पद्धतीतील त्यांचा अर्थ यांचा घोटाळा होण्याचा संभव आहे.
तक्त क्र.४ : आधुनिक भारतीय भाषांतील १ते९ पर्यतचे प्रचलित अंक

अंकपद्धतीत व्यापकीकरणासाठी प हा कोणताही मूलांक घेतल्यास, अशा पद्धतीत ०, १,…, प-१ असे एकूण प अंक येतील. या पद्धतीत…च घ ग ख क अशी कोणतीही संख्या मांडल्यास तिचे मूल्य पुढीलप्रमाणे येईल :
…च घ ग ख क = … च X (प४) + घ X (प३) + ग X (प२) + घ X (प१) + क X (प०).
अशा प्रकारच्या प हा मूलांक असलेल्या पद्धतीत मांडलेली एखादी संख्या, उदा., ४०,२३१ घेतल्यास तिची दशमानपद्धतीतील फोड पुढे दिल्याप्रमाणे करता येईल : प हा मूलांक आहे असे दर्शविण्यासाठी संख्या ४०,२३१प अशी मांडली आहे. ४०,२३१प = ४ X प४ + ० X प३ + २ Xप२ + ३ X प१ + १ X प०. येथे उदा., प = ५ (म्हणजे पंचमान पद्धती) असेल तर –
४०,२३१ पाच = ४ X ५४ + ० X ५३ + २ X ५२ + ३ X ५१ + १ X ५०
= २५०० + ० + ५० + १५ + १
= २५६६ (दशमानपद्धतीतील).
याच संख्येचे द्विमानपद्धतीत रूपांतर करावयाचे असल्यास ते पुढीलप्रमाणे करता येते :
२५६६= १ X २११ + ० X २१०+ १ X २९+ ० X २८ + ० X २७
+ ० X २६ + ० X २५+ ० X २४ + ० X २३+ १ X २२
+ १ X २१+ ० X २०.
२५६६ (दशमानपद्धतीतील) = १,०१,००,००,००,११० (द्विमानपद्धतीतील).
अशाप्रकारे २,५६६ ही दशमानपद्धतीतील संख्या पंचमानपद्धतीत ४०,२३१ पाच अशी द्विमानपद्धतीत १,०१,००,००,००,११० दोन अशी दर्शविता येते. याच पद्धतीने कोणत्याही मूलांकानुसार लिहिलेल्या संख्येची इतर मूलांकपद्धतीत मांडणी करता येते.
पहा : संख्या शून्य.
संदर्भ: 1. Cajori, F. A History of Elementary Mathematics, Londan, 1924.
2. Datta, B. Sing A. N. History of Hindu Mathematics, Bombay, 1962.
3. Gokhale Shobhana L. Indian Numerals, Poona, 1966.
4. Gurjar, L. V. Ancient Indian Mathematics and Vedha, Poona 1947.
5. Satya Prakash, Founders of Sciences in Ancient India New DeIhi, 1965.
6. Smith, D. E. History of Mathematics, 2 Vols., New York, 1923.
७. ओझा गौरीशंकर, भारतीय प्राचीन लिपिमाला, दिल्ली, १९५९.
८. ब्यूलर, जॉर्ज अनु. सिंह, मंगलनाथ, भारतीय पुरालिपिशास्त्र, वाराणसी १९६६.
गुर्जर, ल. वा. गोखले, शोभना ल.
”