प्रकाशवेग

प्रकाशवेग : भौतिकीमध्ये प्रकाशाच्या वेगाला फार महत्त्व असल्यामुळे सतराव्या शतकापासून आजपर्यंत निरनिराळ्या शास्त्रज्ञांनी त्याचे अचूक मापन करण्याकरिता अनेक प्रयोग केलेले आहेत. ⇨ सापेक्षता सिद्धांतात प्रकाशवेग ही एक मूलभूत नैसर्गिक राशी मानलेली आहे, तसेच प्रकाशाचा वेग म्हणजेच ⇨विद्युत्‌ चुंबकीय तरंगांचा वेग असल्यामुळे (रडार वगैरे उपकरणांच्या कार्यांत) या गणनाला विशेषच महत्त्व प्राप्त झाले आहे.

पद्धतींचे वर्गीकरण : प्रकाशवेगाच्या मापनासाठी विविध पद्धती वापरल्या गेल्या आहेत. त्यांचे स्थूलमानाने दोन वर्ग करता येतात. ज्या पद्धतींत प्रकाशाला (किंवा रेडिओ तरंगांना) विशिष्ट अंतर तोडण्यासाठी लागणारा काल काढून त्यावरून प्रकाशवेग काढला जातो, त्यांना प्रकाशवेगमापनाच्या प्रत्यक्ष पद्धती असे म्हणतात (उदा., पुढे दिलेल्या रोमर, फीझो किंवा मायकेलसन इत्यादींच्या पद्धती).

याउलट ज्या पद्धतींमध्ये विद्युत् चुंबकीय तरंगांच्या काही खास गुणधर्मांचा (उदा., वेग = तरंगलांबी  X  कंप्रता) उपयोग करून त्यावरून प्रकाशवेगाचे गणन केले जाते, त्यांना अप्रत्यक्ष पद्धती असे म्हणतात (उदा., ब्रॅड्‌ली यांची पद्धती, अनुस्पंदन पद्धती इत्यादी).

रोमर व ब्रॅड्‌ली पद्धती ज्योतिषशास्त्रीय असून फीझो, मायकेलसन इ. पद्धती भौमिक आहेत. खाली वर्णन दिलेल्या पद्धतींचे वर्गीकरण ज्योतिषशास्त्रीय व भौमिक असे केलेले आहे.

समूहवेग आणि कलावेग : प्रकाशवेग हा शब्द सामान्यतः ‘ज्या वेगाने प्रकाश ऊर्जेचे प्रसारण होते किंवा रेडिओ तरंगांद्वारे संदेशांचे प्रसारण होते तो वेग’ या अर्थाने वापरला जातो. शास्त्रीय परिभाषेत याला प्रकाश तरंगांचा ‘समूहवेग’ असे म्हणतात. प्रत्यक्ष पद्धतीमुळे या समूहवेगाचेच मापन होत असते, हे उघडच आहे. 

समूहवेग म्हणजे अनेक तरंगांच्या समूहाचा वेग होय. या समूहातील घटक तरंगांच्या कंप्रतांमधील (दर सेकंदाला होणाऱ्या कंपनांच्या संख्यांमधील) फरक अत्यल्प असतात. मर्यादित लांबीच्या तरंगमाला या तरंगांचे समूहच असतात [→ प्रकाशकी]. त्यामुळे जेव्हा प्रकाशझोत कोणत्याना कोणत्या उपायाने खंडित करून प्रकाशवेग मोजला जातो तेव्हा समूहवेगच मिळतो. त्याचप्रमाणे विरूपित रेडिओ तरंग [→ विरूपण] हेही तरंग समूहच असतात व त्यांच्या साहाय्याने मोजलेला प्रकाशवेग हाही प्रकाशाचा समूहवेगच असतो. प्रकाशाच्या सर्व अनुप्रयोगांत हा समूहवेगच उपयोगी असतो.

एखाद्या एकवर्णी प्रकाशाच्या शुद्ध ज्या-वक्रीय तरंगाचे तरंगमुख [→ तरंग गति] अनंत माध्यमात ज्या वेगाने प्रसारित होईल, त्याला प्रकाशाचा ‘कलावेग’ किंवा ‘तरंगवेग’ असे म्हणतात. या वेगाचे प्रत्यक्ष मापन करणे अशक्यच आहे. सर्व अप्रत्यक्ष पद्धतींद्वारा मिळतो तो तरंगवेगच असतो.

ज्या माध्यमात सर्व कंप्रतांचे तरंग एकाच वेगाने प्रसारित होतात त्याला अनपस्करणी माध्यम असे म्हणतात. अशा माध्यमात समूहवेग व कलावेग यांची मूल्ये समानच असतात. ‘निर्वात’ हे सुद्धा अनपस्करणी माध्यम असल्याने निर्वातात हे दोन्ही सममूल्य असतात परंतु हवेमध्ये अपस्करण होत असल्याने प्रकाशाचा समूहवेग हा कलावेगापेक्षा ०·००७ टक्क्याने कमी असतो. त्याच कारणाने पाण्यातील समूहवेग १·५ टक्क्याने कमी भरतो. याबद्दलचे सूत्र पुढीलप्रमाणे आहे.

( येथे V_g = समूहवेग व V_p = λ या तरंगलांबीचा कलावेग आहे). कोणत्याही माध्यमाचा प्रणमनांक म्हणजे प्रकाशाच्या निर्वातातील व त्या माध्यमातील कलावेगांचे गुणोत्तर असते. प्रकाशवेगाचे मूल्य देताना प्रयोगाने मिळालेल्या मूल्यावरून गणिताने त्याचा निर्वातातील कलावेग काढून त्याचेच मूल्य देतात. त्यामुळे वेगवेगळ्या पद्धतींवरून मिळणाऱ्या मूल्यांची तुलना करणे सोपे जाते. 

ज्योतिषशास्त्रीय पद्धती

प्रकाशाच्या स्वरूपासंबंधी विचार करताना प्रकाश हा सांत वेगाने प्रवास करतो की त्याचे तत्काल प्रेषण होते, असा प्रश्र प्रथमपासूनच मानवाला पडलेला होता. प्रकाशाचा वेग मोजण्याचा पहिला प्रयत्‍न गॅलिलीओ (१५६४ – १६४२) यांनी केला परंतु अतिसूक्ष्म कालमापनाची साधने त्या काळी उपलब्ध नसल्याने तो अयशस्वी झाला.

रोमर पद्धती : ओलाउस रोमर या डॅनिश ज्योतिषशास्त्रज्ञांनी १६७५ मध्ये केलेल्या प्रकाशवेग मोजण्याच्या या पहिल्याच ज्योतिषशास्त्रीय यशस्वी प्रयोगाची रूपरेषा पुढीलप्रमाणे आहे. पृथ्वी व गुरू हे दोन्ही ग्रह जेव्हा सूर्याच्या एकाच बाजूस व एका सरळ रेषेत येतात, तेव्हा त्यांच्यामधील अंतर किमान असते. त्यानंतर बरोबर ०·५४५ वर्षानंतर पृथ्वी व गुरू सूर्याच्या दोन विरूद्ध बाजूंस असून पुन्हा एका रेषेत येतात. या वेळी या दोन ग्रहांमधील अंतर जास्तीत जास्त असते. म्हणजे पहिल्या खेपेच्या अंतरापेक्षा हे दुसरे अंतर पृथ्वीच्या सूर्याभोवतालच्या कक्षेच्या व्यासाइतके जास्त असते.

गुरूभोवताली फिरणारे त्याचे अनेक चंद्र आहेत. त्यांतील गुरूला सर्वात जवळचा चंद्र जेव्हा गुरूच्या छायेत जातो, तेव्हा त्याला ग्रहण लागले असे म्हणतात व त्याची भ्रमणगती नियमित असल्याने दोन लागोपाठच्या ग्रहणांतील कालखंड अगदी निश्चित (१८ तास २८ मिनिटे) असतो परंतु सूक्ष्म निरीक्षणानंतर रोमन यानां असे दिसून आले की, पृथ्वी व गुरू यांच्यामधील अंतर जसजसे वाढत जाते तसतसा दोन लागोपाठच्या ग्रहणांमधील कालखंड हळूहळू वाढत जातो व त्या दोहोंमधील अंतर जेव्हा कमाल होते तेव्हा गणिताने मिळणाऱ्या वेळापेक्षा ९९६ सेकंद उशीराने ग्रहण दिसते. हा लागणारा जादा वेळ म्हणजे त्या चंद्रापासून निघणाऱ्या प्रकाशाला जे जादा अंतर (पृथ्वी कक्षेचा व्यास) तोडावे लागते त्यासाठी लागणारा वेळ असला पाहिजे, असे रोमर यांनी अनुमान काढले. सूर्य व पृथ्वी यांमधील सरासरी अंतर १४८·४० X १०^६ किमी. धरून त्यावरून रोमर यांच्या पद्धतीने प्रकाशवेगाचे मूल्य सु. ३·०१ X १०^५ किमी./से. येते परंतु प्रत्यक्ष रोमर यांनी केलेल्या मापनात गुरूच्या चंद्राच्या ग्रहणाला लागणारा विलंब मोजण्यात बरीच चूक होती. त्याचप्रमाणे पृथ्वीच्या कक्षेचा व्यासही त्यांना बरोबर माहीत नसल्यामुळे त्यांना मिळालेले प्रकाशवेगाचे मूल्य २,१४,३०० किमी./से. इतकेच आले होते.

ब्रॅड्ली पद्धती : विपथन कोनावर आधारलेली जेम्स ब्रॅड्ली यांनी १७२८ मध्ये शोधून काढलेली दुसरी एक प्रकाशवेग मोजण्याची ज्योतिषशास्त्रीय पद्धती आहे. पृथ्वीच्या सूर्याभोवतीच्या भ्रमण गतीमुळे दूरवरच्या ताऱ्यांची वास्तविक दिशा आणि आपणाला दिसणारी दिशा यांमध्ये एक सूक्ष्म कोन असतो, त्याला विपथन कोन असे म्हणतात. उदग्र (उभ्या) दिशेने पडणारा पाऊस जसा सायकलवरून जाणाऱ्या गतिमान निरीक्षकाला तिरक्या दिशेने येताना दिसतो, तसाच हा प्रकार आहे.

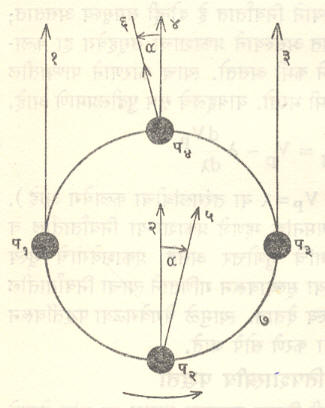
 तारा पृथ्वीच्या कक्षेच्या पातळीत असल्यास पृथ्वीच्या कक्षेत तिच्या दोन स्थिती ( प_१ व प_३ ) अशा येतील की, त्या वेळी पृथ्वीची गती ताऱ्याच्या दिशेला समांतर असल्याने तारा त्याच्या वास्तविक दिशेलाच दिसेल, म्हणजेच विपथन दिसणारच नाही (आ. १). प_२ व प_४ या पृथ्वीच्या स्थिती अशा आहेत की, तेव्हा पृथ्वीची गती ताऱ्याकडून येणाऱ्या प्रकाशाच्या दिशेला लंब आहे. या परिस्थितीतील विपथन कोन α कमाल मूल्याचा येईल. या दरम्यानच्या स्थितीत विपथन कोन मध्यम मूल्याचा येईल. ब्रॅड्ली यांच्या मापनानुसार α = २०’’·४५ असे सिद्ध करता येते की, V (= २९·७ किमी./से.) हा पृथ्वीचा वेग असल्यास प्रकाशवेग c = ^V /sin α · ब्रॅड्ली यांनी यानुसार काढलेले प्रकाशवेगाचे मूल्य ३·०८३०० X १०^५ किमी./से. आले. विपथन कोनाच्या मूल्याचे मापन करण्यात त्रुटी येत असल्यामुळे या पद्धतीनेही मिळणारे प्रकाशवेगाचे मूल्य तितकेसे बिनचूक येऊ शकत नाही.

भौमिक पद्धती 

फीझो पद्धती : ए. एच्. एल्. फीझो (१८१९-९६) यांनी शोधून काढलेल्या या पद्धतीचे तत्त्व म्हणजे एक मर्यादित अंतर तोडण्यासाठी प्रकाशाला लागणाऱ्या वेळाचे मापन फिरत्या दातेरी चक्राच्या साहाय्याने करणे हे होय. 

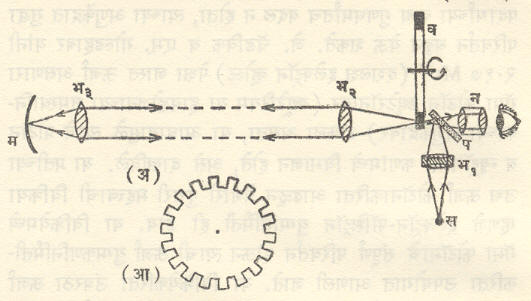
या प्रयोगात एका आडव्या अक्षाभोवती एक दातेरी चक्र (व) खूप वेगाने फिरविता येते (आ. २). स या प्रकाश उद्‌गमापासून निघणारा प्रखर प्रकाश एका काचेच्या पट्टीवरून (प) परावर्तित करून बर्हिगोल भिंगाच्या (भ१) साहाय्याने दातेरी चक्राच्या कडेवर केंद्रित करण्यात येतो. दोन दात्यांमधील फटीतून पलीकडे गेल्यावर, दोन भिंगांच्या (भ२, भ३) साहाय्याने तो प्रकाश एका दूर (सु. ८·५७ किमी.) ठेवलेल्या अंतर्गोल आरशावर (म) पडतो व तेथून परावर्तित होऊन पहिल्या मार्गाने परत येऊन, पुन्हा दातेरी चक्राच्या कडेवर पूर्वीच्याच ठिकाणी केंद्रित होतो. चक्र स्थिर असल्यास दात्यांमधील फटीतून पुढे जाऊन तो प्रकाश तेथे ठेवलेल्या नेत्रिकेतून (न) दिसू शकेल परंतु तो प्रकाश दातेरी चक्रापासून अंतर्गोल आरशापर्यत व तेथून परत चक्रापर्यत येईतो जर चक्राचा एक दाता पुढे सरकला, तर त्याने प्रकाश अडेल व तो नेत्रिकेतून दिसणार नाही.

प्रत्यक्ष प्रयोगात चक्र प्रथम स्थिर ठेवले व नेत्रिकेतून पहात राहून चक्राची गती हळूहळू इतकी वाढविण्यात आली की, प्रकाश दिसेनासा झाला. या वेळी जर चक्राचे प्रती सेकंदाला N फेरे होत असतील, चक्रावरील एकूण दाते n असतील व चक्र ते अंतर्गोल आरसा हे अंतर d असेल, तर या तीन राशींवरून प्रकाशवेग c पुढील सूत्रावरून काढता येतो : c = 2 d X  m X n. फीझो यांनी या पद्धतीने प्रकाशवेगाचे मूल्य ३·१५ X १०^५ किमी./से. इतके काढले. या प्रयोगात चक्राच्या नेमक्या कोणत्या गतीच्या वेळी प्रकाश दिसेनासा होतो हे ठरविणे अवघड जाते व त्यामुळे काढलेल्या प्रकाशवेगाच्या मूल्यात काहीशी चूक येते.

फूको यांची फिरत्या आरशाची पद्धती : एखादा आरसा θ एवढ्या कोनातून असता, त्याच्यावरून परावर्तन पावलेला प्रकाशकिरण २ θ इतक्या कोनातून फिरतो. या तत्त्वाचा जे. बी. एल्. फूको (१८१९-६८) यांच्या पद्धतीत उपयोग केलेला आहे. ए. ए. मायकेलसन, एफ्. जी. पीस, एफ्. पीअर्सन वगैरे शास्त्रज्ञांनी नंतर आपल्या प्रकाशवेग मापनात याच पद्धतीचा (तीत काही सुधारणा करून) अवलंब केला, म्हणून हिला विशेष महत्त्व आहे.

या पद्धतीत (आ. ३) स या प्रकाश उद्‌गमापासून निघालेले किरण एका तिरक्या ठेवलेल्या प या काचेच्या पट्टीतून पलीकडे जाऊन, एका भिंगावर (भ) पडतात. भिंगातून हे किरण बाहेर आल्यावर वेगाने फिरवता येईल अशा र या सपाट आरशावरून परावर्तित होतात व शेवटी एका दूरवर ठेवलेल्या म या अंतर्गोल आरशावर केंद्रित होतात. या आरशाचा वक्रतामध्य फिरत्या आरशाच्या मध्यबिंदूवर असतो. त्यामुळे अंतर्गोल आरशावर पडलेले किरण परावर्तित होऊन पुन्हा बरोबर फिरत्या आरशावरच पडतात परंतु एवढ्या अवधीत फिरता आरसा θया कोनातून फिरलेला असतो. त्यामुळे त्यावरून पुन्हा परावर्तन पावताना ते किरण २ θ या कोनातून फिरलेला व तुटक रेषांनी दाखविलेल्या मार्गाने जाऊन पुन्हा तिरक्या काच पट्टीवर पडतात व शेवटी तेथून परावर्तन होऊन प्र’ या ठिकाणी केंद्रित होतात. म्हणजेच प्र’ येथे स ची प्रतिमा दिसते परंतु आरसा स्थिरच राहिला असता, तर किरण मूळच्याच मार्गाने परत जाऊन प्र या ठिकाणी प्रतिमा तयार झाली असती. म्हणजेच आरशाच्या फिरण्यामुळे प्रतिमेचे प्र प्र’ इतके स्थानांतर झाले. आरशाची फिरण्याची गती वाढविली किंवा रम हे अंतर वाढविले, तर स्थानांतरही वाढते.

प्रतिमेच्या या स्थानांतराचे सूक्ष्ममापकाच्या साहाय्याने काळजीपूर्वक मापन केले. त्याचप्रमाणे आरशाचा कोनीय वेग (ω) आणि सर व रम ही अंतरे नोंद केली व त्यावरून प्रकाशवेग खालीलप्रमाणे काढता आला.

लागलेला वेळ,

 या पद्धतीने फूको यांना प्रकाशवेगाचे मूल्य २·९८ X १०^५ किमी./से. इतके मिळाले. रम येथे पाण्याने भरलेली नळी ठेवून फूको यांनी पाण्यातील प्रकाशवेग मोजला व तो हवेतील वेगापेक्षा कमी असतो, हे सिद्ध केले.

मायकेलसन पद्धती : फूको यांच्या पद्धतीत स्थानांतर फारच कमी म्हणजे ०·७ मिमी. इतकेच आल्यामुळे ते मोजण्यात बरीच चूक होऊ शकते परंतु स्थानांतर वाढविण्यासाठी रम हे अंतर वाढविल्यास  किंवा आरशाचा कोनीय वेग वाढविल्यास प्रतिमा फारच अस्पष्ट होते.

यासाठी मायकेलसन यांनी फूको यांच्या पद्धतीत पुढील सुधारणा केल्या : (१) एक बहिर्गोल भिंग र आणि म यांच्यामध्ये ठेवले. त्यामुळे रम हे अंतर खूपच वाढविता आले. (२) एकच फिरत्या आरशाऐवजी आठ किंवा सोळा कोनी पेटी घेऊन तिच्या सर्व बाजूंवर आरसे बसवून, ती फिरविली. त्यामुळे प्रतिमा अनेक पटीने जास्त तेजस्वी झाली. या सुधारणांमुळे १३३ मिमी. इतके मोठे स्थानांतर मिळविता आले. याशिवाय (३) प्रयोगात लागणारी अंतरे अत्यंत बारकाईने मोजली व (४) आरशाचा कोनीय वेग मोजण्यासाठी मानक (प्रमाणभूत) कंपनशूलाचा [नादकाट्याचा → ध्वनि] उपयोग केला. या सर्व सुधारणांमुळे मायकेलसन यांनी काढलेल्या प्रकाशवेगाच्या मूल्यात असणारी कमाल संभाव्य चूक, एक लाखात फक्त एक या सुमाराची आहे. निर्वात प्रदेशातील प्रकाशवेग मोजण्यासाठी मायकेलसन यांनी सुचविलेल्या पद्धतीने त्यांचे सहकारी पीस व पीअर्सन यांनी एका सु. १·६ किमी. लांबीच्या नळीचा उपयोग केला. पंपाच्या साहाय्याने नळीतील हवेचा दाब ०·५ मिमी. पाऱ्याच्या स्तंभाइतका कमी होईल इतपत निर्वात अवस्था मिळविली. नळीच्या दोन्ही तोंडांवर आरसे लावून प्रकाशकिरणाला नळीतून मागेपुढे असे १० वेळा जावे लागेल अशी व्यवस्था केली, म्हणजेच प्रकाशाचा मार्ग वाढविला. यासाठी लागणारा काल वरील मायकेलसन यांच्या पद्धतीने मोजला परंतु या प्रयोगात पहिल्या प्रयोगापेक्षा जास्त संभाव्य चूक असली पाहिजे, असे नंतर आढळून आले. मायकेलसन यांच्या प्रयोगावरून प्रकाशवेगाचे मूल्य २,९९,७९६ ± ४ किमी./से. इतके मिळाले. 

कर घट : एका काचेच्या भांड्यात नायट्रोबेंझिनासारखा पारदर्शक द्रव भरून, त्यात एकमेकांस समांतर असे दोन धातूचे पत्रे बसविले, तर त्या रचनेस जॉन कर (१८२४-१९०७) या भौतिकीविज्ञांच्या नावावरून कर घट असे म्हणतात. या घटातील पत्र्यांमध्ये विद्युत्‌वर्चोभेद (विद्युत् पातळ्यांमधील फरक) ठेवला, तर त्यांच्या दरम्यानच्या नायट्रोबेंझिनामध्ये द्विप्रणमनाचे गुणधर्म निर्माण होतात. या अवस्थेत त्यातून प्रतल ध्रुवित प्रकाश पाठविल्यास, त्याचे विवृत्ताकृती ध्रुवण होते. हा कर घटाचा विशेष गुण आहे. (‘द्विप्रणमन’ व ‘ध्रुवण’ या संज्ञाच्या स्पष्टीकरणार्थ ‘प्रकाशकी’ ही नोंद पहावी).

दोन जात्य निकोल लोलकांच्या [→ प्रकाशकी] दरम्यान एक कर घट ठेवल्यास त्या तिघांमधून प्रकाश पलीकडे जाऊ शकत नाही परंतु कर घटाच्या पत्र्यांमध्ये विद्युत् वर्चोभेद ठेवल्याबरोबर (वर वर्णन केलेल्या कारणामुळे) त्यांच्यामधून प्रकाश बाहेर येतो. वर्चोभेद काढून टाकला की, ताबडतोब प्रकाश बाहेर येणे बंद होते. म्हणजेच ही रचना एखाद्या विद्युत् प्रकाशीय झडपेसारखी कार्य करते. वर्चोभेद लावण्यासाठी n या प्रचंड कंप्रतेच्या (दर सेकंदाला होणाऱ्या आवर्तनांची संख्या प्रचंड असलेल्या) प्रत्यावर्ती (उलट सुलट दिशेने वाहणाऱ्या) विद्युत् प्रवाहाचा उपयोग केला, तर वर्चोभेद प्रती सेकंदाला 2n वेळा शून्य होत असल्याने या झडपेची उघडझाप अशा रीतीने प्रती सेकंदाला कित्येक कोटी वेळाही होऊ शकते.

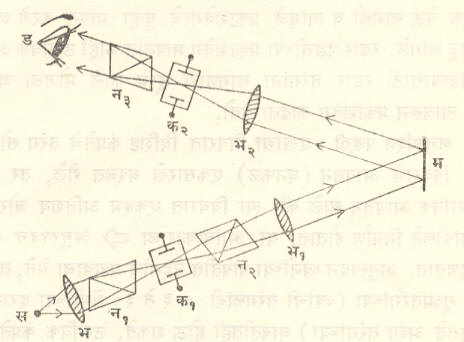
या तत्त्वाचा उपयोग प्रकाशवेग मोजण्यासाठी प्रथम ए. कॅरोलस व ओ. मिटेलस्टेट यांनी केला. त्यांच्या उपकरणात (आ. ४) क_१ व क_२ हे n कंप्रतेच्या एकाच प्रत्यावर्ती प्रवाहाला जोडलेले दोन कर घट असून न_१, न_२ व न_३ हे निकोल लोलक आहेत. न_१ व न_३ यांच्यामधून बाहेर पडू शकणाऱ्या प्रकाशांची ध्रुवण प्रतले एकमेकांना समांतर आहेत पण न_२ च्या ध्रुवण प्रतलाला लंब आहेत. त्यामुळे न_२ मधून बाहेर येणारा प्रकाश न_३ मधून पलीकडे जाऊ शकणार नाही. कल्पना करा की, एका विशिष्ट क्षणाला क_१ वर कमाल वर्चोभेद आहे. त्यामुळे न_१-क_१-न_२ या गटातून एक कमाल तेजाची प्रकाश-शलाका बाहेर पडेल व म वरून परावर्तित होऊन क_२ पाशी पोहोचेल. बरोबर त्याच क्षणी क_२ वर वर्चोभेद शून्य असेल, तर न_३ मधून प्रकाश बिलकुल दिसणार नाही. वर्चोभेद शून्य नसेल, तर काही प्रकाश दिसेल. क_१म व मक_२ ही अंतरे मोजून प्रत्यावर्ती प्रवाहाची कंप्रता n माहीत असल्यास त्यावरून प्रकाशवेग काढता येतो.

n चे मूल्य १०^८ च्या सुमारास असल्याने या प्रयोगात फार मोठी अंतरे वापरावी लागत नाहीत, ही महत्त्वाची सोय आहे. या उपकरणात निरीक्षकाच्या नेत्राच्या ठिकाणी प्रकाशविद्युत् घटाची [→ प्रकाशविद्युत्] योजना करून डब्ल्यू. सी. अँडरसन यांनी या प्रयोगाची अचूकता आणखी वाढविली.

आधुनिक पद्धती : प्रकाश आणि रेडिओ तरंग यांचे स्वरूप मूलतः एकच आहे. त्यामुळे त्यांचा वेगही सारखाच असला पाहिजे. प्रकाशवेग मोजण्याच्या अत्याधुनिक व बिनचूक पद्धतींत रेडिओ तरंगांचाच वेग मोजून तोच प्रकाशवेग समजला जातो.

दुसऱ्या महायुद्धात शत्रूच्या विमानांचे अंतर काढण्यासाठी रडारचा उपयोग होऊ लागला. हे अंतर काढण्यासाठी प्रकाशवेगाचे बिनचूक मूल्य माहीत असावे लागते. त्या काळी माहीत असलेल्या मूल्यावरून रडारच्या साहाय्याने काढलेल्या अंतरात १०,००० भागांत एक भाग इतकी चूक येऊ लागली व त्यामुळे प्रकाशवेगाचे पुन्हा मापन करणे जरूर वाटू लागले. रडार पद्धतीच्या प्रकाशवेग मापनात काही ठराविक अंतर तोडण्यासाठी रडार तरंगांना लागणारा सूक्ष्म काल मोजला जातो व त्यावरून प्रकाशवेग काढता येतो.

अनुस्पंदन पद्धती : एखाद्या विवरात विशिष्ट कंप्रतेचे तरंग सोडले व विवराचे आयतन (घनफळ) एकसारखे बदलत गेले, तर एक ठराविक आयतन झाले की, त्या विवरात एकदम अतिशय जोरदार आंदोलने निर्माण होतात. या आविष्काराला ⇨ अनुस्पंदन असे म्हणतात. अनुस्पंदन ध्वनीच्या बाबतीत नेहमीच प्रत्ययाला येते, तसेच ते सूक्ष्मतरंगांच्या (ज्यांची तरंगलांबी ०·३ ते ३० सेंमी.च्या दरम्यान असते अशा तरंगांच्या) बाबतीतही होऊ शकते. ठराविक कंप्रतेच्या सूक्ष्मतरंगांशी अनुस्पंदी विवराचे आयतन मोजतात. मग ते आयतन व त्या तरंगांची कंप्रता यांवरून तरंगांचा वेग काढता येतो. [→ विवर अनुस्पंदक].

सूक्ष्मतरंग व्यतिकरण पद्धती : (एकाच कंप्रतेच्या दोन अगर अधिक तरंगांचा संयोग होण्याच्या क्रियेला व्यतिकरण म्हणतात). या पद्धतीने काढलेले प्रकाशवेगाचे मूल्य सर्वांत जास्त विश्वसनीय मानले जाते. व्यतिकरणमापकाच्या साहाय्याने सूक्ष्मतरंगांची तरंगलांबी मोजतात [→ सूक्ष्मतरंग]. तसेच त्या तरंगांची कंप्रताही मोजतात. या दोहोंवरून प्रकाशवेग काढता येतो (वेग = कंप्रता X तरंगलांबी).

पुढील कोष्टकावरून प्रकाशवेगमापनातील सूक्ष्मता कशी वाढत गेली त्याची कल्पना येईल. 

प्रकाशवेगात होणारे बदल : कोणत्याही वास्तव माध्यमातील प्रकाशवेगाचे मूल्य त्याच्या निर्वातातील मूल्यापेक्षा कमी असते, याचा उल्लेख वर आलाच आहे. हे वास्तव माध्यम प्रकाशाच्या दिशेने v या वेगाने गतिमान असल्यास त्यामध्ये प्रकाशवेगात

इतकी वाढ होते, असे प्रत्यक्ष प्रयोगावरून आढळून आले (येथे μ हा माध्यमाचा प्रणमनांक आहे). ही वाढ वेगांच्या बेरजेबद्दलच्या सापेक्षता सिद्धांतीय सूत्राबरहुकूम आहे. सापेक्षता सिद्धांताला हा एक अनुकूल पुरावा मानला जातो.

सामान्यतः प्रकाशवेग म्हणजे जेथे गुरुत्वाकर्षणीय क्षेत्र नाही तेथील प्रकाशवेग होय. व्यापक सापेक्षता सिद्धांतानुसार विशिष्ट ठिकाणी गुरुत्वीय वर्चस् ϕ असल्यास तेथे प्रकाशवेग कमी होतो, या बाबतीतले सूत्र असे :

येथे c₀ शून्य गुरुत्वीय वर्चस् असतानाचे प्रकाशवेग मूल्य, c हे ϕ गुरुत्वीय वर्चस् असतानाचे प्रकाशवेग मूल्य, G गुरुत्वाकर्षणीय स्थिरांक, M (वर्चस् निर्माण करणाऱ्या) वस्तूचे वस्तुमान, R त्या वस्तूच्या गुरुत्त्वमध्यापासूनचे अंतर.

द्वैती ताऱ्यांच्या निरीक्षणावरून व इतर ज्योतिषशास्त्रीय प्रयोगांवरून असे सिद्ध झाले आहे की, निर्वातामध्ये सर्व कंप्रतांच्या प्रकाशाचा वेग सारखाच असतो पण वास्तव माध्यमात मात्र कंप्रतेनुसार प्रकाशवेग बदलत जातो. यामुळेच लोलकामध्ये अपस्करण होऊन वर्णपट मिळू शकतो.

 प्रकाशवेग आणि सापेक्षता सिद्धांत : सापेक्षता सिद्धांताला कारणीभूत झालेला व प्रकाशशास्त्रातला सर्वांत प्रसिद्ध प्रयोग म्हणजे  ए. ए. मायकेलसन व ई. डब्ल्यू. मॉर्ली (मोर्ले) यांनी १८८७ साली केलेला प्रयोग होय. 

सर्वव्यापी ईथरामधून [→ ईथर – २] पृथ्वी सूर्याभोवती प्रती सेकंदाला सु. २९ किमी. या वेगाने फिरत आहे. त्यामुळे ईथराला पृथ्वीसापेक्ष गती संभवते. पूर्वीच्या कल्पनेप्रमाणे प्रकाश म्हणजे ईथरामधील तरंग आहेत. नदीमध्ये प्रवाहाच्या दिशेने पोहोणाऱ्याचा वेग वाढतो, पण उलट दिशेने पोहोताना कमी होतो. असाच प्रकार ईथरामध्ये पोहोणाऱ्या प्रकाशतरंगांच्या बाबतीतही व्हावयास पाहिजे.

जर पृथ्वीच्या गतीचा प्रकाशवेगावर याप्रमाणे खरोखरीच परिणाम होत असेल, तर सविस्तर गणित केल्यावर असे दाखविता येते की, जर ईथराचा पृथ्वीसापेक्ष वेग v व प्रकाशवेग  c असेल, तर 1 हे एक ठराविक अंतर v च्या समांतर दिशेने उलट व सुलट जाण्यासाठी प्रकाशाला लागणारा वेळ, हा प्रकाशाला तितकेच अंतर v ला लंब दिशेने उलट व सुलट जाण्यासाठी लागणाऱ्या वेळापेक्षा

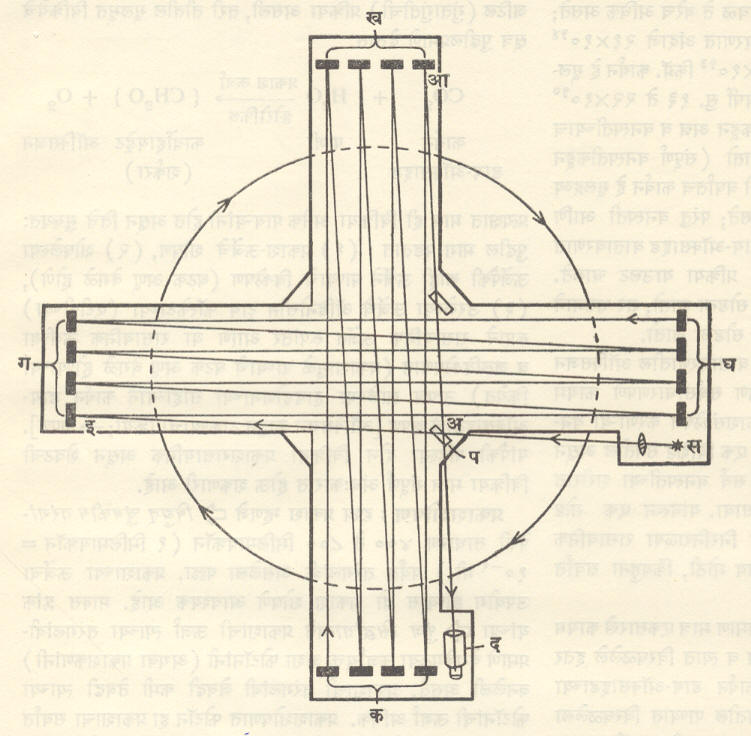
एवढा जास्त असला पाहिजे. हा फरक पडत असेलच, तर तो अत्यंत सूक्ष्मच असणार. त्याचे मापन करण्यासाठी मायकेलसन व मॉर्ली यांनी योजलेल्या उपकरणाची डी. सी. मिलर यांनी केलेली सुधारित रचना आ.५ मध्ये दाखविली आहे.  

प्रथम अ-आ (आ. ५) ही दिशा पृथ्वीच्या वेगाला समांतर ठेवली आहे असे समजू. स या प्रकाश उद्‌गमापासून निघणारा प्रकाश प या अंशतः परावर्तक-पारगामक पट्टीवर पडून दुभंगतो. त्यातील एक भाग अ-आ या दिशेने जाऊन क-ख गटातील आरशांवरून परावर्तन होऊन ८ वेळा मागे-पुढे जातो व शेवटी द या दूरदर्शकात येतो. दुसरा भाग अ-इ दिशेने जाऊन त्याचप्रमाणे ८ वेळा मागे-पुढे जाऊन शेवटी द मध्ये येतो. या दोन भागांत निर्माण झालेल्या पथांतरानुसार (मार्गांच्या लांबीतील फरकानुसार) त्यांच्यामध्ये व्यतिकरण होऊन दूरदर्शकात सुप्रकाशित-अप्रकाशित व्यतिकरण पट्टांची मालिका [→ प्रकाशकी] दिसते. सबंध उपकरण ९०° मधून फिरविल्यास किरणांच्या दोन भागांना आपले मार्ग ओलांडण्यासाठी लागणाऱ्या कालात वर दिल्याप्रमाणे बदल होईल व त्यानुसार त्यांच्यामधील पथांतर बदलून व्यतिकरण पट्ट डावीकडे किंवा उजवीकडे सरकतील. अर्थात पृथ्वीच्या वेगामुळे प्रकाशवेगात बदल होत असेल, तरच हे घडेल परंतु हा प्रयोग वर्षातून वेगवेगळ्या दिवशी अनेकदा करूनही अपेक्षित परिणाम बिलकूल दिसला नाही व म्हणून पृथ्वीच्या वेगाचा प्रकाशवेगावर काहीही परिणाम होत नाही, असे मान्य करावे लागले त्यामुळे प्रकाशवाहक ईथराची कल्पनाच कोसळून पडली. एवढेच नव्हे, तर येथून पुढे भौतिकीच्या एकूण विचारसरणीत एक क्रांतीच घडून आली. या दृष्टीने मायकेलसन-मॉर्ली यांच्या प्रयोगाला अनन्य साधारण महत्त्व आहे. [→ सापेक्षता सिद्धांत].

संदर्भ :  1. Ditchburn, R. W. Light, London, 1963.

            2. Jaffe, B. Michelson and the Speed of Light, Bomaby, 1965.

            3. Jenkins, F. A. White, H. E. Fundamentals of Optics, New York, 1957.

            4. Morgan, J. Introduction to Geometrical and Physical Optics, New York, 1953.

खेर, वि, गो. पुरोहित, वा. ल.

“