प्रकाशमापन

प्रकाशमापन : शाळा,महाविद्यालये,प्रयोगशाळा,यंत्रशाळा,कार्यशाळा,कारखाने इत्यादींमध्ये केली जाणारी कामे, विद्यार्थ्यांच्या वा कर्मचाऱ्यांच्या डोळ्यांवर जादा ताण न पडता पार पाडता आल्यास ती कामे जास्त चांगली होतात व कर्मचाऱ्यांची कार्यक्षमताही वाढते,असे दिसून आले आहे. यासाठी या इमारतींतून प्रकाशनाची यथायोग्य व्यवस्था करणे जरूर असते. प्रकाश तर भरपूर हवाचपण त्याची तजवीज जास्तीतजास्त काटकसरीने कशी करावयाची ते पहावे लागते. यासाठी वेगवेगळ्या प्रकारच्या दिव्यांची प्रकाश देण्याची क्षमता, विशिष्ट कार्य नीट करता येण्यासाठी किमान किती तीव्रतेचा प्रकाश जरूर आहे,दिव्यांना परावर्तकांची जोड देऊन इच्छित दिशेला जास्त प्रकाश कसा उपलब्ध करून देता येईल,दिव्यांच्या प्रखर तिरिपेमुळे डोळ्यांना होणारा त्रास कसा टाळता येईल इ. गोष्टींचा मूलभूत अभ्यास प्रकाशमापन या शास्त्रशाखेमध्ये केला जातो व त्याच्या अनुप्रयोगांचा अभ्यास हा प्रकाश अभियांत्रिकीचा विषय आहे [→ प्रदीपन अभियांत्रिकी].

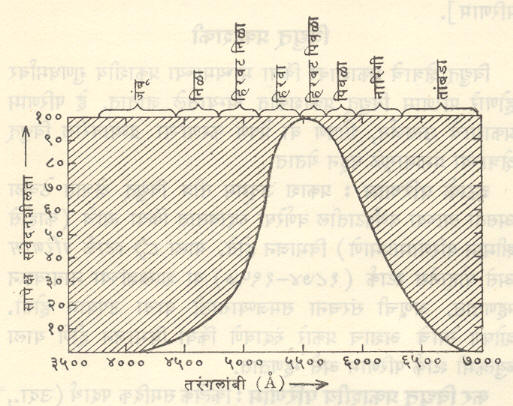
प्रारणमापन व प्रकाशमापन : सर्व तरंगलांब्यांच्या प्रारणाच्या (तरंगरूपी ऊर्जेच्या) शक्तीचे मापन करण्याच्या शास्त्राला प्रारणमापन असे म्हणतात. सकृद्दर्शनी हे शास्त्र प्रकाशमापनासारखेच वाटते,तरीही त्यांमध्ये दोन महत्त्वाचे फरक आहेत. मानवी नेत्र ज्या विद्युत् चुंबकीय तरंगांना (तरंगलांबी सु. ४००० Å ते ७६०० Å १ Å एकक = १०^–१० मी.) संवेदनशील आहेत,त्यालाच फक्त (या संदर्भात) प्रकाश म्हटले जाते व त्याचेच मापन येथे अभिप्रेत असतेपरंतु एकाच शक्तीचे पण दोन वेगळ्या रंगांचे प्रकाशकिरण डोळ्यांना सारखेच तेजस्वी दिसत नाहीत. प्रारणमापनाच्या दृष्टिकोनातून या दोन किरणांची तीव्रता समान असली,तरी प्रकाशमापनाच्या संदर्भात या दोन किरणांची तीव्रता वेगळी आहे,असे म्हणावे लागते. म्हणजेच मानवी नेत्राला जशी प्रकाशाची तीव्रता प्रत्ययाला येते,त्याला अनुसरूनच प्रकाशमापनाचे कार्य करावे लागते. म्हणून प्रकाशमापनासाठी खास उपकरणे व एकके वापरली जातात. आ. १ मध्ये मानवी नेत्राची सापेक्ष संवेदनशीलता व तरंगलांबी यांचा आलेख दाखविला आहे. प्रकाशमापनातील उपकरणाचा अभिलक्षण वक्र यासारखाच करून घेणे आवश्यक असते. काही व्याख्या व एकके : प्रकाशमापनात दृश्य प्रकाशीय दीप्ति-तीव्रता,प्रकाश वितरण,परावर्तनक्षमता इ. राशींच्या मापनाचा समावेश होतो. 

प्रकाशीय स्रोत व दीप्ति-तीव्रता : प्रकाश उद्‌गमापासून सर्व दिशांनी दृग्गोचर प्रकाशाचा स्रोत बाहेर पडत असतो. विशिष्ट क्षेत्रफळातून प्रती सेकंदाला वाहणाऱ्या दृग्गोचर प्रकाश शक्तीला (ऊर्जा प्रतिसेकंद) प्रकाशीय स्रोत (किंवा दीप्ति-स्रोत) असे म्हणतात. 

एखाद्या बिंदुमात्र प्रकाश उद्‌गमापासून विशिष्ट दिशेने प्रती एकक धन कोनामधून [→कोन]जितका प्रकाशीय स्रोत सोडला जातो,तितकी त्या प्रकाश उद्‌गमाची (त्या दिशेची) दीप्ति-तीव्रता आहे,असे म्हटले जाते. सर्व प्रकाशमापनातील आद्य एकक कँडेला हे आहे. त्याची व्याख्या १९३७ साली आंतरराष्ट्रीय परिषदेने पुढीलप्रमाणे निश्चित केली आहे. ⇨ कृष्ण पदार्थ द्रव प्लॅटिनमाच्या घनीभवनाच्या (घन स्थितीत जाण्याच्या) तापमानात (२०४२° के.) असताना त्याच्या एकक क्षेत्रफळाची (एक चौ. सेंमी.) लंब दिशेने दीप्ति-तीव्रता ६० कँडेला असते. वरील प्रकारचा उत्सर्जक वापरण्यास अत्यंत त्रासदायक असतो म्हणून प्रकाशमापनासाठी त्याचा उपयोग केला जात नाही. राष्ट्रीय भौतिकीय प्रयोगशाळांमध्ये या उत्सर्जकाशी तुलना करून प्रमाणित विद्युत् दिवे तयार करतात व सर्वसामान्य प्रयोगशाळांतून मापनासाठी दुय्यम मानक (प्रमाण) म्हणून अशा दिव्यांचाच उपयोग केला जातो. 

अशा तऱ्हेने दीप्ति-तीव्रतेचे एकक निश्चित केल्यानंतर, त्याच्यावरून प्रकाशमापनाची इतर एककेही निश्चित करता येतात. प्रकाशीय स्रोताचे एकक ल्यूमेन हे असून त्याची व्याख्या पुढे दिल्याप्रमाणे आहे. एक कँडेला दीप्ति-तीव्रता असलेल्या बिंदुमात्र एकविध सर्व दिशांनी सारख्याच प्रमाणात प्रकाश उत्सर्जन करणाऱ्या प्रकाश उद्‌गमापासून प्रती एकक घन कोनातून सोडल्या जाणाऱ्या प्रकाशीय स्रोताला एक ल्यूमेन प्रकाश-स्रोत असे म्हणतात. 

---

 प्रकाशन : (प्रकाश-स्रोत घनता). बिंदुमात्र प्रकाश उद्‌गमाला सर्व बाजूंनी वेष्टणारा गोलीय पृष्ठभाग कल्पिल्यास,उद्‌गमापासून निघणारा सर्वच्या सर्व प्रकाश-स्रोत त्या गोलीय पृष्ठभागावर पडेल. हा पृष्ठभाग प्रकाश उद्‌गमाशी 4π स्टरेडियन घन कोन अंतरित करतो. म्हणून प्रकाश उद्‌गमाची दीप्ति-तीव्रता Cकँडेला असल्यास, त्याच्यापासून निघणारा एकूण प्रकाश-स्रोत 4πC ल्यूमेन होईल. समजा, तो प्रकाश उद्‌गम rत्रिज्येच्या गोलाच्या मध्यबिंदूवर ठेवला आहे, तर गोलाच्या पृष्ठभागाचे क्षेत्रफळ 4π r²होईल व प्रकाश उद्‌गमापासून पृष्ठभागाचे लंब अंतर सर्वत्र rहोईल म्हणून प्रती एकक क्षेत्रफळावर पडणारा प्रकाश-स्रोत (E) खालील समीकरणावरून मिळेल.  

E=4πC/4π r² = C/r² …        …        …        … (१) 

कोणत्याही पृष्ठभागाच्या प्रती एकक क्षेत्रफळावर पडणाऱ्या प्रकाशीय स्रोतास त्या पृष्ठभागाचे प्रकाशन असे म्हणतात. समी (१) मधील Eहे गोलाच्या पृष्ठभागाचे प्रकाशन असून त्या समीकरणावरून असे दिसते की,पृष्ठभागावर प्रकाशकिरण लंब दिशेने आपाती होत असल्यास पृष्ठभागाचे प्रकाशन प्रकाश उद्‌गमापासूनच्या अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते. यालाच प्रकाशनाचा ‘व्यस्त-वर्ग-नियम’ असे म्हणतात. प्रत्यक्षात बिंदुमात्र प्रकाश उद्‌गम क्वचितच मिळतात परंतु प्रकाश उद्‌गमाच्या आकारमानाशी तुलना करता अंतर खूपच मोठे असल्यास आसन्न पद्धतीने व्यस्त-वर्ग-नियम लागू करता येतो. 

प्रारंभीच्या काळात प्रकाशमापनासाठी मेणबत्तीची ज्योत किंवा तत्सम प्रकाश उद्‌गमांचा वापर होत असे. त्या ज्योतींचे आकारमान बरेच लहान असल्याने त्यांच्या बाबतीत व्यस्त-वर्ग-नियमाचा उपयोग निरपवादपणे करता येई परंतु अनुस्फुरक नळीसारख्या (फ्ल्युओरेसंट ट्यूबसारख्या) आधुनिक प्रकाश उद्‌गमाचे आकारमान इतके मोठे असते की, त्यांच्या बाबतीत हा नियम सामान्यपणे उपयोगात येऊ शकत नाही. सामान्यतः असे म्हणता येईल की,प्रकाश उत्सर्जकाच्या कमाल आकारमानापेक्षा प्रकाशमापक वगैरेंची अंतरे सु. दहापट मोठी असल्यास व्यस्त-वर्ग-नियम वापरण्यास हरकत नाही. ही अंतरे फक्त पाचपट मोठी असल्यास व्यस्त-वर्ग-नियमाचा वापर करून येणाऱ्या उत्तरात सु. १% त्रुटी येते,

लँबर्ट नियम : पृष्ठभागावर आपाती होणारे किरण पृष्ठलंबाशी θ हा कोन करीत असतील,तर प्रकाशन 

  

E =	C	.cos θ …         …        …                    (२)
	r2

 म्हणजे प्रकाशनcos θ  च्या सम प्रमाणात असते. हा नियम जे. एच्. लँबर्ट (१७२८—७७)या भौतिकीविज्ञांनी मांडला म्हणून त्याला लँबर्ट नियम म्हणतात.  

  प्रकाशन एकक  : प्रकाशनाचे मेट्रिक पद्धतीमधील एकक लक्स आहे. ज्या पृष्ठभागाच्या प्रती चौ. मी. क्षेत्रफळावर एक ल्यूमेन प्रकाश-स्रोत पडतो,त्या पृष्ठभागाचे प्रकाशन एक लक्स आहे असे  म्हणतात. पृष्ठभागाच्या एक चौ. मी. क्षेत्रफळावर Eल्यूमेन प्रकाश-स्रोत पडत असेल,तर प्रकाशन Eलक्स होईल. एक कँडेला दीप्ति-तीव्रतेच्या बिंदुमात्र एकविध प्रकाश उद्‌गमाभोवती एक मीटर त्रिज्येचा गोल काढला अशी कल्पना केल्यास,त्याच्या प्रती चौ. मी. क्षेत्रफळावर एक ल्यूमेन इतकाच प्रकाश-स्रोत पडेलम्हणजेच प्रकाशन एक लक्स होईल. म्हणून लक्सला मीटर-कँडल असेही नाव देतात. त्याचप्रमाणे ब्रिटिश एकक पद्धतीत फूट-कँडल हे एकक निश्चित केले जाते. 

पृष्ठभागाच्या प्रती चौ. सेंमी. क्षेत्रफळावर एक ल्यूमेन प्रकाश-स्रोत पडत असल्यास त्या पृष्ठभागाचे प्रकाशन फॉट आहे असे म्हणतात. फॉट हे एकक लक्सपेक्षा मोठे आहे (१ फॉट = १०^४ लक्स). [→एकके व परिमाणे]. 

---

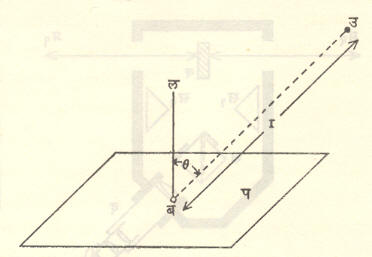
चकासन : एखादा स्वयंप्रकाशित वा परप्रकाशित पृष्ठभाग विशिष्ट दिशेने पाहिला असता कितपत तेजस्वी दिसतो,याचे माप म्हणजे चकासन (दीप्ती किंवा तेजस्विता) होय. विशिष्ट दिशेने त्या पृष्ठभागापासून किती प्रकाश-स्रोत सोडला जातो ते चकासनावरून समजते. पृष्ठभाग स्वयंप्रकाशित असेल (उदा.,अनुस्फुरक नळीचा पृष्ठभाग),तर त्यापासूनच प्रकाश उत्सर्जित होतो. परप्रकाशित असेल,तर त्यापासून परावर्तनाने प्रकाश सोडला जातो. विशिष्ट पृष्ठभागाच्या निरीक्षण दिशेच्या लंब दिशेस प्रक्षेपित केलेल्या,प्रती एकक क्षेत्रफळापासून प्रती एकक घन कोनातून सोडल्या जाणाऱ्या प्रकाशीय स्रोताला,त्या पृष्ठभागाचे त्या दिशेचे चकासन असे म्हणतात. आ. ३ मध्ये दर्शविल्याप्रमाणे δS या अत्यल्प क्षेत्रफळाचे पृष्ठलंब बलशी θ इतका कोन करणाऱ्या दिशेतील चकासन (L_θ) खालील समीकरणाने मिळते. 

Lθ= सीमा	δF/δω	= सीमा	δCθ	=	dCθ	sec θ … (३)
	δS cosθ		δS  cosθ		dS

 

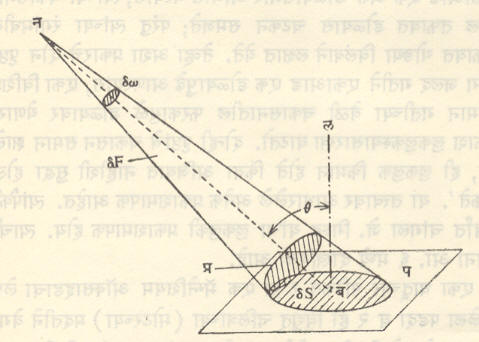
 यावरून हे लक्षात येईल की,विशिष्ट पृष्ठभागाचे चकासन वेगवेगळ्या दिशांना वेगवेगळे असू शकते. 

समी. (३)मध्ये ^δF/_δω = δCθ ही त्या पृष्ठभागाची θ या दिशेने प्रतीत होणारी दीप्ति-तीव्रता आहे व ती कँडेला या एककात मोजली जाते म्हणून चकासनाचे एकक कँडेला प्रती चौ. सेंमी. असे घेतात. यालाच स्टिल्ब हेही नाव दिले आहे. लँबर्ट हे एककही चकासनासाठी वापरले जाते. सर्व दिशांनी सारख्याच प्रमाणात प्रकाशाचे उत्सर्जन किंवा परावर्तन करणाऱ्या पृष्ठभागाच्या प्रती चौ. सेंमी. क्षेत्रफळापासून एक ल्यूमेन प्रकाश-स्रोत निघत असेल,तर त्याचे चकासन एक लँबर्ट असते (गणिताने १ स्टिल्ब= π लँबर्ट हे सिद्ध करता येते). याशिवाय ॲपोस्टिल्ब (= १ ल्यूमेन/चौ.मी.) व निट (= १ कँडेला/चौ.मी.) ही एककेही केव्हा केव्हा वापरली जातात.  

परप्रकाशित पृष्ठभागाच्या बाबतीत प्रकाशनावरून त्या पृष्ठभागावर किती प्रकाश-स्रोत पडतो हे समजते,तर चकासनावरून विशिष्ट दिशेने किती प्रकाश-स्रोत प्रक्षेपित होतो हे समजते.  

 ज्या पृष्ठभागाचे चकासन निरीक्षणाच्या दिशेवर अवलंबून असत नाही, अशा पृष्ठभागाला एकविध किंवा आदर्श विसरण पृष्ठभाग असे म्हणतात. प्रकाशमापनात अशा पृष्ठभागाला फार महत्त्व आहे. मॅग्नेशियम ऑक्साइडाचा लेप दिलेला पृष्ठभाग आदर्श विसरक असतो. 

 प्रकाशमापक : स्थूलमानाने प्रकाशमापकांचे दोन वर्ग करता येतात : (१)नेत्रीय प्रकाशमापक आणि (२)भौतिकीय प्रकाशमापक.नेत्रीय प्रकाशमापकात डोळ्यांचा उपयोग करून प्रकाशाचे मापन केले जाते,तर भौतिकीय प्रकाशमापकात तपयुग्म (दोन निरनिराळ्या प्रकारच्या विद्युत् संवाहकांची टोके एकत्र जोडून व उरलेली टोके विद्युत् प्रवाहमापकास जोडून तयार होणारे आणि एकत्र जोडलेल्या टोकांचे तापमान मोजणारे साधन) किंवा प्रकाशविद्युत् घट [→ प्रकाशविद्युत्] यासारख्या साधनाने मापन केले जाते. 

नेत्रीय प्रकाशमापक : डोळ्याच्या साहाय्याने प्रकाशाच्या तीव्रतेचे मापन फारसे बिनचूक होऊ शकत नाहीपरंतु दोन जवळजवळ ठेवलेल्या पृष्ठाभागांवर पडलेल्या प्रकाशांच्या रंगांत फारशी तफावत नसेल,तर त्या पृष्ठभागांच्या चकासनातील थोडा फरकही डोळ्यांना ओळखू येतो. या तत्त्वावर अनेक नेत्रीय प्रकाशमापक आधारलेले आहेत. 

आदर्श वितरक पांढऱ्या पृष्ठाभागाचे चकासन हे त्याच्या प्रकाशनाच्या सम प्रमाणात असते. असे दोन पृष्ठभाग एकमेकांशेजारी ठेवून,दोन वेगवेगळ्या (C₁व C₂दीप्ति-तीव्रता असलेल्या) प्रकाश उद्‌गमांनी प्रकाशित केले व त्यांची प्रकाश उद्‌गमांपासूनची अंतरे अनुक्रमे r₁व r₂असली, तर त्यांचे प्रकाशन समी. (१)प्रमाणे अनुक्रमे  

अनुक्रमे E1 =	C1	व E2 =	C2	असते.
	r12		r22

 त्यांचे चकासन अनुक्रमे L₁ व L₂ असल्यास

L1 =KE1 =	KC1	L2 = KE2 =	KC2
	r12		r22

 (K—स्थिरांक). प्रकाश उद्‌गमांची अंतरे (r₁वा r₂) बदलून दोन्ही पृष्ठांचे चकासन एकसारखे केल्यास 

KC1	=	KC2	व म्हणून	C1	=	r12	…                   …                    (४)
r12		r22		C2		r22

म्हणजे त्या दोन प्रकाश उद्‌गमांच्या दीप्ति-तीव्रता पृष्ठभागापासूनच्या अंतरांच्या वर्गांच्या सम प्रमाणात असतात. या नियमाला प्रकाशमापकाचा नियम असे म्हणतात. 

या तत्त्वावर आधारलेले अनेक प्रकाशमापक प्रचारात आहेत. काउंट रम्फर्ड (सर बेंजामिन टॉम्पसन) यांचा छाया-प्रकाशमापक व  आर्. डब्ल्यू, बन्सन यांचा पारभासी (अर्धपारदर्शक) तेलाच्या ठिपक्याचा प्रकाशमापक या जातीचे आहेतपण इतर आधुनिक प्रकाशमापकांच्या मानाने हे दोन्हीही प्रकाशमापक कमी दर्जाचे असल्याने त्यांचे वर्णन प्रस्तुत नोंदीत दिलेले नाही.  

---

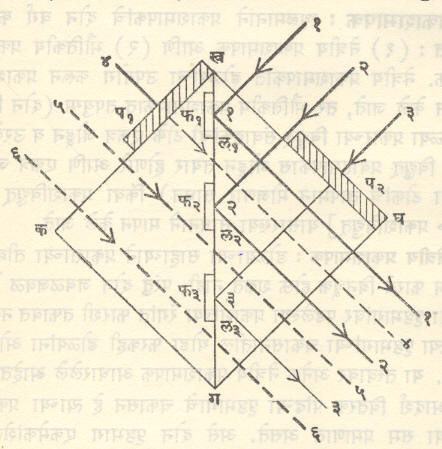
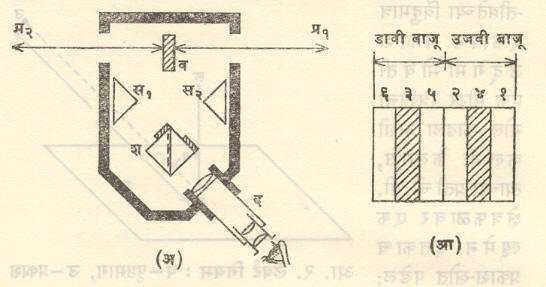
 लुमर-ब्रोडहुन भेददर्शी प्रकाशमापक : नेत्रीय प्रकाशमापकांत ओ.आर्.लुमर व ई. ब्रोडहुन यांनी तयार केलेला हा प्रकाशमापक सर्वांत जास्त अचूक आहे कारण यात निरीक्षण क्षेत्राच्या दोन भागांमध्ये समान चकासन-भेद आणावयाचा असतो. समान चकासनापेक्षा समान चकासन-भेद डोळ्यांना अधिक बिनचूकपणे कळू शकतो. या प्रकाशमापकातील चकासन-भेदकारक शीर्षाची रचना आ. ४ मध्ये दाखविली आहे. 

यात दोन समद्विभुज काटकोनी लोलक त्यांच्या कर्णावर परस्परांना (कॅनडा बाल्सम या) पारदर्शक लुकणाने जोडून एकसंध केलेले असतात. या जोडामध्ये (फ_१,फ_२,फ_३ या) तीन फटी ठेवलेल्या असतात. प्रकाश लोलकातून या फटींकडे जाताना काचेमधून हवेत जात असतो. म्हणून येथील आपाती कोन ४२° पेक्षा जास्त झाल्यास त्याचे संपूर्ण अंतर्गत परावर्तन होते [→ प्रकाशकी] परंतु एकसंध केलेल्या जागांतून मात्र प्रकाश पलीकडे जाऊ शकतो. कख व खग या दोन बाजूंवर प_१ व प_२ या दोन काचेच्या पट्ट्या अशा चिकटविलेल्या आहेत की,त्यांनी या बाजू अर्ध्या झाकल्या जातात. त्यामुळे या पट्ट्यांतून जाणाऱ्या प्रकाशाची तीव्रता सु. ८ टक्क्यांनी कमी होते. अशा तऱ्हेने या प्रकाशमापकाच्या दृष्टिक्षेत्रात चकासन-भेद निर्माण केला जातो. 

 आ. ५(अ) मध्ये संपूर्ण लुमर-ब्रोडहुन प्रकाशमापकाची रचना दाखविली आहे. संपूर्णपणे विसरित परावर्तन करू शकणारे पृष्ठभाग असणारा (उदा.,प्लॅस्टर ऑफ पॅरिसचा किंवा मॅग्नेशियम ऑक्साइडाचा लेप दिलेला) व हा एक पडदा असून तुलना करावयाच्या प्रकाश उद्‌गमांचे प्रकाश या पडद्याच्या दोन बाजूंवर पडून त्या प्रकाशित होतात. त्यांवरून विसरित परावर्तन झालेले काही किरण स_१ आणि स_२ या संपूर्ण अंतर्गत परावर्तन करणाऱ्या लोलकांकरवी शीर्षांच्या कख आणि खग या बाजूंवर (आ. ४ मध्ये दाखविल्याप्रमाणे) पडतात. शेवटी शीर्षातून बाहेर येणारा प्रकाश द या दूरदर्शकात येतो.  

दूरदर्शकाच्या दृष्टिक्षेत्राचे दर्शन आ. ५(आ) मध्ये दाखविले आहे. आ. ४ मधील प_१ व प_२ या काचेच्या पट्ट्यांमधून येणाऱ्या ४ आणि ३ या किरणांमुळे आ. ५(आ) मधील ४ आणि ३ हे काळपट पट्टे दृष्टिक्षेत्रात दिसतात. ३ या पट्ट्याच्या दोन्ही बाजूंचे (६,५ हे) सुप्रकाशित पट्टे कख मधून येणाऱ्या प्रकाशामुळे झालेले असतात. ३ आणि ५,६ यांच्या चकासनातील फरक व ४ आणि १, २ यांच्या चकासनातील फरक समान दिसेतोपर्यंत व पासून प्र_१ किंवा प्र_२ चे अंतर बदलत जातात. हे फरक समान असले म्हणजे व च्या दोन्ही बाजूंच्या चकासनांचे बरोबर संतुलन झालेले असते.मग प्रकाशमापकाचा नियम वापरून त्या दोन प्रकाश उद्‌गमांच्या दीप्ति-तीव्रतांचे गुणोत्तर काढता येते. त्यांतील एक प्रकाश उद्‌गम (दुय्यम) मानक असल्यास दुसऱ्याच्या दीप्ति-तीव्रतेचे मूल्य काढता येते. 

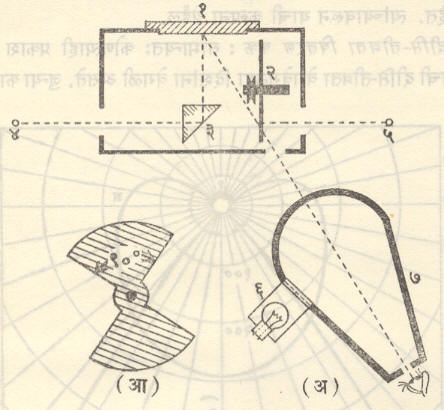
भिन्न रंगाच्या प्रकाशांचे संतुलन : लुकलुकी प्रकाशमापक : वरील प्रकाशमापकाच्या साहाय्याने फक्त दोन समरंगी प्रकाश उद्‌गमांचीच तुलना करणे शक्य होते. दोन भिन्न रंगांच्या प्रकाश उद्‌गमांचीच तुलना करण्यासाठी लुकलुकी प्रकाशमापक वापरावे लागतात. यांचे आधारभूत तत्त्व प्रथमतः ओ. एन्. रूड यांनी शोधून काढले,ते असे : ‘भिन्न रंगांच्या प्रकाशांनी प्रकाशित केलेले दोन पृष्ठभाग एकाआड एक असे डोळ्यासमोर आणीत गेल्यास,त्यांच्या चकासनांतील तफावत डोळ्यास चटकन समजतेपरंतु त्यांच्या रंगांमधील तफावत थोड्या विलंबाने लक्षात येते.तेव्हा अशा प्रकारचे दोन पृष्ठभाग जलद गतीने एकाआड एक डोळ्यापुढे आणल्यास,एका विशिष्ट किमान गतीच्या वेळी चकासनातील फरकामुळे डोळ्यावर येणारा प्रकाश लुकलुकल्यासारखा वाटतो. दोन्ही पृष्ठांचे चकासन समान झाले की,ही लुकलुक किमान होते किंवा अजिबात नाहीशी सुद्धा होऊ शकते’. या तत्त्वावर आधारलेले अनेक प्रकाशमापक आहेत.त्यांपैकी सर्वांत चांगला जे. गिल्ड यांचा लुकलुकी प्रकाशमापक होय. त्याची रचना आ. ६ मध्ये दाखविली आहे. 

एका घातूच्या पेटिकेत १ हा एक मॅग्नेशियम ऑक्साइडाचा लेप दिलेला पडदा व २ ही विद्युत् चलित्राच्या (मोटरच्या) मदतीने वेगवेगळ्या वेगाने फिरविता येईल अशी वृत्तखंडाकार चकती [आ. ६ (आ)]बनविली आहे. चकतीच्या एका बाजूवर मॅग्नेशियम ऑक्साइडाचा लेप दिलेला आहे. १ व २ या दोघांवर अनुक्रमे ४ व ५ या प्रकाश उद्‌गमांचे प्रकाश लंब दिशेने पडतात व ७ या विवृत्ताकार (लंबवर्तुळाकार) पात्रातून १ व २ यांच्या पृष्ठांचे (एकाआड एक) निरीक्षण केले जाते. ७ या पात्राचा अंर्तभागही आदर्श विसरक असून त्याच्या बाजूच्या फाट्यात ठेवलेल्या ६ या दिव्याने पात्राच्या आत एकविध चकासन निर्माण केलेले असते.  

---

वृत्तखंडाकार चकतीचा भ्रमणवेग किमान ठेवून ४(किंवा ५)हा प्रकाश उद्‌गम अशा रीतीने मागेपुढे सरकवितात की,डोळ्यास दिसणारी लुकलुक किमान व्हावी. अशा वेळेस १ व २ यांची चकासने समान होतात व प्रकाशमापकाचा नियम वापरून ४ व ५ या प्रकाश उद्‌गमांच्या दीप्ति-तीव्रतांचे गुणोत्तर काढता येते. 

 भौतिकीय प्रकाशमापक : या प्रकारच्या प्रकाशमापकात डोळ्याऐवजी एखाद्या भौतिकीय साधनाने प्रकाशाचे मापन केले जाते. यामध्ये मुख्य लक्षात ठेवण्याचा मुद्दा हा आहे की,अशा साधनांची विविध तरंगलांब्यांच्या प्रकाशासाठी असणारी संवेदनशीलता मानवी डोळ्यासारखी नसते. त्यामुळे येणारी चूक टाळण्यासाठी योग्य अशा प्रकाशीय गाळण्यांचा उपयोग करणे आवश्यक असते. या प्रकारचे प्रकाशमापक (१)तापविद्युत् परिणाम [उष्णतेचे सरळ विद्युत् ऊर्जेमध्ये रूपांतर होणे→विद्युत्] किंवा (२)प्रकाशविद्युत् परिणाम [→प्रकाशविद्युत्] यांवर आधारलेले असतात. 

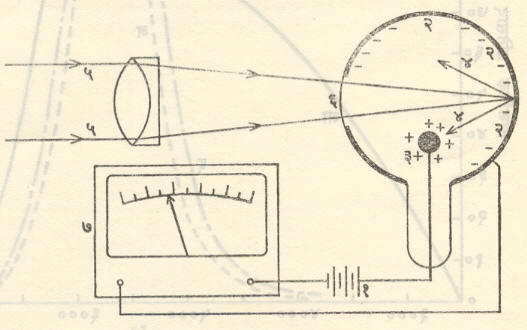
प्रकाशविद्युत् प्रकाशमापक : प्रकाशविद्युत् परिणामावर आधारलेले प्रकाशमापक अत्यंत संवेदनशील असतात. योग्य ती काळजी घेतल्यास या पद्धतीच्या प्रकाशमापकांनी अत्यंत बिनचूक अशी मापने विनासायास करता येतात. म्हणून अलीकडे हेच प्रकाशमापक सर्वत्र वापरले जातात. त्यांचे मुख्य तीन प्रकार आहेत : (१)प्रकाशविद्युत् चालक घट वापरणारे (आ. ७), (२)प्रकाशविद्युत् उत्सर्जक घट (नलिका) वापरणारे (आ. ८) व (३)प्रकाशगुणक नलिका वापरणारे. 

(१) प्रकाशविद्युत् चालक घटयुक्त प्रकाशमापक : पहिल्या प्रकारच्या प्रकाशमापकांची सापेक्ष संवेदनशीलता हिरवी गाळणी वापरल्यास जवळजवळ डोळ्यासारखीच असते. त्यांना वेगळ्या बाह्य विद्युत् घटाची जरूरी लागत नाही आणि ते खूप स्वस्त व आटोपशीर असतात. त्यामुळे त्यांचा वापर फार मोठ्या प्रमाणावर होतोपण त्यांच्या मापनाची अचूकता काहीशी कमी असते. 

प्रकाशविद्युत् चालक घटात धातूच्या (लोखंडाच्या) एका तबकडीवर सिलिनियमाचा किंवा कॉपर ऑक्साइडाचा पातळ थर दिलेला असून त्यावर अतिशय सूक्ष्म जाडीचे सोन्याचे अथवा प्लॅटिनमाचे पारदर्शक पटल असते. या पटलाच्या कडेवरून फवाऱ्याच्या साहाय्याने धातूचे एक कडे तयार केलेले असते. हे कडे व धातूची तबकडी एखाद्या संवेदनशील मायक्रोॲमीटराच्या किंवा ⇨ गॅल्व्हानोमीटराच्या एकेका टोकाला जोडतात. धातवीय पातळ पारदर्शक पटलावर प्रकाश आपाती होऊन सिलिनियमाच्या थरापर्यंत पोचला की,उपकरणातून सूक्ष्म विद्युत् प्रवाह वाहू लागतो व तो मायक्रोॲमीटराच्या साहाय्याने मोजता येतो. पुष्कळ वेळा या मायक्रोॲमीटराचे अंशन [→अंशन व अंशन परीक्षण] सरळ लक्समध्ये केलेले असते,तेव्हा त्या उपकरणाला लक्समीटर म्हणतात. या उपकरणाचा प्रकाशमापक म्हणून मोठ्या प्रमाणावर उपयोग केला जातो. [→छायाचित्रणकॅमेरा]. 

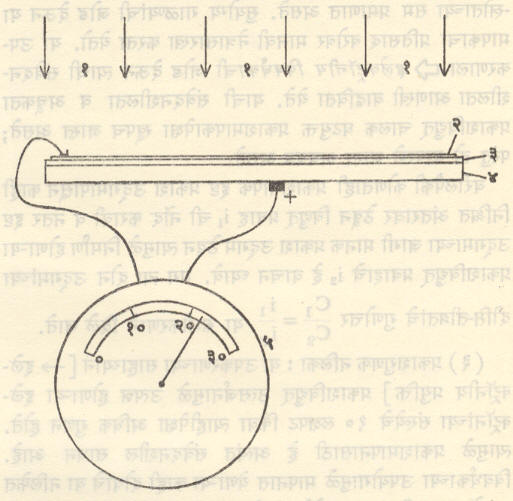
(२)प्रकाशविद्युत् उत्सर्जक घटयुक्त प्रकाशमापक : प्रकाशविद्युत् उत्सर्जक घट वापरून तयार केलेल्या प्राथमिक स्वरूपाच्या प्रकाशमापकाची रचना आ. ८ मध्ये दाखविली आहे. 

यात एका काचनलिकेच्या अंतर्भागावर सिझियम अँटिमनाइडाचा (Cs₃Sb) पातळ थर दिलेला असून तो अत्यंत दुर्बल प्रकाशानेही प्रकाशीय इलेक्ट्रॉनांचे (प्रकाशविद्युत् परिणामामुळे उत्सर्जित होणाऱ्या इलेक्ट्रॉनांचे) उत्सर्जन करू शकतो. हा थर व धनाग्र यांच्यामध्ये विद्युत् घटमालेच्या साहाय्याने सु. ६० ते ९० व्होल्ट विद्युत् दाब लावलेला असतो. सिझियम अँटिमनाइडाच्या थरावर घटावरील पारदर्शक गवाक्षातून प्रकाश पडला असता उत्सर्जित होणारे प्रकाशीय इलेक्ट्रॉन धनाग्राकडे आकर्षित होतात. त्यामुळे उत्पन्न होणारा विद्युत् प्रवाह एका अत्यंत संवेदनशील विद्युत् प्रवाहमापकाच्या (ॲमीटराच्या) साहाय्याने मोजला जातो. या विद्युत् प्रवाहाचे मूल्य आपाती प्रकाशस्रोताच्या सम प्रमाणात असते. सुयोग्य गाळण्यांची जोड देऊन या मापकाचा प्रतिसाद बरोबर मानवी नेत्रासारखा करता येतो. या उपकरणाला ⇨इलेक्ट्रॉनीय विवर्धकाची जोड देऊन त्याची संवेदनशीलता आणखी वाढविता येते. याची संवेदनशीलता व अचूकता प्रकाशविद्युत् चालक घटयुक्त प्रकाशमापकापेक्षा खूपच जास्त असतेपरंतु तो वापरणे जास्त अवघड असते.  

वरीलपैकी कोणताही प्रकाशमापक इष्ट प्रकाश उद्‌गमापासून काही निश्चित अंतरावर ठेवून विद्युत् प्रवाह i₁ची नोंद करावी व नंतर इष्ट उद्‌गमाच्या जागी मानक प्रकाश उद्‌गम ठेवून त्यामुळे निर्माण होणाऱ्या प्रकाशविद्युत् प्रवाहाचे i₂हे वाचन घ्यावे. मग त्या दोन उद्‌गमांच्या दीप्ति-तीव्रतांचे गुणोत्तर  

---

C1	=	i1	या समीकरणाने दिले जाते.
C2		i2

(३) प्रकाशगुणक नलिका : या उपकरणाच्या साहाय्याने [→इलेक्ट्रॉनीय प्रयुक्ति] प्रकाशविद्युत् उत्सर्जनामुळे उत्पन्न होणाऱ्या इलेक्ट्रॉनांच्या संख्येचे १० लक्षपट किंवा त्याहीपेक्षा अधिक गुणन होते. त्यामुळे प्रकाशमापनासाठी हे अत्यंत संवेदनशील साधन आहे. विवर्धकाच्या उपयोगामुळे मापनात येणाऱ्या काही दोषांचे या नलिकेत आपोआपच निराकरण होते. अतिमंद प्रकाशाच्या मापनासाठी ही नलिकाच पसंत केली जाते. 

अंशनपरीक्षण : (इयत्तीकरण). प्रकाशविद्युतीय साधनांचा प्रतिसाद सर्व तरंगलांबांच्या प्रकाशासाठी सारखाच नसतो. त्यामुळे या साधनांच्या साहाय्याने प्रकाशमापन करताना एक तर त्यांचे अंशनपरीक्षण करून त्यांच्या वाचनावरून येणारी मूल्ये मानवी डोळ्याने मापन करून येणाऱ्या मूल्यांशी मिळती जुळती करून घ्यावी लागतात. दुसरा मार्ग म्हणजे प्रकाशविद्युत् साधनाबरोबर सुयोग्य प्रकाशीय गाळण्या वापरून व  त्याच्या विद्युत् मंडलात सुयोग्य रोध वापरून त्यांची वाचने नेत्रीय मापनाशी जुळती करून घ्यावयाची. आ. ९ मध्ये मानवी नेत्र व प्रकाशविद्युत् चालक घट यांचे प्रतिसाद वक्र दिले आहेत. त्यांच्यावरून याची कल्पना येईल. 

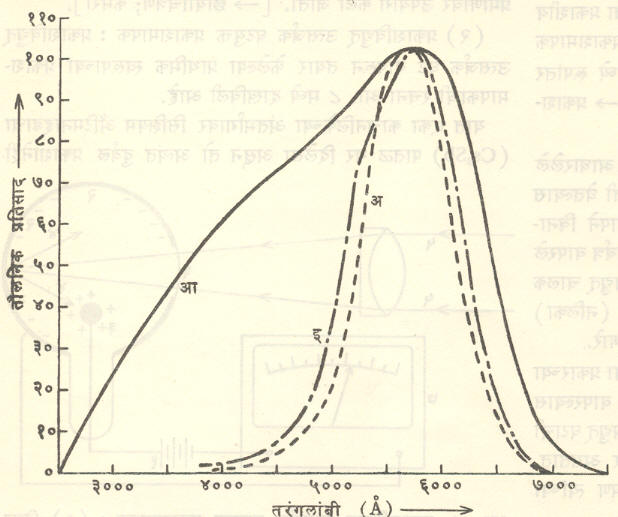
 दीप्ति-तीव्रता वितरण वक्र :सामान्यतः कोणत्याही प्रकाश उद्‌गमाची दीप्ति-तीव्रता वेगवेगळ्या दिशांना वेगळी असते. जुन्या काळची ‘दिव्याखाली अंधार’ही म्हण याचे द्योतक आहे. वेगवेगळ्या दिशांनी दिव्याची दीप्ति-तीव्रता मोजून तीव्रता वितरण दर्शविणारे ध्रुवीय वक्र काढतात. दिव्याला परावर्तकाची जोड देऊन हे वितरण अपेक्षेप्रमाणे बदलता येते. आ. १० मध्ये टंगस्टन तप्त-तंतू दिव्याचे उदग्र प्रतलातील दीप्ति-तीव्रता (कँडेलामध्ये) वितरण वक्र दाखविले आहेत.  

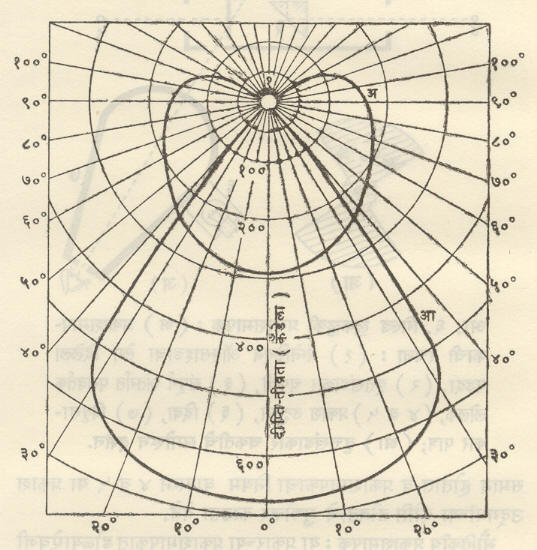
 दिवसा सूर्यप्रकाशाने व रात्री विजेच्या प्रकाशाने कार्यालये व कारखाने यांच्या इमारतीतील निरनिराळ्या भागांचे प्रकाशन कसे आहे,हे पाहण्यासाठी प्रकाशमापकाची मदत घेणे आवश्यक ठरते. 

समाकलक गोलीय प्रकाशमापक : प्रकाश उद्‌गमाची सर्व दिशांना मिळून सरासरी दीप्ति-तीव्रता काढण्यासाठी समाकलक गोलीय प्रकाशमापकाचा उपयोग करतात. एका पोकळ गोलाच्या मध्यावर मापन करावयाचा दिवा ठेवतात. गोलाच्या अंतर्भागावर सर्वत्र आदर्श विसरक पांढऱ्या रंगाचा लेप दिलेला असून त्याच्या एका बाजूला एक छोटेसे छिद्र—गवाक्ष—ठेवलेले असते. या गवाक्षातून मिळणारी दीप्ति-तीव्रताही आतील दिव्याच्या सरासरी तीव्रतेइतकी असते. सरासरी दीप्ति-तीव्रता X ४ π = दिव्यापासून मिळणारा एकूण प्रकाश-स्रोत. या समीकरणावरून दिव्याचा एकूण प्रकाश-स्रोत (ल्यूमेन) काढूत येतो. हीच त्या दिव्याची प्रकाश देण्याची क्षमता होय. 

 परावर्तनमापक :यास प्रेषणमापकही म्हणता येईल. यात प्रकाशविद्युत् चालक घट व समाकलक गोलीय प्रकाशमापक वापरतात. एखाद्या पृष्ठभागावरून परावर्तित झालेल्या प्रकाशाचे मापन करून व त्याची एखाद्या मानक पृष्ठभागावरून परावर्तित झालेल्या प्रकाशाशी तुलना करून त्या पृष्ठभागाची परावर्तनक्षमता काढता येते. त्याचप्रमाणे एखाद्या पदार्थाची प्रेषणक्षमता काढावयाची झाल्यास,दोन समाकलक गोलांच्या गवाक्षांसमोर त्या पदार्थाचे पटल ठेवून ती काढतात. दोन गोलांपैकी एकात प्रकाश उद्‌गम असतो व दुसऱ्यात प्रकाशमापक असतो.

---

सूक्ष्म प्रकाशमापक : (सूक्ष्म घनतामापक). छायाचित्रण काचेवर वर्णपटाचे छायाचित्र घेतल्यानंतर त्यातील वर्णरेषांच्या तीव्रतांचे मापन करण्यासाठी किंवा व्यतिकरण पट्टांच्या [→ प्रकाशकी] छायाचित्रावरून त्या पट्टांची तीव्रता मोजण्यासाठी या उपकरणाचा उपयोग केला जातो. स्थिर दीप्ति-तीव्रतेच्या दिव्यापासून छायाचित्रण काचेवरील पायसाच्या (प्रकाशसंवेदी रसायनाच्या) थरावर भिंगाच्या साहाय्याने प्रथम प्रकाश केंद्रित केला जातो. त्यानंतर दुसऱ्या भिंगाच्या साहाय्याने पायसाची प्रतिमा पायसापासून सु. ३० सेंमी. अंतरावर पाडली जाते. या प्रतिमेच्या प्रतलात एक अरुंद फट (रुंदी सु. ०·०२ ते ०·२ मिमी.) ठेवलेली असते. छायाचित्रण काच योग्य तेथे सरकवून इष्ट वर्णरेषेच्या मधून जाणारा प्रकाश फटीमधून जाऊन एका प्रकाशविद्युत् नलिकेवर पडतो व या पारगमित प्रकाशाच्या तीव्रतेनुसार नलिकेला जोडलेल्या विद्युत् मापकाच्या काट्याचे विचलन होते. त्याचप्रमाणे पायसावर छायाचित्रण न झालेल्या भागातून जाणारा प्रकाश वरीलप्रमाणेच फटीमधून प्रकाशविद्युत् नलिकेवर पाडून त्यामुळे होणारे विचलन मोजतात. या दोन विचलनांवरून इष्ट वर्णरेषेच्या छायाचित्राची घनता मिळते व त्यावरून मूळ वर्णरेषेची तीव्रताही काढता येते. विचलने स्वयंचलित पद्धतीने एका आलेखपत्रावर नोंदण्याचीही सोय करता येते. प्रकाशविद्युत् नलिकेऐवजी अभिज्ञातक म्हणून केव्हा केव्हा तपयुग्माचाही वापर केला जातो. 

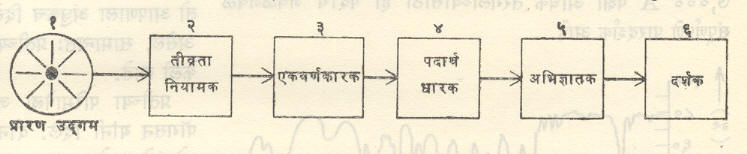
वर्णपट प्रकाशमापक : वर्णपटातील वर्णरेषांच्या प्रकाश ऊर्जा मोजण्यासाठी या उपकरणाचा उपयोग केला जातो. विशिष्ट विद्रावातून प्रकाश जाऊ देऊन त्यामुळे वर्णपटातील विविध भागांचे शोषण किती प्रमाणात होते ते मोजतात. त्यावरून विद्रावातील विद्रुताचे (विरघळलेल्या पदार्थाचे) रासायनिक विश्लेषण अचूकपणे करता येते. जंबुपार (दृश्य वर्णपटातील जांभळ्या रंगाच्या पलीकडील अदृश्य), दृश्य किंवा अवरक्त (दृश्य वर्णपटातील तांबड्या रंगाच्या अलीकडील अदृश्य) अशा वर्णपटाच्या तीनही भागांसाठी हे तंत्र वापरता येते. यासाठी विविध प्रकारची उपकरणे प्रचारात आहेत. आ. १२ मध्ये या उपकरणाचा सर्वसामान्य आराखडा ‘ठोकले पद्धती’ने दाखविला आहे. 

 अखंड वर्णपट देणारा १ हा प्रारण उद्‌गम वर्णपटातील इष्ट विभागानुरूप निवडला जातो उदा., दृश्य प्रकाशासाठी तप्ततंतुदीप, अवरक्त किरणांसाठी नेर्न्स्ट दीप [→अवरक्त प्रारण],जंबुपार किरणासांठी हायड्रोजन प्रज्योत दीप [→जंबुपार प्रारण] इ. प्रारण उद्‌गम वापरले जातात. उद्‌गमापासून उपकरणात जाणाऱ्या प्रकाशाची तीव्रता नियंत्रित करण्यासाठी त्याच्यापुढे २ हे एक लहानमोठे करता येईल असे रंध्र किंवा फट असते. त्यामधून हा प्रकाश ३ या एकवर्णकारकात [लोलक किंवा विवर्तन जालकात→विवर्तन जालक] जातो. त्याच्यातून इष्ट तरंगलांबीच्या भोवतालचा अगदी अरुंद प्रारणपट्ट पुढे जाऊन तो ४ या धारकात बसविलेल्या परीक्ष्य पदार्थांवर पडतो व त्यातून पारगमित झालेला प्रकाश प्रकाश शेवटी ५ या प्रकाशविद्युत् नलिका किंवा तपचिती (एकसरीत जोडलेल्या तपयुग्मांचा संच) किंवा बोलोमीटर [→उष्णता प्रारण] यासारख्या अभिज्ञातकावर पडतो. अर्थात अभिज्ञातकाची निवडही वापरल्या जाणाऱ्या प्रारणपट्टाला अनुरूप अशी करावी लागते. येथे अभिज्ञातकावर पडणाऱ्या प्रारणाच्या ऊर्जेचेच मापन अभिप्रेत असतेदृश्य प्रकाशाचे नव्हे. प्रकाशविद्युत् घटासारख्या नैकरेषीय अभिज्ञातकाचा [→ नैकरेषीय आविष्कार] वापर केल्यास प्रथम त्याचे इयत्तीकरण करून घ्यावे लागते. बोलोमीटर किंवा तपचिती याचे प्रतिसाद रेषीय असल्याने त्यांचा वापर जास्त सोयीचा ठरतो. ६ हा दर्शक घटक म्हणजे एखादा गॅल्व्हानोमीटर किंवा ऋण किरण दोलनदर्शक [→इलेक्ट्रॉनीय मापन] किंवा ⇨ विद्युत् वर्चस्‌मापक असतो. त्याच्या वाचनावरून अभिज्ञातकावर आपाती होणाऱ्या प्रारण ऊर्जेचे मान मिळू शकते. ही वाचने आलेखाच्या स्वरूपात आपोआप नोंदली जावीत अशीही व्यवस्था करता येते. 

 विशिष्ट प्रारण उद्‌गमापासून प्रत्यक्ष येणाऱ्या प्रारणाची तीव्रता I₀ व शोषक माध्यमातून गेल्यानंतर त्याची तीव्रता I असल्यास ^I/I₀ = T या गुणांकाला त्या माध्याचे पारगामित्व असे म्हणतात व log₁₀ (¹/_T) = A या गुणांकाला माध्यमाचे शोषकत्व असे म्हणतात. शोषकत्व हे माध्यमाची जाडी,त्यातील शोषक घटकाची संहती (प्रमाण) व त्याचा शोषक गुणांक यांच्या गुणाकारावर अवलंबून असते.   

---

वरील प्रकारच्या उपकरणाच्या साहाय्याने विशिष्ट शोषकाचे शोषकत्व वेगवेगळ्या तरंगलांब्यांसाठी मोजून त्यांचा आलेख काढतात (आ. १३).या आलेखाला त्या शोषकाचा शोषण वर्णपट असे म्हणतात. आ. १३ वरून असे दिसते की,पेरॉक्सिटिटॅनेटाचे पारगामित्व सु. ४,१०० Å या तरंगलांबीच्या जवळपास किमान असून ७,००० Å पेक्षा अधिक तरंगलांब्यांसाठी हा पदार्थ जवळजवळ संपूर्णपणे पारदर्शक आहे. 

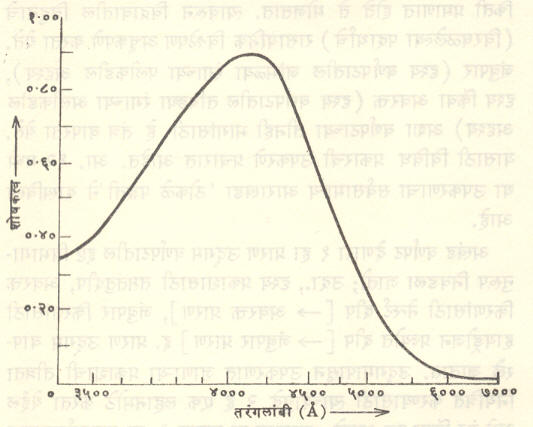
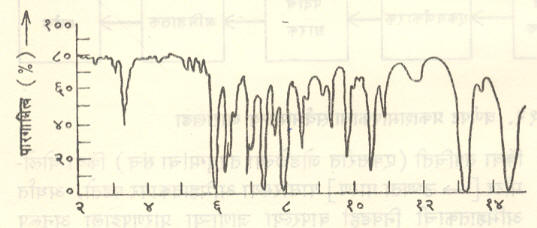
 शोषकत्वाऐवजी पारगामित्व आणि तरंगलांबी यांचा आलेख काढूनही पदार्थाचा शोषण वर्णपट दिग्दर्शिता करता येतो. आ. १४ मध्ये ॲसिटोफेनोनासाठी समीप अवरक्त भागातील असा शोषण वर्णपट दाखविला आहे.  

 विशिष्ट प्रारण उद्‌गमापासून सरळ अभिज्ञातकावर येऊन पडणारी विशिष्ट तरंगलांबीची प्रारणतीव्रता I₀व तीच एखाद्या पृष्ठभागावर पडून परावर्तित होऊन अभिज्ञातकावर पडणारी त्याच तरंगलांबीची प्रारण ऊर्जा I_R यांच्या ^I_R/I₀ = R या गुणोत्तराला त्या पृष्ठभागाची परावर्तकता असे म्हणतात. परावर्तकता व तरंगलांबी यांच्या आलेखाला त्या पृष्ठभागाचा परावर्तन वर्णपट असे म्हणतात. आ. १५ मध्ये जांभळ्या व हिरव्या पृष्ठभागांचे परावर्तन वर्णपट दाखविले आहेत.

  खगोलीय प्रकाशमापन : आकाशात दिसणाऱ्या ताऱ्यांच्या दीप्ती वेगवेगळ्या दिसतात. ताऱ्यांचे वर्गीकरण करण्यासाठी सोयीचे व्हावे म्हणून इ. स. पू. १३० च्या सुमारास हिपार्कस यांनी व नंतर इ. स. १५० च्या सुमाराला टॉलेमी यांनी ताऱ्यांचे सहा वर्ग कल्पिले. डोळ्याने कसेबसे दिसू शकणारे तारे हे त्यांनी सहाव्या प्रतीचे मानले व सर्वांत जास्त तेजस्वी तारे पहिल्या प्रतीचे मानले. प्रत जितकी जास्त तितकी ताऱ्याची दीप्ती कमीपरंतु दीप्तीचे मान केवळ अंदाजानेच केले होते म्हणून या प्रतींमध्ये खूपच अनिश्चितता होती. 

दूरदर्शकाच्या शोधानंतर अधिक अधिक अंधुक तारे पाहता येऊ लागले व त्यामुळे प्रतींच्या संख्येत वाढ करणे आवश्यक झाले. येथे ही गोष्ट लक्षात ठेवणे आवश्यक आहे की,एखाद्या ताऱ्याची निरपेक्ष दीप्ती खूप असली,तरी त्याचे पृथ्वीपासूनचे अंतर फार असल्यास तो आपणाला अंधुकच दिसेल म्हणजेच त्याची भासमान दीप्ती कमी असेल. सामान्यतः प्रतीच्या साहाय्याने ही भासमान दीप्तीच व्यक्त केली जाते. 

प्रतीच्या परिभाषेला जास्त बिनचूक स्वरूप १८५४ मध्ये एन्. पॉगसन यांनी दिले. दोन ताऱ्यांपासून पृथ्वीकडे येणाऱ्या प्रकाशस्रोतांचे गुणोत्तर २·५१२ असेल,तर त्यांच्या प्रतीत एकचा फरक असतो,अशी व्याख्या त्यांनी केली व ती अद्यापही वापरली जात आहे. [→ प्रत]. 

प्रारंभीच्या काळात ध्रुवाच्या ताऱ्याची प्रत २ मानून त्याच्या संदर्भात इतर ताऱ्यांच्या प्रती अजमावल्या जात. १९११ मध्ये ई. हर्ट्‌झस्प्रंग यांच्या हे लक्षात आले की,ध्रुवताऱ्याची दीप्ती स्थिर नसून बदलत असते. त्यामुळे त्याच्या संदर्भात केलेली मापने पुरेशी बिनचूक होणार नाहीत. यासाठी आकाशातील उत्तर भागातील काही ताऱ्यांचा मानक (प्रमाणभूत) म्हणून उपयोग करून प्रती काढण्याची कल्पना पुढे आली. पुढे आकाशाच्या वेगवेगळ्या भागांत कित्येक तारे मानक म्हणून निवडून त्यांच्या संदर्भात त्या त्या भागातील इतर ताऱ्यांच्या प्रती काढल्या जाऊ लागल्या.  

---

नेत्रीय दीप्तिमापन : एकोणिसाव्या शतकाच्या अखेरीला एफ्. त्सल्‌नर यांनी ताऱ्यांसाठी नेत्रीय प्रकाशमापनाची एक पद्धत विकसित केली. या पद्धतीत एका सूक्ष्म छिद्राच्या मागे स्थिर दीप्तीचा विद्युत् दीप ठेवून त्या छिद्राचा ‘कृत्रिम तारा’म्हणून उपयोग केला जाई. मापन करावयाचा तारा व कृत्रिम तारा एकाच वेळी पाहिले जात. कृत्रिम ताऱ्यापासून येणाऱ्या प्रकाशाच्या मार्गात दोन निकोल लोलक [→प्रकाशकी] ठेवून व त्यांपैकी एक फिरवून कृत्रिम ताऱ्याची दीप्ती कमीजास्त करता येई. अशा तऱ्हेने दोनही तारे सारख्याच दीप्तीचे दिसले म्हणजे त्या वेळी त्या दोन निकोल लोलकांच्या प्रधान प्रतलांमधील कोन θ मोजला जाई. त्यावरून कृत्रिम ताऱ्याच्या संदर्भात खऱ्या ताऱ्याची दीप्ती काढता  येई. या पद्धतीत खरा तारा व कृत्रिम तारा यांची स्वरूपे तंतोतंत एकसारखी नसल्याने त्यांचे संतुलन करणे अवघड जाई. 

ई. सी. पिकरिंग यांनी हार्व्हर्ड वेधशाळेत विकसित केलेल्या प्रकाशमापकात इष्ट ताऱ्याची तुलना ध्रुवताऱ्याशीच केली जाई. दोन आरसे व दोन तंतोतंत एकसारखी वस्तुभिंगे वापरून ध्रुवतारा व इष्टतारा यांच्या प्रतिमा शेजारी शेजारी पाडल्या जात. संतुलन करण्यासाठी निकोल लोलकांचाच उपयोग केला जाई. 

छायाचित्रीय दीप्तिमान : इ. स. १९०० च्या सुमाराला ही पद्धती प्रचारात येऊ लागली. नेत्रीय मापनापेक्षा ही पद्धत अनेक दृष्टींनी सरस आहे. १९४५ पर्यंत ताऱ्यांच्या दीप्तिमापनासाठी ही पद्धत सर्वोत्कृष्ट मानली जाई. एकाच छायाचित्रण काचेवर एका वेळी अनेक ताऱ्यांची छायाचित्रे घेऊन त्यांच्या दीप्तींची तुलना करणे या पद्धतीत शक्य होते. अंधुक ताऱ्यासांठी जास्त उद्‌भासन काल (छायाचित्रण काच प्रकाशाची क्रिया होण्यासाठी उघडी ठेवण्याचा काल) देऊन त्यांच्या प्रतिमा जास्त गडद मिळवता येतात हे या पद्धतीचे मुख्य फायदा आहेतपरंतु छायाचित्रण काचेवरील घनता (d),ताऱ्याची दीप्ती (I)व उद्‌भासन काल (t)यांचा संबंध पुढील समीकरणाने दिला जातो. d = It^P येथे P हा एक स्थिरांक असून त्याची मूल्ये वेगवेगळ्या छायाचित्रण पायसांसाठी वेगवेगळी (०·८ ते १·० यांच्या दरम्यान) असतात. या गोष्टींचा दखल मापनात घ्यावी लागते. त्याचप्रमाणे जास्त दीप्तिमान ताऱ्यांच्या छायाचित्राची घनता जास्त असते व त्याचबरोबर त्याच्या प्रतिमेवरचे आकारमानही मोठे असते. दीप्तिमान निश्चित करताना या दोन्हींचा समन्वय करावा लागतो.  

 सामान्यतः आकाशातील इष्ट विभागाचे प्रथम एका छायाचित्रण काचेवर एक छायाचित्र घेतात. नंतर ही काच थोडी बाजूला सरकवून पुन्हा तिच्यावरच त्याच विभागाचे दुसरे छायाचित्र घेतात. हे घेताना त्या विभागातील सर्व ताऱ्यांचा छायाचित्रण काचेवर पडणारा प्रकाश काही निश्चित प्रमाणात कमी होईल असे करतात. यासाठी दुसरे छायाचित्र घेताना दूरदर्शकाचा परिणामी छिद्र व्यास ठराविक प्रमाणात कमी करणे किंवा प्रकाशाच्या मार्गात काचेच्या मानक शोषक पट्ट्या घालणे यासारख्या पद्धतींचा अवलंब केला जातो. या दोन छायाचित्रांतील ताऱ्यांच्या प्रतिमांची घनता व आकारमान लक्षात घेऊन त्यांच्या तौलनिक दीप्तींचे आलेख काढता येतात. या छायाचित्रांची तुलना काही मानक ताऱ्यांच्या प्रतिमांशी करून त्यावरून त्यातील ताऱ्यांच्या भासमान दीप्ती किंवा प्रती निश्चित करता येतात. 

  

 प्रकाशविद्युतीय दीप्तिमापन : ही पद्धत आता सर्वांत जास्त बिनचूक व वस्तुनिष्ठ पद्धत म्हणून मान्यता पावली आहे. दूरदर्शकाच्या साहाय्याने इष्ट ताऱ्याची प्रतिमा एका प्रकाशगुणक नलिकेच्या ऋणाग्रावर पाडली जाते. या नलिकेला पुढे इलेक्ट्रॉनीय विवर्धकाची जोड देऊन प्रकाशविद्युत् प्रवाहाचे सु. १०^१४ पट विवर्धन केले जाते व मग तो प्रवाह विद्युत् मापकाच्या साहाय्याने मोजला जातो किंवा स्वयंचलित यंत्रणेच्या साहाय्याने आलेख पत्रावर नोंदला जातो. या प्रवाहाचे मूल्य हे ताऱ्याच्या दीप्तीचे गमक असते. प्रकाशविद्युत् परिणाम नैकरेषीय असल्यामुळे या मापनाला जरूर ती शुद्धी लावावी लागते किंवा सुयोग्य प्रकाशीय गाळण्या वापराव्या लागतात.  

इतर पद्धती : दूरदर्शकाच्या साहाय्याने विशिष्ट ताऱ्याची प्रतिमा एका धातूच्या काळ्या केलेल्या छोट्या तबकडीवर पाडली असता त्या ताऱ्याकडून येणाऱ्या सर्व प्रारणांचे उष्णतेत रूपांतर होऊन तबकडीचे तापमान वाढते. या तबकडीला एखादे (खास) तपयुग्म किंवा बोलोमीटर किंवा गोले घट [→ अवरक्त प्रारण] यासारख्या साधनाची जोड देऊन त्या उष्णतेचे मापन केले जाते व तेच त्या ताऱ्याच्या दीप्तीचे गमक असते. या पद्धतीने मिळणाऱ्या प्रतीला ताऱ्याची संपूर्ण प्रारणप्रत असे म्हणतात. ही प्रत प्रकाशीय प्रतीपेक्षा कमी मूल्याची असते. ‘थंड’ताऱ्यांच्या दीप्तीचे मापन करण्यासाठी ही पद्धत विशेष उपयुक्त असते.  

वर्णपट प्रकाशमापन पद्धतीच्या साहाय्याने ताऱ्यांच्या वर्णपटातील विविध तरंगलांबीच्या पट्टांच्या प्रकाश-तीव्रताही मोजता येतीलपरंतु फक्त खूप तेजस्वी ताऱ्यांच्या बाबतीतच हे शक्य झाले आहे. 

ताऱ्यांची व दीर्घिकांची पृथ्वीपासूनची अंतर काढणे,त्यांची घटकद्रव्ये अजमावणे,त्यांचे वर्गीकरण करणे इ. ठिकाणी खगोलीय प्रकाशमापनाचा उपयोग होतो. [→ खगोल भौतिकी]. 

संदर्भ :  1. Ditchburn, R.W. Light, London, 1963.

            2. Hewitt, H. Vause, A. S. Ed. Lamps and Lighting, London, 1966.

            3. Smith, S. J. A Degree Physics, Part III : Optics, London, 1960.

            4. Struve, O. Zebergs, V. Astronomy of the 20th Century, 1962.

            5. Walsh, J. W. T. Photometry, New York, 1958.

  भावे, श्री. द.पुरोहित,वा. ल.

“