प्रकाश

प्रकाश : प्रकाशाची सोपी व सुटसुटीत अशी व्याख्या थोडक्यात देणे कठीण आहे परंतु ज्या प्रारण (तरंगरूपी ऊर्जा) विशेषाची मानवी डोळा नोंद घेऊ शकतो त्याला प्रकाश म्हणावे,अशी एक व्याख्या दिली जाते. मात्र येथे हे लक्षात ठेवले पाहिजे की,प्रकाशामुळे आपणाला वस्तू दिसू शकत असल्या, तरीही खुद्द प्रकाश हा आपणाला अदृश्यच असतो. पंचज्ञानेंद्रियांच्या साहाय्याने सृष्टीचे आपणाला जे काही ज्ञान प्राप्त होते त्यापैकी फार मोठा भाग दृष्टीने म्हणजेच प्रकाशाच्या साहाय्याने प्राप्त होतो,म्हणून प्रकाशाच्या अभ्यासाला विशेष महत्त्व आहे.

प्रस्तुत नोंदीत प्रकाशाचे विविध आविष्कार व त्यांच्या संदर्भाने प्रकाशाच्या स्वरूपाविषयीचे सिद्धांत यांचा मागोवा घेतला आहे. आविष्कारांबद्दल जास्त तपशीलवार चर्चा ‘प्रकाशकी’या नोंदीत केली आहे.

प्रकाशाचे काही आविष्कार : प्रकाशाची कोणतीही परिकल्पना मांडताना असे पहाणे आवश्यक आहे की,तिच्या साहाय्याने प्रकाशाच्या विविध आविष्कारांचे सुसंगत स्पष्टीकरण देता येईल. या दृष्टीने प्रथम प्रकाशाच्या प्रमुख आविष्कारांचा थोडक्यात आढावा घेणे जरूर आहे.

रेखीय प्रसारण : स्थूलमानाने पाहता एकविध (सर्वत्र एकसारख्या असलेल्या) माध्यमातून प्रकाश सरळ रेषेत जातो असे दिसते. या गुणालाच प्रकाशाचे रेखीय प्रसारण असे म्हणतात. प्रकाशाच्या या गुणामुळेच अपारदर्शक वस्तूच्या छाया रेखीव अशा पडतात. तसेच छाया-उपच्छाया या प्रकाराचेही यथायोग्य स्पष्टीकरण करता येते. एका बिंदूपासून दुसऱ्या बिंदूपर्यंतचा प्रकाशाचा मार्ग म्हणजेच प्रकाशकिरण होय. ही किरणाची कल्पना रेखीय प्रसारणाच्या तत्त्वावरच राबविली जाते. किरणांच्या साहाय्याने वेगवेगळी भिंगे,आरसे इत्यादींमुळे प्रतिमा कोठे आणि कशा तयार होतील ते समजू शकते. चंद्रसूर्याच्या ग्रहणांची उपपत्तीही समाधानकारकपणे देता येते. ‘भूमितीय प्रकाशकी’चा पाया ‘रेखीय प्रसारण’हाच आहे.

व्यस्त वर्ग नियम : प्रकाश-उद्‌गमापासून जसजसे दूर जावे तसतशी प्रकाशनाची तीव्रता अंतराच्या वर्गाच्या व्यस्त प्रमाणात कमी होत जाते, याला ‘प्रकाशनाचा व्यस्त वर्ग नियम’असे म्हणतात. याचेही सुयोग्य स्पष्टीकरण रेखीय प्रसारणानुसार करता येते.

परावर्तन : कोणत्याही दोन माध्यमांतील आंतरपृष्ठावर प्रकाश पडला असता त्याचा काही अंश परत मूळच्या माध्यमातच फेकला जातो (बाकीच्या भागाचे अंशतः शोषण व/अथवा पारगमन होते). या परिणामाला परावर्तन असे म्हणतात. आरशासारख्या नितळ पृष्ठापासून होणाऱ्या परावर्तनाला खाली दिलेले दोन नियम (परावर्तनाचे नियम) लागू पडतात म्हणून त्याला ‘नियमबद्ध परावर्तन’असे म्हणतात. नियम १ : आपाती किरण, परावर्तित किरण आणि आपात बिंदूच्या ठायीचा पृष्ठलंब हे एकाच प्रतलात असतात. नियम २ : आपाती किरण व परावर्तित किरण हे दोनही किरण पृष्ठलंबाशी समान मूल्याचे कोन करतात. चांगल्या झिलई दिलेल्या पृष्ठापासून सु. ९५% पर्यंत प्रकाशाचे परावर्तन होऊ शकते. कागद किंवा भिंत यासारख्या खडबडीत पृष्ठभागावर पडलेला प्रकाश सर्व दिशांना परावर्तित झालेला दिसतो, याला ‘विसरित परावर्तन’असे म्हणतात. स्वयंप्रकाशी नसलेल्या वस्तू त्यांच्यापासून होणाऱ्या प्रकाशाच्या विसरित परावर्तनामुळेच आपणाला दिसू शकतात. हवेतील धूलिकणांपासून होणाऱ्या सूर्यप्रकाशाच्या विसरित परावर्तनामुळे दिवसा प्रत्यक्ष सूर्याचे उन्ह येत नाही तेथेही आपणाला प्रकाश मिळू शकतो.  

सकृत दर्शनी विसरित परावर्तनाला परावर्तनाचे नियम लागू पडत नाहीत असे वाटते,परंतु ते खरे नाही. खडबडीत पृष्ठाचे अत्यंत लहान भाग कल्पिले, तर या प्रत्येक भागावरून होणारे परावर्तन नियमबद्धच असते. परंतु हे सर्व भाग वेगवेगळ्या दिक्‌स्थितींत असल्याने आपणाला सबंध पृष्ठावरून मिळून सर्व दिशांना परावर्तन होते,असा भास होतो.

काही खास पृष्ठे आपाती किरणांपैकी काही निवडक भागाचेच (कंप्रतांचेचकंप्रता म्हणजे दर सेकंदाला होणारी कंपनसंख्या) प्रकर्षाने परावर्तन करतात. याला ‘विवेचक परावर्तक’ असे म्हणतात.

प्रणमन : प्रकाशकिरण एका माध्यमातून दुसऱ्या माध्यमात जातो तेव्हा माध्यमांमधील आंतरपृष्ठाशी किरणाच्या दिशेत एकदम बदल होतो, याला प्रणमन असे म्हणतात. प्रयोगांवरून असे दिसते की,या आविष्कारात पुढील दोन नियमांचे पालन होते. नियम १ : आपाती किरण,प्रणमित किरण व आपात बिंदूच्या ठायीचा पृष्ठलंब हे एकाच प्रतलात असतात. नियम २ : (व्हिलेब्रॉर्ट स्नेल यांचा नियम). दोन विशिष्ट माध्यमांच्या बाबतीत ^{sin i}/_{sin r} = μ = एक स्थिरांक. येथे i म्हणजे आपाती किरण व पृष्ठलंब यांच्यामधील कोन व r हा प्रणमित किरण व पृष्ठलंब यांच्यामधील कोन होय. या μला दुसऱ्या माध्यमाचा पहिल्या माध्यमासापेक्ष प्रणमनांक असे म्हणतात. उदा.,_aμ_gम्हणजे काचेचा (g) हवेच्या सापेक्ष (a)प्रणमनांक. निर्वात सापेक्ष प्रणमनांकाला माध्यमाचा निरपेक्ष प्रणमनांक असे म्हणतात. या प्रणमनांकाचे मूल्य (१) त्या माध्यमावर,(२) माध्यमाच्या तापमानावर व (३) प्रकाशाच्या रंगावर (कंप्रतेवर) अवलंबून असते.

अपस्करण : पांढरा प्रकाश काचेच्या लोलकातून जाऊ असता दुसऱ्या बाजूस सप्तरंगी वर्णपट मिळतो. या (व इतर) प्रयोगांवरून पांढरा प्रकाश हा या विविध रंगांच्या मिश्रणापासून बनलेला आहे हे सिद्ध होते. हे वेगवेगळे रंग म्हणजे वेगवेगळ्या कंप्रतांचे किंवा तरंगलांब्यांचे प्रकाशतरंग होत. विशिष्ट जटिल प्रकाशकिरणाचे त्याच्या घटक रंगांत पृथक्करण होण्याच्या आविष्काराला अपस्करण असे म्हणतात.

निर्वातात सर्व कंप्रतांच्या प्रकाशतरंगांचा वेग सारखाच असतो परंतु काचेसारख्या घनरूप माध्यमात तरंग-वेग कंप्रतेनुसार बदलत जातो. प्रकाशाच्या तरंग सिद्धांतानुसार यामुळे कंप्रतेनुसार माध्यमाचा 

माध्यमाचा प्रणमनांक=	प्रकाशाचा निर्वातातील वेग
	प्रकाशाचा माध्यमातील वेग

प्रणमनांक बदलत जातो. परिणामी एकाच आपाती कोनासाठी वेगवेगळ्या रंगांच्या प्रकाशकिरणांचे प्रणमन कोन वेगवेगळे होतात व म्हणून ते रंग परस्परांपासून अलग होतात. अशा तऱ्हेने अपस्करण घडून येते.

नियमानुसारी अपस्करण : सामान्यतः प्रकाशाची कंप्रता जसजशी वाढत जाईल किंवा तरंगलांबी कमी होत जाईल,तसतसा माध्यमाचा प्रणमनांक वाढत जातो. अशा पद्धतीने होणाऱ्या अपस्करणाला नियमानुसारी अपस्करण असे म्हणतात. गणिताच्या भाषेत विशिष्ट माध्यमाच्या बाबतीत ^dμ/_dλ (λ प्रकाशाची तरंगलांबी) या अवकलजाला [→ अवकलन व समाकलन] त्या माध्यमाचे अपस्करण असे म्हणतात.

ए. एल्. कोशी यांच्या सूत्रानुसार	dμ	= –	2B
	dλ		λ3

येथे B हा त्या माध्यमाचा विशिष्ट असा स्थिरांक आहे. या सूत्रांवरून असे दिसते की, (अ) तरंगलांबी कमी होईल तसतसा प्रणमनांक वाढत जाईल,(आ) अपस्करणाचे मूल्य तरंगलांबीच्या घनाच्या व्यस्त प्रमाणात बदलत जाते. काच,पाणी यांसारख्या अनेक माध्यमांना कोशी सूत्र लागू पडते, असे प्रयोगावरून दिसून येते. अशा माध्यमात होणारे अपस्करण (कोशी यांच्या) नियमानुसार होते.

नियमविरुद्ध अपस्करण:जेव्हा विशिष्ट तरंगलांबीच्या प्रकाशाचे माध्यमाकडून विवेचक अभिशोषण होते तेव्हा त्या तरंगलांबीच्या आसपास कोशी सूत्र लागू पडत नाही. मग तरंगलांबीच्या वाढीबरोबर प्रणमनांकही वाढत जाण्याचा अनपेक्षित प्रकार अनुभवाला येतो. अशा परिस्थितीत होणाऱ्या अपस्करणाला नियमविरुद्ध अपस्करण असे म्हणतात. त्याचे स्पष्टीकरण प्रकाशाच्या विद्युत् चुंबकीय तरंग सिद्धांतानुसार देता येते.

वर्ण : इंद्रधनुष्यात दिसणारे विविध रंग किंवा वर्ण हे वेगवेगळ्या तरंगलांबींच्या प्रकाशामुळे निर्माण होतात. अशा रंगांना वर्णपटीय रंग असे म्हणतातपरंतु मानवी डोळ्यांना विशिष्ट वर्णाची संवेदना जशी एका विशिष्ट तरंगलांबीच्या प्रकाशामुळे होऊ शकते तशीच ती वेगवेगळ्या वर्णांच्या सुयोग्य मिश्रणापासूनही होऊ शकते. तेव्हा डोळ्याला प्रतीत होणारा वर्ण हा विशिष्ट तरंगलांबीच्या प्रकाशाचे गमक आहे,असे मानता येत नाही. [→ वर्ण व वर्णमापन].

प्रकाशदाब (किंवा प्रारणदाब) : एखाद्या पृष्ठावर प्रकाश पडतो तेव्हा त्या पृष्ठावर प्रकाशाचा अत्यल्प असा दाब पडतो. त्याला प्रकाशदाब असे म्हणतात. संवेदनशील उपकरणाच्या साहाय्याने त्याचे मापनही करता येते. पृथ्वीच्या पृष्ठभागावर सूर्यप्रकाशाचा पडणारा दाब सु. ५·८ X १०^–५ डाइन/सेंमी.^२ इतका असतो. सामान्य परिस्थितीत हा दाब दुर्लक्षणीय असतोपरंतु विशेष परिस्थितीत त्याचा विचार करणे आवश्यक असते. ताऱ्यांच्या अंतर्भागातील समतोलाचा विचार करताना वायुदाबाबरोबरच प्रारणदाबही लक्षात घ्यावा लागतो. धूमकेतूंची पुच्छे सूर्याच्या विरुद्ध दिशेला वळलेली दिसतात ती पुच्छातील अतिसूक्ष्म कणावर पडणाऱ्या प्रारणादाबामुळेच.

संवेग : (द्रव्यमान X वेग या राशीने निर्दिष्ट होणारा गुणधर्म). प्रकाशदाबावरून असा निष्कर्ष निघतो की,प्रकाशाला संवेगही असला पाहिजे. प्रकाशाचा किरण म्हणजे प्रकाश-संवेगाचा एक झोतच असे म्हणता येईल.

ऊर्जा : प्रकाशाला ऊर्जा असते हे अनेक ठिकाणी आपल्या प्रत्ययाला येत असते. पदार्थाकडून प्रकाशाच्या ऊर्जेचे शोषण होऊन सामान्यतः त्याचे उष्णतेत रूपांतर होते. सूर्यप्रकाशाने जमीन तापते ती यामुळेच.

द्रव्याबरोबर विक्रिया : प्रकाश-ऊर्जेचे द्रव्याकडून शोषण होऊन काही इतर आविष्कार उद्‌भूत होतात. प्रकाशविद्युत् परिणाम (विशिष्ट पदार्थावर प्रकाश पडला असता त्याच्या पृष्ठभागातून इलेक्ट्रॉनांचे उत्सर्जन होणे), ⇨ कॉम्पटन परिणाम,प्रस्फुरण आणि अनुस्फुरण [→ संदीप्ति],⇨ रामन (रमण) परिणाम,उत्तेजित उत्सर्जन [→ लेसर] इ. खास नावे या आविष्कारांना दिलेली असून त्यांच्यासंबंधी अधिक माहिती पुढे दिली आहे.

विवर्तन : स्थूलमानाने प्रकाश सरळ रेषेत जातो असे दिसतेपरंतु प्रकाशाच्या मार्गात एखादा अपारदर्शक अडथळा ठेवल्यास प्रकाश अल्प प्रमाणात अडथळ्याच्या कडेवरून वळून छायाभागात जातो असे सूक्ष्म निरीक्षणानंतर दिसून येते. या आविष्काराला विवर्तन असे म्हणतात. [→ प्रकाशकी].

व्यतिकरण : एकाच प्रकाश उद्‌गमापासून निघणाऱ्या दोन अत्यंत अरुंद प्रकाश-शलाका पडद्यावर एकावर एक अशा एकत्र पडल्यास त्यांच्यामध्ये आंतरक्रिया होऊन पडद्यावर एकाआड एक प्रकाशित व अप्रकाशित पट्ट तयार होतात. या पट्टांना व्यतिकरण पट्ट आणि या आविष्काराला व्यतिकरण असे म्हणतात. [→ प्रकाशकी]. 

ध्रुवण :‘पोलरॉइड’या नावाने बाजारात खास प्रकारच्या पारदर्शक चकत्या मिळतात. विशिष्ट परिस्थितीत अशा दोन चकत्यांमधून मिळून प्रकाश अजिबात बाहेर येऊ शकत नाही. एका पोलरॉइडातून बाहेर आलेला प्रकाश रेखीय ध्रुवीत झाला आहे असे म्हणतात व या वर्गातील काही आविष्कारांना ध्रुवण असे म्हणतात. पोलरॉइडाखेरीज प्रकाशाचे ध्रुवण करणारी अन्य साधनेही उपलब्ध आहेत. [→ प्रकाशकी ध्रुवणमिति].

द्विप्रणमन : कॅल्साइटासारख्या काही स्फटिकांवर प्रकाशाचा एक किरण पडल्यास त्यापासून दोन प्रणमित किरण निर्माण होतात याला द्विप्रणमन असे म्हणतात.  

---

 

रासायनिक परिणाम : कित्येक पदार्थांत प्रकाशाचे शोषण झाल्यामुळे काही रासायनिक विक्रिया घडून येतात. ⇨ छायाचित्रण याच परिणामावर आधारलेले आहे. त्याचप्रमाणे सूर्यप्रकाशात वनस्पती शर्करा व इतर पदार्थाच्या रेणूंचे संश्लेषण करू शकतात तो याच परिणामाचा आविष्कार आहे. [→ प्रकाशसंश्लेषण]. 

ऐतिहासिक पार्श्वभूमी : ख्रिस्तपूर्व सहाव्या शतकात पायथॅगोरस या ग्रीक तत्त्वज्ञांनी ‘प्रकाश म्हणजे आपल्या डोळ्यांतून निघणारे (झुरळाच्या स्पर्शक इंद्रियासारखे) स्पर्शक असावेत आणि विशिष्ट वस्तूला या स्पर्शकांचा स्पर्श झाला म्हणजे ती वस्तू आपणाला दिसल्याची जाणीव होते’,अशी कल्पना मांडली. प्रकाशाबद्दलची ही सर्वांत जुनी अशी ज्ञात कल्पना होय. ख्रिस्तपूर्व तिसऱ्या शतकातील एपिक्यूरस या ग्रीक तत्त्वज्ञांनी ‘वस्तूपासून परावर्तित झालेला प्रकाश डोळ्यात शिरला म्हणजे ती वस्तू आपणाला दिसते’,ही कल्पना मांडल्याचे आढळून येते. त्याच शतकातील यूक्लिड या प्रख्यात गणितज्ञांना ‘आपाती कोन व परावर्तन कोन हे सममूल्य असतात’ हा परावर्तनाचा नियम माहीत होता असे दिसते.

ख्रिस्तोत्तर पहिल्या शतकातील टॉलेमी या सुप्रसिद्ध ज्योतिर्विदांना वातावरणीय प्रणमनामुळे ताऱ्यांच्या व ग्रहांच्या आकाशातील स्थानांत भासमान बदल होतो, हे माहीत होते. प्रणमनाचे नियम सतराव्या शतकात व्हिलेब्रॉर्ट स्नेल या डच शास्त्रज्ञांनी शोधून काढले असे सामान्यतः मानले जाते परंतु त्यांच्या आधी अकराव्या शतकातच अल् हसन या अरब शास्त्रज्ञांना या नियमांचे ज्ञान होते असे दिसते. पंधराव्या शतकात लिओनार्दो दा व्हींची या अष्टपैलू बुद्धीच्या शास्त्रज्ञांनी ‘प्रकाशाचे प्रसारण सरळ रेषेत होते’ ही गोष्ट शोधून काढली. ‘प्रकाशनाचा व्यस्त वर्ग नियम’ योहानेस केप्लर या ज्योतिर्विदांनी सतराव्या शतकात शोधून काढला.  

न्यूटन यांचे कार्य : सतराव्या शतकाच्या उत्तरार्धात न्यूटन (१६४२—१७२७) यांनी आधुनिक प्रकाशकीचा पायाच घातला, असे म्हणता येईल. काचेच्या लोलकातून पांढऱ्या प्रकाशाची शलाका जाऊ दिली असता दुसऱ्या बाजूला सप्तरंगांचा वर्णपट मिळतो. हा सप्तरंगी प्रकाश उलट्या दिक्‌स्थितीत ठेवलेल्या लोलकातून जाऊ दिला असता सप्तरंगांचे एकीकरण होऊन परत पांढरी प्रकाश-शलाका मिळते,हा महत्त्वाचा प्रयोग त्यांनी केलात्यावरून ‘पांढरा प्रकाश हा सप्तरंगांच्या मिश्रणाने बनलेला आहे’ असा निष्कर्ष त्यांनी काढला. याला पुष्टिकारक इतर काही प्रयोगही त्यांनी केले. 

भिंगातून पांढरा प्रकाश जातो तेव्हा अपस्करण होऊन वर्ण विपथन नावाचा दोष उत्पन्न होतो. त्यामुळे ⇨ दूरदर्शकातून दिसणारी प्रतिमा पुरेशी सुस्पष्ट नसते. हा दोष टाळण्यासाठी त्यांनी वस्तुभिंगाच्या ऐवजी अंतर्वक्र आरसा वापरून एक दूरदर्शक तयार केला.

काचेच्या सपाट तबकडीवर बहिर्वक्र भिंग ठेवले असता त्या दोघांच्या मध्यंतरी हवेचा एक बदलत्या जाडीचा पातळ स्तर तयार होतो. सूर्यप्रकाशात या स्तराकडे पाहिल्यास तबकडी व भिंग यांच्या स्पर्शबिंदूभोवती एक रंगीत समकेंद्री (समाईक केंद्र असलेली) वर्तुळ श्रेणी दिसते. हा शोध प्रथम न्यूटन यांनी लावला असल्याने या वर्तुळ श्रेणीला ‘न्यूटन वर्तुळे’असे नाव देण्यात आले आहे (चित्रपट ३८) परंतु या आविष्काराची कोणतीही उपपत्ती न्यूटन यांना देता आली नाही.

प्रकाशाच्या स्वरूपासंबंधीचे विविध सिद्धांत : न्यूटन यांचा कण सिद्धांत : ‘प्रकाश हा अतिसूक्ष्म वस्तुमानरहित अशा कणांचा बननेना आहे’ असा प्रकाशाच्या स्वरूपाबद्दलचा आपला सिद्धांत न्यूटन यांनी मांडला. या सिद्धांतानुसार प्रकाशाचे रेखीय प्रसारण, प्रकाशनाचा व्यस्त वर्ग नियम, छाया-उपच्छाया, परावर्तनाचे नियम इत्यादींची सुसंगत उपपत्ती देता येते. विरल माध्यमातून (हवेसारख्या) सघन माध्यमात (काच किंवा पाणी यासारख्या) प्रवेश करताना प्रकाशकिरण प्रलंबाच्या बाजूला वळतो, असा अनुभव येतो. याचे स्पष्टीकरण कण सिद्धांतानुसार देण्याकरिता ‘प्रकाशाचा वेग विरल माध्यमापेक्षा सघन माध्यमात जास्त असला पाहिजे’ असे त्यांना गृहीत धरावे लागले. (पुढे १८५९ मध्ये जे. बी. एल्. फूको यांनी प्रत्यक्ष मापन करून सघन माध्यमात प्रकाशवेग विरल माध्यमातील प्रकाशवेगापेक्षा कमी असतो असे दाखवून दिले. कण सिद्धांताच्या विरुद्ध हा एक निर्णायक पुरावा मानला जातो). कण सिद्धांताच्या आधारे विवर्तन, व्यतिकरण, ध्रुवण, द्विप्रणमन इ. आविष्कारांचे काहीही स्पष्टीकरण देता येत नाही.

याच कालखंडात ओलाउस रोमर (१६४४—१७१०) या डॅनिश ज्योतिर्विदांनी गुरू या ग्रहाभोवती फिरणाऱ्या चंद्रांच्या ग्रहणांमध्ये जाणारा कालावधी मोजून त्यावरून प्रथम ⇨ प्रकाशवेग निश्चित केला. त्याचप्रमाणे एफ्. एम्. ग्रिमाल्डी (१६१८—६३) या इटालियन शास्त्रज्ञांनी प्रकाशाच्या विवर्तनाचा शोध लावला. 

तरंग सिद्धांत : ‘प्रकाश म्हणजे कोणत्या तरी माध्यमातील तरंग आहेत’ या सिद्धांताचे जनक ख्रिस्तीआन हायगेन्झ (१६२९—९५) हे डच शास्त्रज्ञ न्यूटन यांचे समकालीन होते. हायगेन्झ यांचे प्रतिपादन असे होते की, जर प्रकाशझोत म्हणजे वेगाने जाणाऱ्या कणांचे समूह असतील, तर जेव्हा दोन प्रकाशझोत एकमेकांना छेदतील तेव्हा तेथे या कणांच्या परस्परांशी टकरा होऊन काही वेगळे परिणाम घडून यावयास पाहिजेत परंतु तसे काही होताना आढळून येत नाही. त्या अर्थी प्रकाश हा वेगाने जाणाऱ्या कणांच्या स्वरूपाचा नसला पाहिजे.

हायगेन्झ तत्त्व : तरंग सिद्धांतानुसार परावर्तन, प्रणमन इ. आविष्कारांचे स्पष्टीकरण देता यावे यासाठी हायगेन्झ यांनी हे सुप्रसिद्ध तत्त्व मांडले. कोणत्याही तरंगमुखाची [→ तरंग गति] एका विशिष्ट क्षणीची स्थिती व आकार ज्ञात असल्यास या तत्त्वाच्या साहाय्याने त्या तरंगमुखाची पुढील कोणत्याही क्षणीची स्थिती व आकार निश्चित करता येतात. त्याचप्रमाणे भिंगे व आरसे यांच्यामुळे निर्माण होणाऱ्या प्रतिमा कोठे व कशा स्वरूपाच्या असतील तेही काढता येते. हे तत्त्व दोन भागांत पुढे दिल्याप्रमाणे मांडता येईल : (१) कोणत्याही तरंगमुखावरील प्रत्येक बिंदू हा नवीन (दुय्यम) प्रकाश उद्‌गमासारखे कार्य करतो. म्हणजेच त्याच्यापासून नव्याने दुय्यम तरंग निघून ते सर्व दिशांना प्रसारित होतात. (२) विशिष्ट क्षणी अशा सर्व दुय्यम तरंगांना स्पर्श करणारे पृष्ठ हीच त्या तरंगमुखाची त्या क्षणीची स्थिती होय. [→ प्रकाशकी].

हे तरंग एका सर्वव्यापी द्रव माध्यमात प्रसारित होत असावेत व द्रव माध्यमात असल्यामुळे ते अनुतरंग (माध्यमाच्या कणांचे कंपन तरंग प्रसारणाच्या दिशेतच होणारे तरंग) असावेत,असे हायगेन्झ यांचे मत, होते परंतु या माध्यमाच्या कल्पनेचे फारसे स्पष्टीकरण करण्याचा हायगेन्झ यांनी प्रयत्न केला नाही.

हायगेन्झ तत्त्वाचा उपयोग करून परावर्तन व प्रणमनामुळे विविध परिस्थितींत निर्माण होणाऱ्या प्रतिमांची स्थाने व स्वरूपे निश्चित करता येतात. परावर्तन व प्रणमन यांच्या नियमांची उपपत्ती देता येते. इतकेच नाही,तर द्विप्रणमन, व्यतिकरण, विवर्तन या आविष्कारांचाही सुसंगत उलगडा करता येतो.

ईथराची कल्पना : हायगेन्झ यांनी तरंग सिद्धांताचा पाया घातला. त्यात अनेक तपशीलांचा अभ्यास करून टॉमस यंग (१७७३—१८२९) व ए. जे. फ्रेनेल (१७८८—१८२७) यांनी महत्त्वाची भर घातली व तरंग सिद्धांत भक्कमपणे प्रस्थापित केला. ध्रुवण झालेल्या प्रकाशझोतांच्या व्यतिकरणासंबंधीच्या स्वतः केलेल्या प्रयोगावरून फ्रेनेल यांनी तरंग सिद्धांतात एक महत्त्वाची सुधारणा केली. त्यांच्या या प्रयोगावरून त्यांनी असे दाखविले की,प्रकाश हा अनुतरंगरूपी नसून अवतरंगरूपी (ज्यात माध्यमाच्या कणांचे कंपन तरंग प्रसरणाच्या दिशेशी लंब दिशेत होते अशा तरंगांच्या स्वरूपाचा) आहे परंतु अवतरंग हे फक्त घनरूप माध्यमात प्रसारित होऊ शकतात. तेव्हा प्रकाशतरंग ज्या माध्यमातून प्रसारित होतात (या काल्पनिक माध्यमाला ईंथर हे नाव देण्यात आले होते) ते माध्यम घनरूप आहे,असा बुद्धीला न पटणारा निष्कर्ष यावरून निघतो.

---

  

पृथ्वी सूर्याभोवती मोठ्या वेगाने (२९·६ किमी./से.) फिरत असून त्याचबरोबर सबंध सूर्यमाला हर्क्युलस या तारकासमूहाच्या दिशेने प्रचंड वेगाने (२२० किमी./से.) जात आहे. स्थिर अशा घनरूप ईथरामधून जाताना पृथ्वीला किंवा सूर्यमालेला काहीच विरोध कसा होत नाही? त्याचप्रमाणे या ईथरसापेक्ष पृथ्वीच्या गतीमुळे प्रकाशवेगावर काही परिणाम झाला पाहिजे. हा परिणाम मोजण्यासाठी १८८७ मध्ये ए. ए. मायकेलसन व ई. डब्ल्यू. मॉर्ली यांनी आपले विख्यात प्रयोग केले. या प्रयोगांवरून असे निष्पन्न झाले की, पृथ्वीच्या गतीचा प्रकाशवेगावर काहीही परिणाम होत नाही. यामुळे ईथराच्या कल्पनेला कायमची मूठमाती द्यावी लागली परंतु तरंग प्रसारणासाठी माध्यम हे आवश्यक असल्याने तरंग सिद्धांतापुढे हा एक मोठाच कूटप्रश्न शिल्लक राहिला. [→ ईथर–२].

विद्युत् चुंबकीय तरंग : इ. स. १८६४ मध्ये जे. सी. मॅक्सवेल यांनी त्यांची सुप्रसिद्ध ‘मॅक्सवेल समीकरणे’ प्रसिद्ध केली [→ मॅक्सवेल विद्युत् चुंबकीय समीकरणे]. या समीकरणांवरून असे स्पष्ट होते की, निर्वातातून प्रत्यावर्ती (ठराविक कालावधीने ज्यांची दिशा व परिमाण उलटसुलट होते अशा) विद्युत् व (त्याच्याशी संलग्न अशा) चुंबकीय क्षेत्रांचे प्रसारण होऊ शकते. अशा वेळी निर्वातात या क्षेत्रांच्या प्रसारणाचा वेग बरोबर निर्वातातील प्रकाशवेगाइतकाच (= c)असतो. यासंबंधीच्या अवकल समीकरणाचे एकूण स्वरूप या वेगाने प्रसारित होणाऱ्या तरंग गतीच्या समीकरणासारखेच हुबेहूब असते. त्यावरून अशा तऱ्हेने प्रसारित होणाऱ्या परस्परसंलग्न प्रत्यावर्ती विद्युत् चुंबकीय क्षेत्रांना ⇨ विद्युत् चुंबकीय तरंग असे नाव देण्यात आले.

येथे एक महत्त्वाचा मुद्दा लक्षात घेणे आवश्यक आहे तो हा की, विद्युत् चुंबकीय तरंगांमध्ये कुठल्याच प्रकारच्या कणांची आंदोलने होत नसतात. त्यामुळे त्यांच्या प्रसारणाकरिता कोणत्याही माध्यमाची अपेक्षा नाही. विद्युत् चुंबकीय तरंगात विद्युत् क्षेत्राच्या (व चुंबकीय क्षेत्राच्याही) तीव्रतेचे मूल्य प्रत्यावर्ती पद्धतीने बदलत असते व अशी क्षेत्रे संपूर्ण निर्वातातून प्रसारित होऊ शकतात.

विद्युत् चुंबकीय तरंगांचा वेग प्रकाशवेगाइतकाच असल्यामुळे प्रकाश हा विद्युत् चुंबकीय तरंगरूप तर नाहीना,अशा कल्पनेचा जन्म झाला. १८८७ च्या सुमारास एच्. आर्. हर्ट्‌झ यांनी धातूच्या दोन गोलकांमधील लहान फटीतून विद्युत् स्फुल्लिंगाची मालिका जाऊ दिली व त्यामुळे सभोवताली विद्युत् चुंबकीय तरंग प्रसारित होतात हे प्रत्यक्ष प्रयोगाद्वारे सिद्ध केले. म्हणून या तरंगांना हर्ट्‌झियन तरंग असेही म्हणत. प्रारंभीच्या काळात रेडिओ संदेशवहनासाठी हर्ट्‌झ यांच्या पद्धतीचा अवलंब केला जात असे. पुढे प्रयोगावरून असे दिसून आले की, प्रकाशाचे खास असे कित्येक आविष्कार (उदा.,प्रसारणाचा वेग, प्रणमन व परावर्तनाचे नियम, व्यतिकरण, विवर्तन) हर्ट्‌झियन तरंगांच्या बाबतीतही अनुभवाला येतात. इतकेच नाही, तर प्रकाश उद्‌गम तीव्र विद्युत् क्षेत्रात किंवा चुंबकीय क्षेत्रात ठेवल्यास उद्‌गमापासून मिळणाऱ्या वर्णपटातील रेषांचे विभाजन होते असे दिसून आले. या परिणामांना अनुक्रमे ⇨ श्टार्क (स्टार्क) परिणाम (योहानेस श्टार्क यांच्या नावावरून) व झीमान परिणाम (पीटर झीमान यांच्या नावावरून) अशी नावे देण्यात आली आहेत. त्याचप्रमाणे प्रकाश ज्या माध्यमातून जात असतो त्या माध्यमाला तीव्र विद्युत् किंवा चुंबकीय क्षेत्र लावल्यास त्याचे प्रकाशावर काही खास परिणाम होतात,असे दिसून आले आहे [→ प्रकाशकी]. या सर्व पुराव्यांवरून प्रकाश हा विद्युत् चुंबकीय तरंगरूपच आहे असे निश्चितपणे म्हणता येते.

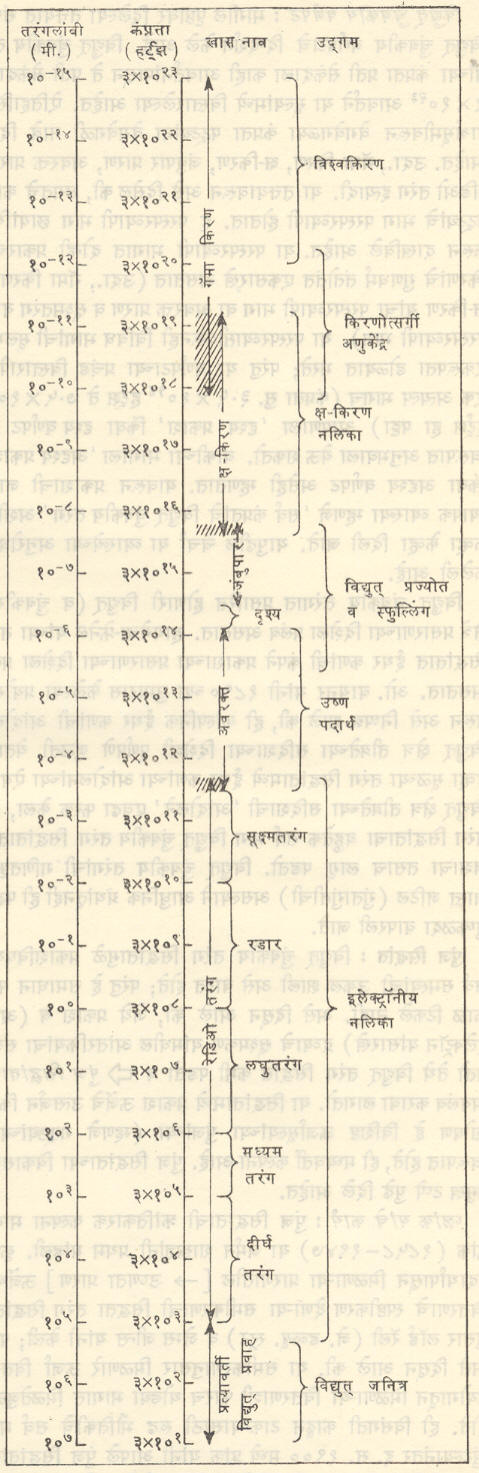
विद्युत् चुंबकीय वर्णपट : मागील पृष्ठावर दिलेल्या तक्त्यात संपूर्ण विद्युत् चुंबकीय वर्णपटाचे दिग्दर्शन केले आहे. विद्युत् चुंबकीय तरंगांच्या कंप्रता प्रती सेकंदाला २ X १०^२३ आवर्तने या मूल्यांमध्ये विस्तारलेल्या आहेत. ऐतिहासिक पार्श्वभूमीवरून वेगवेगळ्या कंप्रता पट्ट्यांना वेगवेगळी नावे दिली आहेत. उदा., गॅमा किरण, क्ष-किरण, जंबुपार प्रारण, अवरक्त प्रारण, रेडिओ तरंग इत्यादी.या तक्त्यावरून असे दिसेल की, लगतचे काही पट्ट्यांचे भाग परस्परव्यापी होतात. हे परस्परव्यापी भाग छायांकित करून दाखविले आहेत. या परस्परव्यापी भागात दोन्ही प्रकारच्या किरणांचे गुणधर्म तंतोतंत एकसारखे असतात (उदा.,गॅमा किरण व क्ष-किरण यांचा परस्परव्यापी भाग वा अवरक्त प्रारण व सूक्ष्मतरंग यांचे परस्परव्यापी भाग). या परस्परव्याप्तीवरूनही विविध भागांची मूलभूत एकरूपता डोळ्यात भरते परंतु या वर्णपटाच्या प्रचंड विस्तारापैकी एक अत्यल्प भागच (कंप्रता सु. ३·५ X १०^१४ हर्ट्‌झ ते ७·५ X १०^१४ हर्ट्‌झ हा पट्टा) आपणाला ‘दृश्य प्रकाश’ किंवा दृश्य वर्णपट या स्वरूपात अनुभवाला येऊ शकतो. बाकीच्या भागाला ‘अदृश्य प्रकाश’ किंवा अदृश्य वर्णपट असेही म्हणतात. यावरून प्रकाशाची जास्त व्यापक व्याख्या म्हणजे ‘सर्व कंप्रतांचे विद्युत् चुंबकीय तरंग’अशीही केव्हा केव्हा दिली जाते. यापुढील चर्चा या व्याख्येच्या अनुरोधाने केलेली आहे.

विद्युत् चुंबकीय तरंगात प्रसारित होणारी विद्युत् (व चुंबकीय) क्षेत्रे प्रसारणाच्या दिशेला प्रलंब असतात. हायगेन्झ-फ्रेनेल यांच्या तरंग सिद्धांतात ईथर कणांची कंपने प्रकाशाच्या प्रसारणाच्या दिशेला प्रलंब असतात. ओ. वायनर यांनी १८९० च्या सुमारास केलेल्या प्रयोगांवरून असे निष्पन्न झाले की, ही काल्पनिक ईथर कणांची आंदोलने विद्युत् क्षेत्र तीव्रतेच्या सदिशाच्या दिशेशी पूर्णपणे जुळती येतात. तेव्हा मूळच्या तरंग सिद्धांतामध्ये ईथर कणांच्या आंदोलनांच्या ऐवजी विद्युत् क्षेत्र तीव्रतेच्या सदिशाची ‘आंदोलने’ एवढा फरक केला, तर तरंग सिद्धांताचा बहुतेक सर्व भाग विद्युत् चुंबकीय तरंग सिद्धांतातही जशाचा तसाच लागू पडतो. विद्युत् चुंबकीय तरंगांची गणितकृत्ये जास्त जटिल (गुंतागुंतीची) असल्याने आधुनिक ग्रंथांतूनही ही पद्धत पुष्कळदा वापरली जाते.

पुंज सिद्धांत : विद्युत् चुंबकीय तरंग सिद्धांतामुळे प्रकाशविषयक सर्व समस्यांची उकल झाली असे वाटत होते परंतु हे समाधान फार काळ टिकले नाही. असे दिसून आले की, जेथे प्रकाश व (अणू, इलेक्ट्रॉन यांसारख्ये) द्रव्याचे सूक्ष्मकण यांमधील आंतरक्रियांचा संबंध येतो तेथे विद्युत् तरंग सिद्धांत कमी पडतो व ⇨ पुंज सिद्धांताचा अवलंब करावा लागतो. या सिद्धांतामध्ये प्रकाश ऊर्जेचे उत्सर्जन किंवा शोषण हे विशिष्ट ऊर्जामूल्यांच्या पुंजांच्या (म्हणजे गठ्ठ्यांच्या) स्वरूपात होते, ही मध्यवर्ती कल्पना आहे. पुंजे सिद्धांताच्या विकासाचे प्रमुख टप्पे पुढे दिले आहेत.

प्लांक यांचे कार्य : पुंज सिद्धांताची क्रांतिकारक कल्पना माक्स प्लांक (१८५८—१९४७) या जर्मन शास्त्रज्ञांनी प्रथम मांडली. कृष्ण पदार्थापासून मिळणाऱ्या प्रारणातील [→ ऊष्णता प्रारण] ऊर्जेच्या वितरणाचे स्पष्टीकरण देणाऱ्या समीकरणाची सिद्धता तरंग सिद्धांतानुसार लॉर्ड रॅली (जे. डब्ल्यू. स्ट्रट) व जेम्स जींन्स यांनी केली परंतु असे दिसून आले की, या समीकरणानुसार मिळणारे ऊर्जा वितरण प्रयोगातून मिळणाऱ्या वितरणाशी फारच थोड्या भागात मिळतेजुळते होते. ही विसंगती काढून टाकण्यासाठी रूढ भौतिकीचे सर्व मार्ग खुंटल्यानंतर इ. स. १९०० मध्ये प्लांक यांनी आपले पुंज सिद्धांतांवर आधारलेले समीकरण प्रसिद्ध केले व ते संपूर्णपणे प्रयोगाशी सुसंगत आहे असे दिसून आले. या समीकरणातील मध्यवर्ती कल्पना म्हणजे ν या कंप्रतेच्या प्रारणाचे उत्सर्जन (व शोषण) hν या ऊर्जामूल्याच्या पुंजांच्या स्वरूपात होत असते (येथे h =६·६२५६ X१०^-३४ जूल-सेकंद, हा प्लांक विश्व स्थिरांक होय). या पुंजाला पुढे ‘फोटॉन’हे नाव देण्यात आले [→ फोटॉन]. शब्दशः फोटॉन म्हणजे ‘प्रकाशकण’ होय. पुढे १९२४ मध्ये सत्येंद्रनाथ बोस या भारतीय शास्त्रज्ञांनी प्लांक सूत्राची सिद्धता देण्यासाठी एक अगदी वेगळी व सोपी पद्धत प्रसिद्ध केली. अर्थात या पद्धतीतही पुंज सिद्धांताचाच वापर केलेला आहे.

प्रकाशविद्युत् परिणाम : कित्येक धातूंवर सुयोग्य कंप्रतेचा प्रकाश पाडल्यास त्या धातुपृष्ठातून इलेक्ट्रॉनांचे उत्सर्जन होते. या आविष्काराला प्रकाशविद्युत् परिणाम असे म्हणतात [→ प्रकाशविद्युत्]. सामान्यतः उत्सर्जित होणाऱ्या इलेक्ट्रॉनांची संख्या आपाती प्रकाशाच्या तीव्रतेच्या सम प्रमाणात असते परंतु आपाती प्रकाशाची कंप्रता विशिष्ट (ν_० या तलसीमा कंप्रतेपेक्षा) मूल्यापेक्षा कमी असेल,तर प्रकाश तीव्रता कितीही वाढविली,तरी इलेक्ट्रॉनांचे उत्सर्जन होऊ शकत नाही. याउलट आपाती प्रकाशाची कंप्रता ν_० पेक्षा जास्त असेल, तर त्याची तीव्रता कितीही कमी असली,तरी प्रकाश पडल्याबरोबर, ताबडतोब (३ x १०^-९ सेकंदापेक्षा कमी वेळात) इलेक्ट्रॉनांचे उत्सर्जन होते. विद्युत् चुंबकीय तरंग सिद्धांतानुसार प्रकाशाची ऊर्जा सबंध तरंगमुखावर पसरलेली असून त्यापैकी अत्यल्प भागच विशिष्ट अणूवर पडू शकेल. त्या अणूकडून ऊर्जेचे शोषण होऊन इलेक्ट्रॉनाचे उत्सर्जन होण्यापुरतीच ऊर्जा साठण्याला कित्येक तासांचा किंवा दिवसांचा अवधी जावा लागेल. त्याचप्रमाणे उत्सर्जित इलेक्ट्रॉनाची कमाल गतिज ऊर्जा विद्युत् चुंबकीय तरंग सिद्धांतानुसार प्रकाश तीव्रतेवर अवलंबून असावयाला हवी परंतु प्रत्यक्षात ती प्रकाशाच्या कंप्रतेवर अवलंबून आहे असे आढळते. एकंदरीत पाहता या आविष्कारात विद्युत् चुंबकीय तरंग सिद्धांत कमी पडतो. १९०५ मध्ये आइन्स्टाइन यांनी या परिणामाचे संपूर्णपणे समाधानकारक स्पष्टीकरण दिले. या स्पष्टीकरणात ν या कंप्रतेच्या प्रकाशाचे शोषण hν ऊर्जामूल्याच्या पुंजांच्या किंवा फोटॉनांच्या स्वरूपात होते हीच मूलभूत कल्पना आहे. यामुळे पुंज सिद्धांताला अधिक मान्यता मिळू लागली.

---

  

बोर यांची परिकल्पना : विशिष्ट परिस्थितीत अणूपासून उत्सर्जित होणाऱ्या प्रकाशाच्या वर्णपटात काही निश्चित कंप्रतांच्या वर्णरेषा मिळतात [→ वर्णपटविज्ञान]. या वर्णरेषांची उत्पत्ती कशी होते, याचे सुयोग्य स्पष्टीकरण विद्युत् चुंबकीय तरंग सिद्धांतानुसार देता येत नव्हेत.

नील्स बोर यांनी १९१३ मध्ये हायड्रोजनाच्या वर्णपटाच्या उपपत्तीबदल एक नवीन परिकल्पना मांडली [→ अणू व आणवीय संरचना]. तिच्या साहाय्याने वर्णपटाविषयीच्या अनेक कूटप्रश्नांची चांगल्या तऱ्हेने उकल करता येऊ लागली. या परिकल्पनेमध्येही ‘प्रकाशाचे उत्सर्जन (व शोषण) हे प्रकाशपुंजांच्या स्वरूपात होते’ हे एक महत्त्वाचे गृहीतक होते.

कॉम्पटन परिणाम : कमी अणुभाराच्या अणूवर ν या कंप्रतेची क्ष-किरण शलाका पाडली असता त्या अणूमधून एक इलेक्ट्रॉन बाहेर फेकला जातो व त्याचबरोबर ν’ या (ν’ &lt ν) कंप्रतेच्या क्ष-किरणाचे प्रकीर्णन (विखुरणे) होते. याला ⇨ कॉम्पटन परिणाम असे म्हणतात. आपाती व प्रकीर्णित क्ष-किरण हे फोटॉनस्वरूपी आहेत असे मानूनच या परिणामातील वैशिष्ट्यांची समाधानकारक उपपत्ती देता येते. त्याचप्रमाणे ⇨ रामन (रमण) परिणामाचे स्पष्टीकरणही फक्त पुंज सिद्धांतांनुसारच करता येते. सारांश, वरील सर्व आविष्कारांत निर्विवादपणे प्रकाश हा पुंजात्मक किंवा कणस्वरूपी आहे, असे आढळून येते.  

फोटॉनाचे काही विशेष : फोटॉन म्हणजे प्रकाशकण असे जरी असले, तरी सर्वसामान्य कणापेक्षा (उदा., धुळीचा कण) तो बराच वेगळा आहे. वर म्हटल्याप्रमाणे ν या कंप्रतेच्या फोटॉनाची ऊर्जा E = hν इतकी असते. फोटॉनाला कणाप्रमाणेच रेखीय व कोनीय संवेगही असतात. ν कंप्रतेच्या फोटॉनाची रेखीय संवेग 

p =	hν	=	h	इतका असतो. (c प्रकाशवेग, λ प्रकाशाची तरंगालांबी =	c	).
	c		λ		ν

वृत्त ध्रुवित प्रकाशाच्या (प्रकाशकी) फोटॉनाचा कोनीय संवेग j =	h	असतो.
	2π

हे सर्व (कणासारखे) गुणधर्म प्रयोगांच्या कसोटीला उतरतात व या अर्थाने त्याला कण मानता येते.

आइन्स्टाइन यांच्या E = mc²या समीकरणानुसार फोटॉनाचे वस्तुमान

m =	E	=	hν	=	p	इतके येते
	c2		c2		c

परंतु हे वस्तुमान c या वेगाने जाणाऱ्या फोटॉनाचेच वस्तुमान आहे व फोटॉन नेहमीच या वेगाने जात असतो. फोटॉनाचे शून्यगति-वस्तुमान शून्यच असते, हे ⇨ सापेक्षता सिद्धांतानुसार दाखविता येते. सर्वसामान्य कणाप्रमाणे फोटॉनांनाही ऊर्जा, रेखीय संवेग व कोनीय संवेग यांच्या अक्षय्यतेचे सिद्धांत लागू पडतात. [→ द्रव्य आणि ऊर्जा यांची अक्षय्यता संवेगाची अक्षय्यता].

एकवर्णी प्रकाश  :शास्त्रशुद्ध दृष्टीने एकवर्णी प्रकाश म्हणजे कोणत्याही एका निश्चित कंप्रतेचा (किंवा निश्चित तरंगलांबीचा) प्रकाश होय. रेखा वर्णपटात [→ वर्णपटविज्ञान] मिळणारी एखादी वर्णरेषा ही एका निश्चित कंप्रतामूल्याची आहे असे सामान्यतः मानले जाते परंतु ते केवळ स्थूलमानानेच खरे असते. कोणत्याही ν या (नामधारी) कंप्रतेच्या वर्णरेषेती कंप्रता ν +¹/₂ Δ ν व ν –¹/₂ Δν या मर्यादांत असते. Δν ला वर्णरेषेची जाडी असे म्हणतात. आदर्श एकवर्णी प्रकाश म्हणजे अनंत लांबीची तरंगमाला असावयास हवी परंतु प्रत्यक्षात मर्यादित लांबीच्या तरंगमाला उत्सर्जित होत असतात व अशी तरंगमाला फक्त एकच कंप्रतामूल्याची असू शकत नाही, हे गणिताने दाखविता येते. यामुळे कितीही काळजी घेतली, तरी वर्णरेषेला काही थोडीशी जाडी असणे अपरिहार्य आहे, हे गणिताने सिद्ध करता येते. वर्णरेषेची मूलभूत जाडी ही ती रेषा उत्सर्जित करणाऱ्या अणूंची संबंधित क्षुब्धावस्था किती काळ टिकू शकते यावर अवलंबून असते. क्षुब्धावस्थेचा सरासरी काळ सु. १०^–८ से. असतो व त्यामुळे वर्णरेषेची मूलभूत जाडी सु. १०^–८ हर्ट्‌झ येते. या १०^–८ सेकंदभर एकाच फोटॉनाचे उत्सर्जन होत होते असे मानल्यास, फोटॉनाची ‘लांबी’= प्रकाशवेग x १०^–८ से.= ३ मी. (सुमारे). ही लांबी म्हणजे फोटॉनाच्या स्थानामधील अनिश्चितता (Δx) आहे व ती Δν च्या व्यस्त प्रमाणात असते परंतु

फोटॉनाच्या संवेगातील अनिश्चितता Δp=	hΔν	. यावरून इलेक्ट्रॉनसारख्या कणाप्रमाणेच
	c

फोटॉनांनाही ⇨ अनिश्चिततेचे तत्त्व लागू पडते हे लक्षात येईल.

फोटॉनाचा वेग : कोणत्याही माध्यमात फोटॉनांचा वेग नेहमी c म्हणजे निर्वातातील प्रकाशवेगाइतकाच असला पाहिजे परंतु प्रयोगावरून असे सिद्ध होते की, पदार्थीय माध्यमात प्रकाशाचा वेग c पेक्षा कमी असतो. या विसंगतीचे निराकरण करण्यासाठी असे सुचविण्यात आले आहे की, प्रत्यक्षात फोटॉनांचा पदार्थीय माध्यमातलाही वेग c इतकाच असतो परंतु अशा माध्यमातून जात असताना मार्गातील पदार्थाच्या अणूंकडून फोटॉनाचे पुनःपुन्हा लागोपाठ शोषण व पुनरुत्सर्जन होत जाते. या क्रियांसाठी जो काही जादा वेळ लागतो त्यामुळे एकंदरीत त्याचा म्हणजेच प्रकाशाचा वेग कमी झाला असे वाटते.

पुंज सिद्धांत व तरंग सिद्धांत यांमधील विरोधाभास : वरील विवेचनावरून असे लक्षात येईल की, ध्रुवण, व्यतिकरण, विवर्तन इ. आविष्कारांच्या संदर्भात प्रकाश तरंगरूपच आहे असे वाटते. उलट प्रकाशविद्युत् परिणाम किंवा कॉम्पटन परिणाम यासारख्या आविष्कारात प्रकाशाचे पुंज-स्वरूपच उठावदारपणे व्यक्त होते. मग साहजिकच असा प्रश्न उभा राहातो की, प्रकाशाचे नक्की स्वरूप कोणते आहे? तरंग की पुंज?

 प्रतिमाने व त्यांच्या मर्यादा : भौतिकीमधील कित्येक परिकल्पना स्पष्ट करण्यासाठी काही प्रतिमानांचा (मॉडेल्सचा) उपयोग केला जातो. विशिष्ट आविष्काराचे सुलभतेने आकलन होण्यासाठी तत्संबंधित प्रतिमान उपयोगी पडते ही गोष्ट खरीच. तरीही तो आविष्कार आणि त्याचे प्रतिमान यांमध्ये संपूर्णपणे एक एकरूपता नसते, ही गोष्ट लक्षात ठेवणे जरूर आहे.

‘सुंदर स्त्रीचे मुख कमलासारखे आहे’ असे कवी म्हणतो तेव्हा मुख व कमल यांच्यामध्ये कोमलता, सौंदर्य अशा काही बाबतींतच समानता असते. ‘कमलाप्रमाणे मुखाला पाकळ्या कोठे आहेत’? असा प्रश्न आपण उभा करीत नाही. त्याचप्रमाणे तरंगसिद्धांताचा विचार करताना प्रकाशाचे कित्येक गुणधर्म तरंगांसारखे आहेत, इतकाच मर्यादित अर्थ घ्यावयास हवा. हीच गोष्ट फोटॉन सिद्धांतालाही लागू आहे. फोटॉन हा काही सर्वस्व सर्वसामान्य कणासारखा कण नाही, तर काही प्रयोगांत त्याचे गुणधर्म कणासारखे आढळतात, इतकाच मर्यादित अर्थ घेणे जरूर आहे. फोटॉन व तरंग ही प्रकाशाच्या स्वरूपाचे आकलन होण्यासाठी वापरलेली केवळ प्रतिमाने आहेत. दुर्दैवाने वेगवेगळ्या परिस्थितींत कण किंवा तरंग या दोहोंचेही गुणधर्म दाखविणारी रोजच्या परिचयातली एखादी गोष्ट आपणाला उपलब्ध नाही. त्यामुळे असे दुहेरी प्रतिमान स्वीकृत करावे लागले आहे परंतु गणिती समीकरणांच्या भाषेत या दोन्ही स्वरूपांचा सांगड घालता येते व तोच पुंज सिद्धांताचा मुख्य आशय आहे. 

 प्रयोग सापेक्षता : विशिष्ट परिस्थितीत प्रकाशाचे कोणते स्वरूप आपणास प्रतीत होईल किंवा कोणते प्रतिमान जास्त समर्पक होईल, ते त्या प्रयोगाच्या स्वरूपावर अवलंबून राहते. व्यतिकरण किंवा विवर्तन यासारख्या प्रयोगात तरंगस्वरूपच मनावर ठसते, तर प्रकाशविद्युत् परिणाम किंवा कॉम्पटन परिणाम यासारख्या प्रयोगात फोटॉन स्वरूप जास्त उठावदार होते.

‘हत्ती आणि सात आंधळे’या प्रसिद्ध कथेच्या साहाय्याने हा मुद्दा कदाचित अधिक स्पष्ट होऊ शकेल. हत्तीचे खरे स्वरूप कसे आहे ते ठरविण्यासाठी सात आंधळे हत्तीला चाचपून पाहू लागले व ज्याच्या हाती जो अवयव (उदा., पाय, शेपटी इ.) लागला त्यानुसार त्याने हत्तीचे वर्णन (उदा., खांबासारखा, दोरीसारखा इ.) केले परंतु डोळस माणूस असे म्हणेल की, ‘हत्तीच्या बाबतीत ही सर्व वर्णने अंशतःच खरी आहेत. हत्तीचे प्रत्यक्ष स्वरूप या सर्व वर्णनांपेक्षा खूपच वेगळे आहे’. या आंधळ्यांप्रमाणेच प्रकाशविषयक प्रयोगांत आपली परिस्थिती आहे.

पूरकतेचे तत्त्व : वस्तुतः तरंगत्व व कणत्व हे प्रकाशाच्या बाबतीत परस्पर पूरक असे भाव आहेत. यांतील कोणत्याही एकाच्या साहाय्याने प्रकाशाचे संपूर्णपणे अभिज्ञान होऊ शकत नाही. सम्यक्‌ज्ञानासाठी या दोहोंचीही एकमेकांना जोड देणे आवश्यक आहे. हे पूरकतेचे तत्त्व बोर यांनी १९२८ मध्ये मांडले. बोर यांच्या प्रतिपादनानुसार, प्रकाशाचे हे दोन्ही भाव एकाच प्रयोगात व्यक्त होईल असा प्रयोग प्रत्यक्षात तर नाहीच पण कल्पनेतसुद्धा करणे अशक्य आहे. हे त्यांचे प्रतिपादन डब्ल्यू. के. हायझेनबेर्क यांच्या अनिश्चिततेच्या तत्त्वावर आधारलेले आहे.

अगदी आदर्श प्रयोगाद्वारे आपण फोटॉनाचे स्थान निश्चित करण्याचा प्रयत्न करीत आहो अशी कल्पना करा. मग त्याच्या स्थानामधील अनिश्चितता Δx आपण कमीत कमी करण्याची कोशीस करू (स्थान हा एक कणाचा विशेष गुण आहे म्हणजे येथे आपण कण जास्त निश्चित करण्याचा प्रयत्न करीत आहोत) परंतु Δx जसे कमी होईल तशी संवेगातील अनिश्चितता Δ p वाढेल. कारण अनिश्चितता तत्त्वानुसार

Δ x · Δ p ≥	h	परंतु संवेग p =	h	.
	2π		λ

त्यातील अनिश्चितता काढणे म्हणजे तरंगलांबी λ जास्त अनिश्चित होणे म्हणजेच तरंगत्त्वाचा भाव जास्त अस्पष्ट होणे. याउलट तरंगलांबी जास्त अचूकपणे मोजू पाहिल्यास त्यामुळे Δx वाढते व फोटॉनाचे स्थान नक्की कोठे ते समजणे अशक्य होते, म्हणजेच कणत्व अस्पष्ट होते. अशा प्रकारचे दोन काल्पनिक आदर्श प्रयोग (वैचारिक प्रयोग) बोर यांनी चर्चिले असून त्यांवरून त्यांनी आपले पूरकतेचे तत्त्व प्रस्थापित केले आहे.

समर्पकतेची क्षेत्रे : पुंज व तरंग यांपैकी कोणते प्रतिमान केव्हा जास्त समर्पक होते याबद्दल बोर यांनी मार्मिक चर्चा केली आहे. त्यांच्या मते पुंज व तरंग यांना जोडणारा दुवा म्हणजे h हा प्लांक स्थिरांक होय.

वर दाखविल्याप्रमाणे p =	h	. यावरून h = pλ हे समीकरण मिळते.
	λ

उजव्या बाजूचे p हे पद म्हणजे संवेग असून ते कणत्वाचे प्रतिनिधित्व करते. λ म्हणजे तरंगत्वाचा प्रतिनिधी होय. या दोहोंचा गुणाकार h हा स्थिरांक असून त्यांचे मूल्य फार अल्प आहे, हे लक्षात घेणे जरूर आहे.  

गॅमा किरण किंवा क्ष-किरण यांच्या बाबतीत तरंगलांबी सर्वांत अल्प व फोटॉन ऊर्जा अती उच्च. त्यामुळे संवेग pचे मूल्य जास्त होते व कणसदृश गुणधर्म प्रकर्षाने प्रत्ययाला येतात. उलट रेडिओ तरंगांच्या तरंगलांब्या फार मोठ्या असतात. त्यामुळे फोटॉन ऊर्जा E व संवेग pचे मूल्य अत्यंत कमी होते व म्हणून रेडिओ तरंगांच्या बाबतीत तरंगात्मक गुणधर्मच फार प्रभावी होतात. दृश्य किरण किंवा जंबुपार किरण यांच्या तरंगलांब्या मध्यम मूल्यांच्या असल्याने त्यांच्या बाबतीत परिस्थितीनुसार केव्हा कणत्व तर केव्हा तरंगत्व असे दोन्ही भाव अनुभवाला येतात.

प्रकाश आणि सापेक्षता सिद्धांत : सापेक्षता सिद्धांतानुसार होणारे काही प्रकाशीय आविष्कार पुढीलप्रमाणे आहेत.

प्रकाशवेग : मायकेलसन-मॉर्ली प्रयोगावरून हे स्पष्ट झाले की, संदर्भाव्यूहाच्या (किंवा निरीक्षक व प्रकाश उद्‌गम यांमधील परस्परसापेक्ष) वेगाचा प्रकाशवेगावर काहीही परिणाम होत नाही परंतु प्रकाशवेगाचे मापन ज्या प्रदेशात केले जात असेल तथील गुरुत्वाकर्षणाच्या परिणामामुळे प्रकाशवेग बदलतो. हा बदल पुढील समीकरणाने व्यक्त केला जातो.

c = c₀ (1 +Φ / c²)

(येथे Φ = — ^GM/_R M वस्तुमानाच्या गुरुत्व मध्यापासून R अंतरावर उत्पन्न होणारे Φ गुरुत्वाकर्षणीय वर्चस् असून त्याचे मूल्य ऋण चिन्हयुक्त आहे. c हा Φगुरुत्वाकर्षणीय वर्चसामधील व c₀हा Φ = 0असतानाचा प्रकाशवेग होय. G = गुरुत्वाकर्षणाचा स्थिरांक = ६·६७X १०^–११ एम. के. एस. एकके). Φ चे मूल्य ऋण असल्यामुळे गुरुत्वाकर्षणीय क्षेत्रात प्रकाशवेग कमी होतो. उदा., सूर्याच्या गुरुर्वाकर्षणामुळे त्याच्या पृष्ठावर प्रकाशवेगात एक लक्ष भागांत ०·२ भाग इतका अल्प बदल होतो. [→ प्रकाशवेग].

  आइन्स्टाइन ताम्रच्युती: प्रकाश उद्‌गम गुरुत्वाकर्षणीय क्षेत्रात असल्यास त्यापासून निघणाऱ्या प्रकाशाची कंप्रता पुढील समीकरणानुसार कमी होते.  

ν = ν0	(	1 +	Φ	)
			c2

(येथे ν₀शून्य मूल्य गुरुत्ववर्चसात व νगुरुत्ववर्चस् असतानाची कंप्रता). यामुळे वर्णपटातील वर्णरेषा तांबड्या रंगाच्या बाजूला सरकल्यासारख्या दिसतात. म्हणून हिला गुरुत्वाकर्षणीय ताम्रच्युती किंवा आइन्स्टाइन ताम्रच्युती असे म्हणतात. सूर्यावरील गुरुत्ववर्चस् पुरेसे उच्च नसल्याने सूर्यावरील ताम्रच्युती मोजता येत नाही परंतु व्याधाचा अंधुक युग्मताऱ्यावर (सिरिअस बी) हे वर्चस् अती उच्च असल्यामुळे त्याच्या वर्णपटातील एका विशिष्ट वर्णरेषेची [बामर βरेषेची → वर्णपटविज्ञान] तरंगलांबी ३X १०^–११ मीटरने वाढल्याचे डब्ल्यू. एस्. ॲडम्स यांना दिसून आले. ही वाढ वरील सूत्राशी मिळतीजुळती आहे. आर्. व्ही. पाउंड व जी. ए. रेब्‌का यांनी १९६० साली (Fe³⁷) या लोहाच्या समस्थानिकापासून (अणुक्रमांक तोच पण भिन्न अणुभार असलेल्या त्याच मूलद्रव्याच्या प्रकारापासून) निघणाऱ्या गॅमा किरणांची कंप्रता पृथ्वीच्या गुरुत्वाकर्षणीय क्षेत्राने किती बदलते, त्याचे ⇨ मॉसबावर परिणामाचा उपयोग करून अत्यंत अचूक मापन केले. तेही वरील सूत्राशी जुळणारेच आले.

किरणाचे विचलन : एखाद्या प्रचंड वस्तुमानाच्या वस्तूजवळून प्रकाशकिरण जात असतो तेव्हा तेथील गुरुत्वाकर्षणीय क्षेत्रामुळे किरण जणू काही त्या वस्तूकडे आकर्षिला गेला आहे अशा तऱ्हेने त्या किरणाच्या दिशेत जो बदल होतो त्याला विचलन असे म्हणतात. यामुळे दूरच्या ताऱ्यापासून पृथ्वीकडे येणारे किरण जेव्हा सूर्याच्या पृष्ठभागाजवळून येत असतील तेव्हा ते थोडेसे सूर्याकडे झुकतात व त्यामुळे त्या ताऱ्याच्या भासमान स्थितीत फरक पडतो. अर्थात अशी निरीक्षणे फक्त खग्रास सूर्यग्रहणाच्या वेळीच शक्य होतात. १९३१ सालच्या सूर्यग्रहणाच्या वेळी केलेल्या मापनानुसार हा विचलन कोन २·२”इतका आढळला. सूत्रानुसार, त्याचे मूल्य १·७५” यावे अशी अपेक्षा होती. अलीकडे ⇨ क्वासारापासून येणाऱ्या रेडिओ तरंगांच्या विचलन कोनाचे मापन करण्यात आले (यासाठी खग्रास सूर्यग्रहणाची आवश्यक नसते) व ते सूत्राबरहुकूम असल्याचे आढळले.

प्रकाशाचे विपथगमन : प्रकाशाचा वेग प्रचंड असला तरी अनंत नाही. त्यामुळे गतिमान निरीक्षकाला दूरच्या ताऱ्यापासून येणाऱ्या प्रकाशकिरणांची दिशा मुळातल्यापेक्षा काहीशी बदललेली दिसते. याला प्रकाशाचे विपथगमन असे म्हणतात. पाऊस उदग्र दिशेने पडत असला, तरी मोटारीतून जाणाऱ्या निरीक्षकाला तो तिरक्या दिशेने येत आहे असे वाटते. तसाच हा प्रकार असून त्याचे स्पष्टीकरण सापेक्षता सिद्धांताच्या मदतीशिवायही करता येते. सूर्याभोवती होत असलेल्या पृथ्वीच्या भ्रमणाचा वेग सु. २९·६ किमी./से. असतो. यामुळे पृथ्वीवरील निरीक्षकाला आकाशातील ताऱ्यांची स्थाने त्यांच्या वास्तविक स्थानांपेक्षा काहीशी वेगळी वाटतात. दूरच्या अगर नजीकच्या ताऱ्यांच्या बाबतीत हा बदल सारख्याच मूल्याचा असतो. जेम्स ब्रॅड्ली यांनी १७२७ मध्ये हा परिणाम शोधून काढला व त्याच्या साहाय्याने प्रकाशवेगही काढला. [→ प्रकाशवेग].

डॉप्लर-फीझो परिणाम : [सी. जे. डॉप्लर व ए. एच्. एल्. फीझो यांच्या नावाने ओळखण्यात येणारा परिणाम → डॉप्लर परिणाम]. निरीक्षकापासून प्रकाश उद्‌गम दूर जात असल्यास त्याच्यापासून येणाऱ्या प्रकाशाची कंप्रता कमी झाल्यासारखी वाटते व त्यामुळे हा उद्‌गम एखादा तारा असल्यास त्याच्या वर्णपटातील वर्णरेषा तांबड्या रंगाकडे सरकलेल्या दिसतात (याच्या उलट परिणाम उद्‌गम निरीक्षकाकडे येत असल्यास होईल). या ताम्रच्युतीवरून विश्वाचे प्रसरण होत आहे हा आश्चर्यकारक निष्कर्ष काढण्यात आला [→ तारा विश्वोत्पत्तिशास्त्र]. या ताम्रच्युतीवरून क्वासारासारख्या अतिदूरच्या ज्योतींची अंतरे अजमावता येतात. अवकाशयाने, क्षेपणास्त्रे इत्यादींचे वेग मोजण्यासाठी या परिणामाचा सर्रास उपयोग केला जात आहे.

द्रव्यीकरण व नष्टीकरण : योग्य परिस्थितीत गॅमा फोटॉनाचे एक इलेक्ट्रॉन व एक ⇨ पॉझिट्रॉन या जोडीत रूपांतर होते. अशा तऱ्हेने ऊर्जेचे द्रव्यात रूपांतर होण्याच्या क्रियेला द्रव्यीकरण असे म्हणतात. याउलट एक इलेक्ट्रॉन व एक पॉझिट्रॉन एकत्र आल्यास ते दोनही कण नष्ट होऊन गॅमा फोटॉनाचे उत्सर्जन होते. यात द्रव्य नष्ट होत असल्यामुळे याला नष्टीकरण असे म्हणतात.

संदर्भ : 1. Ditchburn, R.W. Light, New York, 1963.

            2. Jenikins, F. A. White, H. E. Fundamentals of Optics, New York, 1957.

            3. Levi, Leod Applied Optics, New York, 1968.

           4. Robertson, J. H. Introduction to Optics, New Delhi, 1965.

           5. Ronchi, Vasco, Trans. Barocas, V. The Nature of Light, London, 1970.

           6. Rossi, Bruno Optics, Reading, Mass., 1967.

          7. Wood, R. W. Physical Optics, New York, 1959.

खेर, वि. गो. पुरोहित, वा. ल. 

“