अवकाश – काल

अवकाश-काल : अवकाश व काल या संकल्पना नित्य परिचयाच्या असूनही त्यांच्या व्याख्या करणे अवघड आहे. अवकाश व काल परस्परांपासून स्वतंत्र, निरपेक्ष व अनंत आहेत येथील चालू क्षण सर्वत्र तोच क्षण आहे, दोन घटनांचे काल निरीक्षकाच्या वेगावर अवलंबून असत नाहीत, अशा समजुती एकोणिसाव्या शतकाच्या अखेरीपर्यंत होत्या. परंतु विसाव्या शतकाच्या पहिल्या काही वर्षांतच त्या चुकीच्या आहेत हे सिद्ध झाले. त्यामुळे अवकाश व काल यांचे स्वतःचे स्वतंत्रत्व नष्ट होऊन ‘अवकाश-काल’अशा त्यांच्या युतीलाच अस्तित्व प्राप्त झाले. वस्तूंचा गुणधर्म म्हणून समजले जाणारे गुरुत्वाकर्षण अवकाश-कालाच्या एका भूमितीचा एक गुणधर्म आहे हे दाखविता आले.

यूक्लिडीय भूमिती : ख्रिस्तपूर्व तिसऱ्या शतकात यूक्लिड या गणितज्ञांनी त्या वेळी उपलब्ध असलेल्या भूमितीची तत्त्वे शास्त्रशुद्ध रीतीने मांडली. उदा., बिंदूस अस्तित्व असून त्यास लांबी, रुंदी व जाडी नसतेरेषेस फक्त लांबी असून रुंदी व जाडी नसते इ. अमूर्त स्वरूपाच्या व्याख्या देऊन त्यांनी पुढे सरळ रेषेबद्दल विचार मांडले. दोन बिंदू अनेक रेषांनी जोडता येतात, पण त्यांपैकी ज्या रेषेवर त्या बिंदूंमधील अंतर मोजले असता ते कमीत कमी येते तिला सरळ रेषा म्हणतात. पाच स्वयंसिद्धकांच्या (कोणत्याही अन्य पुराव्याशिवाय कोणालाही सहज मान्य होण्यासारख्या विधानांच्या) आधारे तयार झालेल्या या भूमितीला ‘यूक्लिडीय भूमिती’असे म्हणतात. स्वयंसिद्धकांमध्ये बदल केले असता निराळी भूमिती तयार होते ही गोष्ट काही शास्त्रज्ञांना आढळून आली. अशा भूमितीस ‘अयूक्लिडीय भूमिती’म्हणतात. या भूमितीत आधारभूत असलेल्या स्वयंसिद्धकांमुळे जे अवकाश तयार होते त्यास ‘वक्र अवकाश’असे म्हणतात [→भूमिती].

वैश्लेषिक भूमितीत दोन अत्यंत जवळच्या बिंदूंच्या सरळ रेषेत मोजलेल्या अंतराचा वर्ग, कार्तीय सहनिर्देशक पद्धतीत (स्थानाचा निर्देश करण्याच्या एका पद्धतीत) पुढीलप्रमाणे लिहिता येतो :

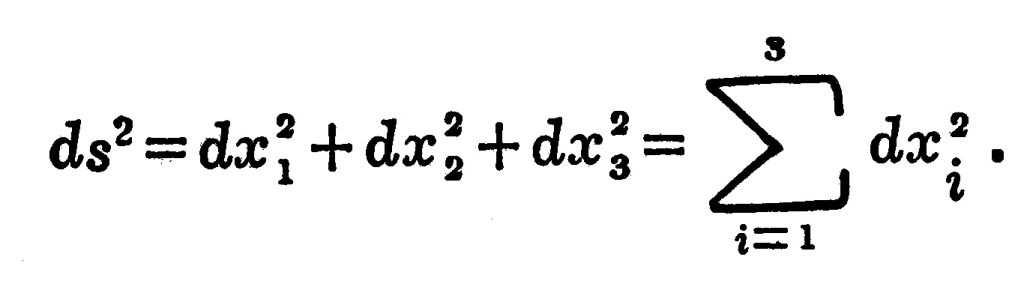
यात x₁, x₂, x₃ हे त्यांपैकी एका बिंदूचे सहनिर्देशक (स्थाननिर्देशक अंक) असून x₁+dx₁,x₂+dx₂,x₃+dx₃ हे दुसऱ्या बिंदूचे सहनिर्देशक आहेत. वरील समीकरण हे द्विमित अवकाशातील पायथॅगोरस प्रमेयाचे व्यापकीकरण असून हे अंतर आदिबिंदू (संदर्भबिंदू) व अक्षांच्या दिशेवर अवलंबून नसते. म्हणजे हे अत्यल्प अंतर सहनिर्देशक व्यूहाच्या स्थानांतरण (दुसऱ्या जागी जाणे) व परिभ्रमण क्रियांमुळे बदलत नाही. अवकाशाच्या ह्या गुणधर्मांना ‘समजातीयता’व ‘समदिक्कता’असे म्हणतात.

अवकाश-कालासंबंधी भौतिकीय रूढ विचार : आइन्स्टाइन यांच्या मर्यादित ⇨सापेक्षता सिद्धांतापूर्वी एकविध (एकसारखा) सापेक्ष वेग असणाऱ्या दोन संदर्भव्यूहांत रूपांतरणाचे नियम कसे होते हे खालील विवेचनावरून समजेल. समजा, दोन संदर्भव्यूहांचे आदिबिंदू सुरुवातीस (t=0 tम्हणजे काल) एकस्थित (एकमेकास खेटून) आहेत आणि त्यांतील एक व्यूह x अक्षाच्या दिशेने V एकविध वेगाने जात आहे व दुसरा स्थिर आहे (पहा : आकृती). स्थिर व्यूहातील एका बिंदूचे सहनिर्देशक जर x व y असतील तर गतिमान व्यूहातील संगत सहनिर्देशक पुढील समीकरणाने दर्शविले जातील :

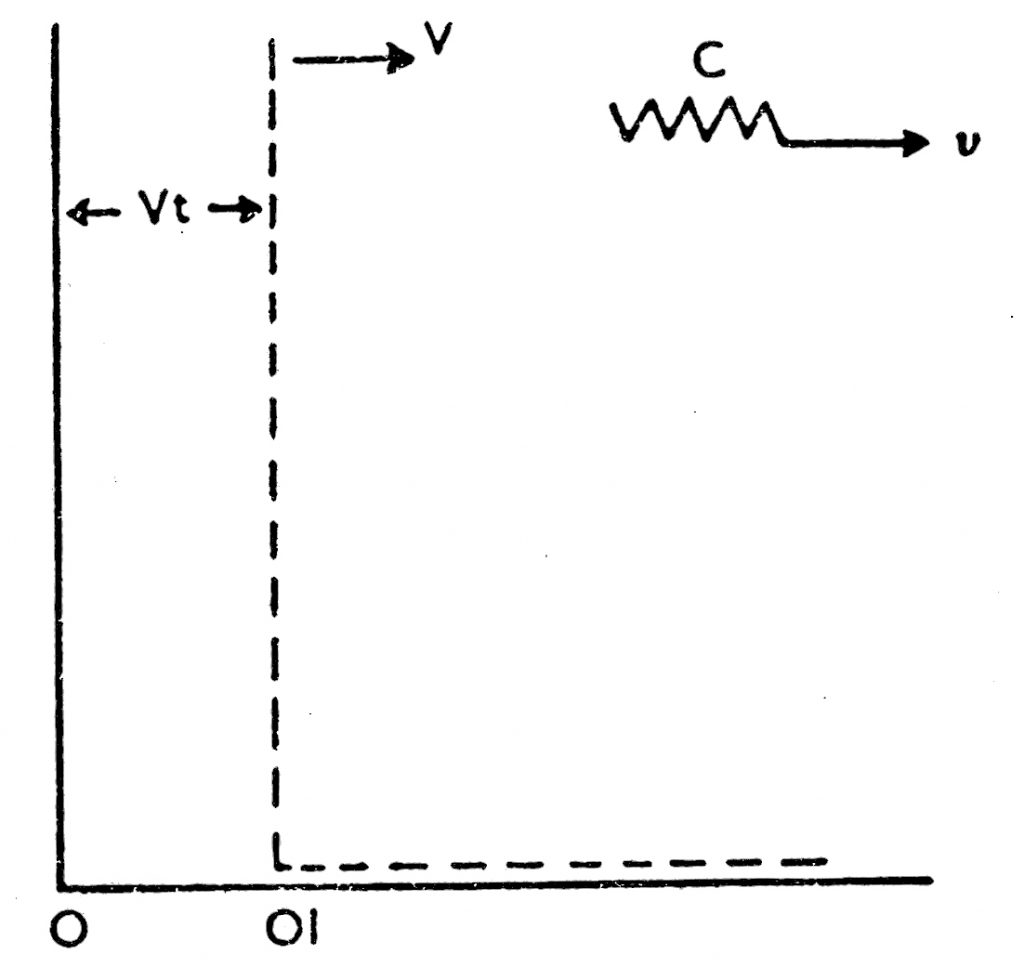
x¹ = x – Vt  y¹ = y t¹= t

सहनिर्देशकांच्या या रूपांतरण सूत्रास ‘गॅलिलीओ रूपांतरणे’ म्हणतात. जर वरील बिंदू x च्या दिशेने v वेगाने जात असेल तर स्थिर व्यूहातील स्थिर निरीक्षकास तो v वेगाने जात असल्याचे दिसेल व गतिमान व्यूहासापेक्ष स्थिर निरीक्षकास v—V वेगाने जाताना दिसेल. त्याचप्रमाणे जर वरील बिंदूतून प्रकाश निघाला, तर ह्या प्रकाशाचा वेग निरीक्षकाच्या व्यूहाच्या गतीवर अवलंबून आहे असे मानल्यास व स्थिर व्यूहामध्ये त्याचा वेग c असल्यास, गतिमान व्यूहातील निरीक्षकास त्याचा वेग c—V वाटेल. तथापि इ. स. १८८७ मध्ये मायकेलसन—मॉर्ली यांच्या प्रयोगांवरून असे सिद्ध झाले की, प्रकाशाचा वेग संदर्भ व्यूहाच्या वेगावर अवलंबून असत नाही. म्हणून गॅलिलीओ रूपांतरण सूत्रात बदल करणे आवश्यक झाले. लोरेन्ट्स नावाच्या शास्त्रज्ञांनी, आइन्स्टाइन यांच्या सापेक्षता सिद्धांतापूर्वीच, प्रकाशाचा वेग निरीक्षकाच्या व्यूहाच्या वेगावर अवलंबून राहत नाही असे गृहीत धरून नवीन रूपांतरण सूत्रे प्रस्थापित केली त्यांस ‘लोरेन्ट्स रूपांतरण’असे म्हणतात. त्यात कालाचेही रूपांतरण करावे लागते.

चतुर्मित भूमिती अवकाश-काळ भूमिती रचना : चतुर्मित अवकाश-कालामध्ये दोन जवळील बिंदूंमधील अंतर कोणत्याही जात्य (ज्यातील अक्ष एकमेकांना काटकोनात असतात अशी) सहनिर्देशक पद्धतीत पुढीलप्रमाणे लिहिता येईल :

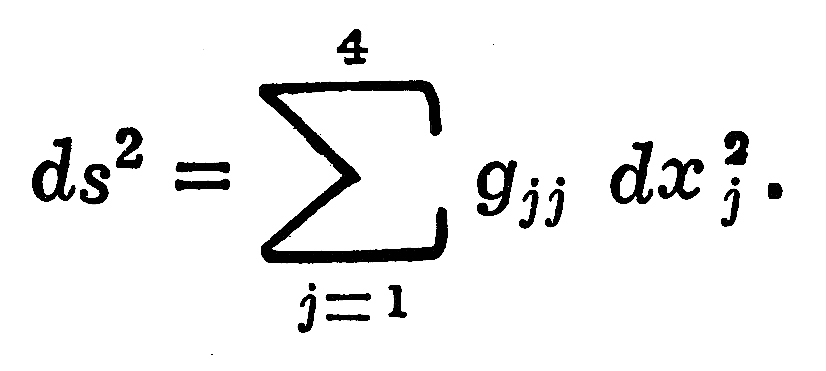
येथे g_jj या राशी सहनिर्देशकावर अवलंबून असतात, म्हणजे g_jj सहनिर्देशकांचे फलन (सहनिर्देशकांवर अवलंबून असलेली राशी)  असते. हा सहनिर्देशक कालदर्शक आहे. g_jj चे सहनिर्देशकावरील अवलंबन लक्षात येण्यासाठी द्विमित अवकाशाचा थोडा विचार करू. त्यात कोणत्याही पृष्ठभागावर एखाद्या बिंदूची स्थिती दाखविण्यास दोन स्वतंत्र प्रचल (विशिष्ट परिस्थितीत अचल राहणाऱ्या राशी) लागतात. सपाट पृष्ठावर दोन जवळील बिंदूंच्या अंतराचा वर्ग असा लिहिता येतो :

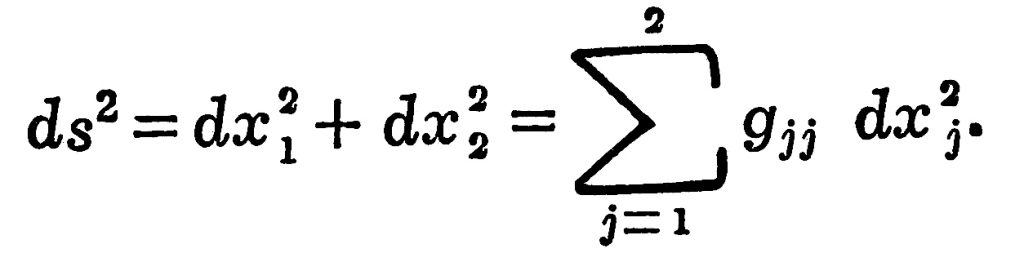
येथे x₁,व x₂हे कार्तीय सहनिर्देशक आहेत. येथे g_jj हे अचल असून त्यांचे मूल्य एक आहे. आता सपाट पृष्ठाऐवजी गोलीय पृष्ठ घेतल्यास तेच अंतर पुढे दिल्याप्रमाणे असते :

येथे g_jj हे x₁,व x₂वर अवलंबून राहतील. महत्त्वाचा मुद्दा म्हणजे गोलीय पृष्ठाच्या संबंधात कोणतीही जात्य सहनिर्देशक पद्धती स्वीकारली तरी g_jj हे अचल होत नाहीत. फक्त सपाट पृष्ठ असल्यासच हे अचल होतात. तसेच गोलीय पृष्ठावर काढलेली सरळ रेषा म्हणजे महावृत्तखंड (गोलीय पृष्ठावर काढलेल्या व ज्याची पातळी गोलाच्या मध्यातून जाते अशा वर्तुळाचा भाग) असून ह्या पृष्ठावर त्रिकोण काढल्यास त्याच्या आंतरकोनांची बेरीज दोन काटकोनांपेक्षा जास्त असते. ह्यावरून लक्षात येईल की, द्विमित अवकाशाचे गुणधर्म या g_jj ने निश्चित होतात. त्रिमित अवकाशामध्ये मांडावयाचे झाल्यास पुढील स्वरूपात मांडता येईल.

पण कोणतीही जात्य सहनिर्देशक पद्धती वापरून हे g_jj अचल राहिले नाहीत तर त्या अवकाशाला वक्र अवकाश म्हणावे लागेल. अशा अवकाशाला यूक्लिडीय भूमिती लागू पडत नाही. पण जर कोणतीही जात्य सहनिर्देशक पद्धती वापरून हे g_jj अचल येत असतील तर त्या अवकाशाला सपाट अवकाश असे म्हणता येईल व त्या अवकाशाची भूमिती यूक्लिडीय

असेल. या g_jj ना ‘मूलभूत प्रदिश’असे म्हणतात. g_jj वर अवकाशाचे गुणधर्म अवलंबून राहतात व त्यांचा उपयोग ‘व्यापक सापेक्षता सिद्धांता’त अनेक ठिकाणी केला आहे.

रीमानीय भूमिती : रीमान या गणितज्ञांनी त्रिमिती अवकाशाचे व्यापकीकरण केले. चतुर्मित अवकाशाचा विचार व्यापक सापेक्षता सिद्धांतात करावयाचा असल्याने या व्यापकीकरणाचे थोडे विवेचन केल्यास ते उपयुक्त ठरेल. N-मित अवकाशामध्ये दोन अगदी जवळील बिंदूंमधील अंतराचा वर्ग पुढे दिल्याप्रमाणे लिहिता येतो :

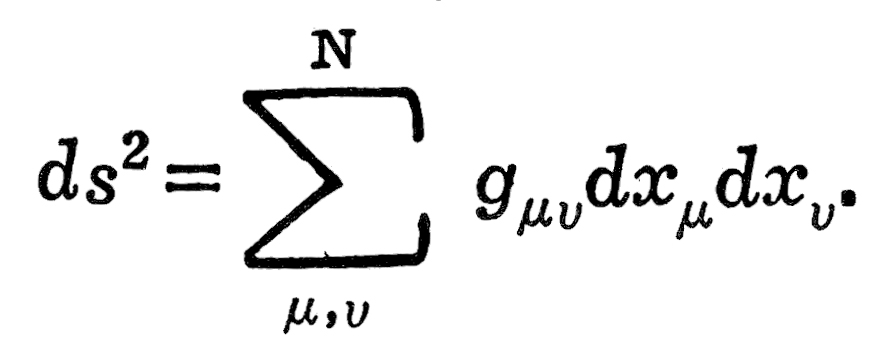
येथे एका बिंदूस N सहनिर्देशक लागतात. g_uv हे या सहनिर्देशकांचे फलन असते. जर एका बिंदूचे सहनिर्देशक x₁, x₂, …,x_N असले व त्याजवळील दुसऱ्या दोन बिंदूंचे सहनिर्देशक अनुक्रमे x₁+dx₁,…, x_N+dx_N, व x₁+δx₁,…, x_N+δx_N असे घेतले तर ते दोन बिंदू x₁,…, x_N या बिंदूंवर जो कोन θ करतील त्याचे कोज्या गुणोत्तर (cosθ) पुढील समीकरणाने दर्शविता येते :

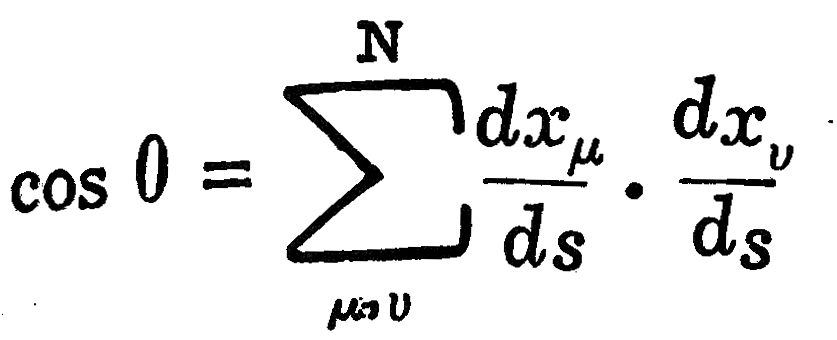
जर याऐवजी दुसरे कोणतेही स्वतंत्र निर्देशक x’_u वापरून ds² ला

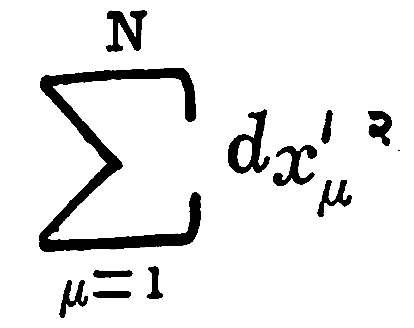
च्या रूपात लिहिता आले, तर g_uv = 1, (μ= v असल्यास) व g_uv = 0, (μ≠ v असल्यास) असे असल्यास या N-मित अवकाशाला ‘सपाट अवकाश’म्हणतात येईल. नाही तर ते वक्र अवकाश समजले जाईल. N-मित सपाट अवकाशामध्ये यूक्लिडीय भूमितीची उभारणी करता येते. जर x₁=F₁(t), …, x_N = F_N(t) असे मांडले, तर t ची निरनिराळी मूल्ये दर्शविणारे बिंदू जोडल्यास येणाऱ्या पथास रेषा म्हणतात. कोणत्याही रेषेवरील दोन निराळ्या बिंदूंमधील अंतर असे लिहिता येते :

⇨चलनकलनाच्या साहाय्याने हे अंतर ज्या रेषेवर स्थिरमूल्य येईल त्या रेषेला अवकाशाची ‘अल्पिष्ट’रेषा म्हणतात. यूक्लिडीय अवकाशामधील सरळ रेषेचे हे व्यापकीकरण होय. अल्पिष्ट रेषेचे समीकरण पुढीलप्रमाणे असते :

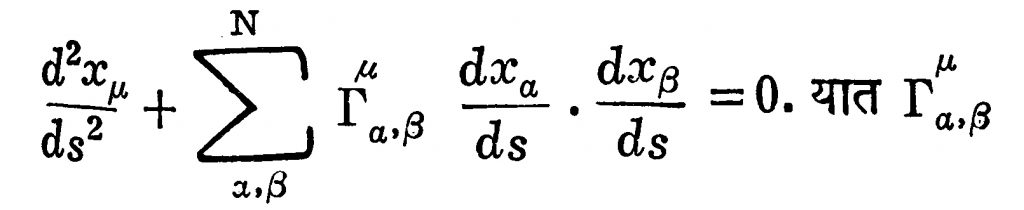
हे g          व       व्याख्याही दिलेल्या आहेत. N-मित अवकाशामध्ये केलेल्या या व्यापकीकरणाचा उपयोग व्यापक सापेक्षता सिद्धांतात होतो. आता चतुर्मित अवकाशाची आवश्यकता भौतिकीत का वाटली व सापेक्षता सिद्धांतावर त्याचा काय परिणाम झाला ते पाहू.

इ. स. १९०५ मध्ये आइन्स्टाइन यांनी ‘मर्यादित सापेक्षता सिद्धांत’ मांडला व लोरेन्ट्स यांच्या रूपांतरण सूत्रास भौतिकीय आधार दिला. या सिद्धांतानुसार कोणत्याही व्यूहातील निरीक्षकाला स्वतःच्या व्यूहात केलेल्या कोणत्याही प्रयोगावरून स्वतःच्या व्यूहाचा एकविध वेग कधीही मोजता येणार नाही. म्हणून भौतिकीय सिद्धांत व्यक्त करणारी समीकरणे एकविध सापेक्ष वेगाने जाणाऱ्या कोणत्याही संदर्भ व्यूहात सारखीच असली पाहिजेत. म्हणून यासाठी जसे एका बिंदूचे तीन अवकाश सहनिर्देशक प्रत्येक व्यूहात असतात, तसा काल सहनिर्देशकही असला पाहिजे. थोडक्यात, भौतिकीय सिद्धांत दाखविणारी समीकरणे लोरेन्ट्स रूपांतरण सूत्रे लागू केल्यावर अचल राहिली पाहिजेत. यास ‘सहचल वैधिकता’म्हणतात. लॉरेन्ट्स रूपांतरणे अशी आहेत :

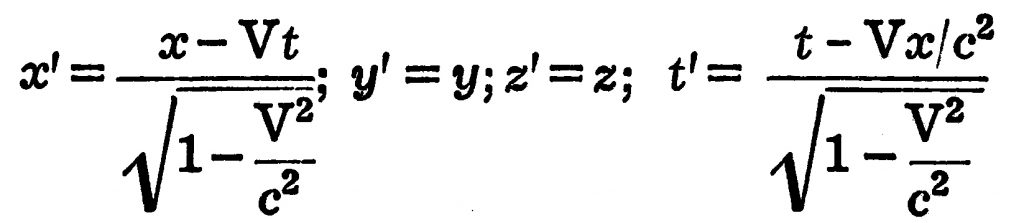
येथपावेतो मर्यादित सापेक्षता सिद्धांताचा विचार झाला. आता व्यापक सापेक्षता सिद्धांताचा विचार करू : आइन्स्टाइन यांच्या गुरुत्वाकर्षणाच्या सिद्धांतानुसार वस्तुरहित अवकाश-काल सपाट असतो म्हणून चतुर्मित अवकाश-कालामध्ये दोन जवळील बिंदूंच्या मधील अंतराचा वर्ग पुढे दिल्याप्रमाणे लिहिता येतो :

येथे dx₄= icdt असून g_μv = δ_u आहे(δ = क्रोनेकर डेल्टा μ = v असल्यास, δ_uv =0 आणि  नसल्यास, δ_uv  = 1). पण जर अवकाशामध्ये वस्तूचे अस्तित्व असेल तर हे g_uv अचल राहणार नाहीत व ते सहनिर्देशकांचे फलन होतील म्हणून ते अवकाश वक्र होईल. तसेच ह्या अवकाशामध्ये दोन बिंदूंमधील अल्पिष्ट रेषा सपाट अवकाशातील अल्पिष्ट रेषेपेक्षा निराळी राहील. याचा अर्थ असा होतो की अल्पिष्ट रेषेवरून जाणाऱ्या प्रकाशकिरणाच्या पथावर वस्तूच्या अस्तित्वाचा परिणाम होईल व ती वस्तू अस्तित्वात नसताना ज्या मार्गावरून तो किरण जात असेल त्यापेक्षा वस्तू असताना तो थोड्या निराळ्या मार्गाने जाईल. वस्तूच्या अस्तित्वामुळे अवकाशामध्ये आलेली ही वक्रता वस्तूपासून दूर जाऊ तसतशी कमी होत जाते. या वक्रतेचा जो परिणाम कणाच्या किंवा प्रकाशकिरणाच्या गतीवर होईल त्यास ‘गुरुत्वाकर्षण’असे ह्या नव्या सिद्धांतात म्हणतात. प्रकाशकिरण सूर्याच्या पृष्ठभागाला खेटून जाताना तेथील अवकाशाच्या वक्रतेमुळे त्याची दिशा बदलते, हे आता प्रयोगाने सिद्ध झाले आहे.

आधुनिक प्रगती : अवकाश व काल यांसंबंधी विचारसरणी तीन भिन्न मार्गांनी प्रगत होत आहे : (१) विश्वरचनेच्या संशोधनात विस्तीर्ण अवकाश-कालाच्या गुणधर्माचाच विचार केला जातो. याचा अर्थ असा की, एखाद्या मोठ्या ताऱ्याभोवतीच्या अवकाश-कालाचे गुणधर्म, किंबहुना दीर्घिकेभोवतीच्या (आकाशगंगेसारख्या इतर तारकासमूहांभोवतीच्या) अवकाश-कालाचे गुणधर्म विचारात न घेता, सर्व विश्वाच्या अवकाश कालाचे भूमितीय गुणधर्म काय असतात याला जास्त प्राधान्य दिले आहे. (२) व्यापक सापेक्षता सिद्धांतात गुरुत्वाकर्षण अवकाश-कालाच्या भूमितीय गुणधर्मावर अवलंबून असते, त्याचप्रमाणे विद्युत् चुंबकीय व अणुकेंद्रीय प्रेरणाही एकीकृत सिद्धांताच्या (गुरुत्वाकर्षण, विद्युत् चुंबकीय व अणुकेंद्रीय या तिन्ही सिद्धांतांच्या एकत्रितपणे विचार करणाऱ्या सिद्धांताच्या) आधारे अवकाश-कालाच्या गुणधर्माचेच परिणाम आहेत. (३) विद्युत् चुंबकीय क्षेत्राच्या पुंज सिद्धांतातील अलीकडच्या प्रगत विचारांनुसार, यापूर्वी जे अवकाश-काल संपूर्ण रिते आहे असे समजले जात असे अशा अवकाश-कालालाही विशिष्ट संरचना आहे, असे समजावयास हवे. या संरचनेवर आधारलेल्या विवरणास ‘निर्वाताचा आधुनिक पुंज सिद्धांत’असे म्हणतात.

पहा : सापेक्षता सिद्धांत.

संदर्भ : 1. Grunbaum, A. Philosophical Problems of Space and Time, New York, 1963.

2. Reichenbach, H. The Philosophy of Space and Time, New York, 1958.

दामले,प्र.शं.