अणुकेंद्रीय भौतिकी : अणुकेंद्रासंबंधी रचना, विस्तार, आकार, प्रेरणा, प्रतिमान (मॉडेल), विक्रिया, परिवलन (स्वत:भोवती फिरणे) आणि चुंबकत्व एवढे विषय अणुकेंद्रीय भौतिकीत मोडतात.
इलेक्ट्रॉन (ऋण विद्युत् भारित कण) आणि अणुकेंद्र हे अणूचे घटक आहेत [→ अणु व आणवीय संरचना]. अणुकेंद्र म्हणजे अणूचा गाभा विस्ताराने तो अत्यंत लहान असून अणूच्या केंद्रस्थानी असतो. अणुकेंद्राची त्रिज्या अदमासे ५ फेर्मी (१ फेर्मी = १०-१३ सेमी.) म्हणजे अणूच्या त्रिज्येच्या (१०-८ सेमी.) मानाने नगण्य असते. अणुकेंद्रावर धन विद्युत् भार असतो व त्याच्या भोवती इलेक्ट्रॉन विशिष्ट परिभ्रमणकक्षांत फिरत असतात. अणुकेंद्रावरील धन विद्युत् भार इलेक्ट्रॉनांच्या एकूण विद्युत् भाराएवढा असल्यामुळे अणू एंकदरीत विद्युत् भाररहित असतो. इलेक्ट्रॉनांचे द्रव्यमान खूप कमी असल्यामुळे अणूचे बहुतेक द्रव्यमान अणुकेंद्रात एकवटलेले असते. सर्व अणुकेंद्रांची घनता सारखीच असते व तिचे मूल्य दर घन मीटरला सु. २·५ x १०१७ किलोग्रॅम इतके प्रचंड असते. अणूचे रासायनिक गुणधर्म अणुकेंद्रावरील विद्युत् भारावर अवलंबून असतात.
अणुकेंद्राचे घटक: प्रोटॉन व न्यूट्रॉन हे अणुकेंद्राचे घटक आहेत. त्यांपैकी प्रोटॉन हा H1 (हायड्रोजन अणुकेंद्र) आहे. त्याच्यावर एक एकक धन विद्युत् भार असतो (आणवीय भौतिकीत एकक विद्युत् भार म्हणजे इलेक्ट्रॉनावरील विद्युत् भार होय). मुक्त प्रोटॉन अगर अणुकेंद्रातील प्रोटॉन स्थिर असतो. न्यूट्रॉनावर विद्युत् भार नसतो. त्याचे द्रव्यमान प्रोटॉनापेक्षा किंचित अधिक असते. मुक्त न्यूट्रॉन किरणोत्सर्गी असून त्याचे अर्धायुष्य (किरणोत्सर्गाची क्रियाशीलता निम्मी होण्यास लागणारा काल) सु. १२ मिनिटांचे आहे. न्यूट्रॉनाचे रूपांतर प्रोटॉन, इलेक्ट्रॉन आणि प्रतिन्यूट्रिनो अशा तीन ⇨ मूलकणांत होते. न्यूक्लिऑन ही संज्ञा प्रामुख्याने अणुकेंद्रातील प्रोटॉन व न्यूट्रॉन यांना वापरतात. अणुकेंद्रातील न्यूक्लिऑनांच्या संख्येस ⇨ द्रव्यमानांक म्हणतात. हा अंक A या अक्षराने दाखवतात. अणुकेंद्रातील प्रोटॉनांच्या संख्येस ⇨ अणुक्रमांक म्हणतात व तो Z या अक्षराने दाखवतात.
अणुकेंद्राची संरचना : यासंबंधीची माहिती अणुकेंद्राची घनता, कवच प्रतिमान आणि सामूहिक प्रतिमान या परिच्छेदांत पुढे दिली आहे.
अणुकेंद्राची बंधनऊर्जा : यासंबंधी काही उपयुक्त संज्ञांचे अर्थ खाली दिले आहेत.
(१) आणवीय द्रव्यमानाचे एकक µ हा C12 या कार्बनाच्या समस्थानिकाच्या (अणुक्रमांक तोच पण अणुभार भिन्न असलेल्या त्याच मूलद्रव्याच्या प्रकाराच्या) द्रव्यमानाच्या १/१२ एवढे असते.
१ आणवीय द्रव्यामानाचे एकक = १·६६०४ ×१०-२७ किलोग्रॅम.
(२) अणुकेंद्रीय ऊर्जा एकक (Mev). १ Mev = १०६ इलेक्ट्रॉन व्होल्ट (ev) = १·६० × १०-६ अर्ग. इलेक्ट्रॉन व्होल्ट म्हणजे १ व्होल्ट विद्युत् दाबाखाली प्रवेगित केलेल्या इलेक्ट्रॉनाची ऊर्जा.
(३) अणुकेंद्रीय संकुलन अंक : समस्थानिकात आढळणारी द्रव्यामान घट (M–A) आणि त्याचा द्रव्यमानांक यांचे गुणोत्तर. याचे चिन्ह ƒ आहे. ƒ = (M–A)/A. या समीकरणात M = अणुकेंद्राचे तौलनिक आणवीय द्रव्यमान-एकक (µ) व्यक्त केलेले द्रव्यमान.
(४) अणुकेंद्रातील सर्व न्यूक्लिऑन एकमेकांपासून अलग करण्यासाठी आवश्यक असलेली लघुतम ऊर्जा म्हणजेच अणुकेंद्रीय बंधनऊर्जा (B). B = [ZMp+(A–Z)Mn–M]c2. या समीकरणात Mp, Mn आणि M अनुक्रमे मुक्त प्रोटॉन, मुक्त न्यूट्रॉन आणि बंधित अणुकेंद्र यांची द्रव्यमाने आणि c प्रकाशाचा वेग आहेत. वरील समीकरण ⇨ सापेक्षता सिद्धांताने सिद्ध करता येते. एका न्यूक्लिऑनाची सरासरी बंधनऊर्जा B¯= B/A अशी असते.
अणुकेंद्रीय प्रेरणा: या प्रेरणेविषयीचे गुणधर्म व माहिती खाली क्रमश: दिली आहे :
(१) संपृक्तता: A = २५ पासून A = २४० पर्यंत न्यूक्लिऑनांची सरासरी बंधनऊर्जा B¯ सामान्यपणे सारखी आहे. (सरासरी ८·० Mev). हलक्या व जड अणुकेंद्रांची सरासरी बंधनऊर्जा B¯, पहिल्यात पृष्ठताणामुळे व दुसऱ्यात कुलंब-प्रतिसारणामुळे (पृष्ठताण व कुलंब-प्रतिसारण हे परिच्छेद पहावेत), ८·५ Mev पेक्षा कमी असते, पृष्ठताण आणि कुलंब-प्रतिसारण या दोन गोष्टी अस्तित्वात नसत्या तर सर्व अणुकेंद्राची B¯ समान असती.
अणुकेंद्रातील प्रत्येक न्यूक्लिऑन एका ठराविक संख्येहून अधिक न्यूक्लिऑनांना आकर्षू शकत नाही. अशा आकर्षण-प्रेरणेस संपृक्त प्रेरणा म्हणतात. प्रत्येक न्यूक्लिऑन जास्तीत जास्त N न्यूक्लिऑनांना आकर्षितो असे मानले असता, अणुकेंद्रातील एकूण आकर्षण-बंध AN/2 एवढे येतात व प्रत्येक बंधाची सरासरी ऊर्जा E मानल्यास, B = ANE/2 आणि B¯ = NE/2 = स्थिरांक, असे सिद्ध होते व ही गोष्ट प्रयोगाशी जुळते. उलटपक्षी अणुकेंद्रीय प्रेरणा असंपृक्त तर B¯ हा A च्या समप्रमाणात वाढेल पण तसे होत नाही असे प्रयोगांती सिद्ध झाले आहे. म्हणून अणुकेंद्रीय प्रेरणा संपृक्त आहे असे मानावे लागते.
(२) लघुक्षेत्र: प्रोटॉन-प्रोटॉन आणि न्यूट्रॉन-प्रोटॉन प्रकीर्णनाच्या (विखुरले जाण्याच्या) अभ्यासावरून अणुकेंद्रीय प्रेरणा अत्यंत लहान क्षेत्रात प्रभावी असते, असे आढळून आले आहे. या क्षेत्राची सरासरी त्रिज्या सु. ३ फेर्मी एवढी असते.
(३) अणुकेंद्रीय प्रेरणेचे विद्युत् भार निरवलंबित्व: अणुकेंद्रीय बंधांचे तीन प्रकार संभवतात, ते असे : (अ) दोन न्यूट्रॉनांमधील बंध (n, n), (आ) प्रोटॉन आणि न्यूट्रॉन यांमधील बंध (p, n) आणि (इ) दोन प्रोटॉनांमधील बंध (p, p). दोन प्रोटॉनांमधील कुलंब-प्रतिसारण विचारात घेतले नाही, तर ते तीनही बंध आकर्षणाचे असून सममूल्य आहेत, असे आढळून आले आहे. यांपैकी (p, p) आणि (p, n) बंधांची समानता (p, p) आणि (n, p) यांच्या प्रकीर्णनाच्या प्रयोगांवरून सिद्ध होते. He3 [ट्रिटियम, हायड्रोजन (३)] आणि He3 [हीलियम (३)] या दोन अणुकेंद्रांतील प्रत्येकात दोन (p, n) बंध समान आहेत. या दोन अणुकेंद्रांच्या द्रव्यमानांत फरक पडण्याची तीन कारणे आहेत ती अशी : (क) न्यूट्रॉनाचे द्रव्यमान प्रोटॉनापेक्षा थोडे जास्त असल्यामुळे H3 चे द्रव्यमान He3 पेक्षा अधिक असणार. (ख) He3 मध्ये कुलंब-ऊर्जा अधिक आहे. (ग) (n, n) आणि (p, p) बंधांची अदलाबदल. सर्व गोष्टींचा एकत्र विचार करता (p, p) बंध = (n, n) बंध असे आढळून आले आहे. येणेप्रमाणे (p, p) = (n, n) = (n, p)
(४) परिवलन-अवलंबित्व : ड्यूटेरॉनामधील (He2 मधील) प्रोटॉन आणि प्रोटॉनाचे परिवलन समसमांतर (एकाच दिशेने व समांतर) आहे उलटपक्षी न्यूट्रॉनाचे प्रोटॉनावरून प्रकीर्णन होत असताना या दोन मूलकणांचे परिवलन समसमांतर अगर प्रतिसमांतर (समांतर परंतु विरुद्ध दिशेने) असू शकते. ड्यूटेरॉनाची बंधनऊर्जा आणि (n, p) प्रकीर्णन या दोन्ही बाबींतील प्रयोगसिद्ध फलिताची उपपत्ती लावण्यासाठी अणुकेंद्रीय प्रेरणा परिवलनावर अवलंबून असते असे मानावे लागते.
(५) कुलंब-प्रतिसारण : प्रोटॉनावर विद्युत् भार असल्यामुळे अणुकेंद्रातील प्रत्येक प्रोटॉन दुसऱ्या प्रोटॉनाला दूर सारतो. अणुकेंद्रीय कुलंब-प्रतिसारण ऊर्जा 3e2Z(Z–1)/5R(4π εo) एवढी असते असे बेटे या शास्त्रज्ञांनी सिद्ध केले आहे. या राशिमालिकेतील e म्हणजे इलेक्ट्रॉनावरील विद्युत् भार आणि R म्हणजे अणुकेंद्राची त्रिज्या होय. εo= मुक्त अवकाशाची विद्युत् पार्यता.
(६) पृष्ठताण : अणुकेंद्र जसजसे हलके होत जाते तसतशी Β¯ कमी होत जाते. अणुकेंद्राला ⇨ पृष्ठताण आहे असे गृहीत धरले असता या गोष्टीची उपपत्ती लावता येते. कमी भाराच्या अणुकेंद्राची त्रिज्या A 1/3 च्या प्रमाणात व क्षेत्रफळ A 2/3 च्या प्रमाणात असते. प्रति न्यूक्लिऑनामागे म्हणजे सापेक्ष क्षेत्रफळ A 2/3÷ A=1/A 1/3च्या प्रमाणात असते. म्हणून त्रिज्या कमी होईल त्या प्रमाणात सापेक्ष क्षेत्रफळ अधिक होईल. एखादे विशिष्ट क्षेत्रफळ सिद्ध होण्यासाठी पृष्ठताणाविरूद्ध कार्य करावे लागते व त्यामुळे Β¯ चे मूल्य कमी होते.
(७) सम-विषम परिणाम : प्रोटॉन-संख्या Z आणि न्यूट्रॉनसंख्या Ν अशा दोन्ही संख्या सम असलेली स्थिर अणुकेंद्रे खूप जास्त (सु.१६० ) व या दोन्ही संख्या विषम असलेली अणुकेंद्रे खूपच कमी (सु. ४ ) आहेत. तसेच या दोहोंपैकी एक सम आणि दुसरी विषम असेल तर स्थिर अणुकेंद्रांची संख्या मध्यम असते. यावरून Z आणि सम N असल्यास अणुकेंद्र अधिक स्थिर असते असे मानावे लागते. Β¯ विरुद्ध A असा आलेख काढल्यास कमी भाराच्या अणुकेंद्राच्या Β‾ ची महत्तम मूल्ये Z आणि N सम असताना येतात. यावरूनही सम-विषम परिणामास पुष्टी मिळते.
अणुकेंद्रीय द्रव्यमान आणि त्याचे अर्ध-अनुभवसिद्ध सूत्र : अणुकेंद्रीय द्रव्यमान, द्रव्यमान वर्णपटलेखकाने [→ द्रव्यमान वर्णपटविज्ञान] अगर अणुकेंद्राच्या विघटनाच्या अभ्यासाने मोजता येते. तत्संबंधीचे अर्ध-अनुभवसिद्ध सूत्र खाली दिले आहे.
M=ZMp+(A-Z)Mn– αΑ+βA 2/3+ εZ2A-1/3
+γ (N-Z)2/A ± δA -3/4
या सूत्रात M= बंधित अणुकेंद्राचे द्रव्यमान Mp आणि Mn अनुक्रमे एका मुक्त प्रोटॉनाचे आणि एका मुक्त न्यूट्रॉनाचे द्रव्यमान α, β, γ, ε आणि δ हे प्रचल (विशिष्ट अणुकेंद्रासाठी अचल राहणाऱ्या राशी) आहेत. Z, N आणि A अनुक्रमे प्रोटॉन संख्या, न्यूट्रॉन संख्या आणि न्यूक्लिऑन संख्या आहेत. या समीकरणाच्या उजव्या बाजूस एकूण सात पदे आहेत. त्यांचा अर्थ समजण्यासाठी अणुकेंद्राची त्रिज्या R ही A 1/3 च्या समप्रमाणात असते हा नियम लक्षात घेणे आवश्यक आहे. उजव्या बाजूची पहिली दोन पदे म्हणजे अणुकेंद्रातील सर्व प्रोटॉनांचे आणि सर्व न्यूट्रॉनांचे द्रव्यमान होय. Β‾ स्थिरांक असल्यामुळे अणुकेंद्राची बंधनऊर्जा A शी समप्रमाणात असते. अशा रीतीने तिसरे पद बंधनऊर्जेसाठी आहे. चौथे पद पृष्ठताणामुळे आहे. कारण अणुकेंद्राच्या पृष्ठाचे क्षेत्रफळ ∝ R2 ∝ A 2/3 (येथे ∝ हे चिन्ह प्रमाण दर्शविते). पाचवे पद कुलंब-ऊर्जेसाठी आहे : कुलंब-ऊर्जा ∝ Z2/R ∝ Z2/A-1/3.
N आणि Z मध्ये जास्त अंतर पडल्यास अणुकेंद्र अस्थिर बनते हे सहाव्या पदाने दर्शविले जाते. सातवे पद सम-विषम परिणाम दाखविते. त्यातील उणे चिन्ह N आणि Z सम असतील तर आणि अधिक चिन्ह दोन्ही विषम असतील तर येते. यांपैकी एक सम व दुसरा विषम असेल तर सातवे पद शून्य असते.
अणुकेंद्राचा आकार : अणुकेंद्र सर्वसाधारणपणे गोलाकार आहे असे मानले जाते. मात्र अनेक अणुकेंद्रांचा आकार गोलत्वाहून काहीसा विचलित झालेला आढळतो.
अणुकेंद्राचा विस्तार : हा विस्तार काढण्यासाठी पद्धती पुढील प्रमाणे आहेत.
(अ) उच्च ऊर्जेच्या इलेक्ट्रॉनाचे प्रकीर्णन : इलेक्ट्रॉनावर अणुकेंद्राची प्रतिक्रिया मुख्यत्वेकरून कुलंब-प्रेरणा ही असते. वस्तू मोजण्याचे माप वस्तूपेक्षा लहान असावे लागते, या नियमानुसार जास्त ऊर्जेचे इलेक्ट्रॉन अणुकेंद्राचा विस्तार मोजू शकतात कारण जास्त ऊर्जेच्या इलेक्ट्रॉनांची तरंगलांबी अणुकेंद्राहून लहान असते. इलेक्ट्रॉनांना खूप ऊर्जा देऊन त्यांची शलाका लक्ष्यावर सोडतात व निरनिराळ्या कोनांतून स्थितिस्थापक अगर अस्थितिस्थापक पद्धतीने प्रकीर्णन पावलेल्या इलेक्ट्रॉनांची संख्या मोजतात (‘विक्रियांचे काही प्रकार’ हा परिच्छेद पहावा). स्थितिस्थापक प्रकीर्णनात कोन लहान असेल तर अणुकेंद्रावरील विद्युत् भारच कळू शकतो कारण अशा वेळी इलेक्ट्रॉन अणुकेंद्रापासून काही अंतरावरून प्रकीर्णन पावतात. उच्च ऊर्जेच्या स्थितिस्थापक प्रकीर्णनात कोन मोठा असतो, तेव्हा इलेक्ट्रॉन अणुकेंद्राच्या आतमध्ये घुसून प्रकीर्णन पावलेले असतात व अशा वेळी अणुकेंद्राचा विस्तार कळू शकतो.
(आ) म्यू मेसॉनीय क्ष-किरणे : म्यू मेसॉन (एक अणुकेंद्रीय अस्थिर मूलकण) वस्तूमधून जाताना वस्तूच्या विरोधाने थांबविला जातो तेव्हा त्याच्यावरील ऋण विद्युत् भारामुळे तो जवळच असलेल्या अणुकेंद्राकडून आकर्षिला जातो व त्या अणुकेंद्राभोवती इलेक्ट्रॉनांप्रमाणे परिभ्रमणकक्षांतून परिभ्रमण करू लागतो. पण म्यू मेसॉनाचे द्रव्यमान इलेक्ट्रॉनाच्या २०७ पट अधिक असल्यामुळे त्याच्या परिभ्रमणकक्षा खूप लहान असतात आणि जड अणुकेंद्राच्या बाबतीत तर काही वेळा या परिभ्रमणकक्षा अणुकेंद्राच्या आत जातात. अशा म्यू मेसॉनांनी उत्सर्जित केलेल्या ⇨ क्ष-किरणांचा अभ्यास करून अणुकेंद्राचा विस्तार काढण्यात आलेला आहे.
(इ) प्रतिबिंब-सदृश अणुकेंद्र : जर एखाद्या अणुकेंद्रात Z प्रोटॉन आणि Z+1 न्यूट्रॉन असतील आणि दुसऱ्या अणुकेंद्रात Z+1 प्रोटॉन आणि Z न्यूट्रॉन असतील तर त्या दोन अणुकेंद्रांस प्रतिबिंब सदृश अणुकेंद्र असे म्हणतात उदा., H3 आणि He3, तसेच C13 आणि N13. प्रतिबिंब-सदृश अणुकेंद्रांच्या द्रव्यमानात फरक पडण्याची कारणे आहेत, ती अशी : (१) न्यूट्रॉन आणि प्रोटॉन यांची अदलाबदल. (२) त्यांच्यातील कलंब-ऊर्जेतील फरक. हा फरक 6 e2Z/5R(4π εo) एवढा असतो. वरील सर्व गोष्टींचा एकत्र विचार केला असता 6 e2Z/5R(4π εo) ह्या पदाचे मूल्य आणि त्यावरून R चे म्हणजे अणुकेंद्राच्या त्रिज्येचे मूल्य ठरवता येते.
(ई) याव्यतिरिक्त प्रोटॉन, न्यूटॉन, आणि पायॉन या मूलकणांचे प्रकीर्णन, α किरणांचे उत्सर्जन, क्ष-किरणांचा वर्णपट इत्यादिकांच्या अभ्यासावरूनही अणुकेंद्राचा विस्तार कळू शकतो.
(उ) प्रचंड ऊर्जेच्या इलेक्ट्रॉनांच्या प्रकीर्णनावरून अणुकेंद्र व न्यूक्लिऑन यांचे आकार व विस्तार यासंबंधीची माहिती कळते. प्रोटॉनाची त्रिज्या सु. एक फेर्मी असते. अमेरिकेतील स्टॅनफर्ड येथील ३·२ किमी. लांबीच्या प्रवेगकाच्या (अणुघटकांचा वेग वाढविण्याचे साधन, → कण वेगवर्धक) साह्याने प्रोटॉनांच्या संरचनेची माहिती त्याच्या त्रिज्येच्या १/१० अंतरापर्यंत (म्हणजे १०-१४ सेंमी.) मिळू शकली.
प्रचंड ऊर्जेच्या इलेक्टॉन-प्रकीर्णनाच्या साह्याने अणुकेंद्रावरील विद्युत् भाराचे वितरण त्याच्या सर्वसामान्य आकारावर कसे होते हे कळून येते. इतकेच नव्हे तर विद्युत् भार घनतेतील सूक्ष्म बदलही कळतो.
अणुकेंद्राची घनता : अणुकेंद्रीय द्रव्याचे वितरण, न्यूक्लिऑनांचे प्रकीर्णन, इलेक्ट्रॉनांचे प्रकीर्णन इ. पद्धतींनी अणुकेंद्रीय घनता काढता येते. मध्याकडून जसजसे परिसराकडे जावे तसतसे अणुकेंद्रीय द्रव्य विरळ होत जाते. इलेक्ट्रॉनांच्या प्रकीर्णनावरून काढलेले वरील द्रव्याच्या घनतेचे वितरण खाली दिलेल्या सूत्राने दाखवता येते :
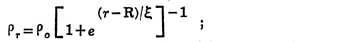
e= स्वाभाविक लॉगरिथमाचा आधारांक
या सूत्रातील ρr म्हणजे मध्यापासून r एवढ्या अंतरावरील घनता, ρo म्हणजे मध्यबिंदूवरील घनता. ξ हा प्रचल आहे. R या अंतरावर अणुकेंद्राची घनता ρoच्या निम्म्याने असते. R ला अणुकेंद्राची त्रिज्या असे म्हणतात. प्रयोगाचा निष्कर्ष R=1·07A 1/3 फेर्मी, या सूत्राने सांगता येतो. या निष्कर्षावरून कोणत्याही अणुकेंद्राची सरासरी घनता सारखी असते असे सिद्ध होते.
अणुकेंद्रीय प्रतिमान : अणुकेंद्रीय विक्रिया समजण्यासाठी अगर तिची उपपत्ती लावण्यासाठी अणुकेंद्रीय प्रतिमानाची आवश्यकता असते. निरनिराळ्या शास्त्रज्ञांनी मांडलेली प्रमुख प्रतिमाने खाली दिली आहेत :
बोर-प्रणीत द्रवबिंदू प्रतिमान अथवा तीव्र अन्योन्यक्रिया प्रतिमान : या प्रतिमानात अणुकेंद्रातील न्यूक्लिऑन परस्परास तीव्रपणे आकर्षितात असे मानले आहे. अणुकेंद्र आणि द्रवबिंदू यांच्यात कित्येक साम्ये आढळतात, ती अशी : (१) दोहोंमधील प्रेरणांमध्ये तीव्र आकर्षण, संपृक्तता आणि लघुक्षेत्रत्व हे गुण आहेत. (२) दोघांनाही पृष्ठताण आहे. (३) दोहांतील कणांना गतिज ऊर्जा असते. (४) ज्याप्रमाणे थेंबांचे बाष्पीभवन होते त्याप्रमाणे अणुकेंद्रातील कणांचे अगर कणसमूहाचे उत्सर्जन होते (उदा., α-उत्सर्जन). (५) अणुकेंद्राच्या भंजनाची उपपत्ती थेंबाच्या भंजनाप्रमाणे असते.
कवच प्रतिमान आणि कूट अंक : या प्रतिमानात न्यूक्लिऑनांची अन्योन्यक्रिया मंद असते असे मानतात. म्हणून हे प्रतिमान बोर-प्रणीत प्रतिमानाच्या उलट आहे.या कवच प्रतिमानाप्रमाणे अणुकेंद्रातील कोणताही न्यूक्लिऑन उरलेल्या A–1 न्यूक्लिऑनांनी निर्माण केलेल्या वर्चस्-कूपात (किमान वर्चसाभोवतीचे क्षेत्र) अडकलेला असतो. ⇨ पुंजयामिकी प्रमाणे अशा कूपात अनेक ऊर्जा-पातळ्या असतात व या पातळ्या भरण्यासाठी २, ८, २०, २८, ५०, ८२ आणि १२६ न्यूक्लिऑन आवश्यक असतात. या अंकांना ‘कूट अंक’ असे म्हणतात. जर अणुकेंद्रात प्रोटॉनसंख्या अथवा न्यूट्रॉनसंख्या कूट अंकाएवढी असेल तर ते अणुकेंद्र अधिक स्थिर असते, कारण अशा वेळी पातळ्या पूर्ण भरलेल्या असतात. कूट अंकांच्या अस्तित्वाचे पुरावे पुढील प्रमाणे : (१) अणुकेंद्राची बंधन-ऊर्जा कूट अंकाजवळ अचानक वाढते. (२)8O17,36Kr87 आणि 54Xe137 ही तीनच अणुकेंद्रे न्यूट्रॉनाचे उत्सर्जन करतात. 8O17 यात 8 हा ऑक्सिजनाचा अणुक्रमांक व 17 हा द्रव्यमानांक आहे आणि असेच इतरांच्या बाबतीत. यांपैकी प्रत्येकात कूट अंकापेक्षा एक न्यूट्रॉन अधिक आहे. (३) नैसर्गिकरीत्या किरणोत्सर्ग (अणुकेंद्र आपोआप फुटून कण अथवा किरण बाहेर पडणे) करणाऱ्या अणुकेंद्र श्रेणींचा शेवट शिशात होतो. अर्थात शिसे खूप स्थिर आहे. शिशाच्या अणुकेंद्रात ८२ प्रोटॉन व १२६ न्यूट्रॉन असतात. हे दोन्ही अंक कूट अंक आहेत. (४) न्यूट्रॉन-शोषणाचा काटछेद (प्रक्षेपित न्यू ट्रॉनाला लक्ष्य म्हणून उपलब्ध असलेले अणुकेंद्राचे परिणामी क्षेत्रफळ) कूट अंकाजवळ लघुतम असतो. (५) जेथे ऊर्जा-पातळ्या किंचित अपूर्ण असतात तेथे समघटकता (द्रव्यमानांक व अणुक्रमांक एकच असलेली परंतु भिन्न ऊर्जा-पातळ्यांत मोजण्याजोग्या कालापर्यंत अस्तित्वात असणारी दोन किंवा अधिक अणुकेंद्रे असणे) हा आविष्कार प्रकर्षाने आढळतो. (६) विद्युत् चतुर्ध्रुवी परिबल [→ अणुकेंद्रीय व आणवीय परिबले] कूट अंकाजवळ लघुतम असते. हे परिबल अणुकेंद्राचे गोल आकारापासून होणारे विचलन दाखवते. कूट अंकाजवळ परिबल लघुतम आहे म्हणजे अणुकेंद्र जवळ जवळ गोलाकार, अतएव अधिक स्थिर आहे. (७) याशिवाय समस्थानिक आणि समन्यूट्रॉन अणुकेंद्रांची विपुलता वगैरे इतर पुरावे पण आहेत.
सामूहिक प्रतिमान : अणुकेंद्रात सर्व न्यूक्लिऑनांना एकाच केंद्राकडे आकर्षण करणारी मध्यवर्ती प्रेरणा नसते त्यांमुळे त्यांतील न्यूक्लिऑन सामूहिक रीतीने कंपन अगर परिवलन पावतात. क्षुब्ध अणुकेंद्रांच्या ऊर्जा-पातळ्यांची उपपत्ती काही वेळा सामूहिक प्रतिमानाने लावता येते.
प्रकाशीय मेघ प्रतिमान : उच्च ऊर्जा असलेले न्यूट्रॉन अणुकेंद्राशी संयुक्त होण्याची संभाव्यता खूप कमी असते. असे न्यूट्रॉन अणुकेंद्रातून सहज बाहेर येतात. अणुकेंद्राच्या अन्योन्यक्रियेमुळे त्यांचे प्रकीर्णन होते. उच्च ऊर्जा असलेल्या न्यूट्रॉनाचे अणुकेंद्र अंशतः शोषण करीत असले, तरी ते प्रामुख्याने भिन्न प्रणमनांक (प्रणमनाच्या म्हणजे वक्रीभवनाच्या क्रियेच्या व्याख्येनुसार आलेले गुणोत्तर) असलेल्या पारदर्शक माध्यमाप्रमाणे वागते. प्रकाशकिरण विरळ मेघातून जाताना त्यांचे अंशतः प्रणमन (प्रकाशकिरणांचे एका माध्यमातून दुसऱ्या माध्यमात दिशा बदलून जाणे) होते ह्या साम्यावरून या प्रतिमानास वरील नाव दिले आहे.
अणुकेंद्रीय विक्रिया : विक्रियेचा काटछेद: लक्ष्यावर ρ, n, d, α आदी प्रक्षिप्त कणांचा मारा केला असता शोषण, क्षुब्धता, प्रकीर्णन आदी विक्रिया घडून येतात. लक्ष्याच्या दर चौ.मी. मध्ये N अणुकेंद्रे असून त्यांवर दर सेकंदास Ι कणांचा मारा होत असेल व त्यामुळे R विक्रिया होत असतील, तर त्या विशिष्ट विक्रियेचा काटछेद σ पुढील सूत्राने मिळतो : σ = R/IN. काटछेदाच्या क्षेत्रफळाचे एकक बार्न आहे एक बार्न =१०-२८चौ.मी.
अणुकेंद्रीय विक्रियेची साधने: H1, H2, H3 आणि He4 हे कण कुलंब-अवरोधामुळे उच्च ऊर्जा असल्याशिवाय अणुकेंद्रात प्रवेश करू शकत नाहीत. या कणांना प्रथम ‘व्हॅन डी ग्रॅफ जनित्र ’ अगर ‘सायक्लोट्रॉन’ यांसारख्या प्रवेगाने खूप ऊर्जा दिली जाते [→ कण वेगवर्धक] आणि मग त्यांचा मारा लक्ष्यावर केला जातो. यामुळे अणुकेंद्रीय विक्रियाहोऊ शकते. न्यूट्रॉनावर विद्युत् भार नसल्यामुळे त्याची ऊर्जा अगदी कमी असली तरी तो अणुकेंद्रात प्रवेश करू शकतो व त्यामुळे विक्रिया करू शकतो. विक्रियेसाठी लागणारे न्यूट्रॉन विक्रियकामधून (अणुभट्टीमधून अगर अन्य अणुकेंद्रीय विक्रियांमधून मिळू शकतात. इलेक्ट्रॉन, क्ष-किरण आगर गॅमा किरण अणूमधील इलेक्ट्रॉनावर जास्त विक्रिया करतात. उलटपक्षी अणुकेंद्रावर त्यांची विक्रिया क्षीण असते. यामुळे अणुकेंद्रीय विक्रियांसाठी त्यांचा उपयोग क्वचित प्रसंगी करतात.
प्रवेश आणि निर्गम मार्ग : समजा, प्रवेश X या लक्ष्यावर ह्या x प्रक्षिप्त कणांचा मारा होतो व नंतर विक्रिया घडते. विक्रियेनंतर Y हे अविशिष्ट अणुकेंद्र आणि y हा उत्सर्जित कण निर्गम-मार्गाने निघून जातात. X आणि Y यांचे द्रव्यमान x आणि y यांच्यापेक्षा खूप जास्त असते.
अणुकेंद्रीय विक्रियेचे Q ऊर्जामूल्य : Q ऊर्जा मूल्य = (विक्रियेनंतर उपलब्ध होणारी गतिज ऊर्जा)–
(विक्रियेपूर्वी असलेली गतिज ऊर्जा). जरूर ते गणितकृत्य करता, Q ऊर्जामूल्य = EY+Ey– Ex= [MX+ Mx–MΥ–My]c2. या समीकरणात EΥ, Ey आणि Ex अनुक्रमे Y, y आणि x यांच्या गतिज ऊर्जा आहेत. लक्ष्य स्थिर असते त्यामुळे त्याची गतिज ऊर्जा शून्य असते. Mχ, Mx, MΥ आणि My अनुक्रमे X, x, Y, y यांचे द्रव्यमान आणि c म्हणजे प्रकाशाचा वेग होय. हे समीकरण सापेक्षता सिद्धांताने सिद्ध करता येते.
उष्मोत्सर्गी आणि ऊष्माग्राही विक्रिया : ज्या विक्रियेचे Q मूल्य धन असते तिला ‘ऊष्मोत्सर्गी विक्रिया’ असे म्हणतात. ज्या विक्रियेचे Q मूल्य ऋण असते तिला ‘ ऊष्माग्राही विक्रिया’ म्हणतात. सर्व नैसर्गिक विक्रिया ऊष्मोत्सर्गी असतात. ऊष्माग्राही विक्रिया करण्यासाठी प्रक्षिप्त कणाला विवक्षित लघुतम ऊर्जेची आवश्यकता असते.
अणुकेंद्रीय विक्रियांचे अक्षय्यतेचे नियम : अणुकेंद्रीय विक्रिया होत असताना कित्येक गोष्टी कायम रहातात म्हणजे त्यांचे मूल्य विक्रियेपूर्वी आणि विक्रियेनंतर सारखे राहते. या नियमामुळे विक्रियेच्या संभाव्यतेवर बंधन पडते. या कायम राहणाऱ्या गोष्टी पुढे दिल्या आहेत : (१) एकूण विद्युत् भार, (२) न्यूक्लिऑन संख्या, (३) एकूण ऊर्जा = द्रव्यमान X c2+ गतिज ऊर्जा. सापेक्षता सिद्धांताप्रमाणे द्रव्यमानाचे ऊर्जेमध्ये रूपांतर होऊ शकते. द्रव्यमान X c2 = द्रव्यमानाची सममूल्य ऊर्जा. एकूण ऊर्जा अक्षय असते. (४) रैखिक संवेग (वस्तुमान X रैखिक वेग), (५) कोनीय संवेग (निरूढी परिबल X कोनीय वेग), (६) समता : तीव्र अन्योन्यक्रियेत ⇨ समता अबाधित राहाते. क्षीण अन्योन्यक्रियेत समता अबाधित राहत नाही (उदा., β उत्सर्जन). समता सम अगर विषम असू शकते. जर Ψ (–x, –y, –z) = Ψ (x, y, z) तर समता सम आणि Ψ (–x, –y, –z) = – Ψ (x,y,z) तर समता विषम असते. या समीकरणातील x, y, z हे अणुकेंद्रातील न्यूक्लिऑनाचे सहनिर्देशक (स्थानदर्शक संख्या) असून Ψ हे फलन आहे. प्रत्येक अणुकेंद्राला त्याच्या प्रत्येक संभाव्य स्थितीत सम अगर विषम अशी कोणती तरी समता असते. समतेच्या आणि कोनीय संवेगाच्या अक्षय्यतेच्या नियमांमुळे अवशिष्ट अणुकेंद्राच्या क्षुब्धावस्थेच्या संभाव्यतेवर बंधन पडते. (७) संख्यिकी : अणुकेंद्राकील न्यूक्लिऑनांची संख्या सम असेल तर बोस-आइन्स्टाइन आणि विषम असेल तर फेर्मी-डिरॅक सांख्यिकीचे पालन होते. अणुकेंद्रीय विक्रियेत न्यूक्लिऑनांची संख्या कायम राहते (नियम २), यामुळे संपूर्ण संचाची संख्यिकी पण तीच राहते [→ सांख्यिकीय भौतिकी].
अणुकेंद्रीय विक्रियेचे प्रक्षिप्त कणाच्या ऊर्जेवरील अवलंबित्व : प्रक्षिप्त कणाची ऊर्जा १० Mev अगर कमी असेल, तर विशिष्ट प्रकारच्या विक्रिया होतात, त्यास ‘लघु-ऊर्जा विक्रिया’ म्हणतात. उलटपक्षी, प्रक्षिप्त कणाची ऊर्जा २०० Mev अगर अधिक असेल तर उच्च ऊर्जा विक्रिया होतात. दोन्ही पद्धतींच्या विक्रियांची वर्णने पुढे दिली आहेत:
अणुकेंद्रीय विक्रिया लिहिण्याच्या पद्धती : नमुन्यासाठी पुढील विक्रिया घेऊ :
F19+ H1= O16 + He4 या समीकरणाचा अर्थ असा की, F19 या लक्ष्यावर H1 या प्रक्षिप्त कणाचा मारा केला असता O16 हे अवशिष्ट अणुकेंद्र राहते आणि He4 (किंवा α कण) चे उत्सर्जन होते. हीच विक्रिया खाली दिल्याप्रमाणे संक्षिप्तपणे लिहिता येते : F19(p, α)O16. कंसातील प्रथम कण हा प्रक्षिप्त कण असून द्वितीय कण उत्सर्जित कण आहे. कंसाबाहेर डाव्या बाजूस लक्ष्य व उजव्या बाजूस अवशिष्ट अणुकेंद्र आहे.
अणुकेंद्रीय विक्रियांचे व्युत्क्रमित्व : रासायनिक विक्रियांप्रमाणे अणुकेंद्रीय विक्रियासुद्धा काही वेळा उलट दिशेने करता येतात. उदा., N14(n, α)B11 आणि B11(α, n)N14 B10(n, α) Li7 आणि Li7(α, n)B10.
विक्रियांचे काही प्रकार : (अ) C12 (d ,dl) C12 (आ) C12 (d , p) C13 (इ) C12 (d , n) N13 आणि (ई) C12 (d , α) B10 या विक्रिया उदाहरणादाखल विचारात घेऊ. (अ) मधील dl ड्यूटेरॉनाची (d) ऊर्जा बदललेली आहे असे दाखवतो. ज्यावेळी लक्ष्य आणि अवशिष्ट अणुकेंद्र एकाच स्वरूपाचे असतात त्यावेळी प्रक्षिप्त कण आणि उत्सर्जित कण पण एकाच स्वरूपाचे असतात. अशा विक्रियेस ‘प्रकीर्णन’ असे म्हणतात. वरीलपैकी (अ) ही प्रकीर्णन विक्रिया आहे. प्रकीर्णन विक्रियेत प्रक्षिप्त कणाची ऊर्जा ही निर्गममार्गातील कणांच्या एकूण गतिज ऊर्जेएवढी असते, त्यावेळी त्या विक्रियेस स्थितिस्थापक प्रकिर्णन म्हणतात. याउलट अस्थितिस्थापक प्रकिर्णनात प्रक्षिप्त कणाच्या ऊर्जेच्या काही अंश अवशिष्ट अणुकेंद्र क्षुब्धावस्थेप्रत नेण्यात खर्च होतो. अर्थात निर्गममार्गाची एकूण गतिज ऊर्जा प्रक्षिप्त कणाच्या ऊर्जेहून कमी असते. वरीलपैकी (आ), (इ) आणि (ई) प्रकार द्रव्यांतरणाचे (एका मूलद्रव्याचे दुसऱ्यात रूपांतरण) अथवा विघटनाचे आहेत. कारण यांपैकी प्रत्येकात अवशिष्ट अणुकेंद्र लक्ष्याहून भिन्न आहे. या प्रकारांतसुद्धा अवशिष्ट अणुकेंद्र क्षुब्धावस्थेत असू शकते.
नीच-ऊर्जा विक्रिया यंत्रणा : यातील प्रमुख यंत्रणा खाली दिल्या आहेत :
(अ) संयुक्त अणुकेंद्र बनणे : या यंत्रणेप्रमाणे प्रक्षिप्त कण अणुकेंद्रात प्रवेश करतो आणि अणुकेंद्राशी एकरूप होतो. अशा रीतीने प्रक्षिप्त कण आणि लक्ष्य यांचे संयुक्त अणुकेंद्र तयार होते. संयुक्त अणुकेंद्र बहुधा क्षुब्धावस्थेत असते. त्याच्यामधील क्षोभ-ऊर्जा कालांतराने गॅमा उत्सर्जनाच्या रूपाने दिली जाते, अथवा एखाद्या न्यूक्लिऑनावर अगर न्यूक्लिऑन समूहावर केंद्रित होते व त्यामुळे तो न्यूक्लिऑन अगर न्यूक्लिऑन समूह उत्सर्जन पावतो. संयुक्त अणुकेंद्र अवस्था काही काळ म्हणजे सु. १०-१६ सेकंद [प्रक्षिप्त कणास अणुकेंद्रातून जाण्यास लागणाऱ्या वेळेपेक्षा (सु. १०-२२ से.) पुष्कळच जास्त] टिकत असल्यामुळे निर्गममार्गाचा प्रवेशमार्गाशी काहीएक संबंध राहत नाही. उदा., प्रवेशमार्ग (Na23+α), (Mg25+d), (Mg26+p) आणि (Al27+γ) या चारांपैकी कोणताही असला तरी त्यातील प्रत्येक प्रवेशमार्गापासून पुढे दिलेले पाचही निर्गममार्ग संभवतात. ते असे : (Na23+α), (Mg25+d),(Mg26+p), (Al27+γ) आणि ( Al26+n). या विलक्षण घटनेचे कारण चारही प्रवेशमार्गांनी Al27* हे संयुक्त अणुकेंद्र तयार होते. (* ही खूण क्षुब्धावस्था दाखवते). Al27* या अणुकेंद्राचा मूळ उत्पत्तीच्या प्रकाराशी संबंध न राहता ते निर्गममार्गाकडे वळते आणि त्याचे वर दिलेले पाचही निर्गममार्ग असल्यामुळे प्रत्येक प्रवेशमार्गापासून ते पाच निर्गममार्ग होऊ शकतात.
(आ)प्रत्यक्ष विक्रिया:कित्येक विक्रियांमध्ये प्रक्षिप्त कण अथवा त्याचा एखादा भाग अणुकेंद्राच्या पृष्ठभागाबरोबर अगर अणुकेंद्राच्या एखाद्या लहानशा भागाबरोबर विक्रिया करतो. अर्थात अशा वेळी संयुक्त अणुकेंद्र तयार होत नाही, तर पुढे दिल्याप्रमाणे विक्रिया घडते. ड्यूटेरॉनामध्ये प्रोटॉन आणि न्यूट्रॉन यांच्यामधील बंध तितकेसे बळकट नसतात. ड्यूटेरॉन एखाद्या अणुकेंद्रावर जोराने आदळल्यास त्यामधील घटक म्हणजे प्रोटॉन आणि न्यूट्रॉन हे विभक्त होतात आणि त्यांपैकी एक अणुकेंद्रात प्रवेश करतो व दुसरा निर्गम पावतो. ( d, p) आणि (d, n) या विक्रिया अशा प्रकारच्या म्हणजे अपखंडनाच्या आहेत. प्रक्षिप्त कण अणुकेंद्रातील एखादा कण शोषून घेतो त्यावेळी त्या विक्रियेस उद्ग्रहण विक्रिया म्हणतात. (p, d) आणि (d, H3) ही उद्ग्रहण विक्रियांची उदाहरणे होत.
(इ) कुलंब-क्षुब्धता : p, d आणि α कण कमी ऊर्जेचे असतात तेव्हा कुलंब-अवरोधामुळे अणुकेंद्रात ते प्रवेश करू शकत नाहीत. मात्र जलद बदलणाऱ्या विद्युत् चुंबकीय क्षेत्रामुळे अणुकेंद्र क्षुब्ध होते.
(ई)प्रकीर्णन : अणुकेंद्र आणि प्रक्षिप्त कण यांच्यामध्ये असलेल्या स्थितिज ऊर्जेमुळे प्रक्षिप्त कणाचे प्रकीर्णन होते. अशा वेळी संयुक्त अणुकेंद्र बनत नाही.
(उ) अणुकेंद्रीय द्विभंजन : या विक्रियेत अणुकेंद्राचे दोन (क्वचित अधिक) तुकडे पडतात. जड अणुकेंद्रावर न्यूट्रॉनांचा मारा करून अशी विक्रिया सुलभतेने घडवता येते. प्रत्येक खंड किरणोत्सर्गी असून या उत्सर्जनामुळे अधिक न्यूट्रॉन मिळतात. अशा विक्रियांपासून अणुभट्टी बनवता येते. [→ अणुकेंद्रीय अभियांत्रिकी अणुऊर्जा].
उच्च-ऊर्जा विक्रिया : विखंडन : प्रक्षिप्त कणाची ऊर्जा २०० Mev अथवा अधिक असल्यास तो संपूर्ण अणुकेंद्रातील अणुकेंद्राबरोबर विक्रिया करीत नसून अणुकेंद्रातील एखाद्या न्यूक्लिऑनावर तीव्र विक्रिया करतो. यामुळे अणुकेंद्राचे अगर त्याच्या मोठ्या भागाचे तुकडे होतात. अशा विक्रियेस विखंडन म्हणतात. उदा., ४०० Mev ऊर्जा असलेल्या α कणांचा आर्सेनिक (७५) या लक्ष्यावर मारा केला असता जे अनेक निर्गममार्ग होतात, त्यांपैकी एकामध्ये क्लोरीन (३८), १८ प्रोटॉन आणि २३ न्यूट्रॉन आढळून आले. या विक्रियेतील निर्गममार्गात असलेले प्रोटॉन आणि न्यूटॉन यांची संख्या जास्त असल्यामुळे अणुकेंद्राचे विखंडन झाले असे स्पष्टपणे दाखवतात. दुसऱ्या निर्गममार्गातही अणुकेंद्राचे विखंडन होते असे आढळून आले आहे.
अणुकेंद्रीय विक्रियांचे प्रकार :
(१) स्थितिस्थापक आणि अस्थितिस्थापक प्रकीर्णन : या प्रकारच्या विक्रियांची उदाहरणे मागे दिली आहेत.
(२) अणुकेंद्रीय द्विभंजन आणि विखंडन : या प्रकारच्या विक्रियांची उदाहरणे नीच ऊर्जा विक्रिया यंत्रणा आणि उच्च-ऊर्जा विक्रिया या परिच्छेदांत दिली आहेत.
(३) अपखंडन, उद्ग्रहण व कुलंब-क्षुब्धता : नीच-ऊर्जा विक्रिया यंत्रणा पहा.
(४) प्रोटॉन विक्रिया : प्रक्षिप्त प्रोटॉन बहुधा (p, γ) विक्रिया करतो. (p, α) विक्रियेची संभाव्यता कमी असते. कारण α कण संयुक्त अणुकेंद्रातून बाहेर पडताना त्याला वर्चस्-अवरोधातून पलीकडे जाणे जास्त कठिण होते. जास्त ऊर्जेच्या प्रोटॉनापासून (p, n) विक्रिया होऊ शकते.
(५) न्यूट्रॉनांच्या विक्रिया : कमी ऊर्जा असलेल्या न्यूट्रॉनांमुळे बहुशः (n, γ) विक्रिया होते. न्यूट्रॉनाची ऊर्जा जास्त असेल तर (n, p) आणि (n, α) विक्रिया होतात. जड अणुकेंद्रावर न्यूट्रॉनाचा मारा केला असता द्विभंजन विक्रिया होऊ शकते (नीच-ऊर्जा विक्रिया यंत्रणा पहा).
(६) α कणांच्या विक्रिया : कमी ऊर्जा असलेले α कण कमी द्रव्यमानाच्या अणुकेंद्रात शिरून (α, p) विक्रिया करतात. ऊर्जा जास्त असेल तर α कण मध्यम आणि जड अणुकेंद्रात प्रवेश करून (α, p) अथवा (α, n)
विक्रिया करतात.
(७) ड्यूटेरॉनांच्या विक्रिया : ड्यूटेरॉन (d, p), (d, n) आणि (d, α) विक्रिया घडवून आणतो.
(८) द्रव्यांतरण अथवा विघटन : या प्रकारात मूलद्रव्य बदलते अर्थात विक्रियेमुळे अणुकेंद्र बदलते.
अणुकेंद्राचे परिवलन परिबल (किंवा थोडक्यात ‘परिवलन’) :
अणुकेंद्राचा अंगभूत कोनीय संवेग ħ या एककात मोजतात.
ħ = h / 2π यातील h हा प्लांक स्थिरांक होय. परिवलनामुळे हा अंगभूत कोनीय संवेग उत्पन्न होतो. कोनीय संवेगाचे, निरपेक्ष मान आणि z अक्षावरील लंब प्रक्षेप, असे दोन प्रकार असून त्यांचा संबंध ⇨ पुंजयामिकीने ठरविला आहे. त्यांपैकी z अक्षावरील प्रक्षेप प्रयोगाने मोजला जात असल्यामुळे नित्याच्या व्यवहारात त्याचाच उपयोग केला जातो. एखाद्या अणुकेंद्राचे परिवलन एक आहे असे म्हटले असता त्याचा संपूर्ण अर्थ त्या अणुकेंद्राच्या परिवलनाचा z अक्षावरील महत्तम लंब प्रक्षेप ħ एवढा आहे असे होतो.
ज्या अणुकेंद्राचा द्रव्यमानांक सम असतो त्याचे परिवलन ०, १, २, … असे म्हणजे पूर्णांक असते याउलट अणुकेंद्राचा द्रव्यमानांक विषम असेल तर त्याचे परिवलन १/२, ३/२,… असे म्हणजे अर्ध अपूर्णांक असते. प्रत्येक न्यूक्लिऑनाचे परिवलन १/२ असल्यामुळे वरील नियम सिद्ध होतो. प्रयोगावरून अणूच्या ऊर्जा-पातळीची अतिसूक्ष्म रचना ठरविता येते आणि त्यावरून अणुकेंद्राचे परिवलन काढता येते.
पहा: सांख्यिकीय भौतिकी पुंजयामिकी अणुकेंद्रीय व आणवीय परिबले.
संदर्भ : 1. Kaplan, I. Nuclear Physics, New York, 1960.
2. Ramsey, N. F. Molecular Beams, 1956.
3. आठवले, वि. त्र्यं, संपा. अणुयुग, मुंबई, १९६९.
केळकर, वा. बा.
“