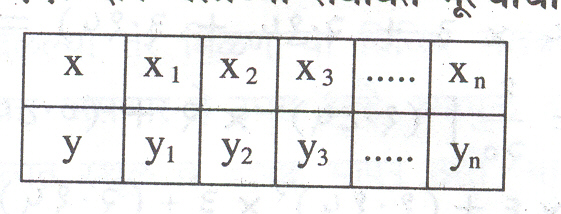सांख्यिकी : कोणत्याही प्रकारच्या संख्यात्मक स्वरूपातअसलेल्या माहितीसंबंधातील उपपत्ती व तिचा सैद्धांतिक अभ्यास याअर्थाने सांख्यिकी हे शास्त्र आता ओळखले जाते. अनेक विषयांच्याअभ्यासात सांख्यिकीचा वापर होतो. मराठी विश्वकोशात याच्याशीसंबंधित जीवसांख्यिकी, कृषि सांख्यिकी, वैद्यकीय सांख्यिकी, विमाविषयक सांख्यिकी, आर्थिक सांख्यिकी, अर्थमिती, निर्देशांक, जनांकिकी,आणि सांख्यिकीय भौतिकी या स्वतंत्र नोंदी आलेल्या आहेत.
ऐतिहासिक सर्वेक्षण आणि विषयांचे कार्यक्षेत्र : सांख्यिकीनावाने आज ओळखल्या जाणाऱ्या ज्ञानशाखेचा उगम म्हणून केवळ एकाच स्रोताकडे निर्देश करता येणार नाही. जवळजवळ तीन शतकांहूनअधिक काळात पसरलेल्या विविध स्रोतांमधून या शास्त्राची उभारणी व बांधणी झाल्याचे दिसून येते. जेव्हापासून राज्यव्यवस्थापन अस्तित्वातआले तेव्हापासून ‘वर्णनात्मक सांख्यिकी’ हा विषय या ना त्या स्वरूपात आल्याचे दिसून येईल. राज्य चालविण्यासाठी शासनाला पैसा लागतो व तो कर रूपाने मिळविला जातो. त्याचप्रमाणे शासनाला काहीप्रसंगी युद्धालाही तोंड द्यावे लागते व त्यासाठी राज्यातील सबळ व्यक्तींची सैन्यात भरती करावी लागते. त्यामुळे प्रजेमधील व्यक्तींचेउत्पन्न व मनुष्यबळ यांची माहिती गोळा करणे, त्या माहितीची योग्य मांडणी व परीक्षण करून त्यातून निर्णय घेणे या राज्यकारभाराच्या आवश्यक व महत्त्वपूर्ण कार्यातून ‘वर्णनात्मक सांख्यिकी’चा उदय झाला. जुगाराशी निगडित असलेल्या, संधीवर आधारित खेळांच्या अभ्यासातून ⇨संभाव्यता व ⇨संभाव्यता सिद्धांत आणि त्यांच्या उपयोगाने सांख्यिकीचा पृथक्करणात्मक अभ्यास हे विषय निर्माण झाले.सागरी विमाशास्त्राची सुरुवात पूर्वकालीन भूमध्य समुद्र भागातीलचाचेगिरी व जहाजांचे अपहरण यातून झाली. आधुनिक जीवन विम्याचा उगम १६६५ मध्ये उद्‌भवलेल्या इंग्लंडमधील प्लेगच्या प्रादुर्भावात आहे. त्रुटींचे शास्त्र, सहसंबंधाची उपपत्ती, प्रयोगांचा अभिकल्प, कालश्रेणी विश्लेषण, घटकांचे विश्लेषण व अनुक्रम उपपत्ती, काय-वर्ग(χ2) रीतींची उपपत्ती या विषयांची मुळे अनुक्रमे खगोलशास्त्र, जीवशास्त्र,कृषिशास्त्र, अर्थशास्त्र व हवामानशास्त्र, मानसशास्त्र आणि समाजशास्त्र याशास्त्रांत सापडतात. मानवी जीवनाचा प्रत्येक कालखंड व जवळजवळ प्रत्येक शास्त्रीय विषय यांचा काही ना काही हातभार सांख्यिकीच्यावाढीला व प्रगतीला लागल्याचे आढळून येते.
जवळजवळ १८५० सालापर्यंत राज्यकारभारात लागणारी व त्यासाठीगोळा केलेली, पूर्णतः नव्हे, तरी मुख्यतः आकडेवारी असलेली माहिती इतपत अर्थानेच सांख्यिकी ही संज्ञा उपयोगात येत असे. त्यानंतरच्याकाळात या संकल्पनेच्या अर्थाचे आणि उपयोगाचे उदात्तीकरण वव्यापकीकरण होऊन मानवी जीवनाशी संबंधित विविध निरीक्षणांतूनउत्पन्न होणाऱ्या निरनिराळ्या प्रकारच्या संख्यात्मक माहितीच्या सर्वांगीण
अभ्यासाला सांख्यिकी ही संज्ञा वापरात येऊ लागली. आज सांख्यिकीही ज्ञानशाखा संभाव्यता सिद्घांतावर मोठ्या प्रमाणावर आधारलेलीआहे. अशा या संभाव्यता सिद्घांताचा उगम खूप पूर्वी म्हणजे⇨किस्तीआन हायगेन्झ (१६५७) यांचे कार्य, ⇨ब्लेझ पास्कालव ⇨प्येअर द फेर्मा यांच्यातील पत्रव्यवहार आणि ⇨झाक बेर्नुली(१७१३) यांचे कार्य यातून झाला असल्याचे दिसून येते. त्यामानानेसांख्यिकीमध्ये संभाव्यताशास्त्राच्या वापराला उशीरा सुरुवात झाली.सांख्यिकीच्या संदर्भात महत्त्वाचा व लक्षात घेण्याचा भाग असा की,सांख्यिकीशास्त्रातील रीतींचा वापर करताना संभाव्यतेची आकडे मोडही नेहमी संधीवर आधारित खेळांतल्याप्रमाणे नेहमी प्रयोगपूर्वकरायची नसते, तर उपयोजित प्रयोगातील अवलोकने लक्षात घेऊन तीठरवायची असते. विशेषतः जेव्हा प्रतिदर्श घेण्यात येतो, तेव्हा त्या प्रतिदर्शातील अवलोकनांवरून संभाव्यता काढाव्या लागतात. ⇨प्येअरसीमाँ मार्की द लाप्लास, मार्क्वस द काँडॉरसे (१७८५) व नंतर⇨ सिमेआँ देनिस प्वासाँ यांच्या कार्यातून संभाव्यताशास्त्राचा उपयोगव्यवहारातील समस्यांमध्ये करण्यास सुरुवात झाली.
आधुनिक सांख्यिकीची सुरुवात साधारणतः १८९० मध्ये झालीअसे म्हणता येईल. त्यानंतर जवळजवळ ४० वर्षे सांख्यिकीमधीलविकास व वाढ मुख्यतः इंग्लंडमध्ये झाली. अर्थात या काळातच,विशेषतः ⇨अंद्र्येई अंद्र्येयेव्ह्यिच मार्को व्ह व अलेक्झांडर कुप्रोव्हयांनी रशियात केलेल्या, संभाव्यताशास्त्रातील योगदानांचा विसर पडूनचालणार नाही. गणितीय सांख्यिकी (या संज्ञेऐवजी आधुनिक सांख्यिकीय उपपत्ती ही संज्ञा अधिक उचित ठरेल ) नावाने ओळखल्याजाणाऱ्या नव्या शाखेचा उदय हळूहळूच झाला. उपयोजित गणितातीलयामिकी यासारख्या शास्त्रातील गणिती पद्घती संख्यात्मक माहितीच्याअभ्यासास उपयोगी पडणाऱ्या नव्हत्या. व्यक्तींच्या उंचींचा समूह(समुच्च्य, समुदाय), शेतीतील उत्पन्नांचा समूह, व्यक्तींच्या उत्पन्नांचासमूह, बंद डब्यातील वायूच्या कणांच्या हालचालींच्या माहितींचासमूह, आकाशातील ग्रह-ताऱ्यांच्या भ्रमंतीसंबंधी माहितींचा समूह, एखाद्यां औषधावर प्राण्यांनी दाखविलेल्या प्रतिक्रियात्मक अवलोकनांचा समूहंअशा समूह म्हणून काही सारखेपणा असणाऱ्या (परंतु प्रत्येक समूहाचेस्वतःचे असे निरनिराळे गुणधर्म दाखविणाऱ्या) समूहांच्या गुणधर्मांच्याअभ्यासासाठी निराळ्या गणिती पद्घती पाहिजे होत्या. या विचारामागचीसंकल्पना ⇨एमील बॉरेल (१८७१–१९५६) यांनी पुढील शब्दांतअधिक प्रकटपणे व अगदी सुयोग्य प्रकारे मांडली आहे : ‘गणितीयसांख्यिकीचा मूलभूत प्रश्न, संधीवर आधारित नाणेफेकीसारखा प्रयोगकेल्यास लागू शकणाऱ्या निकालाची संभाव्यता व एखाद्या घटनेतीलसापेक्ष वारंवारता यांच्यात साम्य आढळून येईल अशी रचना शोधूनकाढणे हा आहे’. नाणेफेकीसारख्या पुनःपुन्हा करता येणाऱ्या प्रयोगातआढळणारी प्रमाणबद्घता किंवा नियमितता सतराव्या शतकातीलगॅलिलीओच्या कार्यात स्पष्टपणे आढळून येते. गणितीय सांख्यिकी याशाखेचा विकास होण्यात लॅम्बर्ट अडॉल्फ झाक केटले, ⇨गुस्टाफटेओडोर फेक्नर, ⇨कार्ल पीअर्सन, ई. चूबर, जी. यू . यूल, व्ही. टी.बर्टकेव्हिच यांचे योगदान सुरुवातीला महत्त्वाचे ठरले.
सांख्यिकीमध्ये वंटन ही अतिशय महत्त्वाची संकल्पना आहे. वंटनाचीकल्पना प्रथम ताऱ्यांच्या गतीशी निगडित मापनांवरून आली असावी.निरनिराळ्या प्रशिक्षित असलेल्या निरीक्षकांनी एकाच वस्तूसंबंधीकेलेल्या त्याच प्रकारच्या मापनांमध्येही फरक आढळून येतो. मापनांतीलया विविधतेचा अभ्यास होऊन त्याबद्दल निरनिराळे सिद्घांत मांडले गेले.थॉमस सिंप्सन यांनी प्रथम (१७५७) अखंड वंटनाची कल्पना मांडली.अठराव्या शतकाच्या अखेरपर्यंत लाप्लास व ⇨कार्ल फीड्रिख गौसयांनी अनेक गणिती वंटनांचा अभ्यास केला व त्यातील सर्वांत महत्त्वाच्या प्रसामान्य वंटनाचा शोध लावला. लंडनमध्ये कार्ल पीअर्सन व वॉल्टरवेल्डन यांनी विविध क्षेत्रांतील वंटनाचा शोध लावला. विशेषतः प्रयोगव निरीक्षण यांच्यातून मिळणाऱ्या वारंवारता वंटनांशी जवळजवळजुळतील-मिळतील अशा वंटन-वक्रां चा शोध पीअर्सन यांनी लावला.स्वीडनमध्ये कार्ल शार्ली, हॉलंडमध्ये ⇨याकोबस कॉर्नेलिस कापटाइनव जोहान व्हान यूव्हेन आणि इटलीत ⇨व्हिलफेदो पारेअतोयांचेया क्षेत्रातील कार्य उल्लेखनीय आहे. [⟶ वंटन सिद्धांत].
एकोणिसाव्या शतकाच्या सुरुवातीला मुख्यतः केटले यांच्या कार्यामुळे सजीवांवरील अवलोकनात वारंवारता वंटन असू शकते हे ध्यानात आले. १८८० साली ⇨सर फान्सिस गॉल्टन व कार्ल पीअर्सन यांनी वंटन काही वेळा समप्रमाणित तर काही वेळा असमप्रमाणित असू शकते हे दाखवून दिले (असमप्रमाणता व शिखरीपणा या गुणधर्मांच्या मापनासंबंधी पुढे वर्णन दिले आहे). १८९० सालीगॉल्टन यांच्या संशोधनातून प्रेरणा घेऊन पीअर्सन यांनी दोन चलांच्या वंटनांचा अभ्यास सुरू केला. यामध्ये दोन गुणविशेषांच्या (उदा., उंचीव वजन किंवा डोळ्यांचा व कातडीचा रंग) संबंधाचा अभ्यास अभिप्रेत होता. यातूनच पुढे गुणात्मक गुणधर्मातील साहचर्य व आसंग आणिपरिमापनात्मक गुणधर्मातील सहसंबंध व समाश्रयण या संकल्पनांचाउदय झाला. तेव्हापासून अशा सांख्यिकीय संबंधांचा सखोल अभ्यास चालू झाला. सुरुवातीला एकरेषीय व नंतर वक्र रेषीय समाश्रयणाचे संशोधन झाले. यात फिशर यांचे योगदान महत्त्वाचे आहे.
अर्थशास्त्राचे प्राध्यापक ⇨फान्सिस इसीड्नो एजवर्थ यांना निवडणुकींच्या निकालात सांख्यिकीय नियमितता आढळून येत होती. तत्पूर्वी अठराव्या शतकाच्या मध्यापासून यूरोपमधील काही राष्ट्रांनी जनगणना करण्यास सुरुवात केली होती. या आधारसामग्री गोळा करण्याच्या धर्तीवर मोठ्या समष्टीमधून (विविध वैज्ञानिक निरीक्षणांच्या समूहातून) प्रतिदर्श घेऊन त्यांच्या अभ्यासावर समष्टीविषयी अनुमाने काढण्याचे प्रयत्न होऊ लागले. प्रतिचयन म्हणजेच योग्य पद्धतीने आधारसामग्री (प्रदत्) जमा करणे ही सांख्यिकीतील महत्त्वाची समस्या आहे. त्याशिवाय प्रतिदर्शातील यदृच्छता हा मूलभूत, परंतु तसाच नाजूक प्रश्न आहे. यदृच्छतेचे महत्त्व ध्यानात आल्यावर योग्य अर्थाने यादृच्छ प्रतिदर्श घेण्याच्या प्रश्नाला बरेच महत्त्व आले. त्यातून प्रत्यर्थि अभिनतीसारखे नवे प्रश्न निर्माण झाले. शेवटी सामाजिक संशोधनासाठी समाजातून प्रतिदर्श घेण्याचे, मानसशास्त्रावर आधारित एक शास्त्रच बनले. १९६०पर्यंत सामाजिक सर्वेक्षणातील त्रुटी बऱ्याच अंशी नियंत्रित झाल्या.कोणतेही यंत्र तयार करताना अथवा घर बांधताना आधी त्याचा नकाशातयार हवा. त्याचप्रमाणे प्रतिदर्श घेण्याच्या पद्घतीची आखणी महत्त्वाचीआहे, या कल्पनेला मान्यता लाभली. [⟶ सामाजिक सर्वेक्षण पद्घतिप्रतिदर्श सर्वेक्षण सिद्धांत ].
एकोणिसाव्या शतकाच्या पूर्वार्धातील कार्ल फ्रीड्रिख गौस यांच्याकामात सोपी प्रतिदर्शी वंटने दिसून येतात. १८७५ मध्ये जर्मन भूगणितज्ञफ्रीड्रिख हेलमर्ट यांनी प्रसामान्य वंटनातून घेतलेल्या प्रतिदर्शाच्या प्रचरणाचेवंटन मांडले, तेव्हा काय-वर्ग वंटन दृष्टोत्पत्तीस आले. तेच काय-वर्गवंटन पुन्हा १९०० मध्ये पीअर्सन यांनी स्वतंत्र रीत्या, अगदी निराळ्यासंदर्भात ( वंटनासंदर्भात ‘गुडनेस ऑफ फीट’च्याकसोटीसाठी ) शोधूनकाढले. तसेच पीअर्सन यांनी प्रतिदर्शाच्या विविध मापनांतीलप्रमाणित त्रुटीसाठी अनंतवर्ती सूत्रे विकसित केली. लहान आकार-विस्ताराच्या प्रतिदर्शाच्या अभ्यासात उद्‌भवणाऱ्या अडचणींचे निराकरण,खूप प्रयत्न करूनही, पीअर्सन करू शकत नव्हते. शेवटी १९०८ मध्ये‘स्टूडंट’ हे टोपणनाव धारण करणाऱ्या विल्यम गॉसेट नामक पीअर्सनयांच्या विद्यार्थ्याने लहान आकाराच्या प्रतिदर्शाच्या अभ्यासात उपयोगीपडेल असे वंटन शोधले. स्टूडंटचे t – वंटन म्हणून ते सुप्रसिद्घ आहे.स्टूडंट व ⇨सर रॉनल्ड एल्मर फिशर यांनी प्रतिदर्शी वंटनाच्याअभ्यासात एक नवीन युग निर्माण केले. पुढील तीस वर्षांत फिशरयांनी या विषयात नवीन अशी मोलाची भर घातली. त्यांनी एकामागोमाग एक, प्रसामान्य समष्टीतून घेतलेल्या प्रतिदर्शातील सहसंबंधगुणांक, समाश्रयणांक इत्यादींसाठी प्रतिदर्शी वंटनांचा शोध लावला.F या प्रतिदर्शी वंटनांचा शोध स्नेडेकॉर यांनी लावला. इंग्लंडमधील जॉनविशार्ट, अमेरिकेतील हॅरॉल्ड होटेलिंग व सॅम्युअल विल्क्स, भारतातील एस्. एन्. रॉय व राजचंद्र बोस या संशोधकांनी यांत – विशेषतः⇨बहुचरात्मक विश्लेषणामध्ये–नवीन शोध लावून मोलाची भरघातली. त्यानंतर टी. डब्ल्यू. अँडरसन यांनी या काहीशा अवघडविषयाच्या ज्ञानाची क्षितिजे अधिक विस्तारली. अशा प्रकारे प्रतिदर्शीवंटनासंबंधी शोध लागत असतानाच आसन्नीकरणाच्या पद्घती मिळविण्यात आल्या. येथेही फिशर आघाडीवर होते. १९२८ मधील त्यांचा‘ k-संख्यांक’ची संकल्पना मांडणारा शोधनिबंध महत्त्वाचा ठरला.
इ. स. १९२५ ते १९३५ च्या दरम्यान सांख्यिकीच्या दोन शाखांचाउदय झाला. फिशर यांच्या प्रेरणेने ‘आगणन किंवा आकलन’ आणिइगॉन पीअर्सन (कार्ल पीअर्सन यांचे पुत्र) व जर्झी नेन यांच्या प्रेरणेनेनिर्माण झालेली गृहीतकांचे परीक्षण या त्या दोन शाखा होत. तसे पाहताऐतिहासिक दृष्ट्या लाप्लास यांनी पहिले गृहीतक-परीक्षण केले होते.परंतु त्यांची पद्घत गणिताधिष्ठित नव्हती ती अधिक अंतःस्फूर्त होती.[⟶ सांख्यिकीय अनुमानशास्त्र].
फिशर यांच्या कार्यामुळे सांख्यिकीकडे बघण्याची नवी दृष्टी निर्माणझाली. १९२२ च्या सुमारास फिशर यांनी ‘अवाढव्य आधारसामग्री तघट करणे’ हा सांख्यिकीय पद्घतीचा महत्त्वाचा हेतू आहे असे सांगूनया पद्घतीने हाताळावयाच्या पुढील तीन मूलभूत प्रश्नांकडे लक्ष वेधले :अभ्यासासाठी घेतलेली आधारसामग्री कोणत्या प्रकारच्या समष्टीमधूनआली आहे ते शोधणे, त्या समष्टीच्या प्रचलांविषयी अनुमान बांधणे आणि‘आगणना’संबंधीच्या संभाव्यशास्त्राशी निगडित प्रश्नांचा मागोवा घेणे.
वरील प्रगतीबरोबरच १९२० ते १९४० च्या दरम्यान फिशर यांच्यासंशोधनावर आधारित प्रयोग व सर्वेक्षणांच्या अभिकल्पाचा सिद्घांतनिर्माण होत होता. जर्मनीतील व्हिल्हेल्म लेक्सिझ यांच्या कल्पनेवरआधारित विचरण-विश्लेषणाची कल्पना फिशर यांनी अधिक व्यापक वसूक्ष्म केली. आता ⇨विचरणाचे विश्लेषण हे सांख्यिकीतील एकमहत्त्वाचे साधन आहे. नंतर ही कल्पना सहप्रचरणाला सुद्घा लावण्यातआली. [⟶ प्रयोगांचा अभिकल्प].
दुसऱ्या महायुद्घाच्या काळात इंग्लंडमधील जॉर्ज बर्नार्ड व अमेरिकेतीलअब्रा हम वॉल्ड यांनी अनुकमात्मक प्रतिदर्शन या उपपत्तीचा शोधलावला. पुढे वॉल्ड यांनी अधिक व्यापक अशी निर्णय-फलांची उपपत्ती(निर्णयफलनांची उपपत्ती) वापरात आणली. [⟶ निर्णय पद्घति].
दुसऱ्या महायुद्घानंतर ⇨यदृच्छ प्रक्रिया ही संभाव्यताशास्त्राचीनवीन शाखा जन्माला आली. १९४५ नंतर या विषयावर बरेच शोधनिबंधप्रसिद्घ झाले. त्यांतील बरेच फ्रेंच व रशियन शास्त्रज्ञांचे होते. १९५०नंतर प्रसामान्य वंटनावर आधारित ⇨बहुचरात्मक विश्लेषण याशाखेचे व्यापकीकरण होऊन बहुचर समस्यांची व्यापक उपपत्तीजन्माला आली. त्यात फलनात्मक विश्लेषण, विहित सहसंबंध विश्लेषण(ज्यातसहसंबंधाची संकल्पना दोन सदिशांना लावण्यात आली), वंटनसिद्घांत आणि प्रतिदर्श पद्घतींचे अनेकमितीय उदाहरणांसाठी व्यापकीकरण या विषयांचा समावेश होतो. फ्रान्समध्ये एमील बॉरेल व पॉललेव्ही तर इटलीमध्ये कोरॉडो जीनी यांच्या नेतृत्वाखाली या विषयावरकार्य होत होते.
दुसऱ्या महायुद्घाच्या शेवटी सांख्यिकीचा अभ्यास व संशोधनाच्याबाबतीत सर्व राष्ट्रीय मर्यादा कोलमडू लागल्या व सर्व जगभर याविषयाचा प्रचंड प्रसार आणि विकास होऊ लागला. सांख्यिकी ही सर्वशास्त्रे, तंत्रविद्या व औद्योगिक जगत यांतील महत्त्वाची आणि सर्वमान्यज्ञानशाखा झाली. विशेष म्हणजे सजीव विश्वाबद्दलच्या संशोधनाचे देखीलहे एक उत्तम साधन बनले. भारतातील ⇨प्रशांत चंद्र महालनोबीस,⇨ कल्यमपुडी राधाकृष्ण राव, एस्. एन्. रॉय, राजचंद्र बोस, ⇨पांडुरंग वासुदेव सुखात्मे, आर्. आर्. बहादुर आणि व. शं. हुजूरबाजार हेसुप्रसिद्घ सांख्यिकीविज्ञ म्हणून ओळखले जातात. [⟶ अनुकमात्मकविश्लेषण अप्राचलात्मक पद्घति गुणवत्ता नियंत्रण जनांकिकी].
या विषयाचा आवाका आता एवढा प्रचंड वाढला आहे की,जवळजवळ प्रत्येक विषयात सांख्यिकीचा उपयोग होत आहे. ज्याप्रश्नांच्या सोडवणुकीसाठी असा उपयोग होऊ शकतो अशांपैकी काहीसमस्या वानगीदाखल पुढे दिल्या आहेत : साहित्याचे परीक्षण व विश्लेषणकरून त्या साहित्याचा अज्ञात लेखक कोण या निर्णयाप्रत येणे विविधखतांमधून एखाद्या पिकाच्या उत्तम उत्पन्नासाठी योग्य खत निवडणेविविध उपलब्ध औषधांमधून रुग्णाचा वयोगट, लिंग, रोगापासून कितीकाळ त्रास होतो आहे इ. घटक विचारात घेऊन अधिक योग्य औषधाचीनिवड करणे विविध खेळाडूंनी किती चेंडू खेळून किती धावा केल्याअशांसारख्या आधारसामगीवरून ‘सातत्य असणे’ या गुणधर्मानुसारखेळाडूंचा कम लावणे परीक्षेत मिळालेल्या गुणांवरून विद्यार्थ्यांनाअक्षरदर्जा प्रदान करणे कारखान्यात तयार होणाऱ्या मालाचे गुणवत्तापरीक्षण करणे प्रश्नावली तयार करून विविध सामाजिक, आर्थिक वराजकीय प्रश्नांवर जनतेने प्रश्नावलीतील प्रश्नावर दिलेल्या उत्तरांचे विश्लेषणकरून या प्रश्नांवर जनतेच्या मतांचे अनुमान बांधणे कोणत्याही अवलोकन-समूहात निरनिराळ्या अवलोकनांमध्ये जे फरक आढळतात तेफरक ज्याकारणांमुळे निर्माण झालेले असतात त्या कारणांमधील महत्त्वाचीकारणे कोणती ते ठरविणे. जीवनाच्या विविध अंगांत सांख्यिकीच्याहोणाऱ्या उपयोगामुळेच जीवसांख्यिकी, कृषि सांख्यिकी, आर्थिकसांख्यिकी, वैद्यकीय सांख्यिकी, विमाविषयक सांख्यिकी अशा विविधशाखांची निर्मिती व वाढ झाली आहे. हे सर्व विचारात घेतल्यावर‘सांख्यिकी ही वैज्ञानिक पद्घतीची तंत्रविद्या आहे’ ही प्रशांत चंद्रमहालनोबीस यांनी केलेली व्याख्या यथायोग्य असल्याची जाणीव होते.
सांख्यिकीमध्ये अभ्यासल्या जाणाऱ्या संख्यात्मक माहितीचामहत्त्वाचा व मूलभूत विशेष लक्षात ठेवावयास हवा. तो असा आहे की,ती माहिती एकाच मापनापुरती मर्यादित नसून अनेक मापनांचा समुच्च्यअसते. अशी माहिती तांत्रिक दृष्ट्या ज्यालासमष्टी म्हणतात अशासमुच्च्यातून आलेली असते. एका व्यक्तीचे वजन दुसऱ्या व्यक्तीच्यावजनाबरोबर नसते ते व्यक्तीगणिक बदलत असते परंतु अनेक व्यक्तींच्यावजनांच्या माहितीवरून त्या व्यक्ती ज्यासमुच्च्यातून येतात त्या समष्टीतीलव्यक्तींच्या वजनाबद्दलचे विश्वासार्ह निर्णय काढता येतात आणि तेसांख्यिकी या शास्त्राचे कार्य आहे.
सांख्यिकीय आधारसामगीची साधने : सांख्यिकी प्रक्रियाउपयोगात आणण्यासाठी आधारसामग्री गोळा करण्याचे चार प्रकारआहेत : (१) ग्रंथालय पद्घती, (२) प्रयोग पद्घती, (३) निरीक्षण पद्घतीआणि (४) प्रश्नावली पद्घती.
(१) रिझर्व्ह बँक, जनगणना खाते, शासनाचे विविध विभाग, औद्योगिक संकुले, निमशासकीय व बिगरशासकीय सामाजिक संस्था या सतत काही सर्वेक्षणे करून माहिती गोळा करतात व त्यांचे अहवाल प्रसिद्घ करीत असतात. असे प्रसिद्घ झालेले अहवाल, विश्वकोश व इतर मार्गदर्शक पुस्तके-पुस्तिका यांतून माहिती घेणे ही माहिती मिळविण्याची ग्रंथालय पद्घती होय. (२) निरनिराळ्या वयोगटांतील व रोगापासून त्रास होण्याच्या विविध कालावधीतील रुग्ण व त्याचबरोबर निरोगी स्त्री-पुरुष-मुले घेऊन त्यांच्यावर निरनिराळ्या औषधांचा व ते देण्याच्या पद्घतींचा (उदा., तोंडावाटे वा इंजेक्शनद्वारे) कसा व काय परिणाम होतो हे पाहण्यासाठी त्याचप्रमाणे कृषी क्षेत्रात वेगवेगळ्या खतांचा धान्याच्या विविध जातींच्या उत्पन्नावर काय परिणाम होतो हे जोखण्यासाठी किंवा सामाजिक क्षेत्रात विविध प्रकारच्या जाहिरातींचा समाजातील निरनिराळ्या घटकांवर कितपत व कसा प्रभाव पडतो हे जाणण्यासाठी प्रयोग आयोजित करून माहिती गोळा करणे या पद्घतीला प्रयोग पद्घती म्हणतात. (३) हवेच्या तापमानात व दाबात काय फरक होत आहेतयांचे, भूकंप झाले असता त्या संबंधातील, तसेच समुद्राच्या भरती-अहोटी, आकाशातील तारे-ग्रह यांच्या गती किंवा त्यांच्यात होणारेफरक या प्रकारचे निरीक्षण करून आधारसामग्री गोळा करणे या पद्घतीला निरीक्षण पद्घती म्हणतात. (४) सामाजिक, राजकीय, आर्थिक, धार्मिक वशैक्षणिक प्रश्नांवर विविध स्तरांतील, वयोगटातील, समाजगटातीलव्यक्तींचे विचार व मते जाणून घेण्यासाठी प्रश्नावल्या तयार करून स्वयंसेवकांतर्फे अशा व्यक्तींनाभेटून किंवा टपालाद्वारे त्यांतील प्रश्नांची उत्तरेजमा करणे ही प्रश्नावली पद्घत होय.
स्वतः प्रश्नावली, प्रयोग व निरीक्षणे करून आधारसामग्री मिळविल्यास त्या साधनांना माहितीची प्राथमिक साधने म्हणतात. दुसऱ्यांनीकेलेल्या सर्वेक्षणांच्या, प्रयोगांच्या व निरीक्षणांच्या अहवालातून माहितीमिळविली तर माहिती मिळविण्याच्या त्या साधनांना माहितीची दुय्यम साधने म्हणून संबोधिले जाते.
आधारसामग्रीचे प्रतिरूपण : बहुतेक वेळा गोळा केलेलीआधारसामग्री म्हणजे माहितीचा प्रचंड साठा असते. त्याच्या साध्यानिरीक्षणाने केवळ अगदी वरवरच्या गोष्टी ध्यानात येतात. उदा., शालान्तपरीक्षेला बसलेल्या सर्व हजारो-लाखो विद्यार्थ्यांचे गुण दाखविणाऱ्यापुस्तिकेच्या पृष्ठांवर नजर टाकली तर, फार तर बहुतेक विद्यार्थ्यांना ४०ते ५० दरम्यान गुण मिळाले आहेत व सर्वांत अधिक गुण मिळविणाऱ्या विद्यार्थ्यांस ९७ गुण मिळाले आहेत, अशी एखादी समजूत होऊ शकते.ती समजूतसुद्घा योग्यच आहे का हे नक्की सांगता येत नाही. ही माहिती योग्य व खऱ्या प्रकारे समजण्यासाठी या कच्च्या माहितीची विशेष प्रकारेमांडणी करावी लागते. याकरिता या आधारसामग्रीचे वर्गीकरण करून तीतक्त्यांच्या अथवा काही आलेख, आकृत्या वा चित्रांच्या स्वरूपातमांडण्याची पद्घत अंगिकारिली जाते. अशा मांडणीमुळे या माहितीबद्दलअधिक अर्थबोध होण्याची शक्यता निर्माण होते. या पद्घतीचे फायदे असेआहेत : (१) अनावश्यक तपशील टाळता येतो, (२) माहितीच्यानिरनिराळ्या भागांत आढळणारे साधर्म्य व विसंगती वाचकांच्या नजरेसआणून देता येते व (३) ही मांडणी बघणारी व्यक्ती आपल्या मनातकाही सोप्या तुलना करून काही विश्वशासार्ह निष्कर्ष काढू शकते.आधारसामग्रीच्या अशा मांडणीचे व प्रतिरूपणाचे प्रकार यांचे वर्णन पुढेदेण्यात आले आहे.
जी माहिती गोळा करण्यात येते ती मुख्यतः दोन प्रकारची असूशकते. बऱ्याच वेळा माहितीचे मापन करता येते व ती संख्या वापरूनव्यक्त करता येते. उदा., झुडपांची उंची ४५ सेंमी. आहे, रोग्याचे वजन६५ किग्रॅ. आहे, शहराचे तापमान ३९० से. आहे, गव्हाचे पीक ५७०टन आले आहे, तिसऱ्या दिवशी सभेला २,००० माणसे जमली होतीइ. वस्तूच्या वा व्यक्तीच्या अशा गुणधर्मांना परिमापनात्मक गुणधर्मम्हणतात. काही वेळा मात्र माहिती संख्या वापरून व्यक्त करता येतनाही. उदा., डोळ्यांचा रंग ( काळा, घारा, हिरवा, निळा ), व्यक्तीशिक्षित वा अशिक्षित असणे, व्यक्ती विवाहित किंवा अविवाहित असणे,व्यक्ती दोषयुक्त अथवा दोषविरहित असणे इत्यादी. व्यक्तींच्या अथवावस्तूंच्या अशा संख्या वापरून मोजता न येणाऱ्या गुणधर्मांना गुणात्मकगुणधर्म म्हणतात.
वारंवारता कोष्टक, सारणी वा तक्ते : उंची, वजन, परीक्षेतील गुण,व्यक्तींचे उत्पन्न, कारखान्यातील वा शेतीतील उत्पन्न अशा अनेक बाबींबद्दल निरनिराळ्या ठिकाणांहून संख्यांच्या स्वरूपात माहिती जमविलीजात असते. लोकांना तिचे आकलन चांगले व्हावे म्हणून, तसेच यामाहितीबद्दल जमा झालेल्या सर्व संख्यांच्या जंजाळातून काय अनुमानकाढता येईल हे पाहण्यासाठी या सर्व संख्या कोष्टकांच्या स्वरूपात व्यवस्थित मांडल्या जातात. उदा., ‘x’ या चलावर माहिती गोळा करीतअसताना हे चल x1, x2, …, xn अशी एकूण ‘n’ मूल्ये घेत आहे असे समजू . एकूण ‘N’ संख्या गोळा झाल्या असून त्यांपैकी f1 संख्यांचे मूल्य प्रत्येकी x1 आहे, f2 संख्या प्रत्येकी x2 आहेत, ….. , fn संख्या प्रत्येकी xn आहेत असे समजा. याचाच अर्थ xm या मूल्याची वारंवारता fm आहे ( m = १, २, … , n ). N ला एकूण वारंवारता म्हणतात. ही माहिती कोष्टकाद्वारे अशी मांडता येईल :
| तक्ता क्र. १. वारंवारता कोष्टक | ||
| x
( चलाचे मूल्य ) |
x1 x2 …. xn | |
| f
( वारंवारता ) |
f1 f2 …. fn | N = f1 + f2 + …. + fn |
या कोष्टकाला x या चलाचे वारंवारता कोष्टक ( तक्ता किंवा सारणी ) अथवा वारंवारता वंटन म्हणतात. पुढील उदाहरण पहा : एका वर्गात २० मुले असून पौष्टिक आहाराच्या योजनेखाली मधल्या सुटीत त्यांना केळी खायला दिली. प्रत्येकाने किती केळी खाल्ली याचे २० आकडे तक्ता क्र . २ मध्ये मुलांच्या हजेरीपटातील क्रमांकानुसार ओळीने दिले आहेत.
| तक्ताक्र. २. वीस मुलांनी प्रत्येकी खाल्लेल्या केळ्यांची संख्या |
| २ ० १ ३ ४ ३ २ १ २ २ |
| १ १ ३ २ १ ० ५ १ २ १ |
वरील माहिती तक्ता क्र. ३ मध्ये दाखविल्याप्रमाणे मांडल्यास अधिक स्पष्टता जाणवते.
| तक्ताक्र. ३. तक्ता क्र. २ वरून केलेले वारंवारता कोष्टक | ||
| खाल्लेल्या केळ्यांची संख्या (X) | ० १ २ ३ ४ ५ | |
| मुलांची संख्या (f) | २ ७ ६ ३ १ १ | २० |
तक्ता क्र. २ मध्ये प्रत्येक आकडा किती वेळा आला आहे याचीमोजदाद करून त्यावरून किती केळी खाणाऱ्यांची संख्या जास्त आहेहे काढीत बसण्यापेक्षा ( आणि ते करताना होणाऱ्या चुकीच्या शक्यतेलातोंड देण्यापेक्षा ) तक्ता क्र. ३ वरून मनातल्या मनात चटकन सरळतुलना करून जास्त मुलांनी प्रत्येकी एक केळ खाल्ले आहे, हे चटकनसमजते. या उदाहरणात एकूण वारंवारता लहान आहे. परंतु एकूणवारंवारता मोठी असल्यास सर्व माहिती वारंवारता तक्त्याच्या स्वरूपातमांडल्यास अशा प्रकारचे फायदे होतात हे समजणे अवघड नाही. तक्ताक्र . २ पेक्षा तक्ता क्र . ३ वरून एक केळ व दोन केळी खाणाऱ्यांचीसंख्या अगदी जवळपास आहे हे साधर्म्यही पटकन लक्षात येते.हजेरीपटावरील कोणत्या क्रमांकाच्या मुलाने किती केळी खाल्ली हेतक्ता क्र . २ वरून सहज समजते. परंतु हा तपशील तसा अनावश्यकअसल्याने तो टाळून तक्ता क्र . ३ तयार केला आहे.
एकूण २० मुलांपैकी २ मुलांनी एकही केळ खाल्ले नाही, ७ जणांनीप्रत्येकी एक केळ खाल्ले, ६ जणांनी प्रत्येकी दोन केळी खाल्ली इ.सांख्यिकी माहिती वारंवारता तक्ता क्र. ३ वरून सहज मिळते. या उदाहरणातील चल ‘खाल्लेल्या केळ्यांची संख्या’ असून तो फक्त ठराविक मूल्ये घेऊ शकतो. १.१६ केळी खाल्ली असे सहसा म्हणता येत नाही. जे चल एखाद्या अंतरालातील ठराविक मूल्ये घेऊ शकते, सर्व मूल्ये घेऊ शकत नाही त्या चलाला पृथक्, विविक्त किंवा असंतत चल म्हणतात. ‘वस्तूमधील दोषांची संख्या’, ‘देशातील जिल्ह्यांची संख्या’ व‘पुस्तकाच्या पानांची संख्या’ ही काही पृथक् चलांची उदाहरणे होत.याउलट जे चल एखाद्या अंतरालातील कोणतेही मूल्य घेऊ शकते अशाचलाला सलग किंवा संतत चल म्हणतात. ‘व्यक्तीची उंची’, ‘चेंडूची त्रिज्या’ ही काही संतत चलांची उदाहरणे होत. तक्ता क्र. ३ मधीलचलाची काही मूल्ये एकत्र करून पुढील कोष्टक तयार करता येते.
| तक्ता क्र. ४. वर्गीकृत वारंवारता वितरण सारणी | ||
| खाल्लेल्या केळ्यांची संख्या (X) | ०–१ २–३ ४–५ | |
| मुलांची संख्या (f) | ९ ९ २ | २० |
तक्ता क्र . ४ सारख्या तक्त्याला ‘वर्गीकृत वारंवारता वितरणसारणी’ म्हणतात. त्यामुळे तक्ता क्र . ३ सारखा तक्ता ‘अवर्गीकृतवारंवारता वितरण सारणी’ म्हणून ओळखला जातो.
तक्ता क्र. ५ मध्ये संतत चलाच्या वर्गीकृत वारंवारता वितरण सारणीचेउदाहरण दाखविले आहे.
| तक्ता क्र. ५. संतत चलाची वर्गीकृत वारंवारता वितरण सारणी | ||
| उंची ( इंच ) | ६०–६३ ६३–६६ ६६–६९ ६९–७२ ७२–७५ ७५–७८ | |
| व्यक्तींची संख्या | २३ ४८ ५८ ३८ २३ १० | २०० |
गुणात्मक गुणधर्माच्या बाबतीत तक्ता क्र. ६ मध्ये दाखविल्यासारखेकोष्टक मिळू शकते. याला आपातिक कोष्टक म्हणतात. कोष्टकातीलआकडे वारंवारताच दाखवितात. लसीकरण घेतलेल्या व तरीही लागण
| तक्ता क्र. ६. आपातिक कोष्टक | |||
| रोगाची लागण झालेल्यांची संख्या | रोगाची लागण न
झालेल्यांची संख्या |
||
| लसीकरण घेतलेल्यांची संख्या | ६ | ६३ | ६९ |
| लसीकरण न घेतलेल्यांची संख्या | २० | १० | ३० |
| २६ | ७३ | ९९ | |
झालेल्या व्यक्तींची वारंवारता सहा आहे.
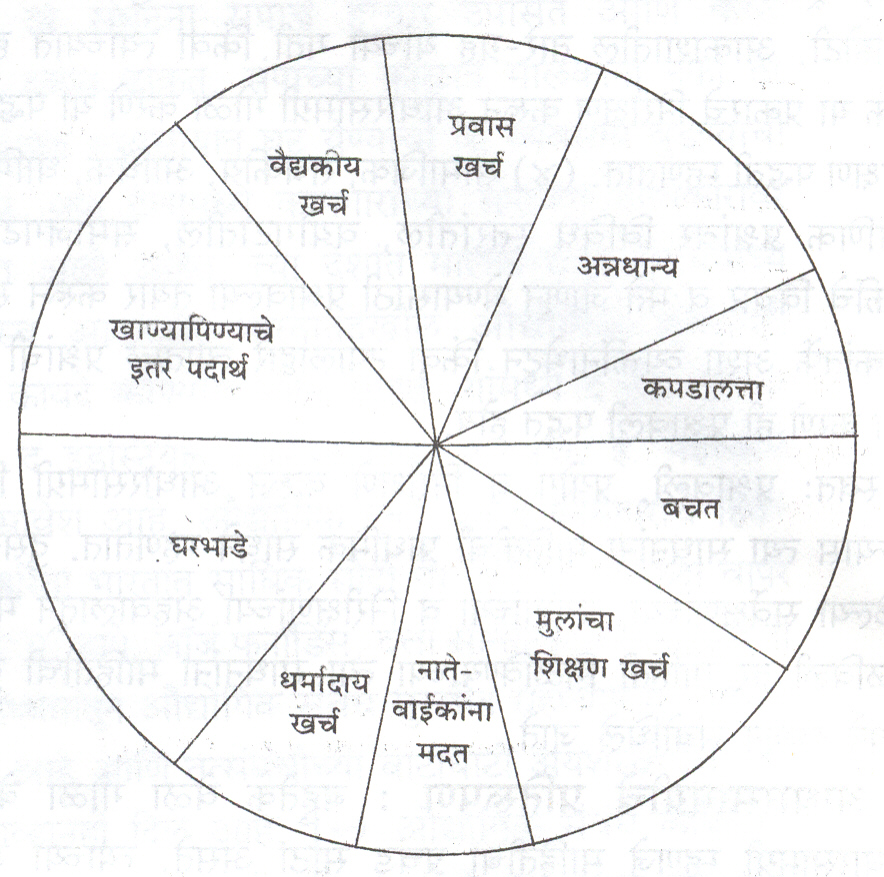माहितीचे चित्ररूप वा आकृती स्वरूपातील प्रतिरूपण : शब्द,वाक्ये, संकेतचिन्हे, सूत्रे, समीकरणे इत्यादींच्या माध्यमातून मांडलेल्यामाहितीपेक्षा, तीच माहिती चित्ररूपाने मांडली तर वाचकाला कळायलासोपी पडते व त्या व्यक्तीला अधिक माहिती सोप्या पद्घतीने थोड्यावेळात मिळाल्याचे समाधान लाभते असा अनुभव अनेक वेळा येतो.लोकसंख्या, पिकांचे उत्पादन, कारखान्यांतील उत्पादन, विद्यार्थ्यांविषयी माहिती, जनगणनेतून मिळालेली माहिती इ. ही विविध अहवालांतूनचित्रे, आकृत्या, आलेख यांचा उपयोग करून मांडलेली असते. उदा.,मासिक उत्पन्नातून घरभाडे, अन्नधान्य, खाण्यापिण्याचे इतर पदार्थ,कपडालत्ता, मुलांचा शिक्षण खर्च, प्रवास खर्च, वैद्यकीय खर्च, धर्मादाय खर्च, जवळच्या नातेवाईकांना मदत व बचत यांसाठी कोणत्या प्रमाणात व्यय होतो, हे दाखविण्यासाठी आ. १ मध्ये दाखविल्यासारखी आकृतीकाढली जाते. अशा आकृतीला वृत्तालेख म्हणतात. वर्तुळ काढून त्याच्यानिरनिराळ्या पाकळ्या माहितीचे निरनिराळे उपविभाग दाखविण्यासाठीप्रमाणानुसार वापरतात. उपलब्ध संपूर्ण माहिती वर्तुळाच्यासंपूर्ण क्षेत्रफळाने दाखविली जाते असे समजून,पाकळीच्या क्षेत्रफळाचे सूत्र वापरून, प्रत्येक उपविभागासाठी किती क्षेत्रफळाची पाकळी करायची हे ठरते.
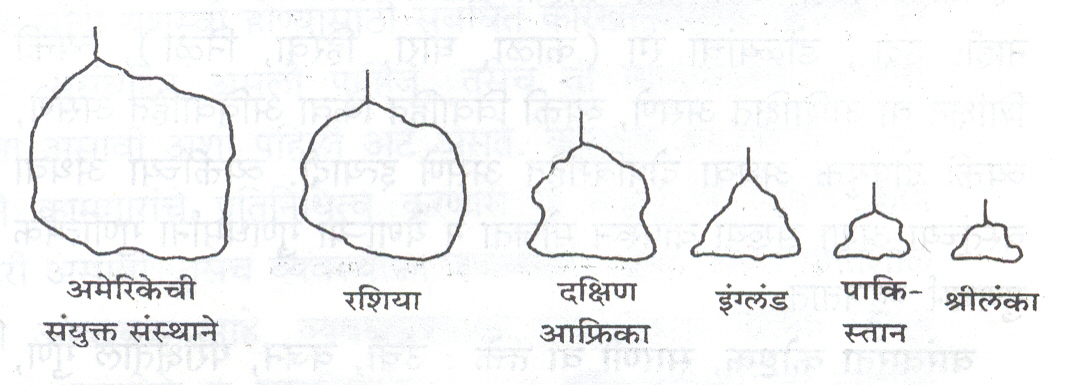
भारताचा वार्षिक व्यापार कोणकोणत्या देशांशीवजनाप्रमाणे किती आहे हे दाखविण्यासाठी आ. २ काढली आहे. यातदिसत असलेले प्रत्येक थैलीचे आकारमान त्या त्या देशाशी असलेल्या व्यापाराच्या वजन संख्येच्या प्रमाणात असले पाहिजे.
गावातील चार शाळांमध्ये प्रत्येकी किती विद्यार्थीशिकतात हे आ. ३ सारख्या आकृतीने दाखविता येते.यातील Ϙ हे चिन्ह ठराविक विद्यार्थ्यांची संख्या ( उदा., २००) दाखविते, असे संकेतन घेऊन या प्रकारची आकृती काढता येते.
परीक्षेत मिळालेल्या गुणानुसार विद्यार्थ्यांचे वर्गीकरण करून ते चित्ररूपाने आ. ४ मध्ये दाखविल्याप्रमाणे मांडता येते. गुणांच्या कोणत्या अंतरालात किती विद्याथ्यांचे गुण मोडतात ते या आकृतीवरून सहज वाचता येते. गुणांच्या प्रत्येक अंतरालात मोडणाऱ्या विद्यार्थ्यांची संख्या एक स्तंभ वापरून दाखविली आहे. अशा प्रकारच्या आकृतीला स्तंभालेख म्हणतात. यात स्तंभाची उंची वारंवारता दाखविते परंतु रुंदी काहीदाखवीत नाही.
गुणांच्या प्रत्येक अंतरालातील विद्यार्थ्यांपैकी किती मुले व कितीमुली आहेत हे आ. ५ प्रमाणे दाखविता येते. प्रत्येक अंतरालासाठीएकमेकांना जोडून, मुलांची संख्या दाखविणारा एक व मुलींची संख्यादाखविणारा दुसरा असे दोन स्तंभ आहेत. अशा आकृतीला विभाजितस्तंभालेख म्हणतात.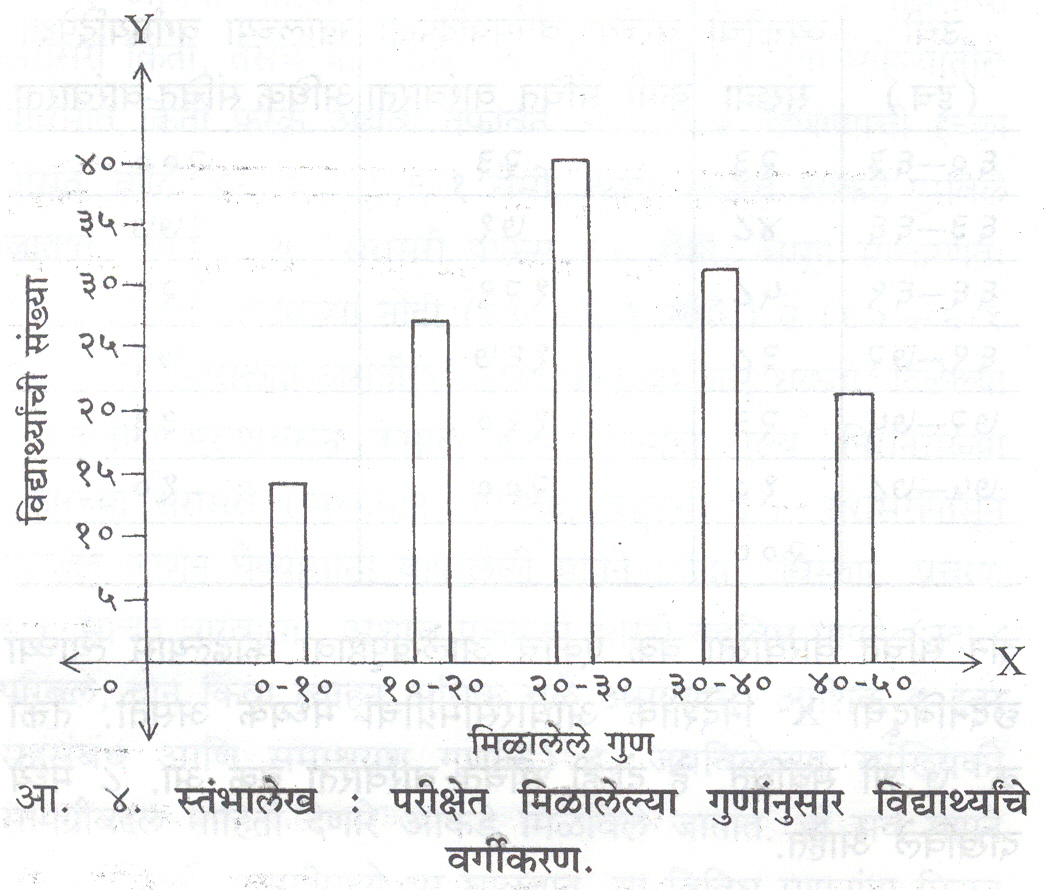 
मुलींची संख्या दाखविणाऱ्या स्तंभात तिरप्या रेषाकाढून त्याचे वेगळेपण दाखविले आहे. माहिती जशी असेल त्यानुसार शेजारीशेजारी दोनपेक्षा अधिक स्तंभही असू शकतात.
अशा प्रकारच्या इतरही विविध प्रकारच्या आकृत्या वा
चित्रे काढतायेणे शक्य आहे. त्यांचा माहितीच्या चित्ररूप प्रतिरूपणासाठी उपयोगहोतो. या आकृत्या काढण्यासाठी भूमितीत वा भूगोलात वापरतात त्याप्रमाणेयोग्य प्रमाण वापरावे लागते. एक सेंमी. लांबी / रुंदी, एक सेंमी.२क्षेत्रफळ यांच्यासाठी वापरलेले प्रमाण लक्षात घेऊन आकृतीचा वतिच्यातील विविध भागांचा तुलनात्मक अभ्यास दृष्टीने आणि मनानेकरून निदान ढोबळ निर्णय ( उदा., भारताचा एखाद्या देशाशी व्यापारदुसऱ्या देशाच्या व्यापाराच्या सु. दुप्पट आहे, एखाद्या शाळेत १,०००विद्यार्थी आहेत इ.) तरी घेता येतात. रंगाच्या छटा वापरून अशाप्रकारच्या आकृत्या अधिक आकर्षकही बनविता येतात. त्रिमितीयआकृत्यांचाही वापर या संदर्भात करता येतो.
या प्रकारच्या प्रतिरूपणास चित्ररूप अथवा आकृती स्वरूपातीलप्रतिरूपण म्हणतात. आयतचित्र, वारंवारता बहुभुज, वारंवारता वक्र वसंचित वारंवारता वक्र या नावांनी ओळखल्या जाणाऱ्या या माहितीच्याप्रतिरूपणाला आलेख स्वरूपातील प्रतिरूपण म्हणतात.
आयतचित्र (आयतालेख ) व वारंवारता बहुभुज : तक्ता क्र.
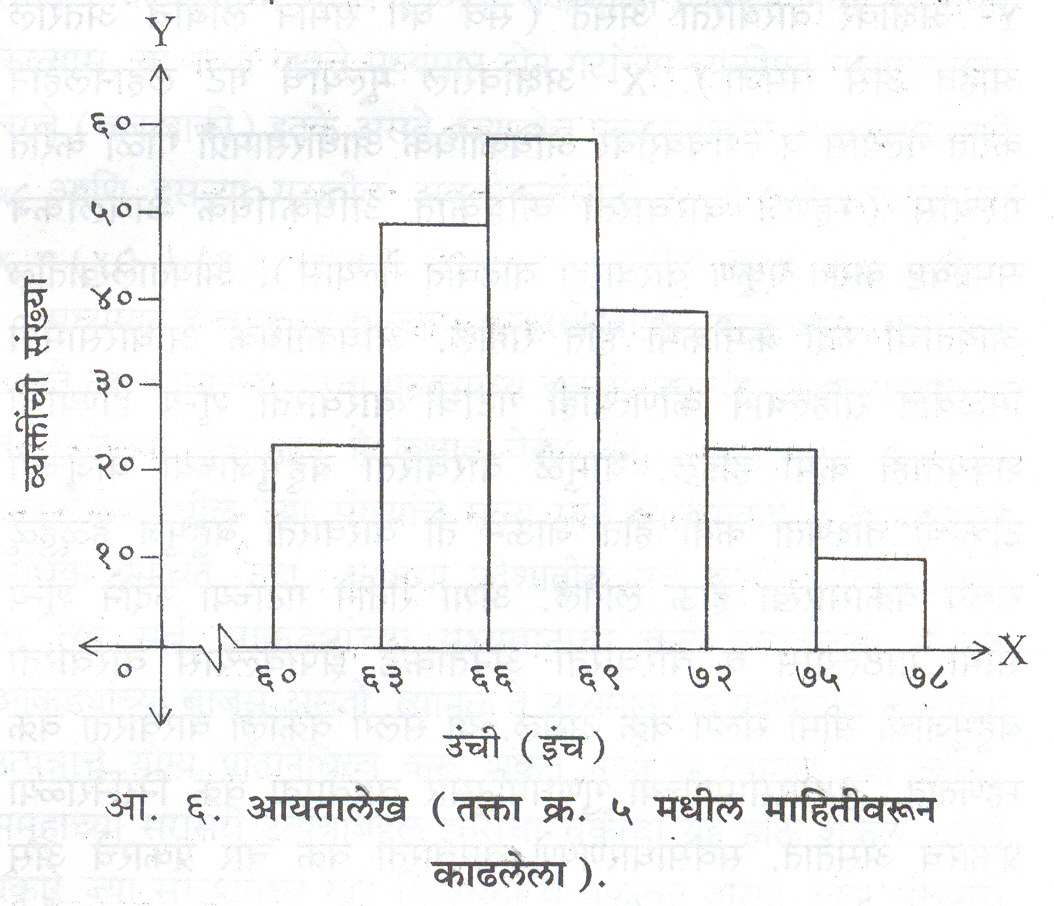
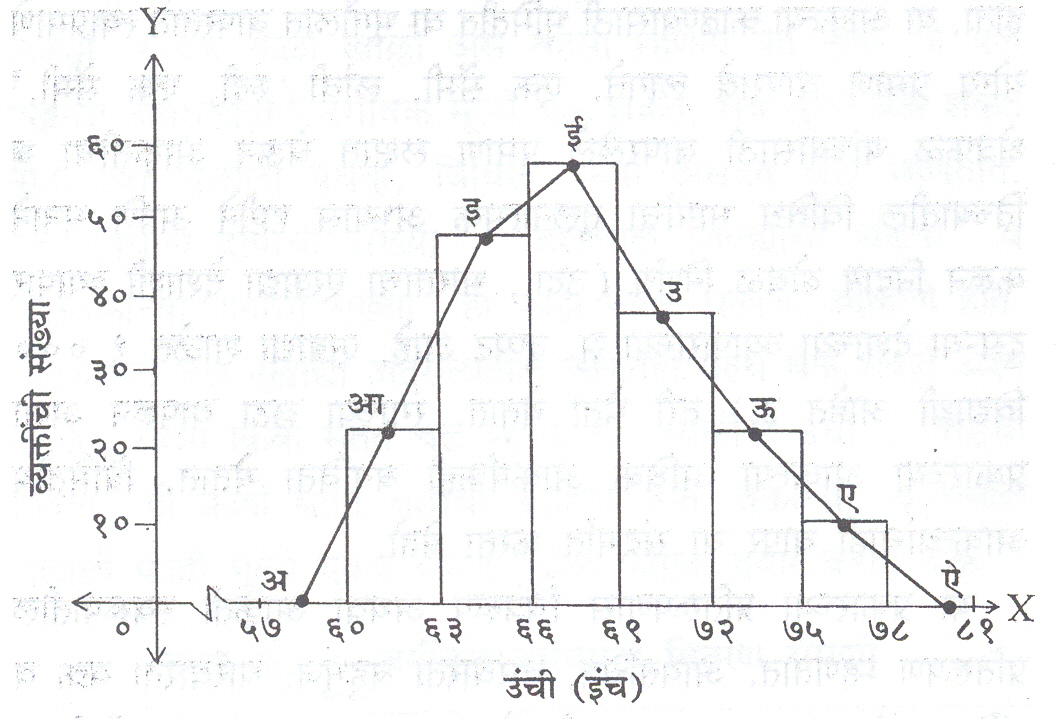
५मधील वारंवारता सारणीतील माहिती आ. ६ मध्ये दर्शविल्याप्रमाणेमांडली तर त्या आकृतीला आयतचित्र अथवा आयतालेख म्हणतात.यात X- अक्षावर चलाच्या मूल्यांचे निरनिराळे वर्ग असतात. यातीलप्रत्येक वर्गावर एक आयत उभा करतात. प्रत्येक आयताचे क्षेत्रफळ संबंधित वर्गाच्या वारंवारतेच्या प्रमाणात असते. प्रत्येक आयताची रुंदीत्या त्या वर्गाच्या वर्गांतराएवढी ( वर्ग-अवकाशाएवढी ) असून ती X-अक्षावर आखली जाते. माहिती ज्यावर्गात वाटली जाते त्या सर्व वर्गांचेअंतराल समान असेल (जसे तक्ता क्र . ४ व ५ यांमध्ये आहे ), तरप्रत्येक वर्गावर उभा केलेल्या आयताची उंची साहजिकच त्या वर्गातीलवारंवारतेच्या प्रमाणात असते. आयतालेखातील X- अक्षावर उभ्याकेलेल्या प्रत्येक आयताच्या वरच्या आडव्या बाजूंचे मध्यबिंदू रेषाखंडांनीक्रमवार जोडले ( आ. ७ पहा ), तर मिळणारी आकृती बहुभुजासारखीदिसते व तिला वारंवारता बहुभुज म्हणतात. हा वारंवारता बहुभुजकाढण्यासाठी X- अक्षावरील सुरुवातीच्या वर्गाच्या आधी एक वर्ग आहेव तसेच शेवटच्या वर्गानंतर एक वर्ग आहे असे मानतात व या मानलेल्यादोन्ही टोकांकडील वर्गांची वारंवारता शून्य आहे असे समजतात. असेकेल्याने वारंवारता बहुभुज पूर्ण होऊन त्याची एक बाजू X- अक्षावरपडते. आ. ७ मधील वारंवारता बहुभुज अआइईउऊएऐ हा आहे.
वारंवारता वक्र आणि संचित वारंवारता वक्र: आधारसामग्री वापरूनवारंवारता कोष्टक (उदा., तक्ता क्र. ५) तयार करून त्याचा उपयोगकरून आयतालेख (उदा., आ. ६) व वारंवारता बहुभुज (उदा.,आ. ७) काढले आहेत. या दोन्ही आकृत्यांमध्ये क्षितिज समांतरX- अक्षावर चलाच्या मूल्यांचे क्रमवार गट (वर्ग) असतात व उभ्याY- अक्षावर वारंवारता असते (सर्व वर्ग समान लांबीचे अंतरालआहेत असे समजा). X- अक्षावरील मूल्यांचे गट लहानलहानकरीत गेल्यास व त्याचबरोबर अधिकाधिक आधारसामग्री गोळा करीतगेल्यास (म्हणजे वारंवारता कोष्टकात अधिकाधिक अवलोकनेसमाविष्ट करीत एकूण वारंवारता वाढवीत गेल्यास), आयतालेखातीलआयतांची रुंदी कमीकमी होत राहील. अधिकाधिक आधारसामग्रीमिळवीत राहिल्याने कोणत्याही गटाची वारंवारता शून्य होण्याचीशक्यताही कमी होईल. यामुळे वारंवारता बहुभुजाच्या बाजूंच्याटोकांची तीक्ष्णता कमी होत जाऊन तो वारंवारता बहुभुज हळूहळूसलग वक्रासारखा होऊ लागेल. अशा रीतीने गटाच्या रुंदीने शून्यसीमा गाठल्यास व वारंवारता अनंताकडे झेपावल्यास वारंवारताबहुभुजाची सीमा सलग वक्र असेल. या सलग वक्राला वारंवारता वक्रम्हणतात. आधारसामग्रीच्या गुणधर्मानुसार वारंवारता वक्र निरनिराळ्याप्रकारचे असतात. सर्वसाधारणपणे वारंवारता वक्र चार प्रकारचे असूशकतात. हे चार प्रकार ‘असमप्रमाणता व ककुदता या गुणधर्मांचीमापने’ यापुढील एका उपविभागात पहायला मिळतील.
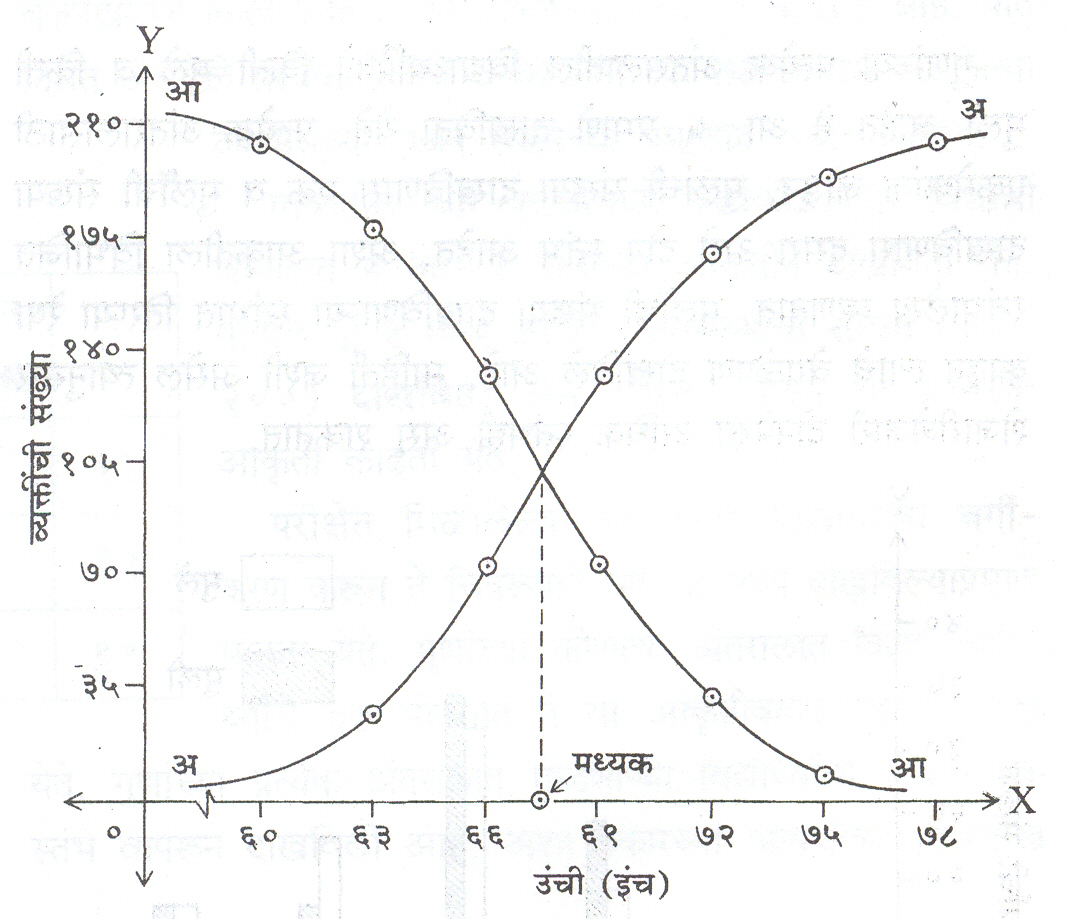
तक्ता क्र. ५ मधील आधारसामग्री तक्ता क्र. ७ मध्ये स्तंभ १ व २मध्ये पुन्हा मांडली आहे. स्तंभ १ व २ मिळून तयार होणाऱ्यावारंवारता सारणीतील गटवार (वर्गवार) वारंवारता क्रमाक्रमाने एकदावरून खाली (स्तंभ ३) आणि एकदा खालून वर (स्तंभ ४) एकत्रितकेल्या आहेत. स्तंभ ३ मधील या आंशिक एकत्रित वारंवारता, २००पूर्ण वारंवारता असणाऱ्या संपूर्ण आधारसामग्रीत, अनुक्रमे ६३ पेक्षाकमी, ६६ पेक्षा कमी, ६९ पेक्षा कमी, ७२ पेक्षा कमी, ७५ पेक्षा कमीव ७८ पेक्षा कमी किती वारंवारता आहेत हे दाखवितात. म्हणून स्तंभ३ मधील या आंशिक एकत्रित वारंवारतांना ‘वरच्या वर्गमर्यादेपेक्षा कमीसंचित वारंवारता’ असे म्हणतात. ६३, ६६, ६९, ७२, ७५ व ७८या स्तंभ १ मधील वर्गाच्या वरच्या मर्यादा आहेत. या स्तंभ ३ मधीलसंचित वारंवारता Y- अक्षावर व स्तंभ १ मधील वर्गांच्या वरच्यावर्गमर्यादा X- अक्षावर घेऊन वक्र काढल्यास त्यास संचित वारंवारतावक्र ( पेक्षा कमी ) म्हणतात. त्याचप्रमाणे स्तंभ ४ मधील आंशिकएकत्रित वारंवारता, अनुक्रमे ६० पेक्षा जास्त, ६३ पेक्षा जास्त, ६६पेक्षा जास्त, ६९ पेक्षा जास्त, ७२ पेक्षा जास्त, ७५ पेक्षा जास्त कितीवारंवारता आहेत हे दर्शवितात. म्हणून स्तंभ ४ मधील आंशिकएकत्रित वारंवारतांना ‘खालच्या वर्गमर्यादेपेक्षा अधिक संचित वारंवारता’म्हणतात. स्तंभ १ मधील खालच्या वर्गमर्यादा X- अक्षावर व स्तंभ ४मधील संचित वारंवारता Y- अक्षावर घेऊन वक्र काढल्यास त्यावक्रास ‘संचित वारंवारता वक्र (पेक्षा जास्त)’ असे म्हणतात.
तक्ता क्र. ७.
| उंची (इंच) | व्यक्तींची संख्या | वरच्या वर्गमर्यादेपेक्षा कमी संचित वारंवारता | खालच्या वर्गमर्यादेपेक्षा अधिक संचित वारंवारता |
| ६०–६३ | २३ | २३ | २०० |
| ६३–६६ | ४८ | ७१ | १७७ |
| ६६–६९ | ५८ | १२९ | १२९ |
| ६९–७२ | ३८ | १६७ | ७१ |
| ७२–७५ | २३ | १९० | ३३ |
| ७५–७८ | १० | २०० | १० |
| २०० |
हे दोन संचित वारंवारता वक्र एकाच आलेखपृष्ठावर काढल्यास त्यांच्याछेदनबिंदूचा X- निर्देशांक आधारसामग्रीचा मध्यक असतो. तक्ताक्र . ७ शी संबंधित, हे दोन्ही संचित वारंवारता वक्र आ. ८ मध्येदाखविले आहेत.
वर्णनात्मक प्रचले : कोणत्याही कारणासाठी जमा केलेल्याआधारसामग्रीची विविध प्रकारे मांडणी केली जाते. वारंवारता कोष्टकहा त्यातीलच एक प्रकार आहे. मूळ माहितीवरून जमलेल्या माहितीतीलकमीत कमी व जास्तीत जास्त मूल्य कोणते हे समजू शकते. वारंवारताकोष्टकावरून मूल्याच्या एखाद्या गटाची (वर्गाची) वारंवारता किती,तसेच जास्तीत जास्त वारंवारता कोणत्या गटाची आहे याचे ज्ञान होते.उदा., वर्षातील ३६५ दिवसांतील प्रत्येक दिवशी एखाद्या ठिकाणीपडलेल्या पावसाचे आकडे जमा केले असल्यास त्या आकड्यांच्यासमुच्च्यावरून त्या वर्षात त्या ठिकाणी किमान पाऊस कोणत्यादिवशी व किती होता, तसेच जास्तीत जास्त पाऊस कोणत्या दिवशीव किती पडला हे समजू शकते. या पावसाच्या कच्च्या माहितीवरूनप्रत्येक महिन्यातील पावसाचे वारंवारता कोष्टक तयार केल्यास त्यावरूनत्या वर्षी त्या ठिकाणी प्रत्येक महिन्यात एकूण पाऊस किती झाला,कोणत्या महिन्यात सर्वांत अधिक पाऊस पडला, कोणत्या महिन्यातसर्वांत कमी पाऊस पडला हे लक्षात येईल. परंतु अनेक वेळा आपल्यालायापेक्षा अधिक माहिती हवी असते. उदा., त्या वर्षाची पावसाचीसरासरी किती, तसेच या सरासरीच्या तुलनेत निरनिराळ्या महिन्यांतीलपावसात किती फरक अथवा तफावत आढळते हे जाणण्याची इच्छाअसते. काही वेळा ६०±६.१ सेंमी. अशा प्रकारचे आकडे पुरविलेजातात. त्याचा अर्थ ‘सरासरी पाऊस ६० सेंमी. असून साधारणतः९५% दिवशी पावसाच्या नोंदी (६० – ६.१ सेंमी.) ते (६०+६.१सेंमी.) या अंतरालात असतील’ अशा प्रकारचा असू शकतो. दिलेल्यामाहितीतील मूल्यांवरून कमाल मूल्य, किमान मूल्य, निरनिराळ्याप्रकारच्या सरासरी (मध्यमान, मध्यक, बहुलक इ.), सरासरीपासूनतफावत जाणून घेण्यासाठी वापरलेली मापने (उदा., विस्तार, प्रचरणइ.), संचित वारंवारता, अशाच प्रकारची इतरही बहुविध मापने (उदा.,परिबले, दोन किंवा त्याहून अधिक चले असल्यास, आंशिक व इतरसहसंबंध आणि समाश्रयण गुणांक) इ. जमविलेल्या सांख्यिकीसामग्रीबद्दल माहिती देणारे आकडे मिळविले जातात. ही सर्व मापनेमूळ सांख्यिकी सामग्रीमध्ये भर घालतात. या विविध मापनांना मिळूनसामग्रीची वर्णनात्मक प्रचले असे संबोधले जाते. प्रचल ही संज्ञा मुख्यतःसमष्टीच्या मध्यमान, विचरण इ. वर उल्लेखिलेल्या मापनांसाठी वापरलीजाते. प्रतिदर्शावरून काढलेली याच प्रकारची मापने समष्टीच्या प्रचलांबद्दलअनुमाने बांधण्यासाठी वापरली जातात.
मध्यमान, मध्यक व बहुलक : परीक्षेत प्रत्येक विषयात मिळालेलेगुण निरनिराळे सांगण्यापेक्षा त्या सर्व आकड्यांचे प्रतिनिधित्व करणारासरासरी हा एक आकडा सांगितला जातो. ‘मला सहामाहीत ९६ टक्केगुण मिळाले’ असे सहजगत्या बोलले जाते. विविध व्यवसायात सरासरी काढण्याला प्रत्येकजण रुळावलेला असतो. याच सरासरीला शास्त्रीयभाषेत अंकगणितीय मध्यमान (अथवा नुसतेच मध्यमान अथवा माध्य) म्हणतात. प्रयोग केल्यावर मोजमापे घेऊन किंवा निरीक्षणाने गणतीकरून जी मूल्ये मिळतात (उदा., प्रत्येक विषयात मिळालेले गुण,प्रत्येक गावाची लोकसंख्या, प्रत्येक नागरिकाची उंची किंवा या प्रकारचीकोणतीही मापे ), त्या सर्व मूल्यांच्या बेरजेला मूल्यांच्या एकूण संख्येनेभागल्यास मिळणारा आकडा त्या सर्व मूल्यांचे मध्यमान म्हणून ओळखलाजातो. X1, X2, X3 …, Xn या n असे दाखवितात. म्हणजे सूत्ररूपाने X= (X1 + X2 + … + Xn)/ n. तक्ता क्र. १ सारखे वारंवारता कोष्टक असल्यास त्यात X चे प्रत्येक मूल्य अनेकदा आलेले असते (उदा., X1 हे मूल्य f1 या वारंवारतेने आले आहे). त्यामुळे तक्ता क्र १ मधील वारंवारता कोष्टकाचे मध्यमान 
या सूत्राने मिळेल. त्यानुसार तक्ता क्र. ३ साठी खाल्लेल्या केळ्यांचे मध्यमान ( सरासरी ) =(०× २+१× ७+२× ६+ ३× ३+ ४×१+५× १)/२०=१.८५ केळी.
मध्यमान या प्रचलाचे काही महत्त्वाचे गुणधर्म पुढीलप्रमाणे आहेत : (१) अवलोकनांच्या मध्यमानापासून घेतलेल्या सर्व विचलनांची बेरीज शून्य असते. सूत्ररूपाने 
तसेच वारंवारता कोष्टकाच्या बाबतीत
(२) n1 अवलोकनांचे मध्यमान x1, आणि n2 अवलोकनांचे मध्यमान x2 असल्यास आणि ही (n1 + n2) अवलोकने एकत्र केल्यास या एकत्रित अवलोकनांचे मध्यमान 
या सूत्राने मिळते. अवलोकनांचे दोनापेक्षा अधिक गट असल्यास या सूत्राचे व्यापकीकरण करता येते.
(३) मध्यमानापासून घेतलेल्या ( इतर कोणत्याही मूल्याऐवजी ) अवलोकनांच्या विचलनांच्या वर्गांची बेरीज सर्वांत कमी असते. म्हणजे सूत्ररूपात 
येथे A ही मध्यमानाव्यतिरिक्त कोणतीही वास्तव संख्या आहे.
(४) दोन गटांतील अवलोकनांची संख्या समान असून दोन्ही गटांतील संगत अवलोकनांची बेरीज (किंवा वजाबाकी) करून नवा गट तयार केल्यास, या नव्या गटाचे मध्यमान दोन गटांच्या व्यक्तीगत मध्यमानांच्या बेरजे ( वजाबाकी ) इतके असते. म्हणजेच एका गटातील अवलोकनांसाठी x1 आणि दुसऱ्या गटातील अवलोकनांसाठी x2 हे चल वापरल्यास, xi = (x1)i ± (x2)i ( i = 1, 2, … , n ) असेल, तर x =x1 ± x2.
मध्यमान हे वस्तूच्या गुरुत्वमध्यासारखे वागते. वस्तू ज्याबाजूस जडअसते त्या भागाकडे त्याचा गुरुत्वमध्य झुकतो. त्याचप्रमाणे मध्यमानाच्यावर दिलेल्या सूत्रावरून हे लक्षात येईल की, x1 , x2, … , xn याअवलोकनांमधील ज्यासंख्यांचे मूल्य मोठे त्यांच्याकडे x हे मध्यमानअधिक झेपावते. उदा., एखाद्या प्रदेशातील सर्व व्यक्तींचे उत्पन्न टिपलेतर त्या सर्व आकड्यांच्या मध्यमानाचा कल उत्पन्नांच्या मोठ्याआकड्यांच्या बाजूस असतो. त्यामुळे ते मध्यमान त्या प्रदेशातील लोकांच्याउत्पन्नांचे योग्य प्रतिनिधित्व करू शकत नाही व त्यामुळे त्या लोकसमूहाच्या सरासरी उत्पन्नाबद्दल इतरांचा चुकीचा ग्रह होऊ शकेल. अशाप्रकारे ज्यासंख्यांमध्ये खूप विविधता व तफावत असते अशा संख्यांचेमध्यमान त्या संख्यासमुच्चयाचा योग्य प्रतिनिधी होत नाही. अशास्थितीमध्ये सर्व संख्यांच्या मधोमध असणारी संख्या ही त्या सर्वसंख्यांची योग्य प्रतिनिधी होऊ शकेल. अशा संख्येला त्या संख्यांचामध्यक म्हणतात. मध्यक ही एक प्रकारची सरासरीच आहे. दिलेल्यासंख्यांचा मध्यक काढण्यासाठी त्या सर्व संख्या त्यांच्या मूल्यानुसारचढत्या ( किंवा उतरत्या ) क्रमाने मांडून मधोमध येणारी संख्या ही त्यादिलेल्या सर्व संख्यांचा मध्यक म्हणून घेतात. उदा., २५, १७, ९२,२, ८१, १९, ५२, २३, ९९ या संख्यांचा मध्यक ( त्या संख्या २,१७, १९, २३, २५, ५२, ८१, ९२, ९९ अशा चढत्या क्रमानेमांडून ) २५ आहे. एकूण संख्या n असतील तर त्या चढत्या क्रमानेमांडल्यावर, n विषम असल्यास ( n +1)/2 वी संख्या आणि n सम असल्यास n व्या आणि (n + 1) व्या संख्यांचे मध्यमान त्या संख्यांचा मध्यक म्हणून घेतात.
मध्यक या प्रचलाचे काही गुणधर्म असे आहेत : (१) मध्यक ही स्थानावलंबित सरासरी आहे. दिलेल्या संख्यांच्या मूल्यांचा मध्यकावर परिणाम होत नाही संख्यासमुच्चयातील संख्यांच्या स्थानाचा होतो. (२) कोणत्याही आधारसामग्रीचा मध्यक त्या आधारसामग्रीला दोन समान भागांत विभागतो. म्हणजे आधारसामग्रीत तिच्या मध्यकाहून कमी मूल्ये असणाऱ्या अवलोकनांची संख्या व मध्यकाहून जास्त मूल्ये असणाऱ्या अवलोकनांची संख्या समान असते. (३) समप्रमाणित वंटनांमध्ये मध्यमान व मध्यक समान असतात. असमप्रमाणित वंटनांची असमप्रमाणता उजवीकडे झुकलेली असेल तर मध्यकाचे मूल्य मध्यमानाच्या मूल्यापेक्षा लहान असते. याउलट असमप्रमाणता वंटनाच्या डावीकडे झुकलेली असेल तर मध्यक मध्यमानापेक्षा मोठा असतो. (४) अवलोकनांची विचलने ( इतर कोणत्याही मूल्याऐवजी ) मध्यकेपासून घेतल्यास, सर्व विचलनांच्या केवलमूल्यांची बेरीज सर्वांत कमी होते. म्हणजेच
येथे A ही मध्यकाव्यतिरिक्त कोणतीही वास्तव संख्या आहे.
बहुलक ही आणखी एक प्रकारची सरासरीच आहे. ज्याप्रमाणेसर्वांतजास्त मते पडणारा उमेदवार निवडून आल्याचे समजतात (जरी त्याला ५० टक्क्यांपेक्षा कमी मते मिळाली असली तरीही ), त्याचप्रमाणे जीसंख्या एखाद्या संख्यासंचात सर्वांत जास्त वेळा येते त्या संख्येला त्यासंख्यासंचाचा बहुलक म्हणतात.
बहुलक या प्रचलाचे काही गुणधर्म असे आहेत : (१) सर्वसाधारणतःफार मोठ्या तसेच फार लहान मूल्यांचा बहुलकावर परिणाम होत नाही.(२) असमप्रमाणित वंटनाची असमप्रमाणता उजवीकडे झुकलेलीअसेल, तर बहुधा मध्यमान मध्यकापेक्षा व मध्यक बहुलकापेक्षा मोठाअसतो. याउलट असमप्रमाणित वंटनाची असमप्रमाणता डावीकडे झुकलेलीअसेल, तर बहुधा मध्यमान मध्यकापेक्षा लहान व मध्यक बहुलकापेक्षालहान असतो.
दिलेल्या संख्यांची सरासरी त्या संख्यांच्या मधे कुठेतरी पडते, बाहेरपडत नाही. त्यामुळे मध्यमान, मध्यक
व बहुलक या सर्वांना मिळूनमध्यप्रवृत्ती मोजणारी मापने म्हणतात. अशा प्रकारची इतरही काही मापनेसांख्यिकीमध्ये वापरतात. आधारसामग्री वर्गीकृत वारंवारता वितरण सारणीवापरून मांडली असेल, तर आकडेमोड करून ही मापने मिळविण्याच्यापद्घती उपलब्ध असून शालेय पुस्तकातही त्या आढळतात. अशा तऱ्हेनेमध्यमान, मध्यक, बहुलक इ. मापने सांख्यिकी सामग्रीची मध्यप्रवृत्तीमोजण्यासाठी वापरली जातात.
विस्तार, प्रचरण, प्रमाणित विचरण इत्यादी : कोणत्याही संख्यासंचाची सरासरी ही त्या संख्यासंचाची प्रतिनिधी म्हणून वापरली जाते. त्यानुसार आधारसामग्रीतील सर्व अवलोकने देण्यापेक्षा त्या सर्व अवलोकनांची योग्य ती सरासरी (मध्यमान, मध्यक, बहुलक) उद्‌धृत केली जाते. परंतु दिलेल्या संख्यासंचाची सरासरी त्या संख्यासंचाचे प्रतिनिधित्व पूर्णपणे करू शकत नाही. उदा., {३४, ३५, ३६} या संख्यासंचाचे मध्यमान ३५ आहे आणि {२०, ३५, ५०} या संख्यासंचाचे मध्यमान देखील ३५ च आहे. परंतु या दोन संख्यासंचांतील अंतर्गत तफावत वेगवेगळी आहे. त्यामुळे एखाद्या संख्यासंचाची सुयोग्य माहिती द्यायची असेल तर त्याची मध्यप्रवृत्ती मोजणाऱ्या मापनाबरोबर त्याचा अंतर्गत विखुरलेपणा म्हणजेच तफावत दाखविणारे मापन म्हणजेच अपस्करणाचे मापन देखील द्यावे लागते.
कोणत्याही संख्यासंचातील सर्व संख्या त्या संचातील कमाल व किमान संख्यांच्या मधे सामावलेल्या असतात. त्यामुळे त्या संचाचा विस्तार केवढा आहे हे या दोन टोकांच्या संख्यांमधील फरक दाखवू शकतो. कमाल संख्या वजा किमान संख्या या फरकाला त्या संख्यासंचाचा विस्तार म्हणतात. ‘विस्तार’ हे आधारसामग्रीच्या अपस्करणाचे एक माप आहे. 
या गुणोत्तराला सापेक्ष अपस्करण म्हणतात. ते एककविरहित मापन आहे.
कमाल व किमान संख्या तशाच ठेवून त्यांच्यामधील संख्या कितीही प्रकारे बदलल्या तर मिळणाऱ्या विविध संख्यासंचाचे ‘विस्तार’ हे मापन एकच असणार हे उघड आहे. त्यामुळे अपस्करणाचे विस्तार हे मापन अत्यंत स्थूल व अपक्व मापन ठरते. यामुळे विस्तार हे मापन अतिशय सोपे असले तरी ते अत्यंत प्राथमिक मापन म्हणूनच वापरता येते. आधारसामग्रीच्या अपस्करणाचे मापन म्हणून ते योग्य न्याय देऊ शकेलच असे नाही. संख्यासंचामधील प्रत्येक संख्या त्या संचाच्या सरासरीपासून किती दूर आहे हे पाहून त्यापासून मिळविलेले मापन त्या संख्यासंचातील अंतर्गत तफावत म्हणजेच अपस्करण अधिक चांगल्या प्रकारे दाखवू शकेल. X1, X2, …, Xn या मूल्यांचे मध्यमान X असल्यास 
हा झाला xi या मूल्याचा मध्यमानापासूनचा फरक त्याला xi चे x पासूनचे विचलन म्हणतात.हा फरक धन किंवा ऋण असू शकतो. 
म्हणजेआधारसामग्रीतील सर्व अवलोकनांच्या मध्यमानापासूनच्या विचलनांचीबेरीज शून्य असते, हे मध्यमानाचा एक गुणधर्म म्हणून पाहिले आहेच. म्हणून विचलनांचे केवलमूल्य घेऊन अशी बेरीज घेतल्यास त्या बेरजेचीसरासरी अपस्करणांचे एक मापन होऊ शकते. त्यानुसार
या आधारसामग्रीच्या अपस्करणाचे मापन म्हणून वापरतात. त्याला ‘मध्य विचलन’ असे म्हणतात. परंतु विश्लेषणात्मक अभ्यासात गणितीदृष्टीने हे मापन नीट हाताळता येत नाही. म्हणून विचलनाचे केवलमूल्यघेण्याऐवजी त्याचा वर्ग घेऊन मिळणारे 
हे मापन वापरले जाते. त्याला प्रचरण म्हणतात. वर्ग नेहमीच धन असल्याने विचलन धन आहे का ऋण याचा परिणाम V वर होत नाही. परंतु आता एककाचा प्रश्न उद्‌भवतो. अवलोकन x सेंमी. असेल तर प्रचरण V चे एकक (सेंमी.)२ होणार. 
चे एकक सेंमी. होईल. त्यामुळे मूळ अवलोकन x, मध्यमान x आणि अपस्करणाचे हे मापन या सर्वांचे एकक समान असेल. 
ला प्रमाणित विचलन म्हणतात. प्रमाणित विचलन भागिले मध्यमान याला विचलनाचा सहगुणक म्हणतात व तो एककविरहित आहे.
अशा तऱ्हेने विस्तार, सापेक्ष अपस्करण, मध्य विचलन, प्रचरण,प्रमाणित विचरण व विचलनाचा सहगुणक ही अपस्करणाची सहामहत्त्वाची मापने असून इतरही काही मापने अस्तित्वात आहेत. तीनिरनिराळ्या प्रकारच्या सामग्रींचे अपस्करण मोजण्यासाठी वापरली जातात.
तक्ता क्र. ३ ( व म्हणून तक्ता क्र. २) मधील प्रदत्ताचे मध्यमान =१.८५ केळी हे वर आलेले आहेच. आता त्याच प्रदत्तासाठी(१) विस्तार = ५−०=५ केळी (२) सापेक्ष अपस्करण =५/(० + ५) =१ (३) प्रत्येक अवलोकनासाठी १.८५ यामध्यमानापासूनचे विचलन,
० – १.८५=−१.८५ (२ वेळा ),
१ – १.८५=−०.८५ (७ वेळा ),
२ – १.८५=०.१५ (६ वेळा ),
३ – १.८५=१.१५ (३ वेळा ),
४ – १.८५=२.१५ (१ वेळ ),
५ – १.८५=३.१५ (१ वेळ ).
∴ मध्य विचलन = १/२० (१.८५ × २ + ०.८५ ×७ + ०.१५ × ६ + १.१५ × ३ + २.१५ + ३.१५) = ०.९६५ केळी.
∴ प्रचरण = १/२० [१.८५)२ × २ + (०.८५)२ × ७ + (०.१५) २× ६ + (१.१५)२ × ३ + (२.१५)२ + (३.१५)२] = १.५२७५ केळी२.
प्रमाणित विचरण 
= १.२३५ केळी.
विचलनाचा सहगुणक = प्रमाणित विचरण/मध्यमान
= १.२३५/१.८५ = ०.६६७.
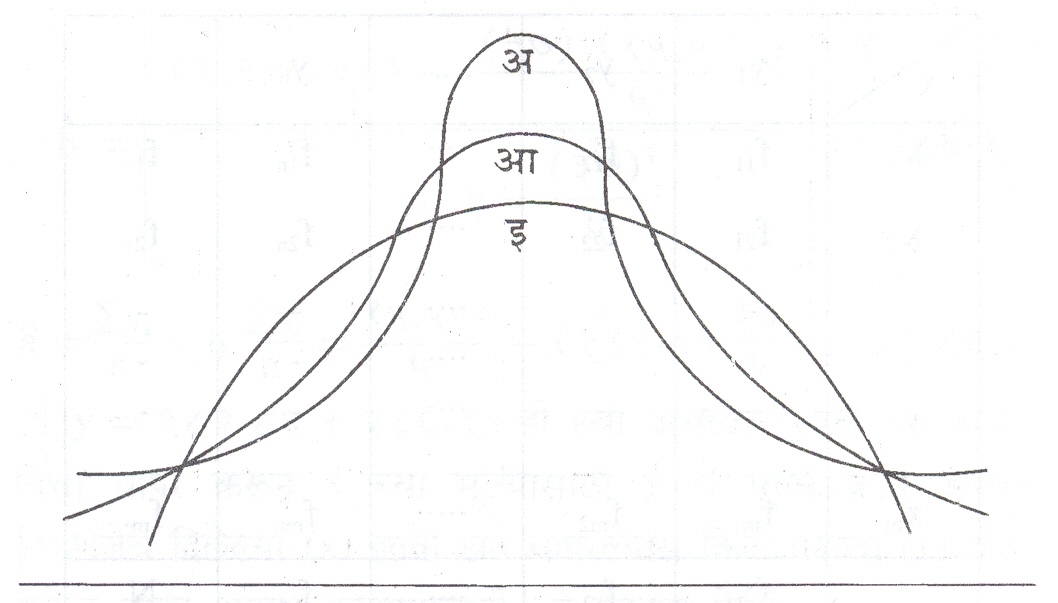
असमप्रमाणता व ककुदता (शिखरीपणा किंवा बहिर्वक्रता) यागुणधर्मांची मापने : वारंवारता वक्र मुख्यतः चार प्रकारचे असतात : (१) समप्रमाणबद्ध, (२) असमप्रमाणबद्घ, (३) J – आकाराचा,(४) U – आकाराचा. [आ. ९].
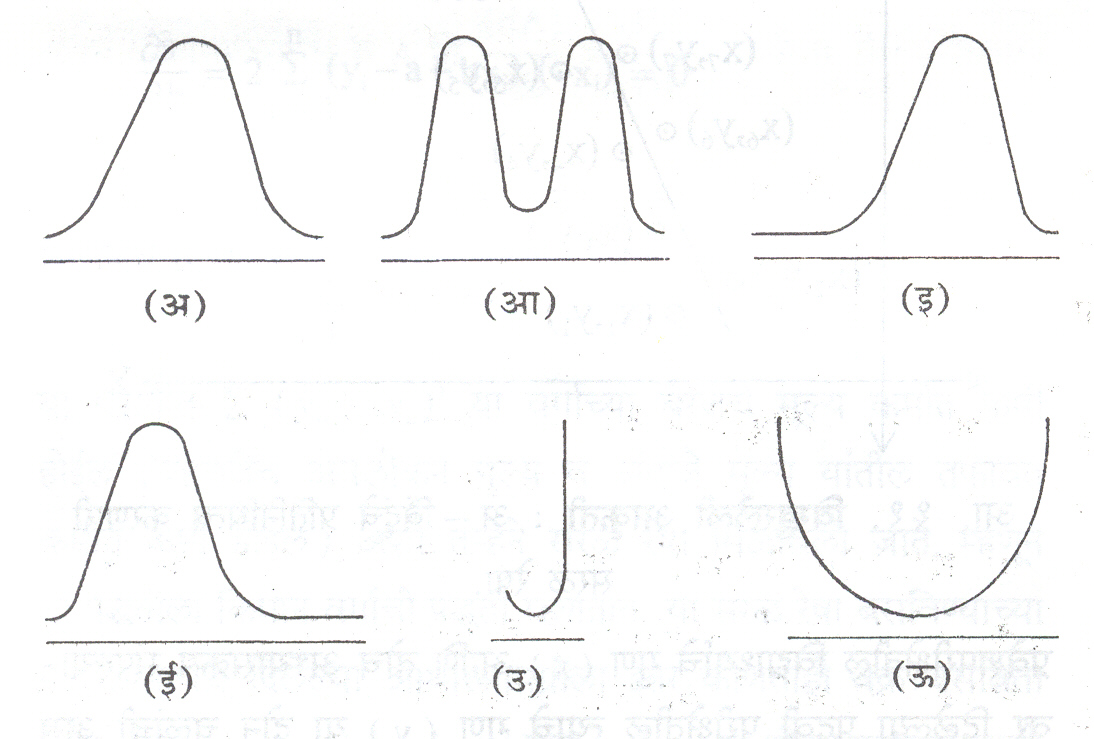
मध्यमान, मध्यक, बहुलक इ. सांख्यिकी-सामग्रीची मध्यप्रवृत्तीमोजणारी मापने आहेत. विस्तार, प्रचरण, प्रमाणित विचरण इ. मापनेसामग्रीचे अपस्करण मोजण्यासाठी वापरतात. ज्यावेळीसांख्यिकी-सामग्री समप्रमाणित असते त्यावेळी तिचे तिसरे केंद्रीय प्रबलक µ3 = 0. त्यामुळे शून्यापासून µ3 जितका वेगळा त्या प्रमाणात सामग्रीची समप्रमाणता कमी होते किंवा असमप्रमाणता वाढते. सामग्रीच्या असमप्रमाणतेच्या मापनासाठी पुढील विविध मापने वापरतात :
(१) µ3/ µ2 3/2 µ3/σ3 हे मापन एककविरहित आहे
(२) मध्यमान–बहुलक (३) ( मध्यमान – बहुलक)/σ
येथे Q1, Q3 हे अनुक्रमे पहिले व तिसरे चतुर्थांशक आहेत D1, D5, D9 हे अनुक्रमे पहिले, पाचवे व नववे दशांशक आहेत P10, P50, P90 हे अनुक्रमे दहावे, पन्नासावे व नव्वदावे शतांशक आहेत. ज्याप्रमाणेमध्यक आधारसामग्रीला दोन समान भागात विभागतो, त्याचप्रमाणेचतुर्थांशक, दशांशक व शतांशक हे आधारसामग्रीला अनुक्रमे चार, दहाव शंभर समान भागात विभागतात.
वक्राच्या बहिर्वक्रतेला पीअर्सन या सांख्यिकीविज्ञांनी
ककुदता हेनाव दिले. या गुणधर्माच्या मापनाने दिलेल्या माहितीचा वारंवारतावक्र शिखराशी किती प्रमाणात सपाट आहे हे ठरविले जाते. याची तुलनागौस यांच्या प्रसामान्य वक्राशी केली जाते ( आ. १० पहा ). पीअर्सनयांनी प्रसामान्य वक्राला किंवा प्रसामान्य वक्राइतकी बहिर्वक्रता असणाऱ्यावक्राला मध्यककुदी ही संज्ञा दिली. प्रसामान्य वक्रापेक्षा जास्त सपाट शिखर कमी सपाट आहे अशा वक्रास अतिककुदी म्हणतात. प्रसामान्यवक्रापेक्षा जास्त सपाट शिखर असणाऱ्या वक्रास अल्पककुदी म्हणतात.ककुदाच्या मापनासाठी प्रबलक वापरून β2 = µ4 /µ22 = µ4/σ 4 हे प्रमाण वापरले जाते. प्रसामान्य वक्रासाठी β2 = 3 असते. म्हणून K = β2 − 3 हे मापन ककुदाच्या (शिखरीपणाच्या म्हणजे बहिर्वक्रतेच्या) मापनासाठी वापरतात.
दोन चलांशी संबंधित आधारसामग्री : एखाद्या समूहातील प्रत्येक व्यक्तीची उंची व वजन नोंदले गेले आहे किंवा एका गावातील सरासरी तापमान व सरासरी पाऊस मोजला आहे असे समजा. या किंवा अशा उदाहरणांमध्ये दोन चले आहेत ( वरील उदाहरणात उंची व वजनकिंवा तापमान व पाऊस ). दोन चले x व y अशा वेगवेगळ्या चिन्हांनीदाखवितात. x चलाची किंमत ज्यावेळी Xi ( i =1, 2, … , n) असेल त्यावेळी y चलाची किंमत yi आहे असे समजा. हीच माहिती कोष्टक स्वरूपात तक्ता क्र. ८ प्रमाणे मांडतात.
| तक्ता क्र. ८. दोन चलांची माहिती | ||||
| x | x1 | x2 | …… | xn |
| y | y1 | y2 | …… | yn |
अशा माहितीला दोन चलांची माहिती म्हणतात. खूप मोठ्या प्रमाणावर माहिती गोळा केली असल्यास ( X1, Y1 ) या मूल्याची जोडी बऱ्याच वेळा मिळाल्यास ती वारंवारता f11 अशी दाखवितात. x हे चल x1, x2, …. , xm ही एकूण m मूल्ये घेत असेल आणि y हे चल y1, y2, …. , yn ही एकूण n मूल्ये घेत असेल असे समजा. म्हणजे x व y या चलांच्या मूल्यांच्या ( xi, yj) (i = 1, 2, … , m j = 1, 2, … , n ) अशा एकूण mn जोड्या असतील. (xi, yj) या जोडीची वारंवारता fij अशी दाखवितात. अशा वेळी x व y या दोन चलांच्या माहितीचे कोष्टक तक्ता क्र. ९ प्रमाणे असते.
| तक्ता क्र. ९. दोन चलांचे वारंवारता वंटन किंवा वारंवारता वितरण सारणी. | |||||
| Xy | y1 | y2 | —- | yn | |
| x1 | f11 | f12 | —- | f1n | f1. |
| X2 | f21 | f22 | —- | f2n | f2. |
| – | – | – | —- | – | – |
| – | – | – | —- | – | – |
| – | – | – | —- | – | – |
| xm | fm1 | fm2 | —- | fmn | fm. |
| f.1 | f.2 | —- | f.n | N | |
अशा कोष्टकाला दोन चलांची ‘वारंवारता वितरण सारणी’ किंवा ‘वारंवरातावंटन’ म्हणतात. एकूण वारंवारता ‘N’ ने दाखवितात. Xया चलाचे मूल्य x1 व त्यावेळी y चलाचे मूल्य काहीही असेल अशा ( x1, yj ) ( j = 1, 2, … , n ) अशा जोड्या एकूण f11 + f12 +… + f1n आहेत. याला x1 ची समासीय वारंवारता म्हणतात व ती f1. अशी दाखवितात. त्याचप्रमाणे x2, … , xm या मूल्यांच्या f2., … , fm. या समासीय वारंवारता असून त्या वारंवारता सारणीत शेवटच्या स्तंभात दाखवितात. अगदी त्याचप्रमाणे y च्या y1, y2, … , yn या मूल्यांच्या समासीय वारंवारता f.1, f.2, …, f.n अशा दाखवितात आणि त्या कोष्टकाच्या शेवटच्या ओळीत मांडतात.
अशा दोन चलांच्या वारंवारता वंटनांच्या अभ्यासाला पीअर्सन यांनी १८९० च्या सुमाराला सुरुवात केली. यासाठी विशेषतः जीवशास्त्रातील खूप कच्ची माहिती मिळत गेली. अशा माहितीमध्ये दोन चलांच्यामध्ये काही संबंध असल्याचे दिसून येते. परंतु भौतिकीमध्ये दोन चलांतील संबंध गणिती पद्घतीने समीकरण मांडून दाखविता येतात, तशा रेखीव पद्घतीने येथे मांडणी करता येत नाही. त्यामुळे दोन चलांमध्ये आधारसामग्रीतून दिसून येणारे संबंध दाखविण्यासाठी नव्या पद्घती अस्तित्वातआल्या. या नव्या प्रकारच्या अभ्यासाची परिणती गुणात्मक गुणधर्माच्यासंबंधात साहचर्य व आसंग आणि परिमापनात्मक गुणधर्माच्या बाबतीतसहसंबंध व समाश्रयण या विषयांत होते. दोन चलांच्या आधारसामग्रीचेएक उदाहरण तक्ता क्र. १० मध्ये दिले आहे.
आधारसामग्रीला वक्र बसविणे : निरीक्षण अथवा मोजणी करूनx व y या दोन चलांच्या संबंधित मूल्यांचा तक्ता क्र. ११ तयार झालाआहे. यातील (x, y) च्या (x1, y1), …. , (xn, yn) या मूल्यांच्या
| तक्ता क्र. १०. पडलेला पाऊस व मिळालेले भाताचे हेक्टरी पीक | ||||
| पडलेला पाऊस
(सेमी. मध्ये) |
दर हेक्टरी भाताचे पीक (१०० टनांमध्ये ) | |||
| ०-१५ | १५-३० | ३०-४५ | ४५-६० | |
| ०-२० | १० | ४ | ३ | ० |
| २०–४० | १२ | ६ | ३ | ० |
| ४०–६० | १४ | ७ | ५ | १ |
| ६०–८० | १५ | ९ | ७ | २ |
| ८०–१०० | १८ | १० | ९ | ४ |
| (या कोष्टकातील वारंवारता ही हेक्टरांची संख्या दाखविते.)
तक्ता क्र. ११. दोन चलांच्या संबंधीत मूल्यांचा तक्ता
|
||||
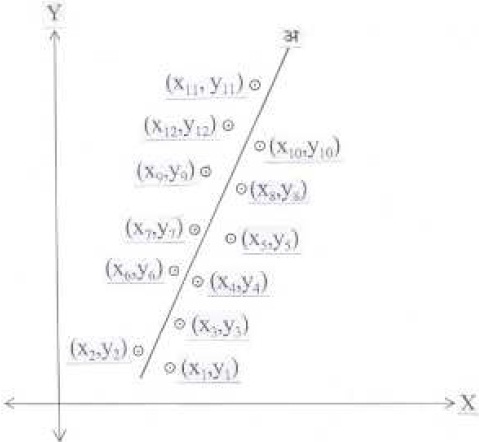n जोड्या मांडून मिळालेल्या आलेखाला विखुरलेली आकृती म्हणतात (आ. ११). ही माहिती अभ्यासकमास प्रवेश घेण्यासाठी दिलेल्या प्रवेशपरीक्षेतील विद्यार्थ्याचे गुण (x) आणि तोच अभ्यासकम संपल्यावरदिलेल्या पदवी परीक्षेतील त्याचे गुण (y) या दोन चलांची असूशकेल. ही माहिती वापरून, साधारणतः त्याच प्रकारची गुणवत्ताअसणाऱ्या नंतरच्या वर्षीच्या दुसऱ्या एखाद्या विद्यार्थ्यास प्रवेशपरीक्षेतमिळालेले गुण (x) माहीत असल्यास, तो त्याच्या पदवी परीक्षेत कितीगुण (y) मिळवेल याचा अंदाज बांधता येईल का ? कोणत्याहीव्यावहारिक समस्येशी संबंधित आधारसामग्रीवरून काढलेल्या अशाप्रकारच्या विखुरलेल्या आकृतीच्या सर्व बिंदूंतून जाणारी एकच सरळरेषा किंवा ज्यातकोठेही टोकदारपणा नाही असा वक्र असणे केवळअशक्य आहे. तेव्हा अशी एखादी सरळ रेषा (किंवा वक्र) असेल का,की जी त्यातल्या त्यात सर्व बिंदूंच्या जवळून जाईल व त्या सर्वबिंदूंचे प्रतिनिधित्व करीत असल्याचे मानता येईल ? अशी सरळ रेषा(किंवा वक्र) मिळाल्यास माहीत असलेले x चे मूल्य तिच्यासमीकरणात घालून y चे हवे असलेले मूल्य काय असेल याचा अंदाजबांधणे शक्य आहे. अशा प्रकारे ज्याच्यावरून x च्या विविध मूल्यांसाठी y च्या मूल्यांचा अंदाज बांधता येईल असा वक्र आधारसामग्रीतील माहितीवरून शोधून काढण्याच्या कृतीला ‘आधारसामग्रीला वक्र बसविणे’ असे म्हटले जाते.
आधारसामग्री वापरून (x, y) च्या काढलेल्या विखुरलेल्या आकृतीच्या सर्व बिंदूंतून जवळपास जाणारी व त्या सर्व बिंदूंचे प्रतिनिधित्व करणारी सरळ रेषा शोधणे म्हणजेच त्या सरळ रेषेचे समीकरण मिळविणे. तेव्हा ती सरळ रेषा y = a + bx आहे असे समजू. मोजून अथवा निरीक्षण करून मिळालेले व विखुरलेल्या आकृतीसाठी वापरलेले y चे मूल्य y० आणि या सरळ रेषेवरून मिळणारे y चे अंदाजे मूल्य ye यातील तफावत सर्व अवलोकनांसाठी कमीत कमी असावी हा उद्देश ठेवून y = a + bx या समीकरणातील a व b ठरविले जातात आणि ते अनुक्रमे 
या संकेतनांनी दाखविले जातात. (yo – ye) हा फरक धन किंवा ऋण असू शकतो. त्यामुळे सर्व अवलोकने विचारात घेऊन 
या राशीचे मूल्य कमीत कमी झाले पाहिजे. त्यासाठी कलनशास्त्रानुसार 
असले पाहिजे. अशा तऱ्हेने मिळणारी ही दोन समीकरणे â व bयांची मूल्ये ठरवितात. तेव्हा
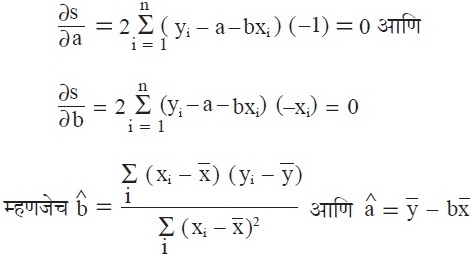
या पद्घतीत Σ (yo – ye)2 या वर्गाच्या बेरजेचे मूल्य कमीत कमी होईल (म्हणजेच अवलोकन मूल्य व अंदाजे मूल्य यांतील तफावत कमीत कमी होईल) अशा तऱ्हेने सरळ रेषा मिळविली जाते. म्हणून या पद्घतीला किमान वर्गाची पद्घती म्हणतात. या सरळ रेषा बसविण्याच्या पद्घतीप्रमाणेच दिलेल्या आधारसामग्रीला इतर कोणताही वक्र बसविता येईल. उदा., y = a + bx + cx2 यात a, b, c या तीन प्रचलांची मूल्ये ठरविली जातील. याकरिता S = Ρ ( yi – a – bxi – cx2)2 कमीत कमी करावे लागते व त्यासाठी 
ही तीन समीकरणे सोडवावी लागतात.
उदाहरण म्हणून तक्ता क्र. १२ मधील स्तंभ १ व २ यांनी दिलेल्या आधारसामग्रीला y = a + bx ही सरळ रेषा बसवूया. त्यासाठी त्या तक्त्यातच स्तंभ ३ व ४ मधील आकडेमोड दाखविली आहे.
वरील विवेचनानुसार 
तक्ता क्र. १२. सरळ रेषा बसविण्याचे उदाहरण
| वापरलेले खत
x ( किलो ) |
विकीतील फायदा
y ( रु. ) |
X2 | xy |
| २ | १,५०० | ४ | ३,००० |
| ५ | २,५०० | २५ | १२,५०० |
| ७ | ३,००० | ४९ | २१,००० |
| ११ | ४,००० | १२१ | ४४,००० |
| १२ | ४,५०० | १४४ | ५४,००० |
| ३७ | १५,५०० | ३४३ | १,३४,५०० |
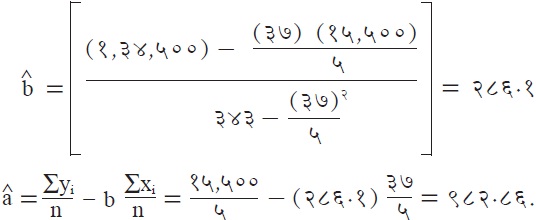
∴y =९८२.८६ + २८६.१x ही हवी असलेली सरळ रेषा आहे.तिचा वापर करून x च्या मूल्यासाठी y चे मूल्य काय असेल[म्हणजेच दिलेल्या (x) इतके खत वापरल्यास किती फायदा (y) होऊशकेल याचा अंदाज काढण्यासाठी] हे काढता येईल.
दोन चलांच्या आधारसामग्रीला बसविलेल्या y =a + bx या सरळरेषेला y ची x वरील समाश्रयण रेषा असे म्हणतात. b ला ‘y चा xवरील समाश्रयण गुणांक’ म्हणतात. समाश्रयण ही संज्ञा प्रथम ⇨सरफान्सिस गॉल्टन यांनी आनुवंशिकतेसंबंधी काही विवेचन करतानावापरली. आता ही संज्ञा दोन वा अनेक चलांधील रेषीय किंवा अरेषीयसंबंध दाखविण्यासाठी वापरली जाते.
सांख्यिकीतील अवलंबित्वाचे (अधीनतेचे) स्वरूप :सांख्यिकीतील अवलंबी व निरवलंबी (अधीनता व अनधिनता) यासंकल्पना संभाव्यतेच्या संकल्पनेवर आधारित आहेत. त्यामुळे त्यांच्याआकलनासाठी संभाव्यताशास्त्राची उपपत्ती योग्य रीत्या समजणेआवश्यक बनते.
A व B या दोन घटनांसंबंधित संभाव्यता
P(AB) =P(A).P(B) …. …. …. …. …. (१)
या सूत्राने व्यक्त होत असतील तर A व B या घटनांना निरवलंबीम्हणतात. B ही घटना घडली असता A या घटनेची संभाव्यताP(A|B) अशी दाखवितात. तिला ‘B घडली असतानाची A ची सशर्तसंभाव्यता’ म्हणतात. या संदर्भात A ची विनाअट ( बिनशर्त ) संभाव्यताP(A) अशी दर्शवितात.
P(A) =P(A | B) …. …. …. …. …. …. (२)
असेल तर, A व B या घटना निरवलंबी असतात. समी. (२) सत्यअसेल तर
P(B) =P(B | A) …. …. …. …. …. …. (३)
हेही सत्य असते. P(A | B) ची व्याख्या अशी आहे.
P(A |B) = P(AB) / P(B), P(B) ≠ 0 …. …. (४)
सूत्र (२) मध्ये (४) वापरून (१) मिळते. म्हणजेच (२) व (१) या दोन्ही निरवलंबतेच्या कसोट्या म्हणून वापरता येतात. त्यातील(१) ही (२) पेक्षा अधिक व्यापक आहे. कारण P(B) =0 असताना (२) वापरता येत नाही, परंतु (१) नेहमीच वापरता येते.
दोनपेक्षा अधिक घटना असल्यास निरवलंबतेची संकल्पना अधिक व्यापक आहे. ती अशी : ‘A1, A2, …. , An या n घटना निरवलंबी आहेत’ असे म्हणण्यासाठी पुढील दोन गुणधर्म सत्य असावे लागतात.
(१) P(A1 A2 … An) = P(A1).P(A2) … P(An)
आणि (२) i1, i2, … , ik या 1, 2, 3, … , n च्या कोणत्याही k क्र मपर्यायासाठी P(Ai१ Ai२ … Aik) =P(Ai1).P(Ai2) … P(Aik) येथे k = 2, 3, 4, … , n−1.
यादृच्छिक चलाच्या घनता-फलनांच्या माध्यमातून सांख्यिकीतील निरवलंबतेची संकल्पना पुढीलप्रमाणे मांडली जाते : x व y ही यादृच्छिक चले असून f1, f2 व f ही अनुक्रमे x चे, y चे आणि x व y यांचे, संयुक्त घनता-फलन असल्यास सर्व x व y साठी f (x, y) =f1(x).f2(y) असेल तर x व y ही यादृच्छिक चले निरवलंबी असतात असे म्हणतात. याच धर्तीवर दोनपेक्षा अधिक यादृच्छिक चलांच्या निरवलंबतेची संकल्पना मांडली जाते.[⟶ संभाव्यता संभाव्यता सिद्धांत].
साहचर्य आणि सहसंबंध : उंची, वजन, परीक्षेतील गुण ववस्तूची किंमत या प्रकारच्या चलांची मूल्ये आकड्यांच्या माध्यमातूनमांडता येतात. उदा., ५२.१ सेंमी., १७.८ ग्रॅम, ८७ गुण, ३.७० रूपये.माणसांचे व वस्तूंचे काही गुणधर्म असे असतात की ते या प्रकारे संख्यावापरून सांगता येत नाहीत. उदा., वस्तूचा रंग ( लाल, काळा, हिरवाइ.), चव/आवड ( गोड, तिखट, आंबट, कडू इ.), व्यक्तीचे लिंग( स्त्री, पुरुष ), धर्म इ. माहिती गोळा करीत असताना अशा प्रकारच्यागुणधर्मांशी संबंधित माहिती देखील जमवावी लागते. अशा गुणधर्मांनागुणात्मक गुणधर्म म्हणतात व त्यांचा सांख्यिकीय अभ्यास निराळ्याप्रकारे करावा लागतो. अभ्यासासाठी निवडलेला गुणात्मक गुणधर्मव्यक्तींध्ये/वस्तूंध्ये आहे की नाही हे पाहून तशी नोंद केली जाते.अशा गुणधर्माचे वस्तूतील/व्यक्तीतील अस्तित्व अथवा अभावA, B, C, … , a, b, c, … इ. अक्षरांनी दर्शविले जाते. त्या संबंधीचाप्रघात असा आहे : जर ‘पुरुष’ या गुणधर्मासाठी ‘A’ हे अक्षरवापरले, तर ‘a’ हे अक्षर ‘स्त्री’ गुणधर्मासाठी वापरतात. ‘B’ हे अक्षर‘साक्षर’ या गुणधर्मासाठी उपयोगात आणले, तर ‘b’ हे अक्षर‘निरक्षर’ हा गुणधर्म दाखविते. या अक्षरांचा संयोग करून ती एकत्रितपणेवापरून अनेक गुणधर्म एकत्रितपणे हाताळता येतात. ‘AB’ म्हणजेसाक्षर पुरुष, ‘ab’ म्हणजे निरक्षर स्त्री. ही अक्षरे कंसात घालून त्या त्यासंबंधित गुणधर्मांची वारंवारता दाखविली जाते. उदा., (A) म्हणजेप्रदत्तामधील पुरुषांची एकूण संख्या (Ab) म्हणजे निरक्षर पुरुषांचीएकूण संख्या इत्यादी.
ह्या ठिकाणी मुख्यत्वे A व B हे गुणधर्म निरवलंबी आहेत का हेपाहावे लागते. त्यासाठी एकूण N व्यक्ती / वस्तू आहेत असे समजा.A या गुणधर्माची वारंवारता (A) आहे. म्हणून एखाद्या दिलेल्याव्यक्तीत/वस्तूत A हा गुणधर्म असण्याची संभाव्यता = (A)/N .तसेच एखाद्या व्यक्तीत/वस्तूत A व B हे गुणधर्म एकत्रितपणे असण्याची संभाव्यता (A)/N X (A)/N त्यामुळे N या एकूण वारंवारतेपैकी A व B हे दोन्ही गुणधर्म असणाऱ्या व्यक्तींची/वस्तूंची अपेक्षित वारंवारता = N x (A)/N x (B)/N = (A)(B)/N. अशा तऱ्हेने N व्यक्ती/वस्तूंमध्ये A व B हे दोन्ही गुणधर्म असणाऱ्या व्यक्तींची/वस्तूंची प्रत्यक्ष अवलोकित वारंवारता (AB) असून, अपेक्षित वारंवारता (A)(B)/N ही आहे. या दोन्ही वारंवारता समान असतील म्हणजेच (AB) = (A)(B)/N असेल, तर A व B हे दोन्ही गुणधर्म निरवलंबी असल्याचे मानले जाते ( येथे संभाव्यताशास्त्रातील संकल्पनेचा वापर केला आहे ). A व B या गुणधर्मांच्या बाबतीत प्रत्यक्ष वारंवारता अपेक्षित वारंवारतेहून अधिक असेल [म्हणजेच (AB) > (A)(B)/N असेल], तर A व B या गुणधर्मात धन-साहचर्य असल्याचे मानतात. उलट (AB) < (A)(B)/N असेल], तर A व B या गुणधर्मात ऋण-साहचर्य आहे असे समजतात. याचप्रमाणे कोणत्याही दोन गुणधर्मांमधील ( उदा., A व b, a व B, a व b )निरवलंबिता, धन-साहचर्य व ऋण-साहचर्य तपासले जाते.
A व B हे गुणधर्म निरवलंबी असल्यास (AB) (ab) =(Ab) (aB) असल्याचे दाखविता येते म्हणून ही समानता A व Bनिरवलंबी आहेत का हे तपासण्यासाठी कसोटी म्हणून वापरता येते. Aव B हे गुणधर्म निरवलंबी असल्यास (B) व (b) या दोन्ही वारंवारतेतA चा अनुपात समान असला पाहिजे, म्हणजेच 
हीगुणोत्तरे समान असली पाहिजेत. म्हणून
ही A व B च्या निरवलंबितेची कसोटी, 
ही A व B याच्यामधील ऋण-साहचर्याची कसोटी आणि 
ही A व B यांच्यामधील धन-साहचर्याचीकसोटी म्हणून वापरता येईल. याचप्रमाणे, (A) व (a)मधील B चा अनुपात वापरून इतर कसोट्या तयार करता येतील. याकसोट्या लक्षात ठेवण्यासाठी तक्ता क्र. १३ मधील कोष्टक वापरतायेईल. तक्ता क्र. १३ ला A व B या गुणात्मक गुणधर्मांचे आपातिककोष्टक म्हणतात.
तक्ता क्र. १३. A व B या गुणात्मक गुणधर्मांचे आपातिक कोष्टक
| गुणविशेष | B | b | एकूण |
| A | (AB) | (Ab) | (A) |
| a | (aB) | (ab) | (a) |
| एकूण | (B) | (b) | N |
A व B या गुणात्मक गुणधर्मांधील निरवलंबिता, धन-साहचर्य व ऋण-साहचर्य यांसाठीच्या वरील सर्व कसोट्या तक्ता क्र. १४ मध्ये एकत्रित केल्या आहेत. त्यातील ओळ १ मधील कोणतेही पद ‘α’ या संकेतनाने व त्याच्या संबंधित त्याच्या बरोबर खाली दुसऱ्या ओळीत येणारे पद ‘β’ या संकेतनाने दाखविले आहे. आता सर्व सहा कसोट्या एकत्रितपणे पुढीलप्रमाणे मांडता येतील.
ज्याप्रमाणे (१) α = β(२) α> βकिंवा (३) α < β असेल त्याप्रमाणे अनुक्रमे (१) A व B निरवलंबी आहेत (२) A व B यांच्यात धन-साहचर्य हे व (३) A व B यांच्यात ऋण-साहचर्य आहे असा निष्कर्ष निघतो.
तक्ता क्र. १४. A व B यांच्यातील अनधिनता, धन-साहचर्य व ऋण-साहचर्य तपासण्यासाठी.
| (α) | (AB) | (AB)
(B) |
(AB)
(A) |
(AB) (ab) | (aB)
(B) |
(Ab)
(A) |
| (β) | (A) (B)
N |
(Ab)
(b) |
(aB)
(a) |
(Ab) (aB) | (ab)
(b) |
(ab)
(a) |
यूल या विख्यात सांख्यिकीविज्ञांनी A व B या गुणात्मक गुणधर्मांतील साहचर्य मापनासाठी
हा साहचर्य गुणांकदिला. Q = 0 हे A व B निरवलंबी असण्याचे लक्षण आहे. Q > 0 असेल तर त्याचा अर्थ A व B यांच्यात धन-साहचर्य असते. Q < 0
असल्यास A व B यांच्यात ऋण-साहचर्य असते. Q जास्तीत जास्त +१ व कमीत कमी –१ असतो. Q = +१ असल्यास A व B यांच्यात संपूर्ण धन-साहचर्य आहे असे म्हणतात. Q = –१ असल्यास A व B यांच्यामध्ये संपूर्ण ऋण-साहचर्य आहे असे म्हणतात.
उदाहरण म्हणून यूल यांचे सूत्र तक्ता क्र. ६ साठी लावूया. त्यासाठी A = लसीकरण घेणारे व B= रोगाची लागण झालेले आणि a = लसीकरण न घेणारे व b = रोगाची लागण न झालेले असे मानू. त्यामुळे तक्त्यातील वारंवारता पुढीलप्रमाणे होतील :
म्हणून या आधारसामग्रीत ‘लसीकरण घेणे’ व ‘रोगाची लागण होते’ यात ऋण-साहचर्य आहे. याचा अर्थ लसीकरण घेण्याने रोगाची लागण होण्याची शक्यता कमी होते असा आहे.
जेव्हा दोन चलांची मूल्ये संख्यांच्या माध्यमातून मांडता येतात तेव्हात्या दोन चलांधील संबंधाचा अभ्यास पुढीलप्रमाणे केला जातो. दोनचलांची मूल्ये एकमेकासमवेत बदलत असतात. म्हणजेच एकाचलाचे मूल्य बदलले की दुसऱ्याचे मूल्यही बदलते असे आढळूनयेते, तेव्हा त्या दोन चलांत सहसंबंध आहे असे म्हटले जाते. एकाचलाचे मूल्य वाढले की दुसऱ्या चलाचे मूल्यही वाढत असेलआणि त्या दोघांमधील एखाद्याचे मूल्य कमी झाले की दुसऱ्याचेहीमूल्य कमी होत असेल तर त्या दोन चलांत धन सहसंबंध आहेअसे म्हणतात. उदा., वधुवरांच्या तक्ता क्र. १५ पहा.
तक्ता क्र. १५. वधुवरांच्या वयांतील धन सहसंबंध
| वराचे वय (x) | २५ | २६ | २७ | २८ | २९ | ३० | ३१ | ३२ |
| वधूचे वय (y) | १८ | २० | २२ | २५ | २६ | २७ | २९ | ३० |
या तक्त्यात दिलेल्या माहितीवरून वराचे व वधूचे लग्नाच्या वेळचे (तसेच त्यानंतर केव्हाही) वय यांच्यात धन सहसंबंध असल्याचे दिसून येते.
याउलट एका चलाचे मूल्य जेव्हा वाढते तेव्हा दुसऱ्या चलाचे कमीहोते आणि त्या दोन चलांधील एकाचे मूल्य कमी होते त्यावेळीदुसऱ्याचे वाढते अशी स्थिती असल्यास त्या दोन चलांतऋण सहसंबंध आहे असे म्हणतात. उदा., तक्ता क्र. १६मध्ये पोलिसांची संख्या व समाजातील गुन्ह्यांची संख्या यादोन चलांत ऋण सहसंबंध असल्याचे आढळून येते.
एका प्रदत्तात दोन चलां ध्ये धन सहसंबंध असूनत्यातील एका चलाचे प्रदत्तातील कोणतेही मूल्य माहीतअसल्यास दुसऱ्या चलाचे त्या प्रदत्तातील संबंधितमूल्य, रेषीय समीकरण वापरून, अगदी तंतोतंत ओळखता येत असेल,तर त्या दोन चलांत परिपूर्ण धन सहसंबंध असल्याचे म्हटले जाते. उदा.,ज्याप्रश्नपत्रिकेत सर्व प्रश्न वस्तुनिष्ठ स्वरूपाचे आहेत व ऋण गुण
तक्ता क्र. १६. पोलिसांची व गुन्ह्यांची संख्या यांच्यातीलऋण सहसंबंध.
पोलिसांची संख्या (x) २००० २५०० ३००० ३५०० ४५००
गुन्ह्यांची संख्या (y) ५०० ३८० ३१० २४० ९०
तक्ता क्र. १७. बरोबर उत्तरांची संख्या व मिळालेले गुण यांच्यात परिपूर्ण धनसहसंबंध असणारा प्रदत्त.
बरोबर उत्तरे असलेल्या
प्रश्नांची संख्या (x) ० १ २ ३ ४ ५ ६ ७ ८ ९ १०
मिळालेले गुण (y) ० २ ४ ६ ८ १० १२ १४ १६ १८ २०
देण्याची पद्घत वापरात नाही अशा परीक्षेत विद्यार्थ्यांना मिळालेले गुणतक्ता क्र. १७ मध्ये दिले आहेत. यात x व y या चलांत y =२x हे रेषीय सूत्र आहे. त्यामुळे त्या दोन चलांमध्ये या प्रदत्तात असलेला धनसहसंबंध परिपूर्ण आहे.
एका प्रदत्तात दोन चलांध्ये ऋण सहसंबंध असून त्यातील एकाचलाच्या प्रदत्तातील प्रत्येक मूल्यासाठी दुसऱ्या चलाचे त्या प्रदत्तातीलसंबंधित मूल्य, रेषीय समीकरण वापरून, अगदी तंतोतंत ओळखता येतअसेल तर त्या दोन चलांत परिपूर्ण ऋण सहसंबंध आहे असे म्हणतात.उदा., तक्ता क्र. १८ मधील प्रदत्त पहा.
तक्ता क्र. १८. बहुभुजाची कोनसंख्या व त्यातील एका कोनाचे माप( अंशामध्ये ) यांत परिपूर्ण ऋण सहसंबंध असणारा प्रदत्त.
बहुभुजाच्या बाजूंची संख्या (x) ३ ४ ५ ६ ७ ८
बहुभुजातील एका कोनाचे माप (y) १६५ १६० १५५ १५० १४५ १४०
यात x व y चलात y = 180 – 5x हे रेषीय सूत्र आहे. त्यामुळे त्यादोन चलांत या प्रदत्तात असलेला ऋण सहसंबंध परिपूर्ण आहे.
अशा प्रकारच्या दोन चलांधील सहसंबंध मोजण्यासाठी सांख्यिकीविज्ञांचे पितामह असणाऱ्या कार्ल पीअर्सन यांनी r हा पुढील सहसंबंधगुणांक सुचविला. x व y या दोन चलांच्या मूल्यांच्या (x1, y1), (x2, y2), … , (xn, yn) या n जोड्यांनी प्रदत्त बनला असेल, तर त्या
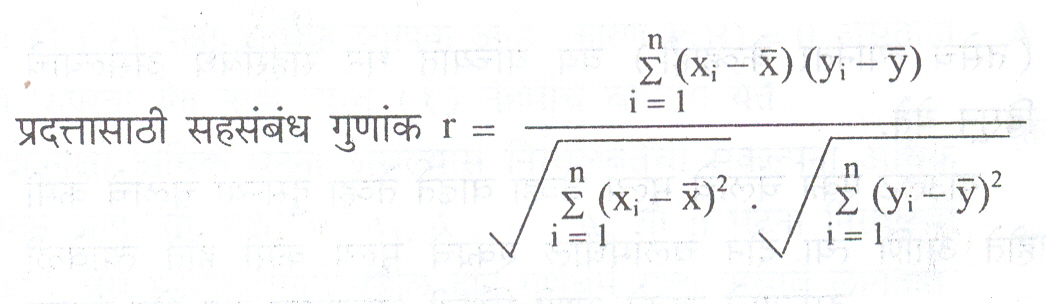
या सहसंबंध गुणांकाचे काही गुणधर्म पुढीलप्रमाणे आहेत : (१) −१⪯r ⪯+१ (२) x व y ही निरवलंबी चले असतील, तर r = ० परंतु r = ० असल्यास x व y निरवलंबी असतातच असे नाही (३) जर x व y यांच्यामध्ये पूर्ण रेषीय संबंध असेल तर y = a +bx, (b ≠ ०) (b < ०) ⇔(r = −१) आणि (b > ०) ⇔ (r =+१) (४) y =a +bx ही y ची x वरील समाश्रयण रेषा असून x =á+b´y ही x ची y वरील समाश्रयण रेषा असेल, तर r2 =bb´ (५) x व y यांच्यात धन सहसंबंध असल्यास r > ० व ते धन सहसंबंध परिपूर्ण असल्यास r =+१ व याच्या उलट (६) x व y यांच्यात ऋण सहसंबंध असतील तर r < ० व ते ऋण सहसंबंध परिपूर्ण असल्यास r = −१ व याच्या उलट (७) r = ०.८ याचा अर्थ y मधील ६४% विचलन x व y मधील रेषीय संबंधाने स्पष्ट करता येते. म्हणजेच x व y मध्ये ६४% समान विचलन आहे. r च्या इतर मूल्यांचे स्पष्टीकरण अशा प्रकारेच करता येते (८) r च्या मूल्यांवरून y मधला चढ-उतार x मुळे होतो असे म्हणता येत नाही.
तक्ता क्र. १२ मधील x व y या दोन चलांच्या प्रदत्तासाठी r काढूया. तेथे ∑ x =३७, ∑y =१५,५००, ∑x2 =३४३, ∑xy =१,३४,५०० आहेतच. आणखी ∑y2 =१०४ (२२५+ ६२५+९००+१,६००+२,०२५) =५,३७५×१०४. आता
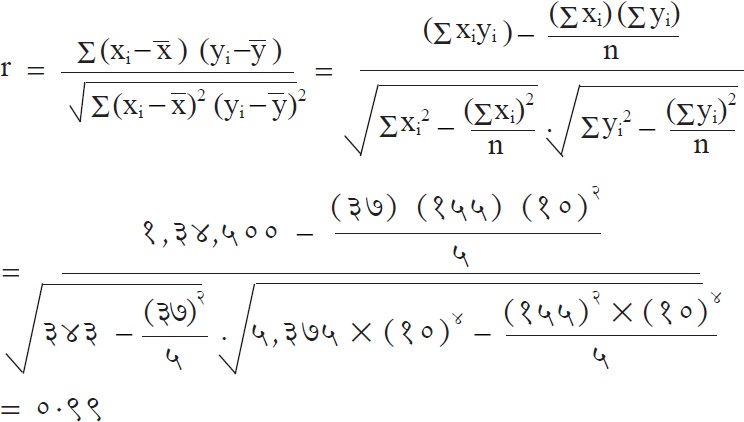
म्हणजे वापरलेले खत व विकीतील फायदा या दोन चलांध्ये धनसहसंबंध आहे.
प्रामाणिकपणा, कार्यक्षमता, सौंदर्य अशा प्रकारच्या गुणधर्मांवर मापनेघेणे अशक्य वा निदान अतिशय अवघड असते, परंतु या गुणधर्मांनुसारव्यक्तींचे/वस्तूंचे कम लावता येतात. काही वेळा चलावर मापने घेणेशक्य असते परंतु तशी मापने न घेता मापने ज्यांच्यावरघ्यायची त्याव्यक्तींची / वस्तूंची चलाच्या संबंधात कमवार मांडणी करतात. काहीवेळा मापने घेऊन त्या मापनांच्या अनुषंगाने व्यक्तींची/वस्तूंची क्र मानुसारयादी केली जाते. अशा प्रकारचा दोन चलांनी निर्देशित केलेल्या गुणधर्मांनुसार व्यक्तींची / वस्तूंची कमवार यादी देणारा प्रदत्त तक्ता क्र. १९मधील स्तंभ १, २ व ३ यांनी दाखविल्याप्रमाणे मांडता येतो. अशाप्रकारच्या प्रदत्तातील दोन गुणधर्मांमधील सहसंबंधाचे मापन चार्ल्स एडवर्ड–स्पिअरमनयांनी दिलेला पुढील गुणांक वापरून करतात.
येथे N = क्रमांकाच्याएकूण जोड्या, D =प्रत्येकवस्तूच्या/व्यक्तीच्या दोन क्र मांकांतील फरक आणि R ला क्र मसहसंबंध गुणांकम्हणतात. त्यासाठीची आकडेमोड तक्ता क्र. १९ मध्ये दाखविली आहे.
तक्ता क्र. १९. क्र मसहसंबंध गुणांकाची आकडे मोड
| व्यक्ती/वस्तू | चल (x) नुसार क्रम (R1) | चल (y) नुसार क्रम (R2) | D = R1 –R1 | D2 |
| A | २ | २ | ० | ० |
| B | ३ | १ | २ | ४ |
| C | ६ | ६ | ० | ० |
| D | ५ | ३ | २ | ४ |
| E | १ | ५ | –४ | १६ |
| F | ४ | ४ | ० | ० |
| N = ६ | २४ |
वरील संपूर्ण विवेचनात ज्याठिकाणी विविध संकल्पनांचे व रीतींचेउल्लेख केले आहेत, त्यातील आवश्यक ठिकाणी उदाहरणांद्वारे त्यासंकल्पना व रीती विशद केल्या आहेत. सांख्यिकीच्या निरनिराळ्याउपयोजनांसंबंधीचे वर्णन मराठी विश्वकोशात अनुकमात्मक विश्लेषण,कालश्रेढी विश्लेषण, गुणवत्ता नियंत्रण, निर्णय पद्घती, प्रतिदर्श सर्वेक्षणसिद्घांत, प्रयोगांचा अभिकल्प, प्रोबिट विश्लेषण, माँटी कार्लो पद्घती,
विचरणाचे विश्लेषण, सांख्यिकीय अनुमानशास्त्र, सामाजिक सर्वेक्षणसिद्घांत या नोंदींत आलेले आहे.
संदर्भ : 1. Mood, A. M. Introduction to the Theory of Statistics, 1974.
2. Triola, M. F. Elementary Statistics, 2000.
टिकेकर, व. ग.
“