विचरणाचे विश्लेषण

विचरणाचे विश्लेषण : हे सांख्यिकीय तंत्र ⇨सर रॉनल्ड एल्मर फिशर यांनी प्रथम शोधून काढले. हे तंत्र प्रयोगातून मिळणाऱ्या फलांच्या सांख्यिकीय विश्लेषणासाठी विशेष उपयुक्त आहे. या तंत्राचा उपयोग फिशर यांनी विज्ञानाच्या निरनिराळ्या शाखामध्ये, विशेषतः जीवविज्ञानातील संशोधनात वापरण्यात येणाऱ्या प्रयोगांच्या अभिकल्पासाठी केला [⟶ प्रयोगांचा अभिकल्प]. लहान प्रतिदर्शाच्या (नमुन्यांच्या) बाबतीत हे तंत्र विशेषत्वाने उपयुक्त आहे व मोठ्या प्रतिदर्शाकरिताही ते वापरता येते. तथापि ते योग्य प्रकारे वापरण्यासाठी संशोधने आपले प्रयोग विशिष्ट विनिर्देशांनुसार अभिकल्पित करणे आवश्यक आहे. प्रस्तुत नोंदीतील माध्य, विचरण, सहविचरण, समाश्रयण, प्रतिदर्श, समष्टी, सार्थता कसोटी, गृहीतकाची कसोटी, आकलन, विश्वास सीमा, मुक्तता मात्रा, प्रसामान्य वंटन, F−वंटन, काय-वर्ग (X²) वंटन, t−वंटन, लॅटिन चौरस अभिकल्प, याइच्छित खंड अभिकल्प वगैरे मूलभूत सांख्यिकीय संज्ञा समजण्यासाठी मराठी विश्वकोशातील ‘वंटन सिद्धांत’, ‘प्रयोगांचा अभिकल्प’ आणि ‘सांख्यिकीय अनुमानशास्त्र’ या नोंदी पहाव्यात.

चलनाचे विभाजन व गृहीतकांची कसोटी : समजा, x₁, x₂,  …..x_n ही एका प्रयोगामध्ये निरिक्षण केलेल्या काही चलांची मूल्ये आहेत. गृहीत धरू की, ही निरीक्षणे अनेक प्रसामान्य वंटनांतून स्वतंत्रपणे आलेली आहेत. असेही गृहित धरू की, या सर्व प्रसामान्य वंटनांचे एकच पण अज्ञात विचरण σ² आहे व त्यांची माध्ये μ_i मात्र निरनिरांळी असून प्रयोगावर परिणाम करणाऱ्या एखाद्या घटकाशी (उदा., जमिनीचा सुपीकपणा, निरनिराळे उपचार, निरनिराळ्या जातींचे जनावरे अथवा वनस्पतींची रोपे इ.) निगडित आहेत. प्रयोगाचा उद्देश या μ_i माध्यांशी संबंधित असलेल्या गृहीतकाची कसोटी घेणे हा आहे. उदा., निरनिराळ्या उपचारांचा माध्यावर काहीच परिणाम होत नाही हे मूळ गृहीतक.

एखाद्या मूळ गृहीतकानुसार जर निरीक्षण केलेल्या X_i मूल्यांची माध्ये तीच असतील, तर या प्रतिदर्शांच्या माध्याच्या विचलनांच्या वर्गांची एकूण बेरीज म्हणजे

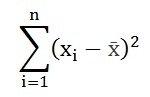याला मुक्तता मात्रांनी म्हणजे (n−1) ने भागले असता आपल्याला σ² चे निरभिमत आकलन मिळेल. विचरणाचे विश्लेषण या तंत्राची मूलभूत कल्पना अशी आहे की, माध्यातील चलनाच्या अनेक विशिष्ट कारणांशी संवादी होईल असे वरील बेरजेचे अनेक घटकांत विभाजन करावयाचे म्हणजे या विभाजनामुळे माध्याशी संबंधित असलेल्या अनेक गृहीतकांची कसोटी घेता येईल आणि शिवाय प्रयोगकर्त्याचा काही हेतू सफल होईल अशा पुष्कळशा अवलंबित राशींची आकलने मिळतील.

आता असे गृहीत धरू की, निरीक्षण केलेल्या n मूल्यांचे p गटांत विभाजन केलेले असून i व्या गटात ni निरीक्षित मूल्यांचा समावेश होते व ती प्रसामान्य घटनाचा नियम पाळतात आणि त्यांचे माध्य μ_i व विचरण σ^₂ आहे. सर्व गटांची माध्ये ही एकमेकांच्या बरोबर आहेत [म्हणजेच μ₁ = μ₂ =………. = μ_p] या मूळ गृहीतकाचा विचार करू. i व्या गटातील j वे निरीक्षित मूल्य x_ij असे दर्शविले, तसेच  x_i· हे i व्या गटातील निरीक्षित मूल्यांचे माध्य असेल व x जर सर्व निरीक्षित मूल्यांचे माध्य असेल, तर खालील नित्य समीकरण मिळेल.

किंवा संक्षिप्त रूपात T=T₂ + T₁

यावरून असे दिसून येते की, विचलनाच्या वर्गाची एकूण बेरीज दोन भागांत विभागता येते. ते भाग म्हणजे (१) गटांमधील विचलनांच्या वर्गाची बेरीज (T₂) व (२) गटांच्या माध्यांच्या एकूण निरीक्षित मूल्यांच्या माध्यापासून होणाऱ्या विचलनांच्या वर्गाचा भाग (T₁) या दोन भागांच्या मुक्तता मात्रा अनुक्रमे (n − p) व (p − 1) आहेत. वर नमूद केलेल्या मूळ गृहीतकानूसार T व T₁ हे काय-वर्ग (Χ²) वंटनाचा नियम पाळतात आणि त्यांच्या मुक्तता मात्रा अनुक्रमे (n−1) व (p−1) आहेत. असेही दिसून येईल की, T₁ व T₂ यांच्या मुक्तता मात्रांची बेरीज T च्या मुक्तता मात्राबरोबर आहे आणि त्यामुळे T₁ हे T₂ पासून स्वतंत्र आहे. यावरून हे उघड आहे की, T₂ सुद्धा काय-वर्ग वंटनांचा नियम पाळेल व त्याच्या मुक्तता मात्रा (n−p) असतील. वरील भाग कोष्टक क्र. १ मध्ये दिल्याप्रमाणे मांडण्याचा प्रघात आहे.

कोष्टक क्र. १. विचरणाचे विश्लेषण

हे डब्ल्यू. जी. कॉक्रन यांच्या प्रयोगाचे विशेष उदाहरण आहे. s₁²/s₂² हे गुणोत्तर जी. डब्ल्यू. स्नेडेकर यांच्या F−वंटनाचा नियम पाळत असून त्याच्या मुक्तता मात्रा अनुक्रमे (p−1) व (n−p) आहेत. याच्यामुळे सर्व माध्ये μ_i एकमेकांच्या बरोबर आहेत या मूळ गृहीतकाची कसोटी उपलब्ध होते. जर मूळ गृहीतक स्वीकारले, तर s₁²−s₂² [ (p-1)/n] ही राशी μ_i माध्यमांतील चलनाचे निरभिनत आकलन उपलब्ध करून देते. तसेच (μ_i −μ_j) या कोणत्याही दोन माध्यांतील फरकाकरिता α% (संभाव्यता) विश्वास सीमा खालीलप्रमाणे उपलब्ध होतील.

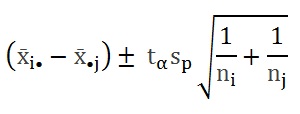येथे t_αहा (n−p) मुक्तता मात्रा असलेल्या t −वंटनाचा α% बिंदू आहे. 

वर विवेचन केलेले मूळ गृहीतक हे ‘माध्ये μ_iही काही विशिष्ट रेखीय (एकघाती) समीकरणांची पूर्तता करतात’ या व्यापक गृहीतकाचे (हे ‘रेखीय गृहीतक’ या नावाने ओळखण्यात येते) एक विशेष उदाहरण आहे. यात एकूण वर्गांची बेरीज अनेक घटकांत (उदा., मुख्य परिणाम, उपचार परिणाम, खंड परिणाम, आंतरक्रिया इ.) अशा तऱ्हेने विभागम्यात येते की, जर मूळ गृहीतक सत्य असेल, तर दोन वर्ग माध्यांच्या आकलनाची मूल्ये एकच होतील व त्यांचे गुणोत्तर वरील मूळ गृहीतकाच्या सार्थकतेची कसोटी उपलब्ध करून देईल, ही मूलभूत कल्पना आहे.

दोन नमुनेदार प्रयोग अभिकल्पांतील विचरणाचे विश्लेषण : वैज्ञानिक संशोधनात नेहमी वापरण्यात येणाऱ्या यादृच्छित खंड अभिकल्प व लॅटिन चौरस अभिकल्प या प्रयोगांच्या अभिकल्पांत विचरणाच्या विश्लेषणाचा कसा उपयोग करतात, याचे विवरण खाली दिले आहे.

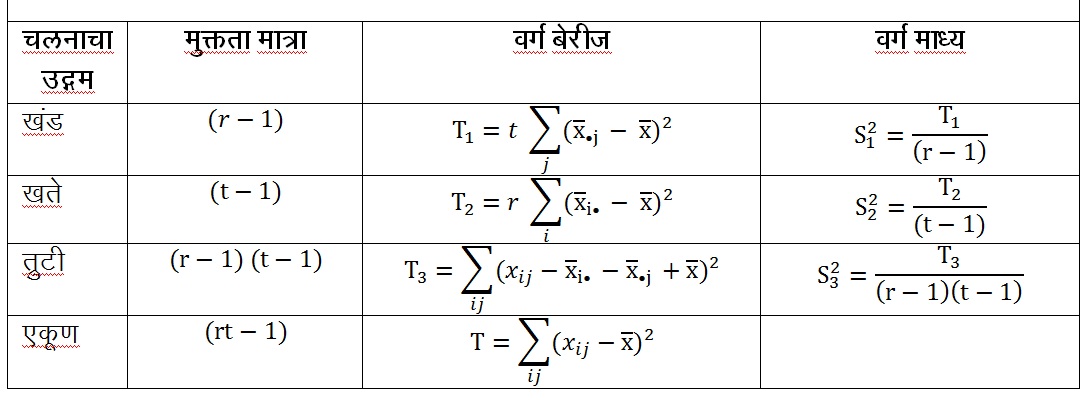
यादृच्छित खंड अभिकल्प : समजा, एखाद्या प्रयोगात आपल्याला निरनिराळ्या t खतांच्या वापराचा भाताच्या उत्पन्नावर काय परिणाम होतो याचा तौलनिक अभ्यास करावयाचा आहे. या प्रयोगासाठीजमिनीचे समान असे r खंड करण्यात येतात, प्रत्येक खंडाची t समान वाफ्यांत विभागणी करून त्यांना प्रत्येक एक याप्रमाणे t खते यदृच्छपणे देतात. सर्व वाफ्यांना जमिनीचा सुपीकरण एकसारखा वाट्याला येईल अशा प्रकारे शक्य तो प्रत्येक खंडाचे वाफे पाडण्यात येतात. समजा X_ij हे i व्या खतामुळे j व्या खंडातून निघालेले भाताचे उत्पन्न आहे. सर्व X_ij स्वतंत्र असून प्रसामान्य वंटनाचा नियम पाळतात व त्यांचे माध्य f_i + b_j असून विचरण एकच पण अज्ञात (σ²) आहे, असे गृहीत धरू. येथे f_i हे i व्या खताचा व b_j हे j व्या खंडाचा उत्पन्नावरील परिणाम दर्शवितात. X_i. व X._j ही जर अनुक्रमे i व्या खताच्या व j व्या खंडाच्या प्रतिदर्शाची माध्ये असतील व X हे उत्पन्नाच्या सर्व मूल्यांचे माध्य असेल, तर विचरणाचे विश्लेषण कोष्टक क्र. २. मध्ये दर्शविल्याप्रमाणे मांडता येईल.  

 यातील त्रुटी ह चलन उदगम प्रायोगिक त्रुटींमुळे उद्‌भवणारा परिणाम आहे व तो गृहीतकात विचारात घेतला जात नाही. या त्रुटी अप्रस्तुत चलांमुळे उदभवतात व त्या बऱ्याचदा ‘यदृढ चलन’ या व्यापक शीर्षकाखाली एकत्रित करण्यात येतात. येथे ‘त्रुटी’ या शब्दाचा अर्थ ‘चूक’ असा मात्र नाही.

वरील विश्लेषण ‘या खतांमध्ये भाताचे उत्पन्न वाढविण्याच्या दृष्टीने आपापसात काहीच फरक नाही’ या मूळ गृहीतकाची कसोटी F−वंटन व (t−l) व (r−l) (t−l) अनुक्रमे मुक्तता मात्रा असलेल्या s₂²/s₃² या गुणोत्तराच्या मूल्यावरून घेता येईल. पण जर मूळ गृहीतक स्वीकारले नाही, तर (f_i−f₁’) या कोणत्याही दोन खतांच्या परिणामामधील फरकाच्या α% विश्वास सीमा खालीलप्रमाणे उपलब्ध होतील.

याशिवाय  (t −1)(s₂²/s₃²)/r हे निरनिराळ्या खतांच्या परिणामातील विचरणाचे म्हणजे

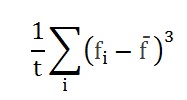याचे निरभिनत आकलन उपलब्ध करून देईल.  

कोष्टक क्र. २. विचरणाचे विश्लेषण : यादृच्छित खंड अभिकल्प

कोष्टक क्र. ३. विचरणाचे विश्लेषण : लॅटिन चौरस अभिकल्प

लॅटिन चौरस अभिकल्प : जर जमिनीच्या सुपीकपणाचा उतार कोणत्या तरी एकाच विशिष्ट दिशेकडे असेल, तर यादृच्छित खंड अभिकल्पाच्या साय्याने जमिनीच्या सुपीकपणामुळे खंडाखंडात निर्माण होणारे चलन टाळता येते आणि यामुळे चलनाच्या त्रुटी घटकाचे निरभिनत व जास्त सुनिश्चित आकलन उपलब्ध होते. परंतु जर जमिनीच्या सुपीकपणाचा उतार दोन दिशांकडे असेल, तर जास्त कार्यक्षम अशा लॅटिन चौरस अभिकल्पाचा उपयोग करून या दोन्ही दिशांकडील सुपीकपणाचा परिणाम टाळता येतो. या अभिकल्पात r² वाफे चौरस आकारात मांडून त्यांना r खते अशा रीतीने देण्यात येतात की, प्रत्येक खत एकदाच एका स्तंभात व एकदाच एका पंक्तीत (ओळीत) येईल. समजा, x_ij हे i व्या पंक्तीतील व j व्या स्तंभावरील वाफ्याला देण्यात आलेल्या k व्या खताच्या उपचारामुळे आलेले भाताचे उत्पन्न दर्शविते. असेही गृहीत धरू की, x_ij हे स्वतंत्र असून प्रसामान्य वटंनाचा नियम पाळतात व त्याचे माध्य r_i + c_j + f_k असून विचरण एकच पण अज्ञात (σ²) आहे. येथे r_i हा i व्या पंक्तीचा, c_j हा j व्या स्तंभाचा व f_k हा k व्या खताचा होणारा परिणाम आहेत. x_i व x_j हे अमुक्रमे पंक्ती माध्य व स्तंभ माध्य, xk हे k वे खत दिलेल्या वाफ्यांपासून येणाऱ्या उत्पन्नांचे माध्य व x हे सर्वसाधारण माध्य आहेत. यावरून या अभिकल्पाच्या बाबतीत विचरणाचे विश्लेषण कोष्टक क्र. ३ मध्ये दर्शविल्याप्रमाणे मांडता येईल.   

‘या खतांच्या उपचारांत आपापसामध्ये काहीच फरक नाही’ या मूळ गृहीतकाची कसोटी F−वंटन आणि (r −l) व (r − l) (r − 2) या अनुक्रमे मुक्तता मात्रा असलेल्या s₁²/ s₄² या गुणोत्तराच्या मूल्यावरून घेता येईल. पण जर मूळ गृहीतकाचा स्वीकार केला नाही, तर वर सांगितल्याप्रमाणे निरनिराळ्या खतांमुळे होणाऱ्या परिणामांच्या वा कोणत्याही दोन खतांच्या परिणामांतील फरकाच्या विचरणाचे आकलन करता येईल.   

सहभागी चल व समाश्रयण : पुष्कळदा असे आढळून येते की, यदृच्छ चल y हा यदृच्छ नसलेल्या u, v, w, x, z, … वगैरे काही चलांवर अवलंबून असतो. अशा u, v, w, x, z, … वगैरे चलांना सहगामी चल किंवा सहचल म्हणतात आणि y ला अवलंबी चल किंवा परचल म्हणतात. येथे y व हे सहचल यांच्यातकाही संबंध आहे की काय याची कसोटी घेऊन नंतर हे सहचल y च्या मूल्याचे भाकित करण्यास कितपत उपयोगी पडतात याचा विचार करावयाचा आहे. उदा. एखाद्या नारळाच्या झाडाचे उत्पन्न y असून त्याचे वय x आहे. या दोहोंमध्ये असलेला संबंध शोधावयाचा आहे. समजा, (x₁, y₁), (x₂, y₂), …. (x_n, y_n) ही n झाडांपासून निरीक्षण करून मिळालेल्या जोड्यांची मूल्ये आहेत. y₁ हे स्वतंत्र असून प्रसामान्य वंटनाचा नियम पाळतात असे गृहीत धरू. त्यांचे माध्य α+ βx_i असून विचरण एकच पण अज्ञात (σ²) आहे. या उदाहरणात एकूण वर्गांची बेरीज दोन घटकांत विभागता येईल : (१) समाश्रयामुळे व (२) अवशिष्ट चलन (समाश्रयणापासून आलेले नाही असे). येथे विचरणाचे विश्लेषण कोष्टक क्र. ४ मध्ये दर्शविल्याप्रमाणे मांडता येते. यांत ^β हे y  च्या x वरील समाश्रयणांकाचे आकलन असून ते

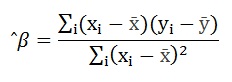समाश्रयणांकाच्या सार्थतेची कसोटी F−वंटनाचा नियम पाळणाऱ्या आणि १ व (n−2) अनुक्रमे मुक्तता मात्रा असलेल्या s₁²/ s₂² या गुणोत्तराच्या मूल्यावरून करता येईल. जर समाश्रयणांक सार्थ नसेल, तर सहचल x हा y च्या मूल्याचे भाकित करण्यास विशेष उपयोगी ठरणार नाही, हे स्पष्टच आहे.

सहविचरण विश्लेषण : समजा, आपल्याला निरनिराळी खाद्ये मिळणाऱ्या काही प्राण्यांच्या गटांच्या वाढीच्या वेगाचा तौलनिक अभ्यास करावयाचा आहे. जर खाद्यांची संख्या n व प्रयोगाच्या  

कोष्टक क्र. ४. विचरणाचे विश्लेषण : समाश्रयण

कोष्टक क्र. ५. सहविचरण विश्लेषण

कोष्टक क्र. ६. सहविचरण विश्लेषण : समायोजित वर्गाची बेरीज

आवृत्त्या (खंडाची संख्या) r असतील, तर खांद्यांच्या वर्ग माध्याच्या व त्रुटीच्या वर्ग माध्याच्या परिमाणांवरून ‘‘प्राण्यांच्या वाढीच्या वेगावर खाद्यांचा काहीच परिणाम नाही’’ या मूळ गृहीतकाची कसोटी घेता येईल. एखाद्या वेळेस या खाद्यांमधील फरक सार्थ नसण्याचीही शक्यता आहे. प्रत्येक आव-त्तीत प्राण्यांच्या सुरुवातीच्या वजनात फार तपावत असल्यामुळे खाद्यांच्या फरकातील सार्थता लपून राहण्याची सुद्धा शक्यता आहे. हा जो x सहचलाचा (सुरुवातीच्या वजनाचा) y चलावर (वाढीच्या वेगावर) होणारा परिणाम आहे त्याचे मूल्यमापन करून y च्या x वरील समाश्रयणाने दर्शविलेल्या संबंधाप्रमाणे y च्या मूल्याचे समायोजन करावे लागते. या समायोजन करण्याला व तत्संबंधी करण्यात येणाऱ्या विश्लेषणालाच सहविचरणाचे विश्लेषण म्हणतात. 

सहविचरणाचे विश्लेषण करताना प्रथम एकूण विचलनांच्या गुणाकारांची बेरीज

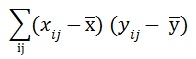विचरणाच्या विश्लेषणाप्रमाणेच अनेक घटकांत विभागावयाची असते (उदा., कोष्टक क्र. ५ मध्ये दर्शविल्याप्रमाणे)

अशा रीतीने विचरणाचे व सहविचरणाचे कोष्टक मांडल्यावर उपचार व त्रुटी यांच्यासाठी समायोजित वर्गाची बेरीज कोष्टक. क्र. ६ मध्ये दाखविल्याप्रमाणे मिळेल.

‘उपचारांमध्ये काहीच फरक नाही’ या मूळ गृहीतकाची कसोटी F−वंटन व (n−l) व (n−l) (r−l)−l या अनुक्रमे मुक्ताता मात्रा असलेल्या S’₂²/S’₃² या गुणोत्तरांच्या मुल्यावरून घेता येईल.

विचरणाच्या तंत्राचा उपयोग सोप्या रीतीने ज्यांत करण्यात आलेला आहे अशा काही उदाहरणांचाच येथे केलेला आहे. हे तंत्र खूप प्रगत झालेले असून अनेक संशोधन क्षेत्रांतील (उदा., जीवविज्ञान, वैद्यक, कृषिविज्ञान, विविध उद्योग) प्रयोगांच्या अभिकल्पांत, त्यांच्या विश्लेषणात व संबंधित गृहितकांच्या कसोट्या घेण्याकरिता ते व्यापक प्रमाणावर वापरण्यात येते.

पहा : प्रयोगांचा अभिकल्प वंटन सिद्धांत सांख्यिकीय अनुमानशास्त्र.

संदर्भ : 1. Cochran, W. G. Cox, G. M. Experimental Designs, Bombay, 1963.

2. Cochran. W. G. Snedecor, G. W. Statistical Methods, 1980.

3. Fisher, R. A. Statistical Method for  Research Workers,  Edinburgh, 1963.

4. Hoel. P. G. Elementary Statistics, New York, 1976.

5. Panse. V. G. Sukhatme, P. V. Statistical Methods for Agricultural Workers, New Delhi, 1961.

सुखात्मे, वा. वा.