ऊष्मागतिकी : यांत्रिक ऊर्जेचे उष्णतेत व उष्णतेचे यांत्रिक ऊर्जेत रूपांतर आणि उष्णताजन्य चालकशक्ती या गोष्टींच्या अभ्यासाचाच अंतर्भाव सुरुवातीस ऊष्मागतिकीत होत असे. नंतर ऊर्जेची अविनाशिता, कार्नो तत्त्व (फ्रेंच अभियंते कार्नो यांनी मांडलेले तत्त्व), व्युत्क्रमी (उलटसुलट दिशेने होऊ शकणाऱ्या प्रक्रियांचे) चक्र इ. गोष्टींचाही अंतर्भाव यात होऊ लागला. ऊष्मागतिकीय नियम व साध्या पदार्थांचे भौतिकीय गुणधर्म यांचा परस्परसंबंध दाखविणे हा या लेखाचा मुख्य उद्देश आहे.
रूढ यामिकीप्रमाणे (प्रेरणांची वस्तूंवर होणारी क्रिया व त्यांपासून निर्माण होणारी गती यांचा अभ्यास करणाऱ्या शास्त्राप्रमाणे) ऊष्मागतिकीतही अनुभवावर आधारलेल्या काही मूलभूत सिद्धांतांवरून अनुमाने काढली जातात या मूलभूत सिद्धांतांचे समर्थन करणे हे ऊष्मागतिकीचे काम नव्हे, ते काम सांख्यिकीचे (संख्याशास्त्राचे). पण ऊष्मागतिकीय अनुमाने प्रत्यक्षात बिनचूक ठरल्याने ऊष्मागतिकीस भौतिकीत महत्त्वाचे स्थान प्राप्त झाले आहे.
यामिकीत पदार्थांच्या बाह्य स्थितीवर उदा., स्थिती, गती, प्रवेग (दर सेकंदास होणारा वेगामधील बदल) इत्यादींवर लक्ष केंद्रित केले जाते, तर ऊष्मागतिकीत पदार्थांच्या (व्यूहाच्या) आंतरस्थितीवर लक्ष केंद्रित असते. वायूसारख्या रासायनिक दृष्ट्या एकजातीय पदार्थाची ऊष्मागतिकीय स्थिती, ती समतोल असल्यास, वायूचा दाब P व त्याचे आयतन (घनफळ) V या दोन राशींनी संपूर्णपणे दर्शविता येते म्हणून दाब व आयतन यांस ‘ऊष्मागतिकीय स्थितिदर्शक चल’ (बदलणाऱ्या राशी) म्हटले जाते. असे इतरही चल आहेत त्यांचा क्रमाने उल्लेख येईलच. या लेखात P, V, U इ. मोठी अक्षरे व p, v, u इ. लहान अक्षरे अनुक्रमे ग्रॅमरेणवीय (ग्रॅममध्ये मोजलेल्या रेणुभाराच्या) वस्तुमानाच्या संबंधात व एकक वस्तुमानाच्या संबंधात वापरली आहेत.
कोणत्याही व्यूहाचा ऊष्मागतिकीय विचार, तो समतोलाच्या– अगर त्याजवळपासच्या– स्थितीत असतानाच केला जातो. ऊष्मागतिकीय समतोल हा (१) यांत्रिक, (२) औष्णिक व (३) रासायनिक या तीन समतोलांचा समन्वय आहे, हे लक्षात ठेवले पाहिजे.
ऊष्मागतिकीय व्यूह रासायनिक, चुंबकीय, विद्युत् इत्यादींपैकी कोणताही एक असू शकेल. रासायनिक व्यूह एकजातीय (उदा., हायड्रोजनासारखा वायू) अगर भिन्नजातीयही असू शकेल. एकजातीय व्यूहात रासायनिक वा भौतिकीय दृष्ट्या सर्वत्र एकजिनसीपणा असावयास हवा. भिन्नजातीय संच अनेक एकजातीय घटकांचा बनलेला असून, त्या एकजातीय घटकांचे पृष्ठभाग एकमेकांपासून अलग पडलेले आढळतात (उदा., बंद भांड्यातील पाणी व त्यावरील वाफ).
ऊष्मागतिकीचा शून्यावा सिद्धांत : कोणत्याही पदार्थाच्या ऊष्मागतिकीय स्थितीची व्याख्या करताना त्याच्या तापमानाचा निर्देश आवश्यक असल्याने, तापमानाच्या अस्तित्वाच्या सिद्धांतास काही वेळा ‘ऊष्मागतिकीचा शून्यावा सिद्धांत’ असे म्हणतात. कोणत्याही समतोल ऊष्मागतिकीय व्यूहात, स्थितिदर्शक चल P व V यांचे एकमेव मूल्य असलेले फलन (चलांमधील गणितीय संबंध) f म्हणून तापमानाचा निर्देश करता येतो व त्याचे मूल्य व्यूहाच्या सर्व भागांत एकच असते, हेच तत्त्व गणितीय भाषेत पुढील समीकरणाच्या रूपाने मांडता येईल :
f1 (P1, V1) = f2 (P2, V2) =… = f (P, V) = t … (१) यात १, २ … हे आकडे व्यूहाच्या निरनिराळ्या घटकांस अनुलक्षून असून t हे व्यूहाचे तापमान आहे. यावरून t [अगर T निरपेक्ष तापमान, → केल्व्हिन निरपेक्ष तापक्रम] हेही व्यूहाच्या ऊष्मागतिकीय स्थितीचे एक निर्देशक होऊ शकते.
समीकरण (१) अथवा त्याच अर्थाचे समीकरण f (P, V, T)=0 … … (२)
यास पदार्थाचे स्थितिदर्शक समीकरण म्हणतात. समी. (२) अथवा समी. (१) मध्ये P व V हे स्वचल (ज्यांच्यातील बदल इतर चलांच्या बदलांवर अवलंबून नाहीत असे चल) आहेत आणि T चे मूल्य P व V च्या मूल्यांमुळे आपोआप ठरते. ही दोन्ही समीकरणे पदार्थाच्या समतोल स्थितीतच लागू पडतात. यातील P, V आणि T या राशी स्थूलमानीय (मोठ्या प्रमाणावरील) आहेत.
कार्य : ज्यात (अ) कार्य घडते व (आ) उष्णता संक्रमण होते, अशा तर्हेच्या क्रिया कोणत्याही ऊष्मागतिकीय व्यूहात होतात असे धरून चालले जाते. व्यूहावर अथवा व्यूहाकडून घडणाऱ्या कार्यास बहिःकार्य म्हणतात व हे बहिःकार्य अंत:कार्याहून अगदी भिन्न आहे. अंतःकार्य व्यूहाच्या एका घटकाकडून, त्याच व्यूहाच्या दुसऱ्या घटकावर घडते. उदा., वायू प्रसरण पावत असताना रेणवीय आकर्षण प्रेरणेविरुद्ध घडत असलेले कार्य. घडणारे बहिःकार्य (यास यापुढे नुसते कार्य म्हणून संबोधू) व्यूहाच्या सुरुवातीच्या व अखेरच्या स्थितीवरच ते केवळ अवलंबून नसून, झालेला बदल कोणत्या मार्गाने घडला त्या मार्गावरही अवलंबून असते.

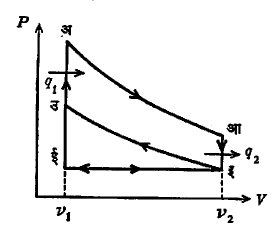
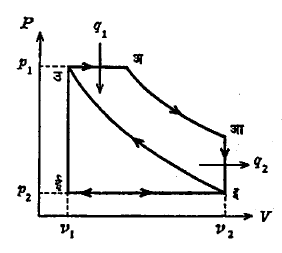
दर्शक रेखाचित्र : ज्यात दाब य अक्षावर व आयतन क्ष अक्षावर रेखित केले जाते अशा रेखाकृतीस ‘दर्शक रेखाचित्र’ अगर ‘दाबआयतन रेखाचित्र’ असे म्हणतात. आ. १ (अ) मध्ये वायू प्रसरण पावत असताना होणारे दाब व आयतन यांमधील फरक वक्र I ने दाखविले आहे. घडणारे कार्य, W= ∫ PdV, त्या वक्राखालील काळसर केलेल्या क्षेत्रफळाने दाखविले आहे. तसेच आ. १ (आ) मधील वक्र II खालील काळसर क्षेत्रफळ, वायू दाबाखाली संकुचित होत असताना त्यावर घडणारे कार्य, दर्शविते. चिन्हांच्या रूढ प्रघातास अनुसरून (अ) मध्ये दर्शविलेले कार्य अधिक चिन्ही (+) व (आ) मधील ऋण चिन्ही (–) समजले जाते. आ. १ (इ) मध्ये वक्र I व II एकत्र काढलेले असून, दोन्ही वक्र मिळून एकामागून एक अशा घडणाऱ्या क्रिया दाखविल्या आहेत अंतिम पदार्थ (वायू) सुरुवातीच्या स्थितीत परत आणला जातो. हे प्रक्रम म्हणजे बदल (इ) मध्ये बंद वक्र III ने दाखविले आहेत व त्यास चक्री प्रक्रम अथवा नुसतेच ‘चक्र’ म्हणून संबोधतात. वक्र III मधील क्षेत्रफळ, वक्र I व II याखालील क्षेत्रफळांमधील फरक असून, ते नक्त कार्य दाखविते. वक्र III मध्ये बाणाने दाखविलेल्या दिशेप्रमाणे हे नक्त कार्य (+) आहे दिशा उलटी झाल्यास त्याचे चिन्ह (–) होईल. ही दर्शक रेखाचित्रे एंजिनाची कार्यपद्धती दाखविण्याच्या दृष्टीने फार उपयुक्त आहेत.
अंतस्थ ऊर्जा : काही व्यूह असे आढळतात की, ज्यांत वरवर पाहता यांत्रिकी ऊर्जा स्पष्ट दिसू शकत नाही, परंतु ते कार्यक्षम असू शकतात अशा व्यूहांना अंतस्थ ऊर्जा असलेले व्यूह म्हणतात. हायड्रोजन व ऑक्सिजन या वायूंच्या मिश्रणाचे आपण उदाहरण घेऊ. हे मिश्रण आहे त्या स्थितीत, काही बदल न होता राहू शकेल पण त्यात जर ठिणगी पडली, तर त्याचा स्फोट होऊन कार्य घडू शकेल. ऊष्मागतिकीत या अंतस्थ ऊर्जेचे मापन आवश्यक ठरते.
कल्पना करू की, बहिःकार्य W मुळे एक उष्णता निरोधित (बाहेरची उष्णता आत व आतली उष्णता बाहेर जाणार नाही असा) व्यूह A स्थितीतून B स्थितीत गेला व म्हणून त्याची सुरुवातीची अंतस्थ ऊर्जा UA चे मूल्य अखेरीस UB झाले, तर ऊर्जेच्या अविनाशितेच्या तत्त्वाप्रमाणे
UB – UA = – W … … (३)
या समीकरणाच्या मदतीने आपणास अंतस्थ ऊर्जेची व्याख्या करता येते व तिच्या बदलाचे मापन करता येते. विशेषत: एखाद्या विशिष्ट समतोल स्थितीत UA शून्य आहे असे मानल्यास (उदा., निरपेक्ष तापमान शून्य असताना),
UB= – W … … (४)
व म्हणून अंतस्थ ऊर्जेस, सर्वस्वी पदार्थांच्या स्थितीवर अवलंबून असलेले व एकमेव मूल्य असलेले, फलन मानता येईल आणि ती अंतस्थ ऊर्जा ऊष्मागतिकीय चल होऊ शकेल. स्पष्टच आहे की, अंतस्थ ऊर्जेतील बदल व्यूहाच्या सुरुवातीच्या व अखेरच्या स्थितीवरच फक्त अवलंबून राहील, बदलाच्या मार्गावर नव्हे. समी. (४) प्रमाणे पदार्थाची अंतस्थ ऊर्जा म्हणजे त्यात असणारी कार्य करण्याची क्षमता असा अर्थ होतो.
उष्णता : उष्णतेची व्याख्या फक्त तापमानाच्या फरकामुळे घडणारी ऊर्जेची देवघेव अशी करता येईल. ‘उष्णतेचा साठा’ याचा अर्थ सतत एक विशिष्ट तापमान असलेले व भोवतालच्या पदार्थाशी त्याच तापमानात फक्त उष्णतेची देवघेव करणारे साधन, असा करू. यापुढील सर्व समीकरणांतून उष्णता ही कार्याच्या एककातच व्यक्त केली आहे, ही गोष्ट लक्षात ठेवावी.
उष्मागतिकीचा पहिला सिद्धांत : समी. (४) वरून उष्णता निरोधित व्यूहात घडणाऱ्या अंतस्थ ऊर्जेच्या छोट्या बदलाविषयी पुढील समीकरण मांडता येईल :
Δ U + Δ W = 0 … … (५)
परंतु उष्णातेस प्रतिबंध नसल्यास काही उष्णता ΔQ व्यूहात प्रवेश करू शकेल व मग व्यूहात प्रवेश करणारी नक्त ऊर्जा ΔQ-ΔW इतकी होईल. ऊर्जेच्या अविनाशितेच्या तत्त्वाप्रमाणे
Δ Q = Δ U + Δ W … … (६)
हे समीकरण मांडता येईल. बदल अत्यल्प असल्यास हेच समीकरण
Dq = dU + dW … … (६ अ)
असे मांडता येईल. समी. (६) व (६अ) गणितीय भाषेत मांडलेला ऊष्मागतिकीचा पहिला सिद्धांत दर्शवितात. यात दोन तत्त्वे ग्रंथित झाली आहेत. (१) उष्णता ही ऊर्जेचा एक आविष्कार आहे व (२) ऊर्जा अविनाशी आहे.
समीकरण (६) नुसार पदार्थाच्या अंतस्थ ऊर्जेची वाढ, त्यात मिळविलेली उष्णता व घडलेले कार्य यांमधील फरकाइतकी असते. कार्याचे मूल्य ¦ PdV आहे,पण ते साध्या रासायनिक व्यूहाच्या संबंधात असते. जरूर पडल्यास व्यूहाच्या भिन्नत्वामुळे तो ज्या जातीचा असेल त्याप्रमाणे, (उदा., पृष्ठदाबीय, कर्षुकीय म्हणजे चुंबकीय, विद्युत्), कार्याच्या मूल्यात फरक करावा लागेल.
पहिल्या सिद्धांताचे अनुप्रयोग: अंतस्था ऊर्जा व्यूहाच्या स्थितीचे फलन असल्याने
U = f (V, T) … … (७)
असे मांडता येईल. यात V व T हे स्वचल असून U त्यांवर अवलंबून असलेला चल आहे. समी. (७)चे भागशः अवकलन [कलन शास्त्रातील एक कृत्य, → अवकलन व समाकलन] करता
| dU = | ( | ∂U | )v | dt + | ( | ∂U | )T | dv … (८) |
| ∂T | ∂V |
हे समीकरण मिळते. परिपूर्ण वायूंच्या बाबतीत (∂U/∂V)T =0 व व्हॅन डर व्हाल्स यांच्या स्थितिदर्शक समीकरणाप्रमाणे [→ स्थिति समीकरण] वागणाऱ्या वायूंच्या बाबतीत (∂U/∂V)T = a/V2; dW = Pdv असल्याने, पहिला सिद्धांत dQ = dU + PdV …. (९)
असाही मांडता येईल. आयतन स्थिर राहिल्यास dV = 0, म्हणून समी. (९) वरून dT ने भागता
(∂Q/∂T)v = (∂U/∂T)v = Cv … … (१०)
याता Cv ही स्थिर आयतनाची ग्रॅमरेणवीय उष्णता धारिता (तापमान एक अंशाने वाढविण्यास लागणारी उष्णता) आहे. समी. (८) प्रमाणे dU चे मूल्य समी. (९) मध्ये घालता व dT ने भागता
| dQ | = ( | ∂U | )V + [ P + ( | ∂U | )T ] | dV | (११) |
| dT | ∂T | ∂V | dT |
यात dQ/dT ग्रॅमरेणवीय उष्णता धारिता आहे. दाब P स्थिर समजल्यास, (∂Q/∂T)P = Cp, स्थिर दाबाची ग्रॅमरेणवीय उष्णता धारिता. समी. (११) वरून
| CP = ( | ∂U | )v + [ P + ( | ∂U | )T ] ( | ∂V | )p |
| ∂T | ∂V | ∂T |
अथवा समी. (१०) वरून
| CP = CV + [ P + ( | ∂U | )T ] | ∂V | )P … (१२) |
| ∂V | ∂T |
म्हणून कोणत्याही पदार्थाच्या बाबतीत Cp व Cv या दोन उष्णता धारितांचा फरक
| CP – CV=[P +( | ∂U | )T ] | ∂V | )P … (१३) इतका असतो. |
| ∂V | ∂T |
परिपूर्ण वायूंच्या बाबतीत (∂U/∂V)T = 0 असल्याने, त्यांच्या स्थितिदर्शक समीकरणावरून (PV = RT ) आणि (∂V/∂T)P = R/P. म्हणून परिपूर्ण वायूंच्या बाबतीत
CP – CV = R … … (१३अ)
असे दाखविता येते की,
| P + ( | ∂U | )T = T | ∂P | )v | |
| ∂V | ∂T | ||||
व म्हणून समी. (१३) पासून
| CP – CV = T ( | ∂P | )v ] | ∂V | )p … … (१४) |
| ∂T | ∂T |
समताप व अक्रमी प्रक्रम : ज्यात व्यूहाचे तापमान स्थिर राहते अशा बदलास किंवा प्रक्रमास ‘समताप’ म्हणतात, अशा बदलाची शर्त T = स्थिरांक … … (१५)
ही होय. अशा प्रक्रमात कार्य घडणे शक्य असते व त्यामुळे तापमान बदलू पाहते. ते स्थिर राखण्यासाठी व्यूहास जरूरीप्रमाणे उष्णता द्यावी तरी लागते किंवा त्यातून उष्णता काढून घ्यावी लागते. उदा., परिपूर्ण वायूच्या समताप प्रसरणाचा विचार केल्यास, घडणारे कार्य
![]()
व त्यामुळे वायूचे तापमान घसरू पाहते. ते स्थिर रहावे म्हणून उष्णता Q = W बाहेरून द्यावी लागते.
ज्या व्यूहात बदल होत असताना त्यातून उष्णता बाहेर जाऊ दिली जात नाही, अगर बाहेरून उष्णता त्यात प्रवेश करू शकत नाही, अशा प्रक्रमास ‘अक्रमी’ म्हणतात. अशा बदलाची शर्त
dQ=0 … … (१७)
ही होय. उष्णतेची देवघेव होऊ शकत नसल्याने अशा बदलात परिणामी तापमान बदलते. समी. (९) मध्ये dq = 0 मांडता, dU = – dW व
W अक्रमी = U1 – U2 … (१८)
अक्रमी बदलास ‘स्थिर एंट्रॉपी बदल’ म्हणूनही संबोधतात [एंट्रॉपी ही उष्णता व तापमान यांचे एक महत्त्वाचे गुणोत्तर आहे, → एंट्रॉपी]. उदाहरण म्हणून अक्रमी प्रसरण पावतार्या परिपूर्ण वायूचा विचार करू. अशा बदलास
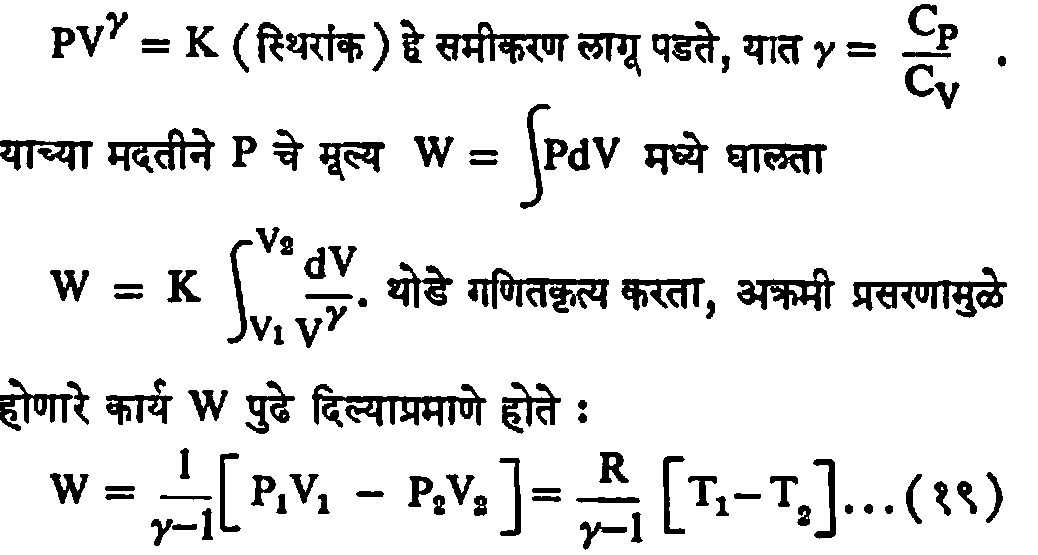
व्युत्क्रमी व अव्युत्क्रमी प्रक्रम : कोणत्याहीऊष्मागतिकीय प्रक्रमात, ज्या परिसराचा व्यूहाशी देवाण-घेवाण दृष्ट्या प्रत्यक्ष संबंध येतो, त्यास ‘लगतचा परिसर’ म्हणू. ज्याचा व्यूहाची संबंध येणे अशक्य नाही अशा पलीकडे असलेल्या परिसरास ‘इतर विश्व’ असे म्हणण्याचा प्रघात आहे (येथे विश्व हे मर्यादित अर्थाने समजावयाचे नेहमीच्या अर्थाने नव्हे.). ऊष्मागतिकीय प्रक्रम ‘व्युत्क्रमी’ अगर ‘अव्युत्क्रमी’ असू शकेल. ज्यात प्रक्रमाच्या शेवटी खुद्द व्यूह व लगतचा परिसर त्यांच्या पहिल्या स्थितीत परत येतात व घडलेल्या प्रक्रमाने इतर विश्वात कोणताही बदल होत नाही, अशाला ‘व्युत्क्रमी प्रक्रम’ म्हणतात. ज्या प्रक्रमात वरील शर्ती पाळल्या जात नाहीत त्यास ‘अव्युत्क्रमी प्रक्रम’ असे म्हणतात. दरेक चक्री प्रक्रमाच्या अखेरीस व्यूह पूर्वस्थितीत येतो म्हणून प्रत्येक चक्री प्रक्रम व्युत्क्रमी असेलच असे नाही.
सैद्धांतिक विचारासाठी जरी प्रक्रम व्युत्क्रमी आहे असे आपण समजून चालणार असलो, तरी हे लक्षात ठेवावयास हवे की, सर्व नैसर्गिक प्रक्रम अव्युत्क्रमीच असतात. प्रक्रम व्युत्क्रमी होण्यासाठी त्याच्या प्रत्येक अनुक्रमात व्यूह व परिसर यांमध्ये यांत्रिक व औष्णिक समतोल राहणे अवश्य आहे. एखाद्या वायूचे प्रसरण व्युत्क्रमी होण्यास त्याचा व बाहेरील दाब समान हवा नाहीतर यांत्रिक समतोल राहणार नाही. त्याचप्रमाणे उष्णता संवहन (येथे उष्णतेची सुलभतेने होणारी एक प्रकारची वाहतूक) व्युत्क्रमी होण्यास, ज्यात संवहन घडत आहे अशा शेजारील दोन भागांचे तापमान समान राहणे अवश्य आहे नाहीतर औष्णिक समतोल बिघडेल. पण वरील दोन्ही शर्ती प्रत्यक्षात खऱ्या असल्यास वायू प्रसरण पावणार नाही, अगर उष्णता संवहनही घडणार नाही. म्हणून वायूचे प्रसरण, उष्णता संवहन यांसारख्या नैसर्गिक प्रक्रिया अव्युत्क्रमीच असतात.
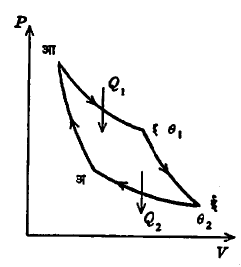
कार्नो एंजिन व कार्नो चक्र : एंजिनामधील वाफेसारख्या कार्यकारी पदार्थाकडून चक्राच्या एका भागात उच्च तापमानाच्या उष्णता साठ्याकडून काही उष्णता घेतली जाते व दुसऱ्या भागात नीच तापमानाच्या उष्णता साठ्यास शिल्लक उष्णता दिली जाते. या दोन (उष्ण व थंड) उष्णता साठ्यांमध्ये एंजिन काम करीत राहते. थंड साठ्यास एंजिन काहीतरी प्रमाणात उष्णता देत असल्याने, कोणत्याही एंजिनाची कार्यक्षमता शंभर टक्के असणे अशक्य असते. एंजिनाच्या कामाचा विचार करताना आपणापुढे पुढील गोष्टींचा विचार प्रामुख्याने असतो : (१) प्राप्त झालेल्या दोन उष्णता साठ्यांच्या मदतीने काम करीत असलेल्या एंजिनाची सर्वोच्च कार्यक्षमता किती असू शकेल? (२) एंजिनाची विशेष लक्षणे कोणती ? (३) एंजिनामध्ये वापरल्या जाणाऱ्या कार्यकारी पदार्थाच्या जातीवर एंजिनाची कार्यक्षमता कितपत अवलंबून आहे ? या सर्व महत्त्वाच्या प्रश्रांची दखल प्रथम फ्रेंच अभियंते सादी कार्नो (१७९६–१८३२) यांनी घेतली व १८२४ मध्ये एका सर्वोच्च कार्यक्षम एंजिनाची माहिती दिली. या एंजिनाचा चक्री प्रक्रम अतिसरळ असून त्यास ‘कार्नो चक्र’ असे नाव मिळाले. हा चक्री प्रक्रम कोणत्याही ऊष्मागतिकीय व्यूहाच्या बाबतीत घडू शकेल असा आहे. यात सर्व प्रक्रम व्युत्क्रमी असून ते पुढीलप्रमाणे आहेत : (१) कार्यकारी पदार्थ सुरुवातीस θ2 तापमान असलेल्या थंड साठ्याशी संबंधित असल्याने त्या व्यूहाचे किंवा पदार्थाचे तापमानही θ2 असणार. (२) हा प्रक्रम अक्रमी असून त्यात दाबाने झालेल्या पदार्थाच्या संकोचामुळे त्याचे तापमान वाढून ते उष्ण साठ्याएवढे म्हणजे θ1 होते. (३) आता त्याचा संबंध उष्ण साठ्याशी जोडला जाऊन θ1 तापमानात तो पदार्थ समताप प्रसरण पावतो व त्यासाठी तो उष्ण साठ्यातून Q1 इतकी उष्णता शोषून घेतो आणि प्रसरणामुळे W1 इतके कार्य घडते. (४) यानंतर तो पदार्थ अक्रमी प्रसरण पावतो व त्यामुळे त्याचे तापमान θ2 होते. (५) आता त्याचा संबंध थंड साठ्याशी जोडला जाऊन त्याचा θ2 तापमानात समताप संकोच केला जातो यासाठी त्यातून काही उष्णता Q2 थंड साठ्यास दिली जाते व W2 कार्य घडते. याप्रमाणे पदार्थ पूर्वस्थितीत येतो व चक्र पुरे होते. (३) व (५) मध्ये घडणारी कार्ये W1 व W2 विरुद्ध चिन्ही आहेत व उपयोगी नक्त कार्य W या दोहोंच्या फरकाइतके W1 -W2 आहे. म्हणून
W = Q1 – Q2 … … … (२०)
अशा तर्हेने काम करणाऱ्या एंजिनास कार्नो एंजिन म्हणतात; यात होणारे सर्व प्रक्रम व्युत्क्रमी असल्याने असे एंजिन फक्त कल्पनेतच असू शकते. पण ऊष्मागतिकी व्यूहांचा अभ्यास करताना याचा फार उपयोग होतो.
कार्नो एंजिनामधील कार्यकारी पदार्थ वायू आहे असे समजून त्याच्या चक्राचे दर्शक रेखाचित्र अआइई आ. २ मध्ये दाखविले आहे त्यावरून कळून येईल की, हे चक्र दोन समतापांचे आइ आणि ईअ व दोन अक्रमींचे आअ आणि इई बनलेले आहे. चक्राचे क्षेत्रफळ एंजिनाने केलेले उपयोगी कार्य दाखविते. कार्नो चक्र व्यत्क्रमी प्रक्रमांचे बनलेले असल्यामुळे, ते वर वर्णन केलेल्या व चित्रात दाखविलेल्या दिशेने अगर विरुद्ध दिशेने (म्हणजे अईइआ या क्रमाने) आखता येईल. विरुद्ध दिशेने आखल्यास ते ‘प्रशीतनाचे’ थंड करण्याच्या क्रियेचे चक्र बनेल. पण यात वैशिष्ट्य असे की, प्रशीतन चक्रातही Q1 Q2 व W या राशी बदलत नाहीत ही गोष्ट सर्व प्रक्रम व्युत्क्रमी असल्यामुळेच केवळ शक्य आहे.
या अनुषंगाने कार्नो यांनी एक सिद्धांत व एक उपसिद्धांत दिला आहे. तो सिद्धांत असा : ‘दिलेल्या उष्ण व थंड साठ्यांमध्ये काम करणारे कोणतेही एंजिन, त्याच दोन साठ्यांत काम करणाऱ्या कार्नो एंजिनापेक्षा अधिक कार्यक्षम असू शकणार नाही’ आणि उपसिद्धांत असा : ‘दिलेल्या उष्ण व थंड साठ्यांमध्ये काम करणाऱ्या सर्व कार्नो एंजिनांची, त्यांत कोणताही कार्यकारी पदार्थ वापरलेला असो, कार्यक्षमता समान असते’. या सिद्धांताचा व उपसिद्धांताचा अर्थ अखेरीस असा होतो की, दिलेल्या उष्ण व थंड साठ्यांच्या तापमानात (θ1 व θ2) काम करणाऱ्या सर्व एंजिनांमध्ये कार्नो एंजिन सर्वांत अधिक कार्यक्षम आहे व त्याची कार्यक्षमता θ1 व θ2 या दोन तापमानांवरच सर्वस्वी अवलंबून आहे म्हणजे कार्यक्षमता η फक्त θ1 व θ2 यांचेच फलन आहे. व्याख्येप्रमाणे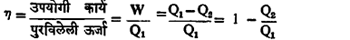
कार्नो यांच्या सिद्धांत-उपसिद्धांताप्रमाणे η हे θ1, θ2 यांचे फलन असल्याने, वरील समीकरणावरून
Q1/Q2 = F (θ1 , θ2) … … … (२१)
आता θ1 व θ2 या तापमानात काम करणारे दुसरे एक कार्नो एंजिन कल्पू. हे एंजिन Q2 उष्णता आत घेऊन Q3 उष्णता बाहेर फेकीत असल्यास, समी. (२१)प्रमाणे त्याच्या बाबतीतही Q2/Q3 = F (θ2, θ3). ज्याअर्थी पहिल्या कार्नो एंजिनाने बाहेर फेकलेली उष्णता Q2 दुसरे कार्नो एंजिन उष्ण साठ्याकडून घेतलेली उष्णता म्हणून वापरते, त्याअर्थी दोन्ही एंजिने मिळून एक मोठे कार्नो एंजिन तयार होते व हे एंजिन θ1 व θ3 तापमानामध्ये Q1 उष्णता आत घेऊन आणि Q3 उष्णता बाहेर टाकून काम करते; म्हणून त्यासाठीही Q1/Q3 = F (θ1, θ3). पण Q1/Q3 = Q1/Q2 X Q2/Q3 असल्याने, F(θ1, θ3) = F(θ1, θ2). F(θ2, θ3) अथवा Q1/Q2 = F (θ1, θ2) = F (θ1, θ3) / F (θ2, θa) … (२२)
θ3 हे तापमान स्वेच्छ घेता येईल; म्हणून ते एक विवक्षित तापमान (उदा., पाण्याचा गोठणबिंदू) आहे, असे समजू. मग फलन F मधून ते ताढून टाकण्यास हरकत नाही. तसे करता व फलनाचे रूप त्यामुळे बदलणे शक्य आहे हे लक्षात घेता.
| Q1 | = F (θ1, θ2) = f (θ1) /(θ2) … (२३) |
| Q2 |
कार्नो एंजिनाच्या कार्यक्षमतेच्या कल्पनेवर आधारलेला असा एक तापक्रम केल्व्हिन यांनी प्रस्थापित केला. कार्नो एंजिनात घेण्यात येणारी अगर त्यातून फेकण्यात येणारी उष्णता त्या त्या तापमानाच्या समप्रमाणात असते, म्हणून जर T1, T2 हीकेल्व्हिन यांच्या तापक्रमाप्रमाणे असणारी, अनुक्रमे q१ व q२ यांच्या समान तापमाने असल्यास,
Q1/Q2 = T1/T2 … … … (२४)
कार्नो एंजिनाची कार्यक्षमता कार्यकारी पदार्थावर मुळीच अवलंबून नसल्याने हे केल्व्हिन तापमान खरोखरी निरपेक्ष आहे. या तापमानास केल्व्हिन अगर निरपेक्ष तापमान म्हणतात. आता कार्नो एंजिनाची कार्यक्षमता अगर निरपेक्ष तापमान म्हणतात. आता कार्नो एंजिनाची कार्यक्षमता h पुढीलप्रमाणे लिहिला येईल.
| η = | Q1 – Q2 | = | T1 – T2 | = 1 – | T2 | … (२५) |
| Q1 | T1 | T1 |
T तापमानात प्राप्त झालेल्या Q उष्णतेपासून आपणास जास्तीत जास्त किती कार्य (W अधिकतम) मिळू शकेल, हे माहीत करून घ्यावयाचे असल्यास दिलेले तापमान T व शक्य ते खालचे तापमान T0 (प्राप्त होण्यासारखे असेल ते), यामध्ये एक कार्नो एंजिन चालवू व त्यात Qही उष्णता साठ्याकडून घेतलेली उष्णता समजू. कार्नो एंजिनाची कार्यक्षमता h सर्वाधिक असल्याने,
| Wअधिकतम = η Q = Q ( 1 – | T0 | ) … (२६) |
| T |
ऊष्मागतिकीचा दुसरा सिद्धांत : कार्नो प्रशीतकाचे काम लक्षात आणता आपणास असे आढळून येते की, थंड साठ्यापासून उष्ण साठ्याकडे उष्णता संक्रमण होऊ शकेल, पण ते सर्वस्वी बाहेरून पुरविलेल्या कार्याच्या मदतीच्या मदतीमुळेच. या कार्याच्या अभावी तसे संस्कमण होणे अशक्य आहे. यावरून आपणास ‘ऊष्मगतिकीचा दुसरा सिद्धांत’ मिळतो. हा सिद्धांत निरनिराळ्या रीतींनी सांगता येतो पैकी क्लॉसियस यांची रीती अशी आहे : ”बाहेरील कार्यरूपी साहाय्याविना कोणत्याही स्वयंचलित’ यंत्रास थंड पदार्थाकडून उष्ण पदार्थाकडे उष्णता नेणे शक्य होणार नाही”.
एंट्रॉपी : कार्नो एंजिनासारख्या व्युत्क्रमी एंजिनाच्या बाबतीत लागू पडणारे समी. (२४) हे
| Q1 | – | Q2 | = 0 … … … (२७) |
| T1 | T2 |
या स्वरूपातही लिहिला येईल. क्लॉसियस यांच्या म्हणण्याप्रमाणे प्रशीतकाकडून –Q2 उष्णता घेतली जाते असे समजल्यास,
| समी. (२७) | Q1 | + | (–Q2) | = 0 असे अथवा ∑ | Q | = 0 … … … (२८) |
| T1 | T2 | T |
असे लिहिता येईल. उष्णतेची देवाण-घेवाण लहान लहान हप्त्यांनी होते असे मानल्यास, म्हणजे तापमान T असता अल्प उष्णता dQ दिली गेली असे समजल्यास, समी. (२८)
| ∲ | dQ | = 0 … … … (२९) |
| T |
असे मांडता येईल. या समी. (२९) ला ‘क्लॉसियस सिद्धांत’ असे म्हणतात. हा सिद्धांत कोणत्याही व्युत्क्रमी चक्रास लागू पडतो. आता
| dQ | = ds … … … (३०) |
| T |
असे मांडल्यास आपणास एक नवीन ऊष्णागतिकीय राशी S मिळते, त्यात एंट्रॉपी हे नाव आहे. समी. (२९) प्रमाणे कार्नो यांच्या एंजिनाच्या व्युत्क्रमी चक्री प्रक्रमाच्या शेवटी एंट्रॉपीमधील एकंदर फरक शून्य असतो. समी. (३०) हा एंट्रॉपीचा अल्प बदल आहे व
| ∫B | dQ | = | ∫B | dS = SB – SA … … … (३१) |
| A | T | A |
हा परिमित बदल होईल. याप्रमाणे आपणास एंट्रॉपीचा कोणताही बदल, ती क्रिया व्युत्क्रमी आहे असे समजून काढता येईल. समी. (३१) मध्ये SAव SB हे टराविक स्थितीतील एंट्रॉपीची मूल्ये दर्शवितात म्हणून एंट्रॉपी-बदल पदार्थावरील क्रिया कोणत्या मार्गाने केली गेली यावर अवलंबून नसून, तो फक्त त्याच्या सुरुवातीच्या (A) व शेवटच्या (B) स्थितीवरच अवलंबून असतो. याचा अर्थ एंट्रॉपी ही एक ऊष्मागतिकीय स्थितिदर्शक चल आहे असा होतो. जर एखाद्या विशिष्ट ठराविक स्थितीत SA चेमूल्य शून्य असेल, तर समी. (३१) वरून आपणास पदार्थाच्या कोणत्याही स्थितीतील एंट्रॉपीचे संपूर्ण मूल्य मिळणे शक्य होइल. याविषयी अधिक विवेचन पुढे नेर्न्स्ट यांच्या उष्णता सिद्धांताच्या संबंधात येईल.
तापमाना – एंट्रॉपी दर्शक रेखाचित्र : समी. (३०) प्रमाणे dQ=Tds. अक्रमी प्रक्रियांत dQ=0 ही शर्त असल्यामुळे व T शून्य होऊ शकत शकत नसल्यामुळे, dQ=0 अथवा अक्रमी क्रियांत S= स्थिरांक. म्हणून अशा क्रियांत एंट्रॉपीत बदल होत नसल्याने, त्यांस ‘सम एंट्रॉपी क्रिया’ असेही म्हणण्याचा प्रघात आहे. आता य अक्षाने तापमान व क्ष अक्षाने एंट्रॉपी दर्शित केल्यास, तयार होणार्या रेखाचित्रात, समताप (T= स्थिरांक) क्ष अक्षात समांतर अशा रेषांनी व अक्रमी (S= स्थिरांक) य अक्षास समांतर अशा रेषांनी दर्शविले जातील. अशा तर्हेच्या दर्शक रेखाचित्राक कार्नो चक्र एक चौकोन होईल. या तापमान-अक्रमी दर्शक रेखाचित्रांचा उपयोग अभियांत्रिकीत फार होतो.
अव्युत्क्रमी एंजिन : त्याच उष्ण व थंड साठ्यांमध्ये काम करणारी, एक व्युत्क्रमी व दुसरे अव्युत्क्रमी, एंजिने कल्पिल्यास व त्यांची कार्यक्षमता अनुक्रमे ηr व ηi असल्यास, कार्नो सिद्धांताप्रमाणे ηr >ηi असते. आता
| ηr = 1 – | T2 | व ηi = 1 – | Q2 | असल्याने, 1 – | Q2 | < 1 – | T2 | अथवा | Q2 | > | T2 | व म्हणून | Q2 | – | Q1 | > 0 … (३२) |
| T1 | Q1 | Q1 | T1 | Q1 | T1 | T2 | T1 |
| याचाच अर्थ अव्युत्क्रमी एंजिनाच्या बाबतीत | ∲ | dQ | > 0 … (३३) |
| T |
| म्हणून अव्युत्क्रमी चक्राच्या शेवटी, जरी कार्यकारी पदार्थ व एंजिन पूर्वस्थितीत आली, तरी | ∲ | dQ | म्हणजे एकंदर एंट्रॉपी (विश्वाची) वाढते. एंट्रॉपी वाढीचे हे तत्त्व कोणत्याही |
| T |
अव्युत्क्रमी चक्राच्या बाबतीत सत्य आहे, हे आपणास सिद्धा करता येईल. म्हणून आपणास म्हणता येईल की,‘कोणत्याही अव्युत्क्रमी घटनेचा परिणाम म्हणून -मग ती चक्रीय स्वरूपाची असली तरी – एकंदर एंट्रॉपी वाढते’ [→ एंट्रॉपी].
यावरून सर्व नैसर्गिक अव्युत्क्रमी असल्याने त्यांच्या पडण्यामुळे क्लॉसियस यांच्या तत्त्वाप्रमाणे ‘विश्वाची एंट्रॉपी वाढत असून ती अधिकतम होऊ पाहते’. या नैसर्गिक घडामोडीसंबंधी केल्व्हिन यांनीही स्वतःचे असे तत्त्व मांडले की, ‘नैसर्गिक घटकांचा परिणाम म्हणून विश्वातील उपयोगी पडण्याजोगी ऊर्जा कमी होत असून ती लघुतम होऊ पाहते’. ही दोन तत्त्वे दिसावयास भिन्न वाटली, तरी एकच आहेत व वाढणाऱ्या एंट्रॉपीचा व कमी होमार्या उपयुक्त ऊर्जेचा परस्पर संबंध आहे. तो संबंध असा की, उपयुक्त ऊर्जेचा र्हास हा नेहमी शक्य ते नीच तापमान गुणिले एंट्रॉपीची वाढ इतका असतो. निर्वात जागेत होणाऱ्या परिपूर्ण वायूच्या मुक्त समताप प्रसरणाच्या पुढील उदाहरणावरून ही गोष्ट पटेल. अशा प्रसरणामुळे झालेले कार्य W समी.(१६) प्रमाणे RT log V2/V1 इतके होते व तितकीच उष्णता Q (= W) आत घेतली जाते. यामुळे झालेली एंट्रॉपीची वाढ
| ∑ | dQ | = | Q | = R log | V2 | … … (३४) |
| T | T | V1 |
आता त्या वायूचा समताप संकोच करून त्यास पूर्वस्थितीत आणले, तर साहजिकच त्यावर W कार्य करावे लागेल व उष्णता Q = W बाहेर पडेल. ही उष्णता Q आपणास T तापमात प्राप्त झाली आहे व त्यापासून मिळणारे अधिकतम कार्य, W अधिकतम, समी. (२६) प्रमाणे Q (1 – T0/T) किंवा W (1 – T0/T) आहे. आता
W – Wअधिकतम = RT0 log V2/V1 … … (३५)
पण W – Wअधिकतम हा फरक उपयोगी पडणाऱ्या ऊर्जेतील ऱ्हास आहे व समी. (३४) लक्षात घेता तो T0 X एंट्रॉपी वाढ, असा आहे. आणखी एका नैसर्गिक क्रियेचे — दोन निष्क्रिय परिपूर्ण वायूंचे एकमेकांत विसरण (आपोआप मिसळणे) – उदाहरण घेऊ व त्यामुळे एंट्रॉपी वाढते हे दाखवू. दोन वायूंचे हे विसरँ म्हणजे त्यांतील प्रत्येक वायूंचे समताप मुक्त प्रसरण समजावयास हरकत नाही. एका वायूच्या मुक्त प्रसरणाने एंट्रॉपीची वाढ समी. (३४) प्रमाणे R log V2/V1 असून, विसरणात भाग घेणार्या वायूंचे प्रत्येकी वस्तुमान ग्रॅमरेणवीय आहे असे समल्यास V1=V व V2=2V असे मांडता येईल. म्हणून दोन व्यूंच्या मिश्रणाच्या एंट्रॉपीची एकंदर वाढ 2Rlog2 होईल.ही एंट्रॉपी राशी ऊष्मागतिकीत अत्यंत उपयुक्त ठरली आहे.
इतर चक्रे : यांचा विचार करताना यांत घडणार्या सर्व क्रिया व्युत्क्रमी आहेत व घर्षण, प्रवेग, संक्षोभ इ. क्रिया अव्युत्क्रमी करणाऱ्या गोष्टींचा अभाव आहे असे समजून. अर्थांत या गृहीतांखाली म्हणजे आदर्श परिस्थितीत काढलेली एंजिनाची कार्यक्षमता प्रत्यक्षात (म्हणजे घर्षण इत्यादींमुळे घट येत असताना) मिळणार्या कार्यक्षमतेपेक्षा पुष्कळच अधिक असेल, हे ध्यानात ठेवावयास हवे. सर्व एंजिनांत कार्यकारी पदार्थांचे प्रसरण वा संकोच होण्यासाठी लागणारे जरूर ते चितिपात्र (दंडगोलाकार नळकांडे, सिलिंडर) व दट्ट्या आहेत असे समजू.
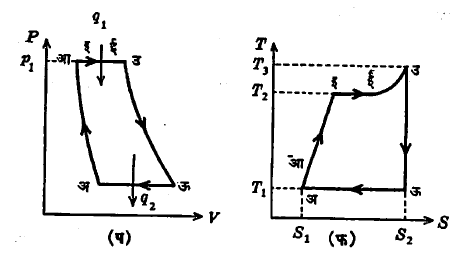
(अ) रँकिन चक्र : हे वाफेवर चालणाऱ्या आदर्श एंजिनाचे चक्र असून, त्याचे दर्शक रेखाचित्र (P–V व T–S) आ. ३ मध्ये अनुक्रमे प व फ यांनी दाखविले आहे. या चक्रात सहा प्रक्रम आहेत, ते असे : (१) अ ते आ : बाष्पित्रामधील (वाफ तयार करणाऱ्या साधनामधील, बॉयलरमधील) दाबाचे P1 इतके मूल्य होईलतो पाण्याचा संकोच. यात पाण्याचे तापमान, T1 जवळजवळ तेच राहते. (२) आ ते इ :दाब स्थिर राहून पामी त्याच्या उकळबिंदूपर्यंत तापविले जाते तापमानT1 पासून T2 पर्यंत चढते. (३) इ ते ई : दाब P1व तापमान T2 स्थिर राहून मिळालेल्या उष्णतेमुळे पाण्याची वाफ बनते. (४) ई ते उ : दाब P1 राहून, दिलेल्या उष्णतेमुळे वाफ तापून अतितप्त होते व तिचे तापमान T3 होते. [प्रक्रम (२), (३) व (४) मध्ये उष्णता शोषली जाते.] (५) उ ते ऊ :वाफेचे अक्रमी प्रसरण घडते व चितिपात्रामधील दट्ट्या जोरात बाहेर ढकलला जातो आणि बहिःकार्य घडते परिणाम म्हणून अतितप्त वाफ परिप्लुत बनते (ज्या पाण्यापासून वाफ तयार झालेली आहे त्याच्या तापमानाइतकेच वाफेचे तापमान होते). (६) ऊ ते अ : दाब स्थिर राहून T1 तापमानात परिप्लुत वाफेचे पाण्यात रूपांतर होते व यामुळे उष्णता बाहेर टाकली जाते.
समजा प्रक्रम (२), (३) व (४) मध्ये शोषलेली उष्णता q1 आहे. ती शोषली जात असताना, दाब स्थिर रहात असल्याने
q1 = h3 – hआ … … (३६)
येथे h ही एकक वस्तुमानाची ऊष्मसंपत (एंथाल्पी) अगर समग्र उष्णता आहे. तिची व्याख्या पुढील समीकरणाने होते :
h = u + pv … … (३७)
या राशीचा विचार इतर ऊष्मागतिकीय राशींबरोबर केला जाईल. तूर्त एवढेच म्हणू की, ऊष्मसंपत हीही एक ऊष्मागतिकीय स्थितिदर्शक चल राशी आहे.
त्याचप्रमाणे ऊ ते अ या प्रक्रमातही दाब स्थिर रहात असल्याने, बाहेर फेकलेली उष्णता q2 असल्यास
q2 = hऊ – hअ
म्हणून रँकिन एंजिनाची कार्यक्षमता
ηr = q1 – q2/q1
= hउ – hआ – hऊ + hअ/hउ – hआ … (३८)
वाफेच्या कोष्टकावरून (विविध तापमानाला परिप्लुत वाफेचे दाब, घनता, समग्र उष्णता, एंट्रॉपी इ. गुणधर्म देणार्या कोष्टकावरून) h ची मूल्ये मिळतात. ती समी.(३८) मध्ये वापरून गृहीत आदर्श परिस्थीत रँकिन चक्राची कार्यक्षमता शेकडा ३२ च्या आसपास येते.
(आ) अंतर्ज्वलन एंजिने : अशा एंजिनात चितिपात्रातच इंधन द्रव जाळून कार्यकारी पदार्थाला (हवेला) उष्णता दिली जाते व दट्ट्याद्वारे तिचे यांत्रिक कार्यात रूपांतर होते. दोन प्रकारच्या अशा एंजिनांची माहिती पुढे दिली आहे, ते दोन प्रकार म्हणजे (१) ओटो एंजिन, ज्यात आयतन स्थिर राहून उष्णता शोषली जाते व (२) डीझेल एंजिन, ज्यात दाब स्थिर राहून उष्णता आत घेतली जाते, हे होत. दोन्ही एंजिनांत हवा हा मुख्य कार्यकारी पदार्थ असून, पेट्रोल, वायु वा इंधन तेल यांचा उपयोग पेट घेऊन हवा तापविणे याकडे होतो. या एंजिनांचा विचार करताना नेहमीच्या चितिपात्र व दट्ट्या यांशिवाय, आत व बाहेर उघडणार्या झडपा व ठिणग्या पाडणारा ‘ठिणगी प्लग’ त्यात आहेत व त्यांची उघडझाप दट्ट्याच्या हालचालीने नियंत्रित केली जाते असे समजू.
(१) ओटो चक्र : आ. ४ मध्ये ओटो चक्र दाखविले आहे, त्याचे प्रक्रम पुढीलप्रमाणे आहेत : (१) ई. ते इ : यात शुद्ध हवा व इंधनवायू यांचे योग्य प्रमाणातील मिश्रण झडपेतून चितिपात्रामध्ये खेचले जाते. (२) इ ते उ :झडपा बंद होऊन मिश्रणाचा अक्रमी संकोच होतो व मिक्षणाचे आयतन पहिल्याच्या सु. १/५ इतके आणि तापमान सु. ६००० से. इतके होते व दाब ५ वातावरणीय दाबाइतका होतो. (३) उ ते अ : आयतन v1 स्थिर राहून ठिणगी प्लगाने उडविलेल्या ठिणगीमुळे मिश्रण पेटते व स्फोट पावते आणि त्याचे तापमान सु. २,०००० से. होते. दाबही त्या प्रमाणात वाढून १५ वातावरणीय दाबाइतका होतो. (४) अ ते आ : यात मिश्रणाचे अक्रमी प्रसरण घडते. (५) आ ते इ : यात झडप उघडून मिश्रणाचा बाहेरच्या वातावरणाशी संबंध जोडला जातो व त्याचा दाब व या स्थितीत बाहेरील वातावरणीय दाबाइतका होतो. (६) इ ते ई : निरुपयोगी झालेली वायूंचे मिश्रण दट्ट्याच्या मागे येण्याने बाहेर फेकले जाते व चक्रास पुन्हा सुरुवात होते.
चक्राच्या ईअ या भागात शोषलेली उष्णता q1 आहे असे समजल्यास q1 = CV (Tअ – Tई ) … … (३९)
त्याचप्रमाणे आइ या भागात बाहेर फेकलेली उष्णता q2 आहे असे मानल्यास, q2 = CV (Tआ – Tइ ) … … (४०)
| म्हणून ओटो चक्राची कार्यक्षमता समी. (३९) व (४०) वरून η0 = 1 – | q2 | = 1 – | Tआ – Tइ | … … (४१) |
| q1 | Tअ – Tई |
गृहीत आदर्श परिस्थितीत η0 चे मूल्य ५२ टक्क्याच्या आसपास येते.
(२) डीझेल चक्र : यात ठिणगी प्लग नसतो याचे दर्शक रेखाचित्र आ. ५ मध्ये दाखविले आहे. त्यातील प्रक्रम असे : (१) ई ते इ : वातावरणीय दाबात (p2) शुद्धा हवा चितिपात्रात घेतली जाते. (२) इ ते उ : त्या हवेचा अक्रमी संकोच होऊन त्याचे आयतन पहिल्याच्या सु. १/११ इकते होते व तापमान सु. १,०००० से. होते. हे तापमान तेलाच्या ज्वलनबिंदूच्या वर असल्याने, दरम्यान स्थिर (p1) दाबात झडपेतून फवार्याने चितिपात्रातील हवेस पुरविलेले तेल पेट घेते. (३) उ ते अ : दाब p1 स्थिर राहून आयतन वाढते व तेलाच्या जळण्यामुळे मिश्रणाचे तापमान वाढून कते सु. २,०००० से. होते. यानंतर तेलाचा पुरवठा बंद होतो. (४) अ ते आ : यात अक्रमी प्रसरणामुळे दट्ट्या खूप जोराने बाहेर ढकलला जातो व बहिःकार्य घडते. (५) आ ते इ : झडप उघडून मिश्रणाचा दाब बाहेरील वातावरणीय दाबाइतका होतो. (६) इ ते ई : निरुपयोगी मिश्रण बाहेर फेकले जाते. यानंतर चक्रास पुन्हा सुरुवात होते.
प्रक्रम (३) उअ मध्ये शोषलेली उष्णता q1 आहे असे मानल्यास दाब स्थिर रहात असल्याने,
q1 = CP (Tअ – Tउ) … (४२)
तसेच प्रक्रम (५) आइ मध्ये बाहेर टाकलेली उष्णता q2 आहे असे मानल्यास,
q2 = CV (Tआ – Tइ) … (४३)
म्हणून डीझेल चक्राची कार्यक्षमता ηD = 1 – q2/q1 अथवा
| ηD = 1 – | CV (Tआ – Tइ) | … (४४) |
| CP (Tअ – Tउ) |
गृहीत आदर्श परिस्थितीत ηD चे मूल्य सु. ५५ टक्के येते.
याशिवाय वाफचक्की (वाफ टरबाइन), झोत (जेट) इंजिन इ. फार महत्त्व पावलेली व फार उपयुक्त अशी साधने उपलब्ध झालेली आहेत. पैकी वाफचक्की मोठ्या नौकांत व झोत एंजिन भारी वेगांच्या विमानांत वापरतात[àअतंर्ज्वलन एंजिन डीझेल एंजिन झोत प्रचालन वाफ टरबाइन].
इतर ऊष्मागतिकीय चल :P, V, T, U व S यांव्यतिरिक्त आणखीही काही ऊष्मागतिकीय चल आहेत व ते म्हणजे ऊष्मसंपत अथवा समग्र उष्णता H, हेल्महोल्ट्स फलन (मुक्त ऊर्जेचे) F व गिब्ज फलन G. त्यांच्या व्याख्या पुढे समीकरणरूपाने दिल्या आहेत.
H = U + PV … … (४५अ)
F = U – TS … … (४५आ)
G = U – TS + PV … … (४५इ)
वरील राशींपैकी एक राशी कोणत्याही दोन राशींचे फलन म्हणून मांडता येईल. पुढे दिलेल्या समी. (४६ इ) च्या साहाय्याने येणारे S चे मुल्य S = – (∂F/∂T)V समी. (४५ आ) मध्ये घालता ते समीकरण
| F = U + T ( | ∂F | )V … (४५ई) |
| ∂T |
याही स्वरूपात मांडता येते. यास ‘गिब्ज-हेल्महोल्ट्स समीकरण’ अशी संज्ञा आहे व ते फार उपयुक्त ठरले आहे.
एखादा रासायनिक व्यूह पहिल्या समतोल स्थितीतून दुसर्या नजीकच्या समतोल स्थितीत जात आहे व त्यात होणारी क्रिया अल्पशी व व्युत्क्रमी आहे असे समजू. समी. (६ अ) मध्ये dQ ऐवजी समी. (३० अ) प्रमाणे TdS घालता, त्या व्यूहाच्या बाबतीत समी. (६ अ) पुढील स्वरूपात मांडू :
dU = TdS – PdV … (४६अ)
त्याचप्रमाणे समी. (४५ अ, आ, इ) चे अवकलन करता पुढे दिल्याप्रमाणे समीकरणे मांडता येतील :
dH = TdS + PdV … (४६आ)
dF = PdV – SdT … (४६इ)
dG = VdP – SdT … (४६ई)
वरील चार समीकरणांपासून आंशिक अवकलनाच्या नियमान्वये पुढे दिलेली मॅक्सवेल यांची महत्त्वाची समीकरणे मिळतात. त्यांचा उपयोग रूपांतरणासाठी विशेषेकरून होतो.
| ( | ∂T | )S = – | ∂P | )V … (४७अ) |
| ∂V | ∂S |
| ( | ∂T | )S = | ∂V | )P … (४७आ) |
| ∂P | ∂S |
| ( | ∂P | )V = | ∂S | )T … (४७इ) |
| ∂T | ∂V |
| ( | ∂V | )P = – | ∂S | )T … (४७ई) |
| ∂T | ∂P |
S हे V व T चे फलन मांडता, S = f (V, T) व त्याचे अवकलन करून येणार्या समीकरणास T ने गुणता
| TdS = T ( | ∂S | )V dT + T ( | ∂S | )T dV … (४८) |
| ∂T | ∂V |
व्याख्येप्रमाणे T (∂S/∂T)V = CV व मॅक्सवेल यांच्या तिसर्या समीकरणाप्रमाणे [(४७ इ)], (∂S/∂V)T = (∂P/∂T)V व म्हणून समी. (४८) पासून
| TdS = CV dT + T ( | ∂P | )V dV … (४९) |
| ∂T |
हे उपयुक्त समीकरण मिळते. त्याचप्रमाणे S=f (P, T) लिहून व त्याचे अवकलन करून येणार्या समीकरणास T ने गुणता,
| TdS = T ( | ∂S | )P dT + T ( | ∂S | )T dP … (५०) |
| ∂T | ∂P |
पण व्याख्येप्रमाणे T (∂S/∂T)P = CP व मॅक्सवेल यांच्या चौथ्या समीकरणाप्रमाणे [(४७ ई)],
| ( | ∂S | )T = – ( | ∂V | )P |
| ∂T | ∂T |
म्हणून समी. (५०) वरून,
| TdS = CPdT – T ( | ∂V | )PdP … (५१) |
| ∂T |
हे दुसरे उपयुक्त समीकरण मिळते. ही दोन्ही समीकरणे एकमेकासमान लिहून, पक्षांतरण (समीकरणाच्या एका बाजूकडून एक किंवा अधिक पदे दुसर्या बाजूस नेण्याची क्रिया) करून व dT ने भागता आणि P स्थिर राहतो असे समजता (dP=0)
| CP – CV = T ( | ∂P | )V ( | ∂V | )P … … (५२) |
| ∂T | ∂T |
आंशिक अवकलनाच्या नियमान्वये,
| ( | ∂P | )V = – ( | ∂V | )P ( | ∂P | )T हे मूल्य समी. (५२) मध्ये वापरता |
| ∂T | ∂T | ∂V |
| CP – CV = –T ( | ∂V | )P2 ( | ∂P | )T … … (५३) |
| ∂T | ∂V |
या समीकरणावरून कळते की (१) (∂P/∂V)T नेहमी ऋण चिन्ही असल्यामुळे (दाब P वाढविल्यास आयतन V नेहमी कमी होते) व (∂V/∂T)2 नेहमी अधिक चिन्ही असल्यामुळे, Cp चे मूल्य Cv पेक्षा केव्हाही कमी असू शकत नाही (२) T शून्याकडे झुकू लागल्यास (T→0), Cp चे मूल्य Cv च्या जवळजवळ येऊ लागते (Cp → Cv) व (३) जेव्हा (∂V/∂T)P असते, (उदा., ४० से. तापमानात पाण्याची घनता महत्तम होते तेव्हा) (Cp =Cv). शिवाय व्याख्येप्रमाणे 1/V (∂V/∂T)P = ∝, स्थिर दाबाचा आयतन प्रसरण गुणांक, व म्हणून (∂V/∂T)P = V∝, तसेच व्याख्येप्रमाणे –1/V (∂V/∂P)T = K, समताप संकोच्यता गुणांक (पदार्थाचा आकुंचन पावण्याचा मापांक), व म्हणून (∂V/∂P)T = – KV ही दोन्ही मूल्ये समी. (५३) मध्ये घालता, पुढील उपयुक्त समीकरण मिळते :
| CP – CV = | TV∝2 | … (५४) |
| K |
Cp चे प्रायोगिक मूल्य मिळविणे सोपे असते. त्याचे ज्ञात मूल्यावरून आणि a व K ची मूल्ये ज्ञात असल्याने Cv चे मूल्य समी. (५४) वरून काढता येते.
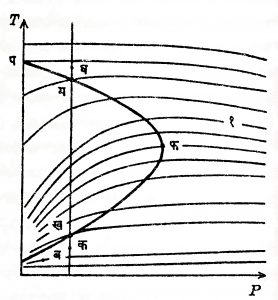
जूल-टॉमसन परिणाम : ऊष्मागतिकीचा एक अनुप्रयोग म्हणून जूल-टॉमसन परिणामाचा विचार करू. औष्णिक निरोधन करून, म्हणजे बाहेरील उष्णता आत व आतील बाहेर जाणार नाही अशी व्यवस्था करून, सच्छिद्र गुडदीतून (प्लगमधून) एखादा वायू उच्च दाबातून नीच दाबात प्रसरण पावत असताना, दाबाच्या बदलामुळे होणार्या तापमानाच्या बदलास ‘जूल-टॉमसन परिणाम’ म्हणतात.या पद्धतीने होणार्या वायूच्या प्रसरणास ‘गळचेपी प्रसरण’ अशी संज्ञा आहे अशा प्रसरणात वायूची ऊष्मसंपत स्थिर राहते. सच्छिद्र गुडदीऐवजी निमुळती होत जाऊन टोकास छिद्र असलेली नळीही (तोटी) वापरली जाते. प्रत्यक्ष प्रयोगात गुडदीच्या अगर तोटीच्या आतील बाजूस उच्च पण स्थिर दाब ठेवून, त्याच्या दुसर्या बाजूस स्थिर पण नीच दाब राखला जातो व या दोन्ही बाजूंस वायूच्या दाबाचे व तापमानाचे मापन केले जाते. पसरणार्या वायूचा होणारा तापमान-बदल, त्याच्या सुरुवातीचे तापमान व दाब, आणि अखेरचा दाब, यांवर सर्वसाधारणपणे अवलंबून असतो व तो बदल तापमानातील वाढ व क्षय दाखवितो, अगर तो शून्यही असू शकतो. प्रत्यक्ष प्रयोगात वायूच्या समतोल स्थितीतील काही सम-ऊष्मसंपताबिंदू शोधून त्यामधून जाणारा वक्र काढतात. नायट्रोजन वायूच्या बाबतीतील असे वक्र आ. ६ मध्ये दाखविले आहेत. ऊष्मसंपताचे मूल्य एका वक्रापासून दुसर्या वक्रावर बदलते पण एकाच वक्रावर ते स्थिर असते. हे वक्र T—P रेखाचित्रावर काढले असून कोणत्याही वक्राच्या कोणत्याही बिंदूची स्पर्शिका (स्पर्शरेषा) जूल-टॉमसन परिणामगुणांक µ दाखविते म्हणजे
µ = (∂T/∂P)H … … … (५५)
ज्या स्थितीत या गुणांकाचे मूल्य शून्य असते अशी स्थिती दर्शविणार्या बिंदूंतून काढलेल्या वक्रास ‘पर्यसन वक्र’ म्हणतात. आ. ६ मधील पफब हा पर्यसन वक्र आहे. या वक्राच्या आतील भागात mचे चिन्ह अधिक (+) रहात असल्याने त्यात असणार्या कोणत्याही स्थितीत तोटीतून अगर गुडदीतून बाहेर पसरलेला वायू थंड होतो, म्हणून या आतील भागास ‘शीत भाग’ म्हणतात. वक्राबाहेरच्या भागातील एखाद्या बिंदूने दर्शविलेल्या कोणत्याही ‘स्थितीत बाहेर पसरलेला वायू उष्ण होत असल्याने. त्या भागास उष्ण भाग’ म्हणतात. खुद्द वक्रावरील बिंदूंनी दर्शविलेल्या स्थितीत, बाहेर पसरलेला वायू थंडही होत नाही किंवा उष्णही होत नाही म्हणजेच त्याचे तापमान बदलत नाही. पर्यसन वक्रातून जाणारी स्थिर दाबाची कखगघ रेषा अनुसरली असता, क स्थितीत बाहेर पसरलेला वायू तापतो, ख आणि ग स्थितीत त्याच्या तापमानात कोणताही बदल होत नाही, खग दरम्यानच्या स्थितीत तो थंड होतो आणि घ स्थितीत तो पुन्हा तापतो. आता समी. (५१) पुन्हा मांडता
| TdS = CPdT – T ( | ∂V | )P dP अथवा |
| ∂T |
| dH – VdP = TdS = CPdT – T ( | ∂V | )P dP. |
| ∂T |
या समीकरणात H स्थिर राहतो असे समजता व dP ने भागता,
| ( | ∂T | )H = μ = | 1 | [ T ( | ∂V | P – V ] … (५६) | |
| ∂P | CP | ∂T | |||||
असे m चे मूल्य मिळते. योग्य अशा तापमानाचा वायू घेऊन, दाबाखाली गुडदीतून अगर तोटीतून बाहेर पडताना तो थंड होतो या गोष्टीचा उपयोग वायूच्या द्रवीकरणात तसेच नीच आणि अतिनीच तापमान मिळविण्यासाठी करून घेतला आहे आणि या दृष्टीने हा परिणाम फार महत्त्वाचा आहे. याच्या जोडीस अक्रमी निकर्षणधर्माचा (कर्षुकत्व नाहीसे करण्याच्या गुणधर्माचा) उपयोग करून अत्यंत नीच तापमाने (निरपेक्ष शून्याच्या किंचित वर) मिळविणे शक्य झाले आहे. शिवाय µ च्या ज्ञात मूल्यामुळे वायुतापमापकाने मोजलेली तापमाने, त्यांस शुद्धी लावून, केल्व्हिन यांची निरपेक्ष तापमाने म्हणून मांडता येतात. याप्रमाणे शुद्ध केलेले वितळणार्या बर्फाचे तापमान २७३.१६५ ± ०.०१५० के. (के. म्हणजे केल्व्हिन तापमान एकक) इतके आहे.
ऊष्मागतिकीय समतोलाचे नियम : हे नियम गिब्ज यांनी प्रथम व्यवस्थित मांडले. सर्व ऊष्मागतिकीय संचांच्या बदलांची अंगभूत प्रवृत्ती समतोल स्थिती प्राप्त करून घेण्याकडे असते. एकतर अंतस्थ ऊर्जा ही स्थितिज (स्थितीमुळे प्राप्त होणार्या) ऊर्जेच्या जातीची असल्याने, यामिकीच्या तत्त्वाचे सादृश्य लक्षात घेता, अगदी अलग असलेल्या ऊष्मागतिकीय संचात होणारा बदल अंतस्थ ऊर्जा कमी होण्याच्या दिशेने होतो. शिवाय अशा बदलांमुळे अंतस्थ ऊर्जेची प्रवृत्ती स्वतःचे मूल्य शक्य तितके किमान होण्याकडे असते.
नैसर्गिक बदलांच्या शर्ती : कल्पना करू की, म या व्यूहाच्या सभोवतालचे व पदार्थाशी (उदा., हवा, ज्यात ती वस्तू ठेवली असेल ते भांडे इ.) संबंध जोडला गेला, तर त्यामुळे बनणार्या जोड व्यूहात घडणार्या प्रत्येक बदलाच्या बाबतीत
δS + δS0 ≧ 0 … … … (५७)
या dS व dS० अनुक्रमे म व ब मध्ये होमारा एंट्रॉपीचा बदल आहे. समी. (५७) व समतोलाच्या अनुषंगाने पुढे येणारी समीकरणे, यात खालचे समानतेचे चिन्ह व्युत्क्रमी क्रियांस व वरचे अधिकतेचे चिन्ह अव्युत्क्रमी क्रियांस अनुलक्षून आहे. भोवतालच्या परिसरात घडणारे बदल व्युत्क्रमी आहेत असे मानल्यास δS0 = – δQ/T = – δU+δW/T व हे मूल्य समी. (५७) मध्ये घालता,
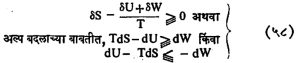
बदल अक्रमी असल्यास dQ = dU + dW = 0 व म्हणून समी. (५८) चे रूप पुढीलप्रमाणे होईल :
dS ≧ 0 … … … (५८अ)
बदल समताप असल्यास T स्थिर राहते, म्हणून समी. (५८) d (U – TS) ≦ – dW असे अथवा U – TS = F असल्याने
dF ≦ – dW … … … (५९)
असे होईल. खेरीज T स्थिर राहून आयतनही स्थिर राहिल्यास, त्या प्रक्रियांच्या बाबतीत कार्य dW=० होत असल्याने समी. (५९) मधील शर्त आता पुढीलप्रमाणे होईल :
dF ≦ 0 … … … (६०)
जेव्हा बदलात दाब व तापमान स्थिर राहते, तेव्हा dW च्या ऐवजी PdV मांडता, समी. (५९) चे रूप dF ≦ – PdV असे अथवा d (U – TS + PV) ≦ 0 असे किंवा U – TS + PV च्या ऐवजी गिब्ज फलन G घालता,
dG ≦ 0 … … … (६१)
असे होईल. δG=0 या शर्तींचा उपयोग करून आपणास स्थिर दाब समताप प्रक्रियांस लागू पडणारे समीकरण
| log KP = | QP | + | logT | δCP + log I … (६२) |
| RT | R |
मिळू शकते. यात KP समतोल स्थिरांक असून QP स्थिर दाबाच्या प्रक्रियेची उष्णता व Iही प्रक्रियेत भाग घेणार्या पदार्थाच्या ग्रॅमरेणूंच्या संख्येवर अवलंबून असणारी राशी आहे. तसेच dF=0 या शर्तीपासून स्थिर आयतन समताप प्रक्रियांचे समीकरण मिळू शकते.
प्रथम क्रमाची अवस्थांतरे : यांची उदाहरणे म्हणजे एखाद्या घन पदार्थाचे त्याच्या वितळबिंदूवर वितळणे, एखाद्या द्रवाचे त्याच्या उकळबिंदूवर बाष्पीभवन होणे, ही होत. ही अवस्थांतरे ठराविक स्थिर दाबात व स्थिर तापमानात होतात व त्यात गिब्ज फलन G बदल पावत नाही. जर १ हा अनुप्रत्यय सुरुवातीची व २ हा अखेरची अवस्था दर्शवितो असे समजले, तर T तापमानात व P दाबात होणार्या अवस्थांतराच्या संबंधात G1=G2असे लिहिता येईल. याहून किंचित वरच्या T + dT तापमानात व P + dP दाबात होणार्या अवस्थांतराच्या बाबतीत G1 + dG1 = G2 + dG2 असे लिहिता येईल. वरील दोन समीकरणांची वजाबाकी करता, dG1 = dG2असे समीकरण मिळेल व dG1 व dG2 ची मूल्ये समी. (४६ ई) प्रमाणे घालता – S1dT + V1dP = – S2dT + V2dP हे अथवा
| dP | = | S2 – S1 | … … … (६३) |
| dT | V2 – V1 |
हे समीकरण मिळते. L या अक्षराने अवस्थांतराची सुप्त उष्णता दर्शविल्यास,
L = T (S2 – S1) … … (६४)
व म्हणून समी. (६३) पासून
| dP | = | L | … … … (६५) |
| dT | T (V2 – V1) |
हे समीकरण मिळते व त्यास क्लॅपिरॉन यांचे अथवा ‘सुप्त उष्णतेचे पहिले समीकरण’ म्हणतात. याचा विचार करू जाता अवस्थांतरे दोन तर्हेची उद्भवतात : (१) पहिल्यात V2 > V1 (उदा., उकळबिंदूवर पाण्याची वाफ होताना, एक ग्रॅम पाण्याचे आयतन सु. १ घ. सेंमी. व त्याच्या वाफेचे आयतन सु. १,६६० पट मोठे) व V2 – V1 चे चिन्ह अधिक होत असल्याने समी. (६५) वरून कळते की dP/dT चे चिन्हही अधिक येते. याचा अर्थ, दाब वाढविला असता उकळबिंदू वर चढतो; त्याच्या उलट, दाब कमी केला असता उकळबिंदूही खाली येतो. उदा., उंचीवर वातावरणीय दाब कमी होत असल्याने पाण्याचा उकळबिंदू १००० से. च्या खाली येतो व खाली येण्याचे हे प्रमाण साधारणपणे दर ३०४.८ मीटरास १० से. इतके असते. (२) दुसर्यात V2 < V1 (उदा. वितळबिंदूवर बर्फाचे पाणी होताना) व V2 – V1 चे चिन्ह आता उणे होत असल्याने dP/dT चे चिन्हही उणे होते. याचा अर्थ दाब वाढविला असता वितळबिंदू खाली उतरेल, बर्फाचा वितळबिंदू त्यावरील दाब वाढविला असता खाली जातो. २ हा अनुप्रत्यय बाष्प अवस्था दाखवितो असे मानल्यास, V2 च्या मानाने V1 अल्प व म्हणून उपेक्षणीय समजण्यास काहीच हरकत नाही; म्हणून V1 उपेक्षित मानल्यास व परिपूर्ण वायूंचे समीकरण बाष्पास (परिप्लुत स्थितीतही) लागू पडते असे गृहीत धरता, V2 च्या ऐवजी RT/P लिहून समी. (६५) पुढीलप्रमाणे लिहिता येईल :
| dP | = | L | . | dT | … … (६६) |
| P | R | T2 |
(अ) L तापमानावर अवलंबून नसून स्थिर आहे अगर (आ) तापमानाप्रमाणे विशिष्ट पद्धतीने Lचे मूल्य बदलते, असे मानून समी. (६६) चे समाकलन [àअवकलन व समाकलन] करता येते. उदा., L = L0 + cT असे समजता व समाकलन करता
| L = – | L0 | + c log T + A (स्ठिरांक) … (६७) |
| RT |
हे समीकरण मिळते. तापमानाचा पल्ला फार मोठा नसल्यास कोणत्याही तापमानास अनुलक्षून L चे मूल्य समी. (६७) वरून काढता येते. संप्लवनाच्या (घन पदार्थ द्रवरूप न होता सरळ वायू स्थितीत रूपांतरित होण्याच्या) बाबतीत किरखोफ यांचे समीकरण

(या समीकरणात अनुप्रत्यय १ घनासाठी व ३ बाष्पासाठी वापरले आहेत) त्यापासून येणारे Lसं चे मूल्य समी. (६६) मध्ये वापरून समाकलन करता बाष्मदाबाचे महत्त्वाचे समीकरण मिळते, ते असे :
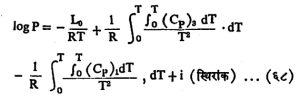
द्वितीय क्रमाची अवस्थांतरे : दुसर्या क्रमाच्या अवस्थांतरांचा विचार करून एहरेनफेस्ट यांची समीकरणे मिळतात. असल्या अवस्थांतरांची उदाहरणे म्हणजे (अ) द्रव हीलियम I चे द्रव हीलियम II मध्ये रूपांतर, (आ) क्यूरी बिंदूवर (क्यूरी यांच्या नावाने ओळखण्यात येणार्या तापमानावर) लोखंडासारख्या लोहकर्षुक पदार्थाचे समकर्षुक (निर्वातापेक्षा जास्त कर्षुकीय पार्यता असलेल्या) पदार्थात रूपांतर इत्यादी. यांचा विचार या लेखात केलेला नाही.
समी. (६४) प्रमाणे उकळबिंदूवर असलेल्या द्रवाच्या एक ग्रॅम वस्तुमानाच्या बाबतीत l/T = S2-S1 (l म्हणजे सुप्त उष्णता) व त्याचे T ला अनुलक्षून अवकलन करता, 1/T.dl/dT – T2 = dS2/dT – dS1/dT, अथवा T ने त्यास गुणता, dl/dT – l/T = TdS2/dT – TdS1/dT हे समीकरण मिळते. व्याख्येप्रमाणे TdS1/dT = C1 द्रवाची विशिष्ट उष्णता व TdS1/dT = C2 बाष्पाची परिप्लुत स्थितीतील विशिष्ट उष्णता; म्हणून
| dl | – | l | = C2 – C1 … … (६९) |
| dT | T |
हे समीकरण मिळते, यात क्लॉसियस यांचे अथवा ‘सुप्त उष्णतेचे दुसरे समीकरण’ म्हणतात. परिप्लुत स्थितीत दाब देऊन बाष्पाचा संकोच केला असता, (१) ती अतिपरिप्लुत होत असल्यास अथवा (२) ती अपरिप्लुत होत असल्यास C2 अनुक्रमे (१) अधिक चिन्ही वा (२) ऋण चिन्ही असते. C2 चे अधिक चिन्ही, ऋण तिन्ही किंवा शून्यही असणे बाष्पाच्या जातीवर अवलंबून असून सर्वस्वी तापमानावर अवलंबून असते. उदा., पाण्याच्या परिप्लुत वाफेच्या बाबतीत तापमान १००० से. असताना C2 ऋण चिन्ही असते, सु. १५०० से. तापमानात C2 शून्य होते व त्यावरील तापमानात C2 अधिक चिन्ही बनते. ज्या परिप्लुत बाष्पांची विशिष्ट उष्णता ऋण चिन्ही आहे अशांचे द्रवीकरण करावयाचे असल्यास, त्यांचे प्रसरण होऊ देणे अवश्य आहे संकोच केल्यास द्रवीकरण न होता ते अपरिप्लुत होतील.
विद्रावांची ऊष्मागतिकी : विरल विद्राव व वायू यांत बरेच साम्य आहे, कारण (१) ज्याप्रमाणे वायूचे रेणू खूप मोठ्या आयतनात पसरलेले असतात, त्याप्रमाणे विद्रुताचे (विरघळलेल्या पदार्थाचे) कणही विद्रावकाच्या (विरघळविणार्या द्रवाच्या) ***मोठ्या आयतनात पसरलेले असतात, (२) वायूस दाब असतो, तर विद्रावातही तर्षणीय दाब (विद्रुत पदार्थाच्या रेणूंच्या गतीमुळे निर्माण होणारा दाब) असतो. यावरून व्हांट हॉफ यांनी असे सिद्ध केले की, परिपूर्ण वायूंचे स्थितिदर्शक समीकरण विरल विद्रावासही लागू पडते.
विद्रावाशी संलग्न असलेल्या परिप्लुत बाष्पाचा दाब (p) विद्रावकाशी संलग्न असलेल्या परिप्लुत बाष्पाच्या दाबा (p0) पेक्षा नेहमी कमी असतो व या दोन दाबांतील फरक p0 — p तर्षणीय दाब P शी संबंधीत असतो व सिद्ध करता येते की,
| p0 – p = | d | P … … … (७०) |
| d0 |
यात d बाष्पाची घनता व d0 विद्रावाची (व विद्राव विरल असल्याने प्रायः विद्रावकाची) घनता दर्शविते. बाष्पदाबाचा सापेक्ष फरक
| p0 – p | = | d | . | P | … … … (७१) |
| p0 | d0 | p0 |
पण परिपूर्ण वायूचे नियम बाष्पास व विद्रावास लागू करता, p0 = nR’T व P = n1R’T. येथे n व n1 अनुक्रमे एकक आयतनातील बाष्पाच्या व विद्रुताच्या रेणूंची संख्या दर्शवितात. शिवाय n2 ने विद्रावकाच्या एकक आयतनातील रेणुसंख्या दर्शविल्यास d/d0 = n/n0 व म्हणून या किंमती समी. (७१) मध्ये घालता आणि उजव्या बाजूस n अंशातून व छेदातून काढून टाकता
| p0 – p | = | n1 | … … … (७२) |
| p0 | n2 |
अथवा
| p0 – p | = | एकक आयतनातील विद्रुताची रेणुसंख्या |
| p0 | एकक आयतनातील विद्रावकाची रेणुसंख्या |
जर विद्रावात विद्रुताचा एक ग्रॅमरेणू विद्रावकाच्या N ग्रॅमरेणूंत मिसळला असेल, तर n1/n2 = 1/N व म्हणून समी. (७२) आता असे होईल :
| p0 – p | = | 1 | … … … (७२अ) |
| p0 | N |
यास ‘राऊल सिद्धांत’ म्हणतात.
विद्रावाचा उकळबिंदू विद्रावकाच्या उकळबिंदूच्या नेहमी वर असतो, त्या दोहोंतील फरक लहान असतो व तो प्रयोगाने शोधून काढता येतो. त्यावरून व सुप्त उष्णतेचे मूल्य L माहीत असल्यास ग्रॅमरेणू M ज्याच्या साहाय्याने काढता येते, ते समीकरण (७५) पुढे दिले आहे. क्लॅपिरॉन समीकरण मांडून त्याचे समाकलन करता,
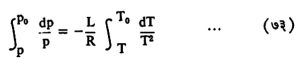
यात T0व PP अनुक्रमे विद्रावकाचे विद्रावकाचे उकळबिंदूचे तापमान व दाब असून T व P विद्रावकाच्या संबंधीच्या त्याच राशी आहेत. L स्थिर आहे असे गृहीत धरले आहे. समाकलन करून व सीमामूल्ये घालून, वरील समी. (७३) log p0/p = L/R (1/T0 — 1/T) = L/R . T — T0/TT0 असे होते. (T — T0) ऐवजी ΔT लिहिता व T आणि T0 मधील फरक थोडा असल्याने T T0 ऐवजी T02 लिहिता,
| log | p0 | = | L | . | ΔT | … … … (७४) |
| p | R | T02 |
आता P0/ P चे ऐवजी 1 + P— P0/ P असे लिहून P0 — P/ P अल्प राशी असल्याने log (1+ P0 — P/ P)=P0 — P/ P जवळजवळ व P0 — P/ P=n1/n2 आसन्नतेने. n विद्रुतरेणूंचे विद्रावकाच्या १०० रेणूंत विद्रावण केले आहे असे समजल्यास n1/n2 = n/100 व म्हणून समी. (७४) वरून वरील मूल्ये घालून ΔT चे मूल्य मांडता,
| ΔT = | nR T02 | = | 0.02T02n | … … (७५) |
| 100 L | L |
यात R वायुस्थिरांक = सु. २ कॅलरी/ग्रॅमरेणु,० से.
विद्रावाचा गोठणबिंदूही विद्रावकाच्या गोठणबिंदूच्या नेहमी खाली असतो. त्या दोहोंतला फरक लहान असून त्याच्यावरूनही ग्रॅमरेणू समीकरण (७८) च्या साहाय्याने काढता येते. या गोठणबिंदूसंबंधीचे परिप्लुत बाष्प दाब व तापमान यांतील संबंध दाखविणारे P—T रेखाचित्र आ. ७ मध्ये दिले आहे. यातील यर वक्र विद्रावकास आणि लव वक्र विद्रावास अनुलक्षून आहे. य विद्रावकाचा गोठणबिंदू असून त्याचा बाष्पदाब p0 व तापमान T0 आहे. ल हा विद्रावाचा गोठणबिंदू असून त्याचा बाष्पदाब p0 व तापमान T0 आहे. तापमान T0 असताना विद्रावाचा बाष्पदाब p आहे. यह वक्र गोठलेला विद्रावक (बर्फ) व बाष्प यांचा संबंध दाखवितो. L’ गोठण्याची सुप्त उष्णता आहे असे मानल्यास, ल बिंदूस अनुलक्षून गोठलेल्या विद्रावकाचे सरळ परिप्लुत बाष्पात अवस्थांतर होताना, संपूर्ण सुप्त उष्णता L + L’ होईलती लक्षात घेऊन समी. (७४) प्रमाणे समीकरण मांडल्यास
| log (p0/p) = | L + L’ | ( | 1 | – | 1 | ) … … (७६) |
| R | T | T0 |
तसेच द्रवांचे परिप्लुत बाष्पात होणार्या अवस्थांतरास अनुलक्षून समीकरण लिहिता,
| log (p/p’) = | L | ( | 1 | – | 1 | ) … … (७७) |
| R | T | T0 |
समी. (७६) तून समी. (७७) वजा करता,
| log (p0/p) = | L’ | ( | 1 | – | 1 | ) व समी. (७४) नंतर अनुसरलेल्या क्रमाबरहुकुम जाता, गोठणबिंदूच्या खाली येणारे तापमान |
| R | T | T0 |
| ΔT = | 0.02T02n | … … (७८) |
| L’ |
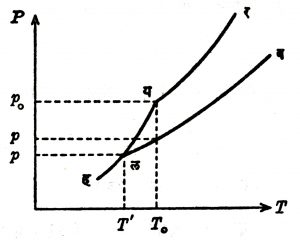
नेर्न्स्ट यांचा उष्णता सिद्धांत: कोणत्या परिस्थितीत रासायनिक विक्रिया संपूर्णपणे पुरी होईल, याता शोध घेत असताना नेर्न्स्ट यांचा हा उष्णता सिद्धांत अगम पावला. गिब्ज-हेल्महोल्ट्स समीकरण (४५ ई) मध्ये उजवीकडील दुसऱ्या पदात आयतन स्थिर रहावयास पाहिजे ही गोष्ट लक्षात ठेवून, ते समीकरण आता असे लिहू :
| F = U + T ( | dF | ). याचे T स अनुलक्षून अवकलन करता |
| dT |
| –T | d2F | = | dU | = ∑nCV … (७९) |
| dT2 | dT |
हे समीकरण मिळते. यात n ग्रॅमरेणूंची संख्या आहे व बेरीज विक्रियेत भाग घेणाऱ्या सर्व घटकांवर करावयाची आहे. समी. (७९) चे समाकलन करता
| dF | = – ∫T0 | ∑nCV | dT + ( | dF | )0 … … (८०) |
| dT | T | dT |
यात (dF/dT)0 समाकलन स्थिरांक आहे व त्याचा अर्थ शुन्य निरपेक्ष तापमानात एकक विक्रिया होऊ दिली असता, होणारा व्यूहाचा एंट्रॉपी-बदल—∑ΔS0 असा आहे. याचे मूल्य समजल्याशिवाय (dF/dT) चे मूल्य मिळणे शक्य नाही. यावर नेर्न्स्ट यांचे म्हणणे की, ∑ΔS0 चे मूल्य शून्य समजावे, म्हणजे त्यांच्या म्हणण्याचा अर्थ हा होतो की, निरपेक्ष शून्य तापमानात गोठलेल्या व्यूहामधील बदल न घडता होतात. या त्यांच्या म्हणण्यासच ‘ उष्णता सिद्धांत’ हे नाव प्राप्त झाले. या सिद्धांताप्रमाणे निरपेक्ष शून्य तापमानात
| F0 = U0, ( | dF | )0 = 0 व ( | dU | )0 = 0 … (८१) |
| dT | dT |
शिवाय त्या तापमानात F व U यांचे वक्र समतल (एकाच प्रतलात) होऊन एकमेकांस मिळतात.
प्लांक हे यापुढे जाऊन म्हणतात की, वर म्हटल्याप्रमाणे एकंदर एंट्रॉपी-बदल शुन्य होतो, एवढेच नव्हे, तर प्रत्येक गोठलेल्या घटकाची व्यक्तिगत एंट्रॉपी शून्य होते, म्हणजे ०० के. तापमानात एंट्रॉपी
S0 = 0. … … (८२)
हे सत्य मानल्यास पदार्थाच्या कोणत्याही स्थितीत एंट्रॉपी S चे समग्र मूल्य व त्याचबरोबर F आणि U यांचीही समग्र मूल्ये आपणास काढता येतील. नेर्न्स्ट यांचा उष्णता सिद्धांत प्लांक यांच्या पुस्तीसह प्रयोगांती खरा ठरला आहे. सांख्यिकीय द्दष्टीनेही यातील तत्त्व खरे आहे, हे फाउलर यांनी सिद्ध केले आहे.
फाउलर यांच्या मताप्रमाणे, प्रथम नर्न्स्ट यांनी १९१२ मध्ये मांडलेले ‘निरपेक्ष शून्य तापमानाच्या प्राप्तीच्या अशक्यतेचे तत्त्व’ अधिक मूलभूत आहे व या तत्त्वास त्यांनी सिद्धांताचे स्थान दिले आहे, यासच ‘ऊष्मागतिकीचा तिसरा सिद्धांत’ म्हणतात.
पहा : उष्णता; सांख्यिकीय भौतिकी.
संदर्भ : 1. Roberts, J. K. Heat and Thermodynamics, London.
2. Saha, M. N.; Shrivastava, B. N. Theatise on Heat, Allahabad, 1965.
3. Zemansky, M. W. Heat and Thermodynamics, New York, 1957.
भावे, श्री. द.