उष्णता संवहन : तांब्याच्या पट्टीच्या एका टोकाला उष्णता देऊन दुसरे टोक हातात धरले असता उष्णता भासते, तेच काचेची पट्टी वापरली असता तितकी उष्णता भासत नाही. यावरून असे दिसून येईल की, निरनिराळ्या पदार्थांची उष्णता संवहन करण्याची (वाहून नेण्याची) पात्रता निरनिराळी असते. उष्णता संवहन करण्याच्या पात्रतेस ऊष्मीय संवाहकता म्हणतात. सर्वसाधारणपणे धातू सुसंवाहक असतात. काच, लाकूड यांसारखे पदार्थ कुसंवाहक असतात. बहुतेक द्रव पदार्थ कुसंवाहक असतात. एखाद्या भांड्यातील पाण्यात तरंगत असलेल्या बर्फास वगळून पाण्यास वरील बाजूने उष्णता दिली असता बर्फ वितळत नाही, यावरून हे स्पष्ट होईल. वायूसुद्धा कुसंवाहकच असतात. उष्णता संवहन होत असताना पदार्थाचे कण (अणू वा रेणू) स्थिरच असतात. ते फक्त उष्णता एका कणाकडून (अणू वा रेणूकडून) दुसऱ्याकडे पोहोचविण्याचे कार्य करतात.
तपमान चढ-उतार : एखाद्या पदार्थाच्या दोन बिंदूंमधील अंतर जर ड असेल व त्या बिंदूचे तपमान जर अनुक्रमे त१ व त२ असेल तर याला तपमान चढ-उतार असे म्हणतात.
| त१ – त२ | याला तपमान चढ-उतार असे म्हणतात. |
| ड |
स्थिर स्थिती : ज्यावेळी एखाद्या पदार्थापासून निघून जाणारी उष्णता त्या पदार्थाला मिळणाऱ्या उष्णतेबरोबर असते, तेव्हा त्या पदार्थाच्या कोणत्याही बिंदूचे तपमान स्थिर राहते. या स्थितीला स्थिर स्थिती म्हणतात.
ऊष्मीय संवाहकता : समजा, एका घन पदार्थाच्या, एकमेकांपासून थोड्या अंतरावर असलेल्या दोन समांतर पृष्ठभागांचे तपमान त१ व त२ आहे (त१ > त२) आणि प्रत्येकाचे क्षेत्रफळ क्ष आहे व त्यांच्यामधील अंतर ड आहे, तर उच्च तपमानाच्या त१ पृष्ठभागापासून नीच तपमानाच्या त२ पृष्ठभागाकडे उष्णता संवहन होते. समजा, उ उष्णता ट वेळेमध्ये वाहते. प्रयोगाने असे दाखवून देता येते की,
| उ ∝ क्ष; उ ∝ (त१–त२); उ ∝ | १ | उ ∝ ट |
| ड; |
| म्हणून उ ∝ | क्ष (त१–त२) ट |
| ड |
| उ = | क × क्ष (त१–त२) ट | … (१) |
| ड |
हे समीकरण प्रथम फूर्ये यांनी प्रयोगाने काढले. येथे क हा स्थिरांक असून त्याला ‘ऊष्मीय संवाहकता’ म्हणतात. निरनिराळ्या पदार्थांची संवाहकता निरनिराळी असते.
वरील समीकरणावरून ऊष्मीय संवाहकतेची व्याख्या पुढीलप्रमाणे करता येते : ‘एकक क्षेत्रफळ व एकक जाडी व समांतर पृष्ठभाग असलेल्या पदार्थाच्या दोन्ही बाजूंकडील स्थिर तपमानांतील फरक जर एकक असेल, तर दर सेकंदाला वरील क्षेत्रफळातून लंब दिशेने वाहणाऱ्या उष्णतेला त्या पदार्थाची ऊष्मीय संवाहकता म्हणतात’. संवाहकता मोजण्याचे एकक, कॅलरी / (सेकंद) (क्षेत्रफळ) (तपमान चढ-उतार) असे आहे.
संवाहकता काढण्यासाठी पाऱ्याच्या तापमापकापेक्षा तपयुग्म (दोन भिन्न धातूंच्या तारांचे सांधे निरनिराळ्या तपमानांत ठेवल्यास जो विद्युत् दाब निर्माण होतो त्याचा उपयोग करणारी) तापमापके अधिक उपयोगी ठरली आहेत. सुरुवातीला ज्या पदार्थांची संवाहकता काढावयाची त्याच्या एका बाजूस वाफ व दुसऱ्या बाजूस बर्फ अथवा पाणी यांचा उपयोग केला जात असे. सध्या अनेक पद्धतींनी संवाहकता काढता येते.
घन पदार्थाची संवाहकता : सर्ल यांची पद्धती : या पद्धतीत ज्या पदार्थाची संवाहकता काढावयाची असेल त्याचे एक टोक एका पेटीत व दुसरे दुसऱ्या पेटीत ठेवलेले असते. पहिल्या पेटीतून वाफ खेळवलेली असते व दुसऱ्या पेटीतून पाणी वाहत ठवलेले असते. पाणी पेटीतून जाताना व बाहेर पडताना त्याचे तपमान मोजण्यासाठी त३ व त४ तपमापके योजिलेली असतात. तसेच काही अंतरावर असलेल्या पदार्थाच्या कोणत्याही दोन बिंदूंचे तपमान त१ व त२ मोजण्यासाठी तपमापके असतात. काही वेळाने स्थिर स्थिती प्राप्त होऊन तपमापके स्थिर तपमान दर्शवितात. नंतर दर सेकंदाला किती ग्रॅम पाणी वाहते ते म आणि निवडलेल्या दोन बिंदूंमधील अंतर ड मोजतात. यावरून ऊष्मीय संवाहकता पुढील समीकरणाने काढता येते :
| म (त४ – त३) = क × क्ष × | (त१ – त२) | |
| ड |
प्रारणाने (उष्णता तरंगांच्या उत्सर्जनाने) उष्णता वाया जाऊ नये म्हणून पदार्थाभोवती त्याच्या इतकेच तपमान असलेले आवरण घालतात. या आवरणाला संरक्षक कडे असे म्हणतात.
फोर्ब्स यांची पद्धती : या पद्धतीत ज्या पदार्थाची संवाहकता काढावयाची असेल त्याची एक लांब पट्टी घेतात. तिचे एक टोक उष्ण करण्यासाठी वितळलेले शिसे किंवा चांदी यामध्ये बुडविलेले असते. या पट्टीमध्ये भोके पाडून त्यांमध्ये तपमापके बसविलेली असतात. चांगला संपर्क साधण्यासाठी पाऱ्याचा उपयोग करतात. पट्टी जसजशी उष्ण होईल तसतशी उष्णता प्रारणाने बाहेर पडू लागते. काही वेळाने स्थिर स्थिती प्राप्त होऊन तपमापके स्थिर तपमान दाखवू लागतात. यावरून तपमान चढ-उतार (त१–त२) / ड काढता येतो. दर सेकंदाला प्रारित होणारी उष्णता उ / ट काढण्यासाठी त्याच पदार्थाचा एक नमुनावजा तुकडा घेऊन त्याचे तपमान वाढवतात व मग त्याची थंड होण्याची त्वरा घड्याळाचा उपयोग करून काढतात. थंड होण्याची त्वरा, पदार्थाची विशिष्ट उष्णता (१ ग्रॅम पदार्थाचे तपमान १० से. ने वाढविण्यास लागणारी उष्णता) व नमुना तुकड्याचा भार यावरून उ / ट काढता येते. नंतर फूर्ये समीकरणावरून क चे मूल्य काढता येते.
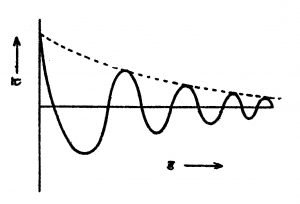
अँगस्ट्रॉम यांची पद्धती : (आवर्ती प्रवाह पद्धती). या पद्धतीत पट्टीचे एक टोक एका बंद पेटीत असते. या पेटीत प्रथम वाफ सोडून पट्टीचे टोक उष्ण करता येते, नंतर पेटीत पाणी सोडून पट्टीचे टोक थंड करता येते. याप्रमाणे आवर्तनाने पट्टीचे टोक उष्ण व थंड करून अँगस्ट्रॉम यांनी पट्टीवरील निरनिराळ्या बिंदूंंचे तपमान ठराविक वेळेच्या अंतराने मोजले. पट्टीचे टोक तापविण्याची क्रिया १२ मिनिटे व थंड करण्याची क्रिया १२ मिनिटे चालू ठेवली होती. याप्रमाणे २४ मिनिटांचे एक आवर्तन घेतले होते. बिंदूंचे टोकापासूनचे अंतर ड व त्यांचे तपमान त यांचा आलेख आकृतीमध्ये दाखविला आहे. पट्टीवरील कोणत्याही दोन बिंदूंचे तपमान दर मिनिटाला पाहून त्यावरून फूर्ये समीकरणाच्या साहाय्याने संवाहकता मिळते. या पद्धतीने पृथ्वीच्या भागाची संवाहकता काढता येते. सूर्याच्या उन्हामुळे पृथ्वीचा पृष्ठभाग दिवसा तापतो व रात्री थंड होतो. त्यामुळे पृष्ठभागाखालील तपमानातही बदल होत असतो. आवर्त-काल एक दिवसाचा असतो, त्यामुळे निर्माण होणाऱ्या उष्णता तरंगांना दैनंदिन तरंग म्हणतात. याशिवाय उन्हाळ्यात हिवाळ्यापेक्षा पृष्ठभाग जास्त तापत असल्याने वार्षिक तरंगही निर्माण होतात. हे तरंग जवळजवळ सरल हरात्मक (ज्या तरंगांचे स्वरूप, एखाद्या बिंदूची वर्तुळावरील एकसारखी गती वर्तुळाच्या व्यासावर प्रक्षेपित करून दखविता येते असे) असतात व ते पृथ्वीच्या अंतर्भागाकडे जातात. या तरंगांचे समीकरण सोडवून त्यावरून कोणत्याही ठिकाणच्या तपमानातील फेरफार काढता येतात. त्याचप्रमाणे तरंगाची लांबी, वेग व परमप्रसर (स्थिर स्थितीपासून लंब दिशेने होणारे कमाल स्थानांतर) हे काढता येतात. तपमापकाच्या साहाय्याने पृष्ठभागाखालील निरनिराळ्या अंतरांवरील बिंदूंचे तपमान मिळते. या सर्व माहितीवरून पृष्ठभागाची संवाहकता काढता येते. भूविज्ञानामध्ये अँगस्ट्रॉम पद्धतीचा बराच उपयोग होतो.
वरील आलेखात उष्णता तरंग दाखवले आहेत. तरंगाचा परमप्रसर ड च्या वाढत्या मूल्याबरोबर कमी होत जातो. दैनंदिन तरंगाचा वेग बराच असतो, त्यामुळे दिवसा घराचे छप्पर तापले तरी खोल्या थंड राहतात. याउलट सायंकाळी छप्पर थंड होऊ लागते आणि खोल्या गरम राहतात, कारण भिंतीतून उष्णता तरंग बाहेर पडू लागतात.
बदलत्या प्रवाहाची पद्धती : नॉयमान यांनी ही पद्धत अमलात आणली. या पद्धतीत पट्टीचे एक टोक तापवतात व नंतर ते आपोआप थंड होऊ देतात. नंतर टोकाच्या व टोकापासून काही अंतरावर असलेल्या दुसऱ्या एका बिंदूच्या तपमानात होणारे बदल व त्याकरिता लागणारा वेळ पाहून त्यावरून पट्टीची संवाहकता काढता येते. याकरिता वापरलेली सूत्रे बरीच क्लिष्ट आहेत. किरखोफ व हॅन्समान यांनी घनाकार (सहा प्रतलांनी बंदिस्त असलेल्या, क्यूब) पदार्थाच्या बाबतीत ही पद्धत वापरली. शुल्टसे, ग्रुनॅझेन व गिबे यांनी ही पद्धती बरीच सोपी केली, तसेच आकडेमोडही पुष्कळ कमी केली.
या पद्धतीचा महत्त्वाचा उपयोग म्हणजे तिच्या साहाय्याने पृथ्वीची निर्मिती केव्हा झाली आसावी ह्यासंबंधी अनुमान काढता येते. भूविज्ञानीय सिद्धांतानुसार सुरुवातीला पृथ्वी अतिशय उष्ण असल्याने द्रवरूप असावी अशी एक कल्पना होती. त्या द्रवाला शीलारस म्हणतात. नंतर ती थंड होत गेल्याने घनरूप बनली. द्रवरूप पृथ्वीचे तपमान साधारण ३,९००० से. असावे. पृथ्वी थंड होण्याची क्रिया घनरूप बनल्यानंतरही सुरूच राहिली. पृथ्वीचे आयुष्य ती घनरूप बनल्यापासून मोजतात. केल्व्हिन यांनी पृथ्वीची संवाहकता व तिच्या पृष्ठभागावरील सध्याचा तपमानाचा चढ-उतार यांवरून तिचे वय काढले. त्यांच्या आकडेमोडीवरून पृथ्वीचे वय अंदाजे १,००० लक्ष वर्षे असल्याचे दिसून आले.
विद्युत् पद्धती : या पद्धतींपैकी डॉन डसन पद्धतीत पदार्थाची एक कांब वापरतात. कांबीच्या एका टोकाला विद्युत् प्रवाहाने उष्णता दिलेली असते व दुसरे टोक एका अखंड-प्रवाह जल-उष्णतामापकामध्ये असते. उष्णतामापकामध्ये जाणाऱ्या व मापकातून बाहेर पडणाऱ्या पाण्याचे तपमान दोन तपमापके मोजतात. कांबीभोवती त्याच पदार्थाचे नळकांड्याच्या आकाराचे संरक्षक कडे असते. याचेही एक टोक त्याच विद्युत् प्रवाहाने उष्ण केलेले असते व दुसरे टोक दुसऱ्या एका तशाच पाण्याच्या प्रवाहाने थंड केलेले असते. यामुळे कोणत्याही पातळीमधील कांबीचे तपमान व नळकांड्याचे तपमान सारखे होते व त्यामुळे कांबीच्या बाजूंनी उष्णता प्रारण होत नाही आणि तपमान चढ-उतार फक्त कांबीच्या अक्षाच्या दिशेनेच होतो. तपयुग्मे तपमापके म्हणून वापरून तपमान चढ-उतार मिळतो. तसेच वापरलेल्या विद्युत् ऊर्जेवरून, जूल यांचा नियम वापरून कांबीला दिलेली उष्णता काढता येते. नंतर फूर्ये समीकरणाने पदार्थाची संवाहकता काढता येते.
लीज यांनी ही पद्धती कुसंवाहक पदार्थाची संवाहकता काढण्यासाठी वापरली. तसेच द्रव हवेच्या तपमानात धातूंची संवाहकता काढण्यासाठीही त्यांनी ही पद्धती वापरली.
होंडा व सिमिडू या जपानी संशोधकांनी एक अतिशय सोपी पण उपयुक्त पद्धती वापरली. या पद्धतीत एकाच पदार्थाच्या दोन एकसारख्या तबकड्या वापरलेल्या असतात व त्यामध्ये विद्युत् तापक असतो आणि त्यापासून दोन्ही तबकड्यांना सारखीच उष्णता मिळते. तबकड्यांच्या बाहेरच्या बाजूस कमी पण स्थिर तपमान असलेल्या आणथी दोन तबकड्या असतात. फूर्ये यांच्या समीकरणाने तबकड्यांची संवाहकता मिळते.
कुसंवाहक पदार्थाची संवाहकता : ही मोजण्यासाठी लीज यांची पद्धती वापरतात. या पद्धतीत पितळेच्या दोन एकसारख्या तबकड्या एकमेकींवर ठेवलेल्या असतात. या प्रत्येकीत एकेक तपमापक असतो. या दोन तबकड्यांमध्ये ज्या पदार्थाची संवाहकता काढावयाची असेल, त्या पदार्थाची तेवढ्याच त्रिज्येची एक पातळ (जाडी ढ) तबकडी ठेवलेली असते. पितळेच्या वरील तबकडीवर एक पेटी असते. या पेटीतून वाफ खेळवून वरील तबकडीचे तपमान वाढवता येते. वाफेऐवजी विद्युत् प्रवाहही वापरता येतो. मधील तबकडी कुसंवाहक असली, तरी पितळेच्या दोन्ही तबकड्यांच्या तपमानात फरक (त१–त२) दिसून येतो. यावरून तपमान चढ-उतार (त१–त२)/ड मिळतो. प्रयोगाच्या या भागाला स्थितिक भाग म्हणतात.
स्थिर स्थिती प्राप्त झाल्यानंतर वरील तबकडीला जेवढी उष्णता मिळते तेवढीच खालील तबकडीपासून प्रारणाने बाहेर पडते, हे उघड आहे. प्रारणाने जाणारी ही उष्णता उ काढण्याचे काम प्रयोगाच्या गतिमान भागात केले जाते. या प्रयोगासाठी फक्त खालची तबकडी लागते. तिचे तपमान १०० से. ने वाढवून (त२ + १००) नंतर ती त२ पेक्षा १०० से. कमी तपमान होईपर्यंत थंड होऊ देतात. वेळ व तपमान ठराविक अंतराने पाहून वेळ ट व तपमान यांचा आलेख काढतात. आलेखावरून तबकडीची थंड होण्याची त्वरा थ मिळते. समजा या तबकडीचे वजन म आहे, तिची विशिष्ट उष्णता व आहे. जाडी ज आहे व त्रिज्या त्र आहे. मग दर सेकंदाला प्रारणाने बाहेर पडणारी उष्णता पुढील समीकरणाने मिळते :
| उ | = म × व × थ | ( | π त्र२ × २ π त्र ज | ) | |
| ट | २ π त्र२ + २ π त्र ज |
गतिमान भागामध्ये तबकडीच्या दोन्ही बाजूंनी प्रारण होते, तर स्थितिक भागामध्ये ते एकाच बाजूने होते. त्यामुळे वरील समीकरणातील कंसातील राशी येते. कुसंवाहक तबकडीचे क्षेत्रफळ क्ष असेल, तर फूर्ये समीकरणाने तिची संवाहकता मिळते.
याशिवाय कुसंवाहक पदार्थाची संवाहकता काढण्याचा अनेक पद्धती आहेत. सर्व पद्धतीत फूर्ये समीकरणाचाच उपयोग होतो. उदा., रबराची संवाहकता काढण्यासाठी रबरी नळी उष्णतामापकामधून नेऊन तीमधून बाष्प सोडतात. संवहनाने उष्णतामापक व त्यामधील पाणी यांना उष्णता मिळते आणि त्यांचे तपमान वाढते. यावरून रबराची संवाहकता काढता येते. काचेची संवाहकता काचेची नलिका वापरून मिळते. ही नलिका एका बाष्पपेटीत ठेवलेली असते व तिच्यातून कायम दाबाखाली पाण्याचा स्थिर प्रवाह सोडतात. काचेतून संवाहित होणारी उष्णता पाण्याला मिळते व त्याचे तपमान वाढते. नळीत शिरताना व नळीतून बाहेर पडताना पाण्याचे तपमान मोजतात व त्यावरून काचेची संवाहकता मिळते.
घन पदार्थांच्या संवहनाचे उपयोग : संवहनाचे अनेक उपयोग आहेत. एखादा पदार्थ शिजविण्यासाठी भांड्यात ठेवून आपण भांड्याला उष्णता देतो. संवहनानेच ती पदार्थाला मिळते. भांडे जर सुसंवाहक नसेल, तर बरीच उष्णता प्रारणाने फुकट जाईल. उष्ण पदार्थ उचलण्यासाठी जी सांडशी आपण वापरतो तिचा दांडा लाकडासारख्या कुसंवाहक प्रदार्थाचा असल्याने हाताला चटका बसत नाही. याप्रमाणे सुसंवाहक व कुसंवाहक पदार्थांचे अनेक उपयोग रोजच्या व्यवहारात आपण करतो. आणखी कiही उपयोग खाली दिले आहेत.
डेव्ही संरक्षक दिवा : एखाद्या ज्योतीवर तांब्याची जाळी ठेवली असता ज्योत जाळीच्या वर येत नाही, कारण तांबे सुसंवाहक असल्याने जाळीवरील वायूचे तपमान ज्वलनबिंदूपर्यंत वाढत नाही. खाणींमध्ये निर्माण होणाऱ्या धोकादायक वायूंच्या अस्तित्वाची सूचना देणारा डेव्ही यांचा संरक्षक दिवा याच तत्त्वावर आधारलेला आहे.
थर्मॉस पात्र (देवार पात्र) : ही एक दुहेरी भिंत असलेली काचेची बाटली असून तिच्या भितींमधील जागा निर्वात केलेली असते. भिंतींचे समोरासमोरचे पृष्ठभाग चकचकीत केलेले असतात. काच कुसंवाहक असल्याने व काचेच्या दोन्ही भिंतींमधील जागा निर्वात केल्याने उष्णतेचे संवहन अथवा संनयन (उष्ण कणांचा प्रवाह थंड कणांकडे जाऊन उष्णता वाहणे) होत नाही. शिवाय काचेचे पृष्ठभाग चकचकीत केल्यामुळे उष्णतेचे प्रारणही होत नाही. यामुळे बाटलीच्या आतील पदार्थाचे तपमान बराच वेळ कायम राहू शकते.
द्रव पदार्थाची संवाहकता : द्रवाची संवाहकता काढणे घन पदार्थाइतके सोपे नाही. कारण द्रवामध्ये संवहनाबरोबर उष्णतेचे संनयनही होत असते. या कारणास्तव द्रवांची संवाहकता काढताना संनयन टाळणे आवश्यक आहे. हे दोन प्रकारांनी साधता येते. (१) द्रव पदार्थ वरील बाजूसच तापवायचा किंवा (२) द्रव पदार्थाचा अगदी पातळ थर वापरावयाचा. या दोन्ही प्रकारांनी द्रवांची संवाहकता काढता येते.
पहिला प्रकार : या प्रकारात द्रव एका नलिकेत घेऊन नलिकेला वरील बाजूने उष्णता देतात व द्रवस्तंभाच्या निरनिराळ्या उंचीवर तपमापके वापरून तपमान मोजतात. नंतर फूर्ये समीकरणाने द्रवाची संवाहकता काढता येते. वेबर यांनी स्तंभाच्या वरील बाजूस उष्णता देण्यासाठी विद्युत् प्रवाहाने तापवलेल्या तेलाचा उपयोग केला होता. स्तंभाभोवती संरक्षक कडे वापरले होते व स्तंभाचा तळभाग बर्फाच्या साहाय्याने थंड केला होता. संवहनाने बर्फाला उष्णता मिळून बर्फ वितळतो.
दुसरा प्रकार : लीज, मिल्नर वगैरेंनी द्रवाचा पातळ थर वापरून संवाहकता काढली. द्रव कुसंवाहक असल्याने लीज यांची पद्धती कुसंवाहक घन पदार्थासाठी वापरलेल्या पद्धतीसारखीच आहे. या पद्धतीत दोन तांब्याच्या तबकड्यांमध्ये द्रवाचा पातळ थर असतो. द्रव स्थिर रहावा म्हणून एक एबोनाइटाची चकती वापरतात. तांब्याच्या वरील तबकडीवर एक काचेची तबकडी व त्यावर पुन्हा दोन तांब्याच्या तबकड्या असतात व त्यांच्यामधून उष्णता निर्माण करणारी विद्युत् वाहक तार नेलेली असते. द्रवाखालील व वरील तबकड्यांचे तपमान मोजण्यासाठी तपयुग्माची योजना केलेली असते. यावरून जर काचेची संवाहकता माहीत असेल, तर द्रवाची संवाहकता काढता येते.
वायूची संवाहकता : वायूंमध्ये उष्णतेचे संक्रमण संवहन, संनयन व प्रारण या तिन्ही प्रकारांनी होते. त्यामुळे वायूंची संवाहकता काढणे अधिकच कठीण होते. कुंट व वॉरबर्ग यांनी असे सिद्ध केले की, हवेच्या किंवा वायूंच्या दाबाचा संवाहकतेवर फारसा परिणाम होत नाही परंतु संनयनावर मात्र होतो. अर्थातच, वायूचा दाब अतिशय कमी केला असता संनयन जवळजवळ होतच नाही व उष्णता फक्त संवहन व प्रारण यांनीच संक्रमित होऊ शकते. भांड्यातील जवळजवळ सर्वच वायू काढून टाकला असता फक्त प्रारणानेच उष्णतेचे संक्रमण होऊ शकते. यावरून या दोन्हीतील फरकाइतकी उष्णता संवहनाने संक्रमित होते हे उघड आहे.
अशा रीतीने संवाहित होणारी उष्णता काढून फूर्ये समीकरणाने वायूंची संवाहकता काढता येते. याशिवाय वायूचा पातळ थर वरील बाजूने तापवूनही द्रवाप्रमाणेच वायूची संवाहकता काढता येते. वायूंची संवाहकता दर्शविणारा एक सोपा प्रयोग पुढीलप्रमाणे करता येईल. एका काचेच्या नलिकेतून प्लॅटिनमाची एक बारीक तार न्यावी व त्यातून विद्युत् प्रवाह सोडावा. नलिकेमध्ये कोणताही वायू भरण्याची सोय असावी. प्रथम हवा ठेवूनच प्रयोग करावा. तार तापून प्रकाशित झालेली दिसेल. नंतर नलिकेतील हवा काढून हायड्रोजन वायू भरावा व पुन्हा प्रयोग करावा. आता तार प्रकाशित होणार नाही पण नलिका मात्र अधिक तापेल. यावरून असे दिसून येईल की, हवेपेक्षा हायड्रोजन वायू अधिक संवाहक असल्याने तो तारेपासून नलिकेकडे त्वरित उष्णता संवहन करतो. त्यामुळे तारेचे तपमान प्रकाशित होण्याइतके तापत नाही पण नलिका मात्र बरीच तापते.
वायूची संवाहकता काढण्याच्या पद्धती : अँड्रूज यांच्या पद्धतीमध्ये वायू एका नळकांड्यात घेऊन नळकांड्याच्या अक्षाबरोबर विद्युत् तार नेलेली असते. तारेमधील विद्युत् प्रवाहामुळे उष्णता निर्माण होऊन ती संवहनाने व प्रारणाने नळकांड्यास मिळते. नळकांड्यातील हवेचा दाब कमी ठेवल्यामुळे व तपमान चढ-उतार नळकांड्याच्या आडव्या छेदाच्या दिशेने होत असल्यामुळे उष्णतेचे संनयन होत नाही. प्रारणाने संक्रमित होणारी उष्णता नळकांड्यातील वायू अजिबात काढून टाकून मोजता येते. नंतर फूर्ये समीकरणाने वायूची संवाहकता मिळते. विद्युत् संपर्क साधण्यासाठी उपयोगात आणलेल्या जोडतारांतून संक्रमित होणाऱ्या उष्णतेबद्दल गणितात योग्य ती दुरुस्ती करावी लागते.
वायूचा पातळ थर वापरून संवाहकता काढण्याची पद्धती टॉड यांनी प्रथम अमलात आणली. नंतर त्यात हरकस व लॅबी यांनी सुधारणा केल्या. या पद्धतीत तांब्याच्या दोन तबकड्यांमध्ये वायू भरलेली पातळ तबकडी ठेवलेली असते. वरील तबकडीमधून विद्युत् तार नेलेली असते व खालील तबकडी पाण्याने थंड केलेली असते. प्रारणाने उष्णता संक्रमित होऊ नये म्हणून वरील तबकडीवर तांब्याचीच तेच तपमान असलेली आणखी एक तबकडी ठेवलेली असते. शिवाय संरक्षक कडेही वापरलेले असते. तपमान मोजण्यासाठी तपयुग्मांचा उपयोग केलेला असतो. संनयन टाळण्याकरता सर्वांत वरील तबकडीचे तपमान त्याखालील तबकडीपेक्षा किंचित जास्त ठेवतात. पण त्यामुळे थोडे प्रारण होते व त्यासाठी गणितात दुरुस्ती करावी लागते. ही दुरुस्ती केवळ पाच टक्के असते व ती देवार निर्वात काचपात्र वापरून स्वतंत्रपणे मोजता येते.
संदर्भ : 1. Gosh, S. N.; Deb, S. Heat, Calcutta, 1963.
2. Noakes, G. R. A Textbook of Heat, London, 1960.
देशपांडे, अ. शा.