चुंबकीय मंडले

चुंबकीय मंडले : विद्युत्‌ यंत्रातील वा उपकरणातील चुंबकीय स्रोताच्या (चुंबकीय रेषांच्या प्रवाहाच्या) सबंध मार्गाला चुंबकीय मंडल म्हणतात. या मंडलाचा बराचसा भाग लोखंडातून अथवा पोलादातून जातो व काही थोडा भाग हवेतून जातो. विद्युत् चलित्रामध्ये (विद्युत् शक्तीचा उपयोग करून यांत्रिक शक्ती उत्पन्न करणाऱ्या यंत्रामध्ये) किंवा विद्युत् जनित्रामध्ये (यांत्रिक शक्तीचा उपयोग करून विद्युत् शक्ती उत्पन्न करणाऱ्या यंत्रामध्ये) चुंबकीय स्रोताचा मार्ग चुंबकाच्या उत्तर ध्रुवापासून सुरू होऊन हवेच्या एका फटीतून आर्मेचराच्या (विद्युत् चालक प्रेरणा म्हणजे मंडलात विद्युत्‌ प्रवाह वाहण्यास कारणीभूत होणारी प्रेरणा उत्पन्न करणाऱ्या गुंडाळीच्या) पोलादी गाभ्यात जातो व पुन्हा हवेच्या दुसऱ्या फटीतून जाऊन चुंबकाच्या दक्षिण ध्रुवामध्ये शिरतो व तेथून यंत्राच्या बाहेरील पोलादी कड्यामधून आरंभस्थानाकडे येतो.

चुंबकीय मंडलाचे विद्युत् मंडलाशी बरेच साम्य आहे. विद्युत् मंडलात ज्याप्रमाणे प्रवाह निर्माण करण्यासाठी विद्युत् चालक प्रेरणा लागते, त्याचप्रमाणे चुंबकीय मंडलात चुंबकीय स्रोत निर्माण करण्यासाठी चुंबकीय चालक प्रेरणा (चुं. चा. प्रे.) लागते. अशी प्रेरणा चुंबकत्व सतत कायम टिकविणाऱ्या चिरचुंबकातून मिळू शकते किंवा सभोवती गुंडाळलेल्या तारेच्या वेटोळ्यातून विद्युत् प्रवाह जात असेपर्यंतच चुंबकीय शक्ती असणाऱ्या विद्युत् चुंबकातून मिळू शकते. चुंबकीय मंडलातील स्रोत φ, चुंबकीय चालक प्रेरणा व स्रोताच्या मार्गातील रोध R’ यांचे संबंध दाखविणारे सूत्र आणि विद्युत् मंडलातील प्रवाह I, विद्युत् चालक प्रेरणा E व रोध R यांचे संबंध दाखविणारा ओहम यांचा नियम यांचे स्वरूप अगदी सारखे आहे, म्हणजे φ = ^{चुं. चा. प्रे.}/_R’ हा संबंध I = ^E/_R यासारखा आहे. चुं. चा. प्रे. ही विद्युत् गुंडाळीमधील तारेच्या वेढ्यांची संख्या T व त्यांमधून जाणारा विद्युत् प्रवाह I यांच्या गुणाकाराबरोबर असते. ही अँपिअर-वेढे (AT) या एककात मोजतात. चुंबकीय रोध व विद्युत् रोध यांची सूत्रेही साधारणतः सारखीच आहेत. चुंबकीय रोध R’ = ¹/_μ · ^L/_a या समीकरणात μ = चुंबकीय पार्यता (चुंबकीय रेषांना आरपार जाऊ देण्याची पदार्थांची क्षमता), L= चुंबकीय स्रोताच्या मार्गाची लांबी व a = चुंबकीय स्रोत मार्गाच्या आडव्या छेदाचे क्षेत्रफळ आहे. पार्यता μ= μ₀ · μ_r.या समीकरणात μ_० =  हवा किंवा निर्वाताची पार्यता = ४ π  × १०^-७ हेन्‍री प्रतिमीटर आणि μ_r  = सापेक्ष पार्यता आहे.

विद्युत् आणि चुंबकीय मंडलातील साधर्म्यांमुळे चुंबकीय मंडलात येणाऱ्या एकापेक्षा अधिक रोधांचा परिणामी रोध काढण्याची सूत्रेही सारखीच आहेत. एकसरी (एकापुढे एक लावलेल्या) पद्धतीने जोडलेल्या R₁‘, R₂‘, R₃‘ या रोधांचा परिणामी ऱोध

R’ = R₁‘ + R₂‘ + R₃‘

या सूत्राने काढता येतो आणि अनेकसरी ( सर्व रोधांची एकेक टोके एकत्र जोडूल दुसरी टोके दुसऱ्या ठिकाणी एकत्र जोडण्याच्या) पद्धतीने जोडलेल्या रोधांना परिणामी रोध

या सूत्राने मिळतो किंवा S = ¹/_R’ असे मांडल्यास

S = S₁ + S₂ + S₃

या सूत्राने मिळतो . या सूत्रातील S या राशीला चुंबकीय पार्यता म्हणतात.

चुंबकीय आणि विद्युत् मंडलांतील फरक : प्रत्येक चिरचुंबकामध्ये प्रत्येक उत्तर ध्रुवाबरोबर दक्षिण ध्रुवही असतो आणि विद्युत् चुंबकीय स्रोताच्या बाबतीतही अशीच परिस्थिती असते, म्हणजे चुंबकीय स्रोताचे मंडल नेहमी पूर्ण बंदिस्त झालेले असते. विद्युत् मंडल खंडित करता येते, तसे चुंबकीय मंडल खंडित करता येत नाही. विविध पदार्थांच्या चुंबकीय पार्यतेमध्ये जरी फरक असला, तरी कोणताही पदार्थ चुंबकीय रेषांना रोखू शकणारा (निरोधक) नाही. हवेच्या फटीमुळे चुंबकीय मंडलातील रोध पुष्कळ वाढतो. त्यामुळे सर्व चुंबकीय मंडलात हवेची फट शक्य तितकी लहान ठेवतात. काही चुंबकीय स्रोत आर्मेचराच्या पोलादी गाभ्यातून न जाता हवेतूनच उत्तर ध्रुवाकडून परस्पर दक्षिण ध्रुवाकडे जातो त्यामुळे चुंबकीय मंडलाचे गणित करताना पोलादी गाभ्याबाहेरूनच गळून जाणाऱ्या झिरप स्रोताचाही विचार करावा लागतो. चुंबकीय रोध स्रोत घनतेप्रमाणे बदलतो. विद्युत् प्रवाह हा ज्याप्रमाणे इलेक्ट्रॉनांचा प्रवाह असतो, तसा चुंबकीय स्रोत हाही चुंबकीय रेषांचा प्रवाहच असतो. चुंबकीय स्रोत उत्पन्न करताना जी ऊर्जा खर्च करावी लागते, ती स्रोत नाहीसा होताना परत मिळू शकते.

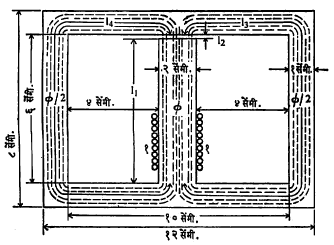
चुंबकीय मंडलांचे गणित : चुंबकीय मंडलात पाहिजे तितकी स्रोत घनता मिळण्यासाठी लागणारी एकंदर प्रेरणा मोजण्याकरिता प्रथम मंडलाच्या निरनिराळ्या भागांकरिता लागणारी प्रेरणा वेगवेगळी मोजतात व त्या सर्वांवरून एकूण परिणामी राशी काढतात.

आ. १ मधील चुंबकीय मंडल २०० सापेक्ष पार्यता व १ सेंमी. जाडी असलेल्या ओतीव लोखंडाचे असून मधल्या शाखेवर एक मिमी. रुंदीच्या फटीमध्ये ०·१ मिलिवेबर स्रोत उत्पन्न करावयाचा आहे. तर त्याकरिता किती अँपिअर-वेढ्यांची चुं. चा. प्रे. लागेल, हे काढावयाचे आहे. या मंडलात मधल्या शाखेमध्ये व फटीमध्ये φ स्रोत आहे. नंतर या स्रोताचे दोन समांतर भाग होतात. या 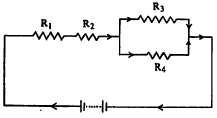दोन्ही भागांची लांबी व त्यांच्या छेदाचे क्षेत्रफळ सारखे असल्याने त्या प्रत्येकातून φ/२ इतका स्रोत आहे. या चुंबकीय मंडलासमान विद्युत् मंडल आ. २ मध्ये दाखविले आहे. मंडलातील एकूण चुंबकीय रोध काढण्यासाठी खालील कोष्टक वापरले आहे. त्यामध्ये μ = μ₀ X μ_r, μ₀ = ४ π X १०^-७ हेन्ऱी प्रतिमीटर, μ_r = २०० आहेत. l₃ व l₄ या समांतरमार्गाचा एकूण

चुंबकीय रोध  R₅‘ = ३·५७ X १०^६ व मंडळाचा एकूण चुंबकीय रोध

R’ = R₁‘ + R₂‘ + R₅‘  = ८·७२ X १०^६

आहे. स्रोत φ =  ०.१ मिलिवेबर = १०^-४ वेबर आहे म्हणून त्याकरिता लागणारी चुं. चा. प्रे. =स्रोत × रोध = १०^-४ X ८.७२ X १०^६ = ८७२ अँपिअर-वेढे असेल. या उदाहरणात झिरप स्रोत नाही असे गृहीत धरलेले आहे.

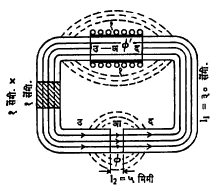
झिरप स्रोत असेल अशा मंडलातील चुं. चा. प्रे. काढण्याची पद्धत खालील उदाहरणामध्ये दाखविली आहे. (आ. ३). यामध्ये उपयुक्त स्रोत अखंड रेषांनी व झिरप स्रोत तुटक रेषांनी दाखविला आहे. झिरप स्रोतामुळे आ या फटीतील उपयुक्त स्रोत ( φ ) हा गुंडाळीच्या मध्यभागी असलेल्या एकूण स्रोतापेक्षा ( φ‘ पेक्षा) कमी असतो. म्हणून आ येथे जर स्रोत पाहिजे असेल. तर अ येथे थोडा जास्त φ‘ स्रोत उत्पन्न केला पाहिजे. अ आणि आ येथील स्रोतांमध्ये जे गुणोत्तर असते, ते कड्याची पार्यता व सभोवतालच्या वातावरणातील पार्यता यांवर अवलंबून असते. φ‘/φ या गुणोत्तराला झिरप गुणक म्हणतात. आ. ३ मधील कड्याची लांबी l₁ = ३० सेंमी. = ^३०/_१०२ मी. आहे.  कड्याच्या काटछेदाचे क्षेत्रफळ a = ^१/_१०^४ चौ. मी. आहे. μ_r = १५० आहे. म्हणून μ = μ₀ X μ_r  = ^{४ π} / _१०^७ X १५०, उपयुक्त स्त्रोत φ = ०·०५ मिलिवेबर आहे. झिरप गुणक १·४ धरला आहे.

कड्यातील चुंबकीय रोध

कड्यातील एकंदर स्त्रोत φ‘ = उपयुक्त स्रोत X झिरप गुणक

      = ०·०५ X १·४

      =  ०·०७ मिलिवेबर

कड्याकरिता लागणारी

 चुं. चा. प्रे. = R1′ φ‘

       = १५·९ X १०^६ X ०·०७ X १०^-३

       = १,११३ अँपिअर-वेढे… …(१)

आ फटीचा रोध R₂‘ =  ^l₂/μ₀ a

l₂ = ^०·५/_१०^२ मी. μ₀ = ^{४ π} X _१०^७ a = ^१/_१०^४ चौ. मी. 

आ फटीतील स्रोत = ०.०५ मिलीवेबर

आ फटीकरिता लागणारी

    चुं. चा. प्रे. = R₂‘ φ‘

 = ३९·८ X १०^६ X ०.०५ X १०^-३

 = १,९९० अँपिअर-वेढे… …(२)

म्हणून एकंदर मंडलास लागणारी चुं . चा. प्रे. = (१) + (२)

= १,११३ +१,९९० = ३,१०३ अँपिअर-वेढे.

स्रोत घनता व पार्यता यांतील संबंध : चुंबकीय मंडल आणि विद्युत् मंडल यांतील मुख्य फरक म्हणजे विद्युत् संवाहकाच्या संवाहकतेप्रमाणे चुंबकीय पदार्थाची पार्यता (आणि त्यावर अवलंबून असलेला रोध) स्थिर नसून त्यामध्ये निर्माण झालेल्या स्रोत घनतेनुसार बदलते.

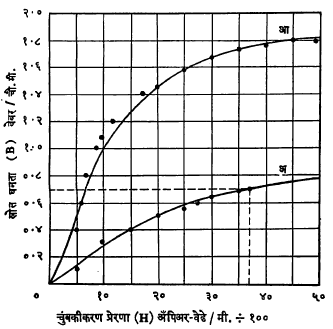लोखंड आणि पोलाद यांची पार्यता त्यांच्या प्रकारानुसार निरनिराळी असते, परंतु ती हवेच्या पार्यतेपेक्षा बरीच जास्त असते. सर्वसाधारणतः स्रोत घनता जशी वाढत जाते तशी पार्यता कमी होते. आ. ४ मध्ये दिलेल्या आलेखात य अक्षावर स्रोत घनता (वेबर/चौ.मी.) व क्ष अक्षावर स्रोत घनतेला लागणारी चुंबकीकरण प्रेरणा (चुं. प्रे. अँपिअर-वेढे / मंडलाची लांबी, मी.) दाखविली आहे. या आलेखावरून दिलेल्या चुंबकीय पदार्थात दिलेली स्रोत घनता निर्माण करण्यासाठी किती चुं. प्रे. लागेल ते काढता येते. उदा., आ. ३ मधील कड्यातील स्रोत घनता ०·७ वेबर/ चौ.मी. आहे. ओतीव लोखंडाच्या आलेखावरून (आ.४) या स्रोत घनतेकरिता लागणारी चुं. प्रे. ३,७१० अँपिअर-वेढे/मी. आहे. म्हणून लोखंडातील ३० सेंमी लांबीकरिता १,११३ अँपिअर-वेढे लागतील. ज्या यंत्रभागात चुंबकीय स्रोत बदलत असतो (उदा., प्रत्यावर्ती म्हणजे उलट सुलट दिशेने वाहणाऱ्या विद्युत् प्रवाहामुळे), त्याच्या बाबतीत गणित करताना मंदायन (लोखंडी वा पोलादी भागावर बदलते चुंबकीय क्षेत्र लावले असता त्यामध्ये चुंबकीकरण होण्यास लागणारा विलंब) व आवर्त प्रवाह (बदलत्या चुंबकीय स्रोतामुळे संवाहक पदार्थात निर्माण होणारे स्थानिक विद्युत् प्रवाह) यांच्या परिणामांचाही विचार करावा लागतो. चुंबकीय स्रोत बदलत असला म्हणजे मंदायनामुळे लोखंड किंवा पोलादी भागामध्ये उष्णता निर्माण होते व शक्तीचा क्षय होतो. हा क्षय त्या वस्तूच्या मंदायन वक्रातील (चुंबकीकरण प्रेरणा व स्रोत घनता यांतील संबंध दाखविणाऱ्या वक्रातील) बंदिस्त क्षेत्रफळांवरून किंवा स्टाइनमेट्स यांच्या

^P(मंदायन क्षय)= η f V B ^1·6 × 10^-7 वॉट

या आनुभविक समीकरणाने काढता येतो. त्यामध्ये P = शक्तिक्षय, η = स्टाइनमेट्स गुणक,  f = कंप्रता (प्रत्यावर्ती विद्युत्‌ प्रवाहाची दर सेकंदातील आवर्तन संख्या), V = गाभ्याचे घनफळ (सेंमी.^३), B = स्रोत घनता/ चौ.सेंमी. आहे. η चे मूल्य चुंबकीय पदार्थाच्या द्रव्यावर अवलंबून असते.

लोखंड व पोलाद विद्युत् संवाहक असल्यामुळे बदलत्या स्रोतामुळे त्यांमध्ये आवर्त प्रवाह निर्माण होतात. या प्रवाहामुळे निर्माण झालेल्या उष्णतेमुळेही शक्तिक्षय होतो. हा क्षय स्रोत घनता (B), कंप्रता (f) व लोखंडी पत्र्याची जाडी (d) यांच्या वर्गाच्या सम प्रमाणात आणि पत्र्याच्या द्रव्याच्या रोधकतेच्या (ρ) वर्गाच्या व्यस्त प्रमाणात असतो.

चुंबकीय मंडलात निरोधक रंग लावलेले पातळ पत्रे वापरून आवर्त प्रवाहामुळे होणारा शक्तिक्षय पुष्कळ कमी करता येतो.

संदर्भ : 1. Dawes, C. L. Electrical Engineering, Vol. I, New York, 1955.

           2. Meares, J. W. Neale, R. E. Eletrical Engineering Practice, London, 1958.

           3. Pumphrey, F. H. Fundamentals of Electrical Engineering, Engelwood Cliffs, N. J., 1960.

पेंढारकर, चं. तु.

“