पराशय

पराशय : निरीक्षकाचे स्थान बदलले असता निरीक्षकापासून वेगवेगळ्या अंतरावर असणाऱ्या दोन वस्तूंमध्ये एकमेकांच्या संदर्भात जे भासमान स्थानांतर होते त्याला पराशय असे म्हणतात. आगगाडीतून प्रवास करीत असताना, दूरच्या डोंगरांच्या संदर्भात नजीकची झाडे गाडीच्या वेगाच्या उलट दिशेने जात आहेत असा भास होतो, तर त्या झाडांच्या संदर्भात डोंगर, गाडीच्या वेगाच्याच दिशेने जात आहेत असे भासते. हे पराशयाचे नेहमीच्या अनुभवाचे उदाहरण आहे.

उपकरणीय पराशय : लंघक तंतू (ज्यांच्या प्रतलात प्रतिमा मिळवावयाची असते असे एकमेकांना काटकोनात असलेले दोन केसांसारखे सूक्ष्म तंतू) बसविलेल्या दूरदर्शकातून किंवा सूक्ष्मदर्शकातून पहाताना वस्तूची प्रतिमा लंघक तंतूंच्या प्रतलात नसेल, तर निरीक्षकाने आपले डोके थोडे डावी-उजवीकडे हलविल्यास वरीलप्रमाणेच प्रतिमा व लंघक तंतू यांच्यामध्ये स्थानांतर झाले असे वाटते. व्हर्नियर पट्टी व मुख्य पट्टी [→ व्हर्नियर] यांची प्रतले वेगळी असतात. त्याचप्रमाणे तापमापकातील पारा व त्याच्यावर आरेखित केलेली मोजपट्टी यांचीही प्रतले भिन्न असतात. त्यामुळे त्यांच्या वाचनात पराशयामुळे काही त्रुटी येऊ शकते. त्या दोहोंच्या प्रतलांना दृष्टिरेषा लंब ठेवून वाचन केल्यास ही त्रुटी येत नाही. गॅल्व्हानोमीटर, विद्युत् मापक, घड्याळ, इत्यादींच्या वाचनाच्या बाबतीतही हेच तत्त्व अनुसरणे आवश्यक असते.

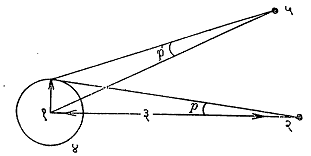
खगोलीय पराशय : एखाद्या खस्थ ज्योतीकडे दोन वेगळ्या स्थानांवरून पाहिल्यास त्या दोन दृष्टिरेषांमध्ये अंतरित होणाऱ्या कोनाला पराशय कोन किंवा पराशय असे म्हणतात. हा कोन नेहमी सेकंदात (अंशाचा १/३६० भाग) दिला जातो. दोन निरीक्षण स्थानांना जोडणाऱ्या रेषेला आधार रेषा किंवा पाया असे म्हणतात. पराशय (p) आधार रेषेच्या लांबीच्या (a) सम प्रमाणात असून त्या ज्योतीच्या अंतराच्या (r) व्यस्त प्रमाणात असतो, म्हणजेच p=a/r. यावरून r=a/p हे समीकरण वापरून त्या ज्योतीचे अंतर काढता येते आणि याचसाठी पराशय मोजला जातो.

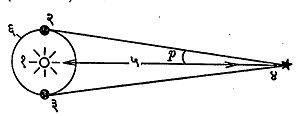
प्रकार : खगोलीय पराशय मोजण्यासाठी आधाररेषा पृथ्वीची त्रिज्या किंवा पृथ्वीचे सूर्यापासूनचे सरासरी अंतर घेण्याची वहिवाट आहे. आधार रेषा पृथ्वीची त्रिज्या घेतल्यास मिळणाऱ्या पराशयाला दैनिक किंवा भूकेंद्रीय पराशय असे म्हणतात. (आ.१). आधार रेषा पृथ्वीचे सूर्यापासूनचे सरासरी अंतर घेतल्यास मिळणाऱ्या पराशयाला वार्षिक किंवा सूर्यकेंद्रीय पराशय असे म्हणतात (आ.२). अती दूरच्या ताऱ्यांचे पराशय मोजण्यासाठी पृथ्वी व सूर्य यांमधील अंतरसुद्धा फार तोकडे पडते. एक वर्षात सू्र्य ( व त्याची ग्रहमाला) अती दूरच्या ताऱ्यांच्या संदर्भात, सूर्य–पृथ्वी अंतराच्या सु. चौपट अंतर तोडतो. या अंतराचा

आधार रेषा म्हणून उपयोग करून मिळणाऱ्या पराशयाला दीर्घकालीय पराशय असे म्हणतात (आ.३).

ताऱ्याचा पराशय त्रिकोणमितीय पद्धतीने मोजल्यास त्याला प्रत्यक्ष किंवा त्रिकोणमितीय पराशय असे म्हणतात. काही फार दूरच्या ताऱ्यांच्या बाबतीत त्रिकोणमितीय मापन अशक्य होते. तेव्हा त्यांचा पराशय (केव्हा केव्हा) वर्णपटीय पद्धतीने काढता येतो. या पद्धतीने काढलेल्या पराशयाला वर्णपटीय पराशय असे म्हणतात. कित्येक युग्म ताऱ्यांचे पराशय ( त्यांच्या आवर्तकालावरून म्हणजे समाईक द्रव्यमान केंद्राभोवती होणाऱ्या एका आवर्तनास लागणाऱ्या कालावरून) गतिकीच्या (प्रेरणा आणि तीमुळे निर्माण होणाऱ्या गतीचा अभ्यास करणाऱ्या शास्त्राच्या) सिद्धांताच्या उपयोगाने काढता येतात, त्याला गतिकीय पराशय असे म्हणतात.

पराशयावरून दूरच्या ज्योतीचे पृथ्वीपासूनचे अंतर (आधार रेषेची लांबी या एककामध्ये) मिळू शकते. म्हणून त्याच्या मापनाला ज्योतिषशास्त्रात फार महत्त्व आहे.

भूकेंद्रीय पराशय : हा पराशय फक्त सूर्यमालेत अंतर्भूत होणाऱ्या ज्योतींच्या बाबतीतच मोजणे शक्य होते. दूरच्या ताऱ्यांच्या बाबतीत त्याचे मूल्य इतके अल्प असते की, त्याचे यथायोग्य मापन अशक्यच होते. विशिष्ट ज्योती जेव्हा मापनस्थळाच्या क्षितिजावर असते तेव्हा त्या ज्योतीचा भूकेंद्रीय पराशय φ ( यालाच क्षैतिज पराशय असे म्हणतात) कमाल मूल्याचा असतो. ज्योती जशी खस्वस्तिकाजवळ (निरीक्षकाच्या डोक्यावरील खगोलावरील बिंदूजवळ) जाईल तसे तिच्या पराशयाचे मूल्य p’ (आ. १) कमी होत जाऊन ती खस्वस्तिकावर येईल तेव्हा p’ चे मूल्य  शून्य होते. म्हणून भूकेंद्रीय पराशय म्हणजे क्षैतिज पराशयच असे मानले जाते.

पृथ्वीला सर्वांत जवळची ज्योती म्हणजे चंद्र होय. त्याचा भूकेंद्रीय पराशय काढण्यासाठी (१) जवळजवळ एकच रेखावृत्तावरील परंतु परस्परांपासून खूप दूर अशा दोन वेधशाळांमधून एकाच वेळी चंद्राची आकाशातील दिशा निश्चित केली जोते. मग त्या दोन वेधशाळांचे अक्षांश व भूमापन यांवरून चंद्राचा भूकेंद्रीय पराशय काढता येतो किंवा (२) एकाच वेधशाळेतून चंद्राच्या दिशा दोन वेगवेगळ्या वेळी निश्चित केल्या जातात. मग पृथ्वीच्या स्वत:च्या अक्षाभोवतीच्या परिभ्रमणाचा वेग लक्षात घेऊन त्यावरून पराशय काढला जातो.

पृथ्वी ही संपूर्णपणे गोल नसल्याने वेगवेगळ्या दिशांनी तिच्या त्रिज्या वेगवेगळ्या येतात. यामुळे येणारी अनिश्चितता टाळण्यासाठी पृथ्वीच्या विषुववृत्तीय त्रिज्येचे सरासरी मूल्य नेहमी विचारात घ्यावे असा संकेत आहे. वरील पहिल्या पद्धतीने चंद्राचा पराशय प्रथम १८३७ मध्ये टी. हेंडरसन यांनी मोजला आणि त्याचे मूल्य त्यांना ५७’ २”·३  इतके मिळाले. चंद्रपृष्ठावरील एका विवराचा पराशय पुढे (१९०५–१० या काळात) मोजला असता त्यावरून चांद्र पराशय ५७’ २”·५ इतका मिळाला. हिपार्कस ( इ. स. पू. १५०) या प्राचीन ग्रीक ज्योतिषशास्त्रज्ञांनी चांद्र पराशयाचे मूल्य ५८’ इतके काढले होते.

ज्योतिषशास्त्रीय एकक : सूर्याच्या पराशयाच्या मापनावरून सूर्य व पृथ्वी यांच्या मधील सरासरी अंतर (वर दिलेल्या समीकरणाचा वापर करून) काढता येते. खगोलीय मापनावरून इतर सर्व ग्रह ताऱ्यांची अंतरे या सूर्य–पृथ्वी अंतराच्या पटीतच मिळू शकतात. म्हणून या अंतराला ज्योतिषशास्त्रीय एकक असे म्हणतात. त्याचे मूल्य जास्त अचूकपणे ज्ञात होणे फार महत्त्वाचे असल्याने विविध पद्धतींनी ते निश्चित केले गेले आहे.

सौर पराशय : चंद्राप्रमाणेच त्रिकोणमितीय पद्धती वापरून सूर्याच्या पराशयाचे प्रत्यक्ष मापन करता येईल. पण एक तर या पराशयाचे मुल्य कमी आहे आणि सूर्याच्या प्रखर तेजामुळे त्या पराशयाचे प्रत्यक्ष मापन करणे कठीण होते. यासाठी पृथ्वीनजीकचा शुक्र किंवा मंगळ यासारखा ग्रह किंवा ⇨ एरॉससारखा लघुग्रह यांचे पृथ्वीपासूनचे अंतर निश्चित करून त्यावरून अप्रत्यक्ष पद्धतीने ज्योतिषशास्त्रीय एककाचे मूल्य काढले जाते.

तीन ग्रहांचे सूर्यप्रदक्षिणाकाल T₁, T₂, T₃,···· इ. असतील व त्यांची सूर्यापासूनची अंतरे अनुक्रमे Q₁, Q₂, Q₃,···· इ. असतील, तर केप्लर यांच्या तिसऱ्या नियमानुसार [→ खगोलीय यामिकी]

इ. असे मांडता येईल. ग्रहांचे सूर्यप्रदक्षिणाकाल अचूकपणे मोजणे सहजच शक्य होते व म्हणून वरील समीकरण वापरून कोणत्याही दोन ग्रहांच्या सूर्यापासूनच्या अंतराचे गुणोत्तर सहज काढता येते. कोणत्याही एका ग्रहाचे सूर्यापासूनचे अंतर निश्चित झाल्यास त्यावरून इतर ग्रहांची अंतरे काढता येतील.

पृथ्वीला सर्वांत नजीक असलेल्या ग्रहाचे पृथ्वीपासूनचे अंतर प्रत्यक्ष पद्धतीने निश्चित करणे सोपे असते. त्यावरून सूर्य–पृथ्वी हे अंतर किंवा सौर पराशय अचूकपणे काढता येतो.

मंगळाचा पराशय मोजून त्यावरून सूर्याचा पराशय प्रथम १६७२ मध्ये काढण्यात आला. यावरून सौर पराशय ९”·५ आला. शुक्र पृथ्वीला मंगळापेक्षाही जास्त जवळ येऊ शकत असल्याने त्याचा पराशय जास्त अचूकपणे मोजणे शक्य असते व त्यावरून सौर पराशयाचे जास्त अचूक मूल्य मिळू शकते. ही सूचना प्रथम एडमंड हॅली यांनी १६७९ मध्ये केली. त्यानुसार १७६१ व १७६९ मध्ये शुक्राचे सूर्यबिंबावर ⇨ अधिक्रमण होताना त्याचा पराशय मोजण्यात आला. त्याचप्रमाणे १८७४ आणि १८८२ सालीही शुक्राच्या अधिक्रमणाच्या वेळी मापने करण्यात आली.

एरॉस हा लघुग्रह पृथ्वीला सर्वांत जवळ (४,८०,००,००० किमी.वर) आला त्या वेळी त्याचा पराशय मोजून त्यावरून सौर पराशय त्याहूनही अधिक अचूक निश्चित करता आला. हे मूल्य ८”·७९० + ०”·४०१ आले. यावरून ज्योतिषशास्त्रीय एककाचे मूल्य १४,८८,०८,००० किमी. आले.

रडार पद्धती : यात रडार स्पंद शुक्रावर सोडून त्याचा रडार प्रतिध्वनी पृथ्वीवर मिळण्यास लागणारा काल मोजण्यात आला. रडार तरंगांचा वेग (२,९९,७९२·५ किमी./से.) ज्ञात असल्याने यावरून शुक्राचे पृथ्वीपासूनचे अंतर काढता आले आणि त्यावरून काढलेले ज्योतिषशास्त्रीय एककाचे मूल्य १४,९५,९८,५०० + ५०० किमी. आले. हे मूल्य सर्वांत जास्त अचूक मानले जाते.

सूर्यकेंद्रीय पराशय : (तारकीय पराशय). तारे पृथ्वीपासून फारच दूर असल्याने पृथ्वीची त्रिज्या हे आधार अंतर घेतल्यास मिळणाऱ्या  

ताऱ्यांच्या पराशयाचे मूल्य मोजता न येण्याइतपत सूक्ष्म येते. हे मूल्य मापनीय होण्यासाठी पृथ्वीच्या सूर्याभोवतालच्या कक्षेची त्रिज्या हे

अधिक मोठे अंतर वापरले जाते. तरीही तारकीय पराशयांची मूल्ये फारच लहान येतात.

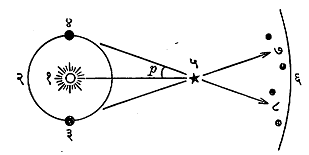
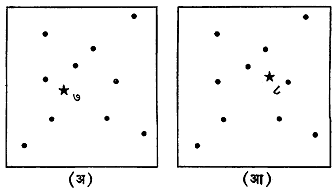
विशिष्ट ताऱ्याचा (सूर्यकेंद्रीय) पराशय मोजताना अती दूरच्या अंधुक ताऱ्यांचा पराशय शून्य आहे असे प्रथमारंभी मानतात आणि त्यांच्या संदर्भात इष्ट नजीकच्या ताऱ्याची भासमान स्थानच्युती मोजतात. आ. ४ व ५ वरून हे मापन कसे करतात हे समजू शकेल. एका विशिष्ट वेळी इष्ट ताऱ्याचे अती दूरच्या ताऱ्यांच्या पार्श्वभूमीवर एक छायाचित्र घेतले जाते. सहा महिन्यांनंतर पुन्हा तसेच छायाचित्र घेतले जाते. या दोन छायाचित्रांत इष्ट ताऱ्याचे स्थान पार्श्वभूमीवरील ताऱ्यांच्या संदर्भात किती ढळलेले दिसते त्याचे सूक्ष्ममापकाच्या साहाय्याने अचूक मापन केले जाते. पृथ्वीच्या दोन स्थानांपासून इष्ट ताऱ्याकडे जाणाऱ्या दृष्टिरेषांमधील कोन हा पराशयाच्या दुप्पट असतो (आ. ४ पहा) व त्याचे अरीयमानामध्ये [→ कोन] मूल्य पुढील समीकरणावरून मिळते.

मग त्यावरून पराशयाचे मूल्य (सेकंदात) काढणे सोपे असते.

प्रत्यक्ष मापन करताना केवळ दोनच छायाचित्रे घेऊन भागत नाही. थोड्या थोड्या कालानंतर पुन:पुन्हा छायाचित्रे घेऊन ज्या दोन स्थानांमध्ये ताऱ्याचे स्थानांतर कमाल असेल त्यावरूनच पराशयाचे मूल्य काढले जाते. दुसरी गोष्ट म्हणजे दूरच्या ताऱ्यांचेही अल्पसे स्थानांतर होतेच. त्यासाठी इष्ट ताऱ्याच्या स्थानांतराला शुद्धी करावी लागते. वातावरणीय प्रणमनासाठीही (प्रकाश एका माध्यमातून दुसऱ्या माध्यमात जाताना त्याच्या दिशेत होणाऱ्या बदलासाठीही) शुद्धी करणे आवश्यक असते.

पृथ्वी सूर्याभोवती फिरत असल्यास तारकीय पराशय दिसणे आवश्यक आहे. म्हणून या पराशयाचा शोध घेण्याचे अनेक प्रयत्न चालू होते. प्रथम १८३७ मध्ये एफ्. जी. डब्ल्यू. श्ट्रूव्हे यांनी अभिजित ताऱ्याचा पराशय मोजला. त्या पाठोपाठ हेंडरसन यांनी आल्फा-सेंटॉरी (नरतुरंगामधील सर्वांत ठळक तारा) या ताऱ्याचा आणि एफ्. डब्ल्यू. बेसेल यांनी हंस तारकापुंजातील ६१ सिग्नी या ताऱ्याचा पराशय मोजला.

आल्फा-सेंटॉरी हा तारा सूर्याला सर्वांत जवळचा तारा असल्याने त्याचा पराशय सर्वांत जास्त मोठा म्हणजे फक्त ०”·७६ इतकाच आहे. इतर ताऱ्यांचे पराशय अर्थातच याहून कमी आहेत. यावरून पराशय मोजण्याचे काम किती अवघड आहे, याची कल्पना येईल. आतापर्यंत सु. ६,००० ताऱ्यांच्या पराशयांची मापने करण्यात आलेली आहेत. पराशय मोजण्याच्या सर्वांत अचूक मापनातही संभाव्य त्रुटी + ०”·००८ आहे. त्यामुळे ०”·०१ पेक्षा कमी मूल्याच्या पराशयाचे बिनचूक मापन वर दिलेल्या पद्धतीने करणे अशक्यच होते.

प्रकाशमापनीय पद्धती : स्वयंप्रकाशित वस्तूचे निरीक्षकापासूनचे अंतर जसजसे वाढत जाते तसतसे तिचे भासमान दीप्तिमान कमी होत जाते. हीच गोष्ट ताऱ्यांची निरपेक्ष प्रत (M) व भासमान प्रत (m) यांना लागू आहे [→ प्रत]. या दोहोंमधील संबंध पुढील समीकरणाने दिला जातो.

M= m+5+5 log p.

ताऱ्याची भासमान प्रत प्रत्यक्ष निरीक्षणावरून काढता येते. कित्येकदा ताऱ्याची निरपेक्ष प्रत त्याच्या वर्णपटीय गटावरून अजमावता येते [→ तारा]. मग वरील समीकरण वापरून त्याचा पराशय अजमावणे शक्य होते. १०० पार्सेकपेक्षा (१ पार्सेक = २,०६,२६५ ज्योतिषशास्त्रीय एकक) अधिक दूर असणाऱ्या ताऱ्यांचे पराशय अनेकदा या पद्धतीने काढले जातात. या पद्धतीत आंतरतारकीय द्रव्यामध्ये होणाऱ्या शोषणामुळे पडणाऱ्या प्रतीतील फरकासाठी शुद्धी करणे जरूर असते.

वर्णपटीय पराशय : ताऱ्यांच्या वर्णपटानुसार त्यांचे O, B, A  इ. गटांत वर्गीकरण केले आहे. विशिष्ट वर्गातील जास्त दीप्तिमान पिवळ्या व तांबड्या ताऱ्यांचे तापमान त्याच वर्गातील कमी दीप्तिमानाच्या ताऱ्यांपेक्षा कमी असते. यामुळे त्यांच्या वर्णपटातील काही वर्णरेषांच्या तीव्रतेवर परिणाम होतो. आ. ६ मध्ये ताऱ्याची निरपेक्ष प्रत व त्याच्या वर्णपटातील स्ट्राँशियमाची ४२१५ A (A अँगस्ट्रॉम एकक = १० ^-८ सेंमी.) तरंगलांबीची (परिवर्तनशील) रेषा व त्याशेजारील लोहाच्या वर्णपटातील ४२६० A तरंगलांबीची रेषा (जिच्या तीव्रतेत प्रतीनुसार फरक पडत नाही) यांच्या तीव्रतांचे गुणोत्तर यांचा आलेख दाखविला आहे. ज्ञात निरपेक्ष प्रत असणाऱ्या ताऱ्यांच्यावरून

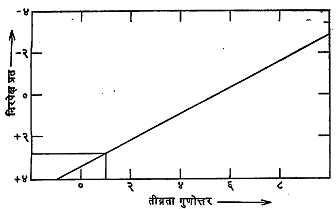
हा आलेख काढतात. मग अज्ञात ताऱ्याच्या वर्णपटातील वरील गुणोत्तराचे मापन करून या आलेखाच्या साहाय्याने त्याची निरपेक्ष प्रत काढतात. त्याची भासमान प्रत प्रत्यक्ष प्रयोगाने काढतात. मग M = m  + 5 + 5 log  p या समीकरणावरून त्याचा पराशय काढता येतो. मौंट विल्सन वेधशाळेतील ओ. सी. विल्सन आणि भारतीय खगोल भौतिकीविज्ञ एम्. के. व्ही. बाप्पू यांनी कॅल्शियमाच्या H व K वर्णरेषांच्या रुंदीवरून ताऱ्यांच्या निरपेक्ष प्रती काढण्याची एक नवीन पद्धत १९५९ मध्ये शोधून काढली. G, K व M गटांतील ताऱ्यांनाच ही पद्धत लागू पडते. त्यावरून काढलेल्या पराशयाच्या मूल्यात १० ते १५ पर्यंत त्रुटी येऊ शकते. या पद्धतीमुळे अधिक दूरच्या अनेक ताऱ्यांचे पराशय पूर्वीपेक्षा जास्त अचूकपणे काढता येऊ लागले आहेत.

गतिकीय पराशय : युग्म ताऱ्यांचे पराशय काढण्यासाठी या पद्धतीचा उपयोग होतो. अशा ताऱ्यांचे संयुक्त द्रव्यमान (m₁ + m₂) माहीत असल्यास त्यांचा आवर्तकाल P (वर्षे) व त्यांच्या कक्षेची सरासरी कोनीय त्रिज्या a (सेकंदात) मोजून त्यावरून त्यांचा पराशय पुढील समीकरणावरून काढता येतो.

p = ³√a³ / P² (m₁ + m₂)

हे समीकरण गतिकी व गुरुत्वाकर्षणाच्या नियमांवरून काढता येते. या पद्धतीने काढलेल्या पराशयाला गतिकीय पराशय असे म्हणतात.

दीर्घकालीय पराशय : आकाशगंगेच्या परिवलनामुळे सूर्यमालेला १९·५ किमी./से. इतका वेग प्राप्त होतो. यामुळे इतर ताऱ्यांना सूर्याच्या गतीच्या विरुद्ध गती प्राप्त झाल्यासारखे वाटते परंतु इतर ताऱ्यांना त्यांची स्वत:ची अशी गती असतेच. तिचे निराकरण करण्यासाठी विशिष्ट गटातील ताऱ्यांचे सरासरी विस्थापन विचारात घेऊन त्यावरून त्या गटाचा सरासरी पराशय काढला जातो. त्यावरून आकाशगंगेची व्याप्ती समजू शकते. यूग्मताऱ्यांचे पराशय मोजता आल्यास त्यावरून त्यांचे संयुक्त द्रव्यमान आणि सूर्याचे द्रव्यमान यांचे गुणोत्तर काढता येते. पराशयाच्या मापनावरून विश्वाच्या काही गुणधर्मांची कल्पना येते. त्याचप्रमाणे ताऱ्यांच्या निजगतीही (दृष्टिरेषेला लंब असणाऱ्या दिशेतील ताऱ्यांच्या गतीचा घटक म्हणजेच खगोलावरील ताऱ्यांच्या स्थानांतील भासमान बदल) काढता येतात.

संदर्भ : 1. Baker, R. H. Astronomy, Princeton, 1960.

2. Struve, O. Zebergs, V. Astronomy of the 20th Century, New York, 1962.

पुरोहित, वा.ल. नेने य. रा.

“