पदार्थांचे बल: अभियांत्रिकीय शास्त्रामध्ये कोणत्याही यंत्राची किंवा वास्तूची निर्मित करण्यापूर्वी त्यातील विविध भागांवर किंवा अवयवांवर येणाऱ्या भारांचे विश्लेषण करावे लागते. यंत्रावर किंवा यंत्रभागावर येणारे भार यामिकीतील [वस्तूंवर होणारी प्रेरणांची क्रिया आणि त्यामूळे निर्माण होणारी गती यांचा अभ्यास करणाऱ्या शास्त्रातील ⟶ यामिकी] तत्त्वानुसार काढतात. काही वेळा विश्लेषण करताना सर्वच भार विचारात घेता येत नाहीत परंतु मुख्य भारांचे मूल्य काढून यंत्राचा अथवा वास्तूचा अभिकल्प (आराखडा) तयार करावा लागतो. काही अभियांत्रिकीय संरचना स्थिर असतात आणि काही गतिशील असतात. त्यामुळे यामिकीच्या स्थितिकी व गतिकी या दोन्ही शाखांचा या कामासाठी उपयोग करावा लागतो. यंत्रभागावर येणाऱ्या भारामुळे यंत्रभागाच्या पदार्थात विकृती निर्माण होते. यंत्रभागाच्या आकारमानात वाढ किंवा घट झाल्यास त्या यंत्रभागाचे कार्य समाधानकारक होणार नाही. म्हणून यंत्राच्या आयुर्मर्यादेत भारामुळे कोणत्याही भागात विकृती उत्पन्न होऊ नये असे उद्दिष्ट असते. तसेच पदार्थांची भार सहन करण्याची क्षमताही माहीत असावी लागते. यंत्राच्या किंवा वास्तूच्या निर्मितीत लोखंड, पोलाद, लोहेतर धातू, दगड, विटा, सिमेंट, काँक्रीट, लाकूड इ. अनेक पदार्थांचा उपयोग करावा लागतो. या पदार्थांच्या अंतिम बलाचे यथार्थ ज्ञान असल्याशिवाय त्यांचा जास्तीत जास्त काटकसरीने उपयोग करणे शक्य नसते. म्हणून पदार्थांचे बल हा अभियात्रिकीमध्ये एक महत्त्वाचा विषय गणला जातो. या विषयाचा येथे दोन विभागांत विचार केलेला आहे : (१) यंत्रभागावर येणाऱ्या भारांचे विश्लेषण व त्यामुळे पदार्थांत निर्माण होणारे परिणाम आणि (२) पदार्थांच्या संबंधित गुणधर्मांचे मापन.
भारांचे विश्लेषण: भारांचे विश्लेषण करताना काही वेळा आसन्नीकरण (बहुतांशी जवळजवळ असणारे उत्तर शोधून काढण्याची क्रिया) करावे लागते किंवा काही गृहीत परिस्थिती कल्पावी लागते परंतु यामुळे अभियांत्रिकीय संरचना जास्त खर्चिक न होता जास्त सुरक्षित होत असेल, तर त्यापासून काही तोटा होत नाही.
भारांचे प्रकार: काही अभियांत्रिकीय वास्तू स्थिर असतात व त्यांवर येणारे भार कालांतराने स्थिर झालेले असतात. इमारतीतील विविध भागांवर येणारे भार स्थिर असतात. बंधाऱ्यावर पाण्यामुळे येणारे भार स्थिर असतात. जर भार कार्यान्वित होण्याचा वेग फार कमी असेल व महत्तम मूल्याला स्थिर असेल, तर अशा भाराला स्थितिक भार म्हणतात. इमारतीत खांबावर येणारा भार लहान क्षेत्रावर येतो. असे भार एका बिंदूवर केंद्रित झाले आहेत असे कल्पिताता व त्यास केंद्रित भार म्हणतात. खांबाच्या अनुप्रस्थ (आडव्या) छेदाच्या सममितीय (छेदाचे सारखे भाग करणाऱ्या) अक्षावर केंद्रित भार कार्यान्वित असेल, तर त्यास अक्षीय भार म्हणतात. इमारतीतील सज्याचा खांबावर येणारा भार खांबाच्या अक्षापासून काही अंतरावर कार्यान्वित असतो. सममितीय अक्षापासून काही अंतरावर कार्यान्वित असणाऱ्या अशा भाराला विकेंद्रि भार म्हणतात. तुळईवर जमिनीचा येणारा भार एका ठिकाणी केंद्रित आहे असे म्हणता येणार नाही. हा भार तुळईंच्या लांबीवर वितरित झालेला असतो व त्यास वितरित भार म्हणतात. वितरित भार सगळीकडे सारखा-समवितरित-असेल किंवा भाराचे वितरण एखाद्या फलनाप्रमाणे (चलांमधील संबंध दर्शविणाऱ्या एखाद्या गणितीय संबंधाप्रमाणे) बदलणारे असेल. पुलावरून आगगाडी जात असताना पुलाच्या विविध भागांवरील भार बदलतो. असा गतिमान भार पुलाच्या निरनिराळ्या ठिकाणी आहे असे समजून महत्तम भार काढावा लागेल. तसेच आगगाडीची चाके रुळांच्या सांध्यावरून जाताना आघात निर्माण होतो. कांडण यंत्राच्या मुसळावरही आघात येतो. अशा भारांना आघाती भार म्हणतात. यंत्रभागावर किंवा त्याच्याशी संलग्न असणाऱ्या भागावर गतीमुळे भार उत्पन्न होतात व त्यांना गतिक भार म्हणतात. एंजिनाच्या प्रचक्रामध्ये (गतीमध्ये होणारे फेरबदल कमी करण्यासाठी वापरण्यात येणाऱ्या जड चक्रामध्ये) गतीमुळे अपकेंद्री (केंद्रापासून दूर ढकलणारा) भार येतो. या ठिकाणी गतीचे मूल्य स्थिर असल्यास अपकेंद्री भार स्थिर असतो. एंजिनाच्या संयोग दांड्यावर येणारे गतिक भार सारखे बदलत असतात. अशा भारांना चक्रीय भार म्हणतात. यात भाराची कार्य करण्याची दिशा व मू्ल्य बदलत असते. चक्रीय भारामुळे पदार्थात शिणवटा येतो. मळसूत्राकार स्प्रिंग वा यंत्रातील शक्तिप्रेषणाकरिता उपयोगात आणलेला दंड यांमध्ये पिळण्याची क्रिया येते. पिळण्याची क्रिया परिबलांमुळे (वाकविण्याच्या वा वळविण्याच्या परिणामांमुळे) होते व त्या भारास परिपीडक भार म्हणतात.
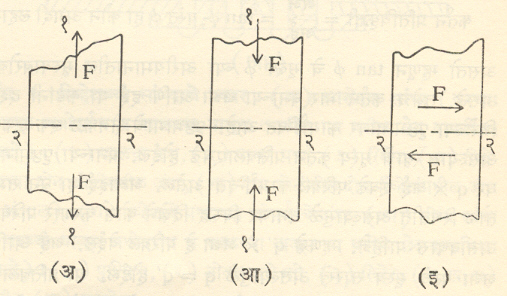
वर दिलेले विविध भार निरनिराळ्या प्रकारांनी कार्यान्वित होत असले, तरी भारामुळे पदार्थात निर्माण होणाऱ्या विकृतिप्रमाणे त्यांचे तीन वर्ग करता येतात. (१) ताण भार : या भारामुळे पदार्थातील तंतूंची लांबी वाढते. झोपाळ्याच्या कड्या, विहिरीतून पाणी काढण्याचा दोर यांमध्ये ताण भार येतो. (२) संपीडक भार : या भारामुळे पदार्थातील तंतूची लांबी कमी होते. इमारतीतील खांबावर येणारा भार, विजेच्या तारांचा खांबावर येणारा भार हे संपीडक भार आहेत. ताण भार व संपीडक भार यांची क्रिया वस्तूच्या अक्षाला लंब असणाऱ्या प्रतलावर होते. तसेच वस्तूचा अक्ष व भारांचा अक्ष एका रेषेत असतात. (३) कर्तन भार : कात्रीने कापण्याची क्रिया, खोबरे किसण्याची क्रिया किंवा दाबछिद्रकाने पत्र्यास छिद्र पाडण्याची क्रिया या उदाहरणात कर्तन भार येतो. भारास समांतर असलेल्या प्रतलावर कर्तन भार कार्यान्वित होत असतो. परिपीडक भारामुळे पदार्थावर कर्तन भार येतो.
प्रतिबल : भारित पृष्ठभागाच्या क्षेत्रफळाच्या एककावर येणाऱ्या बलास प्रतिबल म्हणतात. भारामुळे येणारे प्रतिबल खालील समीकरणाने काढतात.
|
प्रतिबल (f) = |
अक्षीय भार (F) |
|
कार्य प्रतलाचे क्षेत्रफळ (A) |
भार क्षेत्रफल मोजण्याच्या परिमाणावर प्रतिबलाचे परिमाण अवलंबून असते. उदा., किग्रॅ./सेंमी.२, टन/मी.२ प्रतिबलाचे परिणाम प्रकार भाराच्या प्रकारानुसार ताण प्रतिबल, संपीडक प्रतिबल व कर्तन प्रतिबल असे करता येतात. ताण प्रतिबल व संपीडक प्रतिबल यांना अनुक्रमे धन (+) व ऋण (-) चिन्ह वापरतात. वरील समीकरणात कार्य प्रतल ताण व संपीडक भारांच्या बाबतीत अनुप्रस्थ छेद व कर्तन भाराच्या बाबतीत समांतर छेद होईल (आ. १).
प्रतिविकृती : भार आला असता सर्व पदार्थ कमीजास्त प्रमाणात विकृत होतात. ताण आणि संपीडक प्रतिविकृती खालील समीकरणाने काढतात.
|
प्रतिविकृति (e) = |
मापातील बदल |
|
मूळ माप |
वरील समीकरणात उजव्या बाजूच्या गुणोत्तराच्या अंश व छेदाचे परिमाण सारखेच असावे लागते आणि त्यामुळे प्रतिविकृती हा परिमाणविरहित असा अंक असतो. प्रतिबलाप्रमाणे प्रतिविकृतीचे ताण, संपीडक व कर्तन प्रतिविकृती असे तीन मुख्य प्रकार आहेत. प्रतिविकृतीच्या वरील व्याख्येमध्ये उल्लेखिलेला मापातील बदल हा पदार्थामध्ये एकाच वेळी दोन अथवा तीन अशा एकमेकांस काटकोन करणाऱ्या अक्षांमध्ये होऊ शकेल.
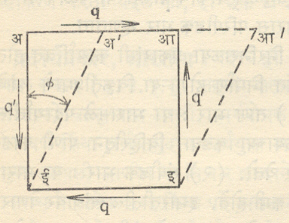
कर्तन भारामुळे निर्माण होणारी प्रतिविकृती आ. २ मध्ये दाखविली आहे. प्रति-विकृती कोनाच्या अरीयमानात [⟶ कोन] मोजतात.
|
कर्तन प्रतिविकृति = |
अअ’ |
= tan ϕ परंतु ϕ हा कोन अगदी लहान असतो |
|
अई |
tan ϕचे मूल्य ϕ च्या अरीयमानातील मूल्याबरोबर असते. तसेच कर्तन भार घनाच्या अआ आणि इई या कडांनी दर्शविलेल्या पृष्ठभागावर कार्यान्वित आहे. पृष्ठभागाचे क्षेत्रफळ एक एकक असल्यास त्याचे मूल्य कर्तन प्रतिबलाएवढे होईल. घनाच्या पृष्ठभागावर q x अई एवढे परिबल कार्यान्वित असेल. अआइई हा घन समतोल स्थितीत असल्यामुळे घनावर विरुद्ध दिशेने कार्य करणारे परिबल असावयास पाहिजे. म्हणजे q’ x अआ हे परिबल येईल. अई आणि अआ यांचे मूल्य सारखे असल्यामुळे q = q’ होईल. या प्रतिबलास पूरक कर्तन प्रतिबल म्हणतात. कर्तन प्रतिबलामुळे ज्या वेळी परिबल कार्यान्वित असते त्या वेळी त्या परिबलांच्या विरुद्ध दिशेने कार्य करणारे परिबल अस्तित्वात असते. दोन्ही परिबले एकमेकांस लंब असणाऱ्या प्रतलात कार्यान्वित असतात.
प्वासाँ गुणोत्तर : (एस्. डी. प्वासाँ या फ्रेंच शास्त्रज्ञांच्या नावावरून ओळखण्यात येणारे). एखादा लोखंडी गज यंत्रात धरून ताणला, तर त्याची लांबी वाढेल पण त्याचबरोबर त्याचा व्यासही किंचित कमी होईल. या एकमेकांशी काटकोनात होणाऱ्या पार्श्वीय व अन्वायामी (लांबीच्या दिशेतील) प्रतिविकृतीच्या गुणोत्तराला प्वासाँ गुणोत्तर (µ) म्हणतात.
|
µ = |
पार्श्वीय प्रतिविकृती |
|
अन्वायामी प्रतिविकृती |
लोखंड व काँक्रीटसाठी या गुणोत्तराचे मूल्य अनुक्रमे सु. ०.३० व ०. १५ एवढे असते.
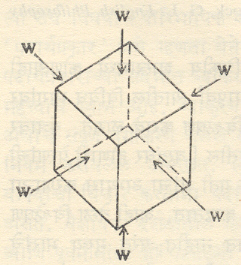
घनफळ प्रतिविकृती : एकमेकांस काटकोनात असणाऱ्या तीन अक्षांवर होणाऱ्या प्रतिविकृतीचा परिणाम घनफळ प्रतिविकृतीमध्ये दर्शविलेला असतो. समजा आ. ३ मध्ये दाखविल्याप्रमाणे एखाद्या पदार्थाच्या लहानशा घनाच्या सहाही पृष्ठांवर सारखा संपीडक भार W एवढा दिला आहे. या स्थितिकीय भारामुळे घनाचे घनफळ कमी होईल. म्हणजेच त्यामध्ये घनफळ प्रितविकृती निर्माण होईल. घनफळ प्रतिविकृती खालील समीकरणाने काढता येईल.
|
घनफळ प्रतिविकृती (ev) = |
घनफळातील बदल (δV) |
|
मूळ घनफळ (V) |
स्थितिस्थापकता :पदार्थाची स्थितिस्थापकता म्हणजे ज्या भारामुळे विकृती निर्माण होते तो दूर होताच विकृतावस्थेतून मूळ स्थितीत येण्याचा पदार्थाचा गुणधर्म. आदर्श स्थितिस्थापक पदार्थ विकृतीचे कारण नाहीसे होताच विकृतीविरहित स्थितीत येतात एवढेच नव्हे तर भार वाढत असता, विशिष्ट भारापर्यंत जेवढी प्रतिविकृती पदार्थात निर्माण झाली असेल तेवढीच प्रतिविकृती भार कमी करत असता त्या विशिष्ट भाराच्या वेळी पदार्थात असते. पदार्थाच्या स्थितिस्थापकतेची मर्यादा हुक सिद्धांताने सांगतात.

हुक सिद्धांत: रॉबर्ट हुक या इंग्रज शास्त्राज्ञांनी असे दाखवून दिले की, पृथ्वीवरील प्रत्येक पदार्थ कमीअधिक प्रमाणात स्थितिस्थापक असून तो प्रतिबलाच्या विशिष्ट मर्यादेपर्यंत भारित केला, तर या मर्यादांतर्गत विकृत अवस्थेत प्रतिबल हे तज्जन्य प्रतिविकृतीशी प्रमाणित असते. या शेवटच्या विधानाला हुक सिद्धांत असे म्हणतात. प्रतिबल व प्रतिविकृती या दोन राशींचा परस्पर संबंध आ. ४ मध्ये कख या सरळ रेषेने दाखविला आहे. ख या बिंदूच्या पुढे प्रतिबल वाढले असता रेषेची सरलता संपून तिला वक्रता येते. ख या बिंदूला स्थितिस्थापकतेची सीमा असे म्हणतात.
स्थितिस्थापकता गुणांक : हुक नियमानुसार कोणत्याही वस्तूवरील स्थितिस्थापकतेच्या सीमांतर्गत असे प्रतिबल व तज्जन्य प्रतिविकृती यांचे गुणोत्तर कायम असते. या गुणोत्तराला स्थितिस्थापकता गुणांक असे म्हणतात. याचे मूल्य खालील सूत्राने काढतात.
|
स्थितिस्थापकता गुणांक (E) = |
प्रतिबल (f) |
|
प्रतिविकृती (e) |
ताण किंवा संपीडक प्रतिबल आणि त्यांच्या प्रतिविकृती वापरून काढलेल्या या गुणांकास यंग यांचा स्थितिस्थापक गुणांक असे म्हणतात आणि तो सामान्यपणे E या अक्षराने दर्शवितात. E चे परिमाण किग्रॅ./सेंमी.२ मध्ये असून त्याचे विविध धातूंसाठी असणारे मूल्य ०.७ ते २.१ x १०६ किग्रॅ./सेंमी.२ एवढ्या कक्षेमध्ये असते.
दृढता मापांक: कर्तन प्रतिबल व प्रतिविकृती यांच्या वरीलप्रमाणे येणाऱ्या गुणोत्तरास दृढता मापांक असे म्हणतात व तो C, G अथवा N या अक्षरांनी दर्शविणे रूढ आहे. या मापकांचे परिमाण हे कर्तन प्रतिबलाचे परिमाणच असते. दृढता मापांक व यंग मापांक यांचा संबंध खालील समीकरणाने दर्शवितात.
|
G = |
E |
|
2 (1 + µ) |
येथे µहे प्वासाँ गुणोत्तर आहे.
घनफळ मापांक: घनाच्या कोणत्याही पृष्ठावरील प्रतिबल व घनफल प्रतिविकृती यांच्या गुणोत्तरास घनफळ मापांक असे म्हणतात.
|
घनफळ मापांक (K) = |
प्रतिबल (fv) |
|
घनफळ प्रतिविकृती (ev) |
|
|
= |
E |
|
3(1 – 2 µ) |
एकेरी प्रतिबले: कोणत्याही प्रकारचे प्रतिबल एकाच वेळी स्वतंत्रपणे कार्यान्वित होत असल्यास त्यास एकेरी प्रतिबल म्हणतात. एकेरी प्रतिबले येणारी अनेक उदाहरणे देता येतील. त्यातील विविध अशा परिस्थितींत येणाऱ्या अशा चार प्रमुख एकेरी प्रतिबलांची उदाहरणे खाली दिलेली आहेत.
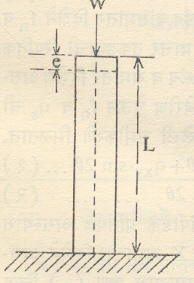
खांब: आ. ५ मध्ये एक फारसा उंच नसलेला खांब दाखवला आहे. त्यावर W किं.ग्रॅ. एवढा अक्षीय भार येतो. जर खांबाच्या आडव्या छे दा चे क्षेत्रफळ A चौ. सेंमी. एवढे असेल, तर खांबामधील एकेरी
|
संपीडक प्रतिबल (f) = |
भार (W) |
|
क्षेत्रफळ (A) |
असे काढता येईल आणि त्यामुळे निर्माण होणारी
|
प्रतिविकृती e = |
WL |
|
AE |
या समीकरणाने मिळेल. येथे E हा स्थितिस्थापक गुणांक आहे.
रिव्हेटाचा सांधा: दोन किंवा तीन पत्रे एकमेकांना जोडण्यासाठी रिव्हेटाचे सांधे वापरतात. या सांध्यांचे दोन मुख्य प्रकार आहेत : (१) आरोहक सांधा (२) सीमा सांधा. आ. ६ (अ) मध्ये रिव्हेटाच्या दोन ओळींचा आरोहक सांधा व आ. ६ (आ) मध्ये रिव्हेटाच्या दोन ओळींचा आणि पत्र्याच्या तुकड्याची दोन पुष्टिपत्रे असलेला सीमा सांधा दाखविलेला आहे. अशा रिव्हेटाच्या सांध्याचे बल अजमावणे हा मुख्य भाग असतो. हे बल व्यास, एका ओळीतील दोन रिव्हेटांमधील अंतर (अंतराल), पत्र्याची जाडी. इ. गोष्टींवर अवलंबून असते. रिव्हेटाचा सांध्याचा भंग हा सांध्याचे पत्रे फाटून अथवा रिव्हेट आडवा कापला जाऊन अथवा रिव्हेटाचा चुराडा होऊन होऊ शकतो. म्हणून वरील गोष्टींसाठी रिव्हेटाचे बल अजमावणे जरूर असते. सांध्याचे बल खालील सूत्राने काढता येते.
(१) सांध्याचा पत्रा फाटण्यास लागणारा भार (Pt):
Pt = ft (p – d) t
या सूत्राने मिळतो. यात ft पत्र्याची अंतिम तन्य शक्ती, p जवळील दोन रिव्हेटांमधील अंतराल (आकृतीत हे ख ने दाखविले आहे), d रिव्हेटाचा व्यास आणि t पत्र्याची जाडी आहे.
(२) रिव्हेट आडवा कापला जाण्यास लागणारा भार (Ps) :
|
Ps = fs · |
π |
. d2 |
|
4 |
या सूत्राने मिळतो. यात fs हे रिव्हेटाच्या धातूचे अंतिम कर्तन बल आहे.

आ. ६ (अ) मधील सांध्याच्या पत्र्याच्या दोन्ही बाजू बाणाच्या दिशेने ओढल्यास रिव्हेट एकाच
पातळीत कापला जाण्याची शक्यता असते म्हणून त्यास एकेरी कर्तन पातळीतील रिव्हेट असे म्हणतात. परंतु आ. ६ (आ) मधील रिव्हेट दोन ठिकाणी कापला जाण्याची शक्यता असते म्हणून त्यास दुहेरी कर्तन पातळीतील रिव्हेट असे म्हणतात. दुहेरी कर्तन पातळीतील रिव्हेटाचे बल हे एकेरी पातळीतील रिव्हेटाच्या बलाच्या दुप्पट असते.
(३) रिव्हेटाचा चुराडा होण्यास लागणारा भार
(Pb) : Pb = fb·d·t
या सूत्राने मिळतो. यामध्ये fb रिव्हेटाच्या धातूचे चुराडा बल आहे.
अर्थातच वर दिलेल्या रिव्हेटाच्या बलांपैकी जे बल सर्वांत कमी असते त्या बलाचा सांध्याचे बल म्हणून उपयोग करतात. रिव्हेटाचा व्यास (सेंमी.) d = t +1 या अथवा अशा प्रकारच्या अनुभवसिद्ध नियमांनी ठरविला जातो.
रिव्हेटाच्या सांध्याची कार्यक्षमता (η) ही अच्छिद्रित पत्र्याच्या ताणबलाशी सांध्याच्या कमीत कमी बलाची तुलना करून काढतात. अच्छिद्रित पत्र्याचे ताणबल (P) म्हणजे ft·p·t हे होय.
|
∴ सांध्याची कार्यक्षमता = |
[वरीलपैकी Pt, Ps, Pb सर्वात कमी असलेले बल] |
|
ft· p·t |
वरील कार्यक्षमता ४० ते ८०% पर्यंत असते. सीमा सांध्याची कार्यक्षमता आरोहक सांध्याच्या पेक्षा जास्त असते. अलीकडील काळात वितळजोडकामाच्या (वेल्डिंगच्या) शास्त्रात व तंत्रात खूपच प्रगती झाल्या कारणाने पत्रे जोडण्याच्या कामात रिव्हेटाचा उपयोग मागे पडला आहे. वितळजोडाची कार्यक्षमता १००% अथवा अधिक करता येते. [⟶ रिव्हेट वितळजोडकाम].
उष्णताजन्य प्रतिबले: वस्तू तापवली असता ती प्रसरण पावते व थंड केली असता आकसते. या प्रसरणास व आकुंचनास जर प्रतिबंध केला, तर त्यामुळे वस्तूत दाब व ताण प्रतिबले निर्माण होतात. अशा प्रतिबलांना उष्णताजन्य प्रतिबले म्हणतात. उष्णताजन्य दाब व ताण प्रतिबले खालील सूत्राने काढता येतील.
प्रितबल = α. T. E. यामध्ये α पदार्थाचा रैखिक प्रसरण (वा आकुंचन) गुणांक (प्रती ° से.), T तापमानातील बदल (° से), आणि E पदार्थांचा स्थितिस्थापक गुणांक आहेत. लोखंडी वा सलोह काँक्रिटाच्या पुलांचे अभिकल्प करताना तापमान बदलाने निर्माण होणारे प्रतिबल विचारात घ्यावे लागते.
पातळ दंडगोल, गोल पात्रे आणि नळ: जेव्हा पात्राच्या पत्र्याच्या जाडीच्या मानाने त्याचा व्यास, अंदाचे ५० पट अथवा अधिक मोठा असतो तेव्हा त्यास पातळ पात्रे म्हणतात. बाष्पित्र (बॉयलर), संपीडित हवापात्रे ही याची उदाहरणे होत. पात्रामध्ये द्रायूचा (द्रवाचा वा वायूचा) दाब आला असता पत्र्यामध्ये तीन मुख्य प्रतिबले निर्माण होतात. ती अशी-परिघीय (परिघाशी स्पर्शरेषीय), अक्षीय व अरीय (त्रिज्येच्या दिशेने). अरीय प्रतिबल दाब जातीचे असून त्याची महत्ता फार कमी असते व म्हणून ते विचारात घेत नाहीत. पहिली दोन प्रतिबले ताण जातीची असून त्यांची महत्ता पुढील सूत्रांवरून काढतात.

|
(१) f1= |
P·d |
|
|
2t |
||
|
(२) f2 = |
P·d |
. |
|
4t |
वरील सूत्रांत आ. ७ मध्ये दाखविल्याप्रमाणे f1 परीघ स्पर्शरेषी ताण प्रतिबल, f2 अक्षीय दिशेचे ताण प्रतिबल, p पात्रांतर्गत द्रायुदाब, d पात्राचा व्यास आणि t पात्राच्या पत्र्याची जाडी आहे.
गोल पात्रात सर्वत्र फक्त p·d/4t इतके परिघीय प्रतिबल अस्तित्वात असते. उघड्या नळातील प्रतिबले दंडगोल पात्रातल्याप्रमाणेच असतात. परंतु अक्षीय दिशेने प्रतिबल नसते.
प्रतिविकृती उर्जा: पदार्थ भारित असता त्यावर प्रतिबल व प्रतिविकृती निर्माण होतात. यामुळे पदार्थात प्रतिविकृती ऊर्जा निर्माण होऊन ती पदार्थात साठविली जाते. जर ‘W’ हा अक्षीय भार, / एवढ्या लांबीच्या व A एवढे छेदाचे क्षेत्रफळ असलेल्या गजावर हळूहळू लावला, तर त्यात δ/ एवढी विकृती निर्माण होईल. अशा पदार्थांची प्रतिविकृती ऊर्जा ही 1/2 W δ/ एवढी होईल. पदार्थावर भार एकदम-आघाती-आल्यास ऊर्जेचे मूल्य Wδ / इतके होईल. प्रतिविकृती ऊर्जा पदार्थाचा लवचिकपणा दर्शविते.
मिश्र प्रतिबले व प्रतिविकृती: यंत्राच्या भागामध्ये सहसा एकाच प्रकारचे प्रतिबल असत नाही. विशिष्ट भागावर कार्यान्वित असलेल्या भारामुळे त्या भागातील विविध बिंदूवर एकाच वेळी तिन्ही दिशांनी प्रतिबले कार्यान्वित असतात. आ. ८ (अ) मध्ये यंत्राचा एक भाग दाखविला आहे. हा यंत्रभाग एक पोकळ नळी असून तिची दोन्ही तोंडे बंद आहेत व नळीच्या आत द्रायूचा दाब आहे. त्यावर परिबल (F.a) कार्यान्वित असल्यामुळे कर्तन प्रतिबल येते.
यंत्रभागातील लहानसा घन निराळा काढून त्यावर असलेली प्रतिबले व सहनिर्देशक अक्ष आ. ८ (आ) मध्ये दाखविले आहेत. हा घन स्थितिक समतोल अवस्थेत असल्यामुळे त्यावर असलेले एकक भार (प्रतिबल) कसे असतात ते दाखविले आहेत. आकृतीच्या लंब दिशेने प्रतिबले नाहीत असे मानले आहे व द्विमितीय प्रतिबलांचाच विचार केला आहे. Y अक्षास θ हा कोन करणारे प्रतल घेऊन पाचरीच्या आकाराचा (कखग) तुकडा निराळा काढून तो आ. ८ (इ) मध्ये दाखविला आहे. कग या प्रतलाच्या लंब व समांतर दिशेने fn व qs अशी दोन प्रतिबले दाखविली आहेत. पाचर तुकड्याची स्थितिक समतोल अवस्था असल्यामुळे कग प्रतलाला लंब व समांतर दिशेत असणाऱ्या सर्व प्रतिबलांच्या घटकांची सदिश बेरीज घेऊन fn व qs ची मूल्ये काढता येतात. त्यांवरून खाली दिलेली समीकरणे मिळतात.
fn = 1/2 (fx + fy) + 1/2 (fx – fy) .cos 2θ + qxy .sin 2θ ….. (१)
qs = 1/2 (fx + fy) .sin 2θ – qxy .cos 2θ ….. ….. (२)
वरील समीकरणांत ताण प्रतिबलाऐवजी संपीडक प्रतिबल असल्यास ऋण (-) चिन्ह वापरावे. Qxy ची दिशा X अक्षाच्या दिशेने असल्यास धन (+) आणि विरुद्ध दिशेने असल्यास ऋण (-) चिन्ह वापरावे.
वरील समीकरणांतील fnव qs ची मूल्ये रेखाकृतीने काढण्याची पद्धत आ. ८ (ई) मध्ये दाखविली आहे. अक्ष व अय हे अनुक्रमे X व Y सहनिर्देशक अक्ष आहेत. X अक्षावर लंब प्रतिबले व Y अक्षावर कर्तन प्रतिबल मोजतात. अआ =fx, अइ fy, इउ = आई =qxy प्रमाणात मोजून घेतले आहे. उई जोडल्यास वर्तुळाचा केंद्रबिंदु ओ मिळतो. इउ आणि आई Y अक्षास समांतर आहेत.
तसेच अओ =1/2 (fx + fy) आणि अच =1/2 (fx – fy).
ओउ या त्रिज्येने वर्तुळ काढले आहे. ओक ही त्रिज्या उईं शी २० इतका कोन करून काढली आहे. कग प्रतलाला लंब व समांतर दिशेने असलेली प्रतिबले का या बिंदुचे सहनिर्देशक अख, कख यांच्या लांबीवरून मिळतात. कोणताही कोन करणाऱ्या प्रतलावरील प्रतिबले अशा प्रकारे काढता येतील. अशा तऱ्हेने काढलेल्या वर्तुळाला जर्मन अभियंते ओटो मोर यांच्या नावावरून मोर वर्तुळ म्हणतात. मोर वर्तुळावरून खालील निष्कर्ष काढता येतात.
(१) महत्तम कर्तन प्रतिबल = qs max = √ 1/4 (fx – fy)2 + qxy2 … … … … … …(3)
हे प्रतिबल ओग या प्रतलावर येते व Y अक्षाशी त्याचा कोन ½ ∠ गओई इतका असतो.
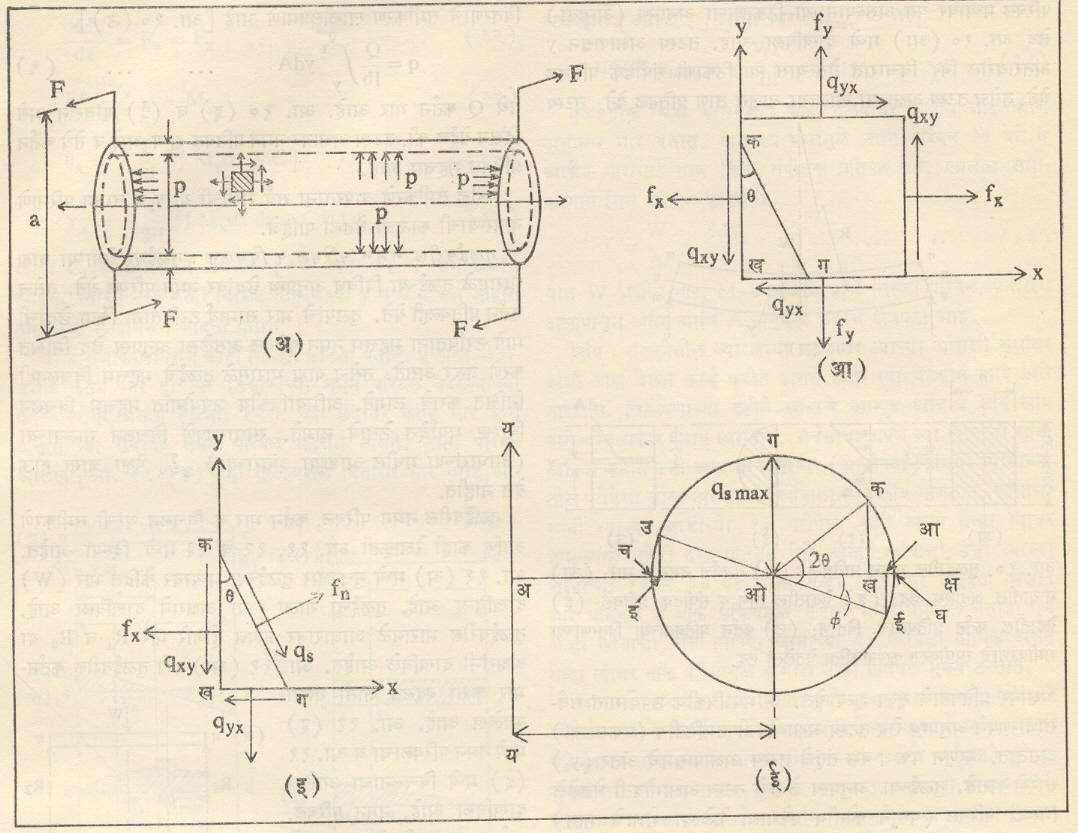
(२) महत्तम लंब प्रतिबल = अघ = fn1 = ½ (fx + fy) + √ ¼ (fx – fy) + qxy2 …….. (४)
या प्रतलाचा Y अक्षाशी कोन ϕइतका असतो.
लघुत्तम लंब प्रतिबल = अच = fn2= ½ (fx + fy) – √ ¼ (fx – fy)2 + qxy2 …….. (५)
या प्रतलाचा Y अक्षाशी कोन ½ (2ϕ + π) इतका असतो.
महत्तम व लघुतम लंब प्रतिबले असणाऱ्या प्रतलावर कर्तन प्रतिबलांचे मूल्य शून्य असते. अशा लघुतम आणि महत्तम लंब प्रतिबलांना प्रमुख प्रतिबले म्हणतात. यंत्रभागाचा अभिकल्प करताना प्रमुख प्रतिबलांचा उपयोग करतात. प्रमुख प्रतिबले एकमेकास काटकोनात असतात.
(३) महत्तम कर्तन प्रतिबल qs max = ½ (fn1 – fn2) …………. (६)
(४) फक्त कर्तन प्रतिबल असल्यास fx=fy=0 होऊन अ आणि ओ हे बिंदु एकस्थित होतील आणि महत्तम व लघुतम लंब प्रतिबले + qxy बरोबर होतील व qxy शी ४५° कोन करणाऱ्या प्रतलावर कार्यान्वित असतील. म्हणजे ताण व संपीडक प्रतिबले कर्तन प्रतिबलाशी ४५° कोन करणाऱ्या प्रतलावर येतील.
(५) कर्तन प्रतिबल शून्य असेल तर 2ϕ = 0 आणि qsmax = ½(fx-fy). Y अक्षाशी ४५° चा कोन करणाऱ्या प्रतलावर हे कर्तन प्रतिबल असेल. fn1=fxव fn2=fy.

तुळई: संरचनेतील ज्या आडव्या घटकावर त्याच्या अक्षाशी अभिलंब असे बाह्य भार येतात, त्या घटकाला तुळई म्हणतात. हे बाह्य भार पेलण्याकरिता तुळईला एक किंवा जास्त आधार दिलेले असतात. आधाराच्या प्रकारानुसार तुळयांचे प्रकार असतात. आ. ९ मध्ये तुळयांचे तीन प्रकारचे आधार दाखविले आहे. जेव्हा तुळईला एकच आधार असतो त्या वेळी तिला अर्धबहाल म्हणतात. मुक्ताधारामध्ये फक्त आधाराच्या दिशेने प्रतिक्रिया मिळते. पक्क्या आधारामध्ये सरळ व परिबल विरोधी प्रतिक्रिया मिळतात आणि खीळ-आधारामध्ये कोणत्याही दिशेने प्रतिक्रिया मिळते.
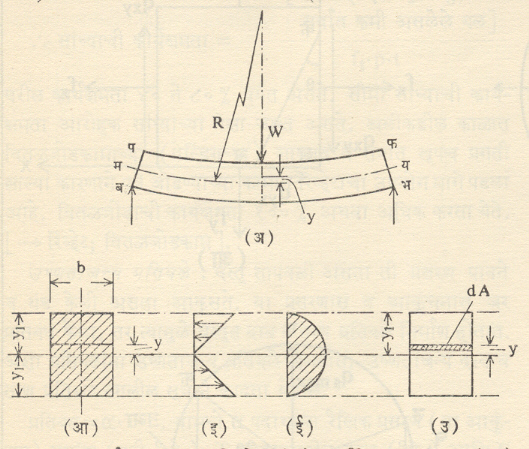
तुळईतील जमन प्रतिबले: आ. १० (अ) मध्ये मुक्ताधार असलेल्या तुळईवर मध्यभागी केंद्रित भार दाखविला आहे. या भारामुळे तुळईचे नमन झाल्याने (वाजवीपेक्षा जास्त प्रमाण घेऊन काढलेले चित्र) तुळईच्या खालील बाजूच्या तंतूंची (बभ) लांबी वाढली आहे व वरच्या बाजूच्या तंतूंची (पफ) लांबी कमी झालेली आहे. या दोन्ही तंतूच्या मध्ये असलेल्या (मय) तंतूंची लांबी स्थिर राहते. या तंतूला (मय) तटस्थ अक्ष असे म्हणतात. तुळईवर महत्तम नमन परिबल मध्यावर येत असल्याने त्या ठिकाणाचा अनुप्रस्थ (आडवा) छेद आ. १० (आ) मध्ये दाखविला आहे. तटस्थ अक्षापासून y अंतरावरील बिंदु विचारात घेतल्यास त्या ठिकाणी संपीडक प्रतिबल येते, तसेच तटस्थ अक्षाच्या खालच्या बाजूस ताण प्रतिबल येते. तटस्थ अक्षावर प्रतिबलाचे मूल्य शून्य येते. अभियांत्रिकीय उपयोगात सर्वसाधारणपणे अनुप्रस्थ छेद तटस्थ अक्षाभोवती सममितीय (एकसारखे) असतात. म्हणून पफ व बभ तंतूचे तटस्थ अक्षापासूनचे अंतर (y1) सारखे असते. तुळईच्या अनुप्रस्थ छेदाचे तटस्थ अक्षाभोवती घेतलेले निरूढी परिबल (वस्तूने कोनीय प्रवेगाला केलेल्या रोधाचे मान) I ह्या अक्षराने निर्देशितात. I/y या गुणोत्तरास छेद मापांक म्हणतात. छेद सममितीय नसेल, तर
|
Z1 = |
I |
आणि Z2 = |
I |
|
y1 |
y2 |
असे दोन छेद मापांक येतील आणि तो सममितीय असल्यासा Z = I/y असा एकच छेद मापांक येईल. नमन परिबलाची समीकरणे पुढीलप्रमाणे आहेत.
|
f |
= |
M |
= |
E |
… … …. (७) |
|
y |
I |
R |
|||
|
M = f |
I |
= fZ … …. …. (८) |
|||
|
y |
|||||
यात f स्थिर अक्षापासून y अंतरावरील प्रतिबल, R तुळईला येणाऱ्या बाकाची त्रिज्या, E तुळईच्या पदार्थाचा स्थितिस्थापकता गुणांक आणि M = छेदावरील नमन परिबल आहे. वरील समीकरणांचा उपयोग करून अनुप्रस्थ छेदातील विविध बिंदुंवरील प्रतिबले आ. १० (इ) मध्ये दाखविली आहेत. तुळईच्या मध्यभागातील अनुप्रस्थ छेदावर कर्तन भारही आहे व त्याचे मूल्य W/2 आहे. त्यामुळे छेदावर कर्तन प्रतिबल येते. त्याचे छेदावरील वितरण आ. १० (ई) मध्ये दाखविले आहे तटस्थ अक्षावर त्याचे मूल्य महत्तम आहे आणि तुळईच्या वरच्या व खालच्या पृष्ठभागांवर त्याचे मूल्य शून्य आहे. कर्तन प्रतिबलाच्या वितरणाचे समीकरण खालीलप्रमाणे आहे [ आ. १० (उ) ].
|
q = |
Q |
⨛ |
y1 |
ydA .. …. (९) |
|
Ib |
y |
येथे Q कर्तन भार आहे. आ. १० (इ) व (ई) यांवरून असे दिसून येईल की, तटस्थ अक्षावर नमन प्रतिबल शून्य आहे व तेथे कर्तन प्रतिबल महत्तम आहे.
वरील समीकरणे वापरताना सर्व राशींची योग्य व समान परिमाणे वापरण्याची काळजी घेतली पाहिजे.
तुळईवरील नमन परिबल व विचलन: तुळईवर येणाऱ्या बाह्य भारामुळे तुळईच्या विविध अनुप्रस्थ छेदांवर नमन परिबल येते. तसेच कर्तन प्रतिबलही येते. तुळयांचे भार सामर्थ्य ठरविताना किंवा छेदांची मापे ठरविताना महत्तम नमन परिबल असलेला अनुप्रस्थ छेद निश्चित करणे जरूर असते. तसेच बाह्य भारामुळे तुळईचे महत्तम विचलनही निश्चित करावे लागते. अभियांत्रिकीय उपयोगात महत्तम विचलन विशिष्ट मर्यादेत ठेवावे लागते. साधारणपणे विचलन गाळ्याच्या (आधारांच्या मधील आडव्या अंतराच्या) १/३२५ पेक्षा जास्त होऊ देत नाहीत.
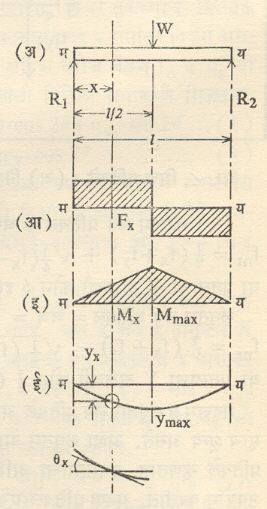
तुळईवरील नमन परिबल, कर्तन भार व विचलन यांची समीकरणे आणि काही रेखाकृती आ. ११, १२ व १३ मध्ये दिल्या आहेत. आ. ११ (अ) मध्ये मुक्ताधार तुळईच्या मध्यावर केंद्रित भार (W) दाखविला आहे. तुळईचा गाळा I या अक्षराने दाखविला आहे. तुळईवरील भारामुळे आधारावर उत्पन्न होणारे भार R1व R2 या अक्षरांनी दाखविले आहेत. आ. ११ (आ) मध्ये तुळईवरील कर्तनभार कसा बदलत जातो याचा आलेख आहे. आ. ११ (इ) मध्ये नमन परिबलाचा व आ. ११ (ई) मध्ये विचलनाचा आलेख दाखविला आहे. नमन परिबल, कर्तन भार आणि विचलन यांचे परस्परसंबंध खालील समीकरणांनी मिळतात. डाव्या बाजूच्या आधारापासून x अंतरावरील अनुप्रस्थ छेद विचारात घेतला आहे. त्या छेदावर Mx नमन परिबल, Fx कर्तन भार, Yx विचलन, ϕx विचलन वक्राच्या स्पर्शरेषेचा तुळईशी होणारा कोन [ हा कोन आ. ११ (ई) च्या खाली मोठा करून दाखविला आहे ज्या बिंदूपाशी हा कोन होतो तो बिं दु (ई) म ध्ये वर्तुळांकित करून दाखविला आहे तसेच कोन आ. १२ (ई) व आ. १३ (ई) च्या खाली दाखविले आहेत], E तुळईच्या पदार्थाचा स्थितिस्थापकता गुणांक आणि I तटस्थ अक्षाभोवती तुळईच्या अनुप्रस्थ छेदाचे निरूढी परिबल आहे. E व I ची मूल्ये सर्व ठिकाणी समान आहेत असे गृहीत धरले आहे.
Fx = R1 = W/2 … … … … … … … … … … … … … (१०)
Mx = R1x = W/2 x … … … … … … … … … (११)
dMx /dx = R1 = Fx … … … … … … … … … … … …(१२)
EI d2yx / dx2 = – Fx … … … … … … … … … … … (१३)
Ox = – 1/EI [∫ Mxdx + C] … … … … … … … (१४)
Yx =- 1/EI ∫∫ Mxdx dx = Cx + C1 … … … … … … …(१५)
C व C1 हे समाकलन स्थिरांक [⟶ अवकलन व समाकलन] आहेत. त्यांची मूल्ये काही विशिष्ट ठिकाणच्या y व ϕ यांच्या माहीत असलेल्या मूल्यांवरून काढता येतात.
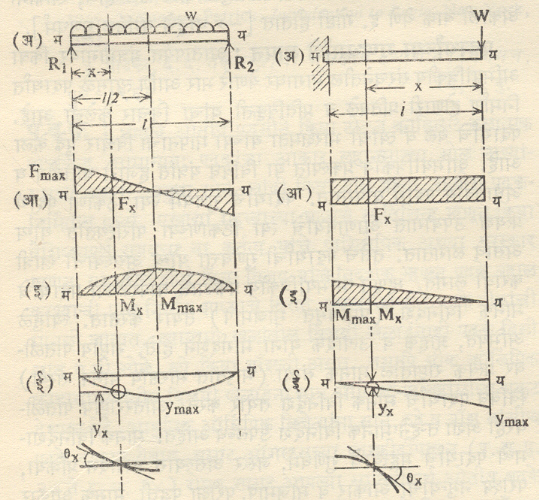
वरील समीकरणांवरून काही निष्कर्ष काढता येतात. एखाद्या छेदावरील कर्तन भार हा त्या ठिकाणाच्या नमन परिबल बदलण्याच्या प्रमाणाबरोबर असतो (समी. १२). ज्या छेदावर कर्तन भार शून्य असतो त्या छेदावर नमन परिबल महत्तम असते. नमन परिबल आलेख [आ. ११ (इ)] हा तुळईवरील वितरित भार आहे, असे धरून एखाद्या छेदावरील नमन परिबल काढल्यास ते त्या ठिकाणच्या विचलनाबरोबर येते.
आ. १२ मध्ये समवितरित भार असलेली मुक्ताधार तुळईवरील व. आ. १३ मध्ये टोकावर केंद्रित भार असलेली अर्धबहाल आणि त्यावरील कर्तन भार, नमन परिबल व विचलन आलेख दाखविले आहेत. महत्तम नमन परिबल व महत्तम विचलन खाली दिल्याप्रमाणे असते.तुळईच्या मध्यावरचा छेद : [आ. ११]
Mmax = WI/4 ymax = 1/48. WI3/EI … … … (१६)
तुळईच्या मध्यावरचा छेद :[आ. १२]
Mmax = WI2/8 ymax = 5/384· WI4 / EI … … (१७)
(येथे w एकक लांबीवरील भार).
अर्धबहाल [आ. १३] आधारावर Mmax = WI
टोकावर ymax = 1/3 WI3/ EI … … … … … (१८)
तुळईतील मिश्र प्रतिबले: काही तुळयांवर अक्षीय भार आणि अनुप्रस्थ भार येतात. अनुप्रस्थ भारामुळे नमन परिबल M येते व अक्षीय भारामुळे ताण किंवा संपीडक प्रतिबल येते. खालील समीकरणाने मिश्र प्रतिबल काढतात.
f = W/A + My/I … … … … … … … … … … (१९)
यात W अक्षीय भार, M नमन परिबल,I निरूढी परिबल, y तटस्थ अक्षापासून अंतर आणि A अनुप्रस्थ छेदाचे क्षेत्रफळ आहे.
खांब: संरचनेतील ज्या उभ्या घटकावर त्याच्या अक्षाशी समांतर अशी बाह्य प्रेरणा कार्य करीत असते तेव्हा त्या घटकास खांब असे म्हणतात. विश्लेषणाच्या दृष्टीने खांबाचे आखूड खांब व लांब खांब असे दोन प्रकार करावे लागतात. सर्वसाधारणपणे ज्या खांबाची लांबी त्याच्या कमीत कमी आडव्या मापाच्या (जाडीच्या) अथवा व्यासाच्या तीस पटींपेक्षा जास्त असते, त्या खांबाला लांब खांब म्हणतात. खांबाची लांबी त्याच्या जाडीच्या १० पटींपेक्षा कमी असते तेव्हा त्यावर प्रामुख्याने एकेरी दाब प्रतिबल येते. जेव्हा खांबाची उंची त्याच्या जाडीच्या १० ते ३० पट असते तेव्हा त्याच्यावर मुख्यतः अक्षीय भार प्रतिबल वा बाक प्रक्रियेमुळे येणारी नमन प्रतिबले येतात पण जेव्हा खांबाची लांबी त्याच्या जाडीच्या ३० पटींपेक्षा अधिक असते तेव्हा त्यावर बाक प्रक्रियेमुळे होणारी नमन प्रतिबले मुख्य ठरतात.
खांबाच्या बाबतीत त्याचे कृशता गुणोत्तर महत्त्वाचे असते. खांबाची प्रभावी लांबी व त्याची घूर्णीय त्रिज्या (दिलेल्या अक्षाभोवतील निरूढी परिबलाला द्रव्यमानाने भागून मिळणाऱ्या राशीचे वर्गमूळ) यांच्या गुणोत्तरास खांबाचे कृशता गुणोत्तर म्हणतात. खांबाची प्रभावी लांबी काढताना त्या खांबाच्या दोन टोकांना असणाऱ्या आधारांचा विचार करावा लागतो. आ. १४ मध्ये खांबाच्या टोकांचे विविध आधार व त्यांवर येणाऱ्या प्रेरणा दाखविलेल्या आहेत. जर I एवढी खांबाची लांबी असल्यास आ. १४ (अ) मधील आधारासाठी I एवढी प्रभावी लांबी घेतात. तसेच (आ), (इ), (ई) साठी अनुक्रमे २ I, I/२ व I/√2 एवढी प्रभावी लांबी धरतात.
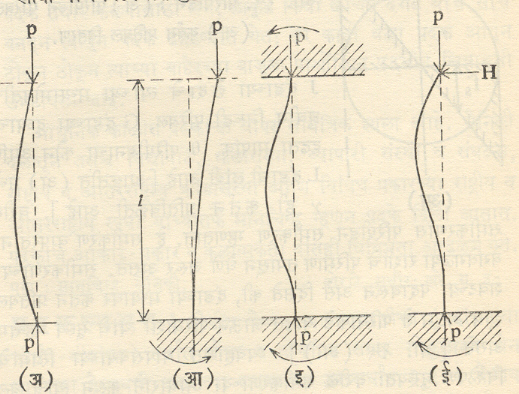
खांबाच्या विश्लेषणात मुख्यतः त्यावरील सीमा भाराचे मूल्य ठरविणे हा भाग येतो. वर दिलेल्या खांबाचे आधार व त्यावर येणाऱ्या भार परिस्थितीनुसार सूत्रामध्ये फरक होतो. आ. १४ (अ) मध्ये दिल्या प्रमाणे दोन्ही टोकाला मुक्ताधार असणाऱ्या उंच खांबाकरिता लेनर्ड ऑयलर यांचे सूत्र खालीलप्रमाणे आहे.
p = π2EI/I2
यात p हा खांबावरील सीमा भार आहे. वरील सूत्राशिवाय (१) रँकिन-गॉर्डन सूत्र, (२) सरल रेषीय सू्त्र, (३) जॉन्स्टन अन्वस्तीय सूत्र, (४) भारतीय मानक संस्थेचे सूत्र इत्यादींचाही वापर करतात. भारतीय मानक संस्थेने तयार केलेले सूत्र अनेक प्रकारच्या परिस्थितींत वापरता येते (भारतीय मानक क्र. ८००-१९६२). खांबाचा उपयोग इमारती, विविध प्रकारच्या संरचना, यंत्रे इत्यादीमध्ये सर्रास करतात. म्हणून त्यासंबंधीच्या सूत्रांना विशेष महत्त्व आहे.
परिपीडन: एखाद्या दोरीच्या तुकड्याचे एक टोक एका हातात घट्ट पकडून दुसरे टोक वळवीत राहिले, तर दोरील पीळ पडतो. पीळ पडण्याच्या किंवा घालण्याच्या क्रियेला परिपीडन असे म्हणतात. अक्षीय किंवा अभिलंबित प्ररेणेने परिपीडन होऊ शकत नाही. त्यासाठी परिबलच लावावे लागते. उदा., बोल्टवरील नट फिरवून बसविणे. परिपीडनाने वस्तूत कर्तन प्रतिबल निर्माण होते. परिपीडनाने निर्माण होणारे कर्तन प्रतिबल हे खालील समीकरणाने काढतात. आ. १४ मध्ये दंडाचे परिपीडन परिबल दाखविले आहे.
|
fs |
= |
T |
= |
Gθ |
… …. …. (२०) |
|
r |
J |
L |

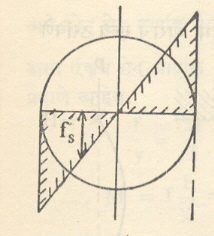
यामध्ये fs हे r एवढ्या अंतरावरील कर्तन प्रतिबल, r दंडाच्या मध्यापासून एखाद्या बिंदुचे त्रिज्यात्मक अंतर, T परिपीडन परिबल, J दंडाच्या छेदाचे त्याच्या मध्याभोवतीचे ध्रुवीय निरूढी परिबल, G दंडाच्या द्रव्याचा दृढता मापांक, ϕ परिपीडनाचा कोन आणि L दंडाची लांबी आहे [ आकृतीत (अ) मध्ये y ही कर्तन प्रतिविकृती आहे]. वरील समीकरणास परिपीडन समीकरण म्हणतात. हे समीकरण वापरताना वेगवेगळ्या राशींचे परिमाण तपासून घेणे जरूर असते. समीकरणाच्या शेवटच्या पदावरून असे दिसते की, दंडाच्या मध्यावर कर्तन प्रतिबल शून्य असून ते परिघाकडे वाढत जाऊन परिघाशी त्यांचे मूल्य महत्तम असते [ आ. १५ (आ) ]. व्यवहारात वापरावयाच्या स्प्रिंगांचे विश्लेषण मुख्यतः वरील समीकरणाच्या आधाराने करून त्यांचे बल ठरवितात.
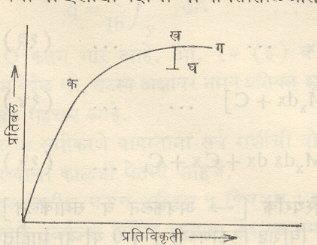
विसर्पण व प्रतिबल शिथिलन: कुठल्याही वस्तूवर बाह्य प्रेरणांमुळे येणारे प्रतिबल कायम असूनही तीत होणारी कालावलंबी प्रतिविकृती म्हणजेच पदार्थाचे विसर्पण होय. आ. १६ मध्ये ताण परीक्षा करता येणाऱ्या एखाद्या पदार्थाच्या बाबतीतील प्रतिबल-प्रतिविकृतीचा आलेख दाखविलेला आहे. जेव्हा या परीक्षेत पदार्थावरील प्रतिबल ख या आकार्य ( आकार देता येण्या सारख्या) अवस्थेतील बिंदूइतके कायम ठेवले तरीही पदार्थातील प्रतिविकृती काही काळ वाढत जाते. या अवस्थेच्या बदलाला विसर्पण म्हणतात. या उलट ख या आकार्य अवस्थेतील बिंदूइतकी प्रतिविकृतीं कायम ठेवण्याचा प्रयत्न केला, तर प्रतिबल कमीकमी होऊन घ या बिंदूशी स्थिरावते. पदार्थाच्या या क्रियेला विसर्पणित प्रतिबल शिथिलन असे म्हणतात. पदार्थाच्या विसर्पणामुळे आणि प्रतिबल शिथीलनामुळे बोल्ट सेल होणे, खांबांना अकाली बाक येणे इ. गोष्टी होतात [⟶ धातूंचे यांत्रिक गुणधर्म].
पदार्थांच्या गुणधर्माचे मापन: आतापर्यंत यंत्रभागावर किंवा अभियांत्रिकीय संरचनेतील भागावर येणारे भार आणि त्यामुळे पदार्थात निर्माण होणारी प्रतिबले व प्रतिविकृती यांचा विचार केलेला आहे. पदार्थांचे बल व त्यांची भारक्षमता यांच्या मापनाचा विचार पुढे केला आहे. अभियांत्रिकीय प्रकल्पात वा विविध यंत्रात हजारो धातवीय व अधातवीय पदार्थ वापरतात. पदार्थांचे गुणधर्म ज्या ठिकाणी पदार्थ प्रत्यक्ष उपयोगात आणावयाचे त्या ठिकाणच्या परिस्थितीत योग्य असावे लागतात. तसेच पदार्थांची गुणवत्ता योग्य असल्याची खात्री करावी लागते. म्हणून अभियांत्रिकीय प्रकल्यात वापरलेल्या पदार्थांचे मानक विनिर्देश (प्रमाणभूत मोजमापे) तयार करतात. त्यामुळे अभियंते, ग्राहक व उत्पादक यांना मार्गदर्शन होते. राष्ट्रीय पातळीवर प्रत्येक राष्ट्रातील मानक संस्था (भारतात भारतीय मानक संस्था) विविध पदार्थांचे मानक विनिर्देश तयार करते. आंतरराष्ट्रीय पातळीवरही अशा तऱ्हेने मानक विनिर्देश उपलब्ध आहेत. मानक विनिर्देशामध्ये पदार्थांचे महत्त्वाचे गुणधर्म, जरूर असल्यास उत्पादन प्रक्रिया, परीक्ष्य नमुन्याचा आकार व मोजमाप, परीक्षा पद्धती, मानक आकार (गोल, चौरस इ.) असल्यास त्यांची मोजमापे यांची माहिती असते.
पदार्थांच्या महत्त्वाच्या गुणधर्मांचे मापन केले जाते. धातूंच्या बाबतीत स्थितिस्थापकीय ताण, परिपीडक व कर्तन बल हे महत्त्वाचे गुणधर्म असतात. तसेच विशिष्ट परिस्थितीत कठिनता, आकार्य विरूपण, आघातक्षमता, शरण बिंदु (ज्या प्रतिबलाला भार स्थिर व कमी असताना पदार्थात आकार्य विरुपण येते ते प्रतिबल), शिणवटा, विसर्पण इ. गुणधर्म तपासून पहावे लागतात. या परीक्षा यंत्राच्या साहाय्याने धातूंच्या लहान नमुन्यावर केल्या जातात व त्यात नमुन्याचा विनाश होतो. पदार्थाच्या नमुन्यावर केल्या जातात व त्यात नमुन्याचा विनाश होतो. पदार्थाच्या नमुन्यावर विशिष्ट प्रकारचा भार लावून प्रतिबल व प्रतिविकृती यांचा संबंध दर्शविणारा आलेख काढला जातो (आ. ४). काही यंत्रात स्वयंचलित रीत्या प्रतिबल व प्रतिविकृती यांचा आलेख कागदावर काढण्याची सोय असते. विनाशी परीक्षासंबंधी माहिती ‘धातूंचे यांत्रिक गुणधर्म’ या नोंदीमध्ये दिलेली आहे.
स्थापत्यशास्त्रात मोठ्या प्रमाणावर लगणाऱ्या सिमेंट, काँक्रीट, भाजलेल्या विटा, लाकूड यांसारख्या अधातवीय पदार्थांचे ताण व संपीडक बल हे धातूंचे बल काढण्यास लागणाऱ्या यंत्रावर किंवा तत्सम यंत्रावर काढले जाते. त्याकरिता नमुन्याचा मानक आकार निराळा असतो. तसेच प्रत्येक पदार्थाकरिता आणखी काही परीक्षा कराव्या लागतात. उदा., सिमेंटचे कण सूक्ष्म असणे जरूर असते. त्याकरिता विशिष्ट चाळणीतून सिमेंट चाळून तिच्यातून न जाणारा भाग वर्ज्य करतात. काँक्रीटमधील घटकांचे (सिमेंट, खडी, वाळू व पाणी) प्रमाण ठरलेले असते [⟶ काँक्रीट]. वीट किंवा दगड यांमध्ये पाणी शोषणाचे प्रमाणसुद्धा जास्त असता कामा नये. ठिसूळ अधातवीय पदार्थांचे लहान तुळईच्या आकाराचे नमुने करून यंत्रामध्ये आडवा भार देऊन त्याच्या ताण बलाची परीक्षा केली जाते. काही अधातवीय पदार्थांचे रासायनिक घटक संशोधन करून ठरविंतात. उदा., प्लॅस्टिक, रबर इत्यादी. अग्निसह विटा बाष्पित्राच्या भट्ट्यांमध्ये उच्चतम तापमानाला टिकाव्या लागतात. अशा विटांची उच्च तापमानात परीक्षा केली जाते.
वर दिलेले गुणधर्म काढताना नमुना तुटेपर्यंत परीक्षा करतात. त्यामुळे अंतिम बल मिळू शकते. तसेच विशिष्ट भारापर्यंत भार काढल्यावर प्रतिविकृती पूर्णपणे नाहीशी होते. ह्या विशिष्ट भारास स्थितिस्थापकतेच्या भारापर्यंत भार काढल्याबर प्रतिविकृती पूर्णपणे नाहीशी होते. ह्या विशिष्ट भारास स्थितिस्थापकतेची मर्यादा म्हणतात. यंत्रामध्ये किंवा संरचनेमध्ये कोणत्याही भागात भारामुळे प्रतिविकृती कायम राहता कामा नये. त्यामुळे यंत्राचे कार्य सुरळीत चालू शकत नाही म्हणून स्थितिस्थापकतेच्या मर्यादेपेक्षा प्रतिबल बरेच कमी ठेवावे लागते. नमुन्याची परीक्षा ज्या परिस्थितीत करतात त्यापेक्षा प्रत्यक्षात परिस्थिती पुष्कळच निराळी असते. परीक्षा पद्धतीत नमुन्याचा अनुप्रस्थ छेद लहान असतो त्यामुळे प्रतिबलाचे वितरण सर्व ठिकाणी समान असू शकते. प्रत्यक्ष यंत्रभागाचा छेद मोठा असतो व त्यात समान वितरण असत नाही. काही ठिकाणी प्रतिबल सरासरी प्रतिबलापेक्षा जास्त असते. यंत्रभागाच्या छेदामध्ये अकस्मात बदल होत असल्यास किंवा त्यात छिद्र, खाच असल्यास काही ठिकाणी प्रतिबल केंद्रित होते व त्याचे मूल्य सरासरीपेक्षा खूपच जास्त असू शकते. परीक्षा पद्धतीत नमुन्यावर भार देण्याचा वेग अत्यंत कमी असतो. प्रत्यक्षात वेग इतका कमी नसतो किंबहुना भार आघाती स्वरूपाचा असण्याचा संभव अधिक असतो. परीक्षा पद्धतीत भोवतालचे वातावरण नेहमीचे तापमान व आर्द्रात असलेले असते परंतु प्रत्यक्षात उच्च व नीच तापमान तसेच गंजकारक परिस्थिती असू शकते. बाष्पीत्रामध्ये दाबामुळे प्रतिबल येते तसेच तापमान उच्च असते. प्रशीतकात किंवा अती थंड प्रदेशात नीच तापमान तसेच सुमुद्रावर किंवा रासायनिक प्रक्रियांत गंजकारक परिस्थिती असते. काही ठिकाणी भार चक्रीय असतात व तेथे पदार्थात शिणवटा उत्पन्न होतो. शक्य तितकी प्रत्यक्षात असलेली परिस्थिती कृत्रिम रीत्या निर्माण करून परीक्षा घेण्याच्या नवनवीन परीक्षा पद्धती उपलब्ध होत आहेत. याशिवाय यंत्रभागास लागणारा विशिष्ट आकार व मोजमापे आणण्याकरिता उत्पादक कारखान्यामध्ये विविध प्रक्रिया वा यंत्रे वापरतात व त्यामुळे यंत्रभागात प्रतिविकृती राहतात किंवा दोष निर्माण होतात. अशा सर्व बाबींचा विचार करून यंत्रभागाची सुरक्षित भारक्षमता ठरवावी लागते. ⇨ सुरक्षा गुणांकाचा व पदार्थाच्या यांत्रिक बलाचा उपयोग करून यंत्रभागाचे सुरक्षित प्रतिबल ठरवितात. जास्त खर्च येत नसल्यास प्रत्यक्ष यंत्रभाग तुटेपर्यंत वापरून पाहतात व त्यानुसार त्या यंत्रभागाचा अभिकल्प करतात.
धातूंच्या अनाशी परीक्षांमध्ये क्ष-किरण व गॅमा किरण पद्धत, श्राव्यातीत तरंग पद्धत, चुंबकीय पद्धत, विद्युत् चुंबकीय पद्धत, आवर्ती विद्युत् प्रवाह पद्धत इ. परीक्षा समाविष्ट असून त्यांच्या संबंधीची महिती ‘धातूंचे परीक्षण’ या नोंदीमध्ये दिलेली आहे. यांपैकी काही पद्धती अधातवीय पदार्थाच्या परीक्षणातही वापरतात. यंत्रभाग न मोडता प्रत्यक्ष कार्य करण्याच्या परिस्थितीत भारक्षमतेची परीक्षा करता येते. काही पद्धतींत यंत्रभागाची प्रतिकृती तयार करून तीवर परीक्षा करून विविध प्रतिबले ठरविता येतात. अशा पद्धतींपैकी आणखी काही पद्धती येथे दिल्या आहेत.
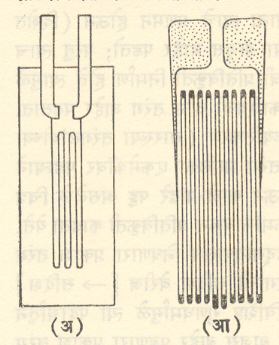
विद्युत् प्रतिविकृतीमापक : विद्युत् संवाहक तारेत विकृती उत्पन्न झाल्यास तिच्या रोघात फरक पडतो. या तत्त्वावर विद्युत् प्रतिविकृतिमापक बनविलेला असतो. या मापकाचा प्रथम उपयोग १९३८ मध्ये अमेरिकेत केला गेला. या मापकाच्या रचनेचे दो न प्रकार आ. १७ मध्ये दाखविले आहेत.

तार किंवा प्रतिविकृती संवेदक वर्ख यांच्या दोन्ही बाजूंना एक प्रकारचे लुकण लावून संरक्षक कागदाच्या पट्ट्या लावतात. मापकाची लांबी ०.८ मिमी. पासून २२५ मिमी. पर्यंत असते. तसेच मापकाचा विद्युत् रोध ६० ते ५,००० ओहम असतो. विद्युत् प्रतिविकृतिमापक यंत्राच्या विभागाच्या विशिष्ट जागी एका प्रकारच्या लुकणाने चिकटवितात. त्या भागावर जेव्हा भार येतात त्या वेळी विद्युत् प्रतिविकृतिमापकाच्या तारेमध्ये किंवा वर्खामध्ये प्रतिविकृती निर्माण होते व त्याचा विद्युत् रोध बदलतो. अशा तऱ्हेने रोधात झालेला बदल ⇨ व्हीट्स्टन सेतुने किंवा ⇨ विद्युत् वर्चस्मापकाने मोजतात. त्यावरून प्रतिविकृतिमापकाच्या लांबीमध्ये म्हणजे पर्यायाने यंत्राच्या भागात उत्पन्न झालेली प्रतिविकृती काढता येते. प्रतिविकृती व प्रितिबल यांची सांगड डुक यांच्या सिद्धांताप्रमाणे घालता येते. अर्धसंवाहक (ज्याची विद्युत् संवाहकता धातू व निरोधक यांच्या दरम्यान असते असा पदार्थ वापरलेला मापक असल्यास त्याला विवर्धक [⟶ इलेक्ट्रॉनीय विवर्धक] वापरावा लागतो. विद्युत् प्रतिविकृतिमापकाच्या लांबीच्या दिशेने प्रतिबल नसल्यास प्रतिविकृती बरोबर मिळणार नाही. प्रमुख प्रतिबलाची दिशा माहीत असल्यास त्या दिशेत मापक बसविता येईल परंतु माहीत नसल्यास एकापेक्षा जास्त म्हणजे दोन किंवा तीन निरनिराळ्या दिशांनी बसविलेले मापक असलेले समूह वापरतात. आ. १८ मध्ये असे मापक दाखविले आहेत.
विद्युत् प्रतिविकृतिमापकाशी संलग्न अशी विविध प्रकारची दर्शक उपकरणे वापरतात. एका विद्युत् प्रतिविकृतिमापकापासून शंभर मापकांचे विद्युत् रोध फरक वाचण्याची क्षणता असलेली उपकरणे उपलब्ध आहेत. रेडिओ प्रेषणाचा उपयोग करून दूरच्या ठिकाणी मापक दर्शक उपकरणे बसविता येतात. ऋण किरण दोलनदर्शकाचा किंवा दोलनलेखकाचा [⟶ इलेक्ट्रॉनीय मापन] व चुंबकीय फितीचाही उपयोग करतात.
प्रकाश स्थितिस्थापकता पद्धती : प्रकाश तरंग भाररहित स्थितीत असलेल्या समदिक् (तेच गुणधर्म सर्व दिशांनी सारखेच असलेल्या) पारदर्शक पदार्थातून जात असताना त्याचे प्रणमन होऊन (दिशेत बदल होऊन) एकच तरंग दुसऱ्या बाजूस बाहेर पडतो परंतु त्याच पदार्थावर भार दिल्यास त्यामध्ये जी प्रतिविकृति निर्माण होते त्यामुळे दुसऱ्या बाजूला द्विप्रणमनामुळे एकाऐवजी दोन तरंग बाहेर पडतात. त्यांचे वेग निराळे असल्यामुळे व्यतिकरण (सारख्या तरंगलांबीच्या दोन वा अधिक तरंगलांबीच्या तरंग मालिका एकमेकींवर पडल्याने निर्माण होणारा आविष्कार) होऊन काळे-पांढरे पट्ट असलेले चित्र तयार होते. व्यतिकरण पट्टाच्या क्रमांकावरून प्रतिविकृती काढता येते.

कोणत्याही एकवर्णी प्रकाश उद्गमापासून निघणारा प्रकाश तरंग हा विविध प्रतलांत असलेल्या तरंगांची सदिश बेरीज [⟶ सदिश] असते परंतु काही पदार्थांच्या विशिष्ट गुणधर्मामुळे त्या पदार्थातून प्रकाश तरंग पाठविल्यास दुसऱ्या बाजूस बाहेर पडणारा प्रकाश तरंग एकाच प्रतलात असतो. बाकीचे तरंग पदार्थात शोषिले जातात. अशा तरंगास प्रतल ध्रुवित प्रकाश तरंग म्हणतात. प्रतलास समांतर असलेल्या अक्षास ध्रुवण अक्ष असे म्हणतात. काही पदार्थांतून ध्रुवित प्रकाश पाठविल्यास त्यातून द्विप्रणमन होऊन दोन प्रतलांत असलेले दोन प्रकाश तरंग निर्माण होतात. प्रकाश स्थितिस्थापक पद्धतीत पदार्थातील प्रतिबले मोजण्याचा हेतू असल्यामुळे व प्रमुख प्रतिबले काटकोनात असल्यामुळे ज्या पदार्थामुळे द्विप्रणमन काटकोनात असलेल्या दोन प्रतलांत होते असेच पदार्थ वापरतात. द्विप्रणमनानंतर प्रकाश तरंगांचा वेग भिन्न असतो व बाहेर पडणाऱ्या तरंगांमध्ये कलांतर (एखाद्या समाइक संदर्भांच्या सापेक्ष असणाऱ्या कोनात्मक स्थितींमधील म्हणजे कलांमधील अंतर) येते. हे कलांतर पदार्थाची जाडी व प्रकाशाची तरंगलांबी यांवर अवलंबून असते. द्विप्रणमनानंतर दोन तरंगांतील कलांतर जर ९०° असेल, तर त्या पदार्थाच्या पट्टीला चतुर्थांश तरंग पट्टी म्हणतात. एका विशिष्ट जाडीची पट्टी विशिष्ट तरंगलांबीच्या प्रकाश तरंगाकरिताच चतुर्थांश तरंग पट्टी असू शकते. वरील पट्टीच्या दोन प्रतलांना समांतर असलेल्या अक्षांना शीघ्र तरंग अक्ष व मंद तरंग अक्ष असे म्हणतात. ध्रुवित प्रकाश तरंग ध्रुवण अक्षाशी θ कोन करीत असला, तर पदार्थातून बाहेर पडणारा तरंग हा ध्रुवित प्रकाश तरंगाच्या ध्रुवण अक्षास समांतर असलेल्या घटकाइतकाच असतो. ध्रुवण अक्षास लंब असणारा घटक पदार्थात शोषणामुळे विरून जातो. जर दोन ध्रुवण पट्ट्यांचे ध्रुवण अक्ष काटकोनात असतील, तर दुसऱ्या ध्रुवण पट्टीतून प्रकाश तरंग बाहेरच येणार नाही. चतुर्थांश तरंग पट्टीचे अक्ष ध्रुवण पट्टीच्या अक्षाशी जर ४५° चा कोन करत असतील, तर द्विप्रणमन होऊन बाहेर पडणाऱ्या प्रकाश तरंगांचे परमप्रसर (एखाद्या स्थिर स्थानापासून होणारे कमाल स्थानांतरण) सारखे होतील. अशा प्रकाश तरंगास वृत्त ध्रुवित प्रकाश तरंग म्हणतात [⟶ प्रकाशकी]. वरील तत्त्वाचा प्रतिविकृती मोजण्याकरिता ध्रुवणदर्शक या उपकरणात उपयोग केला जातो (आ. १९)

यात गाळणी वापरून प्रकाश शक्य तितका एकवर्णी केला जातो. समांतरित्र भिंगामुळे प्रकाश किरण समातंर होतात. ध्रुवकामुळे प्रकाश तरंगाचे ध्रुवण होते. चतुर्थांश तरंग पट्टीमळे प्रकाश तरंगाचे वृत्त ध्रुवण होते व कलांतर ९०° होते. ज्या यंत्राच्या भागातील प्रतिबले काढावयाची असतात त्या भागाची विशिष्ट द्विप्रणमनी पदार्थांच्या पत्र्यापासून बनविलेली प्रतिकृती किंवा नमुना तयार करतात. या प्रतिकृतीवर यंत्राच्या भागावर येणाऱ्या भाराप्रमाणेच भार देण्याची व्यवस्था असते. दोन्ही चतुर्थांश तरंग पट्ट्यांचे शीघ्र तरंग अक्ष समांतर किंवा एकीचा शीघ्र व दुसरीचा मंद अक्ष समांतर ठेवण्याची व्यवस्था असते. विश्लेषक हा ध्रुवकच असतो. त्याचा ध्रुवण अक्ष ध्रुवकाच्या ध्रुवण अक्षास समांतर किंवा काटकोनात ठेवण्याची व्यवस्था असते. ध्रुवक व विश्लेषक पोलरॉइड प्लॅस्टिकापासून बनवितात. चतुर्थांश तरंग पट्ट्या चिरप्रतिविकृत प्लॅस्टिकापासून बनवितात. प्रतिकृतीकरिता सेल्युलॉइड, बेकेलाइट एपॉक्सी रेझीन, यूरेथेन रबर असे विविध पदार्थ वापरतात. आ. २० मध्ये ध्रुवणदर्शकाच्या साहाय्याने दोन दंतचक्रांच्या दात्यांमध्ये भार आला असताना कशा तऱ्हेचा आकृतिबंध दिसतो ते दाखविले आहे. अशा चित्रांवरून प्रत्यक्ष प्रतिविकृती काढून प्रतिबले काढणे इतके सोपे नसते परंतु अशा चित्रांवरून प्रतिबलांचे केंद्रीकरण किंवा वितरण कसे होते याची कल्पना येते. वर दिलेल्या पद्दतीने यंत्राच्या भागाची प्रतिकृती तयार करावी लागते आणि यंत्राचा भाग व प्रतिकृती यांचा आकार तंतोतंत सारखा नसतो. दुसऱ्या एका पद्धतीत प्रत्यक्ष यंत्राच्या भागावर आकार्य़ (प्लॅस्टिक) पदार्थांचा पातळ थर देतात. यंत्रात बसविल्यानंतर त्या भागावर जे भार येतात त्याप्रमाणे भार दिल्यास भागावरील थराला चिरा पडतात व त्यांचे ध्रुवणदर्शकाने छायाचित्र घेता येते व प्रतिबलाविषयी कल्पना येते.
अनुस्पंदन पद्धती: पदार्थामधून जाणाऱ्या ध्वनीचे प्रसारण हे ⇨ अनुस्पंदन पद्धतीतील मूलतत्त्व आहे. एखाद्या आडव्या तुळईंची नैसर्गिक कंप्रता (दर सेकंदात होणारी कंपनसंख्या) आणि तिच्या द्रव्याचा स्थितिस्थापक गुणांक, संपीडक व ताण भार यांचा एकमेकांशी संबंध असतो. खाली दिलेल्या अथवा इतर समीकरणांवरून हा संबंध दिसून येईल.
|
E = Er |
[ |
1 – 0.15 |
f – 40 |
] |
… … …. (२१) |
|
100 |
Er = 52,000 3√ fc … … … … … … … … … … … … … … … … … … (२२)
Er = 70,000 √ ft … … … … … … … … … … … … … … (२३)
यामध्ये E पदार्थाचा (द्रव्याचा) स्थितिस्थापक गुणांक, Er अनुस्पंदन मापांक, f प्रतिबल (किग्रॅ./सेंमी.२ ), fc संपीडक प्रतिबल (किग्रॅ./सेंमी.२ ), आणि ft तणा प्रतिबल (किंग्रॅ./सेंमी.२) आहे.
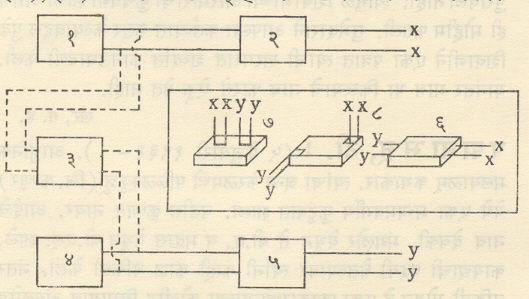
अशा प्रकारच्या परीक्षेमध्ये परीक्ष्य नमुन्याचे कृत्रिम रीत्या अक्षीय, आडव्या अथवा परिपीडक स्थितीमध्ये कंपन करून त्याची कंप्रता मोजतात. मग वरीलप्रमाणे सूत्रे वापरून पदार्थाचे गुणधर्म ठरविता येतात. अशा प्रकारच्या पद्धतीसाठी आ. २१ मध्ये दाखविल्याप्रमाणे मांडणी करतात. हीमध्ये चालक मंडल व उद्ग्रहण मंडल असे दोन भाग असतात. चालक मंडलात विविध कंप्रता निर्माण करणारा आंदोलक व विवर्धक असतात. जरुरीप्रमाणे परीक्ष्य नमुन्याची जोडणी (६),(७),(८) मध्ये करतात. उद्ग्रहण मंडलात कंप्रतामापक व विवर्धक कंप्रतेचे मापन करून मग वर दिल्याप्रमाणे पदार्थाचे गुणधर्म काढता येतात.
तरंग वेग पद्धती: या पद्धतीत परीक्ष्य नमुन्यामधून जाणाऱ्या श्रवणीय तरंगाचा वेग मोजतात. श्रवणीय तरंग हातोड्याने अथवा इतर साधनाने परीक्ष्य नमुन्याच्या एका बाजूला निर्माण करतात व त्या तरंगाला परीक्ष्य नमुन्याच्या दुसऱ्या बाजूला येण्यास किती वेळ लागतो हे मोजावयाचे असते. परीक्ष्य नमुन्याची लांबी माहीत असल्याने श्रवणीय तरंगाचा वेग काढता येतो. श्रवणीय तरंगाचा वेग व पदार्थाचे संपीडन परिबल यांचा संबंध खालील समीकरणावरून अथवा इतर प्रकारे दाखविता येईल.
Fc = 1·52 Ci … … … … … … … … … … … … … … … (२४)
यामध्ये fc संपीडक भार (किग्रॅ./सेंमी.२) व Ci श्रवणीय तरंगाचा अक्षीय वेग आहे.
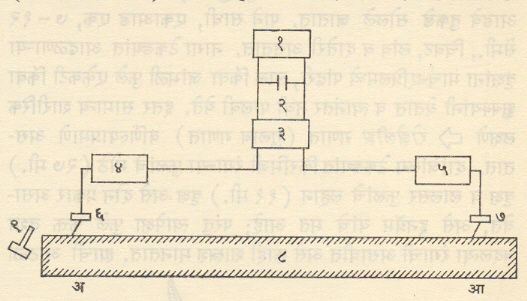
आ. २२ मध्ये दाखविल्याप्रमाणे या पद्धतीतील परीक्षांकरिता मांडणी करतात. हीमध्ये परीक्ष्य तुकड्यावर होतोडा अथवा इतर साधन वापरून श्रवणीय तरंग निर्माण करतात. क्र. १ व २ मधील स्विचद्वारा अ व आ या ठिकाणी तरंग आल्यावर त्यांची नोंद होते. अशा तऱ्हेने अआ हे अंतर कापण्यास तरंगास किती वेळ लागला हे अचूक कळते. या वेळावरून तरंगाचा वेग काढता येतो.
वरील अनुस्पंदन पद्धती व तरंग वेग पद्धती या काँक्रीट, खडक यांसारख्या अधातूंच्या तसेच धातूंच्या परीक्षेकरिता वापरतात.
इ. स. १९५० नंतर विद्युत् उत्पादन, शेती, वैद्यकीय इ. असैनिकी वे सैनिकी क्षेत्रांत अणुऊर्जेचा उपयोग केला जात आहे. त्याकरिता लागणाऱ्या उपकरणात वापरलेल्या पदार्थांवर अणुकेंद्रीय प्रारणांचा (तरंगरूपी ऊर्जेंचा) परिणाम होऊन त्या पदार्थांची कार्याक्षमता कमी होणे अनिष्ट असते. तसेच कृत्रिम उपग्रह आणि अवकाशयान यांमध्ये वापरलेल्या पदार्थांवर विश्वकिरणांचा (बाह्य अवकाशातून येणाऱ्या अतिशय भेदक किरणांचा) परिणाम होऊन या पदार्थांचे कार्य बिघडता कामा नये. म्हणून अणुकेंद्रीय प्रारणांच्या किंवा विश्वकिरणांच्या विविध पदार्थांवर होणाऱ्या परिणामांची परीक्षा घेण्याच्या पद्धती प्रचारात आल्या आहेत.
जमिनीत पुरलेल्या नळांचे संरक्षक, रंग, वेष्टने अथवा व्हिनील प्लॅस्टिकपासून केलेले नळ, जमिनीत पुरलेल्या अभियांत्रिकीय संरचना, जमिनीतील टाक्या, पोहण्याच्या तलावाच्या किंवा कालव्याच्या आतून लावलेले पॉलिथिलीन प्लॅस्टिक अस्तर यांच्यावर शैवल, कवक (बुरशीसारख्या हरितद्रव्यरहित वनस्पती) व सूक्ष्मजंतू यांचे परिणाम होतात, असे दिसून आले आहे. शैवल, कवक आणि सूक्ष्मजंतू यांचा परिणाम होऊ नये म्हणून विविध रसायानांचा उपयोग करतात. त्यांच्या कार्यक्षमतेची परीक्षा करण्याच्या पद्धती उपलब्ध झाल्या आहेत.
विशिष्ट क्षेत्रातील जमिनीत मातीचे जैव घटक माहीत नसतात. त्या वेळी मातीच्या नमुन्यातून कवक, सूक्ष्मजंतू, शैवल, हे घटक अलग करून त्यांची नेहमीच्या पद्धतीने प्रयोगशाळेत वाढ केली जाते. अशा तऱ्हेने उपलब्ध झालेले जैव घटक वापरून विविध पदार्थांवर होणाऱ्या त्यांच्या परिणामांचा अभ्यास केला जातो.
संदर्भ :1. Cement Research Institute of India, Non-destructive Methods of Testing Concrete, New Delhi, 1969.
2. Douglas, R. A. Introduction to Solid Mechanics Wadsworth, 1963.
3. Dove, R. E. Adams, P.H. Experimental Stress Analysis and Motion Measurement, New Delhi, 1965.
4. Jensen, A. Statics and Strength of Materials, New York, 1962.
5. Junnarkar, S. B. Mechanics of Structures, Bombay, 1965.
6. Khanna, P. N. Indian Practical Civil Engineer’s Handbook, New Delhi, 1963.
7. Marin, J. Mechanical Behaviour of Engineering Materials, New Delhi, 1966.
8. Stepin, P. Trans. Konyaeva, M. Strength of Materials, Moscow, 1964.
9. Timoshenko, S. Strength of Materials, 2 Vols. New Delhi, 1965.
10. Warnock, F. V. Benham, P. P. Mechanics of Solids and strength of Materials, London, 1965.
ओगले, कृ. ह. भिडे, गं.का. पाटणकर, मा. वि. सप्रे, गो. वि.
“