तरंग गति : तरंग गती हा भौतिकीतील अत्यंत महत्त्वाचा आविष्कार आहे. समुद्राच्या पाण्यावरील लाटा, ध्वनितरंग, प्रकाश, रेडिओ तरंग, क्ष–किरण, रडार तरंग हे सर्व तरंग गतीचेच वेगवेगळे प्रकार आहेत. इतकेच नव्हे तर डोंगराजवळ वातावरणात तयार होणाऱ्या तरंगांचा हवामानावर होणारा परिणाम, ध्वनीपेक्षा जास्त वेगाने जाणाऱ्या क्षेपणास्त्रे अथवा विमानासारख्या वस्तूंना होणारा वातावरणाचा विरोध, अवकाशयानाचे पृथ्वीवर पुनरागमन होताना त्याच्यावर वातावरणाचा होणारा परिणाम या सर्व घटनांत तरंग गतीचा महत्त्वाचा वाटा असतो. इतकेच नव्हे तर अतिशय वाहतूक असलेल्या रस्त्यांवर मध्यंतरी काही अकस्मात अडथळा आल्यास त्याचे वाहतुकीवर होणारे परिणाम विशिष्ट प्रकारच्या तरंगाप्रमाणेच (आघात तरंग) असतात. त्यांना तरंग गतीचे गणित लावून त्यावरून वाहतूक अधिक सुकर कशी करावी, याबद्दल निष्कर्ष काढता येतात. भूकंपाच्या केंद्रापासून दूरवर होणारे दुष्परिणाम भूकंपाच्या तरंगांच्या पृथ्वीमधून होणाऱ्या प्रसारणामुळे होतात ते कसे कमी करता येतील हे तरंग गतीच्या अभ्यासावरून समजते. इतकेच नव्हे तर आधुनिक भौतिकीनुसार इलेक्ट्रॉन, प्रोटॉन यांसारखे मूलकण आणि म्हणून त्यांच्यापासून बनलेले यच्चयावत वस्तुमात्र तरंगमयच आहे म्हणून गणितात आणि भौतिकीत तरंग गतीच्या अभ्यासाला अनन्यसाधारण स्थान आहे.
माध्यमातून होणाऱ्या कोणत्याही क्षोभांच्या स्थानांतरणास (पुढे जाण्याच्या गतीस) तंरग गती म्हणता येईल. यात माध्यमाच्या कणांचे स्थानांतरण होत नाही परंतु माध्यमाच्या निरनिराळ्या भागांत काही तात्पुरती विकृती (कोणत्याही मूळ भौतिक स्थितीतील बदल) होऊन त्या स्थितीचे स्थानांतरण होते. पाण्याच्या पृष्ठभागावर निर्माण होणारे व पुढे पुढे जाणारे तंरग सर्वांच्या परिचयाचे आहेत. तसेच ध्वनी, प्रकाश वगैरे तरंगरूपानेच स्थानांतरण करतात.
साधारणतः सर्व पदार्थ विकृतीक्षम असून त्यांच्या अंगी स्थितिस्थापकत्व (विकृती घडवून आणणाऱ्या प्रेरणा काढून घेतल्यावर मूळ स्थितीत येण्याचा पदार्थांचा गुण) असते. अशा पदार्थांच्या माध्यमास पदार्थीय माध्यम व त्यात निर्माण होणाऱ्या तरंगांना स्थितिस्थापकीय तरंग असे म्हणतात.
पदार्थीय माध्यमांत तरंग कसे निर्माण होतात व ते प्रवास कसा करतात, हे पाहण्यासाठी साधा प्रयोग करता येईल. एका संथ पाणी असलेल्या लहानशा तळ्यात किंवा पाणी असलेल्या पसरट भांड्यात लहानसा दगड किंवा अन्य तत्सम वस्तू टाकल्यास त्या ठिकाणी पाण्याचे कण वरखाली हालू लागतील. या कणांची (खालीवर होण्याची) गती शेजारच्या कणांना मिळून तेही हालू लागतील व अशा प्रकारे तरंगांचा प्रवास चारी दिशांनी होईल. तरंगांचा प्रवास होत असताना बुचाचा एक लहान तुकडा पाण्यावर तरंगत ठेवल्यास तो त्याच ठिकाणी फक्त खालीवर हालताना दिसेल म्हणजे माध्यमाचे कायमचे स्थानांतरण होत नाही. त्याचप्रमाणे समुद्राच्या लाटा एकसारख्या किनाऱ्याकडे येताना दिसतात पण येथे किनाऱ्याकडे वाहणारा पाण्याचा ओघ निर्माण होत नाही, यावरूनही हे स्पष्ट होईल.
निरूढी (स्थितिबदलास विरोध करण्याचा पदार्थाचा गुणधर्म) आणि स्थितिस्थापकत्व हे पदार्थाचे गुणधर्म आहेत. क्षोभामुळे माध्यमाच्या काही कणांना मिळालेली गती शेजारच्या कणांना मिळते व माध्यमात गतिजन्य ऊर्जेचा संचय होतो. शिवाय कणांचे थोडेबहुत स्थानांतर झाल्यामुळे स्थितिजन्य ऊर्जेचाही संचय होतो. ज्या माध्यमांत गतिजन्य व स्थितिजन्य ऊर्जांचा संचय होऊ शकेल त्यांत स्थितिस्थापकीय तरंग गती संभवते. तरंगाची ऊर्जा म्हणजे माध्यमातील गतिजन्य आणि स्थितिजन्य ऊर्जा होय. या ऊर्जेचा प्रसार एका ठिकाणापासून दुसरीकडे एकदम होत नाही. तो माध्यमाच्या एका थरातून नजीकच्या थरात, तिथून पुढल्या थरात असा होत जाऊन एकूण माध्यम मात्र आहे त्याच ठिकाणी राहते.
विद्युत् चुंबकीय तरंग मात्र अगदी वेगळ्याच प्रकारचे असून त्यांत विद्युत् क्षेत्र व चुंबकीय क्षेत्रातील क्षोभ कोणत्याही माध्यमाशिवाय प्रवास करतो. उदा., प्रकाश तरंग, निरनिराळ्या ताऱ्यांपासून पृथ्वीवर येणारे प्रकाश तरंग निर्वात अवकाशातून येतात.
तरंग वर्गीकरण : तरंगांचे वर्गीकरण निरनिराळ्या पद्धतींनी करतात. पाण्यावरील तरंग, प्रकाश तरंग, ध्वनितरंग वगैरे हे वर्गीकरण भौतिक गुणधर्मांवरून केलेले आहे. त्याचप्रमाणे माध्यमातील कणांची कंपन गती तरंग प्रसारणाच्या दिशेशी निगडित असल्याने या दोन गतींच्या परस्परसापेक्ष दिशांवरूनही तरंगांचे वर्गीकरण करता येते. यानुसार तरंगांचे अवतरंग आणि अनुतरंग असे दोन प्रकार पडतात. अवतरंगात माध्यमाच्या कणांचे कंपन तरंग प्रसारणाच्या दिशेशी लंब दिशेत असते. आ. १ मध्ये दोरीवरील तरंगाच्या साहाय्याने अवतरंगाचे उदाहरण दाखविले आहे. आकृतीत दोरीवरील कणांची कंपन गती तरंग प्रसारणाच्या दिशेशी लंब आहे हे बाणांनी दाखविले आहे.
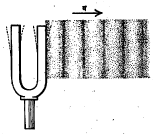
माध्यमाच्या कणांचे कंपन तरंग प्रसारणाच्या दिशेतच असल्यास त्या तरंगास अनुतरंग म्हणतात. अनुतरंगाचे उदाहरण आ. २ मध्ये दाखविले आहे. या आकृतीत दाखविलेली स्प्रिंग अ च्या बाजूने उजव्या बाजूस दाबल्यास प्रत्येक वेटोळे शेजारच्या वेटोळ्यावर दाब देईल व कंपने (अ ने दाखविल्याप्रमाणे) निर्माण होतील. प्रत्येक वेटोळ्याचे स्प्रिंगच्या लांबीच्या दिशेने कंपन होईल व तरंगही त्याच दिशेने प्रवास करेल. ध्वनितरंग हे अनुतरंगाचे उदाहरण आहे. नादकाटा (दोन शाखा असलेले, इंग्रजी Y अक्षरासारखा आकार असलेले आणि आपटल्यास ठराविक नाद देणारे धातूचे साधन) आपटल्यास तो कंप पावू लागतो व ध्वनी प्रसारणाच्या दिशेत एकापाठोपाठ हवेचा जास्त दाबाचा थर व कमी दाबाचा थर अशी मालिका निर्माण होऊन त्यांच्या स्वरूपात तरंगाचे प्रसारण होते. अवतरंगात एकामागोमाग उंचवटा व खोलगट भाग असे तरंगाचे प्रसारण होते. या उंचवट्यास शीर्ष व खोलगट भागास द्रोणी म्हणतात. एक संपूर्ण शीर्ष व नजीकची संपूर्ण द्रोणी मिळून एक पूर्ण तरंग होतो. कधीकधी तरंगात एकच शीर्ष असते व द्रोणी नसतेच अशा तरंगांना एकाकी तरंग म्हणतात.
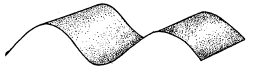
पाण्याच्या पृष्ठभागावरील तरंगात कणांची गती तरंग प्रसारणाच्या दिशेला समांतर व लंब अशा दोन कंपन गतींच्या संयोगाने तयार होते. त्यामुळे कणांचे चलन वर्तळाकृती अथवा दीर्घवर्तुळाकृती असते. आ. ३ मध्ये अशी गती दाखविली आहे व त्याचबरोबर तरंग प्रसारण दिशाही दाखविली आहे.
प्रकाश तरंग (किंवा जंबुपार म्हणजे वर्णपटातील जांभळ्या रंगाच्या पलीकडील किरण, क्ष–किरण, गॅमा किरण वगैरे) हे स्थितिस्थापकीय तरंग नाहीत. यांत प्रसारित होणारा क्षोभ म्हणजे माध्यमाच्या कणांचे चलन किंवा विकृती नसून विद्युत् आणि चुंबकीय क्षेत्रांतील प्रत्यावर्ती (एकाआड एक होणारा) बदल असतो. विद्युत् क्षेत्रातील व चुंबकीय क्षेत्रातील बदल एकमेकांस लंब दिशेने होत असून तरंग प्रसारणाच्या दिशेलाही लंब असतात म्हणून विद्युत् चुंबकीय तरंग हे अवतरंग (किंवा अनुप्रस्थ तरंग) आहेत, असे म्हणतात [→ विद्युत् चुंबकीय तरंग].
तरंगांचे वर्गीकरण आणखी एका पद्धतीने करतात. हे वर्गीकरण मितींवर अवलंबून असते. या पद्धतीत तरंग प्रसारणामुळे किती दिशांत ऊर्जा दिली जाते त्या दिशांच्या संख्येवरून हे वर्गीकरण करतात व त्यानुसार एकमितीय तरंग, द्विमितीय तरंग व त्रिमितीय तरंग असे वर्गीकरण होते. आ.१ मधील दोरीवरील तरंग किंवा आ.२ मध्ये दाखविलेला स्प्रिंगमधील तरंग हे एकमितीय तरंग होत. पाण्याच्या पृष्ठभागावर उमटणारे तरंग हे द्विमितीय तरंग असून ध्वनितरंग व प्रकाश तरंग ही त्रिमितीय तरंगांची उदाहरणे आहेत.
ताणलेल्या दोरीचे एक टोक थोडे बाजुला हालवून उद्‌भवणारा क्षोभ हा दोरीवरून पुढेपुढे सरकत असता (म्हणजे तरंगाचा प्रवास होत असता) दोरीचा कोणताही लहान भाग तरंग त्या ठिकाणी येईपर्यंत स्थिर असतो. तरंग त्याच्यापाशी येताच त्याचे स्थानांतरण होते व पुन्हा तो मूळ ठिकाणी येऊन स्थिर होतो. दोरीच्या टोकास ⇨ सरल हरात्मक गती दिल्यास दोरीवरून तरंगमालिका पाठविता येईल. दोरीच्या प्रत्येक कणास सरल हरात्मक गती मिळेल व सर्व कणांचा आवर्तकाल (ठराविक कालखंडानंतर पुनःपुन्हा घडणाऱ्या घटनांच्या म्हणजे आवर्ती घटनांच्या पूर्ण आवर्तनास लागणारा काळ) एकच असेल परंतु प्रत्येक कणाची कला (आवर्त गतीतील ठराविक संदर्भापासून कोनात मोजली जाणारी गतिविषयक स्थिती) मात्र भिन्न असेल. अशा प्रकारच्या तरंगांना सरल हरात्मक तरंग असे म्हणतात.
तरंगमुख : सर्व दिशांत सारख्या वेगाने जाणाऱ्या तरंगाचा आता आपण विचार करू. एका विशिष्ट क्षणी ज्या ज्या ठिकाणी तरंग पोहोचला असेल ते सर्व बिंदू जोडून जर एक पृष्ठ कल्पिले, तर कालानुसार हे पृष्ठ पुढेपुढे सरकेल व तरंग प्रसारण कसे होते ते कळेल. या पृष्ठातील प्रत्येक बिंदूची एकच कला असेल, अशा पृष्ठास तरंगमुख असे म्हणतात. एकजिनसी व समदिक् (सर्व दिशांत सारखे गुणधर्म असणारे) माध्यम असल्यास तरंग प्रसारणाची दिशा या पृष्ठास म्हणजे तरंगमुखास लंब असते. तरंग प्रसारणाची दिशा दर्शविणाऱ्या रेषांना किरण असे म्हणतात.
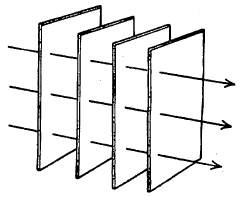
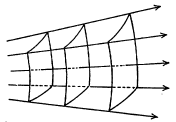
एकाच दिशेत तरंग प्रसारण होत असल्यास तरंगमुख प्रतलीय असते कारण समान कला असणारे बिंदू प्रसारण दिशेशी लंब असलेल्या प्रतलात असतात आणि म्हणून सर्व किरण परस्परांना समांतर असतात. अशा तरंगांना प्रतलीय तरंग असे म्हणतात. आ. ४ मध्ये प्रतलीय तरंग दाखविले आहेत. एका बिंदूपासून सर्व दिशांत सारख्या वेगाने जाणाऱ्या तरंगांना गोलीय तरंग असे म्हणतात कारण यांत तरंगमुख गोल असते. आ. ५ मध्ये उगमबिंदूपासून तरंगमुखांना किरण लंब कसे आहेत, ते दाखविले आहेत. आकृतीतील तरंगमुखे गोलीय पृष्ठे आहेत.
तरंग समीकरण : ताणलेल्या दोरीवरील अवतरंग क्ष अक्षाच्या धन दिशेने पुढेपुढे जातो असे समजू. काल क = ० या विशिष्ट क्षणी दोरीवरील कोणत्याही क्ष ह्या ठिकाणच्या कणाचे स्थानांतर य हे क्ष च्या फलन रूपाने (गणितीय संबंधाच्या रूपाने)
य = फ (क्ष) … … … (१)
असे देता येईल. तरंग प्रसारणाचा वेग व असल्यास क कालानंतर तरंगाचे वक इतक्या अंतरातून प्रसारण होईल. त्या वेळी वरील समीकरण
य =फ (क्ष–व क) … … … (२)
असे होईल. आ. ६ मध्ये समीकरण (१) व (२) यांचे वक्र दिले आहेत.
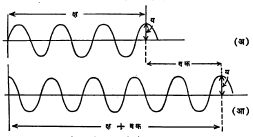
आ. ६ (आ)मध्ये क्ष+ वक या अंतरावरील बिंदूपाशी तरंगाचे स्वरूप आ. ६ (अ) मधील क्ष या अंतरावरील बिंदूप्रमाणेच आहे. फक्त ते व क इतके अंतर पुढे गेलेआहे.
तरंग प्रसारणाचा विचार करताना य ची विशिष्ट मूल्य असणारी स्थिती क्ष व क नुसार कशी बदलते, हे पहावे लागेल. य चे मूल्य स्थिर राहण्यासाठी फ(क्ष–वक) चे म्हणजेच क्ष–वक चे मूल्य स्थिर राहिले पाहिजे. म्हणजे क चे मूल्य जसजसे वाढेल तसतसे क्ष चेही मूल्य त्याच प्रमाणात वाढेल म्हणजेच तरंगवक्र पुढेपुढे सरकेल.
विरुद्ध दिशेने म्हणजे क्ष अक्षाच्या ऋण दिशेने त्याच वेगाने येणाऱ्या तरंगाचे समीकरण
य =फ (क्ष+व क) … … … (३)
असे होईल.
(क्ष–व क) या राशीच्या एखाद्या मूल्यासाठी य चे मूल्य सर्वत्र एकच असते म्हणून (क्ष–व क) यास तरंगाची कला म्हणतात. विशिष्ट कला मूल्यासाठी य ची सर्व मूल्य समान असतात. तरंगाची कला ठराविक असण्यासाठी क्ष–व क = स्थिरांक असले पाहिजे. याचे क सापेक्ष अवकलन केल्यास [→अवकलन व समाकलन]
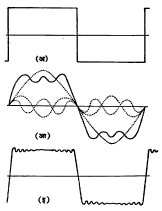
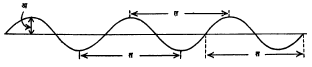
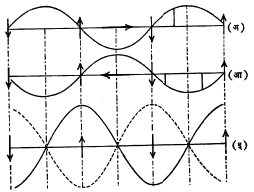
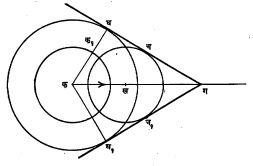
dक्ष = व … … … (४) dक हे समीकरण मिळते. याचा अर्थ व हा तरंगाचा ‘कला वेग’ (कला ज्या वेगाने पुढे सरकते तो वेग) आहे. विरुद्ध दिशेने जाणाऱ्या तरंगाचा कला वेग–व असतो हे समीकरण (३) वरून दाखविता येईल. तरंग समीकरण (२) चा विचार करता असे दिसते की, विशिष्ट क्षणी म्हणजे क ला काही विशिष्ट मूल्य दिल्यास (समजा १० सेकंद) व क हा स्थिरांक होतो आणि मग फ(क्ष–व क) यामध्ये फक्त क्ष हेच चलपद राहते. यामुळे य हा फक्त क्ष चे फलन होते. या परिस्थितीतत क्ष आणि य यांचा आलेख काढल्यास मिळणारा वक्र त्या विशिष्ट क्षणी त्या दोरीची (किंवा माध्यमाची) परिस्थिती दर्शवितो. त्याचप्रमाणे दोरीवर (किंवा माध्यमात) एका विशिष्ट बिंदूपाशी क्ष स्थिरमूल्य असतो. त्या ठिकाणी यहे क चे फलन होते आणि काल क जसजसा बदलतो तसतसे त्याचे स्थानांतर होते म्हणजेच य ही बदलते. क आणि य यांच्या आलेखावरून हा बदल कसा होत जातो, ते स्पष्ट होते. अनुतरंगाच्या आणि इतरही तरंगांच्या बाबतीत अशाच प्रकारचे समीकरण मांडता येईल. ज्या–वक्र तरंग : [त्रिकोणमितीतील ‘ज्या’ गुणोत्तराच्या वक्राच्या आकारासारखे असणारे तरंग→त्रिकोणमिति]. विषयाच्या सुलभतेसाठी क्ष अक्षाच्या दिशेने जाणाऱ्या ज्या-वक्राकृती तरंगांचा विचार करू. सरल हरात्मक तरंगाच्या बाबतीत माध्यमातील सर्व कणांची गती सरल हरात्मक असते, म्हणून त्याचे समीकरण अशा स्वरूपाचे असेल [→सरल हरात्मक गती]. येथे ख हा एक प्रचल (ज्याला परिस्थितीनुरूप मूल्ये देता येतात अशी राशी) असून त्याचा अर्थ पुढे स्पष्ट होईल. य हे बिंदूचे मूळ स्थानापासून होणारे क्षणिक स्थानांतरण (क्षोभ), प आवर्तकाल आणि अ हा कणांचा परमप्रसर (मूळस्थानापासून होणारे जास्तीत जास्त स्थानांतर)आहे. अनुतरंगात य ची दिशा क्ष च्या दिशेत असेल व अवतरंगात ती क्ष च्या दिशेशी लंब दिशेत असेल. उगमापासून क्ष, क्ष+त, क्ष+२त, क्ष+३त वगैरे अंतरांवरील बिंदूंसाठी य ची मूल्ये एकच असल्यास त ने दर्शविलेल्या अंतरास तरंग लांबी म्हणतात. त अंतरावर असणाऱ्या दोन बिंदूंच्या कलांमधील फरक असे लिहिता येईल. या समीरणावरून असे दिसते की, (क+प) कालानंतर (क्ष+त) या बिंदूपाशी समीकरणाचे स्वरूप आहे तसेच राहते म्हणजे प कालात तरंग त इतके अंतर आक्रमितो, म्हणून अध्यारोपण : विशिष्ट माध्यमातून अनेक तरंग जात असल्यास त्यांचा एकमेकांवर काहीही परिणात होत नाही म्हणजेच प्रत्येक तरंग स्वतंत्र असतो. दोन किंवा अनेक तरंग एकत्र आल्यास त्या ठिकाणी होणारा परिणाम हा त्या तरंगांमुळे होणाऱ्या त्या ठिकाणच्या स्थानांतरांच्या सदिश बेरजेने [→सदिश] दिला जातो, या तत्त्वाला अध्यारोपण तत्त्व म्हणतात. विशिष्ट प्रकारचे तरंग विशिष्ट परिस्थितीत एकत्र आल्यास त्यांचा एकमेकांवर परिणाम होऊन काही वैशिष्ट्यपूर्ण आविष्कार प्रतीत होतात, यास व्यतिकरण असे म्हणतात [→प्रकाशकी]. व्यतिकरणाचे स्पष्टीकरण अध्यारोपण तत्त्वानुसार करता येते. व्यतिकरण हा तरंग गतीचा खास आविष्कार आहे. दोन जवळजवळ सारख्या कंप्रतेचे ध्वनितरंग एकदम निर्माण केल्यास त्यांचे व्यतिकरण होऊन परिणामी ध्वनीचा नियमितपणे चढउतार ऐकू येतो. यास विस्पंदन असे म्हणतात. अशा प्रकारच्या व्यतिकरणास कालानुसार होणारे व्यतिकरण म्हणता येईल. दोन सारख्या कंप्रतेच्या, सारख्याच परमप्रसराच्या व सारख्या वेगाने परस्परविरुद्ध दिशेने जाणाऱ्या तरंगांचे व्यतिकरण होऊन अप्रगामी (पुढे न जाणारे) म्हणजेच स्थिर तरंग निर्माण होतात. अशा तरंगांत क्षोभाचे प्रसारण होत नाही. यास अंतरानुसार होणारे व्यतिकरण म्हणता येईल. दोन विरुद्ध दिशांत प्रसारण होणारे तरंग समीकरण (७) व (११) यांनी व्यक्ती करता येईल. समीकरण (१२) हे अप्रगामी तरंगाचे समीकरण आहे. या समीकरणावरून असे दिसते की, सर्व बिंदू सरल हरात्मक गतीने हालतात परंतु २ अ असतो, म्हणून येथे स्थानांतर (क्षोभ) जास्तीत जास्त असते. या बिंदूंना प्रस्पंद बिंदू म्हणतात. दोन शेजारच्या प्रस्पंदांच्या दरम्यानचे अंतरही त/२ म्हणजे अर्ध्या तरंगलांबीइतके असते. आ. (८) मध्ये तरंग प्रसारणाची दिशा उजव्या बाजूच्या दिशेने (+ क्ष च्या) आहे. आ. ८ (आ) मध्ये तरंग प्रसारणाची दिशा डाव्या बाजूच्या दिशेने (–क्ष च्या) आहे. दोन्ही तरंगांचा एकत्रित परिणाम आ.८ (इ) मध्ये दाखविला आहे. हाच अप्रगामी तरंग होय. व्यवहारात अप्रगामी तरंग अनेक प्रकारे मिळतात. तंतुवाद्याच्या तारांवरील तरंग अप्रगामी असतात. बासरी, सनई यांसारख्या सुषिर वाद्यांच्या नळींतील वायूतही अप्रगामी तरंग प्रस्थापित होतात. अप्रगामी तरंगांचे प्रात्याक्षिक एफ्. मेल्डे यांच्या प्रयोगाने दाखविता येते. यात एका नादकाट्याला एक बारीक दोरा बांधून तो दोरा एका कप्पीवरून नेऊन त्याला पाण्यावरील तरंग : पाण्याच्या पृष्ठभागावर उठणारे तरंग किंवा इतर द्रवांवर निर्माण होणारे तरंग. यांची समीकरणे वरील समीकरणांसारखीच परंतु बरीच गुंतागुंतीची असतात. आ.११ मध्ये हे तरंग आपल्या दृष्टीस कसे दिसतात ते दाखविले आहे. पाण्याच्या पृष्ठभागावर कोणत्याही बाह्यकारणाने (उदा., वारा) क्षोभ झाल्यास तरंग निर्माण होतात. गुरुत्वाकर्षण व पृष्ठताण या दोन कारणांनी पाण्याचा पृष्ठभाग सपाट राहण्याची प्रवृत्ती असते. तज्जन्य प्रेरणांमुळे पाण्याच्या (किंवा कोणत्याही द्रवाच्या) पृष्ठभागावर तरंग प्रस्थापित होऊ शकतात. विशिष्ट मर्यादेपेक्षा तरंगलांबी जास्त असेल (पाण्याच्या बाबती १·७ सेंमी. पेक्षा जास्त), तर पृष्ठताणाचा परिणाम दुर्लक्षणीय होतो आणि तरंगांचे नियमन केवळ गुरुत्वाकर्षणामुळे होत असते. मग अशा तरंगांना गुरुत्वाकर्षणीय तरंग असे म्हणतात. याउलट तरंगलांबी विशिष्ट मर्यादेपेक्षा कमी असल्यास तरंगांचे नियमन मुख्यतः पृष्ठताणजन्य प्रेरणांमुळे होत असते. मग त्या तरंगांना वीची किंवा केशाभ तरंग म्हणतात. पाण्यावर केशाभ तरंगांचा वेग २३ सेंमी./से.पेक्षा कमी असतो आणि गुरुत्वाकर्षणीय तरंगांचा वेग या मर्यादेपेक्षा जास्त असतो. समुद्रावरील लाटा : समुद्रपृष्ठावरील लाटा प्रायः वाऱ्याच्या परिणामामुळे उत्पन्न होतात. त्यांची उंची ही वाऱ्याचा वेग व किती लांबीच्या सागरपृष्ठावर त्या वाऱ्याचे कार्य होते, त्यांवर अवलंबून असते. लाटांची उंची पाण्याच्या खोलीवरही अवलंबून राहते. विशिष्ट मर्यादेपेक्षा लाटांची उंची वाढली, तर लाटांची शीर्षे पुढल्या बाजूला वक्र होऊन शेवटी कोसळतात आणि खळबळाट व फेस निर्माण होतो. अशा लाटांमुळे सागरात तरंगणारे पदार्थ किनाऱ्यावर फेकले जातात. उंच लाटा किनाऱ्यावरील खडकांवर किंवा धक्क्यावर किंवा जहाजावर आपटून त्यांचे परावर्तन होते. ही परावर्तित लाट व मूळ लाट परस्परांना पूरक होतात आणि त्यामुळे किनाऱ्यावरील बांधकामाचे नुकसान होते किंवा जहाजाजवळ लाटांची उंची इतकी वाढते की, ती लाट जहाजावरून जाऊ शकते. गोदीतील पाण्यात अप्रगामी तरंग निर्माण होऊन प्रस्पंद बिंदूपाशी लाटा खूप उंच होतात. महोर्मी : पाण्याच्या प्रवाहातील झडप एकदम उघडण्यामुळे किवा झाकण्यामुळे पाण्याच्या ओघात एकदम बदल होतो त्यामुळे एक मोठ्या उंचीची लाट तयार हाते, तिला महोर्मी म्हणतात. भरतीची लाट खाडीत घुसते तेव्हा ही अशी महोर्मी (टायडल बोअर) निर्माण होते. जलविद्युत् केंद्रातील जलटरबाइनाला पाणी पुरविणाऱ्या नळाची झडप उघडली किंवा झाकली जाते तेव्हा अशी जोरदार महोर्मी निर्माण होऊन नळ फुटण्याचा धोका असतो. त्याचप्रमाणे विद्युत् प्रवाहात एकदम फेरबदल झाल्यास विद्युत् वाहकात विद्युत् महोर्मी निर्माण होऊन तिच्यामुळे नुकसान होऊ नये म्हणून व्यवस्था करावी लागते. नळामधून वाहणाऱ्या पाण्याच्या गतीत अचानक बदल झाल्यास पाण्याच्या दाबातही एकदम बदल हातो. त्यामुळे नळामध्ये दाब तरंग निर्माण होतात. दाबातील बदलामुळे पाण्यात महोर्मी तयार होऊन हातोड्याने मारल्यासारखा खाडSS खाड आवाज उत्पन्न होतो, याला जल मुद्‌गल किंवा जलाघात असे म्हणतात. पंप चालू असता जलाघात सुरू होण्याचा विशेष संभव असतो. जलाघातामुळे नळाची नुकसानी होण्याचे भय असते. महोर्मी हा एक प्रकारे आघात तरंगाचाच आविष्कार असतो. आघात तरंग : ध्वनितरंगात दाबामध्ये फेरबदल होत जातात म्हणून त्या तरंगांना ‘दाब तरंग’ असेही म्हणता येते परंतु सामान्यतःध्वनितरंगातील दाबातील चढ–उतार वातावरणीय दाबाच्या एक दशलक्षांश या सुमाराचे म्हणजे अत्यल्प असतात. ज्या दाब तरंगात दाबातील फेरबदल फार मोठे असतात, त्यांना आघात तरंग असे म्हणतात. या प्रकारचे तरंग घन, द्रव किंवा वायुरूप यांपैकी कोणत्याही माध्यमात निर्माण होऊ शकतात. वातावरणात मोठा बाँबस्फोट झाला किंवा वीज पडली, तर तेथे तात्कालिक स्वरूपात प्रचंड दाब निर्माण होऊन आघात तरंग निर्माण होतात. ध्वनिवेगापेक्षा जास्त वेगाने उड्डाण करणाऱ्या विमानाची पुढची हवा दाबली जाऊन आघात तरंग उत्पन्न होतो व हा आघात तरंग जेव्हा जमिनीवर येऊन पोहोचतो तेव्हा तेथे स्फोटासारखा प्रचंड आवाज निर्माण होतो, त्याला श्राव्य गर्जना (सॉनिक बूम) असे म्हणतात. आघात तरंगमुखात कित्येक दशलक्ष वातावरणीय दाबाइतका प्रचंड दाब निर्माण होतो आणि त्यामुळे तेथील तापमानातही कित्येक सहस्र अंश से.ची वाढ होते. मात्र ही परिस्थिती सु. एक सहस्रांश सेकंद इतकी अल्पकालिक असते. आघात तरंगांचा वेग ध्वनिवेगापेक्षा जास्त असतो. दाबातील वाढ जितकी जास्त तितका आघात तरंगाचा वेगही जास्त असतो. आघात तरंग जसजसा पुढे जातो तसतसा प्रसरणामुळे त्यातील दाब व तापमान कमी कमी होत जातात आणि दाब पुरेसा कमी झाल्यानंतर पुढे त्या तरंगाचे प्रसारण मग ध्वनिवेगानेच होत जाते. घन पदार्थातही आघात तरंगांचे गुणधर्म सामान्यतःवरीलप्रमाणेच असतात. अशनिपात (बाह्य अवकाशातील पदार्थ पृथ्वीवर पडणे), भूगर्भातील उद्रेक किंवा बाँबस्फोट यांमुळे जमिनीत आघात तरंग निर्माण होतात. धातूंमधून आघात तरंग जाऊ देऊन त्यावरून अती उच्च दाब व उच्च तापमान यांमुळे धातूच्या गुणधर्मात काय फरक होतात, त्याचा अभ्यास करणे शक्य होते. अशा प्रकारच्या अभ्यासातून विस्फोटक पद्धतीने धातूंचे जोडकाम, झाळकाम, विलेपन यांसारख्या क्रिया करण्याच्या पद्धती प्रगत झालेल्या आहेत. आघात नलिका या उपकरणात वायू भरून त्यातून आघात तरंग सोडता येण्याची व्यवस्था केलेली असते. आघात तरंगामुळे त्या वायूत सु. १५,०००° के. इतके उच्च तापमान निर्माण होऊ शकते. यामुळे रासायनिक गतिकीमधील (रासायनिक विक्रियांचा वेग, या वेगांवर परिणाम करणारे घटक व त्यांवर अवलंबून असलेली विक्रियांची यंत्रणा यांचा अभ्यास करणाऱ्या शास्त्रामधील) काही प्रयोग करणे शक्य झालेले आहे. आघात तरंगामुळे निर्माण होणाऱ्या उच्च तापमानाचा उपयोग करून नियंत्रित अणुसंघटन करण्याचे (दोन निरनिराळ्या अणूंचा संयोग करण्याचे) प्रयत्न चालू आहेत. एखादे पातेले, नादकाटा वगैरे वस्तूंस धक्का लागल्यास त्यांत कंपने सुरू होतात आणि जास्त दाब व कमी होतात. हे कानावर पडल्यास आवाजाची संवेदना होते. आ. १२ मध्ये नादकाट्याच्या कंपनाने दाब तरंग कसे निर्माण होतात ते दाखविले आहे. त्यात एका मागोमाग संपीडन (माध्यमाचे आकुंचन) व विरलता कशी असते हे दिसून येते. व्हायोलिनाच्या तारेच्या कंपनामुळे, घशातील स्वरयंत्रातील कंपनामुळे किंवा तबल्यावरील थापेमुळे ध्वनितरंग निर्माण होतात. यांत कंप्रता २० पासून २०,००० हर्ट्‌झपर्यंत असल्यास तो ध्वनी मनुष्यास ऐकू येतो म्हणजे तो श्रवण गोचर असतो. २०,००० हर्ट्झपेक्षा जास्त कंप्रता असल्यास त्या ध्वनितरंगास श्राव्यातीततरंग असे म्हणतात. अशा तरंगांचे अनेक शास्त्रीय आणि व्यावहारिक उपयोग होतात [→ श्राव्यातीत ध्वनिकी]. २० ते २०,००० हर्ट्‌झ कंप्रता असणाऱ्या तरंगास श्राव्य तरंग असे म्हणतात. भूकंप तरंग : काही अंतर्गत घडामोडींमुळे पृथ्वीच्या कवचात (पृथ्वीच्या पृष्ठाखाली थोड्या अंतरापर्यंतच्या भागात) काही विक्षोभ (उदा., खडकांच्या सापेक्ष हालचाली) निर्माण होतात व त्यामुळे तरंग निर्माण होतात. या तरंगांपैकी प्राथमिक तरंग ध्वनितरंगासारखे म्हणजे अनुतरंग असून द्वितीयक तरंग हे अवतरंग असतात. प्राथमिक तरंगांचे पृथ्वीच्या सर्व भागातून प्रसारण होऊ शकते, तर द्वितीयक तरंगांचे पृथ्वीच्या गाभ्यातील काही भागातून प्रसारण होऊ शकत नाही. यावरून पृथ्वीचा गाभा द्रवरूप असावा असे अनुमान निघते. प्राथमिक तरंगांचा वेग द्वितीयक तरंगांच्या वेगाच्या सु. दुप्पट असतो. या दोहोंचा परिणाम म्हणून निर्माण होणाऱ्या पृष्ठीय (किंवा दीर्घ) तरंगांचे पृथ्वीच्या फक्त पृष्ठभागातून प्रसारण होते [→भूकंप]. असे तरंग भूपृष्ठाखाली स्फोट करूनही निर्माण करता येतात आणि त्यांच्या प्रसारणाच्या अभ्यासावरून खनिज संपत्तीचा शोध घेणे शक्य होते [→ खनिज पूर्वेक्षण]. नाळ तरंग : एखाद्या माध्यमातून वस्तू त्या माध्यमातील तरंगवेगाहून जास्त वेगाने जात असल्यास तरंगमुख आ. १३ मध्ये दाखविल्याप्रमाणे निर्माण होते. माध्यमातून एकसम वेगाने जाणारी वस्तू क या बिंदूपाशी आल्यावर तिथून गोल तरंग प्रसारित होईल. काही कालानंतर वस्तू ख या बिंदूपाशी येईल, परंतु तरंग प्रसारणाचा वेग वस्तूच्या वेगापेक्षा कमी असल्याने तरंग कक१इतके अंतर जाईल. ख पासून दुसरा तरंग निघेल व ट इतक्या अधिक कालानंतर क पासून निघालेला तरंग घ या बिंदूशी, ख पासून निघालेला तरंग च या बिंदूपाशी आणि वस्तूपासून निघणारा तरंग ग या बिंदूपाशी असल्याने तरंगमुख घचग व दुसऱ्या बाजूला घ१च१ग निर्माण होईल. नाव पाण्यावरून वेगाने जात असताना असे तरंग निर्माण होतात. तरंग प्रसारण सर्व दिशांत होत असल्यास तरंगमुख शंकूच्या आकाराचे असते. तरंग गती समीकरण : तरंग गतीच्या समीकरणात दोन चल पदे असल्याने तिचे समीकरण आंशिक अवकलजयुक्त मिळते [→अवकल समीकरणे]. न्यूटन यांच्या गतिकीविषयक नियमाने हे समीकरण काढता येते. एकमितीय तरंगासाठी ते असे येते. या व हा तरंग प्रसारणाचा वेग असून य, क्ष आणि क यांचे अर्थ मागे दिल्याप्रमाणेच आहेत. हे समीकरण सोडवल्यास य = फ (क्ष–व क) + प (क्ष + व क) … … (१४) हा निर्वाह (उत्तर) मिळतो. फ आणि प ही स्वेच्छ फलने आहेत. याच प्रकाराने तीनही दिशांत प्रसारण होणाऱ्या तरंगांचेही समीकरण मांडता येते. द्रवात प्रसारण होणारे ध्वनितरंगदेखील वरील अवकल समीकरणाची पूर्तता करतात. द्रवात त्या तरंगांचा वेग वायूतील प्रसारणाच्या वेगापेक्षा जास्त असतो. घन पदार्थातून जाणाऱ्या ध्वनितरंगांच्या प्रसारणाचा वेग त्या त्या पदार्थांच्या गुणधर्मावर अवलंबून असतो. एकमितीय तरंग गतीचे समीकरण वरीलप्रमाणेच असते. परंतु धातूच्या गजातून किंवा फलकातून जाणाऱ्या तरंग गतीचे अवकल समीकरण चतुर्थ कोटीचे असते. गज वाकविल्यास त्याचा खालचा भाग आकुंचन पावतो व वरचा भाग ताणला जातो. वाकविण्याची क्रिया थांबविल्यास गज आपला मूळचा आकार धारण करू पाहतो आणि आपणांस तरंग गती मिळते. या तरंग गतीच्या समीकरणात यंग मापांकाचा समावेश होतो, तर फलकातील तरंग गतीच्या समीकरणांत प्वासाँ मापांक विचारात घ्यावा लागतो [→स्थितिस्थापकता]. जटिल तरंगाचे विश्लेषण : सर्वांत सोप्या प्रकारचा तरंग म्हणजे ज्या-वक्र तरंग होय परंतु सामान्यतः व्यवहारात आढळणारे तरंग खूपच जटिल असतात. काही प्रकारच्या जटिल तरंगांचे विश्लेषण तरंग विश्लेषक या खास उपकरणाच्या साहाय्याने करता येते. फूर्ये यांच्या गणिती पद्धतीच्या साहाय्याने [→फूर्ये श्रेढी] कोणताही जटिल तरंग किंवा वक्र हा विशिष्ट ज्या-वक्रीय तरंगांच्या एकत्रित परिणामामुळे बनलेला आहे हे दाखविता येते व हे ज्या-वक्रिय घटक काढता येतात. फूर्ये सिद्धांतानुसार कोणत्याही तरंगाचा आवर्तकाल प असून कोणत्याही काली त्यामुळे होणारा क्षोभ य (क) या फलनाने दिला जात असेल, तर या अनंत श्रेढीने व्यक्त करता येतो. आ. १४ (अ) मध्ये एक आयताकार तरंग दाखविला आहे. या तरंगाचे विश्लेषण करण्यासाठी वरील पद्धतीनुसार श्रेणीतील पहिले तीन घटक घेतल्यास त्यांच्या संयुक्त परिणामामुळे मिळणारा निष्पन्न तरंगाकार आ.१४ (आ) मध्ये दाखविला आहे आणि १५ घटकांच्या संयुक्त परिणामामुळे मिळणारा निष्पन्न तरंगाकार आ. १४ (इ) मध्ये दाखविला आहे. जितके जास्त घटक विचारात घ्यावेत तितका निष्पन्न तरंगाकार मूळच्या तरंगाकाराशी जास्त चांगला जुळतो. तरंगाकार : विशिष्ट तरंगाचा वक्र काढल्यास त्याच्या आकाराला तरंगाकार असे म्हणतात. सरल हरात्मक तरंगांची रूपरेखा ज्या-वक्रीय असते, तर जटिल तरंगांची खूप गुंतागुंतीची असते. ऋण किरण दोलनदर्शकाच्या [→ इलेक्ट्रॉनीय मापन] साहाय्याने अशा तरंगांच्या वक्राचे विश्लेषण करून त्यातील घटक सरल हरात्मक तरंग निश्चित करता येतात. यांचा उपयोग गोंगाट कमी करण्याची साधने, यंत्र सामग्रीची आंदोलने कमी करणे, संगीत वाद्यांची गुणवत्ता पारखणे अशा विविध गोष्टींसाठी होतो. तरंगपुंज : समजा की, विविध तरंगलांब्यांचे तरंग एकाच माध्यमातून प्रवास करीत आहेत व त्यांच्यामधील कलांतरे अशी आहेत की, माध्यमाच्या फक्त छोट्या अशा भागातच सर्व तरंगांमुळे होणारे क्षोभ परस्परांना पूरक आहेत इतर सर्वत्र हे क्षोभ परस्परांचे निराकरण करीत आहेत. मग जेथे सर्व तरंग परस्पर पूरक आहेत तेथे तरंगपुंज तयार झाला असे म्हणतात. तरंग गतीमुळे हा तरंगपुंजही पुढेपुढे जातो. तरंगपुंजाच्या वेगाला पुंजवेग असे म्हणतात. पुंजवेग तरंग वेगाहून वेगळा असू शकतो.⇨पुंजयामिकीमध्ये मूलकण हा एक प्रकारचा तरंगपुंज मानला जातो. तरंग व द्रव्ये : आतापावेतो आपण तरंग म्हणजे काही क्षोभाचे प्रसारण असते व त्यात द्रव्याचे प्रसारण होत नाही हे पाहिले म्हणजे द्रव्य व तरंग यांचे गुणधर्म वेगवेगळे असतात. तथापि द ब्रॉग्ली या फ्रेंच शास्त्रज्ञांनी १९२४ मध्ये असे सिद्ध केले की, कोणत्याही वस्तूस वेग दिला असता त्याच्या ठिकाणी तरंग गुणधर्म दृग्गोचर होतात. त्याची तरंगलांबी त = प/वXवे या सूत्राने मिळते. या सूत्रात प हा प्लांक स्थिरांक असून व आणि वे त्या वस्तूचे वस्तुमान आणि वेग होत. मोठ्या आकारमानाच्या वस्तूची तरंगलांबी इतकी लहान असते की, ती मोजणे अशक्य होते परंतु लहान कणांच्या बाबतीत (उदा., इलेक्ट्रॉन, न्यूट्रॉन वगैरे) तरंग परिणाम दिसून येतात. संदर्भ : 1. Coulson, C. A. Waves, New York, 1955. 2. Sears, F. W. Mechanics, Wave Motion and Heat, Reading, Mass., 1958. 3. Wood, A.Acoustics, London, 1962. गुर्जर, ल. वा. “
एक सुयोग्य वजन टांगतात. नादकाट्याची कंपने सुरू केल्यास दोऱ्यावर आ.९ मध्ये दाखविल्याप्रमाणे अप्रगामी तरंग मिळतात. त्याचप्रमाणे ए. ए. कुंट यांच्या नलिकेच्या साहाय्यानेही अप्रगामी तरंग चांगल्या प्रकारे दाखविता येतात. यात आ. १० मध्ये दाखविल्याप्रमाणे एक आडवी काचेची नळी (१) आणि एक मध्यावर पक्की धरलेली धातूची सळई (२) एका रेषेत ठेवलेल्या असतात. सळईच्या टोकाला एक बुचाचा तुकडा (३) नळीतून सहज मागेपुढे हलू शकेल असा बसविलेला असतो. नळीचे दुसरे टोक (४) या बुचाने बंद केलेले असते व नळीत थोडा लाकडाचा भुस्सा (५) पसरलेला असतो. सळई कापडाच्या किंवा कातडयाच्या साहाय्याने मागेपुढे अशी घासल्यास कंप पावते व ध्वनितरंग निर्माण होतात. नळीत तरंगांचे प्रसारण होऊन त्यांचे (४) या बुचापासून परावर्तन होते व त्यामुळे अप्रगामी अनुतरंग निर्माण होतात आणि भुशाचे पुंजके आ. १० (आ) मध्ये दाखविल्याप्रमाणे आकार धारण करतात.
