ध्वनि

ध्वनि : ध्वनी किंवा आवाज म्हणजे कानाला ऐकू येऊ शकतो तो आविष्कार अशी व्यावहारिक व्याख्या देता येईल. शास्त्रीय परिभाषेत असे म्हणता येईल की, श्रवणेंद्रियाला ज्या उद्दीपनामुळे संवेदना होऊ शकते ते उद्दीपन म्हणजे ध्वनी होय. हे उद्दीपन नेहमी एखाद्या वायू, द्रव किंवा घन माध्यमातील यामिकीय (भौतिक प्रेरणांमुळे निर्माण होणाऱ्या) तरंगांच्या स्वरूपात असते. हे तरंग माध्यमाच्या स्थितिस्थापकतेमुळेच (विकृती निर्माण करणाऱ्या प्रेरणा काढून घेतल्यावर मूळ स्थितीत येण्याच्या पदार्थाच्या गुणधर्मामुळेच) प्रस्थापित होऊ शकतात. म्हणून त्यांना स्थितिस्थापकीय तरंग किंवा ध्वनितरंग असे म्हणतात. मानवी श्रवणेंद्रियाला फक्त सु. १६ हर्ट्‌झ ते २०,००० हर्ट्‌झ या मर्यादांमधील कंप्रतेच्या (दर सेकंदाला होणाऱ्या कंपनसंख्येच्या) तरंगांचाच बोध होऊ शकतो. या प्रकारच्या तरंगांना श्राव्य ध्वनी असे म्हणतात. १६ हर्ट्झपेक्षा कमी कंप्रतेच्या तरंगांना अवश्राव्य ध्वनी व २०,००० हर्ट्‌झपेक्षा जास्त कंप्रतेच्या तरंगांना श्राव्यातीत ध्वनी असे म्हणतात [→श्राव्यातीत ध्वनिकी]. व्यापक अर्थाने सर्वच कंप्रतांच्या यामिकीय तरंगांना ध्वनी असे म्हटले जाते आणि सामान्यपणे याच अर्थाने हा शब्द येथे वापरला आहे. ध्वनीच्या वेगवेगळ्या आविष्कारांचे आणि उपाययोजनांचे भौतिकीच्या दृष्टीतून येथे विवरण केले आहे.

ऐतिहासिक पार्श्वभूमी : आदिमानवाला स्वतःच्या संरक्षणासाठी त्याचप्रमाणे भक्ष्याचा शोध घेण्यासाठी ऐकू येणाऱ्या वेगवेगळ्या ध्वनींवरून योग्य ते निष्कर्ष काढणे व आवश्यक ती क्रिया करणे भाग होते. यामुळे मानवाच्या कर्णेंद्रियाच्या गुणवत्तेत उत्तरोत्तर सुधारणा होत गेली. ध्वनी निर्माण करण्याच्या वेगवेगळ्या साधनांची ओळखही दैनंदिन अनुभवामधूनच झाली असावी. उदा., धनुष्याच्या दोरीच्या टणत्कारावरून तंतुवाद्यांची कल्पना स्फुरणे स्वाभाविक आहे. पुढे काही ध्वनी कानाला गोड लागतात हे पाहून अशा ध्वनींचे संकलन व समायोजन करून त्याने (प्राथमिक स्वरूपाचे) संगीत निर्माण केले असावे.

संगीतातील स्वरांना भौतिकीच्या कल्पना लावण्याचे कार्य पायथॅगोरस या ग्रीक तत्त्वज्ञांनी  इ. स. पू. सहाव्या शतकात केले. हीच ध्वनीच्या शास्त्रीय अभ्यासाची सुरुवात म्हटली पाहिजे. इ. स. पू. पहिल्या शतकात होऊन गेलेल्या मार्क्स व्हिट्रूव्हिअस पोलिओ या रोमन स्थापत्यशास्त्रज्ञांना ध्वनीचे प्रसारण तरंगाद्वारे होते याची स्पष्ट कल्पना होती, असे दिसते परंतु मध्ययुगात ही कल्पना लुप्त होऊन ध्वनी म्हणजे अदृश्य कणांचा प्रवाह होय अशी कल्पना रूढ झाली.

पी. गासँदी यांनी इ. स. १६३५ मध्ये दूरवर उडवलेल्या तोफेचा जाळ दिसणे व बार ऐकू येणे, या घटनांमधील कालखंड मोजून त्यावरून ध्वनीच्या हवेमधील वेगाचे मूल्य काढले. सतराव्या शतकात ध्वनी हा तरंगमय आहे हे गृहीत धरून आयझॅक न्यूटन यांनी ध्वनीच्या हवेतील वेगाचे एक समीकरण शोधून काढले. त्यातील त्रुटी अठराव्या शतकात पी. सी. लाप्लास यांनी दुरुस्त केली. १८७७ मध्ये लॉर्ड रॅली यांनी ध्वनिशास्त्रावर एक ग्रंथ (थिअरी ऑफ साऊंड ) प्रसिद्ध केला. ध्वनीच्या आधुनिक अभ्यासाची हीच सुरुवात होय, असे पुष्कळजण मानतात. त्याआधी जर्मन शास्त्रज्ञ जी. एस्. ओहम व एच्. एल्. एफ्. फोन हेल्महोल्ट्स यांनी एकोणिसाव्या शतकात ध्वनिशास्त्रात, विशेषतः श्रवणक्रियेच्या संदर्भात महत्त्वाची भर घातली होती.

ध्वनितरंगांचे प्रसारण : प्रकाशतरंग निर्वातातून प्रसारित होतात परंतु ध्वनितरंगांच्या प्रसारणासाठी कोणते तरी वास्तव किंवा पदार्थीय माध्यम आवश्यक आहे. या माध्यमाच्या कणांची निरूढी (स्थितिबदलास विरोध करण्याचा गुणधर्म जडत्व) व स्थितिस्थापकता या दोन गुणांमुळेच त्यातून ध्वनितरंगांचे प्रसारण होऊ शकते. निर्वातात ध्वनितरंग प्रस्थापित होऊ शकत नाहीत. सामान्यतः ध्वनीच्या प्रसारणाचे माध्यम हवा हे असते परंतु कोणत्याही द्रायूत (द्रवात किंवा वायूत) फक्त अनुतरंगच (माध्यमाच्या कणांचे कंपन तरंग प्रसारणाच्या दिशेत होणारे तरंगच) संभवू शकतात [→तरंग गति] तेव्हा ध्वनितरंग हे अनुतरंगच असतात, हे उघड आहे. ध्वनितरंगांचे कोणत्याही माध्यमातून प्रसारण होत असताना माध्यमाचे कण आंदोलन पावू लागतात. त्यामुळे काही ठिकाणी माध्यमाचे कण परस्परांच्या अधिक जवळ येतात व त्यामुळे तेथील दाब वाढतो. या ठिकाणी माध्यमात ‘संकोचनʼ उत्पन्न झाले आहे असे म्हणतात. उलट इतर काही ठिकाणी माध्यमाचे कण परस्परांपासून अधिक दूरदूर होतात व त्या ठिकाणचा दाब कमी होतो. अशा ठिकाणी ‘विरलीकरणʼ झाले असे म्हणतात. ध्वनितरंगांच्या मार्गात एकाआड एक अशा परस्परांपासून सारख्या अंतरावर असणाऱ्यासंकोचन व विरलनांची मालिकाच तयार होते. ही मालिका आपल्या कानातील पडद्यावर येऊन पडली म्हणजे तिच्यामुळे त्या पडद्याची आतबाहेर अशी आंदोलने सुरू होतात व तो ध्वनी आपल्याला ऐकू येतो [→श्रवण]. अशा तऱ्हेने ध्वनितरंगात एकामागून एक दाबाचे चढउतार निर्माण होऊन त्यांचे प्रसारण होत असते म्हणून त्याला दाबतरंग असेही म्हणतात.

ध्वनीची तीव्रता फार नसल्यास विशिष्ट माध्यमातील ध्वनीचा वेग केवळ त्या माध्यमाचा स्थितिस्थापक गुणांक व त्याची घनता यांच्यावरच अवलंबून असतो. न्यूटन यांनी गणिताने असे दाखविले की, ध्वनीचे प्रसारण होताना परिणामी होणारा माध्यमाचा स्थितिस्थापक गुणांक E व घनता ρ असल्यास ध्वनीचा त्या माध्यमातील वेग C हा पुढील समीकरणाने दिला जातो.

C =	√	E	…	…	…	(१)
		p

घन पदार्थाच्या गजातून ध्वनीचे प्रसारण होताना ठिकठिकाणी गजाचे आकुंचन व प्रसारण होत असते. तद्‌विशिष्ट स्थितिस्थापक गुणांक म्हणजे यंग गुणांक (Y) होय [→स्थितीस्थापकता]. म्हणून गजातील अनुतरंगांचा वेग

	C =	√	Y
			p

या समीकरणाने मिळतो. वायूतून ध्वनीचे प्रसारण होताना ठिकठिकाणी वायूचे तात्कालिक आकुंचन वा प्रसारण होऊन तेथील तापमान वाढते वा कमी होते परंतु वायू हा उष्णतेचा अत्यंत मंदवाहक असल्याने व ही आकुंचन-प्रसरणे अत्यंत अल्पकालिक असल्याने तेथे उष्णतेचे फारसे संक्रमण होत नाही म्हणजे ही असंक्रमी क्रिया असते ही गोष्ट लाप्लास यांनी स्पष्ट केली. या परिस्थितीत वायूचा  दाब P असल्यास

E = γ P व म्हणून C =	√	γ P	असे समीकरण मिळते.
		p

[येथे γ =	वायूची स्थिर दाब विशिष्ट उष्णता	→ उष्णता.]
	त्याची स्थिर आयतन विशिष्ट उष्णता

वायूंच्यापेक्षा द्रव व घन पदार्थांच्या बाबतीत E/p चे मूल्य जास्त असते त्यामुळे त्यांमध्ये ध्वनीचा वेग जास्त असतो. वायूचे तापमान वाढल्यास त्याची घनता कमी होते त्यामुळे उष्ण वायूत ध्वनीचा वेग वाढतो. गणितावरून हे सिद्ध करता येते की, वायूतील ध्वनीचा वेग वायूच्या निरपेक्ष (केल्व्हिन) तापमानाच्या (T च्या) वर्गमूळाच्या समप्रमाणात असतो.

T_१ आणि T_२ या निरपेक्ष तापमानाला विशिष्ट वायूत ध्वनीचे वेग अनुक्रमे C_१ आणि C_२ असल्यास

	C१	=	√	T१	…	…	(२)
	C२			T२

हवेतील आर्द्रता वाढल्यास हवेची घनता कमी होते आणि त्यामुळे कोरड्या हवेपेक्षा आर्द्र हवेत ध्वनीचा वेग जास्त होतो. या सर्व गोष्टींमुळे ध्वनीच्या प्रसारणात काही गमतीदार आविष्कार अनुभवास येतात. त्यांची चर्चा पुढे येईल. प्रतलीय तरंगांचे एकविध द्रायू माध्यमातील X- अक्षाच्या दिशेत होणारे प्रसारण पुढील अवकल समीकरणाने [ →अवकल समीकरण] दिले जाते.

	∂2ξ	=	E	.	∂2ξ	= C2	∂2ξ	…	…	(३)
	∂t2		p		∂x2		∂x2

येथे ξ हे कणांचे आंदोलनजन्य स्थानांतरण असून E ही माध्यमाची आकारमान-स्थितिस्थापकता ρ ही त्याची घनता आणि t हा काळ होय. ध्वनि-प्रसारणाचे जास्त सार्वत्रिक अवकाल समीकरण पुढीप्रमाणे आहे.

	∂2θ	= C2	∂2θ	…	…	(४)
	∂t2		∂X2

येथे θ = ξ तसेच υ (कणांचा आंदोलनजन्य वेग), s (संकोचन), ρ (माध्यमाची घनता) किंवा p  (तरंगामुळे निर्माण होणारा जादा दाब) यांपैकी कोणतीही राशी घेता येईल. या समीकरणाचा व्यापक निर्वाह [→अवकल समीकरणे]

θ = Af₁ (Ct – x) + Bf₂ (Ct + x)

असा  मिळतो. येथे A व B हे स्थिरांक f₁ असून व f₂ ही दोन स्वतंत्र फलने आहेत.  + X अक्षाच्या दिशेने प्रसारित होणाऱ्या  सरल हरात्मक तरंगांचे [→सरल हरात्मक गति] समीकरण,

θ = a sin	2 π	(Ct – x) = a sin	[	2πCt	–	2πx	]	…	(५)
	λ			λ		λ

असे मिळते. –X अक्षाच्या दिशेने प्रसारित होणाऱ्या तरंगांचे समीकरण,

θ=a sin	2 π	(Ct + x)=a sin	[	2πCt	+	2πx	]	…	(६)
	λ			λ		λ

असे  येते. येथे a हा तरंगांचा ‘परमप्रसरʼ (त्या त्या राशीत होणारा कमाल बदल) व λ ही तरंगलांबी होय.

जास्त तपशीलात न शिरता येथे इतकेच म्हणता येईल की, तरंगांमुळे वायूत होणारे संकोचन फार नसले तरच तरंगवेग C = γP/ρ या समीकरणानुसार मिळतो. परंतु संकोचन विशिष्ट मर्यादेपलीकडे गेल्यास (उदा., बाँबस्फोटाच्या आवाजात) ध्वनीचा वेग वाढतो. ही गोष्ट सैद्धांतिक त्याचप्रमाणे प्रायोगिक रीत्याही सिद्ध झालेली आहे.

कोष्टक क्र. १ मध्ये काही माध्यमांतील ध्वनीच्या वेगाची मूल्ये दिली आहेत. नळ्यांमधील हवेतील ध्वनिवेग मुक्त हवेतील ध्वनिवेगापेक्षा काहीसा कमी असतो.

कोष्टक क्र. १ काही मध्यमांतील ध्वनीचा वेग
माध्यम	ध्वनिवेग (मी./से.)
हवा (तापमान ०° से.)	३३१·४५
हीलियम (तापमान ०° से.)	९७०
हायड्रोजन (तापमान ०° से.)	१,२६९·५
पाण्याची वाफ (१००° से.)	४०४·८
पितळ	३,४२०
पोलाद	५,०५०
लाकूड	१,०१० ते ४,१००
समुद्राचे पाणी (१५° से.)	१,५०४·१५
शुद्ध पाणी (२५° से.)	१,४८६·५

परावर्तन, प्रणमन व पारगमन : हे आविष्कार सर्व प्रकारच्या तरंगांच्या बाबतीत प्रत्ययाला येतात व त्याला ध्वनीही अपवाद नाही.

प्रतिध्वनी : ध्वनितरंग मोठ्या आकाराच्या अडथळ्यावर (उदा., डोंगराचा कडा) आपटून जो परावर्तित ध्वनी ऐकू येतो त्याला प्रतिध्वनी असे म्हणतात. ध्वनीमधील शब्दोच्चार स्पष्ट समजण्यासाठी मूळ ध्वनी व परावर्तित ध्वनी कानावर पडण्यामध्ये किमान १/१५ सेकंद इतका वेळ गेला पाहिजे. ध्वनिवेग लक्षात घेता यासाठी ऐकणाऱ्यापासून अडथळ्याचे अंतर किमान २० मी. तरी असावे लागते. दोन अडथळ्यांमध्ये उभे राहणाऱ्यास त्या अडथळ्यांवरून पुनःपुन्हा होणाऱ्या परावर्तनांमुळे एकाच शब्दाचे प्रतिध्वनी अनेक वेळा ऐकू येऊ शकतात. शोषणामुळे प्रतिध्वनींची तीव्रता कमीकमी होत जाऊन शेवटी तो ऐकू येईनासा होतो. ⇨ कुजबुजणाऱ्या सज्जातून अंतर्गोल भिंतीवरून परावर्तन होऊन ध्वनी एका बिंदूपाशी केंद्रित होतो. भिंती जितक्या जास्त टणक व गुळगुळीत असतील तितका हा प्रकार जास्त प्रकर्षाने अनुभवाला येतो. त्याचप्रमाणे नीच कंप्रतांपेक्षा उच्च कंप्रतांच्या ध्वनीचे परावर्तन जास्त प्रमाणावर होऊ शकते [→प्रतिध्वनि].

निनादन : इमारतीची जमीन, छत व भिंती यांवरून ध्वनीची अनेकदा परावर्तने होऊन तोच आवाज बराच वेळ रेंगाळल्यासारखा वाटतो पण स्पष्ट असे ऐकू येत नाही. याला निनादन असे म्हणतात [→ध्वनिकी].

मोठ्या अडथळ्याऐवजी ध्वनीच्या मार्गात मोठा धुक्याचा थर किंवा ढग आला, तर त्यावरून ध्वनीचे परावर्तन होऊन त्याच्यापलीकडे ध्वनी (नीटसा) ऐकू येत नाही. समुद्रात कित्येक ठिकाणी खडकांचे इशारे देण्यासाठी बसविलेल्या घंटा किंवा कर्णे यांचे आवाज धुक्यामध्ये ऐकू न आल्यामुळे अपघात घडलेले आहेत.

परावर्तनाचे नियम ध्वनी व प्रकाश या दोहोंच्या बाबतीत सारखेच आहेत. परंतु ध्वनीची तरंगलांबी प्रकाशाच्या तरंगलांबीच्या तुलनेने खूपच जास्त असल्याने ध्वनीच्या चांगल्या परावर्तनासाठी परावर्तकाचा आकारही मोठा असावा लागतो.  प्रकाशाप्रमाणेच अंतर्वक्र परावर्तकाच्या साहाय्याने ध्वनीचे केंद्रीकरण करता येते व बहिर्वक्र परावर्तकाच्या योगे त्याचे अपसारण होते.

प्रणमन : ध्वनी जेव्हा एका माध्यमातून दुसऱ्या माध्यमात जातो तेव्हा तेथे त्याच्या मार्गाची दिशा बदलते, त्याला प्रणमन असे म्हणतात. प्रत्यक्षात माध्यमाचे द्रव्य बदलले जाणे आवश्यक नाही. एखाद्या पृष्ठाच्या दोन बाजूंच्या माध्यमात ध्वनिवेग वेगळे असले म्हणजे झाले (उदा., मुक्त वातावरणातील हवा व एखाद्या उघड्या तोंडाच्या नळीतील हवा). अशा वेळी या मधल्या पृष्ठांपासून ध्वनीचे अंशतः परावर्तन व अंशतः पारगमन होते.  त्या दोन माध्यमांची घनता अनुक्रमे ρ₁ व ρ₂आणि त्यांमधील ध्वनिवेग C₁ व C₂असतील, तर त्यांच्या मधल्या सीमेवर येऊन पडणाऱ्या ध्वनिशक्तीपैकी किती भाग पलीकडच्या माध्यमात प्रवेश करेल (p_r) ते पुढील समीकरणाने दिले जाते.

pr =	4ρ2 C2/ρ1 C1	…	…	(७)
	(1+ρ2 C2/ρ1 C1)

p_r ही राशी दोन बाजूंच्या ρ.C या गुणाकारावर अवलंबून आहे हे यावरून स्पष्ट होते. ध्वनीच्या गाळण्या बनविणे, गोंगाट कमी करणे, वाद्यांचे आवाज सुयोग्य यावे अशी रचना करणे यांसाठी वरील समीकरणाचा उपयोग होतो. ρ.C या गुणाकाराला माध्यमाचा ‘विशिष्ट ध्वनिकीय रोध’ असे म्हणतात.

प्रकाशाप्रमाणेच ध्वनीचेही प्रणमन होते व त्याच तऱ्हेने नियम येथेही लागू पडतात. हिवाळ्यात किंवा वाऱ्याच्या दिशेने ध्वनी जास्त दूरपर्यंत ऐकू येऊ शकतो वगैरे प्रकार ध्वनीच्या वातावरणीय प्रणमनामुळे होतात [→ ध्वनिकी]. बहिर्गोल भिंगाच्या आकाराच्या पातळ रबरी पिशवीत कार्बन डाय-ऑक्साइड वायू भरल्यास तिच्या साहाय्याने प्रकाशाप्रमाणे ध्वनीचेही केंद्रीकरण करता येते.

अध्यारोपण : ध्वनीचे दोन झोत परस्परांना छेदून जात असतील, तर त्यांचा एकमेंकावर काहीच परिणाम होत नाही परंतु दोन ध्वनितरंग एका बिंदूचे ठायी एकाच क्षणी आल्यास तेथील माध्यमाच्या कणांचा वेग व दाब प्रत्येक तरंगामुळे त्या ठिकाणी होणाऱ्या त्या राशींच्या सदिश बेरजेच्या इतका होतो. म्हणजे एखाद्या ठिकाणी दोन्ही अनुतरंगामुळे दाबात वाढच होणार असेल, तर तेथे निष्पन्न दाबातील वाढ त्या दोन दाबांच्या वाढीच्या बेरजेइतकी होईल. एका तरंगांमुळे दाबात वाढ (संकोचन) व दुसऱ्यामुळे तितकीच घट होणार असेल (विरलीकरण), तर तेथे निष्पन्न दाबात काहीच वाढ किंवा घट होणार नाही. म्हणजेच संकोचन व विरलीकरण परस्परांना नष्ट करून टाकतील.  या तत्त्वाला तरंगांच्या अध्यारोपणाचे तत्त्व असे म्हणतात.

व्यतिकरण : अवतरंगांच्या (ज्यात माध्यमाच्या कणांचे कंपन तरंगाच्या प्रसारणाच्या दिशेशी लंब दिशेत होते अशा तंरगांच्या) बाबतीत, दोन शिखरे (अगर दोन द्रोणी) एकत्र आल्यास तेथे परिणामी मोठे शिखर (किंवा द्रोणी) निर्माण होईल पण एक शिखर व एक द्रोणी एकत्र आल्यास ते परस्परांना नष्ट करून टाकतील. वरील उदाहरणावरून असा सामान्य नियम सांगता येईल की, एकाच ठिकाणी येणाऱ्या दोन तरंगाच्या कला (एखाद्या संदर्भाच्या सापेक्ष असणारी स्थिती) परस्परविरुद्ध असतील, तर ते तरंग एकमेकांचा परिणाम नष्ट करतील. या नष्ट करण्याच्या प्रकाराला ‘विनाशी व्यतिकरण’ व परस्परांना मदत करून मोठे शिखर (वा द्रोणी) होण्याच्या परिणामाला ‘प्रपोषक व्यतिकरण’ असे म्हणतात. या एकूण परिणामाला व्यतिकरण असे म्हणतात. व्यतिकरण हा तरंगांचा खास असा गुणधर्म आहे व त्याचा प्रत्यय सर्व प्रकारच्या तरंगांच्या बाबतीत येऊ शकतो.

प्रकाशाच्या बाबतीत विनाशी व्यतिकरणामुळे त्या ठिकाणी अंधार उत्पन्न होतो. ध्वनीच्या बाबतीत त्या बिंदूच्या ठायी आवाज दुर्बल होऊन ऐकूही येत नाही, उलट प्रपोषक व्यतिकरणाने आवाज मोठा होतो.

कोणत्याही तरंगात दोन विरुद्ध कला असलेल्या बिंदूमधील अंतर

l	च्या विषम पटीइतके	(उदा.,	l	,	३l	,	५l	)	असते.
२			२		२		२

त्यामुळे एकाच उद्‍गमापासून निघालेले ध्वनितरंग दोन वेगळ्या मार्गांनी जाऊन (विशिष्ट बिंदूत) एकत्र आले व या मार्गांच्या लांब्यांमधील फरक l/२ च्या विषम पटीइतके असले, तर त्या बिंदूपाशी आवाज ऐकू येणार नाही.

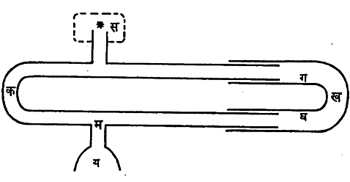
आ.१. मध्ये दाखविलेल्या व्यतिकरण नळीच्या साहाय्याने हे दाखविता येते व ध्वनीची तरंगलांबीही काढता येते. स येथे लहान घड्याळासारखा दुर्बल ध्वनि-उद्‍गम ठेवला असता ध्वनितरंग सकमय आणि सगखघय या दोन वेगळ्या मार्गांनी जाऊन य येथे एकत्र येतात. उजवीकडील सरकती नळी मागे-पुढे सरकवून शेवटी अशी स्थिती आणता येते की, य येथे आवाज अजिबात ऐकू येत नाही. प्रेक्षागृह व सभागृह यांमध्ये विनाशी व्यतिकरणाने काही ठिकाणी आवाज नीट ऐकू येत नाही. याची दखल या इमारतींच्या रचनेच्या वेळी घ्यावी लागते [→ ध्वनिकी]. विस्पंदन व स्थिर तरंग हे ध्वनींच्या व्यतिकरणाचे दोन विशेष आविष्कार आहेत.

विस्पंदन : जवळजवळ समान कंप्रतेचे ध्वनितरंग एकाच माध्यमातून एकाच दिशेने जात असतील, तर ऐकू येणारा आवाज एकसारखा न येता तुटक-‘वाउ–वाउ–वाउ’ असा ऐकू येतो. या प्रकाराला विस्पंदन असे म्हणतात. प्रती सेकंदाला ऐकू येणाऱ्या ‘वाउ’ च्या संख्येला विस्पंद कंप्रता (p) असे म्हणतात.  मूळच्या दोन ध्वनींच्या कंप्रता n₁ व n₂ (n₁ &gt n₂) असतील, तर गणिताने असे दाखविता येते की,

p = n1  – n2

…

…

…

(८)

या समीकरणातील n₁ व n₂ यांपैकी कोणतीही एक कंप्रता ज्ञात असल्यास, प्रयोगाने p मोजून त्यावरून दुसरी अज्ञात कंप्रता वरील समीकरणाच्या साहाय्याने काढता येते. ध्वनिकंप्रता निश्चित करण्याची ही एक अत्यंत अचूक अशी पद्धती आहे. p चे मूल्य ६ पेक्षा जास्त असल्यास विस्पंद नीट मोजता येत नाहीत. सतार, तंबोरा यांसारखी वाद्ये सुरात लावताना या विस्पंदाचा उपयोग केला जातो. विस्पंद ऐकू येऊ लागणे ही दोन स्वरांची कंप्रता जवळजवळ समान असल्याची खूण होय. त्यानंतर खुंटी पिळून तारेवरचा ताण हळूहळू वाढवत (किंवा कमी करत) जातात. तो इतपत की, विस्पंद कंप्रता कमी कमी होत जावी. शेवटी विस्पंद कंप्रता शून्य होईल तेव्हा दोन्ही स्वर बरोबर ‘जुळेलेले’ असतील. सतार, तंबोरा यांच्या स्वरांना येणारी ‘झार’ विस्पंदनामुळेच असते.

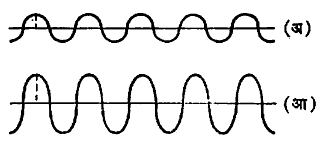
उत्पत्ती : विस्पंदन कसे घडून येते ते आ. २ (अ, आ, इ) वरून समजून येईल. या आकृती हवेतील ध्वनितरंगांच्या विस्थापन आकृती (उद्‍गमापासून विशिष्ट बिंदूंचे अंतर X – अक्षाच्या दिशेने आणि आंदोलनामुळे होणारे त्याचे विस्थापन Y-अक्षाच्या दिशेने दाखवून काढलेले आलेख) आहेत हे लक्षात घ्यावे.

(अ) व (आ) या आकृतींनी दर्शविलेले तरंग एकाच मार्गाने जात आहेत परंतु स्पष्टतेसाठी वेगवेगळे काढले आहेत. १, ३, ५, ७ इ. बिंदूंनी दर्शविलेल्या ठिकाणी दोन्ही तरंगांची शिखरे एकत्र येऊन तेथे निष्पन्न परमप्रसर मोठा होतो. उलट २, ४, ६ इ. बिंदूंवर दोन तरंग परस्परविरुद्ध कलेमध्ये एकत्र येतात आणि तेथे निष्पन्न परमप्रसर शून्य होतो. अशा रीतीने आ. २ (इ) मध्ये दाखविलेल्या आकाराचा निष्पन्न तरंग तयार होऊन तो डावीकडून उजवीकडे जात असतो परंतु आवाजाचा गरिमा (लहानमोठेपणा) परमप्रसराच्या वर्गाच्या प्रमाणात असल्यामुळे १, ३, ५ वगैरे तरंगभाग कानावर पडतात तेव्हा मोठा आवाज ऐकू येतो व २, ४ इ. भाग कानावर पडतात तेव्हा तो ऐकू येत नाही. अशा तऱ्हेने विस्पंदन निर्माण होते. ही गोष्ट गणिताच्या साहाय्यानेही पुढीलप्रमाणे दाखविता येईल.

या दोन्ही तरंगांचे परमप्रसर a आणि कंप्रता अनुक्रमे n₁ व n₂ असल्यास त्यांची समीकरणे पुढीलप्रमाणेलिहिता येतील.

y1 = a·sin 2p{n1t –	x	}
	l

Y2 = a·sin 2∏{n2t –	x	}
	l

अध्यारोपणाच्या तत्त्वानुसार निष्पन्न स्थानांतरण Y = y₁ + y₂,

Y = a [Sin 2p(n1t –	x	)	+ Sin 2p(n2t –	x	)	]
	l			l

त्रिकोणमितीमधील

sin α + sin ß = 2 Cos	α-ß	·sin	α+b
	2		2

हे नित्य समीकरण (चलांच्या, येथे α आणि ß यांच्या, कोणत्याही मूल्यांकरिता सत्य असणारे समीकरण) वापरता,

Y=2a·cos 2∏	(	n1-n2	)	t. Sin2	{	n1-n2	·t-	x	}
		2				2		l

= A sin2∏	{(	n1+n2	·t)	–	x	}	…	…	(९)
		2			l

यावरून निष्पन्न तरंगाची कंप्रता दोन मूळ कंप्रतांच्या सरासरी इतकी आहे व परमप्रसर

A=2a.cos 2∏	(	n1-n2	)	t
		2

इतका आहे व तो काळानुसार बदलतो हे स्पष्ट होते, या ध्वनीचा गरिमा

A2=4a2.cos 2∏	(	n1-n2	)	t
		2

या राशीच्या सम प्रमाणात असेल,

cos θ = 2 cos2	θ	-1
	2

हे नित्य  समीकरण वापरून

A2-2a2{1+cos2∏ (n1-n2)t}

…

(१०)

जेव्हा (n₁  n₂) t = 0, 1, 2, 3, … असेल तेव्हा A² = 4a² व ध्वनी जास्तीत जास्त मोठा ऐकू येईल.

उलट जेव्हा

(n1  n2) t =	१	,	३	,	५	…	…
	२		२		२

असेल, तेव्हा A² = ० आणि ध्वनी ऐकू येणार नाही.

त्याचप्रमाणे (१०) या समीकरणावरून हेही दिसून येते की, कोणत्याही दोन लागोपाठच्या विस्पंदामधील कालखंड  1/n₁ – n₂ से. येतो व म्हणून प्रतिसेकंद (n₁  – n₂)विस्पंद होतात व हीच विस्पंद कंप्रता होय.

स्थिर तरंग किंवा अप्रगामी तरंग : नेहमीच्या तरंगात विशिष्ट क्षोभ किंवा स्थिती पुढे पुढे सरकत असते, परंतु दोन समान कंप्रतेचे व समान (वा जवळजवळ समान) परमप्रसराचे तरंग एकाच रेषेवरून परस्परविरुद्ध दिशेने मार्गक्रमण करीत असतील, तर त्यांच्या अध्यारोपणामुळे होणाऱ्या निष्पन्न गतीला अप्रगामी तरंग किंवा स्थिर तरंग असे म्हणतात, कारण या गतीमध्ये क्षोभाचे मागे किंवा पुढे असे मार्गक्रमण होत नाही. माध्यमाचे सर्व कण एकाच कंप्रतेने आंदोलित होत असतात पण त्यांच्या परमप्रसरांत अंतरानुसार आवर्ती बदल होत जातात.  मूळचे दोन्ही तरंग X–अक्षाच्या दिशेने प्रसारित होत असतील तर संदर्भ बिंदूपासून x अंतरावरील कणाचा निष्पन्न परमप्रसर

A	=	2a. cos	(	2p	)	…	…	…	(११)
				l

या समीकरणाने दिला जातो [→तरंग गति]. येथे a हा मूळ तरंगांचा परमप्रसार आणि λ ही त्यांची तरंगलांबी होय.

समीकरण (११) वरून हे दिसून येते की, ज्या बिंदूच्या बाबतीत

x=0,	l	,	3l	,	5l	……….
	4		4		4

वगैरे असेल त्याच्या ठायी परमप्रसराचे मूल्य शून्य होते व म्हणून येथील माध्यमाचे कण कायमचे स्थिर राहतात. अशा बिंदूंना निःस्पंद बिंदू असे म्हणतात. त्याचप्रमाणे जेथे

x=	l	,	3l	,	5l	……….
	2		2		2

वगैरे मूल्ये असतील तेथे परमप्रसर ±2a म्हणजे कमाल मूल्याचा होईल म्हणजे येथे क्षोभही जास्तीत जास्त होईल. अशा बिंदूंना प्रस्पंद बिंदू असे म्हणतात. (११) या समीकरणावरून हेही स्पष्ट होते की, दोन पाठोपाठच्या प्रस्पंद बिंदूंमधील (वा निःस्पंद बिंदूंमधील) अंतर l/2 असते. त्याचप्रमाणे दोन लगतच्या निःस्पंद बिंदूंच्या मध्यावर एक प्रस्पंद बिंदू असतो. या तत्त्वाचा उपयोग करून ध्वनीची तरंगलांबी मोजता येते [उदा., मेल्डे यांचा प्रयोग, कुंट नलिका इत्यादींमध्ये →तरंग गति].

व्यवहारात एखादा मूळचा तरंग व त्याचे कोणत्या तरी पृष्ठापासून परावर्तन होऊन मिळणारा परावर्तित तरंग यांच्यामध्ये अध्यारोपण होऊन अप्रगामी तरंग तयार होतात. बासरी, सनई वगैरे सुषिर वाद्यांच्या नळ्यांतील हवेच्या स्तंभात अप्रगामी तरंग निर्माण होतात ते यामुळेच.

त्याचप्रमाणे तंतुवाद्याच्या तारांवर अप्रगामी तरंग तयार होतात. त्यामुळेच त्यांची कंपने दीर्घकालपर्यंत चालू राहू शकतात, या स्तंभांच्या व तारांच्या लांबीवर उमटणाऱ्या स्वरांची उच्चनीचता अवलंबून असते.  त्याचप्रमाणे दंड, ताणलेले पटल (उदा., तबल्याचे चामडे) आणि तबकड्या यांवरही अप्रगामी तरंग प्रस्थापित होतात (यांचे वर्णन पुढे दिलेले आहे).

विवर्तन : ध्वनितरंगांच्या मार्गात काही अडथळा आल्यास त्याच्या बाजूने वळून तरंग अडथळ्याच्या मागे जाऊ शकतात, या परिणामाला विवर्तन असे म्हणतात. प्रकाशापेक्षा ध्वनितरंगांची तरंगलांबी खूपच जास्त असल्याने ध्वनीचे विवर्तन प्रकाशापेक्षा खूपच जास्त प्रमाणावर होते. त्यामुळे प्रकाशमार्गावरील अडथळ्याची जशी सुस्पष्ट छाया पडते तसे ध्वनीच्या बाबतीत होत नाही. ध्वनीच्या तीव्रतेच्या मापनासाठी ध्वनीच्या मार्गात एखादा मापक (उदा., ध्वनिग्राहक) ठेवल्यास त्याच्या वाचनात विवर्तनामुळे काही त्रुटी येते, तिची दखल मापन करताना घ्यावी लागते.

अपस्करण : अपस्करण म्हणजे तरंगवेग कंप्रतेनुसार बदलणे. सामान्य ध्वनीचे अपस्करण होत नाही. समूहगान किंवा वृंदवादनाचा कार्यक्रम दुरून ऐकला, तरी त्याच्या एकूण स्वरूपात फरक पडत नाही तो याचमुळे परंतु फार उच्च कंप्रतेच्या व अतितीव्र ध्वनीचे वेग कंप्रतेनुसार बदलतात.

शोषण व क्षीणन : वायूतून ध्वनी जात असताना ध्वनि-उर्जेचे अंशतः उष्णतेत रूपांतर होऊन ध्वनी उत्तरोत्तर क्षीण होत जातो. या परिणामाची कारणे पुढीलप्रमाणे आहेत.

(१) वायूच्या श्यानतेमुळे : वायुकणांच्या आंदोलनांना श्यानतेमुळे (दाटपणामुळे) विरोध होतो. त्यामुळे आंदोलनाच्या ऊर्जेपैकी काही अंशाचे उष्णतेत रूपांतर होते.

(२) उष्णता संवहनामुळे : वायूमध्ये ध्वनितरंगामुळे एकाआड एक संकोचने आणि विरलीकरणे तयार होतात. संकोचनांच्या ठिकाणी दाब वाढल्यामुळे तापमान वाढते. याउलट विरलीकरणाशी तापमान कमी होते. मग वायूमधून जास्त तापमानाच्या भागाकडून कमी तापमानाच्या भागाकडे उष्णतेचे संवहन होऊ लागते. अशा संवहनामुळे ⇨ एंट्रॉपी  वाढते म्हणजेच ऊर्जेचा क्षय होतो.

(३) उष्णता प्रारणामुळे : संकोचनाचे तापमान जास्त असल्याने तेथून काही प्रमाणात उष्णतेचे प्रारणही (तरंगरूपाने ऊर्जेचे प्रसारणही) होते व त्यामुळे ऊर्जाक्षय होतो.

(४) ऊर्जाविनिमयामुळे : पाण्याची वाफ अथवा कार्बन डाय-ऑक्साइड यासारख्या वायूच्या रेणूंतील अणूंची एकमेंकाच्या संदर्भात आंदोलने होतात. त्यामध्ये काही ऊर्जाक्षय होतो. उद्‍गमाजवळ ध्वनीची तीव्रता I₀ आणि तेथून x अंतरावर I_x असेल, तर पुढील समीकरण मिळते

Ix= I0.e-2α x

…

…

(१२)

यातील α हा त्या वायुमाध्यमाचा शोषण गुणांक होय, शोषण गुणांकाचे मूल्य ध्वनिकंप्रतेवर अवलंबून असते आणि सामान्यतः कंप्रता वाढते तसा शोषण गुणांकही वाढतो. ध्वनी जेव्हा एखाद्या पृष्ठभागावर पडतो तेव्हा त्या पृष्ठभागाकडूनही ध्वनीचे काही प्रमाणात शोषण होते. सामान्यतः टणक व गुळगुळीत पृष्ठे अल्प प्रमाणात शोषण करतात, तर मऊ व सच्छिद्र पदार्थ जास्त शोषण करतात. सभागृहांचे निनादनकाल सुयोग्य ठेवण्यासाठी खास शोषक पदार्थ तयार करण्यात आलेले आहेत. मानवी शरीरही ध्वनीचे शोषण करते [→ ध्वनिकी].

गोगांट : नको असलेला आवाज म्हणजे गोंगाट होय परंतु ही गोगांटाची व्यक्तिनिष्ठ व्याख्या झाली.  एकाला नको वाटणारा आवाज दुसऱ्याला हवासा वाटणे शक्य आहे. जो संगीत नाही व भाषणही नाही असा आवाज म्हणजे गोगांट अशीही एक गोगांटाची व्याख्या करण्यात येते. गोंगाटाने संभाषण किंवा संगीत ऐकण्यात व समजण्यात अडथळा येतो. सामान्यतः ज्या ध्वनीच्या बाबतीत निश्चित उच्चनीचता उमगू शकत नाही व ज्याच्या आंदोलनात निश्चित आवर्तने नसतात असा ध्वनी म्हणजे गोंगाट अशी व्याख्या देतात. फटाक्याचा आवाज, यंत्रांची घरघर ही गोंगाटाची उदाहरणे आहेत [→ गोंगाट].

स्वर व त्यांची अभिलक्षणे : संगीतात (किंवा) भाषणात ज्यांचा उपयोग होतो ते ध्वनी म्हणजे स्वर होत.  स्वरांची तीन व्यक्तिनिष्ठ अभिलक्षणे आहेत. दोन स्वरांमध्ये तुलना करताना आपण या तीन अभिलक्षणांचा विचार करतो. ही अभिलक्षणे म्हणजे गरिमा, स्वरपद व स्वराविशेषत्व ही होत.

गरिमा : गरिमा म्हणजे आवाजाचा लहानमोठेपणा.  रेडिओची विशिष्ट (व्हॉल्यूम कंट्रोलची) गुंडी सव्य दिशेने (घड्याळाच्या काट्याच्या हालचालीच्या दिशेने) फिरविली म्हणजे आवाज मोठा होतो किंवा गरिमा वाढतो.  ध्वनि – उद्‍गमापासून जसजसे दूर जावे तसतसे कानावर पडणाऱ्या ध्वनीचा गरिमा कमी होत जातो पण त्या ध्वनीच्या इतर कोणत्याही गुणधर्मात फरक पडत नाही.  गरिमाशी संलग्न वस्तुनिष्ठ राशी ध्वनीची तीव्रता किंवा ध्वनितरंगाचा परमप्रसर ही होय. तीव्रता म्हणजे प्रती एकक क्षेत्रफळातून प्रती सेकंद जाणारी ध्वनि-ऊर्जा होय (याबद्दल सविस्तर विवेचन पुढे दिलेले आहे).

स्वरपद : आवाजाची उच्चनीचता म्हणजे स्वरपद होय.  बाजाच्या पेटीवर सा रे ग म वगैरे सूर क्रमाक्रमाने काढल्यास स्वरपद उत्तरोत्तर उच्च होत जाते, सामान्यतः पुरुषांचे आवाज स्त्रिया किंवा लहान मुलांच्या आवाजाच्या तुलनेने नीच स्वरपदांचे असतात. अशा आवाजाला आपण ढाला आवाज म्हणतो. ध्वनितरंगांची कंप्रता जितकी जास्त वा तरंगलांबी कमी तितका तो ध्वनी उच्च कंप्रतेचा वाटतो (आ. ४).  कंप्रता ही स्वरपदाशी संलग्न वस्तुनिष्ठ राशी होय.

स्वरविशेष : दोन वेगवेगळ्या वाद्यांनी काढलेले स्वर एकाच गरिम्याचे व स्वरपदाचे असले, तरीही आपणाला ते ज्या अभिलक्षणामुळे ओळखू येतात त्याला स्वरविशेष असे म्हणतात. आवाजावरून कोण व्यक्ती बोलते आहे ते आपण ओळखू शकतो. याचे कारण वेगवेगळ्या व्यक्तींच्या आवाजाचे स्वरविशेष वेगळे असतात हे होय. तबल्याच्या थापेचा आवाज, बासरीचे सूर, सारंगीचे सूर इ. आपण ओळखू शकतो ते स्वरविशेषामधील फरकामुळे होय.

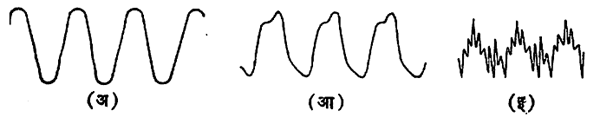
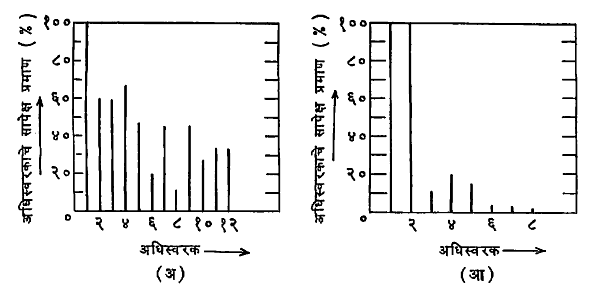
ध्वनितरंगाचा विशिष्ट आकार (तरंगाकार) स्वरविशेषाशी संलग्न आहे असे दिसून येते. त्याचप्रमाणे तरंगाकार हा त्या आवाजात किती अधिस्वरकांचे (मूलकंप्रतेच्या वरील घटकांचे) मिश्रण आहे व त्यांचे परस्पर प्रमाण काय आहे यावर अवलंबून आहे. आ. ५ मध्ये कंपनशूल (नादकाटा), बासरी व व्हायोलिन यांच्या साहाय्याने काढलेल्या एकाच स्वरपदाच्या स्वराच्या तरंगाकृती दाखविल्या असून आ. ६ मध्ये बासरी व व्हायोलिन यांच्या स्वरांमधील अधिस्वरकांच्या सापेक्ष तीव्रता आलेखाने दिग्दर्शित केल्या आहेत. त्यावरून हे दिसेल की, अधिस्वरकांच्या भरण्यामुळे स्वराची रंजकता वाढते. कंपनशूलाच्या स्वरात फक्त एकाच कंप्रतेचे तरंग असतात. त्यांचा तरंगाकार ‘ज्या’ वक्राप्रमाणे (त्रिकोणमितीतील ‘ज्या’ गुणोत्तराच्या वक्राच्या आकाराप्रमाणे) आहे. अशा स्वराला शुद्ध स्वरक असे म्हणतात. असे सूर कानाला फारसे मधुर लागत नाहीत.  इलेक्ट्रॉनीय नलिकांच्या साहाय्याने शुद्ध स्वरक निर्माण करता येतात. बहुतेक सर्व ध्वनि-उद्‍गमापासून मिळणारे ध्वनी म्हणजे अनेक स्वरकांचे मिश्रण असते. ध्वनिविश्लेषक उपकरणाच्या साहाय्याने अशा जटिल स्वरातील घटक स्वरक व त्यांचे प्रमाण काढता येते. सामान्यतः जटिल स्वराचे स्वरपद त्यातील सर्वांत कमी कंप्रतेच्या स्वरकावर अवलंबून असते, त्याला मूलस्वरक असे म्हणतात. इलेक्ट्रॉनीय ऑर्गनच्या साहाय्याने मूलस्वरकाचे सुयोग्य अशा अधिस्वरकांशी योग्य त्या प्रमाणात मिश्रण करून कोणत्याही वाद्याचा आवाज हुबेहुब काढता येतो.

ध्वनीचे उत्पादन : कोणत्याही पदार्थीय माध्यमात एखादी वस्तू आंदोलने करू लागली असता त्या माध्यमात ध्वनितरंग निर्माण होतात आणि उत्पन्न होणाऱ्या ध्वनीची वैशिष्ट्ये या आंदोलनांवर अवलंबून असतात.

मुक्त किंवा नैसर्गिक आंदोलने : समतोलावस्थेत असलेली वस्तू क्षणिक प्रेरणा लावून समतोलापासून ढळविल्यास गुरुत्वाकर्षण किंवा स्थितीस्थापकता यामुळे पुनःस्थापक प्रेरणा तिच्यावर उत्पन्न होतात व ती वस्तू कमी अधिक काळापर्यंत आंदोलने (वा कंपने) करीत राहते. या आंदोलनांना मुक्त आंदोलने म्हणतात आणि या आंदोलनाच्या कंप्रतेला त्या वस्तूची नैसर्गिक कंप्रता म्हणतात. नैसर्गिक कंप्रतांची मूल्ये सर्वस्वी त्या वस्तूवरच अवलंबून असतात. लंबकाची आंदोलने व छेडलेल्या तारेची आंदोलने ही मुक्त आंदोलनाची उदाहणे आहेत.  ध्वनिशास्त्रात ज्यांच्या मुक्त आंदोलनाच्या अभ्यासाला महत्त्वाचे स्थान आहे, अशा काही वस्तूंच्या मुक्त आंदोलनांसंबंधीचे विवरण खाली दिले आहे.

ताणलेल्या तारा व तंतू आणि दंड : तंतू अगर तारांमध्ये अवतरंग आणि दंडांमध्ये अवतरंग व अनुतरंगही निर्माण करता येतात. पूर्णतः नम्य (लवचिक) व ताणलेल्या अशा l लांबीच्या व प्रती एकक लांबीस m वस्तुमान असलेल्या तारेस वा तंतूस T ताण लावला असता तिच्यात निर्माण होणाऱ्या अवतरंगांचा वेग υ खालील सूत्राने दिला जातो.

υ	=	√	T
			m

समजा, एका तारेची क आणि ख ही टोके पक्की केलेली असूनही तार छेडून तिच्यावर तरंग निर्माण केला. क आणि ख या बिंदूपासून मूळ तरंगाचे पुनःपुन्हा परावर्तन होऊन अध्यारोपणामुळे तारेवर स्थिर तरंग प्रस्थापित होतो. तारेत जेव्हा फक्त एकच प्रस्पंद निर्माण होतो तेव्हा तारेची लांबी l ही ध्वनितरंगाच्या अर्ध्या तरंगलांबीइतकी असते. म्हणून अशा वेळी तारेत निर्माण होणाऱ्या ध्वनीची कंप्रता n पुढील सूत्राने दिली जाते.

n	=	1	√	T	…	…	…	(१३)
		2ι		m

या सूत्रावरून असे दिसून येते की, ताण कायम ठेवून तारेची लांबी कमी केली असता कंप्रता वाढते आणि लांबी कायम ठेवून ताण वाढविला असता कंप्रता वाढते आणि लांबी कायम ठेवून ताण वाढविला असता कंप्रता वाढते. या n कंप्रतेच्या स्वराला तारेचा मूल स्वरक म्हणतात व या आंदोलन पद्धतीला मूल आंदोलन पद्धती असे म्हणतात. तारेच्या क आणि ख या बिंदूंची अशी परिस्थिती आहे की, त्यांचे विस्थापन होऊच शकत नाही.  म्हणून तेथे नेहमीच निःस्पद निर्माण झाले पाहिजेत. या तत्त्वाला तारेची मर्यादा अट असे म्हणतात. मर्यादा अटीचे पालन करून तार इतर अनेक प्रकारांनी आंदोलित होणे शक्य आहे. या प्रकारांत तारेमध्ये अनुक्रमे २,३,४,… … … वगैरे प्रस्पंद निर्माण होऊ शकतात. त्या आंदोलनाच्या कंप्रता अनुक्रमे 2n, 3n, 4n, … … … म्हणजे मूल स्वरकाच्या कंप्रतेच्या पूर्णांक पटीत असतात. या कंप्रतांना संनादी किंवा प्रगुण कंप्रता असे म्हणतात. आ. ७ मध्ये तारेची मूल आंदोलन पद्धती आणि पुढील ३ कंपन प्रकार दाखविले आहेत.

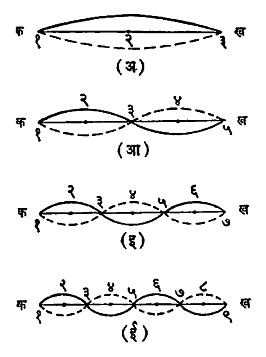
अशा तऱ्हेने अनेक प्रकारांनी आंदोलने होणे शक्य असले, तरी विशिष्ट परिस्थितीत कोणत्या आणि किती प्रकारची आंदोलने प्रत्यक्ष होतील, ती आंदोलने कशी निर्माण केली, त्यासाठी किती प्रेरणा लावली इ. गोष्टींवर अवलंबून असते. उदा., तार मध्यबिंदूवर छेडून आंदोलित केली, तर मध्यबिंदूपाशी प्रस्पंद निर्माण होईल. मग आ. ७ मधील (आ) आणि (ई) हे आंदोलन प्रकार निर्माण होऊच शकणार नाहीत. सर्व तंतुवाद्याचे आवाज एकसारखे लागत नाहीत त्याचे हे एक महत्त्वाचे कारण आहे.

तंतुवाद्य साधारणतः तीन गटांत विभागता येतात : (१) तारा छेडल्या जातात अशी वाद्ये, उदा., सतार, वीणा. (२) ताडनाने (टोला देऊन) तारांतून ध्वनी निर्माण केला जातो अशी वाद्य, उदा., पियानो. (३) तारा धनुकलीने घासून ध्वनी निर्माण करण्यात येतो अशी वाद्ये, उदा., व्हायोलिन, दिलरुबा, सारंगी.

सतारीमध्ये भोपळा व त्याला जोडलेला पोकळ लाकडी दांडा यांवर तारा ताणलेल्या असतात. खुंट्यांच्या साहाय्याने तारांवरील ताण कमीजास्त करता येतो. वेगवेगळ्या पडद्यांवर तार दाबून तिच्या कंपायमान भागाची लांबी कमी करता येते व त्यामुळे वेगवेगळ्या स्वरपदांचे स्वर काढता येतात. तारेमधून निघणारे सर्व संनादी स्वर मूलस्वराशी सहसंवादी असल्याने एकूण आवाज मधुर येतो, यामुळेच अनेक वाद्यांत ताणलेल्या तारांपासून ध्वनी उत्पादन करतात. पियानोमध्ये एकेरी तारा किंवा तारांचे गट एका मोठ्या जड ध्वनिफलकास (की-बोर्डला) जोडलेले असतात. त्यातील पट्टी दाबली असता संबंधित तारेवरील विशिष्ट बिंदूवर फेल्ट आच्छादित हातोडीने आघात होऊन ध्वनी निर्माण होतो. पियानोच्या स्वरांचा स्वरविशेष हा निर्माण होणाऱ्या संनादी स्वरांच्या संख्येवर, हातोडीच्या कठीपणावर तसेच तिच्या ताडन कालावर आणि ध्वनिफलकावर अवलंबून असतो. व्हायोलिनमध्ये एक विशिष्ट आकाराची ध्वनिपेटिका असते. या वाद्यात ठराविक असे पडदे नसल्याने वादकास तारा जरूर त्या ठिकाणी  बोटाने दाबून ध्वनीचे स्वरपद बदलावे लागते. घोड्याच्या राळ लावलेल्या केसांची धनुकली वापरून व्हायोलिनमध्ये टिकणारा सूर निर्माण करता येतो. संनादी स्वरांच्या वैपुल्यामुळे व्हायोलिनचा सूर फार रंजक वाटतो [→वाद्य व वाद्यवर्गीकरण].

ताणलेली पटले : पटल म्हणजे ताणलेल्या तारेचे द्विमितीय स्वरूप असे म्हणता येईल. ताणलेल्या पटलात निर्माण होणाऱ्या अवतरंगांची मूलकंप्रता लावलेल्या ताणावर अवलंबून असते. ढोलावरील कातडीप्रमाणे ताणलेल्या पटलावर आघात केला की ते कंपन पावू लागते. अशी पटले ढोलासारख्या निरनिराळ्या प्रकारच्या वाद्यांत (उदा., तबला, मृदंग, नगारा वगैरे) वापरली जातात. वाद्याच्या भांड्यातील हवेच्या ⇨ अनुस्पंदनामुळे पटलांची कंपने अधिक जोरदार केली जातात.

a त्रिज्या असलेल्या वर्तुळाकार पटलात निर्माण होणाऱ्या ध्वनीची मूलकंप्रता n ही रॅली यांच्या खालील सूत्राने दिली जाते.

	n	=	2.450	√	T	…	…	…	(१४)
			2pa		m

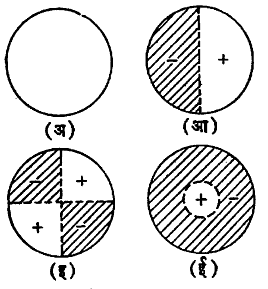
ह्या सूत्रात T म्हणजे पटलावरील ताण व m म्हणजे पटलाच्या एकक क्षेत्रफळाचे वस्तुमान होय. पटल इतर प्रकारांनीही कंप पावू शकते परंतु पटलाच्या या इतर कंपन प्रकारांच्या (आ. ८) कंप्रता अनुक्रमे 1·593n, 2·135n, 2·2295n, 2·917n इ. असतात. या मूलकंप्रतेच्या पूर्णांक पटीत नसल्याने पटलाचा एकूण आवाज कर्कश लागतो. भारतीय तबल्यावर मधे शाई लावल्याने पटलाचे स्वरपद नीच होते. त्याचबरोबर जास्त कर्कशता निर्माण करणारे अधिस्वरक अतिदुर्बल केले गेल्याने तबल्याचा आवाज (पाश्चिमात्यांच्या ड्रमच्या तुलनेने) मधुर होतो. सी. व्ही. रामन यांनी याबाबत मूलभूत संशोधन केले आहे. कंप पावणाऱ्या पटलाच्या सीमेचे कुठल्याही रीतीने आकुंचन केल्यास त्यातून निघणाऱ्या ध्वनीचे स्वरपद उच्च होते. निरनिराळ्या आकारांच्या सारख्या क्षेत्रफळाच्या व सारख्याच स्थितीत कंप पावणाऱ्या पटलांपैकी वर्तुळाकार पटलांतून निघणाऱ्या ध्वनीचे स्वरपद नीचतम असते.

पडदे व पट्ट (तबकडी प्लेट) यांच्यात निर्माण होणाऱ्या कंपनांच्या बाबतीत त्यांची स्थितीस्थापक प्रेरणा प्रधान मानली जाते. सीमा भाग संधृत (घट्ट पकडून ठेवलेल्या) वर्तुळाकार पडद्यात निर्माण होणाऱ्या मूलस्वराच्या कंप्रतेकरिता (n) रॅली यांनी खालील सूत्र मांडले.

n	=	1·62h	√	Y	…	…	(१५)
		a2		12 r० (1-s2)

या सूत्रात h पडद्याची जाडी, a त्याची त्रिज्या, Y त्या पडद्याच्या पदार्थाचा यंग गुणांक, ρ_० त्याची घनता आणि σ प्वासाँ गुणोत्तर [→स्थितिस्थापकता] होय. पडद्यांचे संनाद सहसंवादी नसतात त्यामुळे संगीताच्या स्वरनिर्मितीसाठी त्यांचा उपयोग करीत नाहीत परंतु ध्वनिग्राहक, ध्वनिक्षेपक इ. साधनांत पटले व पडदे यांचा उपयोग केला जात असल्याने त्यांच्या अभ्यासाला फार महत्त्व आहे.

कांड व दंड : यांमध्ये अनुतरंग, अवतरंग व परिपीडन (पिळाकार) तरंग असे तीन प्रकारचे तरंग प्रस्थापित होऊ शकतात. मध्यभागी संधृत असलेल्या कांडात अनुतरंग निर्माण केले असता त्यात सर्व सम संनादी कंप्रतांचा अभाव असतो. अशा कांडाची मूलस्वर कंप्रता खालीलप्रमाणे असते.

मूलस्वर कंप्रता	n	=	p	√	Y		…	…	…	(१६)
			2ι		r

ह्या सूत्रात p हा विषम पूर्णांक असून त्यास १, ३, ५,… अशी मूल्ये दिली असता कांडाच्या निरनिराळ्या कंप्रता मिळतात. यात Y हा कांडाच्या पदार्थाचा यंग गुणांक व ही त्याची घनता होय.  पुढील संनादी आंदोलनाच्या कंप्रता अनुक्रमे 3n, 5n, 7n इ. असतात. आ. ९ मध्ये अशा अन्वायाम (आडव्या दिशेतील) आंदोलनाच्या मूल व प्रथम संनादी पद्धती दाखविल्या आहेत.

क्लाडनी आकृत्या : काचेचा किंवा धातूचा चौकोनी पट्ट एका उभ्या स्तंभावर समतल पातळीत स्क्रूने मध्यभागी घट्ट बसवून त्याच्या एका बाजूवर धनुकलीने घासून तो आंदोलित केला असता त्यामधून निश्चित स्वरपद असलेला ध्वनी निघतो, असे ई. एफ्. एफ्. क्लाडनी या जर्मन भौतिकीविज्ञांनी १७८७ मध्ये शोधून काढले. ह्या पट्टावर वाळू पसरून पट्ट आंदोलित केला, तर वाळू निःस्पंद रेषांवर जमा होते. ह्या रेषा पटाचा आंदोलन न पावणारा भाग दर्शवितात. आंदोलित पट्टांवर तयार झालेल्या या वाळूच्या आकृत्यांना क्लाडनी आकृत्या म्हणतात.

वर्तुळाकार पट्टाच्या निःस्पंद रेषा व्यास किंवा वर्तुळे असतात वा दोन्ही मिळून असतात (आ.१०). अशा आकृत्यांच्या साहाय्याने पट्टांच्या आंदोलन पद्धती चटकन उमगून येतात.

कंपनशूल : (नादकाटा). एकच शुद्ध स्वरक निर्माण करण्यासाठी कंपनशूल वापरले जातात.  पियानोसारख्या वाद्यांचे मेलन (तारांची योग्य सुरांत जुळवणी) करताना संगीतज्ञ या साधनाचा उपयोग करतात. याच्या सुरात संनादी स्वरांचा अभाव असल्याने तो रंजक होत नाही म्हणून वाद्यांत तो वापरला जात नाही. कंपनशूल म्हणजे एक धातूची जाड पट्टी U या इंग्रजी अक्षराच्या आकारात वाकविलेली असून U च्या बुंध्याच्या मध्यावर एक उभा दंड जोडलेला असतो. याच्या कोणत्याही एका टोकावर आघात केला, तरी दोन्ही भुजांची कंपने सुरू होतात. या कंपनात टोके एकदा परस्परांजवळ येतात व नंतर परस्परांपासून दूर जातात.  या क्रिया एकाआड एक होत असतात.

आर्. कोयनिग (१८३२–१९०१) ह्या शास्त्रज्ञांनी या साधनाचा विकास केला. त्यांनी निरनिराळ्या कंप्रतांचे शुद्ध स्वर निर्माण करणारे कंपनशूल बनविले. स्वराची शुद्धता व सातत्य ह्या दोन गुणधर्मांमुळे विद्युत् ऊर्जेच्या साहाय्याने सतत कंपायमान ठेवलेला कंपनशूल विद्युत् कंप्रतेच्या अचूकतेचे प्रमाण म्हणून मानला जातो.

विशिष्ट धातूच्या आणि आकाराच्या कंपनशूलाची कंप्रता त्याच्या भुजांच्या लांबीवर अवलंबून असते.  कंपनशूलाची पट्टी ज्या पातळीत वाकविलेली असते त्या पातळीतील भुजांच्या जाडीच्या सम प्रमाणात कंपनशूलाची कंप्रता असते. कंपनशूलाची निरपेक्ष कंप्रता n त्या धातूतील ध्वनीच्या वेगावर अवलंबून असून ती खालील सूत्राने काढता येते.

n	=	(1·875)2.t	√	Y	…	…	(१७)
		2π√12· ι 2		r

या सूत्रात t म्हणजे ज्या पातळीत भुज वाकविलेले असतात त्या पातळीतील भुजांची जाडी, L  ही भुजांची लांबी, Y हा त्या धातूचा यंग गुणांक व ही त्या धातूची घनता होय. अशा रीतीने कंपनशूलाची कंप्रता भुजांची जाडी व ध्वनीचा वेग √Y/p ह्यांच्या सम प्रमाणात असते व भुजाच्या लांबीच्या वर्गाच्या व्यस्त प्रमाणात असते पण ती भुजांच्या रुंदीवर अवलंबून नसते.

कंपनशूलांची टोके कानशीने घासून टोकाजवळचे वस्तुमान कमी केले असता कंप्रता वाढते, तर मेण किंवा इतर पदार्थ त्यांच्या टोकास चिकटविल्याने कंप्रता कमी होते.

कंपित हवेचा स्तंभ : हवेच्या स्तंभांची फक्त अन्वायाम पद्धतीचीच कंपने होऊ शकतात. हवेच्या स्तंभाची कंपने बासरी, सनई, ऑर्गन व तत्सम वाद्यांमध्ये ध्वनीची निर्मिती करतात. अशा कंपनांचा विचार करताना असे गृहित धरू की, (१) ज्या नलिकेत हवेची कंपने उघडतात त्या नलिकेचा व्यास हवेच्या श्यानतेचा परिणाम उपेक्षिता येईल इतका मोठा आहे, पण तो लांबीच्या मानाने लहान आहे आणि (२) नलिकेच्या भिंती दृढ आहेत.  कंपित हवेच्या स्तंभाचे दोन प्रकार आहेत : (१) नलिकेची दोन्ही टोके खुली असलेला आणि (२) नलिकेचे एक टोक बंद व दृढ आणि दुसरे खुले असलेला.

(१)दोन्ही टोकांस खुला असलेला कंपित हवेचा स्तंभ : यातील हवेच्या कंपनाचे प्रकार आ.११ मध्ये दाखविले आहेत. नळीच्या टोकाशी वायुकणांना अत्यंत मुक्तपणे कंप पावणे शक्य असते त्यामुळे या वायुस्तंभाची मर्यादा अट म्हणजे त्याच्या दोन्ही टोकांना प्रस्पंद असले पाहिजेत अशी येते. प्रत्यक्षात हे प्रस्पंद नळीच्या किंचित बाहेर असतात. मूलस्वराची कंप्रता

n	=	C	…		(१८)
		2(l + e)

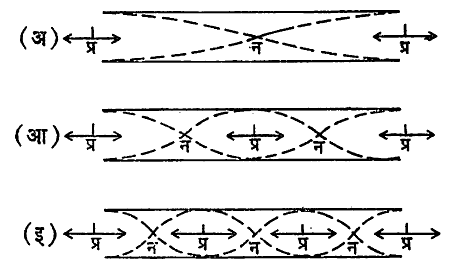
अशी मिळते. येथे C वायूतील ध्वनीचा वेग, I नळीची लांबी आणि e नळीचे टोक व तेथील प्रस्पंद यांच्यामधील अंतर. आ. ११ च्या (अ) भागामधील कंपनांचा परिणाम म्हणून मूलस्वर निघतो आणि (आ) व (इ) यांतील कंपनामुळे अनुक्रमे पहिला व दुसरा संनादी स्वर उत्पन्न होतो. याप्रमाणे निःस्पंदांची संख्या वाढेल त्याप्रमाणे पुढील संनादी स्वर निर्माण होतात. मूलस्वर आणि संनादी स्वर यांच्या कंप्रतांची गुणोत्तरे १ : २ : ३ : ४ ··· इ. अशी येतात. तेव्हा येथेही सर्व संनादी स्वर सहसंवादी असतात, म्हणून एकूण स्वर मधुर लागतो.

(२) एक टोक बंद व दुसरे उघडे असलेल्या नळीतील वायुस्तंभाची कंपने :बंद टोकाशी  असलेले वायुकण कंप पावण्यास मोकळे नसतात.  त्यामुळे बंद टोकाशी निःस्पंद व उघड्या टोकाजवळ प्रस्पंद या अशा वायुस्तंभाच्या मर्यादा अटी येतात.  त्यांना अनुसरून होऊ शकणाऱ्या वायुस्तंभाच्या पहिल्या तीन कंपन पद्धती आ.१२ मध्ये दाखविल्या आहेत.

येथे मूलस्वराची कंप्रता n	=	C	…	…	(१९)
		4(ι +e)

या सूत्राने दिली जाते. येथे C ध्वनीचा त्या वायूतील वेग, ι नळीची लांबी आणि e नळीचे टोक व लगतचा प्रस्पंद यांमधील अंतर होय. अशा तऱ्हेने एक टोक बंद असलेल्या वायुस्तंभाची मूलकंप्रता तितक्याच लांबीच्या दोन्ही टोके उघडी असणाऱ्या वायुस्तंभाच्या कंप्रतेच्या निम्मी असते. एकूण स्वरात मूलस्वराच्या समपटीच्या कंप्रतांचे संनादी नसतात. त्यामुळे हा स्वर कमी रंजक व गंभीर वाटतो.

मूलस्वर व संनादी यांच्या कंप्रतांचे गुणोत्तर १ : ३ : ५ : ७ असे असते. येथे वायुस्तंभाबरोबर तो जिच्यात समाविष्ट झालेला आहे त्या खुद्द नळीचीही काही प्रमाणात कंपने होतात व त्यांचाही परिणाम त्या स्वरावर होतो, ही गोष्ट लक्षात ठेवणे जरूर आहे. वेळूची बासरी व त्याच सुरातील पितळी बासरी यांचे आवाज तंतोतंत एकसारखे लागत नाहीत त्याचे हेच कारण आहे. अशीच परिस्थिती इतर वाद्यांच्या बाबतीतही होत असते.

भोंगा झोत सीमा-नाद : सी. सी. द लातूर यांनी शोधून काढलेल्या मूळच्या भोंग्यात वर्तुळाकार सारख्या अंतरावर छिद्रे पाडून बनविलेली एक परिभ्रमण करणारी तबकडी असते. ह्या तबकडीच्या समोरच्या बाजूस बसविलेल्या नळीतून येणाऱ्या हवेचा झोत ह्या छिद्रांवर पडतो व भोंगा तयार होतो. ह्या भोंग्याच्या ध्वनीची कंप्रता तबकडीवरील छिद्रांची संख्या व तबकडीने एका सेकंदात केलेल्या परिभ्रमणांची संख्या ह्यांच्या गुणाकाराइतकी असते. ए. सीबेक यांनी शोधून काढलेल्या नंतरच्या भोंग्यात तबकडीवरील छिद्रे तिरपी पाडलेली असतात व हवेच्या एकेरी झोताऐवजी स्थिर अशा कड्यांची योजना केलेली असून या स्थिर कड्यांमधून येणारा हवेचा झोत तबकडीच्या तिरप्या छिद्रावर पडतो. यामुळे निर्माण होणाऱ्या प्रतिक्रियेने तबकडीचे परिभ्रमण सुरू होते. अशा प्रकारच्या भोंग्यातून निघणाऱ्या ध्वनीची तीव्रता त्याच्या कंप्रतेच्या सम प्रमाणात असते व ह्या दोन्ही गोष्टी हवेच्या झोताच्या ऊर्जेच्या सम प्रमाणात असतात. आधुनिक भोंग्यात छिद्रयुक्त तबकडी विद्युत् चलित्राच्या (मोटरच्या) साहाय्याने फिरविण्यात येते. या चलित्राला वेगदर्शक लावलेला असतो, शिवाय वेगाचे नियंत्रण करण्याची व्यवस्थाही असते. त्यामुळे या भोंग्यातून निघणाऱ्या ध्वनीचे स्वरपद सहज नक्की करता येते. हवेच्या झोताचा दाब कमीजास्त करून तीव्रता बदलता येते.

प्रवाही पदार्थ व लहान आकारमानाचा घन पदार्थ ह्यांच्यातील सापेक्ष गतीमुळे प्रवाहात गतिमान असलेल्या पदार्थामागे आवर्त व भोवरे निर्माण होतात. एखाद्या तारेभोवतालून हवेचा झोत जात असता असेच आवर्त उत्पन्न होतात. अशा प्रत्येक आवर्ताबरोबर पुढील हवेला एक झटका बसतो. अशा लागोपाठ बसणाऱ्या झटक्यांमुळे हवेत कंपने निर्माण होऊन ध्वनी उत्पन्न होतो. उंच वाढलेल्या गवताभोवतालून किंवा झाडांभोवतालून वाऱ्याची झुळूक जात असता असा ध्वनी ऐकू येतो. अशा ध्वनीचे स्वरपद अडथळ्याच्या लांबीवर किंवा ताणावर अवलंबून नसते, तर ते अडथळा व हवेचा झोत ह्यांच्या सापेक्ष वेगाच्या सम प्रमाणाचा असते.

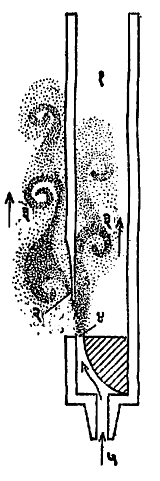
बारीक छिद्रातून येणाऱ्या हवेचा झोत जर एखाद्या तीक्ष्ण पाचरीवर सोडण्यात आला, तर त्या पाचरीच्या दोन्ही बाजूंस हवेचे एकाआड एक भोवरे निर्माण होतात त्यामुळेही वरीलप्रमाणे ध्वनी उत्पन्न होतो. अशा वेळी उत्पन्न होणाऱ्या ध्वनीस सीमा-नाद असे म्हणतात. ह्या पाचरीस जर हवेचा स्तंभ जोडलेला असला, तर त्या स्तंभातील हवेत अनुस्पंदनाने कंपने निर्माण होऊन मोठा ध्वनि उत्पन्न होतो. अलगूज व एक प्रकारच्या ऑर्गन नलिकेत या पद्धतीने ध्वनी निर्माण होतो. आ.१३ मध्ये ऑर्गन नलिकेच्या तोंडावर निर्माण होणारी भोवऱ्यांची मालिका दाखविली आहे.

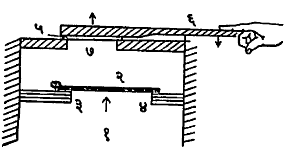
बाजाच्या पेटीत (आ. १४) स्प्रिंगेसारख्या एका पातळ पत्र्याच्या पट्टीची (जिभेची) आंदोलने होऊन ध्वनी निर्माण होतो. पेटीचा भाता हलवून (१) या वायुपेटिकेत हवेचा दाब वाढविला जातो. (३-४) ही एका जाड पत्र्याच्या पट्टीत चौकोनी फट असून तिच्यात (२) ही जीभ फट बंद होईल अशी बसविलेली असते.  जिभेचे (३) हे टोक स्क्रूने पक्के बसविलेले असून (४) या बाजूचे टोक मुक्त असते. (६) ही पट्टी दाबली की, (५) ही बुरणुसासारखी प्रयुक्त लावलेली बाजू वर उचलली जाऊन (७) हे छिद्र उघडते. मग (१) मधील हवेच्या दाबाने पट्टी वर उचलली जाते व स्थितीस्थापकतेमुळे ती काही ठराविक कंप्रतेने कंप पावू लागते आणि त्या कंप्रतेचा स्वर निर्माण होतो. अकॉर्डिअन, माउथ ऑर्गन (तोंडाने वाजवावयाचा बाजा) या वाद्यांत याच तत्त्वावर ध्वनी निर्माण केला जातो.

ब्युगल व तत्सम वाद्ये वाजविणारा आपले ओठ वाद्याच्या तोंडावर दाबून त्यांच्यामध्ये एक फट निर्माण करतो. या फटीमधून जेव्हा हवा जोराने सोडली जाते तेव्हा ओठांची कंपने होतात ती ब्युगलच्या नळीमधील वायूला दिली जाऊन ध्वनी निर्माण होतो. पिपाणी, सनई व मानवी स्वरयंत्र यांतही अरुंद फटीतून हवा सोडल्याने फटीच्या बाजूंच्या होणाऱ्या कंपनामुळे आवाज निर्माण होतो.

युग्मित कंपन प्रणाली : दोन (किंवा अधिक) कंपनक्षम वस्तू जेव्हा एकमेंकाच्या कंपनांवर परिणाम घडवून आणू शकतात तेव्हा त्यांना युग्मित कंपन प्रणाली असे म्हणतात. अ आणि आ या दोन वस्तूंचे युग्मन अनेक प्रकारे केले जाऊ शकते. (१) अ आणि आ सारखेच जोरदार असून परस्परांवर सारखाच परिणाम करू शकतात (२) अ जास्त जोरदार असून त्याचा आ वर भरपूर भरपूर परिणाम होतो, परंतु आ चा मात्र अ वर दुर्लक्षणीय परिणाम होतो (३) किंवा (२) च्या उलट इत्यादी.

ध्वनि-उत्पादनात युग्मित प्रणालींचा मोठ्या प्रमाणावर उपयोग केला जातो व त्यामुळे निर्माण होणाऱ्या ध्वनीच्या गुणधर्मात महत्त्वाचे बदल होतात, उदा., ऑर्गन नलिकेच्या बाबतीत नलिकेतील वायुस्तंभ व पाचरीपाशी भोवरे निर्माण होऊन हवेची कंपने होतात. ही एक युग्मित प्रणाली आहेपरंतु यातील वायुस्तंभाची कंपने जास्त जोरदार असून तीच भोवरे निर्माण होणाऱ्या त्वरेवर परिणाम करतात. त्यामुळे उत्पादित ध्वनीचे स्वरूप या वायुस्तंभाच्या कंपन प्रकारानुसार होते. हेच अलगुजातही होते. अलगुजाच्या नळीवरील भोके बोटांनी मिटून आणि उघडून वायुस्तंभाची परिणामी लांबी बदलली जाते. त्यानुसार सा रे ग म इत्यादी विशिष्ट कंप्रतांचे स्वर निघतातपरंतु अलगुजात फार जोराने फुंकल्यास मग भोवऱ्यांची त्वरा जास्त जोरदार होते व उच्च कंप्रतेचा ध्वनी निघतो. व्हायोलिन, सारंगी, सतार इ. तंतुवाद्यांच्या बाबतीत प्रत्यक्ष वाजविल्या जाणाऱ्या वाद्यांच्या तारा व वाद्याचा बाकीचा सांगाडा यांची मिळून एक युग्मित प्रणाली होते. हा सांगाडाही तारांच्याबरोबर आंदोलित होतो व वाद्यापासून निघणाऱ्या आवाजावर त्याची छाप पडते. सारंगीत वा सतारीत वेगवेगळ्या सुरांना मिळविलेल्या तरफेच्या तारा असतात. अनुस्पंदनामुळे त्या ठराविक कंप्रतांच्या ध्वनीने कंपायमान होऊन तो ध्वनी मोठा करतात. मानवी आवाजात देखील मुख-नासिका इ. पोकळ्या व स्वरतंतूंपासून निर्माण होणारी आंदोलने यांची युग्मित प्रणाली होते आणि त्यामुळे मनुष्याच्या आवाजाला वैशिष्ट्यपूर्ण गुणधर्म येतात. इतकेच नाही तर या पोकळ्यांचे आकार जरूर तसे बदलून वेगवेगळे वर्णोच्चार करणेही आपणाला शक्य होते. वरवर पाहता अगदी सारखी दिसणारी वाद्ये सारखीच का बोलत नाहीत त्याचा यावरून उलगडा होईल.

उर्वरित माहिती ध्वनि – २ मध्ये दिली आहे.

“