द्रव्याचा गत्यात्मक सिद्धांत

द्रव्याचा गत्यात्मक सिद्धांत: वायू द्रव व घन यांपैकी कोणत्याही अवस्थेतील पदार्थ हा कणांचा समूह असतो. त्यामधील कणांना स्वैर गती असते. त्यांच्या गतिवेगाचे मूल्य शून्यापासून अनंतापर्यंत काहीही असू शकते. समूहाचे तापमान या कणाच्या सरासरी स्वैर वेगावर अवलंबून असते. या मूलभूत कल्पनांवर द्रव्याचा गत्यात्मक सिध्दांत आधारलेला आहे. समूहातील कणांची संख्या विलक्षण मोठी असल्यामुळे (१ घ. सेंमी. वायूमध्ये साधारणतः ≈ २ X १०^१९ कण असतात) त्यातील कणांचे निरीक्षण करून कोणत्याही क्षणी त्यांच्या व्याक्तिगत वेगांचे ज्ञान करून घेणे शक्य होत नाही. याकरिता सांख्यिकीय (संख्याशास्त्रीय) पध्दत वापरून समूहाच्या तापमानाचा उपयोग करून त्यामधील वेगवितरणाच्या (वंटनाच्या) स्वरूपात ही माहिती मिळवता येते. समजा एक लक्ष वायुकणांचा समूह घेतला, तर त्यामधील किती कणांचा स्वैर वेग (एक ठराविक तापमान असता) एक ठराविक मूल्याचा आहे ( उदा., ५,००० मी./से.), हे त्याच्या वेगवितरण सूत्रावरून काढता येते. सांख्याकीय पद्धतीचा उपयोग योग्य ठरण्याकरिता समूहातील कणांची संख्या पुरेशी मोठी पाहिजे. उदा., ८–१० कणांच्या समूहाला सांख्यिकीय विवरण लावल्यास त्यापासून मिळणारे निष्कर्ष बरोबर ठरणार नाहीत. कणांचे एकमेकांवर आघात होऊन जी गतिज ऊर्जेची देवघेव होते ती रूढ नियमांनुसार होते, कणांमध्ये परस्परक्रिया किंवा आकर्षण नाही असे मानले, तर जी सांख्यिकी मिळते तिला रूढ अथवा मॅक्सवेल–बोल्टस्‌मान सांख्यिकी असे म्हणतात [→ सांख्यिकीय भौतिकी]. त्यानुसार मॅक्सवेल वेगवितरण सिध्दांत मिळतो. प्रत्यक्षात वायुकणांत परस्परक्रिया किंवा आकर्षण आहे, त्यामुळे खरे पाहिले असता त्यांमधील आघातांचे वर्णन ⇨ पुंज सिध्दांताप्रमाणेच करावयास हवे. याकरिता पुंज सांख्यिकीचा उपयोग केला पाहिजे (उदा., बोस–आइन्स्टाइन व फेर्मी–डिरॅक सांख्यिकी). सर्वसाधारण दाब व तापमान यांकरिता वायुकणांतील अंतर जास्त असल्यामुळे त्यांमधील परस्परक्रिया नगण्य समजून त्याकरिता रूढ सांख्यिकी वापरली, तरी चालू शकते. रूढ सांख्यिकीचे गणित जास्त सोपे आहे म्हणून वायूच्या गुणधर्माचे वर्णन या सांख्यिकीनुसारच केले जाते. अतिनीच तापमानाचा वायू, सर्वसाधारण तापमानाचा द्रव किंवा घन पदार्थ याकरिता या सांख्यिकीचा उपयोग योग्य ठरत नाही. वायूचे तापमान माहीत असेल, तर या सांख्यिकीचा उपयोग करून त्यामधील कणांमधील वेगवितरण काढता येते. या वेगवितरणाचा उपयोग गत्यात्मक सिद्धांतानुसार वायूचा दाब, त्यामध्ये होणारे उष्णता संवहन, श्यानता (दाटपणा) इ. स्थूलमानीय आविष्कारांचे कणांच्या गतीच्या स्वरूपात अचूक विवरण करता येते. या आविष्कारांमध्ये वायूचा दाब व तापमान यांत बदल झाला तर काय परिणाम होतील, हेही या विवरणामुळे सांगता येते. याबरोबरच या निरनिराळ्या आविष्कारांचे परस्परांशी काय संबंध आहेत हे स्पष्ट करता येते. एवढेच नव्हे, तर वायुकणाचे आकारमान इत्यादींविषयीसुद्धा संख्यात्मक अंदाज करता येतात.

मूलभूत गृहीते: मागे वर्णिल्याप्रमाणे या सिद्धांतामध्ये खालील मुख्य गृहीते आधारभूत म्हणून वापरली आहेत. (१) सर्व भौतिक पदार्थ कणसमूहापासून बनलेले आहेत, हे कण अणू किंवा रेणूच्या स्वरूपात असतात. (२) या कणांना संतत गती असून पदार्थातील उष्णता किंवा त्याचे तापमान कणाच्या सरासरी गतिज ऊर्जेवर अवलंबून असते. यांपैकी पहिले गृहीत म्हणजे पदार्थाचा कण सिद्धांत हा प्राचीन काळापासून चालत आलेला आहे. ग्रीक तत्वज्ञ डीमॉक्रिटस (इ. स. पू. पाचवे शतक) व भारतामध्ये कणाद यांनी पदार्थाचे अंतिम घटककण अणु–रेणू असतात, ही कल्पना पुढे मांडली. एकोणिसाव्या शतकाच्या मध्याच्या सुमारास जॉन डाल्टन यांनी या कल्पनेस प्रयोगाद्वारे दुजोरा देऊन तिला निश्चित वैज्ञानिक सिध्दांताचे स्वरूप दिले. जेम्स जूल, जे. आर्. मायर इ. शास्त्रज्ञांच्या प्रयोगांनी पदार्थातील उष्णता म्हणजेच त्यातील रेणूंची गतिज ऊर्जा या गृहीताची प्रचीती मिळाली. 

द्रव्याच्या अवस्था : द्रव्याच्या घन, द्रव व वायू अशा तीन महत्त्वाच्या अवस्था असतात. या तिन्ही अवस्थांमधील कणांची गतिज ऊर्जा सारख्या मूल्याची नसून त्यांमध्ये एक विशिष्ट ऊर्जावितरण आढळते. अवस्थेनुसार योग्य ती सांख्यिकी वापरून या ऊर्जावितरणाचे स्वरूप निश्चित करता येते.

---

वायू अवस्थेमध्ये समूहातील समीपस्थ कणांतील अंतर सर्वांत जास्त असते यामुळे त्यांमधील परस्परक्रिया नगण्य मानता येते. औष्णिक गतीमुळे त्यामध्ये होणारे परस्पर-आघात स्थितिस्थापक (ज्यात एकूण स्थानांतरणीय गतिज ऊर्जेमध्ये बदल होत नाही अशा) स्वरूपाचे असतात व त्यांचे वर्णन रूढ सिद्धांताप्रमाणे करता येते, असे समजणे फारसे चुकीचे ठरत नाही. वायू अवस्थेमधील कण मुक्त असतात व वायू एक-आणवीय (रेणूमध्ये फक्त एकच अणू असलेला) असला, तर त्याची औष्णिक ऊर्जा या कणांच्या स्वैर स्थानांतर गतीच्या स्वरूपातच असते.

घन अवस्थेतील कणसमूहामध्ये समीपस्थ कणांमधील अंतर सर्वांत कमी असते. त्यामुळे त्यांमधील परस्परक्रियेचे प्रमाण मोठे असते. स्फटिकामधील कणांची जालकाच्या (ठराविक ठिकाणी कणांची मांडणी होऊन तयार होणाऱ्या रचनेच्या) स्वरूपातील रचना या परस्परक्रियेमुळेच घडून येते. या परिस्थितीत रूढ सिद्धांताचा उपयोग करणे योग्य ठरत नाही आणि याकरिता पुंज सिद्धांत व सांख्यिकी यांचा वापर करणे आवश्यक ठरते. वायू व घन या अवस्थांतील कणांच्या गतीच्या स्वरूपातसुद्धा फरक असतो. एक-आणवीय वायूमध्ये कण मुक्त असल्यामुळे त्यांना इतस्ततः स्वैर स्थानांतर गती असते. याउलट घन अवस्थेतील कण मुक्त नसून ते जालकामधील विशिष्ट स्थिर स्थानाशी निगडित असतात व ते या स्थानाभोवती फक्त आंदोलतात. घन अवस्थेतील कणसमूहाची औष्णिक ऊर्जा वाढविल्यास कणाच्या आंदोलनात्मक गतिज ऊर्जेच्या स्वरूपात असते. समूहाचे तापमान वाढविल्यास कणाच्या आंदोलनाचा परमप्रसर (स्थिर स्थितीपासून होणारे जास्तीत जास्त स्थानांतरण) वाढतो. उच्च तापमानामुळे कणाच्या आंदोलनाचा परमप्रसर एका ठराविक मर्यादेपलीकडे वाढल्यास त्यांमधील समतोल मोडला जाऊन कणांची विशिष्ट जालक रचना मोडते. समूह वितळून त्याचे द्रवात रूपांतर होते. वितळबिंदूचे एक विशिष्ट तापमान असणे, हा शुद्ध घनाचा एक महत्त्वाचा गुण आहे.

द्रवामधील समीपस्थ कणांमध्ये सरासरी अंतर जास्त असते आणि त्यामुळे घन अवस्थेच्या तुलनेत त्यामधील परस्परक्रियेचे प्रमाण खूप कमी असते. हे कण द्रवामध्ये मुक्तपणे स्थानांतर करू शकतात. सांख्यिकीय सिद्धांताच्या दृष्टीने द्रवरूप समूहाची स्थिती घन व वायू या समूहांच्या मधली असते. द्रवसमूहाकरिता योग्य अशी सांख्यिकी संपूर्णपणे विकसित केली गेलेली नाही. तीन अवस्थांमधील कणसमूहांच्या वर्तनात, या सांख्यिकीय भिन्नत्वामुळे, थोड्याफार प्रमाणात फरक आढळला, तरी त्या सर्वांकरिता गत्यात्मक सिद्धांताच्या मूलभूत संकल्पना यथार्थ ठरतात. वायुरूपी कणसमूहात या संकल्पना समजण्यास आणि गणितीय दृष्ट्या हाताळण्यास सुलभ असल्यामुळे अशा समूहाचा विचार यापुढे मुख्यत्वेकरून केला आहे.

आदर्श वा परिपूर्ण वायुसमूहाचे गुणधर्म : या समूहाच्या गुणधर्माचे विवरण करण्याकरिता खाली वर्णिलेली प्रतिकृती वापरतात. या समूहातील कण संपूर्णपणे स्थितीस्थापक, अगदी परस्परांसारखे असे गोलक असतात. समीपस्थ कणांमधील अंतर त्यांच्या त्रिज्येच्या तुलनेत खूप जास्त असल्यामुळे हे गोलक बिंदुमात्र आहेत, असे मानता येते. कणांच्या मुक्त स्वैर संचार गतीमुळे ते सतत परस्परांवर आदळतात. स्थितिस्थापक-आघात सिध्दांतानुसार त्यांमध्ये ऊर्जेची देवघेव होते. या क्रियेमुळे समूहात स्थिर स्थिती प्रस्थापित होते. याचा अर्थ असा होतो की, समूहातील कणांमधील ऊर्जावितरण स्थिर होते व ते कालपरिवर्ती (काळानुसार बदलणारे) असत नाही. एकूण समूहाची गतिज ऊर्जा अर्थात कायमच राहते. स्थिर स्थितीमध्ये कोणत्याही एका क्षणी, एका दिशेत धावणाऱ्या समूहातील कणांची संख्या सर्व बाजूंस समान असली पाहिजे हे उघड आहे. कारण ही संख्या एका दिशेत जास्त व दुसऱ्या दिशेत कमी, असे असण्याचे काही एक कारण नाही. कणवेगामधील दिशिक वितरण समान असणे यास समदिक्‌ता असे म्हणतात. कणाचे द्रव्यमान = m, समूहातील प्रती घ. सेंमी. मधील त्यांची संख्या = n, समूहाचे तापमान = T, कणाचा स्थानांतर वेग = C असे मानले, तर समूहातील कणाचा वेग C हा – ∞ ते + ∞ या मर्यादेत काहीही मूल्य धारण करू शकतो. ज्याचा संपूर्ण वेग C व C +dC यांमध्ये आहे, अशा समूहातील प्रती घ.सेंमी.कणांची संख्या n_c ही जे. सी. मॅक्सवेल यांनी प्रथम रूढ सांख्यिकी वापरून खालील समीकरणाने मिळते असे दाखविले.

    

                                       (१)  

---

 याला मॅक्सवेल यांचा वेगवितरण सिद्धांत असे म्हणतात. या समीकरणात k हा बोल्टस्‌मान (एल्. बोल्टस्‌मान या भौतिकीविज्ञांच्या नावावरून ओळखण्यात येणारा) स्थिरांक व e हा स्वाभाविक लॉगरिथमाचा आधारांक आहे.

वरील समीकरणावरून असे दिसते की, जर C = 0 तर n_C = 0 आणि तरीही n_C = 0 यावरून यामधील कोठल्या तरी वेगाच्या मूल्याकरिता n_C चे मूल्य महत्तम होईल. या वेगाच्या मूल्याला अतिसंभाव्य वेग C_m असे म्हणतात. याचे मूल्य

                                                  (२)

या सूत्राने मिळते. कणवेगांच्या वर्गांची सरासरी घेऊन त्याचे वर्गमूळ काढून मिळणारे वेगाचे मूल्य (वर्ग माध्य वर्गमूळ वेग व. मा. व. वेग)

या सूत्राने मिळते. हा वेग जास्त महत्त्वाचा आहे कारण हे सूत्र निराळ्या स्वरूपात लिहिले असता

                                                     (३)

यापासून कणाच्या गती मुक्तता मात्रांत होणाऱ्या ऊर्जा विभाजनाबद्दल फार महत्त्वाचा असा सिद्धांत काढता येतो (यासंबंधी पुढे विवरण दिलेले आहे). याशिवाय आपणास कणाचा सरासरी वेग

                                                     (४)

---

 याने मिळतो असे दाखविता येते. वायूमधील उष्णता संवहन, विसरण (रेणू एकमेकांत मिसळण्याची क्रिया) इ. आविष्कारांचे विवेचन करण्याकरिता वायुकणाचा सरासरी वेग C_a हाच महत्त्वाचा ठरतो. C_a, C_m व C‾ यांमधील परस्परसंबंध खाली दाखविले आहेत.

C_a = 1·13 C_m     C‾= 1·22 C_m.

समीकरण (१) पुढील स्वरूपात मांडता येते

                            (५)

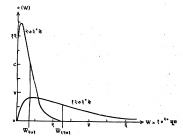
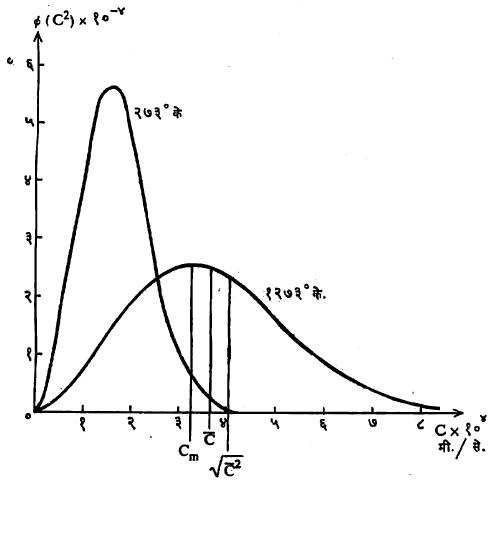ज्याचा वेग आसन्नपणे (जवळजवळ) C एवढा आहे अशा समग्र कणसंख्येचा अंश ⁿC/n ने दर्शविला जातो. मॅक्सवेल सूत्राप्रमाणे मिळणारे हायड्रोजन वायूमधील कणांचे (रेणूंचे) वेगवितरण आ. १ मध्ये दाखविले आहे. 

मॅक्सवेल वेगवितरणाचे आणखी एक रूप काही आविष्कारांकरिता उपयोगी पडते. घटककणाचा संपूर्ण वेग जो C आहे त्याचे X, Y, Z, या अक्षांशी समांतर घटक अनुक्रमे u,v,w, असे असतील, तर फक्त एका घटकवेगाचे मूल्य आसन्नपणे u असणाऱ्या कणांची संख्या खालील सूत्राने मिळते असे दाखविता येते.

                             (६)

---

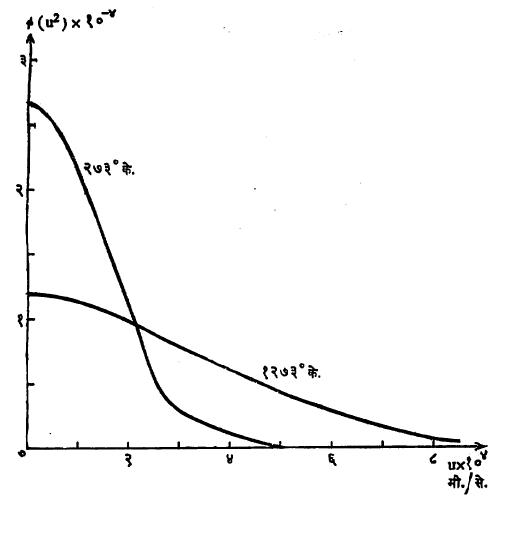
आ. 2 मध्ये हायड्रोजन वायुमधील कणवेग घटक वितरण दाखविले आहे.आ.1 व 2 यांमधील फरक लक्षात घेण्याजोगा आहे. ज्या कणांचा वेग घटक µ आहे त्यांचा संपूर्ण वेग C भिन्न मूल्याचा असू शकतो, हे या फरकाचे कारण आहे. मॅक्सवेल वेगवितरणावरून कणामधील गतिज ऊर्जेचे वितरण मिळू शकते, कारण 1/2 mC² = W = गतिज ऊर्जा, हे वितरण मॅक्सवेल-बोल्ट्‌समान सिद्धांत म्हणून प्रसिद्ध आहे.

 (७)

याप्रमाणे वायुकणांमध्ये मिळणारे ऊर्जावितरण आ. ३ मध्ये दाखविले आहे. वर वर्णन केलेल्या मॅक्सवेल-बोल्ट्‌समान सांख्यिकीचा उपयोग करून आदर्श वायूकरिता (१) त्याचा दाब, (२) त्याची विशीष्ट उष्णता [→उष्णता], (३) त्यामधील रूढ ऊर्जासम विभाजन इ. सिद्धांतांची उपपत्ती लावता येते.

आदर्श वायूचा दाब : येथे वायूचे धारकपात्र आयताकार असून त्याची एक भिंत X अक्षाला लंबरूप आहे असे मानले आहे. वायुकणाच्या स्वैर संचाराची कल्पना आ.४ वरून येईल. वायुकण अवकाशात स्वैर हालचाल करतात, तर काही पात्राच्या भिंतीवर आदळून परावर्तित होतात. वायूच्या कणसमूहातील कोणत्याही एका कणाचा संपूर्ण वेग C व त्याचे X, Y, Z या दिशांत u,v,w असे घटक आहेत. हा कण पात्राच्या भिंतीवर mu या संवेगाने (वेग X द्रव्यमान या राशीला संवेग म्हणतात) स्थितिस्थापक आघात करतो असे मानले, तर आघातानंतर त्याच्या गतीची दिशाच फक्त उलटी होऊन वेगाचे मूल्य जवळजवळ तेवढेच राहील. यामुळे त्याच्या संवेगामध्ये 2mu एवढा बदल होईल. u घटक असणाऱ्या कणाची प्रती घ. सेंमी. संख्या एवढी असेल. एका सेकांदात भिंतीच्या चौ.सेंमी. क्षेत्रफळावर पडणाऱ्या कणांची संख्या

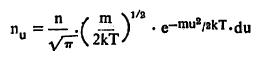
एवढी असेल. एका सेकंदात भिंतीच्या चौ. सेंमी क्षेत्रफळावर पडणाऱ्या कणांची संख्या

---

 

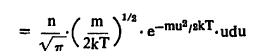
एवढी असते. प्रत्येक कण 2 mu संवेग भिंतीला देतो, त्यामुळे सर्व वेग घटक विचारात घेतले असता भिंतीला प्रती सेकंद, प्रती चौ. सेंमी. संवेग अंतरण खालील समाकलन सूत्राने मिळते.

           (८)

आतापर्यंत एक घ.सेंमी. घनफळ असलेल्या वायूचा विचार केला. जर प्रत्यक्षात M ग्रॅमरेणू द्रव्यमानाचा (ज्याचे ग्रॅममधील मान त्या द्रव्याच्या रेणूभाराच्या इतके असते अशा द्रव्यमानाचा) वायू असेल, तर त्यामधील कणांची संख्या ए ॲव्होगाड्रो यांच्या नियमानुसार N (ॲव्होगाड्रो संख्या) एवढी असणार व त्याचे घनफळ V एवढे असेल. याकरिता n = N/V यावरून सूत्र (८) चे स्वरूप

pV = NkT = RT                                                                             (९) 

असे होते.

समीकरण क्र. ९ हे आदर्श वायूकरिता सर्वसाधारण वायू समीकरण या नावाने प्रसिद्ध आहे.

समीकरण (८) व (९) वरून प्रयोगांद्वारे याआधी सिद्ध झालेल्या अनेक नियमांचे सुलभ विवरण मिळते. समीकरण (८) वरून असे दिसते की, एकच तापमान व दाब असलेल्या निरनिराळ्या वायूंमध्ये वायुकणांची प्रती घ.सेमी. असणारी संख्या सारखीच असते, हा नियम ॲव्होगाड्रो यांनी शोधून काढला. जर वायूचे तापमान स्थिर असेल, तर वायूचा दाब त्याच्या घनफळाच्या व्यस्त प्रमाणात बदलतो हा सिद्धांत (रॉबर्ट बॉइल यांच्या नावावरून ओळखण्यात येणारा) म्हणून प्रसिद्ध आहे समीकरण (९) वरून असा निष्कर्ष निघतो की जर वायूचे घनफळ स्थिर असेल, तर वायूचा दाब त्याच्या तापमानाच्या रेखीव (एकघाती) प्रमाणात वाढेल. वाढ ही भिन्न वायूंच्या बाबतीत सारखीच असते कारण R या स्थिरांकांचे सर्व वायूंकरिता एकच मूल्य असते. जर याऐवजी वायूचा दाब स्थिर ठेवला, तर वायूचे घनफळ त्याच्या तापमानाच्या रेखीय प्रमाणात वाढते असे समजते, यालाच चार्ल्‌स नियम (जे. ए. सी. चार्ल्‌स यांच्या नावाने ओळखण्यात येणारा नियम) म्हणतात. एखाद्या वायुसमूहात अनेक घटक वायू असतील, तर त्या प्रत्येक घटकाचा आंशिक दाब 

p1 = n1kTp2 = n2kT

या समीकरणाने मिळतो. यांतील १ पादांकाच्या राशी पहील्या वायूच्या आहेत व २ पादांकाच्या दुसऱ्या वायूकरिता आहेत असे समजावे, यावरून वरील वायुमिश्रणाचा परिणामी दाब

---

 P = P₁ + P₂ = (n₁ + n₂)kT         (१०)

या सूत्राने मिळतो. समीकरण (१०) मध्ये डाल्टन नियमाचा अंतर्भाव होतो. या नियमाप्रमाणे वायुमिश्रणामधील परिणामी दाब त्याच्या घटक वायूंच्या व्यक्तीशः असलेल्या दाबाच्या बेरजेएवढा असतो. वायुमिश्रणाचे संपूर्ण घनफळ प्रत्येक घटक वायूने व्यापले असता त्यांचे जे दाब मिळाले असते तेवढीच मूल्य या घटक दाबांची असतात, ही गोष्टही येथे लक्षात घेण्यासारखी आहे.

वायुकणांच्या गती मुक्तता मात्रांमधील ऊर्जा विभाजन : सूत्र (३) प्रमाणे वायुकणाचा वर्ग माध्य वर्गमूळ वेग C हा वायूच्या तापमानाशी निगडित असतो.

                          (११)

C या संपूर्ण वेगाच्या तदनुरूप घटकांची मूल्ये u, v, w एवढी असतील, तर गणितीय रीतीने

 (१२)

असे मॅक्सवेल-बोल्ट्‌समान सांख्यिकी वापरून दाखविता येते. एक आणवीय वायुकणास फक्त स्थानांतर गती असते. त्रिमीतीय अवकाशात वायुकण वेगाची दिशा X, Y, Z यांपैकी कोणत्याही एका अक्षाशी संमातर असू शकेल किंवा ही दिशा यांपैकी कोणत्याही अक्षाशी संमातर नसेल. अशा अवस्थेत या वेगाला फक्त u, v, w असे तीनच घटक असू शकतात. यामुळे तांत्रिक भाषेत एक आणवीय वायुकणास फक्त तीन स्थानांतर गती मुक्तता मात्रा आहेत असे म्हटले जाते. समीकरण (१२) वरून असे दिसते की, स्थिर स्थितीत वायुकणाची गतिज ऊर्जा त्याच्या तीन गती मुक्तता मात्रामध्ये सारखीच विभागलेली असते. हा निष्कर्ष व्यापक असून तो तीन पेक्षा अधिक गती मुक्तता मात्रा असलेल्या वायुकण समूहांच्या बाबतीत सुद्धा यर्थाथ असतो, असे बोल्टसमान यांनी दाखविले. जर वायुकण द्विआणवीय असेल, तर आ. ५ मध्ये दाखविल्याप्रमाणे त्यास एकंदर परिणामी गती मुक्तता मात्रा पाच असू शकतात. यांपैकी एक-आणवीय कणाप्रमाणे तीन स्थनांतर गती व त्यांशिवाय परीभ्रमणीय दोन गती असतात (द्विआणवीय कणाच्या बाबतीत त्याच्या द्रव्यमध्यभोवती आंदोलन गतीसुद्धा शक्य असते. सर्वसाधारण तापमानाकरिता या गतीची शक्यता नगण्य असते असे आढळते). बोल्ट्‌समान सिंद्धातानुसार या सर्व पाच गती मुक्तता मात्रांमध्ये ऊर्जा विभाजन सारखेच म्हणजे प्रत्येकी  1/2kT एवढेच असते. ज्या गतीकरिता तदनुरूप ऊर्जा ही गतीच्या सहनिर्देशकाच्या (अंक्षाच्या सापेक्ष स्थान दर्शविणाऱ्या अंकाच्या) वर्गाच्या स्वरूपात मिळते, अशी गती मुक्तता मात्रा करताच सरासरी ऊर्जा 1/2kT एवढी असते, असे दाखविले गेले आहे. जर एखाद्या गतीकरिता असणारी ऊर्जा तिच्या सहनिर्देशकाच्या x घातामध्ये मिळत असेल, तर मॅक्सवेल-बोल्ट्‌समान सांख्यिकी वापरून तदनुरूप सरासरी ऊर्जा kT/x एवढी असेल, असे दाखविता येते.

---

अती उच्च तापमानाकरिता समूहातील वायुकणांचे वेग एवढे मोठे होतात की, ऊर्जा गणन करण्यासाठी रूढ सूत्रे योग्य ठरत नाहीत. जेव्हा kT चे मूल्य साधारणपणे च्या मूल्याएवढे होते (C_o = प्रकाशवेग) तेव्हा अशी परिस्थिती निर्माण होते. ⇨सापेक्षता सिद्धांताप्रमाणे 

हे सूत्र वापरले असता प्रत्येक गती मुक्तता मात्रेकरिता सरासरी कण ऊर्जा अशा वेळी   

1/2 kT (1 + 5/4 . kT/mC_o²⁾                                                                                                                                   (१३)

या सूत्राने मिळते असे दाखविता येते.

मर्यादित सापेक्षता सिद्धांताप्रमाणे कोणत्याही एका कणाचा वेग कोणत्याही परिस्थितीत C_o या प्रकाशवेगापेक्षा जास्त असू शकत नाही या तत्त्वाचा ज्याच्यात अंतर्भाव केलेला आहे असे खाली दिलेले सुधारित वेगवितरण ई. कनिंगहॅम यांनी सुचविले आहे.

                                                                        (१४)

या सूत्रात A आणि α हे स्थिरांक असून W₀ ही कणाची विश्रामी ऊर्जा आहे. या सूत्राप्रमाणे प्रकाशवेगापेक्षा जास्त वेग असणाऱ्या कणांची संख्या शून्य होते. मॅक्सवेल-बोल्ट्‌समान वितरण फलनाकरिता लोरेन्ट्स रूपांतरण [एका सहनिर्देशक व्यूहातून दुसऱ्या सहनिर्देशक व्यूहात रूपांतर करण्याकरिता वापरण्यात येणारे गणितीय रूपांतरण → सापेक्षता सिद्धांत] वापरले असता त्याचे स्वरूप बदलते. या वरून हे वितरण सापेक्षता सिद्धांताच्या निकषानुसार विश्वव्यापी स्वरूपाचे नाही असे समजते. वायुविसर्जनाद्वारे (वायुतून विद्युत् प्रवाह वाहून नेण्याच्या क्रियेद्वारे) मिळणाऱ्या आयनद्रायूकरिता (ज्यात धन आयन–विद्युत् भारित अणु वा अणुगट–व इलेक्ट्रॉन याची संख्या जवळजवळ सारखी आहे अशा उच्च आयनीभूत वायूकरिता) ड्रुइव्हेस्टीन यांनी मॅक्सवेल-बोल्ट्‌समान सदृश असे एक परिवर्तित ऊर्जावितरण फलन सुचविले आहे ई. ए. मिल्न यांनी त्यांच्या विस्तारित सापेक्षता सिद्धांताचा वापर करून वेगवितरण फलन मिळविले आहे. हे फलन लोरेन्ट्स रूपांतरणानंतरही निश्चल राहते. मिल्न याचे वितरण सूत्र खाली दिले आहे.

येथे B हा स्थिरांक आहे. या प्रकारचे वेगवितरण असलेला समूह उपलब्ध नाही. मॅक्सवेल वेगवितरणाचा उपयोग तारासमूहाच्या अवकाश वितरणाचे यथार्थ वर्णन करण्याकरिता केला गेला आहे. अशाच प्रकारच्या परिस्थितीत मिल्न यांच्या वेगवितरणाचा उपयोग हाईल अशी अपेक्षा होती.

---

 विशिष्ट उष्णता : वायुसमुहातील कणांना स्थिर स्थितीमध्ये प्रत्येक गती मुक्तता मात्रेकरिता सरासरी 1/2 kT एवढी ऊर्जा असते, असे वर सांगितले आहे. एक-आणवीय वायूच्या ग्रॅमरेणू द्रव्यमानात एकंदर कणांची संख्या N एवढी असते आणि या प्रत्येक कणाला फक्त तीन स्थानांतर मुक्तता मात्रा असतात हे लक्षात घेतले, तर एकंदर समूहाची सरासरी ऊर्जा

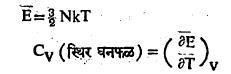 एवढी होते. विशिष्ट उष्णता

म्हणून                (१५)

हीलियम, आर्‌गॉन यांसारख्या वायूंच्या बाबतीत C_v चे प्रयोगान्ती मिळालेले मूल्य एवढेच आढळते (‘वायूमधील उष्णता संवहन’ या उपशीर्षकाखाली दिलेले कोष्टक पहावे).

द्विआणवीय वायुकणाकरिता मागे वर्णन केल्याप्रमाणे तीन स्थानांतर आणि दोन परिभ्रमणीय गती मुक्तता मात्रा असतात. त्यामुळे अशा वायूकरिता 

हायड्रोजन व नायट्रोजन यांकरिता प्रयोगाने C_V करिता जवळजवळ एवढेच मूल्य मिळते (कोष्टक पहा).

वरील सिद्धांत घन पदार्थाकरिताही यथार्थ आहे असे मानून अशा समूहातील कणास स्थिर बिंदूभोवती फक्त आंदोलन गती मुक्तता मात्रा आहे, असे आपण समजू शकतो. आंदोलन गतीमध्ये ऊर्जा ही गतिज आणि स्थितिज या दोन स्वरूपांची असू शकते. सरासरीने अर्धी ऊर्जा गतिज व अर्धी स्थितिज प्रकारची आहे असे मानले तर गतिजकरिता 1/2kT स्थितीजकरिता 1/2kT अशी प्रत्येक आंदोलन दिशेकरिता एकंदर सरासरी ऊर्जा kT एवढी होईल. आंदोलन गती मुक्तता मात्रा तीन त्यामुळे एकंदर ग्रॅमरेणुची सरासरी ऊर्जा E‾ = 6RT अथवा Cv = 5/2R = 4·96 कॅलरी/° (तापमान) अशी उपपत्ती मिळते. डुलाँग व पेटिट सिद्धांत (पी. एल. डुलाँग व ए .टी पेटिट या शास्त्रज्ञांच्या नावाने ओळखण्यात योणारे सिद्धांत) वरील निष्कर्षाशी जुळतो. वरील सुलभ उपपत्तीवरून असे दिसते की, कोणत्याही अवस्थेतील (व विशेषतः वायूकरिता) विशिष्ट उष्णता त्याच्या तापमानावर अवलंबून नसते. प्रत्यक्षात विशिष्ट उष्णता स्थिर नसून ती अतीनीच तापमानाकरिता घन किंवा वायूकरिता बऱ्याच मोठ्या प्रमाणात ऱ्हास पावते, असे प्रयोगाने दिसते. रूढ सांख्यिकी या परिस्थितीत यथार्थ ठरत नाही हेच त्याचे कारण आहे. याचे योग्य विवरण करण्याकरिता पुंज सिद्वांताचीच मदत घ्यावी लागते [→उष्णता].

---

 वायूमधील स्वैर संचार करणारा वायुकण इतर वायूकणांवर आघात करतो.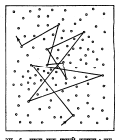

माध्य मुक्त पथ : वायुसमूहातील कणांना स्वैर गती असते त्यामुळे ते एकमेकांवर आदळतात व पात्राच्या भिंतीवर सुद्धा आघात करतात. याचे वर्णन मागे आले आहे. या परस्पर आघाताने वायूमध्ये स्थिर स्थिती प्रस्थापित होते. कणाचि गति स्वैर आहे, त्याचा वेग निरनिराळा आहे यामुळे कोणत्याही एका कणाने दोन अनुक्रमी (लागोपाठच्या) आघातांमध्ये कापलेले अंतर (आ. ६) हे मोठ्या प्रमाणात फेरबदल दाखवील. पुरेशी आघातसंख्या विचारात घेऊन जर दोन आघातांमधील कापलेल्या अंतरांची बेरीज करून त्यास आघातसंख्येने भागिले, तर त्यापासून जे सरासरी अंतर मिळते त्यास माध्य मुक्त पथ म्हणतात. दोन अनुक्रमी परस्पर आघातांमध्ये एका कणाने कापलेले, सरासरी अंतर (λ) अशी त्याची व्याख्या करता येते. गत्यात्मक सिद्धांतानुसार याचे मूल्य काढण्याकरिता वायूतील कण बिंदुमात्र नसून त्यांस एक ठराविक व्यास आहे व त्यांमध्ये परस्परक्रिया होत नाही असे समजणे आवश्यक ठरते. गणितीय सुलभतेकरिता आपण असे मानू की, एक कण C_a या सरासरीने वेगाने संचार करीत आहे व इतर सर्व कण स्थिर आहेत. जर कणाचा व्यास σ असेल तर तो एका सेकंदात ∏σ² = C_a एवढेच अवकाश घनफळ व्यापेल .जर n = कणांची प्रती घ. सेमी संख्या असेल, तर वरील घनफळात जेवढे कण असतील त्या सर्वांवर मूळ कण आघात करतो, असे मानता येईल, त्यामुळे आघात कंप्रता (प्रती सेकंदातील आघातसंख्या) ν = ∏σ²C_an.यावरून λ = माध्य मुक्त पथ = C_{a /ν = 1 /}  n∏σ² हे सूत्र मिळते. आर्. यू. ई. क्लॉसियस व मॅक्सवेल यांनी इतर कणांचा वेग लक्षात घेऊन जास्त काटेकोरपणे गणित वापरून

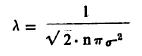                                                                   (१७)

असे दाखविले आहे. वरील सूत्र फक्त आसन्नपणे यथार्थ ठरते हे लक्षात घेणे आवश्यक आहे. कणांमध्ये परस्परक्रिया नाही हे यामध्ये वापरलेले गृहीत अचूकपणे लागू नाही. सूत्र १७ प्रमाणे कणाचा माध्य मुक्त पथ त्याच्या वेगावर अवलंबून नाही असे दिसते. प्रत्यक्षात हे काटेकोरपणे घडत नाही असे प्रयोगावरून दिसून येते.

आदर्श वायूकरिता परिवहन आविष्कार: यामध्ये श्यानता, उष्णता संवहन इ. आविष्कारांचा समावेश होतो. या सर्व आविष्कारांमध्ये वायू स्थिर स्थितीत नसतो पण या स्थितीपासून झालेल्या बदलाचे प्रमाण कमी आहे असे मानून यांचे गणितीय विवरण करता येते.

श्यानता : वायू भरलेल्या एखाद्या नलिकेच्या एका टोकास वायूवर दाब दिल्यामुळे वायूचे तीमधून वाहणे या आविष्कारात श्यानतेचा विचार करावा लागतो. नलिकेमधून हायड्रोजन वायू हा ऑक्सिजनापेक्षा जास्त सुलभतेने वाहतो. प्रवाहीपणास होणाऱ्या रोधाचे प्रमाण वायूच्या श्यानता या गुणधर्मामुळे ठरते. जेवढी श्यानता कमी तेवढी प्रवाहीपणात सुलभता येते. प्रहावीपणास होणारा विरोध वायूच्या रेणूंमधील अंतर्गत क्रियेमुळे अथवा घर्षणामुळे होतो, असे मानले जाते. या दाबामुळे वायुकणांना एकाच दिशेत सामूहिक गती V मिळते.

---

 या गतीवेगाचे प्रमाण त्याच्या स्वैर गतिवेगाच्या तुलनेत अल्प असते असे गृहीत धरले जाते. वायूच्या श्यानतेकरिता गत्यात्मक सिद्धांताचा उपयोग करून त्याकरिता सूत्र मिळवणे हे या सिद्धाताचे एक महत्त्वाचे यश ठरले आहे. या विवरणाचा सुलभ प्रकार पुढे दिला आहे. आ. ७ मध्ये ब हा नलिकेची भिंत व अक्ष यामधील भाग असून त्यातील दाबामुळे तिच्यामधून वायूची सामूहिक गती डावीकडून उजवीकडे होत आहे असे मानले आहे. गणितीय सुलभतेकरिता वायूकण एकाच सरासरी C_a या वेगाने संचार करीत आहेत असे समजू. या स्वैर गतीचे दिशिक वितरण समान असते. त्यामुळे X, Y, Z यापैकी कोणत्याही एका दिशेत एक घ.सेमी. क्षेत्रफळ ओलांडून जाणाऱ्या कणांची संख्या nC_a/6 एवढी असेल, हे उघड आहे. या स्वैर गतीवर लावलेल्या दाबामुळे निर्माण झालेली सामुहीक गती V अध्यारोपित होते. या गतीचे मूल्य अक्षापासूनच्या अरीय अंतराप्रमाणे बदलत जाईल कारण भिंतीजवळ या गतीचे मूल्य शून्य असले पाहिजे, तर नळीच्या अक्षापाशी हिचे मूल्य महत्तम असेल. Z च्या दिशेत यामुळे वेग प्रवणता (अंतरानुसार होणारा वेगबदल) मिळेल. श्यानतेच्या व्याख्येप्रमाणे एकक क्षेत्रफळावर श्यानतेमुळे उत्पन्न होणारी घर्षणाच्या जातीची प्रेरणा F=–ηdV/dZ  या सूत्राने मिळते. येथे η  हा श्यानता गुणांक आहे. गत्यात्मक सिद्धांताप्रमाणे हिचे मूल्य काढण्याकरिता एकमेकास XY प्रतलेस संमातर अशी तीन प्रतले अ, आ, इ विचारात घेऊ. अ आणि आ तसेच आ आणि इ मधील लंब अंतर या वायूच्या माध्य मुक्त पथाएवढे आहे असे धरले आहे. कण अ मधून निघून आ मध्ये त्यांच्या स्वैर गतीमुळे येतात तेव्हा ते दुसऱ्या कणांवर आघात करीत नाहीत. अ या ठिकाणी असणाऱ्या सर्व कणांना C_a एवढा स्वैर गतिवेग व त्यावर अध्यारोपित असा हा फक्त X दिशेत असणारा सामूहिक वेग असतो. इ मधील कणांना स्वैर गतिवेग C_a हाच आहे व त्याशिवाय V₂  हा  X दिशेत असणारा अतिरिक्त वेग आहे. त्यामुळे अ मधून आ च्या एकक क्षेत्रफळावर प्रतिसेकंद आदळणाऱ्या कणामुळे जो संवेग दिला जातो तो इ मधून आ च्या तेवढ्याच क्षेत्रफळावर प्रतिसेकंद आदळणाऱ्या कणांपासून मिळणाऱ्या संवेगापेक्षा जास्त असतो . यामुळेच आ वर प्रेरणा निर्माण होते. अ पासून येणाऱ्या कणांमुळे हा संवेग

nC_a/6[ m(C_a+V₁)]

असेल, तर इ पासून येणाऱ्या कणांमुळे

nC_a/6[ m(C_a+V₂)]

एवढा संवेग दिला जाईल. आ च्या एक घ सेमी. क्षेत्रफळास मिळणारा प्रती सेकंद निव्वळ संवेग

-nC_a/6(V₁–V₂)

एवढा राहील. न्यूटन यांच्या सिद्धांताप्रमाणे आ वरचा हाच दाब असेल, तर

(V₁–V₂)/2λ=dV/dZ

---

 श्यानतेची व्याख्या वापरून

F= -η(V₁–V₂/2λ)= -mnC_a/6(V₁–V₂)

η = 1/3mnC_aλ                                                                                                 (१८)

मॅक्सवेल यांनी जास्त काटेकोर गणितीय रीत वापरून

η = 0·310mnC_aλ=0·310p C_aλ                                                                        (१९)

हे सूत्र मिळविले, वरील p= वायूची घनता. या समीकरणात λ = 1/n हे लक्षात घेतले, तर श्यानता वायुदाबावर अवलंबून नसते, असा निष्कर्ष काढता येतो. त्याचप्रमाणे C_aλ√T म्हणून तापमान वाढविल्यास वायूची श्यानता वाढावी असे दिसते. हे दोन्हीही निष्कर्ष प्रयोगान्ती खरे आहेत, असे आढळले आहे.

सूत्रे (४), (१७)व (१८) यांचा उपयोग करून कणाचा व्यास σ काढता येतो [→ श्यानता].

η= 2/3∏^3/2.1/Nσ^{2 . √MRT …   …   …}   (२०)

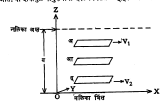
वायूमधील उष्णता संवहन : वायूमधील उष्णता संवहन क्रिया ही धातूमधील याच क्रियेपेक्षा निराळी असते. वायूमध्ये उष्णता संवहन त्यामधील वायुकणांच्या प्रत्यक्ष स्थानांतर गतीमुळे होते. या क्रियेचे वर्णन श्यानतेकरिता दिलेल्या विवरणासारखेच आहे आ. ८ मध्ये या क्रियेचे सुलभ विवरण करण्याकरिता लागणारी परिस्थिती दाखविली आहे. या आकृतीत Z अक्षाच्या दिशेने तापमान प्रवणता मिळते असे मानले आहे. याचा अर्थ या दिशेत वायूच्या तापमानात बदल होतो . आकृतीतील अ प्रतलाचे तापमान T₁ असते व तेथील वायुकणांची ऊर्जा E₁एवढी आहे असे मानले आहे. त्यापासून λ अंतरावर (λ = माध्य मुक्त पथ) आ प्रतल असून त्याचे तापमान T = (T1 + T2/2) एवढे आहे असे मानले आहे. आ. पासून परत λ अंतरावर दुसऱ्या बाजूस इ प्रतल असून त्याचे तापमान T2 व त्यावरील वायुकणांची ऊर्जा E2 आहे. T1 व T2 मधील फरक जास्त नसल्यामुळे अ त इ विभागातील सर्व कणांचा सरासरी वेग C_a एवढा आहे, असे आसन्नपणे समजता येते. अ पासून आ च्या एकक क्षेत्रफळावर प्रतिसेकंद आदळणाऱ्या कणांची संख्या nC_a/6 एवढी होईल व येथील कणांची ऊर्जा E₁ असल्यामुळे तेथे nC_a/6·E1 एवढी ऊर्जा पोहोचविली जाईल. याच न्यायाने इ मधून तेवढ्याच क्षेत्रफळावर nC_a/6·E2 एवढी ऊर्जा पोहोचविली जाईल. आ कडे परिणामी ऊर्जा लाभ

= nC_a/6·(E1–E2)

---

 जर एकक क्षेत्रफळातून dQ एवढ्या उष्णतेचे dT या कालखंडात परिवहन झाले, तर औष्णिक संवाहकतेच्या (K च्या) व्याख्येनुसार

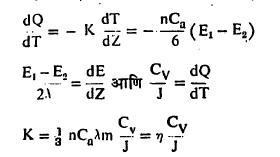   (२१)

हे सूत्र मिळते. येथे Q ही उष्णता राशी, C_v ही वायूची विशिष्ट उष्णता ( स्थिर घनफळ) आणि J हा ⇨उष्णतेचा यांत्रिकतुल्यांक आहे.

वायूचा दाब कमी केला असता श्यानता व औष्णिक संवाहकता कमी व्हावी असे सर्वसाधरणपणे वाटेल कारण दाब कमी झाला म्हणजे या दोन्ही अाविष्कारांना जबाबदार अशा वायुकणांची संख्या कमी होते. गत्यात्मक सिद्धांतानुसार हे दोन्हीही स्थिरांक दाबावर अवलंबून नसतात, हे मॅक्सवेल यानी दाखविले (समी. १८ व २१). हा निष्कर्ष ठराविक दाब मर्यादेत बरोबर आहे, असे प्रयोगाने सिद्ध झाले आहे. त्याबरोबरच जर वायूचा दाब सतत कमी करीत जाऊन त्या ठिकाणी अंती संपूर्ण निर्वात स्थिती निर्माण केली, तर राहिलेल्या माध्यमाला श्यानता किंवा औष्णिक संवाहकता मुळीच असणार नाही हे उघड आहे. या दृष्टीकोनातून या आविष्काराचे विवेचन केल्यास ज्या अवस्थेत वायुकणाचा माध्य मुक्त पथ वायुपात्राच्या आकारमानाचा होतो, त्या स्थितीपासून दाब आणखी कमी करीत गेल्यास या दोन्हीही राशींत घट व्हावी असा निष्कर्ष निघतो. हाही निष्कर्ष प्रयोगाद्वारे बरोबर आहे असे सिद्ध करता येते.

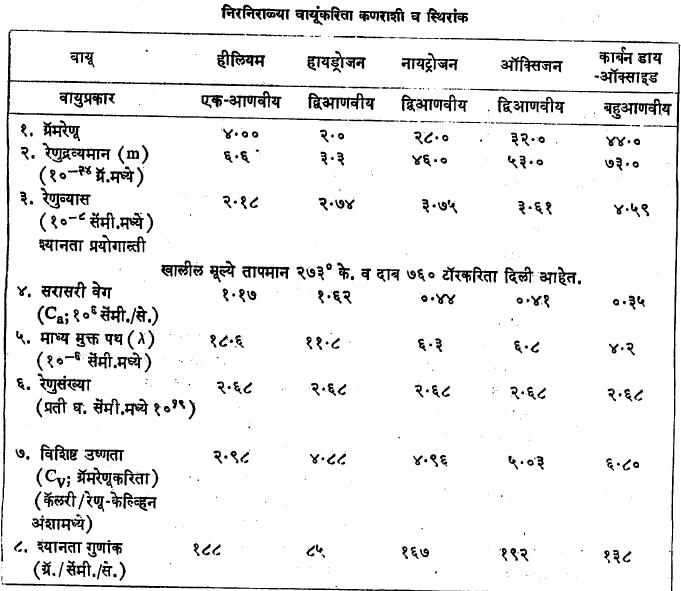
पुढील कोष्टकात काही प्रातिनिधिक वायुकणांकरिता निरनिराळे कण स्थिरांक, त्याकरिता प्रयोगाने मिळालेली श्यानता, विशिष्ट उष्णता (ग्रॅमरेणू), औष्णिक संवाहकता इ. स्थूलमानी स्थिरांक दिले आहेत. यावरून आतापर्यंत केलेल्या विवेचनाचे स्पष्टीकरण होईल.

वायूची श्यानता इ. प्रयोगांपासून वायुकणाच्या व्यासाचे जे मूल्य मिळते त्याला फक्त आसन्न सार्थता असते, हे येथे लक्षात ठेवले पाहिजे. वायुकण काटेकोर गोलकासारखे असून त्यांस एक विशिष्ट व निश्चित व्यास आहे असे समजणे बरोबर होणार नाही. वायुकणाच्या भोवती जे प्रभावक्षेत्र आहे त्याच्या आकारमानाचा सांख्यिकीय अंदाज वरील व्यास गणन पद्धतीने मिळतो, असे समजणे योग्य होईल. वायुकणाचा व्यास काढण्याकरिता अनेक रीती आहेत (उदा., वर्णपटीय, व्हॅन डर व्हाल्स स्थिरांक मापन इ.). या प्रत्येक रीतीनुसार वायुकणाच्या व्यासाची जी मूल्ये मिळतात ती एकरूप नसून त्यांमध्ये नेहमी कमीअधिक फरक आढळतो. या गोष्टीवरून वरील दृष्टिकोनाची सार्थता स्पष्ट होते.

---

वायूचे विसरण : आ. ९ मध्ये दाखविल्याप्रमाणे p दाब असलेला आणि T तापमानाचा एक वायू (उदा.,ऑक्सिजन) अ या पात्रात घेतला आणि आ या दुसऱ्या तशाच पात्रात त्याच दाबाचा व तापमानाचा पण दुसरा वायू (उदा., नायट्रोजन) घेतला आहे. जर या दोन पात्रांमधील अडथळा ( म्हणजे त्यावरील झाकण) दूर केले, तर वायुकणांच्या स्वैर औष्णिक हालचाली मुळे अ ⇆ आ या दिशेत वायुकणांचा संचार होतो व ते वायू एकमेकांत मिसळतात, या क्रियेला वायूचे विसरण असे म्हणतात. P = nkT या सूत्रानुसार दोन्ही वायूंत प्रती घ. सेंमी. कणांची संख्या समानच असणार हे उघड आहे. त्यामध्ये दोन्हीही वायुकणांची सांद्रता x दिशेत बदलते. त्यामुळे सांद्रता प्रवणता मिळते अ ⇆ आ कडे प्रती चौ.सेंमी. प्रतिसेकंद जाणाऱ्या वायुप्रवाहाचे मूल्य

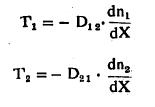
या सूत्रांनी दर्शविले जाते. सांद्रता ज्या दिशेत कमी होत जाते त्या दिशेत हा प्रवाह वाहतो, हे या समीकरणातील ऋण चिन्हाने दर्शविले जाते. संहवन व श्यानता यांकरिता असेच समीकरण वापरले होते D₁₂ व D₂₁ यांना विसरण गुणाकं म्हणतात. वरील दोन आविष्कारांकरिता

---

वापरलेली गणितीय उपपत्ती वापरली असता खालील सूत्र मिळते.

                                             (२२) 

 यातील λ₁, λ2 अनुक्रमे दोन वायूंकरिता माध्य मुक्त पथ तर C_1a, C_2a त्यांच्या वायुकणांचे सरासरी वेग आणि n₁ = n₂ = n वायुकणांची घनता दर्शवितात. जर या दोन वायूंकरिता λ_1 ≈ λ2 = λ आणि C_1a » C_2a = C_a असतील तर

D_{12 =} D₂₁ = D = 1/3 λC_a                                                                                (२३)

D = η/p                                                                                              (२४)

हे सूत्र मिळते. यावरून गत्यात्मक सिद्धांताप्रमाणे या तीन परिवहन अाविष्कारांमधील परस्परसंबंध अशा प्रकारे स्पष्ट होतो.

मॅक्सवेल वेगवितरण फलनाची सरळ प्रायोगिक प्रचीती : याकार्याकरिता मुख्यतः दोन प्रायोगिक रीती उपलब्ध आहेत. एका रीतीमध्ये आणवीय वर्णपट रेघांची [→वर्णपटविज्ञान] नैसर्गिक सांत रुंदी मोजून त्यापासून ⇨ डॉप्लर परिणामाचा उपयोग करून वितरणाची प्रचीती मिळविता येते. दुसऱ्या रीतीमध्ये रेणवीय-किरण तंत्राचा उपयोग केला जातो. अशा प्रकारे ओ.स्टर्न, झार्टमान व लॅमर्ट यांनी केले आहेत. त्यांपैकी लॅमर्ट यांनी वापरलेल्या रीतीचे संक्षिप्त वर्णन खाली दिले आहे.

आ.१० मध्ये अ या उच्च तापमानाच्या भट्टीमधून पाण्याच्या वाफेच्या कणांचा झोत रेखाछिद्र स_१ च्या साहाय्याने मर्यादित केला जातो. उपकरणाच्या पुढील भागात एकाच दांड्यावर (द) बसविलेली दोन चक्रे च_१ व च_२ असतात. ही चक्रे त्यांच्या आसाभोवती वेगात फिरविता येतात. च_१ व च_२ यांवर दोन रेखाछिद्रे असतात. ही रेखाछिद्रे एकमेकांस समांतर नसून च_२ मधिल छिद्र च_१ वरील छिद्राच्या २^° कोनाने मागे ठेवलेले असते. रेणुझोत ज्यावेळी च_१ या छिद्रातून उपकरणात प्रवेश करतो त्यावेळी च_१ ची जी स्थिती असते तिला समांतर अशी स्थिती च_२ मधील छिद्र भ्रमण गतीमुळे धारण करील तरच झोत या दोन चक्र योजनेतून बाहेर पडू शकतो. च_२ वरील छिद्रास भ्रमण गतीने २^° कोनामधून जाण्यास जेवढा वेळ लागतो तेवढाच काळ रेणूंना च_१ च_२ हे अंतर कापण्यास लागणाऱ्या कालखंडाबरोबर असेल, तर ही अट पुरी होते. ही अट पुरी झाल्यास पाऱ्याचे रेणू च_१ व च_२ मधून व स_२ या छिद्रातून जाऊन प या पटलावर निक्षेपित होतील (साचतील). या उपकरणामध्ये वायुकण एकमेकांवर आदळून त्यांचा वेग बदलू नये याकरिता सबंध उपकरणात उच्च प्रकारचा निर्वात असतो. या चक्र योजनेचा वेग विवेचक म्हणून उपयोग होतो. पाऱ्याचे अणू भट्टीच्या तापमानानुसार एकाच वेगाने संचार करीत नसून त्यांमध्ये त्या तापमानानुसार वेगवितरण असते. चक्राची भ्रमण गती बदलून निरनिराळ्या वेगाच्या रेणूंची निवड करता येते. कोणतेही वेगमूल्य असणाऱ्या रेणूंची संख्या प पटलावर तदनरूप मिळणाऱ्या निक्षेपाच्या तीव्रतेवर अवलंबून राहील, हे स्पष्ट आहे. या प्रयोगावरून मॅक्सवेल वेगवितरण फलन हे यथार्थ आहे असे सिद्ध करता येते.

ब्राउनिय गती : द्रव्यातील उष्णतेमुळे त्यामधील रेणूंना सतत स्वैर गती आहे, हे गत्यात्मक सिध्दांताचे एक महत्त्वाचे गृहीत आहे. याची सत्यता सरळ प्रयोग करून पाहणे शक्य नाही. कारण अत्यंत तीव्र शक्तीच्या सूक्ष्मदर्शकाच्या साहाय्याने सुध्दा पदार्थातील रेणूंची गती दिसू शकत नाही. ब्राउनीय गतीचा अभ्यास करून याबद्दल अप्रत्यक्ष पुरावा मिळू शकतो. ब्रिटिश वनस्पतिवैज्ञानिक रॉबर्ट ब्राउन यांनी हा आविष्कार पाण्यातील संधारित (लोंबकळत्या अवस्थेतील) निर्जीव बीजुकांच्या (वनस्पतीच्या सूक्ष्म जननक्षम घटकांच्या) बाबतीत १८२७ मध्ये प्रथम शोधला. शक्तिशाली सूक्ष्मदर्शकातून निरीक्षण केले असता हे कण इतस्तत: स्वैर हालचाल करीत असतात असे त्यांना दिसले. हा आविष्कार ⇨ कलिल विद्रावामध्ये सुद्धा दिसतो. हवेत तरंगणाऱ्या सूक्ष्म धूम्र व धूलिकणांच्या बाबतीत सुध्दा हाच प्रकार आढळतो. कलिल कण रेणूपेक्षा १०-२० पट मोठ्या आकारमानाचे असतात.अतीत सूक्ष्मदर्शकाच्या [→सूक्ष्मदर्शक]साहाय्याने ते दृश्यमान होऊ शकतात. कलिल कणांची स्वैर गती त्यावर होणाऱ्या द्रव रेणूच्या सतत आघातामुळे होते, असे यांचे विवरण करण्यात आलेले आहे व ही गती त्यामुळे रेणूंना सतत स्वैर गती असते याबद्दलचा पुरावा ठरतो.

---

अल्बर्ट आइनस्टाइन ,एम. फोन स्मॉलुकॉव्हस्कि आणि पि . लांझव्हॅ यांनी या कणाच्या गुरुत्वाकर्षणाच्या लंब दिशेत होणाऱ्या हालचालीचे गणितीय रित्या विश्लेषण केले. हा कण a त्रिज्येचा गोलक आहे असे समजून त्यांनी पुढील समीकरण मिळविले.

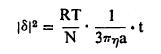 (२५)

यामध्ये R = रेणविय वायूस्थिरांक , T = तापमान, N = ॲव्होगाड्रो संख्या व n = द्रवाचा श्यानता गुणांक [δ]2 हे एका ठराविक t काळात निरीक्षण करून मिळणाऱ्या कणाच्या स्थानांतरणाचे वर्ग माध्य दर्शविते. हे स्थानांतर कोणत्याही एका बिंदूपासून गुरुत्वाकर्षणाच्या लंब दिशेत मोजलेले असते.

प्रत्यक्ष वायूकरिता गत्यात्मक सिध्दांत : मॅक्सवेल-बोल्ट्‌समान सिद्धांतामध्ये वायुकण बिंदुवत आहे असे मानले आहे आणि त्यामध्ये परस्परक्रिया नगण्य आहे असे गृहीत धरले आहे. प्रत्यक्षात ही गृहिते यथार्थ ठरत नाहीत. प्रयोगान्ती असे आढळते की (उदा., दाब वाढविल्यामुळे), वायुकण एकमेकांच्या पुष्कळ जवळ आले, तर त्यांमध्ये आकर्षण होते. या आकर्षणास व्हॅन डर व्हाल्स आकर्षण म्हणतात. याचा विचार केल्यास PV = RT या ऐवजी

 (p+a/V² )(V-b)=RT                                  (२६)

(यात P = दाब, V = घनफळ, T = तापमान व R = वायूस्थिरांक) असे समीकरण मिळते. यामध्ये a व b या दोन राशी आल्या आहेत. त्यांची मूल्ये निरनिराळ्या वायूंकरिता निरनिराळी असतात व ती सर्वसाधारणपणे अचल असतात. प्रयोगावरून असे दिसते की, दोन रेणूंमध्ये काही अंतराकरिता आकर्षण होत असेल, तरी ते त्याहून आणखी जवळ आल्यास त्यांमध्ये प्रतिसारण होते. यातील a ही राशी वायुकणामधील परस्परक्रियेवर अवलबून असते, तर b ही राशी वायुकणाच्या प्रभावी घनफळावर अवलंबून असते. हे घनफळ त्यांमधील आकर्षण व प्रतिसारण प्रेरणांच्या कार्यक्षेत्रावरून निश्चित होते. b ही राशी प्रयोग करून मोजली असता तीपासून वायुकणाचा व्यास काढता येतो. व्हॅन डर व्हाल्स यांचे सुधारित गणित वापरल्यास वायुदाब, श्यानता, संवहन गुणांक इ. सूत्रांमध्ये फार बदल होत नाही. या सूत्रामध्ये येणाऱ्या १/३ या संख्येऐवजी दुसरा एक अपूर्णांक मिळतो. त्यामुळे त्यापासून आतापर्यंत वर्णन केलेल्या सर्वसाधारण निष्कर्षात महत्त्वाचा बदल होत नाही.

वायुकणांमधील परस्परक्रियेमुळे माध्य पथाच्या मूल्यात मात्र महत्त्वाचे बदल होऊ शकतात.आत्तापर्यंत जे आघात विचारात घेतले त्यांमध्ये ऊर्जा अथवा संवेग देवघेव होते असे मानले आहे .या प्रकारच्या आघतांकरिता मिळणाऱ्या माध्य मुक्त पथास संवेगांतरण माध्य मुक्त पथ म्हणतात. आघातामुळे विभाजन किंवा कणामधून प्रारण उद्दीपन होत असेल, तर त्याकरिता प्रत्येक क्रियेकरिता वेगळा असा निराळ्या मूल्याचा माध्य मुक्त पथ मिळू शकतो.

वायूमध्ये रेणवीय परिगमन: नलिकेच्या दोन्ही बाजूंस लावलेल्या दाबामुळे वायूचे श्यानता – नियंत्रित वाहणे याचा विचार मागे केला आहे.यामधील वायूचा दाब कमी झाल्यास (०·०१ मिमी.पाऱ्याच्या दाबापेक्षा कमी )अथवा ज्या परिस्थितीत वायुकणाचा माध्य मुक्त पथ नलिकेच्या त्रिज्येबरोबर किंवा तीपेक्षा जास्त असतो तेव्हा नलिकेमधून वायूचा प्रवाह श्यानतेवर अवलंबून राहत नसून तो रेणवीय परिगमन या प्रकाराचा होतो असे एम्.एच्.सी.नूडसेन(क्नूस्न) यांनी दाखविले आहे. या परीस्थितीत वायुकणाचे परस्पर आघातच महत्त्वाचे ठरतात. नूडसेन यांच्या मते या आघातामुळेच वायुकणात मॅक्सवेल वेगवितरण प्रस्थापित होते, भिंतीवर आदळणारा प्रत्येक कण त्यावर प्रथम शोषला जाऊन नंतर त्याचे परत बाप्पीभवन होते. या परिस्थितीत नलिकेमधून प्रती सेंकद वाहणाऱ्या वायूंचे द्रव्यमान (M*)

                                        

                     (२७)

---

या सूत्राने मिळते असे गत्यात्मक सिद्धांताचा उपयोग करून दाखविता येते. वरील समीकरणात r = नलिकेची त्रिज्या, l = नलिकेची लांबी, m = वायुकणाचे द्रव्यमान, T = त्याचे तापमान, p_1 – p₂ = त्यावरील दाबांतर आणि k = बोल्ट्‌समान स्थिरांक आहे. श्यानता नियंत्रित वायुगमन त्वरेबरोबर याची तुलना केल्यास रेणवीय परिगमन क्रियेचे वैशिष्ट्य लक्षात येते.

                                                               

                    (२८ )

यामध्ये η = श्यानता गुणांक व ρ = वायूची घनता असून इतर राशींचा अर्थ समी. (२७) प्रमाणेच आहे. जे. एल्. एम् पॉयसूली (प्वाझय) यांनी शोधून काढलेले वरील सूत्र वायूच्या वाहण्याकरिता योग्य समजले जाते.

रेणवीय परीगमन क्रियेमध्ये M* हे श्यानतेवर अवलंबून असत नाही व ते r^₃ प्रमाणे बदलते. या गोष्टी महत्त्वाच्या आहेत.

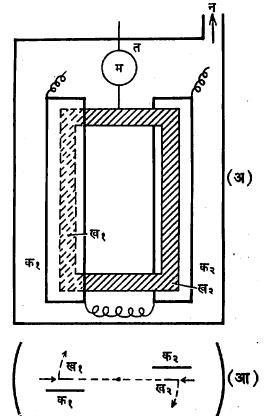
नूडसेन नरपेक्ष वायूदाब मापक : वायूच्या गत्यात्मक सिद्धांतावर आधारित असा अल्प वायुदाबमापक नूडसेन यांनी तयार केला. यामागील मूलभूत तत्त्व आ. ११ वरून समजून येईल. ख_१ ख_२ ही हलक्या वजनाची धातूची पट्टिका आकृतीत दाखविल्याप्रमाणे त या तंतूच्या साहाय्याने टांगलेली असते. तंतूवर म हा आरसा बसविलेला असतो. ख_१ख_२च्या समोर त्यांना समांतर अशा क_१ व क_२ या स्थिर पट्टिका ठेवलेल्या असतात . विद्युत् प्रवाहाच्या साहाय्याने या पट्टिकांचे तापमान ख_१ख_२ पेक्षा जास्त केले जाते. ही सर्व योजना विरल वायूमध्ये प्रस्थापित केलेली असते. वायूचा दाब इतका कमी असतो की, वायुकणाचा माध्य मुक्त पथ क आणि ख पट्टिकांतील अंतरापेक्षा पुष्कळ जास्त असतो. क_१ पट्टिकेच्या जवळचे वायुकण तीवर आघात करून तिच्या तापमानास अनुरूप असे सरासरी ऊर्जामूल्य घेतात. क_१ कडून येणारे वायुकण ख_१ च्या एका बाजूवर येऊन (मध्ये आघात न होता) आदळतात. उपकणातील कमी तापमानाचे कण ख_१ च्या दुसऱ्या बाजूवर आदळतात. परिणामी ख_१ च्या प्रत्येक चौ.सेमी.क्षेत्रफळावर प्रतिसेंकद क_१ → ख_१ या दिशेत संवेग दिला जातो. अशाच ख_१ख_२ च्या चौ. सेंमी.वर F एवढी प्रेरणा मिळते, तिचे मूल्य 

F = P/2√T1/T2–1                       (२९)

या सूत्राने मिळते. येथे ख_१ ख_२ व वायूचे तापमान T₂ क_१ क_२ चे तापमान T₁ P = वायुदाब आहे. या प्रेरणेमुळे ख पट्टिकांचे विचलन होते. या विचलनाचे आरसा व मोजपट्टी यांच्या साहाय्याने मापन करून वायूचा दाब काढता येतो. अवकाशातील वायुकण क_१ क_२ वर पडल्यावर त्याचे तापमान घेतात असे वरील उपपत्तीत गृहीत धरले आहे, हे सर्वस्वी खरे असत नाही. यामुळे हा दाबमापक संपूर्ण निरपेक्ष नसून त्याचे अंशन परीक्षण (इतर अचूक दाबमापकांच्या साहाय्याने अंशाचे परीक्षण) करावे लागते. याच तत्त्वावर आधारित असा दाबमापक एस्. दूश्‌मान यांनी संशोधिला आहे. या प्रकारचे दाबमापक १०^–३ मिमी.पेक्षा कमी दाब मापण्याकरिता योग्य ठरतात. सध्या त्याचा उपयोग इतर दाबमापकांचे अंशन परीक्षण करण्याकरिताच जास्त प्रमाणात केला जातो.

---

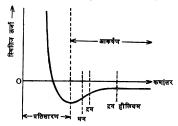 द्रव व घन पदार्थांकरिता गत्यात्मक सिद्धांत : घन, द्रव व वायू या तिन्ही अवस्थांमधील द्रव्यकणांत (रेणूंत) परस्परक्रिया होते असे प्रय़ोगाने आढळते. ही क्रिया जटिल स्वरूपाची असावी असे दिसते कारण दोन द्रव्यकणांमधील अंतर कमी झाले असता ते एकमेकांना आकर्षित करतात पण हे अंतर आणखी कमी केले, तर त्यामध्ये प्रतिसारण मिळते. घन अवस्थेतील स्फटिकामध्ये जी अवकाशीय क्रमरचना आढळते ती या दोन विरुद्ध तऱ्हेच्या प्रेरणांच्या समतोलाशी संबंधित असावी असे वाटते. आ. १२ मध्ये दोन द्रव्यकणांमधील परस्परक्रियेमुळे उत्पन्न होणारी स्थितिज ऊर्जा त्यामधील अंतरानुसार कशी बदलते हे दाखविले आहे. सामान्य घन, द्रव व वायूमध्ये स्थितिज ऊर्जेच्या मर्यादाकक्षा आकृतीत दाखविल्या आहेत. वायूच्या तुलनेत द्रवामधील घटक कण एकमेंकांच्या अधिक जवळ असतात त्यामुळे द्रवात कणाच्या माध्य मुक्त पथाची लांबी अर्थातच कमी असते. घनाप्रमाणे (उदा., स्फटिक) द्रव माध्यमात लांब मर्यादांतराची क्रमवार रचना नसली तरी क्ष-किरण विवर्तन [→ क्ष-किरण] संशोधनावरून त्यामधील कोणत्याही एका कणाच्या सभोवती अल्प मर्यादांतराची क्रमवार रचना असावी असा निष्कर्ष निघतो . आ.१३ मध्ये द्रव अवस्थेतील सोडियम धातूच्या एका प्रातिनिधिक अणूभोवती असणाऱ्या इतर सोडियम अणुकणांची सरासरी संख्या त्यापासूनच्या अंतराप्रमाणे कशी बदलते हे दाखविले आहे. ही माहीती क्ष-किरण विवर्तन पध्दतीने मिळविली गेली आहे .

एका अणूच्या सभोवताली मिळणाऱ्या इतर अणूंच्या स्थितिज ऊर्जा वितरणामधील (काही थोड्या अंतरापर्यंत) सूसूत्रता वरील आकृतीवरून स्पष्ट होते. ही रचना कालानुसार बदलते पण कोणत्याही एका क्षणी द्रवातील कोणत्याही एका कणाभोवती सरासरी ७–१० अणू एक प्रकारच्या स्वैर आकृतिबंधात असतात, असे दिसते. त्यामुळे द्रवामधील कणांची गतिज उर्जा स्थांनातरीय आणि एक प्रकारच्या कंपनीय स्वरूपात विभागलेली असते, असे अनुमान काढता येते. द्रवातील कणांमध्ये मॅक्सवेल-बोल्ट्‌समान सूत्रानुसार ऊर्जा वितरण असते, असे प्रयोगावरून दाखविता य़ेते. घनामध्ये रेणू किंवा कण एका ठराविक आकृतिबंधात (जालकात) पसरलेले असतात . ते आपल्या स्थिर स्थानाभोवती कंपने पूरी करतात. ही कंपने काही ठराविक कंप्रतेने (दर सेंकदाला होणाऱ्या कंपनसंख्येने) होत असतात. या उलट द्रवामधील कणांची कंपने ही ठराविक कंप्रतेची नसल्यामुळे त्यांचे वर्णन गोंगाट या संज्ञेने करणे योग्य ठरते. या दोन अवस्थांतील गतीमधील फरक आ. १४ व १५ वरून स्पष्ट होईल. द्रव्याच्या घटक कणाच्या स्वैर गतीचे दर्शन कोणत्याही सूक्ष्मदर्शक उपकरणाच्या साहाय्याने पाहता येणे शक्य नाही, असा उल्लेख मागे आलाच आहे, पण या गतीचे स्वरूप सद्दशीकरण पद्धतीने ऋण किरण दोलनदर्शक [→ इलेक्ट्रॉनीय मापन] उपकरणाच्या साहाय्याने आ.१४ व १५ मध्ये दाखविले आहे. आ.१५ मधील काळा भाग द्रवाचा बाष्पकण दाखवितो. रु

द्रव अवस्थेमधील गूणधर्मांचे वर्णन करण्याकरिता निरनिराळ्या प्रतिकृती सुचविल्या गेलेल्या असल्या, तरी या अवस्थेकरिता सिद्धांताचे स्वरूप विशेष समाधानकारक नाही.

 २·१८^° के. तापमानाचा द्रव हीलियम काही आश्चर्यकारक असे आविष्कार दाखवितो. या तापमानास त्याचा श्यानता गुणांक एकदम कमी होतो व तो द्रव अतिप्रवाही बनतो. याच तापमानावर त्याची विशिष्ट उष्णता, घनता, संवहन गुणांक यांमध्ये एकदम मोठे बदल होतात. या तापमानाच्या द्रव हीलियमाला, हीलियम ∥ असे नाव दिलेले आहे. याचे गुणधर्म कोणत्याही रूढ द्रवापेक्षा भिन्न असतात. पुंज सिद्धांताचा उपयोग करून या गुणधर्माचे विवरण करण्याकरिता निरनिराळ्या (काही सुलभ तर काही जटिल अशा) प्रतिकृती सुचविल्या गेलेल्या आहेत. त्यांपैकी कोणत्याही एका प्रतिकृतीने सर्व निरीक्षित आविष्कारांचे विवेचन करणे शक्य झालेले नाही [→ अतिप्रवाहिता अतिसंवाहकता].

---

संघनित अवस्था: द्रव (किंवा घन) अवस्थेतील सामान्य तापमानाच्या द्रवाचे बाष्पीभवन होत असते व त्यामुळे एकाच वेळी या दोन्हीही अवस्था मिळतात. उदा., पाणी व त्याच्या पृष्ठभागाजवळ वाफ आढळते. द्रव्याच्या या दोन अवस्थांमध्ये एक गतिज स्वरूपाचा समतोल अथवा स्थिर स्थिती आढळून येते. बाष्प अवस्थेतील काही बाष्पकण संघनित (द्रवीभूत झालेल्या) द्रवाच्या पृष्ठभागाजवळ सतत आदळतात व यांपैकी काहींचे शोषण होऊन ते संघनित अवस्थेत जातात. याउलट संघनित अवस्थेतील ठराविक क्रांतिक मूल्यापेक्षा जास्त वेग असलेले काही कण द्रव पृष्ठभागावरील इतर रेणूंच्यामुळे निर्माण होणाऱ्या आकर्षण प्रेरणेवर मात करून बाष्प अवस्थेत जातात. या क्रियेमध्ये पृष्ठभागी प्रेरणेविरुद्ध कार्य होत असल्यामुळे कणाच्या गतिज ऊर्जेच्या काही अंशाचे स्थितिज ऊर्जेत रूपांतर होते. याचाच अर्थ असा होतो की, जे कण संघनित अवस्थेपासून निसटून बाष्प अवस्थेत येतात तेव्हा त्यांचा वेग कमी होतो. वेगात होणारा क्षय अशा मूल्याचा असतो की, बाष्प अवस्थेतील कणाची सरासरी गतिज ऊर्जा परत संघनित अवस्थेतील कणाच्या सरासरी ऊर्जेएवढी होते. यामुळे बाष्प व संघनित द्रव या दोहोंचे तापमान स्थिर स्थितीमध्ये सारखेच असते असे आढळते. उदा., पाणी व त्यापासून होणारी वाफ या दोहोंचे तापमान उकळबिंदूवर सारखेच असते.

घन अवस्था: घनामधील कण मुक्त नसून ते आपल्या विशिष्ट स्थानाच्या भोवती फक्त आंदोलन करू शकतात, असा उल्लेख मागे आला आहे. धातूवरील कोरीव आकृतीचा आकार कित्येक शतकांपर्यंत जशाचा तसाच राहतो. सोन्याचा मुलामा केलेल्या वस्तूवरील सोन्याचा थर (सामान्य तापमानाकरिता) पृष्ठभागावरच राहतो व तो खाली असलेल्या धातूमध्ये पसरत नाही. ही उदाहरणे घन अवस्थेतील कण मुक्त नाहीत या विधानाच्या पुष्ट्यर्थ देता येतात. घनातील कण आपल्या स्थिर स्थिती स्थानाभोवती आंदोलन करतात. त्यामुळे कोणत्याही एका तापमानाकरिता दोन समीपस्थ कणांमध्ये एक सरासरी अंतर असते, असे म्हणता येते. घनाचे तापमान वाढविले, तर कणांचा परमप्रसर वाढून त्यांमधील सरासरी अंतर वाढते. त्यामुळे तापमान वाढविले असता बहुतेक घनांचे प्रसरण का होते, याचे विवरण करता येते.घनातील कण समीपस्थ कणांतील आकर्षण व प्रतिसारण प्रेरणांचा जेथे समतोल होतो अशी स्थाने व्यापत (पहा आ. १२) असल्यामुळे त्याच्या स्थितिस्थापक गुणधर्माचे विवरण करता येते. घनावर दाब लावून जर कण एकमेकांच्या जास्त जवळ आणण्याचा प्रयत्न केला, तर त्यांमधील प्रतिसारण प्रेरणा जास्त प्रभावी होऊन या प्रयत्नास विरोध केला जातो. याउलट योग्य प्रेरणा लावून त्याची लांबी वाढवावयाचा प्रयत्न केला, तर परिणामी त्यामधील कणांतील अंतर जास्त होऊन प्रेरणेमधील समतोल बिघडून त्यांमधील आकर्षण प्रेरणेचे मूल्य वाढून विस्तारणास विरोध निर्माण होतो.

तापमान जास्त प्रमाणात वाढविल्यास घनातील कणांच्या आंदोलनाचा परमप्रसर आणि त्यामुळे त्याचे विस्थापन इतक्या मोठ्या प्रमाणात होते की, ते परत आपल्या मूळ स्थानी येऊ शकत नाहीत. काही घन पदार्थ उच्च तापमानाला आकार्य (आकार देता येईल असेप्लॅस्टिक) बनतात व त्यामध्ये विसरण आढळते. यामागे वरील क्रिया असते.

घन अवस्थेतील पदार्थांचे बाबतीत सैद्धांतिक परिस्थिती अधिक समाधानकारक आहे. पुंज सिद्धांताचा ऊपयोग करून त्यांच्या अनेक गुणधर्मांचे विवेचन करण्यात यश आले आहे. धन पदार्थांच्या विशिष्ट उष्णतेकरिता आइनस्टाईन व पी. जे. डब्ल्यू. डेबाय यांच्या सिद्धांताचे वर्णन ‘उष्णता’ या नोंदीत दिले आहे. या सिद्धांतात कणांच्या गती मुक्तता मात्रेमध्ये होणाऱ्या उर्जेची विभागणी रूढ तऱ्हेच्या विभागणी पेक्षा निराळी असते हे लक्षात घेण्याजोगे आहे.

संदर्भ : 1. Cunningham, E. Principles of Relativity, Cambridge, 1914.

           2. Glasstone, S. Thermodynamics for Chemists, New York, 1963.

           3. Hildebrand, J. H. Introduction to Molecular Kinetic Theory, London, 1963.

           4. Jeans, J. H. An Introduction to Kinetic Theory of Gases, London ,1940.

            5. Kennard, E. H. Kinetic Theory of Gases with Introduction to Statistical Mechanics, New York, 1938.

            6. Knudsen, M. H. C. Kinetic Theory of Gases, London, 1934.

            7. Loeb, L. B., Kinetic Theory of Gases, New York, 1962.

            8. Rice, S. A. Gray, P. Statistical Mechanics of Simple Liquid, New York, 1965.

            9. Saha, M. N. Srivastava, B. N. A. Treatise on Heat, Allahabad, 1965.

          10. Temperley, H. N. V. Changes of State, London, 1958.

चिपळोणकर, व. त्रिं. भावे, श्री. द.

“