चंद्र : पृथ्वीचा एकुलता एक उपग्रह. चंद्राचे शीतल चांदणे, त्याच्या कला, त्याचे मोहक स्वरूप वगैरे गुणांमुळे चंद्राबद्दल मानवाला पूर्वापार आकर्षण वाटत आले आहे. सर्व धर्मांत चंद्राबद्दल काही संकेत रूढ झालेले दिसतात. ‘ईद’ च्या चंद्राबद्दल मुस्लिमांना वाटणारे महत्त्व, अमावास्या व पौर्णिमा यांना असणारे हिंदूंमधील विशेष स्थान सर्वश्रुत आहे. फलज्योतिषातही चंद्राला फार महत्त्वाचे स्थान दिले आहे.
चंद्राच्या उपपत्तीबद्दल, त्याच्या आकाशातील मार्गक्रमणावर, त्याचप्रमाणे त्याच्या कलांबद्दल आणि त्याच्यावरील डागांबद्दल संस्कृतात वेगवेगळ्या कथा प्रचलित आहेत. विराटपुरुषाच्या मनापासून चंद्रमा उत्पन्न झाला (चंद्रमा मनसो जातः) असे पुरुषसूक्तात म्हटले आहे. २७ नक्षत्रे (या प्रजापतीच्या कन्या) चंद्राच्या बायका होत. त्यांत फक्त रोहिणीवरच तो फार प्रेम करी म्हणून त्याला प्रजापतीचा शाप मिळाला व क्षयरोग जडला, म्हणून कृष्ण पक्षात तो कमी कमी होत जातो. पुढे त्याला उःशाप मिळाला त्यामुळे तो शुक्ल पक्षात वृद्धिंगत होत जातो. अशा अनेक कथा पुराणांत आढळतात. हिंदू धर्मात चंद्राला देवतारूप दिले आहे. शुद्ध द्वितीयेला चंद्रदर्शन घेणे, भाऊबीजेच्या दिवशी चंद्राला ओवाळणे इ. प्रथा हिंदू लोकांत प्रचलित आहेत.
चंद्राच्या ग्रहणांबद्दल मानवाला प्राचीन कालापासून कुतूहल वाटत आले आहे. चंद्राची फलज्योतिषाशी सांगड घातली गेल्याने, पौर्णिमा किंवा अमावास्या नेमकी केव्हा येईल, ग्रहण केव्हा होईल, यांचे आगाऊ अंदाज करण्याच्या प्रयत्नातून चंद्राच्या गतीचा अभ्यास प्राचीन काळापासून सुरू झाला. मुख्यतः चंद्राच्या गतीच्या अभ्यासावरूनच न्यूटन यांना त्यांचा वैश्विक गुरुत्वाकर्षणाचा सिद्धांत मांडता आला आणि या सिद्धांताच्या आधारानेच पुढे चंद्राची स्थाने अधिक अचूकपणे वर्तविता येऊ लागली. दिवस-रात्र हा आविष्कार मानवाला कालमापनाचे नैसर्गिक माप म्हणून लक्षात आला. त्याच्यापेक्षा मोठे काळाचे माप जे महिना ते चंद्राच्या कलांवरून मनुष्याच्या लक्षात आले. त्याहून मोठे माप जे वर्ष, ते ऋतुचक्राच्या पुनरावृत्तीवरून पुष्कळच उशिरा लक्षात आले. अत्याधुनिक आणवीय घड्याळ सोडल्यास चंद्र हा कालमापनाचे सर्वांत अधिक अचूक साधन मानले जाते, म्हणजे चंद्राची गती आता आपणाला अत्यंत अचूकपणे माहीत झालेली आहे.
भारतीय, रोमन, ग्रीक व चिनी प्राचीन ग्रंथांवरून चंद्राबद्दलचे शास्त्रीय ज्ञान सु. ४,००० वर्षांपूर्वीपासून मिळविण्याचे प्रयत्न चालू आहेत असे दिसते. चंद्राच्या गतीचा अभ्यास प्रथम बॅबिलोनियन लोकांनी सुरू केला व प्राचीन ग्रीक तत्त्वज्ञांनी काही महत्त्वाचे सिद्धांत मांडले. चंद्राची एकच बाजू पृथ्वीवरून दिसते हे प्राचीन ग्रीकांना माहीत होते. चंद्राच्या कला व ग्रहणे यांचे वास्तविक कारण ॲनॅक्सॅगोरस (इ. स. पू ५००? — ४२८) यांना समजले होते. हिपार्कस यांनी इ. स. पू. १५०—१३० या सुमारास चंद्राचे पृथ्वीपासूनचे अंतर पृथ्वीच्या त्रिज्येच्या ५९ पट आहे असे भूमितीच्या साहाय्याने निश्चित केले. त्याचप्रमाणे चंद्रकक्षा पृथ्वीच्या सूर्याभोवतीच्या कक्षेशी ५ अंशांचा कोन करते हेही त्यांनी शोधून काढले व ही मूल्ये, प्रचलित मूल्यांशी चांगलीच जुळतात. चंद्राच्या गतीच्या अभ्यासात टॉलेमी (इ. स. दुसरे शतक) व ट्यूको ब्राए (१५४६—१६०१) यांनी आणखी सुधारणा केल्या. त्यानंतर ग्रहगतीबद्दल केप्लर (१५३१—१६३०) यांनी आपले विख्यात तीन नियम मांडले. न्यूटन (१६४२—१७२७) यांनी गुरुत्वाकर्षणाचा सिद्धांत मांडल्यानंतर सर्वच खगोल गणिताला सैद्धांतिक बैठक प्राप्त झाली आणि आणि त्याबरोबर चंद्राच्या गतीची छाननी शास्त्रीय दृष्ट्या सुरू झाली. भरती-ओहोटीच्या आविष्काराचा चंद्राशी घनिष्ट संबंध असल्याचे मानवाला फार पूर्वीपासून माहीत आहे. त्याचाही खुलासा गुरुत्वाकर्षणाच्या सिद्धांतावरून करता येऊ लागला.
पूर्वीच्या काळी ग्रहगोलांचे वेध घेण्याच्या पद्धती फारच सदोष होत्या. ट्यूको ब्राए यांनी त्यात पुष्कळच अचूकता आणली. गॅलिलीओ (१५६४ — १६४८) यांनी दूरदर्शकामध्ये (दुर्बिणीमध्ये) सुधारणा केल्यानंतर चंद्राचे अधिक सूक्ष्म निरीक्षण तर करता येऊ लागलेच पण ग्रहांचे वेधही अधिक बिनचूकपणे घेता येऊ लागले. म्हणजे ग्रह गणिताच्या शास्त्रात जसजशी सुधारणा होत गेली, तसतसे ग्रहांचे (व म्हणून चंद्राचे) वेध अचूक घेण्याची मानवाची क्षमताही वाढली. या दोहोंच्या संयोगाने चंद्रगती अत्यंत काटेकोरपणे सांगणे शक्य झाले.
इ. स. १९५७ सालानंतर चंद्राकडे सोडण्यात आलेल्या अन्वेषक यानांच्या साहाय्याने चंद्राची (पृथ्वीवरून न दिसणाऱ्या भागाचीही) उत्कृष्ट छायाचित्रे मिळविणे शक्य झाले. अमेरिकेची चंद्रावर अलगद उतरलेली सर्व्हेयर मालेतील याने, अपोलो योजनेनुसार १९६९ नंतर चंद्रावर उतरलेल्या अंतराळवीरांनी गोळा केलेले तेथील खडकांचे नमुने व त्याचे पृथ्वीवर मागाहून करण्यात आलेले परीक्षण, अंतराळावीरांनी चंद्रावर ठेवलेली विविध शास्त्रीय उपकरणे, तसेच चंद्रपृष्ठावर प्रवास करणारे रशियाचे ल्यूनोखोड हे स्वयंचलित वाहन व चंद्राभोवती परिभ्रमण करणारी ल्यूना मालेतील अन्वेषक याने या सर्वांच्या द्वारे चंद्रासंबंधी अनेकविध स्वरूपाची आणि विश्वसनीय माहिती मानवाला उपलब्ध झाली आहे.
चंद्राचा आकार : चंद्राचा आकार इतर ग्रहांप्रमाणे स्थूल मानाने गोलाकार आहे. परंतु निरीक्षणांवरून व प्रयोगांवरून असे आढळून आले की, चंद्राची विषुववृत्तीय त्रिज्या त्याच्या ध्रुवीय त्रिज्येपेक्षा काहीशी जास्त आहे. चंद्राची सरासरी त्रिज्या १,७३८ किमी. आहे. पृथ्वीच्या आकर्षणामुळे चंद्रगोलाचा पृथ्वीसमोरचा भाग काहीसा जास्त फुगीर झाला आहे. त्यामुळे या भागाची त्रिज्या २ किमी. ने जास्त आहे आणि उलट बाजूची तेवढीच कमी आहे. यामुळे चंद्राचा गुरुत्वमध्यही त्याच्या दर्शनी मध्यापासून बाजूला सरकला आहे. इतके सूक्ष्म फरक चंद्रावर पाठविलेल्या चांद्रयानांतील उपकरणांनी केलेल्या प्रयोगावरून निश्चित करता आले. हे फरक फार थोडे वाटले तरी त्यांचा चंद्रगतीवर परिणाम होतो. दुसरी गोष्ट, या फरकांवरून चंद्राच्या उत्पत्तिकालाबद्दल काही तर्क करता येतात, या दृष्टीने ते महत्त्वाचे आहेत.
त्रिज्येवरून चंद्राचे आकारमान व चंद्रपृष्ठाचे क्षेत्रफळ काढता येते. चंद्राचे आकारमान पृथ्वीच्या १/९४ आहे व त्रिज्या पृथ्वीच्या त्रिज्येच्या सु. ३/११ आहे.
वस्तुमान : आकाशस्थ ग्रहगोलांचे वस्तुमान न्यूटन यांच्या गुरुत्वाकर्षणाच्या नियमावरून काढता येते. आपल्या गुरुत्वाकर्षणामुळे एखादा ग्रहगोल नजीकच्या दुसऱ्या गोलाच्या गतीत कितपत फेरबदल करू शकतो, हे निरीक्षणाने पाहून त्यावरून त्याच्या गुरुत्वाकर्षणाची प्रेरणा काढता येते. त्यावरून त्या गोलाचे वस्तुमान काढतात. या पद्धतीने पूर्वीं चंद्राचे वस्तुमान काढले होते. यापेक्षा जास्त अचूक आणि सरळ पद्धत म्हणजे सरळ सोडलेली वस्तू त्या गोलावर किती प्रवेगाने आपटते, त्याचे मापन करणे व त्यावरून गोलाचे वस्तुमान काढणे. चंद्रावर गेलेल्या अंतराळवीरांनी या पद्धतीने चंद्राचे निश्चित केलेले वस्तुमान ७·३५३ X १०२२ किग्रॅ. म्हणजेच पृथ्वीच्या वस्तुमानाच्या १/८१·३०२ आहे. चंद्रगतीच्या गणितात त्याचे वस्तुमान विचारात घेणे अर्थातच आवश्यक आहे.
गुरुत्व प्रवेग व मुक्तिवेग : उंचावरून सोडलेली वस्तू ९·८ मी./से.२ या सरासरी प्रवेगाने पृथ्वीवर पडते. हा पृथ्वीवरील गुरुत्व प्रवेग होय. कोणत्याही ग्रहगोलावरील गुरुत्व प्रवेग त्या गोलाचे वस्तुमान व त्रिज्या यांवर अवलंबून असतो. चंद्रावरील गुरुत्व प्रवेग १·६२ मी./से.२ म्हणजे पृथ्वीच्या १/६ हून थोडा कमी आहे. यामुळे चंद्रावरील एखाद्या वस्तूचे वजन पृथ्वीवरील वजनाच्या सु. १/६ भरेल.
विशिष्ट ग्रहाच्या गुरुत्वाकर्षणातून बाहेर पडण्यासाठी ज्या किमान वेगाने एखादी वस्तू फेकली पाहिजे, त्याला त्या ग्रहावरील मुक्तिवेग असे म्हणतात. पृथ्वीवरील मुक्तिवेग ११·२ किमी./से. आहे, तर चंद्रावर तो फक्त २·३२२ किमी./से. आहे. जेव्हा पृथ्वी व सूर्याचे आकर्षण साहाय्याकारी असेल तेव्हा हा मुक्तिवेग २·०७१ किमी./से. इतकाच राहील. चंद्रावरील अल्प मुक्तिवेगामुळेच चंद्राला वातावरण जवळजवळ नाहीच असे म्हटले तरी चालेल. त्याचप्रमाणे अवकाश प्रवासाकरिता चंद्र हा एक उपयुक्त टप्पा होईल. कारण चंद्रावरून अवकाशात उड्डाण करणे खूपच कमी खर्चाचे होईल.
विशिष्ट गुरुत्व : चंद्राचे वस्तुमान व आकारमान यांचा भागाकार म्हणजे चंद्राचे सरासरी विशिष्ट गुरुत्व ३·३८ ग्रॅ./घ. सेंमी. येते. पृथ्वीच्या वि. गु. शी (५·५४ ग्रॅ./घ. सेंमी.) तुलना करता हे बरेच कमी असून पृथ्वीवर सर्वत्र आढळणाऱ्या ग्रॅनाइट दगडाच्या वि. गु. पेक्षा थोडे जास्त आहे. पृथ्वीच्या मध्याजवळच्या भागात लोह, निकेल यांसारख्या वजनदार धातूंच्या आधिक्यामुळे पृथ्वीचे वि. गु. जास्त येते हे लक्षात घेता असा निष्कर्ष निघतो की, चंद्रगर्भात पृथ्वीप्रमाणे लोहासारख्या धातूंचे एकीकरण झालेले नाही. चंद्रावर पृथ्वीच्या तुलनेने फारच दुर्बल चुंबकीय क्षेत्र (पृथ्वीच्या एक लक्षांशाहून कमी) आहे ही गोष्ट वरील निष्कर्षाला पुष्टिदायक आहे.
वातावरणीय दाब : वेगवेगळ्या प्रयोगांवरून असे निश्चित झाले आहे की, चंद्रावर काही वातावरण असलेच, तर त्याचा दाब पृथ्वीवर समुद्रसपाटीवर जो वातावरणीय दाब असतो त्याच्या साठ लक्षांशाहून कमी असला पाहिजे. उत्कृष्ट निर्वात पंपाच्या साहाय्यानेही अद्याप इतका कमी दाब निर्माण करता आलेला नाही. वरील निष्कर्ष काढण्यास पुढील निरीक्षणे साहाय्यक ठरली आहेत. चंद्रावर पृथ्वीसारखे वातावरण असते, तर दूरदर्शकातून चंद्राचे निरीक्षण करताना कधी ना कधी ढग दिसले असते (असे ढग मंगळावर आढळले आहेत). चंद्रावर लक्षात घेण्याइतक्या दाबाचे वातावरण असते, तर दूरदर्शकातून पाहताना त्याच्या कडा इतक्या रेखीव दिसल्या नसत्या. चंद्रावर वातावरण असते, तर त्यामुळे पृथ्वीप्रमाणे तेथेही संधिप्रकाश दिसू शकला असता. हा संधिप्रकाश, चंद्रावरील सूर्योदयापूर्वी अथवा सूर्यास्तानंतर दिसला पाहिजे. म्हणजेच तो चंद्राच्या अप्रकाशित भागाच्या कडेवर दिसावा. संधिप्रकाश हा वायुकणांवरून झालेल्या सूर्यकिरणांच्या प्रकीर्णनामुळे (विखुरण्यामुळे) निर्माण होतो. असा प्रकीर्णन झालेला प्रकाश मूळच्या प्रकाशाच्या दिशेला लंब दिशेने पाहिल्यास त्याचे ध्रुवण झालेले दिसते. म्हणजे त्याच्यातील कंपने काही ठराविक दिशेनेच होत असतात. चंद्राच्या अप्रकाशित पृष्ठाकडून येणाऱ्या प्रकाशात अशा ध्रुवित प्रकाशाचे किती प्रमाण आहे, त्याचे मापन करण्याचा प्रयत्न करण्यात आला. जितके हे प्रमाण जास्त तितक्या प्रमाणात चंद्रावर जास्त वातावरण असले पाहिजे. अशा प्रकारचे प्रयोग प्रथम फेसेनकॉव्ह यांनी आणि त्यानंतर ल्यो यांनी केले. या प्रयोगांत ध्रुवण झालेल्या प्रकाशाचा मागमूसही लागला नाही व त्यावरून चंद्रावर वातावरण जवळजवळ नाहीच ही गोष्ट सिद्ध झाली. वर दिग्दर्शित केलेला प्रयोग या कामासाठी सर्वांत जास्त संवेदनशील आहे.
वातावरणाच्या अभावामुळे चंद्राने आकर्षित केलेल्या उल्का त्याच्या पृष्ठभागावर प्रचंड वेगाने आदळून खड्डे पडतात. असे खड्डे (त्यांना आपण विवरे म्हणतो) चंद्रपृष्ठावर लक्षावधी दिसतात. हाही चंद्रावर वातावरण नसल्याचा एक पुरावा आहे. चंद्रावरील अत्यल्प मुक्तिवेगामुळे तेथे प्रारंभी काही वायू असलेच, तर ते आता जवळजवळ संपूर्णपणे निघून गेले आहेत.
चंद्रावरील पोटॅशियम (४०), युरेनियम (२३८), युरेनियम (२३५), आयोडीन (१२९) या किरणोत्सर्गी (भेदक कण अथवा किरण बाहेर टाकणाऱ्या) मूलद्रव्यांपासून काही प्रमाणात आर्गॉन, क्रिप्टॉन व झेनॉन हे वायू तयार होत असावेत आणि अंदाजानुसार या निघणाऱ्या वायूंमळे चंद्रावर प्रत्यक्ष दिसतो त्याहून पुष्कळच जास्त वातावरणीय दाब उत्पन्न झाला पाहिजे. शेवटी म्हणजे या वायूंचे अणुभार मोठे असल्याने चंद्रावरील तापमानात त्यांना मुक्तिवेग प्राप्त होणे अशक्यप्राय आहे. हेरिंग आणि लिक्ट यांच्या मते सूर्यापासून येणाऱ्या सौरवाताने (यात प्रोटॉन या मूलकणांचे वेगाने येणारे झोत असतात) हे वायू चंद्रापासून दूर लोटले गेले असावेत. ओपिक व सिंगर यांनी अशी उपपत्ती दिली की, सौरवाताने या वायूंचे प्रथम विदलन होऊन त्यांचे धन आयन (धन विद्युत् भारित अणू वा रेणू) बनतात व मग सूर्यप्रकाशित चंद्रपृष्ठावर प्रकाशविद्युत् परिणामाने (प्रकाशाच्या क्रियेमुळे ऋण विद्युत् भार नाहीसा होण्याने) उत्पन्न होणाऱ्या धन विद्युत् भारामुळे प्रतिसारण होऊन ते दूर फेकले गेले असावे.
तापमान : चंद्रावर पडलेल्या सूर्यकिरणांचे अंशतः शोषण होऊन त्यांचे उष्णतेत रूपांतर होते व चंद्रपृष्ठाचे तापमान वाढते. यामुळे चंद्रपृष्ठ विशिष्ट तरंगलांबींच्या विद्युत् चुंबकीय तरंगांचे प्रक्षेपण करू लागते. या प्रक्षेपित तरंगांचे मापन करून त्यावरून चंद्रपृष्ठाचे तापमान काढता येते. यासाठी प्रथम केलेल्या प्रयोगात रॉस यांनी दूरदर्शकाच्या केंद्रबिंदूंवर तपयुग्म ठेवले. तपयुग्मात दोन भिन्न धातूंच्या तारा एकत्र जोडलेल्या असतात. या जोडाला उष्णता मिळाली की, तपयुग्मात विद्युत् प्रवाह निर्माण होतो. या प्रवाहाचे मापन करून त्यावरून तापमान निश्चित करता येते. चंद्रावर जेथे सूर्यप्रकाश लंबरूप पडत असेल तेथील तापमान या पद्धतीने ३९७० के. (= १२४० सें.) मिळाले. या पद्धतीत पुढे अनेक सुधारणा करून ती अधिक सूक्ष्मदर्शी करण्यात आली. तिचा उपयोग करून पेटिट आणि निकल्सन यांनी वेगवेगळ्या परिस्थितींत चंद्राच्या वेगवेगळ्या भागांची तापमाने मोजली. १९२७ साली त्यांनी खग्रास चंद्रग्रहणाच्या वेळी चंद्रावरील एका विशिष्ट भागाची तापमाने ग्रहणाच्या वेगवेगळ्या अवस्थेत मोजली. ग्रहण सुरू होण्यापूर्वी तेथील तापमान ३४२० के. होते. खग्रास होण्यापूर्वी ते २१०० के. इतके उतरले. खग्रास झाल्याबरोबर २० मिनिटांनी ते १७०० के. झाले. तेथून पुढे हळूहळू उतरत ग्रहण सुटू लागण्याच्या वेळी ते १५२० के. (= – १२१० से.) भरले. पूर्ण मोक्ष झाल्यावेळी ते परत ३४२० के. झाले.
तापमानातील हे बदल फार जलद गतीचे व अतिरेकी असून असे बदल पृथ्वीवर कोठेही होताना दिसत नाहीत. चंद्रावर जसा दिवस-रात्र हा बदल होत जाईल तेव्हा त्याबरोबर चंद्रपृष्ठावर ठिकठिकाणी तापमान कसे बदलत जाईल, त्याचा हा नमुनाच म्हटला पाहिजे.
तापमानाच्या या बदलावरून असे समजून येते की, चंद्राचा पृष्ठभाग उष्णतेचा चांगलाच निरोधक असला पाहिजे. पृथ्वीवरील खडक इतके चांगले निरोधक नाहीत. या दर्जाची निरोधकता येण्याला चंद्रपृष्ठावर सर्वत्र बारीक रेतीचा थर असला पाहिजे. चंद्रावर प्रत्यक्ष जाऊन तेथे केलेली याबाबतची प्रत्यक्ष निरीक्षणे वरील गोष्टीशी पूर्णपणे मिळतीजुळती आहेत. चंद्रपृष्ठावर भर दुपारचे तापमान पाण्याच्या उकळबिंदूच्यापेक्षा बरेच जास्त असते, तर रात्री ते हवा द्रवरूप करण्याइतपत कमी असते.
चंद्राचा पृष्ठभाग : चंद्रावरील तापमान, वातावरणीय दाब व इतर परिस्थितीचा विचार करता चंद्रावर जीवसृष्टी असणे अशक्य आहे, याबद्दल आता शंका राहिलेली नाही. सकृत्दर्शनी नितळ वाटणारे चंद्रपृष्ठ, दूरदर्शकातून पाहिल्यास अत्यंत खडबडीत आहे असे दिसून येते. चंद्रावर मोठमोठे पर्वत, विवरे, सपाट प्रदेश इ. दिसतात. चंद्राची जी बाजू आपणाला कधीही दिसत नाही तिची अवकाशयानातून छायाचित्रे घेण्यात आलेली आहेत. त्यांवरून असे दिसते की, सर्वसाधारणपणे त्या बाजूचे स्वरूपही असेच आहे.
चंद्रावरील काही थोडी विवरे अंतर्गत घडामोडीने झालेली असून बहुतेक सर्व अशनिपातानेच निर्माण झालेली आहेत. मोठा अशनी आदळल्यामुळे चंद्रातील खडकांचे तुकडे दूरवर फेकले जाऊन त्यांच्या परत पडण्यामुळे काही दुय्यम विवरे तयार झालेली दिसतात. जुन्या विवरावर नंतर अशनिपात होऊन पुनःपुन्हा नवी विवरे बनलेली आढळतात. विवरांचे वय ओळखण्याची ही एक सोपी युक्ती आहे. अपोलो १५, १६ आणि १७ मधील अंतराळवीरांनी आणलेल्या चांद्र खडकांच्या अभ्यासावरून असे निष्पन्न झाले की, दक्षिणेकडील किरण शलाका विवर हे सर्वांत अलीकडचे असून त्याचा उत्पत्तिकाल २० ते ३० लक्ष वर्षांपूर्वीचा असावा. उंच प्रदेशावरील खडक ४·२ खर्व वर्षांचे म्हणजे सर्वांत पुरातन आहेत. चंद्रावरील सागरप्रदेश लाव्हारसापासून बनलेले असून त्यांचे वय २ ते ३ खर्व वर्षांचे आहे. चंद्रावरील बहुतेक खडक हे ॲल्युमिनियम व कॅल्शियमयुक्त लहान लहान कपच्या व काच एकमेकांना जोडल्या जाऊन बनलेले आहेत. अशा खडकांना कोणाश्म असे म्हणतात. सु. ७० मी. खोलीपर्यंत चंद्राचा पृष्ठभाग अशा कोणाश्मांनीच मुख्यतः बनलेला आहे.
चंद्रावरून आणलेल्या खडकांच्या तुकड्यांचे क्ष-किरणांच्या साहाय्याने परीक्षण केल्यावर त्यांत सोडियम, मॅग्नेशियम, ॲल्युमिनियम, सिलिकॉन व लोह ही मूलद्रव्ये आहेत, असे निश्चित करता आले. त्याचप्रमाणे चंद्रावर केलेल्या आयन शोधक उपकरणाच्या प्रयोगाने, तेथे अल्प प्रमाणात पाण्याची वाफ असल्याचेही उघडकीला आले. ही वाफ चंद्राच्या अंतर्भागातून बाहेर येत असावी. परंतु चंद्रावर कार्बनी संयुगांचा अभावच दिसून आला.
|
कोष्टक क्र. १. चंद्रावरील काही प्रमुख विवरांची नावे व त्यांचे व्यास |
|
|
विवर |
व्यास (किमी.) |
|
क्लेव्हियस |
२३० |
|
आल्फॉन्सो |
११० |
|
प्लेटो |
९६ |
|
कोपर्निकस |
८८ |
|
ट्यूको |
८८ |
|
आर्किमिडीज |
८० |
|
एरॉटास्थीनीझ |
६० |
|
ॲरिस्टार्कस |
४७ |
|
केप्लर |
३५ |
अपोलो अंतराळवीरांनी चंद्रपृष्ठाला १ ते १·५ मी. खोल भोके पाडून त्यांत तापमापके ठेवली. या प्रयोगावरूनच असे दिसून आले की, चंद्राच्या पृष्ठाभागावर पडणारी सूर्याची उष्णता ७० सेंमी. खोलीपलीकडे आत जात नाही. त्याचप्रमाणे चंद्राच्या अंतर्भागातून प्रती सेकंद प्रती चौ. सेंमी. ०·७९ X १०-६ कॅलरी इतकी (म्हणजे पृथ्वीच्या मानाने निम्मी) उष्णता बाहेर येत असते. यावरून चंद्राच्या अंतर्गत भागाचे तापमान खूप उच्च असावे असे दिसते. चंद्रावर नाव घेण्याजोगे ज्वालामुखी उद्रेक अंतराळवीरांना आढळले नाहीत.
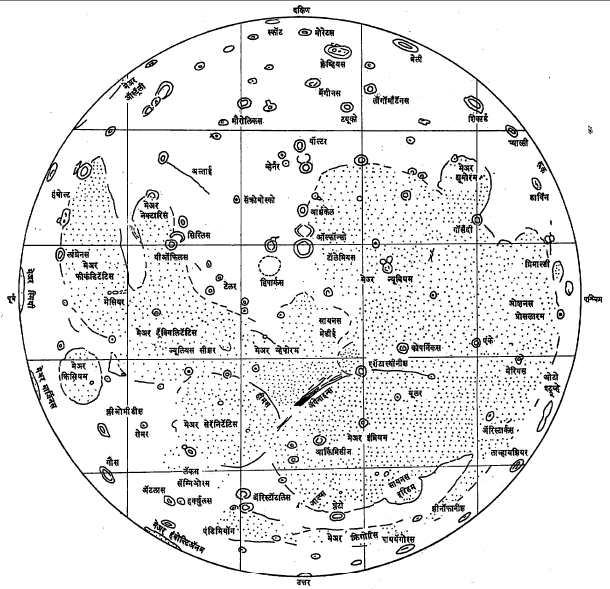
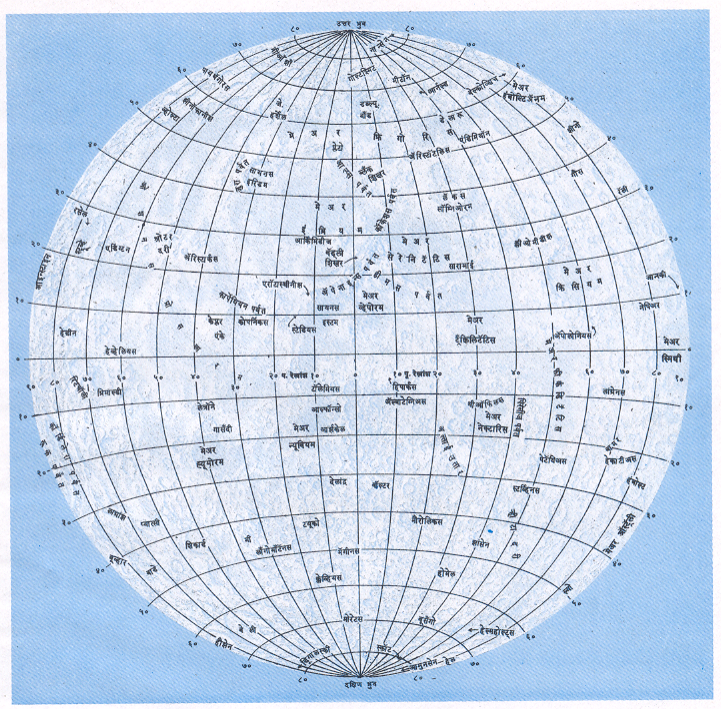
चंद्राचे नकाशे : शास्त्रज्ञांनी चंद्रपृष्ठाचे अवलोकन करून त्याचे प्रमाणशीर नकाशे काढले आहेत. त्यावरील पर्वत, शिखरे, विवरे, सखल भाग वगैरेंना नावेही दिली आहेत. असे म्हटले जाते की, चंद्राच्या दर्शनी भागाचे आपणाला जितके तपशीलवार ज्ञान आहे तितके भूपृष्ठाचेही नाही. चंद्राचा पहिला चांगला नकाशा १६४७ साली हेव्हेलियस यांनी तयार केला. त्यानंतर वेळोवेळी अधिक तपशीलवार व बिनचूक नकाशे काढण्यात आले. परंतु १९५९ पर्यंतचे सर्व नकाशे पृथ्वीवरून दूरदर्शकाच्या साहाय्याने घेतलेल्या छायाचित्रांवरून बनविलेले असल्याने पुरेसे अचूक नव्हते. चंद्रावर मानवाचे पदार्पण होण्यापूर्वी चंद्राचे अचूक नकाशे बनविणे अत्यंत आवश्यक होते. १९६६ सालापासून चंद्राभोवती उपग्रहाप्रमाणे फिरणारी पाच ऑरबाइटर अवकाशयाने पाठविण्यात आली. त्यांनी चंद्रपृष्ठाच्या अगदी जवळून छायाचित्रे घेऊन ती दूरचित्रण पद्धतीने पृथ्वीवर पाठविली. अशा तऱ्हेने चंद्राच्या सर्व पृष्ठांची छायाचित्रे घेऊन त्यांवरून अमेरिकेच्या विमानदलाने अत्यंत अचूक असे नकाशे तयार केले आहेत. त्याचा नमुना चित्रपत्र (३७) मध्ये दाखविला आहे. पृथ्वीच्या नकाशाप्रमाणे यावरही अक्षांश रेखांशाच्या रेषा काढलेल्या असून त्यांच्या साहाय्याने चंद्रावरील कोणत्याही ठिकाणचे निश्चित स्थान देता येते. चंद्रनिरीक्षकांच्या सोयीसाठी चंद्रपृष्ठाचे आराखडे (आ. १) बनविलेले असून त्यांत वेगवेगळे डोंगर, विवरे इत्यादींची स्थाने दिलेली असतात. दूरदर्शकातून पाहताना प्रतिमा उलटी दिसते. तिच्याशी पडताळणे सुलभ जाण्यासाठी अशा आराखड्यातून पूर्व डावीकडे आणि उत्तर खालच्या बाजूला (म्हणजे नकाशातील नेहमीच्या संकेताच्या विरुद्ध) घेतलेली असते.
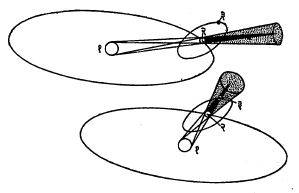
चंद्राची कक्षीय परिभ्रमण गती : चंद्राची गती पूर्णपणे समजणे म्हणजेच कोणत्याही वेळी चंद्राचे आकाशातील स्थान बरोबर काढता येणे होय. चंद्र हा पृथ्वीचा उपग्रह असल्यामुळे तो पृथ्वीभोवती विवृत्ताकार (दीर्घ वर्तुळाकार) कक्षेत फिरतो व त्याचबरोबर पृथ्वी चंद्राला आपल्याबरोबर घेऊन सूर्याभोवती प्रदक्षिणा करीत असते. यामुळे चंद्राच्या गतीवर सूर्याच्या आकर्षणाचा परिणाम होऊन तीमध्ये काही फेरफार होत राहतात. त्यामुळे चंद्राची गती फार गुंतागुंतीची होते. यात भर म्हणून इतर ग्रहांचे, विशेषतः शुक्राच्या आकर्षणाचे, चंद्रावर परिणाम होत असतात. चंद्र आणि पृथ्वी यांच्या कक्षा एकमेकींशी काही कोन करतात व हा कोनही सारखा बदलत असतो चंद्राच्या कक्षेची विकेंद्रता [वर्तुळ आकारापासून विवृत्ताच्या आकाराच्या भिन्नत्वाचे मान दर्शविणारी राशी, ⟶ विवृत्त] हळूहळू बदलत असते भरती-ओहोटीमुळेही चंद्रगतीवर काही सूक्ष्म परिणाम होत जातो, चंद्रकक्षेच्या मध्यातून काढलेल्या लंबाची अवकाशातील दिशाही एकसारखी बदलत असते. त्यामुळे चंद्रगती इतक्या गुंतागुंतीची होते की, कित्येक ज्योतिर्विदांनी व गणितज्ञांनी हा कूटप्रश्न सोडविण्यासाठी वर्षानुवर्षे खर्च करून समाधानकारक निर्वाह (उत्तरे) मिळालेले नाहीत. चंद्राच्या कक्षीय परिभ्रमण गतीशी संबंधित असलेल्या राशी कोष्टक क्र. २ मध्ये दिल्या आहेत.
कोष्टक क्र. २
चंद्राच्या कक्षीय परिभ्रमण गतीशी संबंधित असलेल्या राशी.
(१) चंद्राचे पृथ्वीपासून अंतर किमान (उपभू) ३,६३,३०० ते ३,५६,४०० किमी.
(२) चंद्राचे पृथ्वीपासून अंतर कमाल (अपभू) ४,०६,१०४ ते ४,०६,७०० किमी.
(३) चंद्रकक्षा व पृथ्वीकक्षा यांच्या पातळ्यांमधील कोन i= ५º ८’४३” ± ९’ (१७३ दि. आवर्तकाल)
(४) चंद्रकक्षेची सरासरी विकेंद्रता = ०·०५४९०
(५) पृथ्वीभोवती प्रदक्षिणाकाल नक्षत्र सापेक्ष = २७·३२१६६१४० दिवस.
(६) पृथ्वीभोवती प्रदक्षिणाकाल सूर्य सापेक्ष = २९·५३०५८८२ दिवस.
(७) चंद्रकक्षा व चंद्राचे विषुववृत यांमधील कोन = ६º ४१’.
(८) उपभू-अपभू रेषेच्या भ्रमणाचा आवर्तकाल =+ ८·८५०३ वर्षे (चंद्रभ्रमणाच्या दिशेने).
(९) पातबिंदूच्या भ्रमणाचा आवर्तकाल = – १८·५९९५ वर्षे (चंद्रभ्रमणाच्या विरुद्ध दिशेने).
ज्या राशीचे मूल्य बदलत बदलत विशिष्ट काळानंतर परत पूर्ववत होते त्या राशीला आवर्त राशी म्हणतात व त्या काळाला आवर्तकाल म्हणतात. पृथ्वीची कक्षा आणि चंद्राची कक्षा यांची प्रतले ज्या रेषेत छेदतात ती रेषा खगोलाला ज्या दोन बिंदूंत छेदते त्यांना पात बिंदू म्हणतात.
चंद्राच्या कक्षेत ज्या विशिष्ट स्थानी चंद्र व पृथ्वी यांमधील अंतर किमान असते त्या स्थानाला उपभू बिंदू आणि ज्या स्थानी अंतर कमाल असते त्याला अपभू बिंदू म्हणतात.
वर सांगितल्याप्रमाणे चंद्रकक्षेची विकेंद्रता बदलत असल्याने चंद्राची पृथ्वीपासूनची किमान व कमाल अंतरे बदलत असतात म्हणजे कक्षेचा आकार बदलत असतो. चंद्रकक्षेची विकेंद्रता सरासरीने ०·०५४९० असून तिच्यात ± ०·०११७ इतका फरक होतो. माध्य (सरासरी) गतीने जाणारा एक माध्य चंद्र मानला आणि खरा चंद्र व माध्य चंद्र एकाच वेळी उपभू बिंदूपासून निघाले, तर त्यांची पुन्हा भेट अपभू बिंदूपाशी पडेल पण मध्यंतरी ते मागेपुढे असतील. त्यांच्या स्थानातील जास्तीत जास्त फरकाचे माध्यमान ± ६º १७’ इतके असले, तरी प्रत्यक्षात त्याचे मूल्य ± ५º ३’ ते ± ७º ३१’ इतके असते. या फरकास चांद्रपर्यास म्हणतात. सूर्याच्या व ग्रहांच्या आकर्षणामुळे चंद्राच्या कक्षेच्या विकेंद्रतेत होणारा बदल हे चांद्रपर्यासाचे कारण होय. या बदलाचा आवर्तकाल ३१·८१ दिवस असतो. चंद्रकक्षेचा बृहदक्ष (विवृत्ताच्या मध्यातून व दोन्ही नाभींमधून जाणारा अक्ष) सूर्याच्या दिशेने असतो तेव्हा विकेंद्रता अधिकतम असते.
चंद्राच्या कक्षीय परिभ्रमण गतीचे गणित : पृथ्वीभोवती फक्त चंद्र फिरत असून सूर्य किंवा ग्रहांच्या आकर्षणांचा त्याच्यावर काहीच परिणाम होत नसता, तर त्याची कक्षा एक निश्चित विवृत्त झाली असती व या विवृत्ताच्या एका केंद्रबिंदूवर पृथ्वी असती. मग चंद्राचे गणित फारच सोपे झाले असते. या रचनेत सूर्याच्या परिणामाचा अंतर्भाव केला की, गणित फारच गुंतागुंतीचे होते. अशा तीन वस्तूंच्या परस्परक्रिया होत असताना सिद्ध होणाऱ्या गतीची समस्या (याला त्रिपिंड समस्या असे म्हणतात), ही अद्याप गणितज्ञांना सोडवता आलेली नाही [⟶ खगोलीय यामिकी]. तेव्हा यातून काही व्यवहार्य मार्ग काढावा लागतो.
चंद्राच्या गतीची समीकरणे मांडताना प्रथम चंद्र, सूर्य व पृथ्वी हे बिंदुमान आकारमानाचे आहेत अशी कल्पना करतात. मग न्यूटन यांच्या गुरुत्वाकर्षण सिद्धांतानुसार फक्त पृथ्वीचे चंद्रावरील आकर्षण विचारात घेऊन चंद्रगतीचे समीकरण मांडतात व या समीकरणात सूर्याच्या आकर्षणाचा परिणाम दर्शविणारे एक जादा पद घालून समीकरण पूर्ण करतात. या समीकरणाचा निर्वाह (समीकरण सोडवून मिळणारे उत्तर) एका घातश्रेढीच्या स्वरूपात मिळतो (अशी श्रेढी म्हणजे विशिष्ट स्थिर राशीच्या १, २, …… इ. घातयुक्त पदांची बेरीज असते). याला मुख्य निर्वाह असे म्हणतात. हा मुख्य निर्वाह काढणे हा चंद्रगतीच्या अभ्यासातील पहिला टप्पा होय.
या निर्वाह-श्रेढीत (१) चंद्र आणि इतर ग्रहांच्या आकर्षणामुळे पृथ्वीच्या कक्षेत होणारा बदल, (२) इतर ग्रहांच्या आकर्षणांमुळे खुद्द चंद्रावर होणारे परिणाम, (३) चंद्र व पृथ्वी यांचे आकार काहीसे लांबट गोल असल्याने होणारे परिणाम व (४) आइन्स्टाइन यांच्या ⇨ सापेक्षता सिद्धांतानुसार होणारे फरक, हे परिणाम व्यक्त करणारी जादा पदे घातली म्हणजे त्यावरून चंद्राचे कोणत्याही वेळचे सहनिर्देशक (एखाद्या संदर्भाच्या सापेक्ष स्थान दर्शविणारे अंक) मिळतात.
प्रत्येक सहनिर्देशकाचे मूल्य श्रेढीच्या स्वरूपात असल्याने श्रेढीतील जितकी जास्त पदे विचारात घ्यावी तितकी उत्तराची अचूकता वाढते. या पदांची मूल्ये उत्तरोत्तर कमीकमी होत जातात. उदाहरण द्यावयाचे म्हणजे चंद्राचे सहनिर्देशक काढण्यासाठी वरील निर्वाहात कित्येक हजार पदे येतात. त्यांची काळजीपूर्वक छाननी करून ब्राउन यांनी शेवटी फक्त १५५ पदे ठेवली आणि त्यांची मूल्ये काढून त्यांवरून चंद्राचे सहनिर्देशक काढले.
अर्थात विचारात घेण्यात येणाऱ्या पदांची संख्या जितकी कमी तितकी अचुकता कमी मिळते. परंतु इतक्या प्रचंड संख्येच्या पदांची गणिते करणे अत्यंत किचकट आणि वेळ घेणारे असते. संगणकांच्या (गणित कृत्ये करणाऱ्या यंत्रांच्या) साहाय्याने अशी आकडेमोड थोड्या वेळात व अचूकपणे करता येते. ही पद्धत वारूपन एकहार्ट, रिबेक्का जोन्स व क्लार्क यांनी ६,००० पदे विचारात घेतली आणि चंद्राची वेगवेगळ्या वेळी स्थाने देणारे कोष्टक तयार केलेले आहे. ते सध्या सर्वांत अचूक मानले जाते.
चंद्राची अक्षीय परिभ्रमण गती : पृथ्वी ज्याप्रमाणे आपल्या अक्षाभोवती फिरत आहे (यामुळेच दिवस-रात्र हे आविष्कार होतात) त्याप्रमाणेच चंद्रही स्वतःच्या अक्षाभोवती फिरत असतो. याला चंद्राचे अक्षीय परिभ्रमण असे म्हणतात. या गतीच्या निरीक्षणावरून कासीनी यांनी सतराव्या शतकाच्या अखेरीस तीन नियम प्रसिद्ध केले.
नियम (१) : चंद्र आपल्या स्थिर अक्षाभोवती पश्चिमेकडून पूर्वेकडे या दिशेने फिरत असून या गतीच्या कोनीय वेगाचे मूल्य स्थिर राहते. स्वतःच्या अक्षाभोवती एक फेरी पूर्ण करण्याला चंद्राला लागणारा काळ बरोबर एक नक्षत्र मासाइतका (चंद्र एका नक्षत्रापासून निघून परत त्याच नक्षत्रात येण्यास लागणाऱ्या काळाइतका) असतो. अगदी आधुनिक वेधांनुसार पाहता या नियमात काही चूक असेल, तर ती १/३००००० टक्क्यांपेक्षा कमी असेल. चंद्राची ही गती हे नैसर्गिक अचूक कालमापकच म्हणता येईल.
नियम (२) : चंद्राच्या अक्षीय परिभ्रमणाचा पृथ्वीच्या कक्षेच्या पातळीशी जो कोन होतो त्याचे मूल्य नेहमी स्थिर राहते. त्याचप्रमाणे चंद्राचे विषुववृत्त चंद्राच्या कक्षापातळीशी जो कोन करते त्याचेही मूल्य स्थिर (६० ४०’ ४४”) असते.
नियम (३) : चंद्राच्या आसाचे ध्रुव, क्रांतिवृत्ताचे (सूर्याच्या भासमान मार्गाचे) कदंब (किंवा ध्रुव) व चंद्रकक्षेचे ध्रुव हे एकाच प्रतलात आणि एकाच बृहत्वृत्तावर (ज्या वर्तुळाचा मध्य व खगोलाचा मध्य एकच आहे अशा खगोलावरील वर्तुळावर) असतात.
चंद्राच्या अक्षीय परिभ्रमणाच्या या वैशिष्ट्यांमुळे काही महत्त्वाचे परिणाम होतात. त्यांचा थोडक्यात आढावा खाली दिला आहे.
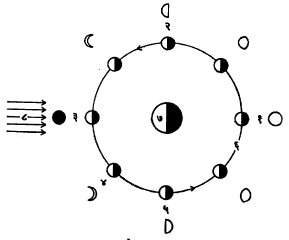
चंद्राचे अक्षीय परिभ्रमण व पृथ्वीभोवतीचे कक्षीय परिभ्रमण यांचे आवर्तकाल एकच असल्याचा एक परिणाम असा होतो की, चंद्रगोलाचा एकच अर्ध नेहमी पृथ्वीसमोर येतो. म्हणजे आपणाला चंद्राचा फक्त ५०% भाग दिसू शकतो. ही गोष्ट आ. ३ वरून स्पष्ट होईल. आकृतीत चंद्राची कक्षा वर्तुळाकार मानली आहे.
अ, आ, इ, ई हे चंद्रावरील चार समान अंतरांवरील बिंदू आहेत. १, २, ३, ४ या चंद्राच्या कक्षेतील चंद्राच्या अवस्था एका आठवड्याच्या अंतराने दाखविल्या आहेत.
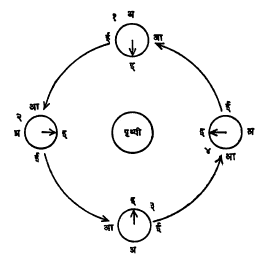
१ या अवस्थेत इ हा बिंदू पृथ्वीला संमुख असून अ उत्तरेकडे आहे. २ या अवस्थेत पुन्हा इ पृथ्वीला संमुख होण्यासाठी चंद्र आपल्या अक्षाभोवती १/४ फेरीमधून फिरला पाहिजे. आता अ पश्चिमेच्या दिशेला असेल. म्हणजेच चंद्राने पृथ्वीभोवती १/४ फेरी पूर्ण केली तेवढ्याच वेळात चंद्राचा आपल्या अक्षाभोवती १/४ वळसा पूर्ण झाला. याप्रमाणे ३, ४ या अवस्थांत प्रत्येकी १/४ फेरे होऊन परत ज्यावेळी चंद्र पृथ्वीप्रदक्षिणा पूर्ण करून १ येथे येईल तेव्हा चंद्राच्या अक्षीय परिभ्रमणाचा एक फेरा पूर्ण होईल. त्यामुळे सर्वत्र इ हाच बिंदू पृथ्वीला संमुख राहील.
दोलना : वरील विधान ढोबळमानानेच खरे आहे. पृथ्वीची कक्षा वर्तुळाकार नसून विवृत्ताकार आहे. त्यामुळे सूक्ष्मपणे निरीक्षण केल्यास चंद्र गोलाच्या सर्वसाधारणपणे दिसणाऱ्या अर्ध्या पृष्ठभागापेक्षा सर्व बाजूंच्या कडेचा काही थोडा अधिक भाग कधी ना कधी दिसू शकतो. त्यामुळे चंद्र किंचित डुलत व अंगविक्षेप करीत जात असल्यासारखा वाटतो. या आविष्कारास चंद्राची दोलना असे म्हणतात. ही दोलना तीन कारणांमुळे घडून येते.
(१) रेखांश-दोलना : चंद्राचे अक्षीय परिभ्रमण एकविध गतीने होते. परंतु चंद्रकक्षा विवृत्ताकार असल्याने तो पृथ्वीच्या कधी जवळून जात असताना थोडा अधिक वेगाने तर कधी लांबून जात असताना थोडा कमी वेगाने जात असतो. त्यामुळे जवळून जात असताना बिंबाचा पश्चिम कडेजवळील भाग अधिक दिसतो, तर दुरून जात असताना बिंबाच्या पूर्व कडेजवळील भाग अधिक दिसतो. एकूण सु. ७० इतका पूर्वपश्चिमेकडील जास्त भाग दृष्टीपथात कधी ना कधी येतो. ही रेखांश-दोलना होय.
(२) अक्षांश-दोलना : चंद्राची कक्षा व त्याचे विषुववृत्त यांच्या पातळ्यांमध्ये ६१०/२ चा कोन आहे. त्यामुळे कधी चंद्राचा उत्तर गोलार्ध थोडासा पृथ्वीकडे कललेला असतो तेव्हा त्याचा उत्तर ध्रुवाकडील चंद्राच्या अक्षांशाच्या दृष्टीने ६१०/२ पर्यंत अधिकात अधिक प्रदेश दिसू शकतो आणि अर्धी प्रदक्षिणा पुरी झाल्यावर दक्षिण गोलार्ध थोडासा पृथ्वीकडे कललेला असतो तेव्हा त्याचा दक्षिण ध्रुवाकडील ६१०/२ पर्यंत अधिकात अधिक प्रदेश दिसू शकतो. या दोलना प्रकारास अक्षांश-दोलना म्हणतात.
(३) दैनिक-दोलना : चंद्र उगवल्यापासून मावळेपर्यंतच्या काळात पृथ्वीच्या अक्षीय भ्रमणामुळे पृथ्वीवरील निरीक्षकाचे ठिकाण चंद्रसापेक्ष बदलते. त्यामुळे निरीक्षकाला चंद्रोदयाच्या वेळी, साधारणतः दिसणाऱ्या चंद्राच्या पृष्ठाभागापेक्षा पश्चिमेकडचा काही अधिक प्रदेश दिसू शकतो, तर अस्ताच्या वेळी पूर्वेकडचा काही अधिक प्रदेश दिसू शकतो. असा फरक फक्त १०च असतो. या तिन्ही दोलनांचा एकत्रित परिणाम म्हणजे चंद्राचा ४१% भाग कधीच दिसत नाही. १८% भाग आळीपाळीने कधीकधी दिसतो आणि ४१% भाग मात्र सतत दिसणारा असतो. म्हणजे चंद्रपृष्ठाचा ५९% भाग दृष्टिपथात येऊ शकतो.
गॅलिलीओ यांना रेखांश व दैनिक दोलना आढळली आणि हेव्हेलियस यांना अक्षांश-दोलना आढळली.
सूर्यसापेक्ष चंद्राचा मार्ग : चंद्र पृथ्वीभोवती फिरत असून त्याला बरोबर घेऊन पृथ्वी सूर्याभोवती फिरत असते. जेव्हा पृथ्वी आणि सूर्य यांच्या दरम्यान चंद्र येतो तेव्हा अमावास्या होते. सकृतदर्शनी असे वाटते की, चंद्रकक्षा पृथ्वीकडून पाहिली असता अंतर्वक्र आहे. तेव्हा अमावास्येच्या आगेमागे, सूर्यावरून पाहिले असता चंद्राचा मार्ग बहिर्वक्र असावा. परंतु ही कल्पना चुकीची आहे. चंद्राच्या अवकाशातील प्रत्यक्ष मार्गाचा आकार हा चंद्राची पृथ्वीभोवतीची गती व पृथ्वीसमवेत सूर्याभोवतीची गती याच्या संयोगाने तयार होतो. पृथ्वी-कक्षेला लंबरूप दिशेने अवकाशातून पाहता हा मार्ग कसा दिसेल ते आ. ४ मध्ये दाखविले आहे. त्यावरून असे दिसेल की, सूर्याकडून पाहता चंद्रामार्ग नेहमी अंतर्वक्रच असतो.
चंद्रोदयाचा काळ : पृथ्वीच्या दैनंदिन अक्षीय परिभ्रमणामुळे चंद्रसूर्य इत्यादींचे उदय-अस्त होतात. त्याशिवाय चंद्राच्या पृथ्वीभोवतालच्या कक्षीय परिभ्रमणामुळे चंद्र पश्चिमेकडून पूर्वेकडे जातो, असे नक्षत्रांच्या तुलनेने वाटते. चंद्राची ही गती प्रतिदिनी सु. १३ अंश आहे. म्हणजे आज चंद्रोदय सायंकाळी ७ वाजता झाल्यास उद्या चंद्र क्षितिजाखाली सु. १३ अंश असेल. त्याचा उदय होण्याला पृथ्वीचे आणखी थोडे परिभ्रमण व्हावे लागेल व तेवढ्या मानाने चंद्रोदय उशीरा होईल. यामुळे दरदिवशी चंद्र सु. ५० मिनिटांनी उशीरा उगवतो.
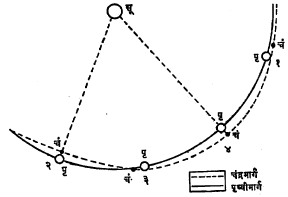
पृथ्वीभोवती ज्या काल्पनिक मार्गातून सूर्य मार्गक्रमण करतो असे वाटते तो मार्ग (म्हणजे क्रांतिवृत्त) व चंद्रकक्षा यांच्यामध्ये ५० ९’ चा कोन होतो. त्यामुळे ती दोन्ही जवळजवळ समांतरच आहे असे मानले, तर फारशी चूक होणार नाही.
उत्तर गोलार्धात वसंत ऋतूमध्ये क्रांतितृत्त क्षितिजाशी सु. ६६ अंशांचा कोन करते. त्यामुळे क्रांतिवृत्तावरील १३ अंश पुढे असलेला बिंदू क्षितिजाच्या बराच खाली जातो. त्यामुळे चंद्रोदयाला दररोज वरीलप्रमाणे सु. ५० मिनिटांचा उशीर होत जातो. परंतु शरद ऋतूतील (सप्टेंबर महिन्यातील) पौर्णिमेला क्रांतिवृत्त व क्षितिज यांच्यामध्ये सु. २३ अंशांचाच कोन असल्यामुळे ते क्षितिजाला जवळजवळ समांतर होते. यामुळे क्रांतिवृत्तावरील १३ अंश पुढचा बिंदू क्षितिजाच्या फारसा खाली जात नाही. त्यामुळे पौर्णिमेनंतर पुढे काही दिवस चंद्रोदय जवळजवळ त्याच वेळेला होतो. त्यामुळे सूर्य मावळल्यानंतर ताबडतोब चंद्रप्रकाश दिसू लागतो व तो प्रकाश शेतातील कामाला उपयुक्त असतो. सप्टेंबर हा उत्तर गोलार्धात सुगीचा हंगाम असल्याने या प्रकाराला सुगीचा चंद्र (हार्व्हेस्ट मून) असे म्हणतात.
चांद्रमास : चंद्राला पृथ्वीभोवती प्रदक्षिणा पूर्ण करण्यास लागणाऱ्या काळाला चांद्रमास म्हणतात. हिंदू पंचांगात कालगणनेसाठी चांद्रमास हाच आधार घेण्यात आलेला आहे [⟶ पंचांग महिना].
चंद्राची तेजस्विता : चंद्राला सूर्याप्रमाणे स्वतःचा प्रकाश नाही. सूर्यप्रकाश चंद्रावरून परावर्तन पावतो व पृथ्वीवर येणारा हा परावर्तित प्रकाश म्हणजेच चांदणे होय. चंद्राची परावर्तन करण्याची क्षमता फारच कमी आहे. त्याच्यावर पडलेल्या प्रकाशऊर्जेपैकी फक्त ७ टक्के ऊर्जेचेच परावर्तन होते, अगदी काजळी किंवा कोळसा यांच्यासारखे अपवाद सोडल्यास पृथ्वीवरील सर्वच पदार्थ याहून अधिक प्रमाणात प्रकाशऊर्जेचे परावर्तन करू शकतात.
चंद्राच्या तेजस्वीपणाची ⇨ प्रत (पौर्णिमेच्या दिवशी) १२·७ आहे. चंद्रापेक्षा सूर्य ४,६५,००० पट जास्त तेजस्वी आहे. अष्टमीला चंद्राचे बिंब अर्धे दिसते. तरी पण पौर्णिमेचा चंद्र अष्टमीच्या चंद्रापेक्षा १३ पट जास्त तेजस्वी असतो. कारण अष्टमीला चंद्रावर सूर्याचे किरण तिरके पडल्याने त्याच्यावरील डोंगर पर्वतांच्या सावल्या त्याच्या पृष्ठभागावर पडतात म्हणून ते अर्धबिंब चांगले प्रकाशित होऊ शकत नाही.
चंद्रग्रहण : सूर्य व चंद्र यांच्या मध्ये पृथ्वी आल्यामुळे चंद्रावर पृथ्वीची छाया पडून चंद्रग्रहण लागते. चंद्रग्रहण अर्थात पौर्णिमेलाच लागण्याची शक्यता असते [⟶ ग्रहण].
चंद्राच्या कला : चंद्राच्या कला कशा होतात हे आ. ५ वरून समजू शकेल. आकृती सोपी करण्यासाठी पृथ्वी स्थिर मानून चंद्रकक्षा वर्तुळाकार दाखविली आहे.
चंद्र जेव्हा (१) या ठिकाणी असेल तेव्हा चंद्राच्या पृथ्वीकडील सर्व पृष्ठभागावर सूर्यकिरण पडल्यामुळे पूर्ण बिंब दिसते. तेथून तो वद्य अष्टमीला (२) या ठिकाणी येतो तेव्हा चंद्राच्या पृथ्वीकडील भागाचा फक्त अर्धाच भाग सूर्यकिरणांनी प्रकाशित होतो म्हणून चंद्राचे अर्धबिंब दिसते. (३) या ठिकाणी चंद्राचा पृथ्वीकडे असलेला सर्वच्या सर्व भाग अप्रकाशित असल्याने चंद्र दिसतच नाही. म्हणजे अमावास्या होते. (४) हे शुद्ध चतुर्थीच्या दिवशीचे चंद्राचे स्थान दर्शविते. यावेळी चंद्राचा पृथ्वीकडील अर्ध्यापेक्षाही कमी भाग प्रकाशित असल्याने चंद्राची कोरच दिसते. कोरीच्या आकाराची नीटशी कल्पना या आकृतीवरून येऊ शकणार नाही. त्यासाठी त्रिमितीय आकृतीची आवश्यकता आहे[⟶ कला].
चंद्राच्या अप्रकाशित भागावर पृथ्वीने परावर्तित केलेला सूर्यप्रकाश पडून तो अंधुक असा दिसू शकतो, चंद्रकोर लहान असताना हा प्रकार विशेष दिसतो [⟶ भूप्रकाश].
चंद्राचे पृथ्वीवर होणारे परिणाम : (१) भूपृष्ठाची भरती-ओहोटी : सागराची ⇨ भरती-ओहोटी हा आविष्कार चंद्राच्या आकर्षणाने (आणि सूर्याच्याही) होतो. परंतु चंद्राच्या आकर्षणामुळे जसा सागराच्या पाण्याला फुगवटा येतो, तसाच तो भूपृष्ठालाही येतो. अशा तऱ्हेने भूपृष्ठाचीही भरती-ओहोटी होत असते. त्यामुळे भूपृष्ठ सु. २२ सेंमी. ने वर किंवा खाली होते. परंतु या कारणामुळे पृथ्वीच्या आकारात कोणताही चिरस्थायी बदल झालेला नाही. याचे कारण पृथ्वीची स्थितिस्थापकता हे होय. चांगल्या पोलादापेक्षाही पृथ्वीची स्थितिस्थापकता काहीशी जास्त आहे.
(२) पृथ्वीच्या अक्षीय परिभ्रमणावर होणारा परिणाम : भरती-ओहोटीमुळे पृथ्वीचा अक्षीय परिभ्रमणाचा वेग हळूहळू मंदावत आहे व यामुळे दिवसाची लांबी हळूहळू वाढत आहे. शंभर वर्षांनी दिवसाची लांबी ०·००१८ सेकंदाने वाढत असली पाहिजे, असे गणिताने सिद्ध करता येते. ही वाढ इतकी अत्यल्प असली, तरी ती खरी असल्याबद्दल काही पुरावे उपलब्ध आहेत. प्राचीन चिनी ग्रंथांतून आणि बायबलमध्ये पूर्वीच्या काही ग्रहणांचे कालनिर्देशासह उल्लेख आहेत. दिवसाची सध्याची लांबी धरून गणिताने या ग्रहणांची वेळ काढता त्यापेक्षा ती ग्रहणे थोडी उशीरा झाली असे दिसते. यावरून त्यावेळी दिवसाची लांबी कमी असावी असे अनुमान काढता येते. याहीपेक्षा एक वेगळा पुरावा वेल्स यांनी सादर केला. सध्या तयार होत असलेल्या प्रवाळाच्या खडकांत प्रतिवर्षी सु. ३६० कंगोरे असतात. पण याच प्रकारच्या ४०० दशलक्ष वर्षांपूर्वी झालेल्या खडकांच्या परीक्षणात प्रतिवर्षी ४०० कंगोरे आहेत असे आढळून आले. म्हणजे त्यावेळी दिवसाची लांबी १/४०० वर्ष इतकीच होती. यावरून गणित करता दिवसाच्या लांबीतील वाढ शंभर वर्षांत सु. ०·००२८ सेकंद असावी असे उत्तर येते.
भरतीचा चंद्रावर होणारा परिणाम : भरतीचा फुगवटा बरोबर चंद्राच्या समोर येतो. पृथ्वीभोवतालच्या परिभ्रमणामुळे चंद्र जसजसा पुढे जातो तसतसा तो या फुगवट्यालाही त्याच वेगाने पुढे रेटण्याचा प्रयत्न करतो. परंतु पृथ्वीचा पृष्ठभाग व म्हणून समुद्रतळ (पृथ्वीच्या दैनंदिन अक्षीय परिभ्रमणामुळे) याहून जास्त वेगाने पुढे जात असतो. परिणामी भरतीचा फुगवटा व समुद्रतळ यांमध्ये घर्षण उत्पन्न होऊन त्यामुळे पृथ्वीच्या अक्षीय परिभ्रमणाचा वेग मंदावतो. म्हणून पृथ्वीचा कोनीय संवेग (कोनीय वेग व निरूढी परिबल यांचा गुणाकार निरूढी परिबल म्हणजे कोनीय प्रवेगाला होणाऱ्या रोधाचे मान) कमी होतो. संवेगाच्या अक्षय्यत्वाच्या सिद्धांतानुसार तेवढ्याच मानाने चंद्राच्या कक्षीय परिभ्रमणाचा कोनीय संवेग वाढतो व म्हणून चंद्र पृथ्वीपासून हळूहळू दूर जात आहे. पृथ्वीचे अक्षीय परिभ्रमण व चंद्राचे कक्षीय परिभ्रमण यांच्या कोनीय गती समान होईपर्यंत या क्रिया चालू राहतील. गणित करता असे दिसते की, ५०,००० दशलक्ष वर्षांनंतर ही परिस्थिती येईल व तेव्हा आपला दिवस चांद्रमास या प्रत्येकाची लांबी हल्लीच्या ४७ दिवसांइतकी येईल.
याउलट फार प्राचीन काळी चंद्र पृथ्वीच्या खूपच जवळ असला पाहिजे व तेव्हा दिवस खूपच लहान असला पाहिजे. या दृष्टीने बरीच गुंतागुंतीची गणितकृत्ये करून गेर्स्टेनकॉर्न यांनी असे दाखवून दिले की, फार पूर्वी (४,००० दशलक्ष वर्षांपूर्वी) चंद्राचे पृथ्वीपासूनचे अंतर किमान म्हणजे पृथ्वीच्या त्रिज्येच्या ४·७ पट इतकेच असावे व तेव्हा दिवस अवघ्या ४·८ तासांचाच असावा. हा काळ साधारणपणे पृथ्वीच्या उत्पत्तीचाच काळ आहे. चंद्राचा पूर्वेतिहास समजून घेण्यासाठी याचा उपयोग करून घेण्यात आलेला आहे.
चंद्राची उत्पत्ती : चंद्राचा जन्म केव्हा व कसा झाला यांबद्दल अद्याप निश्चित असा निर्णय करता आलेला नाही. वेगवेगळ्या अभ्यासकांनी काही परिकल्पना मांडलेल्या आहेत. परंतु त्यांतील कोणतीच सर्वस्वी समाधानकारक नाही.
अपोलो अंतराळवीरांनी चंद्रावरील जुन्यात जुन्या उंचवट्यांवरून आणलेल्या खडकांच्या नमुन्यांचे वय ४,९०० दशलक्ष वर्षे, तर (खोलगट प्रदेशातून आणलेल्या) सर्वांत नवीन खडकांचे वय ३,०००—३,७०० दशलक्ष वर्षे आहे म्हणजे चंद्राचे वय ४,९०० दशलक्ष वर्षांपेक्षा जास्त असावे आणि त्यावर नवे खडक बनण्याची क्रिया ३,७०० दशलक्ष वर्षांपूर्वीच थांबली असावी. ज्वालामुखीमधून निघणाऱ्या लाव्ह्यापासून पृथ्वीवर अजूनही नवे खडक बनत आहेत.
चंद्र पृथ्वीपासूनच निघालेला असावा व या क्रियेत पृथ्वीचा जेथला भाग फुटून निघाला तेथे सध्या पॅसिफिक महासागर आहे अशी एक परिकल्पना डार्विन यांनी मांडली होती. परंतु ती गणिताशी जुळली नाही. दुसरी गोष्ट पृथ्वी आणि चंद्र यांच्यामधील मूलद्रव्यांची प्रमाणे सारखी नाहीत म्हणून ती परिकल्पना सोडून देण्यात आली आहे.
पृथ्वीने दुसरा एखादा छोटा ग्रह आकस्मिकपणे जवळ आला असता त्याला आपल्या गुरुत्वाकर्षणाने आकर्षित करून आपला उपग्रह बनविला असावा अशी एक परिकल्पना गेर्स्टेनकॉर्न यांनी मांडली आहे. या परिकल्पनेनुसार ही घटना घडून आली तेव्हा चंद्र पृथ्वीच्या खूपच जवळ होता. त्यामुळे त्याच्या पृथ्वीला संमुख असलेल्या पृष्ठावरील काही भाग पृथ्वीच्या आकर्षणाने खेचून काढला असावा. पृथ्वी संमुख चंद्रपृष्ठावर (उलट बाजूच्या तुलनेने) खोलगट भाग जास्त आहेत ही वस्तुस्थिती या कल्पनेला पोषक आहे. परंतु ही परिकल्पना अद्याप सर्वमान्य झालेला नाही.
संदर्भ : 1. Branley, F. M. Exploration of the Moon, London, 1965.
2. Burgess, E. Assault on the Moon, London, 1966.
3. Callatay, V. Atlas of the Moon, New York, 1964.
4. Kanwar Lal, Moon in Man’s Stride, Delhi, 1969.
5. Kopal, Z. An Introduction to the Study of the Moon, Dordrecht, Holland, 1966.
6. Kopal, Z. The Moon, London, 1960.
7. Moore, P. Survey of the Moon, London, 1963.
8. Wilkins, H. P. Moore, P. The Moon, London, 1961.
मोडक, वि. वि. काजरेकर, स. ग. पुरोहित, वा. ल.





“