कण अभिज्ञातक

कण अभिज्ञातक : (गणित्र). ह्या साधनांच्या साहाय्याने जलद गतीने प्रवास करणाऱ्या अणूंचा अगर अणूगर्भीय विद्युत्भारित मूलकणांचा शोध घेतला जातो. असा कण अभिज्ञातकातून जाऊ लागला म्हणजे विद्युत् विक्षोभ (क्षुब्धता, खळबळ) निर्माण होतो व या विक्षोभाचे मापन होऊ शकल्याने त्या कणाबद्दल माहिती मिळू शकते. ही साधने आणवीय व अणुगर्भीय भौतिकीत, तसेच विश्वकिरणांच्या ( बाह्य अवकाशातून पृथ्वीवर येणाऱ्या अतिशय भेदक किरणांच्या) संबंधात फार उपयुक्त आहेत. शिवाय किरणोत्सर्गी (कण किंवा किरण बाहेर टाकणाऱ्या) खानिजांचा शोध घेण्यासाठीही त्यांचा फार उपयोग होतो. अभिज्ञातकास काही वेळा गणित्र म्हणून संबोधण्याचाही प्रघात आहे.

मूलभूत तत्त्व व प्रकार : मूलकण म्हणजे इलेक्ट्रॉन, प्रोटॉन, आल्फा कण, मेसॉन यांसारखे कण होत [→ मूलकण]. अभिज्ञातकाच्या भिंतीतून आत प्रवेश होईल व तेथे विद्युत् विक्षोभही निर्माण होईल एवढी या कणांची ऊर्जा असणे आवश्यक असते. अर्थात हे कण विद्युत् भारित व वेगयुक्त असले पाहिजेत, कारण त्यांवरील विद्युत् भार व त्यांचा वेग यांमुळे पदार्थातून इलेक्ट्रॉनांसारखे विद्युत् भारित कण बाहेर पडतात आणि या दुय्यम कणांमुळे मूलकणांचा शोध घेणे शक़्य होते. काही जातीच्या अभिज्ञातकांत मूलकणांमुळे उत्पन्न झालेला विद्युत् विक्षोभ विवर्धकाच्या (वृद्धिंगत करणाऱ्या साधनाच्या) मदतीने वाढविला जातो. अशा तऱ्हेची योजना गायगर-म्यूलर (अगर गायगर) गणित्र किंवा चमक गणित्र यामध्ये वापरलेली असते. दुसऱ्या जातीच्या अभिज्ञातकांत (उदा., बाष्प कोठी व बुद्बुद् कोठी) जलद गतीने जाणाऱ्या कणांचा मार्ग दिसू शकतो व त्याचे छायचित्र घेता येते. अभिज्ञातकांचे निरनिराळे प्रकार पुढे दिल्याप्रमाणे आहेत : (१) आयनीकरण कोठी, (२) बाष्प कोठी, (३) बुद्बुद् कोठी, (४) छायचित्रण पायस, (५) गायगर-म्यूलर (अथवा गायगर) गणित्र, (६) चमक गणित्र, (७) स्फुल्लिंग गणित्र, (८) स्फटिक गणित्र, (९) अर्धसंवाहक गणित्र व (१॰) चेरेनकॉव्ह प्रारण गणित्र. या सर्व अभिज्ञातकांचे वर्णन खाली दिलेले आहे. छायाचित्रण पायसात (प्रकाश संवेदनक्षम पदार्थाच्या लेपात) उच्च ऊर्जा असलेल्या मूलकणांचा परिणाम त्यातील सिल्व्हर ब्रोमाइडाच्या (हॅलाइड) रवाळ भागावर होतो आणि विकाशन केल्यानंतर (सुप्त प्रतिमा रासायनिक विक्रियेने दृश्य स्थितीत पक्की केल्यांनंतर ) उच्च वर्धनक्षमता असलेल्या सूक्ष्मदर्शकाच्या साहाय्याने छायाचित्रण पायसातील मूलकणांच्या पथरेषा तपासता येतात. या पद्धतीचा विशेष उपयोग अणुगर्भीय संशोधनात होतो.

योग्य अभिज्ञातक वापरला असता त्यावरून मूलकणांविषयी पुढील माहिती मिळू शकते : (१) अभिज्ञातकातून दर सेकंदास जाणारी कणसंख्या, (२) त्यास लागणारा काल, (३) कणाचा वेग व संवेग (वस्तुमान आणि वेग यांचा गुणाकार), (४) कणाची स्थिती, (५) कणाची ऊर्जाक्षय त्त्वरा व (६) किरणोत्सर्गी कणाच्या संबंधात त्याचे आयुर्मान. पुष्कळ वेळा कणासंबंधी संपूर्ण माहिती मिळविण्यासाठी एकापेक्षा अधिक अभिज्ञातक वापरावे लागतात. कोणता अभिज्ञातक वापरावा हे (अ) गणनत्वरा, (आ) समानुपातित्त्व (समप्रमाणात असण्याचा गुण) व (इ) अपेक्षित माहिती यांवरुन ठरते.

(अ) गणनत्वरा : गणित्राची गणनत्वरा त्यात उत्पन झालेल्या विद्युत् संकेत कालावर व मिळालेल्या प्रेरणेपासून पूर्वस्थितीत येण्यास लागणारा काल (यास क्रियाशून्य काल म्हणतात) यांवर अवलंबून असते. चमक गणित्राची गणनत्वरा सर्वात अधिक असते यात संकेतकाल १०⁻⁹ सेकंद व क्रियाशून्य काल शून्य असतो. गायगर गणित्राची गणनत्वरा या मानाने जरा कमी असते व क्रियाशून्य काल सु. १०⁻⁴ सेकंद इतका असतो. बहुतेक सर्व बाष्प कोठ्यांचा क्रियाशून्य काल एक मिनिटापेक्षा अधिक असतो व इतर अभिज्ञातकांची गणनत्वरा वरील मर्यादांच्या दरम्यान असते.

(आ) समानुपातित्व : विद्युत् संकेताचे मान गणित्रात घडणाऱ्या ऊर्जाक्षयाच्या समप्रमाणात असल्यास ते गणित्र समानुपाती आहे असे म्हणतात. चमक गणित्र समानुपाती असते तर गायगर-म्यूलर गणित्र तसे नसते.

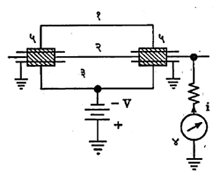
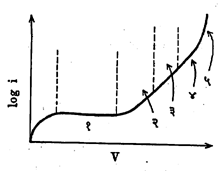
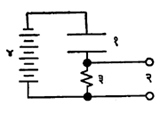
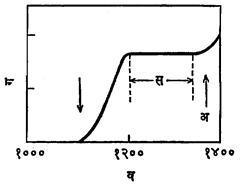
समानुपाती गणित्र : समानुपाती गणित्राचे एक उदाहरण म्हणजे   आर्गाॅनासारख्या वायूने अगर आर्गॉन व दुसऱ्या योग्य वायूच्या मिश्रणाने भरलेली विद्युत् विसर्जन नलिका (वायूतून विद्युत् प्रवाज वाहू देणारी नलिका) हे असून तिच्या मदतीने आयनीकरण करणार्‍या (विद्युत् भारित अणू, रेणू वा अणुगट म्हणजे आयन निर्माण करणाऱ्या) प्रारणाचे (तरंगरुपी ऊर्जेच्या उत्सर्जनाचे) अभिज्ञान होऊ शकते. यात आयनीकरणामुळे आपाती (गणित्रावर पडणाऱ्या) किरणांच्या ऊर्जेच्या समप्रमाणात विद्युतं स्पंद (येथे अल्पकालीन तरंग) उत्पन्न होतो. अशा तऱ्हेचे साधन पुढे वर्णन केल्याप्रमाणे असते. पातळ धातूच्या एका नलिकेच्या अक्षावर एक तार ताणून बसविली असून ती नलिकेच्या दोन्ही तोंडात बसविलेल्या विद्युत् निरोधक (विद्युत् प्रवाहास प्रतिबंध करणाऱ्या) बुचांतून बाहेर आणलेली असते (आ.१), बाहेरून लावलेल्या वर्चसामुळे (विद्युत्दाबामुळे) नलिकेचे आवरण ऋण भारित व तार धन भारित होते आणि आवरण व तार विद्युत् प्रस्थे (अग्रे) बनतात. बाह्य मंडलामध्ये विद्युत् प्रवाह मोजण्याचे साधन ठेवलेले असते. आयनीकरण करणाऱ्या प्रारणाचा उद्गम नलिकेच्या आत आहे असे समजू. आता या प्रारणाचा परिणाम म्हणून नळीतील वायूत आयन निर्माण होतात. व त्यांच्या मार्गावर (मुक्त झालेले इलेक्ट्रॉन इतर पदार्थ कणांशी संयोग पावत नाहीत असे समजल्यास) समान संख्या असलेले घन आयन व इलेक्ट्रॉन उत्पन्न होतात. आवरण व तार यांमधील वर्चसामुळे इलेक्ट्रॉन तारेकडे जोराने खेचले जातात व घन आयन त्यामानने कमी वेगाने आवारणाकडे खेचले जातात आणि याचा परिणाम म्हणून बाह्य मंडलातून विद्युत् प्रवाह सुरु होतो. जसजसे वर्चस् वाढवावेतसतसा प्रवाह वाढत जातो. वर्चस् V व विद्युत् प्रवाह i समजल्यास, V व log i यांचा परस्परसंबंध दाखविणारा आलेख आ. २ मध्ये दिला आहे. या आलेखाचे तीन स्वतंत्र भाग पडलेले दिसतात व त्यासंबंधीचा खुलासा पुढे दिल्याप्रमाणे आहे : वर्चोभेद (वर्चसांमधील फरक) १० ते १०० व्होल्ट दरम्यान असताना विद्युत् प्रवाहाचे परिपूर्ती मूल्य गाठले जाते. या स्थितीत सर्व इलेक्ट्रॉन व धन आयन विद्युत प्रस्थांकडे खेचले जातात व विद्युत् प्रवाहाचे हे परिपूर्ती मूल्य नलिकेच्या प्रभावी आयतनात (घनफळात) दर सेकंदास निर्माण होणाऱ्या आयनव्दयांच्या संख्येच्या समप्रमाणात असते म्हणजे विद्युतु प्रवाह हा आयनीकारक बाह्य उद्गमाच्या तीव्रतेच्या समप्रमाणात असतो. स्थिर परिस्थितीत वर्चोभेद सु. १,००० व्होल्टपर्यंत वाढविला असताही विद्युत् प्रवाहाचे हे परिपूर्ती मूल्य जवळजवळ स्थिर राहते. आलेखाचा हा भाग समानुपातित्त्व दाखवितो. वर्चोंभेदाचे हे कमाल मूल्य नलिकेतील वायू, त्याचा दाब व नलिकेचा आकार-विशेषत: तिचा व्यास-यांवर अवलंबून असते. साधारणपणे असे म्हणता येईल की, वर नमूद केलेली मूल्ये सु. ४ सेंमी. व्यास असलेल्या नलिकेच्या व ॰.२ मिमी. व्यास असलेल्या तारेच्या बाबतीत आणि एक वातावरणीय दाब असलेल्या व १० : १ या प्रमाणात मिश्रण केलेल्या आर्गॉन व मिथेन या मिश्रवायूंच्या बाबतीत आढळतात. आयनीकरण कोठीचे कार्य याच समानुपाती भागातले असते. गायगर गणित्रास समानुपाती गणित्र का म्हणता येत नाही, हे या वक्रावरुन स्पष्ट कळून येते. कारण त्यात जमा झालेला विद्युत् भार व त्यापासून निर्माण होणारा विद्युत् प्रवाह हा मूलकणाने निर्माण केलेल्या सुरुवातीच्या आयनीकरणावर अवलंबून नसतो. आयनीकरण कोठ्यांच्या आकारमानात पुष्कळच भिन्नता आढळते. विश्वकिरणांच्या बाबतीत १.८ मी. लांब व ०.६ मी. व्यास असलेल्या आयनीकरण कोठ‌्या वापरण्यात आल्या आहेत, तर अणुगर्भीय विक्रियकातील (अणुगर्भीय विक्रिया ज्या उपकरणात करण्यात येतात त्यातील) न्यूट्रॉनांची गणती करण्यासाठी ६.३ मिमी. लांब व तितक्याच व्यासाच्या आयनीकरण कोठ्या वापरण्यात आल्या आहेत. विद्युत् प्रस्थांसाठी (नलिकेचे आवरण व तार) पितळ, तांबे अगर अँल्युमिनियम वापरतात व विद्युत निरोधक म्हणून काच, प्लॅस्टिक अथवा अंबर वापरतात.

ऊर्जाक्षय : पदार्थातून जाताना विद्युत् भारित कणाची ऊर्जा पुढील तीनपैकी कोणत्या तरी रीतीन क्षय पावते : (१) अणूंचे आयनीकरण व संक्षोभन (क्षुब्ध करणे), (२) आणवीय क्षेत्रात प्राप्त होणाऱ्या प्रवेगाचा (दर सेकंदास होणाऱ्या वेग बदलाचा) परिणाम म्हणून निर्माण होणारे प्रारण व (३) दुसऱ्या अणुगर्भाशी होणाऱ्या टकरींमुळे घडणारे अणुगर्भाचे रुपांतरण. यापैकी (२) व (३) चा विचार येथे करण्याचे कारण नाही. (१) प्रमाणे होणारा ऊर्जाक्षय प्रकीर्णनाचा (विखुरल्याचा) परिणाम म्हणून होतो. आपाती कणांचे प्रकीर्णन मुख्यत: इतर अणुगर्भांशी होणाऱ्या विक्रियेमुळे घडते, तर ऊर्जाक्षय सर्वस्वी इलेक्ट्रॉनांशी होणाऱ्या टकरींमुळे होतो. कमी वेगापासून सुरुवात करुन वेग जसजसा वाढेल त्याप्रमाणे टकरा व संक्षोभन यांमुळे होणारा ऊर्जाक्षय (यास आघात वा आयनीकरण क्षय म्हणतात) कमी कमी होत जातो व ज्या वेगास कणाचे वस्तुमान त्याच्या स्थिर वस्तुमानाच्या जवळजवळ दुप्पट होते त्यात हा ऊर्जाक्षय नीचतम होतो. आल्फा कणांमुळे होणारे आयनीकरण बीटा कणांच्या (वेगयुक्त इलेक्ट्रॉनांच्या) मानाने पुष्कळच जास्त असते. सर्वसाधारणपणे एक बीटा कण सु. १०० आयन निर्माण करतो, तर एक आल्फा कण १०, ००० आयन उत्पन्न करतो. याचा परिणाम म्हणून अर्थातच कणाची मूळ ऊर्जा प्रत्येक टकरीबरोबर कमी होत जाते. ही कमी झालेली ऊर्जा (ऊर्जाक्षय) आयन निर्माण करते व अणूसही थोडी ऊर्जा प्राप्त करुन देते. आल्फा कणांच्या अशा टकरी पुष्कळच होत असल्याने ते पदार्थाच्या आत फारच थोड्या अंतरापर्यंत घुसू शकतात व म्हणून त्यांची पारगम्यता (आरपार जाण्याची क्षमता) फारच कमी असते. बीटा कणांची पारगम्यता त्यामानाने पुष्कळच अधिक असते. आल्फा, बीटा व गॅमा कणांची सापेक्ष आयनीकरणक्षमता व पारगम्यता कोष्टक क्र. १ मध्ये दिली आहे.

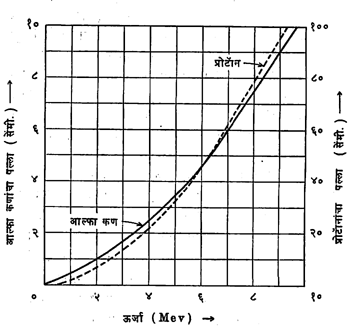
वर सांगितलेच आहे की, एखाद्या पदार्थातून विशिष्ट अंतर गेल्यानंतर विद्युत् भारित कणाची गती नाहीशी होते. या अंतरास त्या कणाचा त्या पदार्थातील पल्ला म्हणतात. ७६० मिमी. (पाऱ्याचा) दाब असताना व १५⁰ से. तापमान असताना आल्फा कणांचा व प्रोटॉनांचा पल्ला आलेख रुपाने आ. ३ मध्ये दाखविला आहे. हा आलेख कणांचा पल्ला व त्यांची ऊर्जा यांचा संबध दाखवितो.

गणित्राची कार्यक्षमता : याची व्याख्या पुढे दिल्याप्रमाणे केली जाते. ε॰ ही गणित्राची अंगभूत कार्यक्षमता असल्यास,

आपाती प्रारणाच्या दिशेवर कार्यक्षमतेचे मूल्य अवलंबून नाही असे समजल्यास,

समाकलित (सर्व मिळून आलेली) कार्यक्षमता εi= ε॰ ω … (२) यात ω हा गणित्राच्या उपयोगात आलेल्या पृष्ठाने उगमबिंदूशी केलेला घनकोन आहे व तो स्टरेडियन या एककात मांडला जातो. ε0 चे मूल्य गणित्राच्या व प्रारणाच्या जातीवर अवलंबून असते.

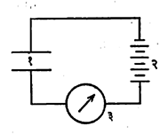
आयनीकरण कोठी : वेगवान विद्युत् भारित कणांनी उत्पन्न केलेले आयनीकरण मोजण्यासाठी व विश्वकिरणांसंबंधीच्या अथवा अणुगर्भीय संशोधनात तसेच प्रारणाचीतीव्रता मोजण्यासाठी ही कोठी वापरतात. सुवर्णपत्री विद्युत् दर्शक (विद्युत् भाराचे अस्तित्त्व दर्शविणारे एक उपकरण) हादेखील एक साधी आयनीकरण कोठीच आहे. आयनीकरण कोठी दोन प्रकारची असते : (१) किरणोत्सर्गी पदार्थ कोठीच्या आत ठेवून त्यातून निघणाऱ्या प्रारणाचे अभिज्ञान होण्यासाठी व (२) कोठीच्या बाहेरुन येणाऱ्या उच्च ऊर्जा असलेल्या कणांच्या (उदा. कणवेगवर्धकातून म्हणजे कणांना उच्च वेग प्राप्त करुन देणाऱ्या उपकरणातून बाहेर पडणाऱ्या) अभिज्ञानासाठी पहिल्या प्रकारात किरणोत्सर्गी पदार्थ कोठीतील एकमेकांस समांतर असलेल्या दोन पातळ पट्‌ट्यांपैकी एकीवर ठेवला जातो व आतील वायूचा दाब असा ठेवला जातो की, उत्सर्जित आल्फा कण समोरील पट्टीपर्यंत पोहोचण्याच्या आतच थांबविला जाईल. या अभिज्ञातकाच्या मदतीने किरणोत्सर्गी पदार्थाचा अर्धायु:काल (किरणोत्सर्गीची मूळची क्रियाशीलता निम्मी होण्यास लागणारा काल) काढता येतो अगर त्याचा अर्धायु:काल माहीत असल्यास, त्या पदार्थाचे मान कळते. सर्वसाधारण बीटा कणांमुळे आयनीकरण थोड्या प्रमाणात होत असल्याने त्यांच्या बाबतीत या कोठ्या वापरीत नाहीत परंतु कणवेगवर्धकातून येणाऱ्या अगर विश्वकिरणांमुळे निर्माण झालेल्या अतिवेगवान इलेक्ट्रॉनांच्या बाबतीत या कोठ्या वापरता येतात. कोठीत आर्गॉन वायू शुद्ध स्वरुपात असतो. मापनाच्या दोन पद्धती आ. ४ व ५ मध्ये दाखविल्या आहेत. आ. ४ मध्ये दाखविल्याप्रमाणे समांतर पट्ट्यांमध्ये विद्युत्क्षेत्र निर्माण केलेले असते व त्यामुळे धन आणि ऋण आयनांची हालचाल होऊन उद्‌‍भवलेला विद्युत्‌ प्रवाह मापकाने मोजला जातो. पट्ट्या सपाट असण्याऐवजी वृत्तचित्तीय (दंडगोलाकार) वा गोलीय असू शकतात.

एकाच कणामुळे निर्माण झालेले आयनीकरण मोजावयाचे झाल्यास मिळणारा विद्युत् प्रवाह सूक्ष्म असल्याने, त्याचे वर्धन करण्यासाठी विवर्धकाची जरुरी असते (आ.५). उच्च रोधकातून हा विद्युत् प्रवाह गेल्यामुळे रोधकाच्या दोन टोकांत विद्युत् वर्चोभेद निर्माण होतो वविवर्धकाच्या साहाय्याने तो वाढविला जातो आणि अखेरीस हे वर्धित विद्युत् स्पंद मोजले जातात.

या कोठीत नुसत्या इलेक्ट्रॉनांचा जमा होण्याचा काल एक मायक्रोसेकंद (१०⁻⁶ सेकंद ) असतो व त्यावेळी गणनत्वरा १०⁵ प्रतिसेकंदापर्यंत असते. अधिक वजनाच्या आयनांच्या बाबतीत ते जमा होण्याचा काल एक मिलिसेकंद (१०⁻३ सेकंद) असतो व गणनत्वरा १०२ प्रतिसेकंदापर्यंत ठेवता येते.

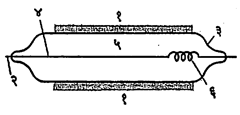
बाष्प कोठी : या साधनाचे वैशिष्ट्य असे आहे की, त्यात नियंत्रित अतिपरिप्‍लुतता (परिप्‍लुत अवस्थेत असणाऱ्या बाष्पाच्या प्रमाणापेक्षा अधिक प्रमाणात बाष्प असणारी अवस्था) निर्माण करता येते व ती काही काल टिकत असल्याने अधिक प्रमाणात असलेल्या बाष्पाचे आयनांवर द्रवीभवन होते. अशा रितीने तयार झालेल्या द्रवाचे थेंब प्रकाशित करुन त्यांची छायाचित्रे घेता येतात आणि या छायाचित्रांत उमटलेल्या पथरेषांवरुन मूलकणांसंबंधीची माहिती प्राप्त होते. या बाष्प कोठ्या अणुगर्भीय संशोधनात वापरल्या जातात. अशा तऱ्हेची कोठी प्रथम सी. टी. आर्. विल्सन यांनी १९११ मध्ये बनविली.

ज्यांचा उकळबिंदू अत्यंत नीच आहे व सर्वसाधारण तापमानात जे वायुरुपात आढळतात असे हवा, आर्गॉन, हीलियमासारखे वायू आणि पाण्याची वाफ व अल्कोहॉलाचे बाष्प यांचे मिश्रण या कोठीत असते. वायूंचा दाब वातावरणीय दाबाइतका अगर त्याहून कमी किंवा ५॰ वातावरणीय दाबाइतकाही असतो. वायू सुरुवातीस परिप्‍लुत असतात व ते अतिपरिप्‍लुत व्हावे म्हणून खालील दोन तऱ्हेच्या योजना असतात :

(१ ) विल्सन बाष्प कोठीमध्ये दट्ट्याच्या अथवा रबरी फुग्याच्या एकाएकी बाहेर सरकण्यामुळे परिप्‍लुत वायू अक्रमी (उष्णतेचा लाभ वा व्यय न होता) प्रसरण पावतात व त्यामुळे त्यांचे तापमान उतरून ते अतिपरिप्‍लुत बनतात. हे प्रसरण नियंत्रित असावे लागते कारण प्रसरण पुरेसे न झाल्यास थेंब तयार होणार नाहीत व अधिक झाल्यास कोठीत दाट धुके निर्माण होईल. (२) दुसरी योजना विसरण (आपोआप एकमेकांत मिसळण्याच्या क्रियेचा उपयोग करणाऱ्या) बाष्प कोठीमध्ये वापरली जाते. कोठीमधील तळ थंड ठेवून वरची बाजू कढत ठेवतात. बाष्प वरच्या बाजूने आत सोडतात व ते विसरणामुळे तळाकडे जाते आणि अशा रीतीने बाष्पामध्ये तापमानाचा उतार तयार होतो. मधील एका विशिष्ट भागात अतिपरिप्‍लुतता निर्माण होते व तेथे आयन आल्यास त्यावर बाष्पाचे द्रवीभवन होऊन थेंब तयार होतात. अशा भागाची कार्यक्षम रुंदी ५—७.५ सेंमी.च असते व यापेक्षा अधिक रुंद भागात कणांचे पथ स्पष्ट मिळणे कठीण असते. विसरण बाष्प कोठी सतत कार्यक्षम राहते, तर विल्सन बाष्प कोठी सतत प्रसरणानंतर काही सेकंदच कार्यक्षम राहते. शिवाय एका प्रसरणानंतर पुन्हा तीच कोठी वापरण्याच्या आधी काही काल (सु. एक मिनिट) सुरुवातीची समतोलित अवस्था प्राप्त होण्यासाठी जाऊ द्यावा लागतो.

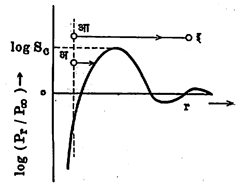
r त्रिज्या असलेल्या व एकविधतेने (सर्वत्र सारख्या प्रमाणात) विद्युत् भारित अशा थेंबावर तो समतोलित रहावा म्हणून जरूर असलेला अधिक दाब Pr पुढील समीकरणाने दिला जातो :

यात S = द्रवाचा पृष्ठताण, D = द्रवाची घनता, R = वायुस्थिरांक, T = निरपेक्ष तापमान, K = विद्युत् अपार्यता, M = बाष्पाचा ग्रॅमरेणुभार (ग्रॅममध्ये मोजलेला रेणुभार), P∞ = सपाट पृष्ठावरील बाष्पदाब आहे आणि e = विद्युत् भार आहे.

विल्सन बाष्प कोठी अल्पकाल कार्यक्षम असते हा तिचा दोष दूर करण्यासाठी ती कोठी प्रतिनियंत्रित करतात. म्हणजेच वेगवान विद्युत्‌ भारित कण आला असल्याचा संदेश देणारे निराळे अभिज्ञातक असतात व त्यामुळे कणाच्या प्रवेशानंतर काही सहस्रांश सेकंदातच कोठीत प्रसरण घडते.

बाष्प कोठी कर्षुकीय (चुंबकीय) क्षेत्रात ठेवली असता कणांचे पथ वर्तुळाकृती होतात त्यांच्या छायाचित्रांवरून वर्तुळाची त्रिज्या मोजता येते. त्यावरून व कर्षुकीय क्षेत्राची तीव्रता ज्ञात असल्याने कणांचा संवेग काढता येतो. p हा संवेग समजल्यास

p = 300 B r …. …. (४)

यात B ओर्स्टेड ही कर्षुकीय क्षेत्राची तीव्रता असून r पथाची त्रिज्या आहे. शिवाय कणाच्या गतीची दिशा माहीत असल्यास कणावरील विद्युत्‌ भार धन वा ऋण आहे हे समजते, कारण धन व ऋण भारानुसार पथाच्या वक्रतेची दिशा बदलते. कणामुळे घडून आलेले आयनीकरण त्याच्या वेगावर अवलंबून असल्याने कणाचा वेग समजतो आणि संवेग व वेग कळून आल्याने कणाचे वस्तुमानही समजते. कणांच्या पल्ल्यांची लांबीही छायाचित्रावरून मोजता येते.

बुद्‍बुद्‌ कोठी : ज्यामध्ये वेगयुक्त विद्युत्‌ भारित कणाचा मार्ग त्याच्या मार्गावर बनलेल्या बुडबुड्यामुळे दृष्टोत्पत्तीस येतो, अशा अभिज्ञातकास बुद्‌बुद्‌ कोठी म्हणतात. डोनाल्ड ग्‍लेसर यांनी १९५२ मध्ये बुद्‌बुद‌्‍ कोठीचा शोध लावला. यात योग्य तापमान व दाब असलेला द्रव असतो व आकस्मिक होणाऱ्या प्रसरणामुळे दाब एकदम कमी होऊन तो द्रव अतितप्त अवस्थेत येतो. यासाठी सुरुवातीस उच्च दाबात उष्णता देऊन द्रवाचे तापमान. त्याच्या उकळबिंदूच्या वर आणतात व नंतर त्या द्रवावरील दाब एकदम कमी करतात. अशा रीतीने अतितप्त झालेल्या द्रवातून वेगवान विद्युत्‌‍ भारित कण जाऊ लागला म्हणजे कणाची ऊर्जा द्रवास दिली जाते, त्याचा परिणाम म्हणून द्रवातील काही जागा आणखी तापतात आणि अशा जागी बारीक बुडबुडे तयार होऊ लागतात. हे बुडबुडे प्रकाशित करून त्यांची छायाचित्रे घेण्यात येतात व अशा रीतीने कणांच्या पथांचे चित्र तयार होते. बुद्‌बुद्‌ कोठीचा उपयोग अणुगर्भीय संशोधनात फार होतो. प्रोपेन व तत्सम द्रव यात वापरले जातात. द्रव झेनॉन, द्रव हायड्रोजन, द्रव ड्यूटेरियम व द्रव हीलियमही वापरतात पैकी शेवटची तीन द्रव्ये अत्यंत नीच तापमानात वापरतात. म्हणून योग्य अशा संबंधित उपकरणांची योजना व कोठी हवाबंद करणे, यांविषयी फार काळजी घ्यावी लागते. द्रव हायड्रोजन असलेली बुद्‌बुद्‌ कोठी २५० ते २९० निरपेक्ष तापमानात व ३ ते ७ वातावरणीय दाबात वापरतात. द्रव हीलियम असलेली बुद्‌बुद्‌ कोठी ३० ते ४० निरपेक्ष तापमानात व वातावरणीय दाबापेक्षा कमी दाबात वापरली जाते. द्रव हायड्रोजन कोठीत प्रसरण गुणोत्तर ०.७ ते २.० टक्के एवढे असते तर द्रव हीलियम कोठीत ते एक टक्क्यापेक्षा कमी असते. दोहोंत उष्णता निरोधन चांगल्या प्रकारचे असावे लागते.

छायाचित्रण पायस : आयनीकरण करणारा कण छायाचित्रण पायसातून जात असताना त्याचा परिणाम पायसातील सिल्व्हर हॅलाइडावर होतो ही गोष्ट१९११ पासून माहीत होती, पण ज्यास अणुगर्भीय पायस असे नाव आहे अशा खास पायसांचा वापर १९५० पासून मोठ्या प्रमाणावर सुरू झाला. या पायसामुळे प्रत्येक कणाचा पथ स्पष्ट रेखीत होतो. या पायसात जिलेटीन माध्यमात सिल्व्हर हॅलाइडाचे ०.१ ते ०.३ मायक्रॉन (μ, १०-३ मिमी.) व्यास असलेले पुष्कळसे सूक्ष्म रव विखुरलेले असतात.

कोडॅक कंपनीच्या अणुगर्भीय पायसांच्या संवेदनक्षमतेबद्दलची माहिती कोष्टक क्र. २ मध्ये दिली आहे त्यात निरनिराळ्या कणांची अधिकात अधिक मापनीयऊर्जा दिलेली आहे. कोष्टकात Mev आणि Kev हे अनुक्रमे मिलियन (दशलक्ष) इलेक्ट्रॉन व्होल्ट आणि किलो (हजार) इलेक्ट्रॉन व्होल्ट (१ इलेक्ट्रॉन व्होल्ट = १.६ X १० -१२ अर्ग) असे दर्शवितात.

साधारणपणे २.५ X ७.६ सेंमी. आकाराच्या काचेच्या पट्ट्यांवर पायसाचा थर दिलेला असतो, पण जरूर असल्यास इतरही आकाराच्या

पट्‌ट्या तयार करता येतात. पायस थराची जाडी ५०-२०० μ इतकी असते. २५० μ जाडीच्या थरांची नुसती पायसेही (काच पट्‌ट्यांवर लावलेली नव्हे) मिळू शकतात. सर्व पट्‌ट्यांना ०.५ ते १ μ जाडीचे जिलेटिनाचे संरक्षक कवच असते. इल्फर्ड कंपनीचीही साधारणपणे अशाच तऱ्हेची पायसे उपलब्ध आहेत.

या पट्‌ट्यांचे उद्‌भासनानंतर (प्रकाश पडल्यानंतर) शक्य तितक्या लवकर विकाशन करणे जरूर असते. हे काम सर्वसाधारणपणे तांबड्या प्रकाशात करता येते, पण काही पट्‌ट्यांच्या बाबतीत संपूर्ण काळोख असणे आवश्यक असते. विकाशन झाल्यानंतर उमटलेले चित्र दोषरहित व एकविध असणे जरूर असते. नंतर या पट्‌ट्या चांगल्या दर्जाच्या, दोन्ही डोळ्यांनी पाहता येईल अशा द्विनेत्री सूक्ष्मदर्शकाच्या साहाय्याने अभ्यासल्या जातात. जरूर तर विवर्धनासाठी तैल-निमज्‍जित वस्तुभिंग (ज्यातून प्रथमतः प्रकाशकिरण जातात असे तेलात बुडवलेले भिंग) आणि लहान कोन मोजण्यासाठी कोनमापी नेत्रभिंग वापरणे इष्ट असते[→ सूक्ष्मदर्शक].

पदार्थातून जाताना विद्युत्‌ भारित कणाची आयनीकरणामुळे झालेली ऊर्जाक्षयत्त्वरा गणिताने काढता येते व त्यावरून कणाचा पल्ला आणि संवेगसमीकरणाच्या मदतीने काढता येतात. शिवाय कणांच्या पथावरील पायस रवांची (पायस कणांची) पथाच्या विशिष्ट लांबीतील (५० वा १०० मायक्रॉन) सरासरी संख्या सूक्ष्मदर्शकाच्या साहाय्याने मोजता येते. चांगले सरासरी मूल्य मिळण्यासाठी अशी बरीच मापने करावी लागतात.

पथांच्या शेवटास गतिमान कणांचे प्रकीर्णन (रदरफर्ड प्रकीर्णन सिद्धांतानुसार) होते असे आढळून आले आहे. प्रकीर्णन कोनांच्या व रवसंख्येच्या मापनावरून कणाचा संवेग आणि त्याचे वस्तुमान काढणे शक्य होते.

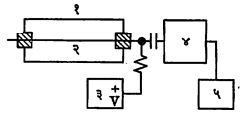
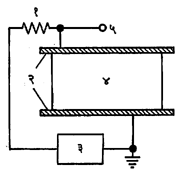
गायगर-म्यूलर (गायगर) गणित्र : हे गणित्र आयनीकरण करणाऱ्‍या प्रारणाचे अभिज्ञातक आहे व अणुगर्भीय प्रारणाची तीव्रता मोजण्याचे ते एक चांगले साधन समजले जाते. ते सुटसुटीत असल्याने उद्योगधंद्यात, वैद्यकशास्त्रात, खनिजांचा शोध घेण्यासाठी व वैज्ञानिक संशोधन कार्यात उपयुक्त ठरते. साधारणतःया गणित्राची रचना व कार्य आ. १ मध्ये दाखविल्याप्रमाणे असते. गणित्रातील दोन्ही विद्युत्‌ प्रस्थांचे पृष्ठभाग अत्यंत स्वच्छअसावे लागतात व आतील वायूही शुद्ध असणे जरूर आहे. आर्‌गॉनासारखा अक्रिय वायू व त्यात थोडया प्रमाणात मिसळलेलेएखादे कार्बनी बाष्प ०.१४ वातावरणीय दाबात गणित्राच्या आत भरलेले असतात. कार्बनी बाष्पामुळे विद्युत्‌ विसर्जनाचे शमनहोते व अनेक दुय्यम स्पंद निर्माण होणे थांबते. परंतु या बाष्पापैकी थोडा भाग दर स्पंदात वापरला जातो व म्हणून या गणित्राचीआयुर्मर्यादा १०८ ते १०९ मापने इतकी राहते. शमन करण्यासाठी हॅलोजन गटातील वायूंचाही उपयोग करतात व त्यामुळेगणित्राची आयुर्मर्यादाही वाढते. अक्षावर ताणलेली तार टंगस्टनाची असून तिचा व्यास ०.०७५ ते ०.१३० मिमी. असतो. यागणित्राचा एक निराळा प्रकार म्हणजे ऋण विद्युत्‌ प्रस्थ बाहेर असलेला असतो. यात काचेच्या वृत्तचित्तीय नलिकेच्या बाहेरीलदोन विरुद्ध बाजूंस तांबे, पितळ अगर ॲल्युमिनियम या धातूचा पातळ थर दिलेला असतो व हे थरच ऋण विद्युत्‌ प्रस्थ होतात. नलिका सोडाग्‍लासची असते व सोडाग्‍लासचीसंवाहकता (सुलभतेने होणारी विजेची वाहतूक) कमी असली तरी तीमधून विद्युत्‌ प्रवाह जाण्यास पुरेशी असते. अशा तऱ्‍हेचे गणित्र आ. ७ मध्ये दाखविले आहे. या गणित्रासपूर्वस्थितीवर येण्यास बराच काळ लागत असला तरी धातूच्या बनविलेल्या गणित्रापेक्षा ते स्वस्त असते. शिवाय चुकीने अधिक वर्चस्‌ लावले गेले तरी त्यास इजा पोहोचतनाही. उपयोग कोठे करावयाचा यावर त्याचे आकारमान अवलंबून असते. ३.८ सेंमी. व्यासाची व ७.६ सेंमी. लांबीचा ॲल्युमिनियमाचा पातळ थर असलेली गणित्रे बीटा कणव विश्वकिरण संशोधनात वापरतात. ५ ते ७.६ सेंमी. व्यासाची, ९० सेंमी. पर्यंत लांबी असलेली गणित्रेही बनविण्यात आली आहेत. या गणित्राचे कार्य आ. ८ वरून समजूशकते. आयनीकरणाचा परिणाम म्हणून इलेक्ट्रॉनांचा लोंढा तयार आ. ८. गायगर गणित्राचे योजनादर्शक चित्र : (१) आवरण (ऋण), (२) तार (धन), (३) वर्चोभेद निर्माण करणारे साधन, (४) विवर्धक, (५) प्रमाण नियंत्रक. होतो आणि विद्युत् स्पंद निर्माण होतो. हा स्पंद ५० व्होल्ट एवढा असतो. इलेक्ट्रॉनांचा लोंढा एवढा विस्तृत असतो की, तोतारेच्या सर्व लांबीभोवती जमा होतो. धन आयन नलिकेच्या बाह्य आवरणाकडे कमी वेगाने खेचले जातात. इलेक्ट्रॉन व धनआयन यांच्या आपसात टकरी शक्य तितक्या होऊ नयेत यासाठी वायू व बाष्प यांचे मिश्रण आणि बाहेरून लावलेल्यावर्चोभेदाचे मूल्य, योग्य असणे जरूर आहे. वर्चोभेद जरूरीपेक्षा कमी ठेवल्यास इलेक्ट्रॉनांचा लोंढा तयार होत नाही व तेअधिक ठेवल्यास धन आयनांमुळे अधिक इलेक्ट्रॉन निर्माण होऊन विद्युत्‌ भाराचे एक सारखे विसर्जन होऊ लागते. हे विसर्जनस्पंदरूपाने व्हावयास हवे. काही एका विशिष्ट वर्चोभेदास गणित्राचे कार्य सुरू होते व या वर्चोभेदास तलसीमा वर्चस्‌ म्हणतात.यानंतर वर्चोभेद वाढवीत गेल्यास त्याच्या विशिष्ट मूल्यानंतर गणनत्वरा व वर्चस्‌ यांचा संबंध दाखविणाऱ्‍या वक्राचा सपाट भागमिळतो (आ. ९). या सपाट भागाच्या मध्यबिंदूने दर्शविलेली परिस्थिती गणित्राच्या कायक्षमतेच्या दृष्टीने अत्यंत अनुकूलअसते. निर्माण झालेले स्पंद विवर्धकामुळे वृद्धिंगत होतात व त्यांची नोंद विद्युत्‌ यांत्रिकी साधनाद्वारे होते, अथवा ध्वनिक्षेपकवापरल्यास त्यात टकटक असा आवाज येतो व त्यामुळे गणन होते. स्पंद अती वेगाने येत असल्यास त्यांची नोंद करणेअशक्य होते व अशा वेळेस स्पंदांचा त्त्वराक्रम, प्रमाण नियंत्रकाच्या मदतीने विशिष्ट प्रमाणात कमी करूनस, नंतर ते स्पंद मोजले जातात अथवा गणित्रास जोडलेले धारित्र(विद्युत्‌ भार साठविणारे साधन) या स्पंदामुळे विद्युत्‌ भारित होते व त्यात वर्चोभेद निर्माण होतो. धारित्राच्या दोन्ही प्रस्थांच्या दरम्यान एक उच्च रोधक ठेवल्यास धारित्रातील विद्युत्‌ भाराचे विसर्जन सावकाश होते व वर्चसाचे मापन होऊ शकते. शमनासाठी हॅलोजन गटातील वायूही वापरण्याचा प्रघात आहे, हे मागे म्हटले आहेच. पाऱ्याच्या एक मिमी. दाबापेक्षाही कमी दाब असलेला ब्रोमीन वायू, एकंदर दाब १० सेंमी. होईल अशा बेताने आर्‌गॉन वायूबरोबरमिसळला तर हे मिश्रण चांगल्यापैकी शमन करणारे व स्थायी असते. या मिश्रणामुळे गणित्राची आयुर्मर्यादा वाढते व कार्यक्षमवर्चस्‌ १,२०० व्होल्टपेक्षाही पुष्कळ खाली येते. त्याखेरीज वापरावयाच्या तापमानाची खालची मर्यादा -७०⁰ से. पर्यंत खालीजाते.

चमकगणित्र: १९०३ साली सर विल्यम क्रुक्स यांस आढळले की, झिंक सल्फाइडाचा थर दिलेल्या पडद्यावर आल्फाकण पडले असता त्या जागी चमक उत्पन्न होते. या गोष्टीचा उपयोग नंतर रदरफर्ड यांनी त्यांच्या प्रसिद्ध प्रकीर्णन प्रयोगातआल्फा कणांची संख्या मोजण्यासाठी केला. पण चमकगणित्राचा खरा उपयोग प्रकाशविद्युत्‌ वर्धकाच्या (प्रकाशाच्या क्रियेने निर्माण होणाऱ्या इलेक्ट्रॉनांच्या साहाय्याने विद्युत्‌ प्रवाहाचे वर्धन करणाऱ्या उपकरणाच्या) शोधानंतर सुरू झाला. असेवर्धक दुसऱ्या महायुद्धात मोठ्या प्रमाणावर बनविले गेले आणि युद्धानंतर अणुगर्भीय प्रारणामुळे झिंक सल्फाइडमध्ये उत्पन्न होणाऱ्या चमकेची नोंद करण्यासाठी वापरले गेले. झिंक सल्फाइडाऐवजी काही कार्बनी व अकार्बनी पदार्थ, द्रव व प्लॅस्टिकआणि हीलियमसारखे वायू चमकद्रव्य म्हणून उपयोगी पडतात असे आढळून आले आहे. या गणित्रात चमक दाखविणारा पदार्थ प्रकाशविद्युत्‌ वर्धकाच्या संवेदनक्षम भागाला जोडलेला असतो व प्रारण ज्याभागातून प्रवेश करते तो सोडून त्याच्या इतर सर्व भागाभोवती परावर्तक पृष्ठ असते (आ. १०). जेव्हा वेगवान कण चमक निर्माण करणाऱ्‍या पदार्थात प्रवेश करतो तेव्हा तेथील अणू उत्तेजित होऊन प्रारण बाहेर टाकतात. हे प्रारण प्रकाशविद्युत्‌ वर्धकावर पडते व त्यातून उच्च मूल्याचा विद्युत्‌ स्पंद मिळू शकतो. 

चमक गणित्र कण अभिज्ञातक या दृष्टीने फार उपयुक्त आहे व त्याची कार्यक्षमता चांगली आहे. आकाराने लहान व पातळ असल्याने त्याच्या मदतीने कणाच्या स्थितीची अचूकपणे निश्चिती करता येते. एकापेक्षा अधिक प्रकाशविद्युत्‌ वर्धक वापरून व चमकद्रव्य म्हणून योग्य असा द्रव (५ ग्रॅम पॅरा-टरफिनिलाचा एक लिटर टोल्यूइनामध्ये केलेला विद्राव) वापरल्यास गणित्राचा आकार मोठा करता येतो. पण अशा गणित्रात उत्पन्न होणारा विद्युत्‌ स्पंद घन चमक गणित्रापेक्षा लहान असतो व गणित्रातील द्रव पेट घेण्याचीही भीती असते. उत्सर्जित प्रकाशाचा स्पंद अल्पकालिक (१०⁻⁸ ते १०⁻⁹ सेकंद) असल्याने योग्य असा प्रकाशविद्युत्‌ वर्धक वापरल्यास चमक गणित्रांची त्त्वरा व विश्लेषणक्षमता चेरेनकॉव्ह गणित्र सोडल्यास इतर गणित्रांपेक्षा अधिक असते आणि त्याची गणनत्वरा खूपच असते. योग्य रीतीने वापरल्यास ही गणित्रे समानुपाती होऊ शकतात.

चमकपदार्थ : (१) अकार्बनी : यात कॅडमियम वा कॅल्शियम टंगस्टेट व थॅलियम यांनी क्रियाशील केलेले सोडियम वसिझियम आयोडाइड यांचा समावेश होतो. स्पंदक्षयाचा काळ सु. १०⁻⁶ से. असतो. या पदार्थातील अणू वजनदार असल्याने त्या अणूंमुळे गॅमा किरणांचे रूपांतर इलेक्ट्रॉनांमध्ये होते व म्हणून गॅमा किरणांचा अभ्यास करण्यासाठी त्यांचा फार उपयोग होतो. (२) कार्बनी : नॅप्थॅलीन, अँथ्रॅसीन, ट्रॅन्सटिल्बिन व टरफिनिल हे कार्बनी चमकपदार्थ म्हणून वापरतात. झायलीन अगर त्याचा कोणताही बहुवारिक (अनेक साध्या रेणूंच्या संयोगाने तयार झालेल्या प्रचंड रेणूंनी युक्त असलेले संयुग) यामध्ये टरफिनिल विरघळवून घन प्लॅस्टिक चमकद्रव्य बनवितात. ही वापरली असता स्पंदाचा क्षयकाळ १०⁻⁸ ते १०⁻⁹ सेकंद असतो, म्हणून उच्च गणनत्त्वरेसाठी ते वापरले जातात.

दुसऱ्‍या कण अभिज्ञातकाबरोबर कार्बनी चमकपदार्थ असलेले चमक गणित्र संपात (एकाच वेळी नोंद करण्याच्या) योजनेनेही वापरता येते. दुसऱ्‍या गणित्रापासून मिळणाऱ्या स्पंदास लागणारा विलंब हा पहिल्या गणित्रातून दुसऱ्या गणित्रात जाण्यासाठी कणास लागणारा काल असतो व त्यावरून कणाचा वेग काढता येतो. या पद्धतीने २.९ × १०⁸ मी./से. पर्यंतचे वेग मोजण्यात आले आहेत.

स्फुल्लिंग गणित्र : यात एकमेकांस समांतर असलेल्या पट्‌ट्या विद्युत्‌ प्रस्थे म्हणून असतात व त्यांमधील जागेत (विद्युत्‌ क्षेत्रात) योग्य असा वायू असतो. आयनीभवनाचा परिणाम म्हणून अगदी थोड्या वेळात विद्युत्‌ भाराचा लोंढा तयार होतो व विद्युत्‌ स्फुल्लिंग उत्पन्न होते. हा वर्चस्‌-स्पंद तयार होण्यास लागणारा काल १०⁻⁹ व १०-१० सेकंद दरम्यान असतो, म्हणून हे गणित्र मापन करण्याचे एक अचूक साधन आहे. पण या गणित्राचे आयुर्मान इतरांच्या मानाने कमी म्हणजे १०⁷ स्पंद इतकेच असते. नेहमी वापरण्यात येणाऱ्या अशा गणित्रात पट्‌ट्यांचा व्यास काही सेंमी. व त्यांमधील अंतर ०.२ मिमी. असते. पट्‌ट्यांचा व्यास जरूरीप्रमाणे बदलतात. विश्वकिरणांचा अभ्यास करण्यासाठी वापरण्यात येणाऱ्‍या गणित्रातील पट्‌ट्यांचा व्यास ३० सेंमी. असू शकतो. काचेवर विद्युत्‌ संवाहकाचा पातळ थर देऊन त्याचे विद्युत्‌ प्रस्थ बनवितात. निर्गत स्पंद १०० व्होल्टच्या आसपास असल्याने या गणित्रात साधारणपणे विवर्धकाची जरूरी नसते. विद्युत्‌ प्रस्थाचा पृष्ठभाग धूलिरहित, तेलकट नसलेला आणि चरे नसलेला असणे जरूर आहे.

स्फटिक गणित्र : यास संवाहक अथवा प्रकाश विद्युत्‌ संवाहक गणित्र असेही म्हणतात. या अभिज्ञातकात दोन विद्युत्‌ प्रस्थांमध्ये संवेदनक्षम असा विद्युत्‌ अपार्य स्फटिक बसविलेला असतो. हे गणित्र किरणोत्सर्गी अणुगर्भातून बाहेर पडणाऱ्या गॅमा किरणांच्या अभ्यासासाठी विशेषतः वापरतात. जेव्हा विद्युत्‌ भारित कण स्फटिकात प्रवेश करतो अथवा गॅमा किरणाच्या योगाने उच्च ऊर्जायुक्त इलेक्ट्रॉन निर्माण होतात तेव्हा या विद्युत्‌ भारित कणांची स्फटिकातील अणूंवर क्रिया होऊन कमी ऊर्जा असलेले अनेक अर्धमुक्त इलेक्ट्रॉन उत्पन्न होतात. विद्युत्‌ प्रस्थांमध्ये वर्चोभेद ठेवल्याने विद्युत्‌ क्षेत्र निर्माण होते व या क्षेत्रामुळे मुक्त इलेक्ट्रॉन धन विद्युत्‌ प्रस्थाकडे खेचले जातात. इलेक्ट्रॉन बाहेर पडल्यामुळे निर्माण झालेल्या धन विद्युत्‌ भारित पोकळया त्या जागीच राहतात, अगर त्याही विद्युत्‌ क्षेत्रामुळे ऋण विद्युत्‌ प्रस्थाकडे खेचल्या जातात. काही वेळेस हे अर्धमुक्त इलेक्ट्रॉन स्फटिकातील अशुद्ध वा अपूर्ण भागात अडकून राहतात, असे इलेक्ट्रॉन सोडल्यास, विद्युत्‌ भाराच्या होणाऱ्या हालचालीमुळे विद्युत्‌ स्पंद निर्माण होतो व त्याचे विवर्धन करून तो मोजला जातो (आ. ११). लागणारे विद्युत्‌ क्षेत्र १,००० ते १०,०००व्होल्ट /सेंमी. इतके असते व स्फटिकाची लांबी काही मिमी. असते. सिल्व्हर क्लोराइड, हिरा, झिंक सल्फाइड, थॅलियम क्लोराइड, थॅलियम आयोडाइड,कॅडमियम सल्फाइड हे स्फटिक वापरले जातात. सिल्व्हर क्लोराइडासारखा आयनीक स्फटिक वापरल्यास, सर्वसाधारण तापमानात तो संवाहक असल्याने, द्रव नायट्रोजनाने थंड करून, त्या तापमानात तो वापरावा लागतो. हिरा, झिंक सल्फाइड व कॅडमियम सल्फाइड हे स्फटिक सर्वसाधारण तापमानात वापरता येतात.

हे गणित्र वापरण्यात बऱ्याच अडचणी आहेत. निर्माण होणाऱ्या स्पंदाचा परमप्रसर (स्थिर स्थितीपासून होणारे कमाल स्थानांतरण) बदलत राहतो व यासाठी चांगल्या प्रतीचा विवर्धक वापरणे जरूरीचे असते शिवाय जमा होणाऱ्या विद्युत्‌ भारामुळे विरोधी विद्युत्‌ प्रेरणा निर्माण होते. हा विरोध प्रत्यक्षात क्षेत्राची दिशा बदलती ठेवून किंवा स्फटिक तापवून अगर अवरक्त (दृश्य वर्णपटातील तांबड्या रंगाच्या अलीकडील अदृश्य) वा शुभ्र प्रकाश त्यावर पाडून दूर करावा लागतो.

अर्धसंवाहक गणित्र : [अर्धसंवाहक म्हणजे ज्यांचा विद्युत्‌ रोध धातू आणि विद्युत्‌ निरोधक पदार्थ यांच्या मध्ये आहे असे पदार्थ, → अर्धसंवाहक]. यातील संवेदनशील भागावर वेगयुक्त विद्युत्‌ भारित कण पडल्याने इलेक्ट्रॉन-पोकळी अशा जोड्या तयार होतात. बाहेरून लावलेल्या विद्युत्‌ क्षेत्रामुळे त्या गोळा केल्या जातात व अशा रीतीने विद्युत्‌ स्पंद तयार होतो. यादृष्टीने हे गणित्र आयनीकरण कोठीसारखे आहे, पण यात प्रत्येक इलेक्ट्रॉन-पोकळी जोडी उत्पन्न होण्यासाठी खर्ची पडणारी ऊर्जा थोडी म्हणजे तीन इलेक्ट्रॉन व्होल्ट इतकीच असल्याने यात ऊर्जायुक्त कणांचा प्रभाव आयनीकरण कोठीपेक्षा दहा पटीने अधिक होतो. पण ज्या कणांमुळे आयनीकरण थोड्याप्रमाणात होते अशा कणांच्या बाबतीत हे गणित्र फारसे उपयुक्त नाही. यात स्पंदाची वाढ होण्यासाठी लागणारा काल अत्यल्प असल्यानेत्याची गणनत्वरा बरीच असते. या गणित्रात सुधारणा करण्याचे प्रयत्न चालू आहेत.

चेरेनकॉव्हप्रारणगणित्र :हे प्रारण म्हणजे विद्युत्‌ चुंबकीय आघात तरंगांचा एक प्रकार होय. याचे समधर्मी उदाहरण म्हणजे ध्वनिवेगापेक्षा हवेत अधिक वेगाने जाणाऱ्याप्रक्षेपित वस्तूमुळे उत्पन्न होणारे आघात तरंग हे होय. एखाद्या पारदर्शक धन व असंवाहक माध्यमातील प्रकाश वेगापेक्षा अधिक वेगाने एखादा मूलकण त्या माध्यमातून जातअसताना, कणाकडून निर्माण होणाऱ्या प्रकाशास चेरेनकॉव्ह प्रारण म्हणतात. या प्रारणाचे पी. ए. चेरेनकॉव्ह यांनी १९३४ मध्ये प्राक्कथन केले होते. हे प्रारण गणित्रामध्येवेगवान मूलकणांचे अस्तित्त्व दाखविण्यासाठी व त्यांची ऊर्जा मोजण्यासाठी वापरले जाते. जी दिशा कणाच्या पथाशी विशिष्ट कोन θ करते, त्याच दिशेला तरंगांचे स्पष्ट असेतरंगमुख मिळते. या θ चे मूल्य पुढील समीकरणाने दिले जाते :

Cos θ = 1 / β n …. …. … (५)

यात β = v/c = कणवेग/प्रकाशवेग व n हा माध्यमाचा प्रणमनांक (प्रारणाचा निर्वातातील वेग आणि त्याचा माध्यमातील वेग यांचे गुणोत्तर) आहे. या समीकरणावरून कळतेकी, जर θ चे मापन होऊ शकले व n ज्ञात असला तर मूलकणाचा वेग काढता येतो. आय्‌. एम्‌. फ्रँक व आय्‌. ई. टॅम यांच्या उपपत्तीप्रमाणे λ1 व λ2 या दरम्यान तरंगलांबीअसणारे चेरेनकॉव्ह प्रारणमूल्य पुढे दिल्याप्रमाणे आहे :

यात N फोटॉन संख्या (फोटॉन म्हणजे प्रकाशाची अविभाज्य किमान राशी किंवा प्रकाशपुंज) व l पथाची लांबी दर्शवितात. वर्णपटीय वितरण 1 / λ3 या प्रमाणात होत असल्यानेया प्रारणाचा नील ते जंबुपार (जांभळ्या रंगाच्या पलीकडील) असा अखंड वर्णपट मिळतो. n चे मूल्य एकापेक्षा कमी असल्यास प्रारण मिळत नाही. पाण्याच्या बाबतीत (n =१.३३), जर β → 1 असेल तर θ महत्तम = ४१० व λ1 आणि λ2 यांची मूल्ये अनुक्रमे ३,५०० A⁰ व ५,५०० A⁰ येतात (A⁰ म्हणजे अँगस्ट्रॉम एकक = १०⁻⁸ सेंमी.)

ज्यांचा वेग जवळजवळ प्रकाशवेगाइतका आहे (उदा., विश्वकिरणात आढळणाऱ्या अथवा कणवेगवर्धकाच्या साहाय्याने अतिवेगवान झालेल्या) अशा कणांच्या अभिज्ञानासाठी हे चेरेनकॉव्ह गणित्र वापरतात. चेरेनकॉव्ह प्रारणाच्या वर्धनासाठी प्रकाशविद्युत्‌ वर्धक वापरतात (आ. १२). आ. १२. अकेंद्रित चेरेनकॉव्ह गणित्र : (१) पाणी, (२) आतील बाजूस पांढरा रंग दिलेले भांडे, (३) प्रकाशविद्युत् वर्धक.या गणित्रामध्ये काच, पाणी अगर स्वच्छ प्लॅस्टिक हे विद्युत्‌ अपार्य पदार्थ म्हणून वापरले जातात. कोणता पदार्थ वापरावा हे कणाच्यावेगावर ठरविले जाते. कणांच्या विशिष्ट वेगपट्‍ट्यास संवेदनक्षम होतील असे दोन विद्युत्‌ अपार्य पदार्थ असलेली दोन संपाती चेरेनकॉव्हगणित्रे एकामागून एक अशी वापरता येतात.

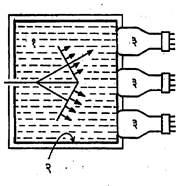
हे अभिज्ञातक केंदित व अकेंद्रित अशा दोन तऱ्हेचे असतात. अकेंद्रित अभिज्ञातकात विद्युत्‌ अपार्य पदार्थाभोवती, जेथे विद्युत्‌ वर्धक जोडावयाचा तो भाग सोडून, प्रकाशाचे परावर्तन करील अशा पदार्थांचा थर आतील बाजूस दिलेला असतो. केंद्रित गणित्रात विशिष्ट कोन करून येणारा प्रकाश केंद्रित करण्यासाठी भिंगांची आणि आरशाची योजना असते. हा अभिज्ञातक समानुपाती आहे व त्याच्या मदतीने कोन θ, तरंगलांबी λ व पदार्थांचे गुणधर्म यांचे फलन (गणितसंबंध) असलेल्या फोटॉनांच्या संख्येचे गणन करता येते आणि प्राथमिक विश्वकिरणांवरील विद्युत्‌ भाराचे वितरण अभ्यासता येते.

न्यूट्रॉनांचेअभिज्ञान: न्यूट्रॉनांच्या अभिज्ञानासाठी वापरण्यात येणारी साधने पुढीलपैकी कोणत्यातरी एका तत्त्वावर आधारलेलीआहेत : (१) अणुगर्भाकडून होणारे न्यूट्रॉनाचे शोषण व त्यामुळे तत्काळ होणारे विद्युत्‌ भारित कणांचे उत्सर्जन. याचे उदाहरण म्हणजे आतील भिंतीवर बोरॉन (१०) यासमस्थानिकाचे (एकाच मूलद्रव्याचा भिन्न अणुभार असलेल्या प्रकाराचे) बरेच प्रमाण असलेल्या बोरॉनाचा लेप दिलेल्या, अथवा बोरॉन ट्रायफ्ल्युओराइड (BF₃) वायू आतभरलेल्या, अशा समानुपाती गणित्राच्या मदतीने न्यूट्रॉनांची गणना होऊ शकते, हे होय. येथे B10 (n, α) Li7 + 2.78 Mev या विक्रियेप्रमाणे आल्फा (α)या विद्युत्‌ भारितकणांचे उत्सर्जन होते (अणुगर्भीय विक्रिया दर्शविताना प्रथम मूळ मूलद्रव्य, कंसात मारा केलेला कण, नंतर उत्सर्जित झालेला कण व शेवटी कंसाबाहेर तयार झालेलेमूलद्रव्य अशा क्रमाने लिहितात). तसेच Li6 (n, α) H3 + 4.78 Mev या विक्रियेप्रमाणे ऊर्जायुक्त कण लिथियम आयोडाइड या स्फटिकावर पडतात व चमक निर्माणकरतात. या चमकांचे प्रकाशविद्युत्‌ वर्धकामुळे विद्युत्‌ स्पंदात रूपांतर होते व नंतर स्पंदांचे मापन होते. कॅडमियम अगर बोरॉन यांचे लवण चमक द्रवात विरघळून मोठ्या आकाराचे व संवेदनक्षम असे न्यूट्रॉन अभिज्ञातक बनविण्यात आलेले आहेत. (२) न्यूट्रॉनांच्या ग्रासामुळे होणारे भंजन : उदा., आयनीकरण कोठीच्या भिंतीच्या आतीलबाजूस युरेनियम (२३५) चोपडले असता, भंजन (अणुकेंद्र फुटून तयार झालेल्या) खंडांच्या ऊर्जेमुळे आयनीभवन होऊन विद्युत्‌ स्पंद निर्माण होतात व त्यांचे मापन होऊशकते. अतिवेगवान न्यूट्रॉनांच्या बाबतीत पॅराफिनासारख्या हायड्रोजनयुक्त पदार्थांचा काही सेंमी. जाडीचा थर अभिज्ञातकाभोवती दिल्यास न्यूट्रॉनांच्या अभिज्ञानाचीसंवेदनक्षमता वाढते कारण अशा हायड्रोजनयुक्त पदार्थातून जाताना न्यूट्रॉनांचा वेग कमी होतो व त्यांच्या अणुगर्भाकडून होणाऱ्या ग्रासाची संभाव्यता वाढते. (३) न्यूट्रॉनांच्याग्रासामुळे होणारी किरणोत्सर्गी द्रव्याची उत्पत्ती : न्यूट्रॉनांनी उद्दीप्त केलेली बरीचशी मूलद्रव्ये किरणोत्सर्गी बनतात व या किरणोत्सर्गामुळे अशा प्रसंगी वापरल्या जाणाऱ्यागणित्रांच्या साहाय्याने न्यूट्रॉनांचे गणन होऊ शकते. (४) अतिवेगवान न्यूट्रॉनांच्या टकरींमुळे निर्माण होणारे प्रतिक्षिप्त (फेकल्या गेलेल्या) अणुगर्भांचे (विशेषेकरून प्रोटॉनांचे)योग्य अशा अभिज्ञातकांच्या साहाय्याने गणन केल्याने मूळ न्यूट्रॉनांची संख्या समजते. ही पद्धती बऱ्याच प्रमाणात वापरण्यात येते.

हायड्रोजनयुक्त पदार्थाच्या भिंती असलेल्या अगर मिथेनसारखा वायू आत भरलेल्या गणित्रात विद्युत्‌ स्पंद निर्माण होतात, कारण अतिवेगवान न्यूट्रॉनांच्या माऱ्यामुळे यापदार्थातील प्रोटॉन प्रतिक्षेपित होतात व त्यामुळे आयनीकरण होते.

न्युट्रिनोंचे अभिज्ञान : न्यूट्रिनोंचे अभिज्ञान होण्यासाठी दुसऱ्या एखाद्या कणाशी त्याची विक्रिया घडावयास हवी, पण तशी विक्रिया घडून येणे ही जवळजवळ अशक्यप्रायघटना आहे कारण पृथ्वीवर न्यूट्रिनोंचा वर्षाव जोरात होत असला तरी १०१० न्यूट्रिनोंपैकी एखाद्या न्यूट्रिनोचीच दुसऱ्या कणाशी आघात होण्याची शक्यता असते. तरीहीत्यांच्या अभिज्ञानाचा व गणनाचा प्रयत्न होत असून अमेरिकेतील ब्रूकहॅव्हन नॅशनल लॅबोरेटरीमध्ये ३० Bev (बिलियन इलेक्ट्रॉन व्होल्ट) प्रोटॉन-वेगवर्धकाच्या एका प्रयोगातम्यू मेसॉनांच्या संबंधात आढळणाऱ्या न्यूट्रिनोंचे अस्तित्त्व सिद्ध झाले, पण ते देखील अल्प प्रमाणात. प्रयोगाच्या एकूण काळात एकंदर १०१४ वेगवान न्यूट्रिनो स्फुल्लिंगगणित्रातून गेले असावे पण त्यांपैकी फक्त ५१ न्यूट्रिनोंचेच, त्यांच्या इतर कणांशी झालेल्या टकरींमुळे, गणन होऊ शकले.

संदर्भ : 1. Crowther, J. A. Ions, Electrons and Ionising Radiations, New York, 1949.

         2. Richtmeyer, F. K. Kennard, E. H. Lauritsen, T. Introduction to Modern Physics, Tokyo, 1965.

         3. Smith, C. M. H. A Textbook of Nuclear Physics, London, 1965.

  भावे, श्री. द.

“